Dimensional Analysis of Superplastic Processes with the Buckingham Π Theorem
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dimensional Analysis
2.2. Experimental Tests
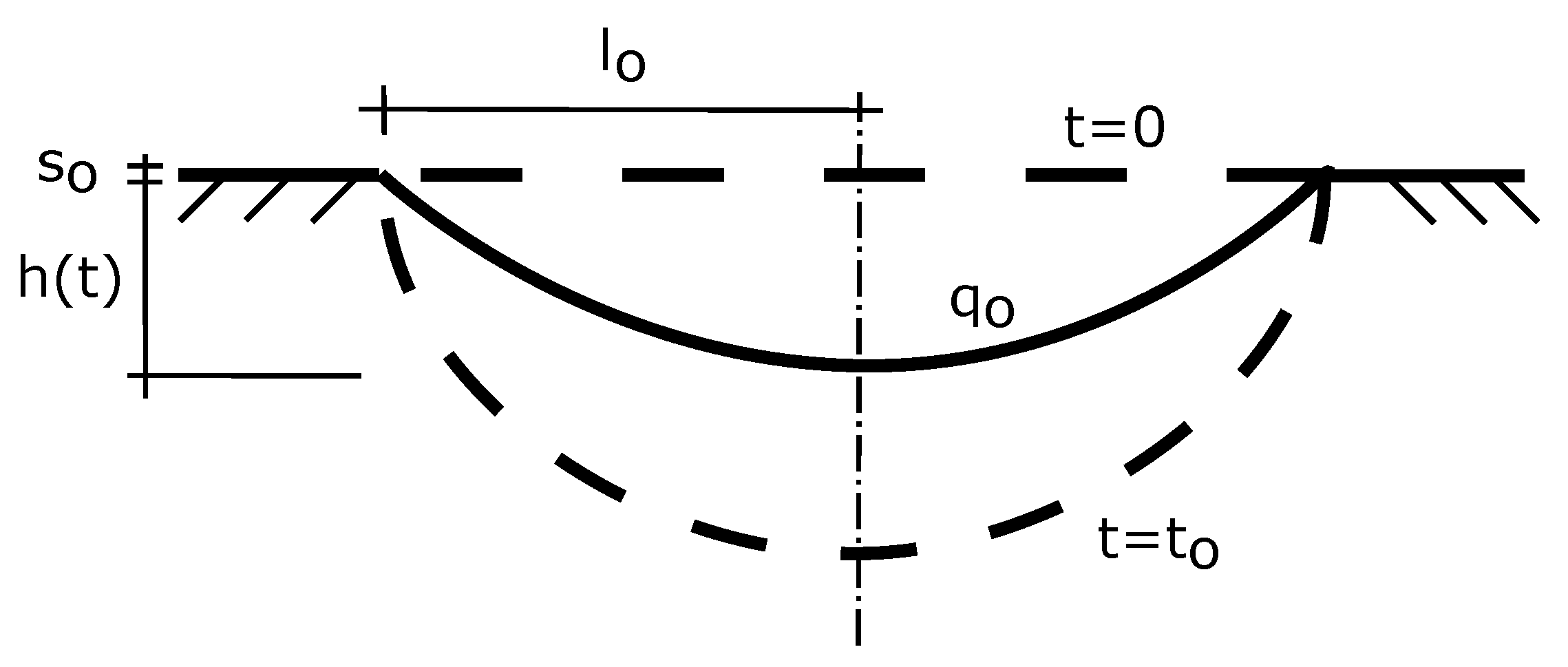
- geometrical information such as the die radius and the initial sheet thickness , that must be joined into the second dimensionless variable .
- external pressure .
- information on the material behaviour based on the parameters K and m. The last one is directly used as the third dimensionless variable.
- the forming time that is used in in a double way, in the numerator directly, and also its inverse in the denominator as the reference point in which the apparent viscosity term is calculated.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barnes, A.J. Superplastic Forming 40 Years and Still Growing. J. Mater. Eng. Perform. 2007, 16, 440–454. [Google Scholar] [CrossRef]
- Friedman, P.A.; Luckey, S.G.; Copple, W.B.; Allor, R.; Miller, C.E.; Young, C. Overview of superplastic forming research at Ford Motor Company. J. Mater. Eng. Perform. 2004, 13, 670–677. [Google Scholar] [CrossRef]
- Hefti, L.D. Advances in fabricating superplastically formed and diffusion bonded components for aerospace structures. J. Mater. Eng. Perform. 2004, 13, 678–682. [Google Scholar] [CrossRef]
- Hefti, L.D. Commercial Airplane Applications of Superplastically Formed AA5083 Aluminum Sheet. J. Mater. Eng. Perform. 2006, 16, 136–141. [Google Scholar] [CrossRef]
- Bonet, J.; Wood, R.D.; Said, R.; Curtis, R.V.; Garriga-Majo, D. Numerical simulation of the superplastic forming of dental and medical prostheses. Biomech. Model. Mechanobiol. 2002, 1, 177–196. [Google Scholar] [CrossRef]
- Sorgente, D.; Palumbo, G.; Piccininni, A.; Guglielmi, P.; Aksenov, S.A. Investigation on the thickness distribution of highly customized titanium biomedical implants manufactured by superplastic forming. CIRP J. Manuf. Sci. Technol. 2018, 20, 29–35. [Google Scholar] [CrossRef]
- Hefti, L.D.; Hefti, L.D. Innovations in the Superplastic Forming and Diffusion Bonded Process. J. Mater. Eng. Perform. 2008, 17, 178–182. [Google Scholar] [CrossRef]
- Ortiz, A.A.; Gago, J.; Sanchez, P.; Gil, V.; Rubio, L. Technical and industrial approaches for super plastic forming and diffusion bonding (SPF/DB) titanium alloy leading edge manufacturing. Mater. Werkst. 2014, 45, 785–792. [Google Scholar] [CrossRef]
- Xun, Y.W.; Tan, M.J. Applications of superplastic forming and diffusion bonding to hollow engine blades. J. Mater. Process. Technol. 2000, 99, 80–85. [Google Scholar] [CrossRef]
- Totten, G.; Funatani, K.; Xie, L. Handbook of Metallurgical Process Design; Materials Engineering; Marcel Dekker lnc.: New York, NY, USA, 2004. [Google Scholar]
- Aksenov, S.A.; Kolesnikov, A.V.; Mikhaylovskaya, A.V. Design of a gas forming technology using the material constants obtained by tensile and free bulging testing. J. Mater. Process. Technol. 2016, 237, 88–95. [Google Scholar] [CrossRef]
- Franchitti, S.; Giuliano, G.; Palumbo, G.; Sorgente, D.; Tricarico, L. On the optimisation of superplastic free forming test of an AZ31 magnesium alloy sheet. Int. J. Mater. Form. 2008, 1, 1067–1070. [Google Scholar] [CrossRef]
- Antoniswarny, A.; Taleff, E.; Hector, L.; Carter, J. Plastic deformation and ductility of magnesium AZ31B-H24 alloy sheet from 22 to 450 °C. Mater. Sci. Eng. A 2015, 631, 1–9. [Google Scholar] [CrossRef]
- Jovane, F. An approximate analysis of the superplastic forming of a thin circular diaphragm: Theory and experiments. Int. J. Mech. Sci. 1968, 10, 403–427. [Google Scholar] [CrossRef]
- Belk, J.A. A quantitative model of the blow-forming of spherical surfaces in superplastic sheet metal. Int. J. Mech. Sci. 1975, 17, 505–511. [Google Scholar] [CrossRef]
- Yu-Quan, S.; Jun, Z. A mechanical analysis of the superplastic free bulging of metal sheet. Mater. Sci. Eng. 1986, 84, 111–125. [Google Scholar] [CrossRef]
- Enikeev, F.U.; Kruglov, A.A. An analysis of the superplastic forming of a thin circular diaphragm. Int. J. Mech. Sci. 1995, 37, 473–483. [Google Scholar] [CrossRef]
- Giuliano, G.; Franchitti, S. On the evaluation of superplastic characteristics using the finite element method. Int. J. Mach. Tools Manuf. 2007, 47, 471–476. [Google Scholar] [CrossRef]
- Huh, H.; Choi, T.H. Modified membrane finite element formulation for sheet metal forming analysis of planar anisotropic materials. Int. J. Mech. Sci. 2000, 42, 1623–1643. [Google Scholar] [CrossRef]
- Bonet, J.; Wood, R.D.; Collins, R. Pressure-control algorithms for the numerical simulation of superplastic forming. Int. J. Mech. Sci. 1994, 36, 297–309. [Google Scholar] [CrossRef]
- Bonet, J.; Gil, A.; Wood, R.D.; Said, R.; Curtis, R.V. Simulating superplastic forming. Comput. Methods Appl. Mech. Eng. 2006, 195, 6580–6603. [Google Scholar] [CrossRef]
- Alabort, E.; Putman, D.; Reed, R.C. Superplasticity in Ti–6Al–4V: Characterisation, modelling and applications. Acta Mater. 2015, 95, 428–442. [Google Scholar] [CrossRef] [Green Version]
- García-Barrachina, L.; Gámez, A.J. A forming time estimator of superplastic free bulge tests based on dimensional analysis. Int. J. Mater. Form. 2020. [Google Scholar] [CrossRef]
- Padmanabhan, K.A.; Vasin, R.A.; Enikeev, F.U. Superplastic Flow: Phenomenology and Mechanics; Springer: Berlin, Germany, 2001; pp. 311–324. [Google Scholar]
- Zohuri, B. Dimensional Analysis Beyond the Pi Theorem; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Lemons, D.S. A Student’s Guide to Dimensional Analysis; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef] [Green Version]
- Tan, Q.M. Dimensional Analysis: With Case Studies in Mechanics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Szirtes, T.; Rózsa, P. Applied Dimensional Analysis and Modeling; Elsevier Science & Technology: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- García-Barrachina, L.; Gámez, A. Superplastic Materials Characterisation Based on Free-Bulge Tests. Solid State Phenom. 2020, 306, 15–22. [Google Scholar] [CrossRef]
- Delaplace, G. (Ed.) Dimensional Analysis of Food Processes; Elsevier: Oxford, UK, 2015. [Google Scholar] [CrossRef]
- Jarrar, F.S.; Abu-Farha, F.; Hector, L.G.; Khraisheh, M.K. Simulation of high-temperature AA5083 bulge forming with a hardening/softening material model. J. Mater. Eng. Perform. 2009, 18, 863–870. [Google Scholar] [CrossRef]
- Ramos, R.E.; Prada, J.C.G.; Giuliano, G. Análisis de las Características Mecánicas de la Superplasticidad: Aplicación a la Aleación de PbSn60. Master’s Thesis, Universidad Carlos III, Madrid, Spain, 2011. In Spanish. [Google Scholar]
- Sorgente, D.; Tricarico, L. Characterization of a superplastic aluminium alloy ALNOVI-U through free inflation tests and inverse analysis. Int. J. Mater. Form. 2014, 7, 179–187. [Google Scholar] [CrossRef]
- Sorgente, D.; Palumbo, G.; Piccininni, A.; Guglielmi, P.; Tricarico, L. Modelling the superplastic behaviour of the Ti6Al4V-ELI by means of a numerical/experimental approach. Int. J. Adv. Manuf. Technol. 2017, 90. [Google Scholar] [CrossRef]
| Material | Ref. | Temp. (°C) | Pressure (MPa) | (s) | |||
|---|---|---|---|---|---|---|---|
| ZnAl22 | [16] | 270 | 0.4 | 365 | 0.04098 | 25 | 0.35 |
| 0.6 | 160 | 0.04082 | 25 | 0.35 | |||
| 0.8 | 87 | 0.04028 | 25 | 0.35 | |||
| AA5083 | [31] | 450 | 0.29 | 1138 | 0.02276 | 41.67 | 0.5 |
| 0.56 | 142 | 0.02170 | 41.67 | 0.5 | |||
| 0.90 | 26 | 0.02105 | 41.67 | 0.5 | |||
| PbSn60 | [32] | 50 | 0.06 | 122 | 0.00936 | 100 | 0.364 |
| 0.07 | 99 | 0.01011 | 100 | 0.364 | |||
| 0.08 | 69 | 0.01014 | 100 | 0.364 | |||
| 0.09 | 50 | 0.01013 | 100 | 0.364 | |||
| 0.10 | 45 | 0.01013 | 100 | 0.364 | |||
| Alnovi-U | [33] | 450 | [0.6] | 1045 | 0.05778 | 16.67 | 0.439 |
| [0.75] | 603 | 0.05674 | 16.67 | 0.439 | |||
| [0.9] | 436 | 0.05902 | 16.67 | 0.439 | |||
| 500 | 0.3 | 2499 | 0.05764 | 16.67 | 0.5 | ||
| 0.4 | 1189 | 0.05519 | 16.67 | 0.5 | |||
| 0.5 | 668 | 0.05620 | 16.67 | 0.5 | |||
| [0.6] | 260 | 0.05052 | 16.67 | 0.642 | |||
| [0.7] | 199 | 0.04964 | 16.67 | 0.642 | |||
| [0.8] | 153 | 0.04798 | 16.67 | 0.642 | |||
| AZ31 | [12] | 450 | [0.2] | 3407 | 0.02954 | 30 | 0.544 |
| [0.25] | 2435 | 0.03076 | 30 | 0.544 | |||
| [0.35] | 1185 | 0.02911 | 30 | 0.544 | |||
| [0.5] | 423 | 0.03107 | 30 | 0.391 | |||
| 520 | [0.11] | 2206 | 0.02553 | 30 | 0.723 | ||
| [0.17] | 1307 | 0.02703 | 30 | 0.723 | |||
| 0.16 | 809 | 0.02498 | 35 | 0.457 | |||
| 0.29 | 200 | 0.02392 | 35 | 0.457 | |||
| Ti-6Al-4V | 800 | [1.25] | 5878 | 0.04398 | 22.5 | 0.382 | |
| [1.5] | 3671 | 0.04409 | 22.5 | 0.382 | |||
| [1.75] | 2924 | 0.04715 | 22.5 | 0.382 | |||
| [34] | 850 | 0.5 | 4597 | 0.03592 | 22.5 | 0.703 | |
| 1.0 | 1815 | 0.03738 | 22.5 | 0.703 | |||
| 1.5 | 924 | 0.03488 | 22.5 | 0.703 | |||
| [17] | 900 | 0.5 | 1500 | 0.02832 | 35 | 0.43 | |
| 0.7 | 678 | 0.02817 | 35 | 0.43 | |||
| 1.0 | 291 | 0.02799 | 35 | 0.43 |
| m | PbSn60 | ZnAl22 | AZ31 | AA5083 | Alnovi-U | Ti-6Al-4V |
|---|---|---|---|---|---|---|
| 0.35 | 50 °C (0.364) | 270 °C (0.35) | 450 °C (0.391) | 800 °C (0.382) | ||
| 0.45 | 520 °C (0.457) | 450 °C (0.439) | 900 °C (0.43) | |||
| 0.5 | 450 °C (0.544) | 450 °C (0.5) | 500 °C (0.5) | |||
| 0.7 | 520 °C (0.723) | 850 °C (0.703) |
| Material | Temp. (°C) | Pressure (MPa) | (s) | ||
|---|---|---|---|---|---|
| ZnAl22 | 270 | 0.4 | 255 | 362 | 365 |
| 0.6 | 113 | 161 | 160 | ||
| 0.8 | 64 | 91 | 87 | ||
| AA5083 | 450 | 0.29 | 1059 | 998 | 1138 |
| 0.56 | 177 | 167 | 142 | ||
| 0.90 | 37 | 35 | 26 | ||
| PbSn60 | 50 | 0.06 | 123 | 127 | 122 |
| 0.07 | 80 | 83 | 99 | ||
| 0.08 | 56 | 58 | 69 | ||
| 0.09 | 40 | 42 | 50 | ||
| 0.10 | 31 | 33 | 45 | ||
| Alnovi-U | 450 | 0.6 | 881 | 1079 | 1045 |
| 0.75 | 530 | 650 | 603 | ||
| 0.9 | 350 | 428 | 436 | ||
| 500 | 0.3 | 2157 | 2226 | 2499 | |
| 0.4 | 1214 | 1252 | 1189 | ||
| 0.5 | 777 | 801 | 668 | ||
| 0.6 | 285 | 252 | 260 | ||
| 0.7 | 224 | 198 | 199 | ||
| 0.8 | 182 | 161 | 153 | ||
| AZ31 | 450 | 0.2 | 3554 | 3153 | 3407 |
| 0.25 | 2358 | 2092 | 2435 | ||
| 0.35 | 1270 | 1127 | 1185 | ||
| 0.5 | 394 | 503 | 423 | ||
| 520 | 0.11 | 2786 | 2431 | 2206 | |
| 0.17 | 1526 | 1331 | 1307 | ||
| 0.16 | 884 | 944 | 809 | ||
| 0.29 | 241 | 257 | 200 | ||
| Ti-6Al-4V | 800 | 1.25 | 4590 | 6291 | 5878 |
| 1.5 | 2848 | 2903 | 3671 | ||
| 1.75 | 1902 | 2607 | 2924 | ||
| 850 | 0.5 | 5361 | 4794 | 4597 | |
| 1.0 | 2000 | 1788 | 1815 | ||
| 1.5 | 1123 | 1004 | 924 | ||
| 900 | 0.5 | 1232 | 1408 | 1500 | |
| 0.7 | 563 | 644 | 678 | ||
| 1.0 | 246 | 281 | 291 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Barrachina, L.; Gámez, A.J. Dimensional Analysis of Superplastic Processes with the Buckingham Π Theorem. Metals 2020, 10, 1575. https://doi.org/10.3390/met10121575
García-Barrachina L, Gámez AJ. Dimensional Analysis of Superplastic Processes with the Buckingham Π Theorem. Metals. 2020; 10(12):1575. https://doi.org/10.3390/met10121575
Chicago/Turabian StyleGarcía-Barrachina, Luis, and Antonio J. Gámez. 2020. "Dimensional Analysis of Superplastic Processes with the Buckingham Π Theorem" Metals 10, no. 12: 1575. https://doi.org/10.3390/met10121575
APA StyleGarcía-Barrachina, L., & Gámez, A. J. (2020). Dimensional Analysis of Superplastic Processes with the Buckingham Π Theorem. Metals, 10(12), 1575. https://doi.org/10.3390/met10121575






