Characterization and Modeling of Intermetallic Phase Formation during the Joining of Aluminum and Steel in Analogy to Co-Extrusion
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Procedure
2.2. Setup of Numerical Model and Subroutine
3. Results and Discussion
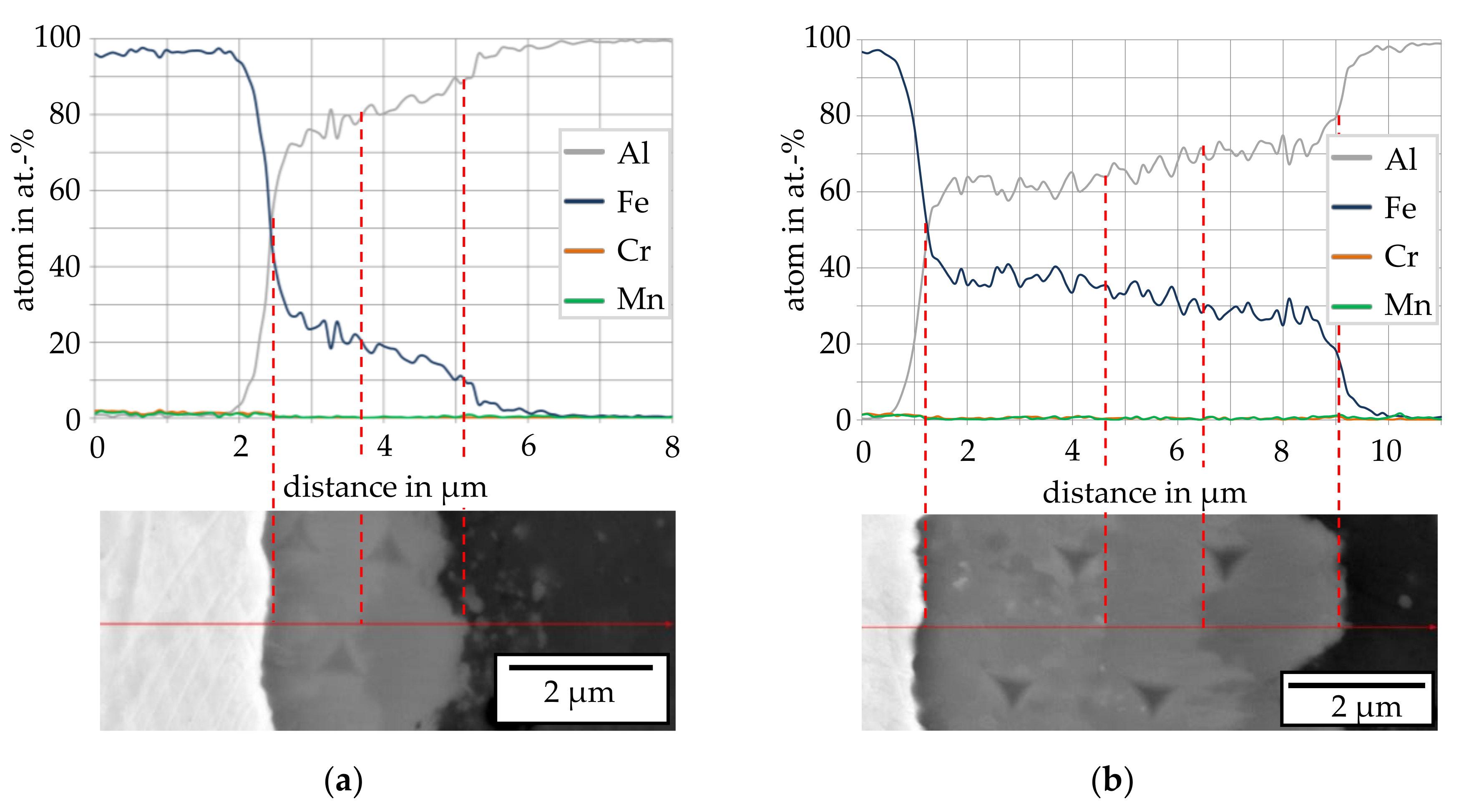
3.1. Evolution of the Intermetallic Phase Seam Thickness
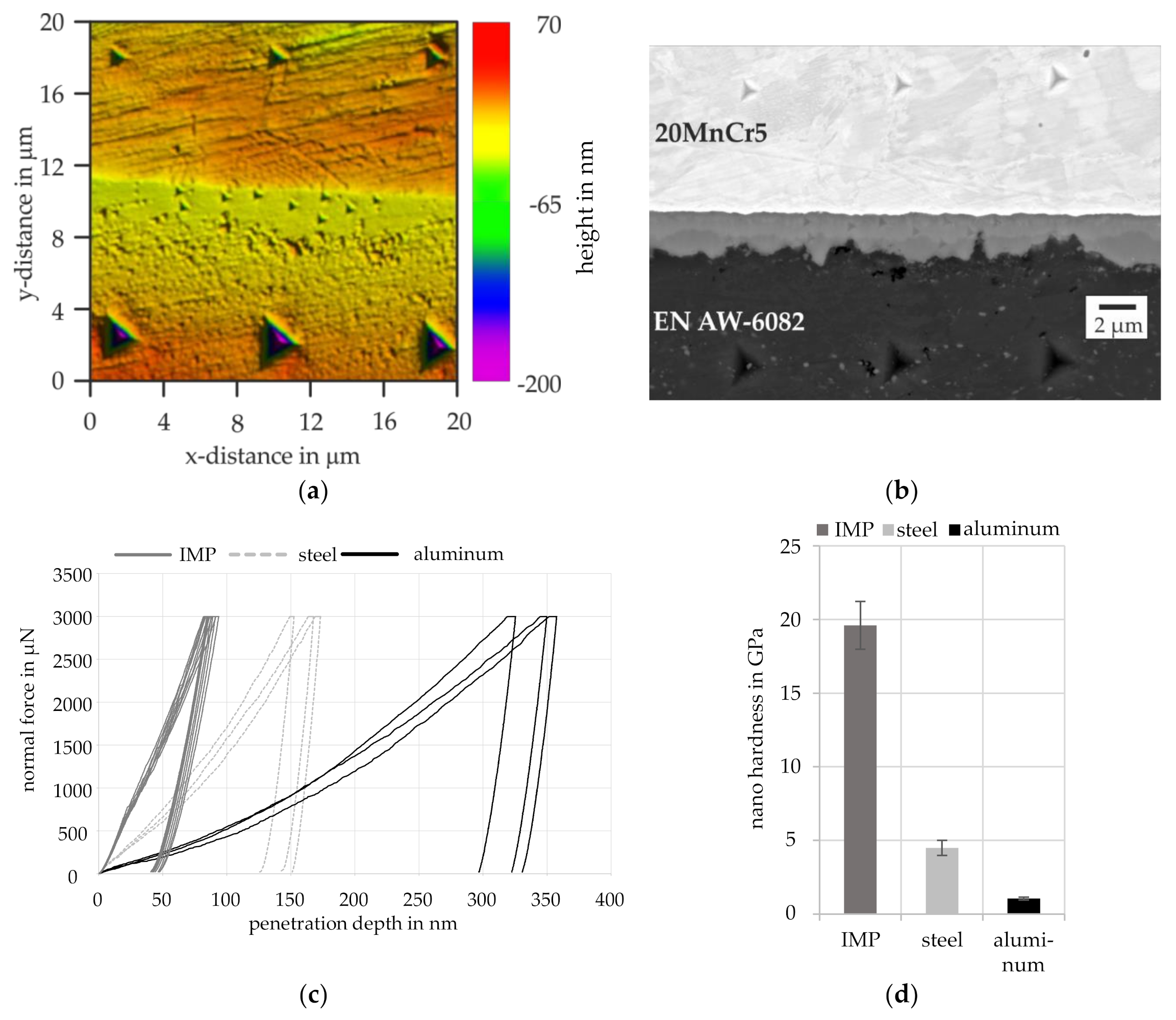
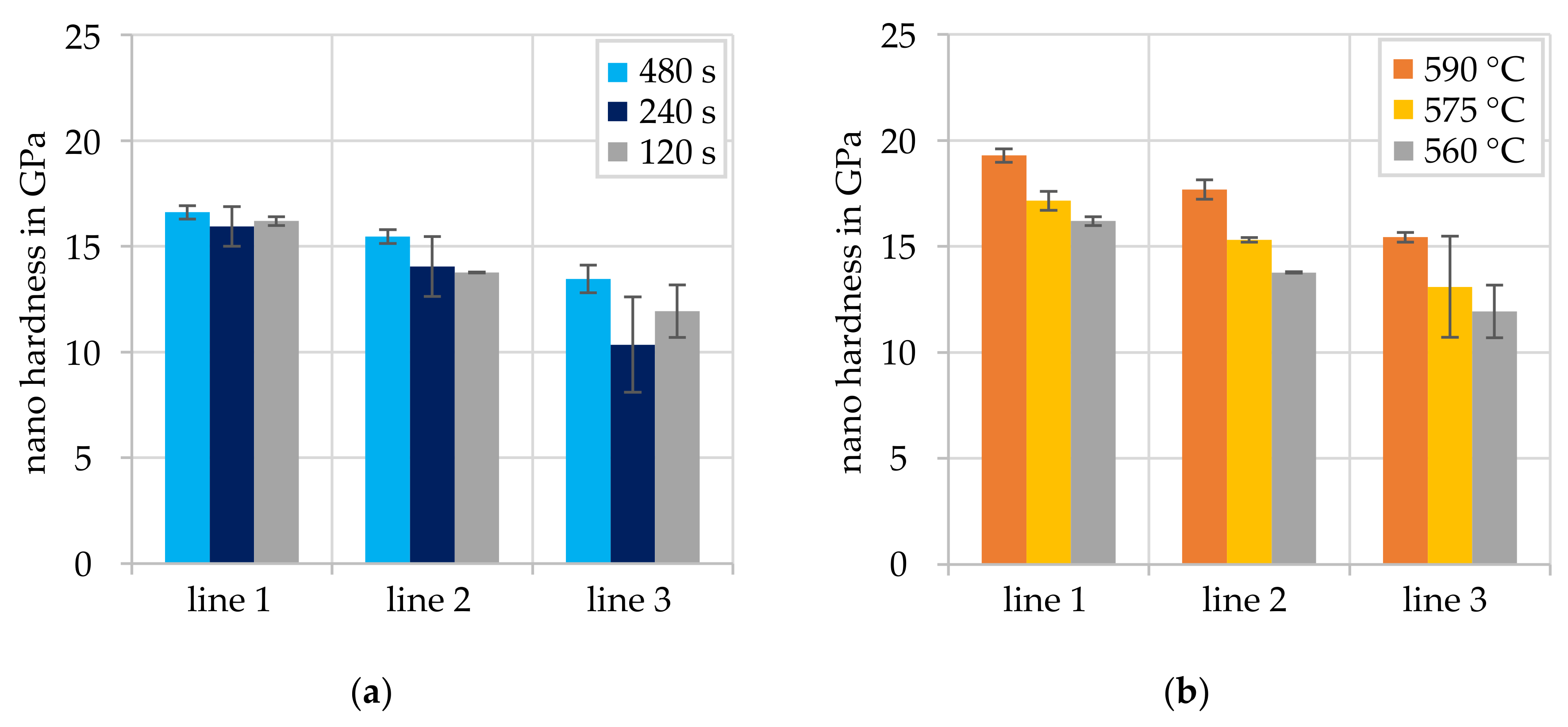
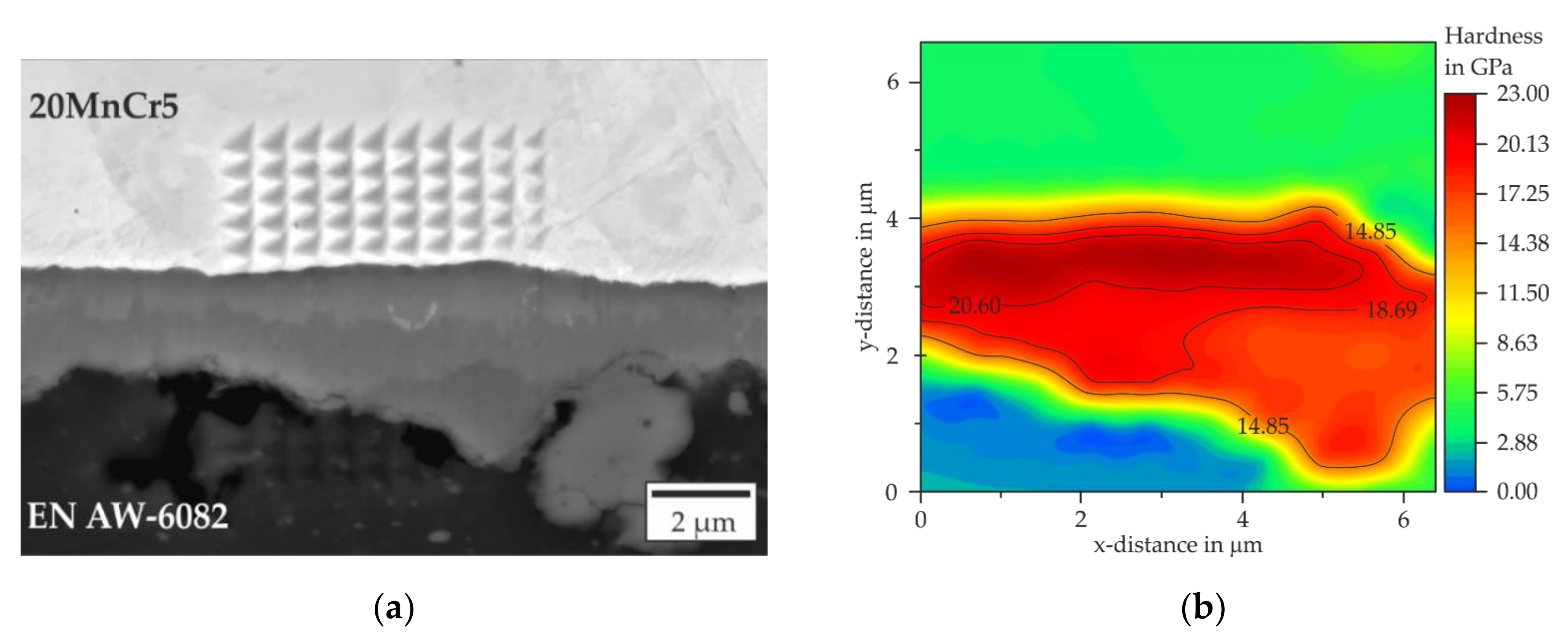
3.2. Nanoindentation Measurement of the Intermetallic Phase Seam
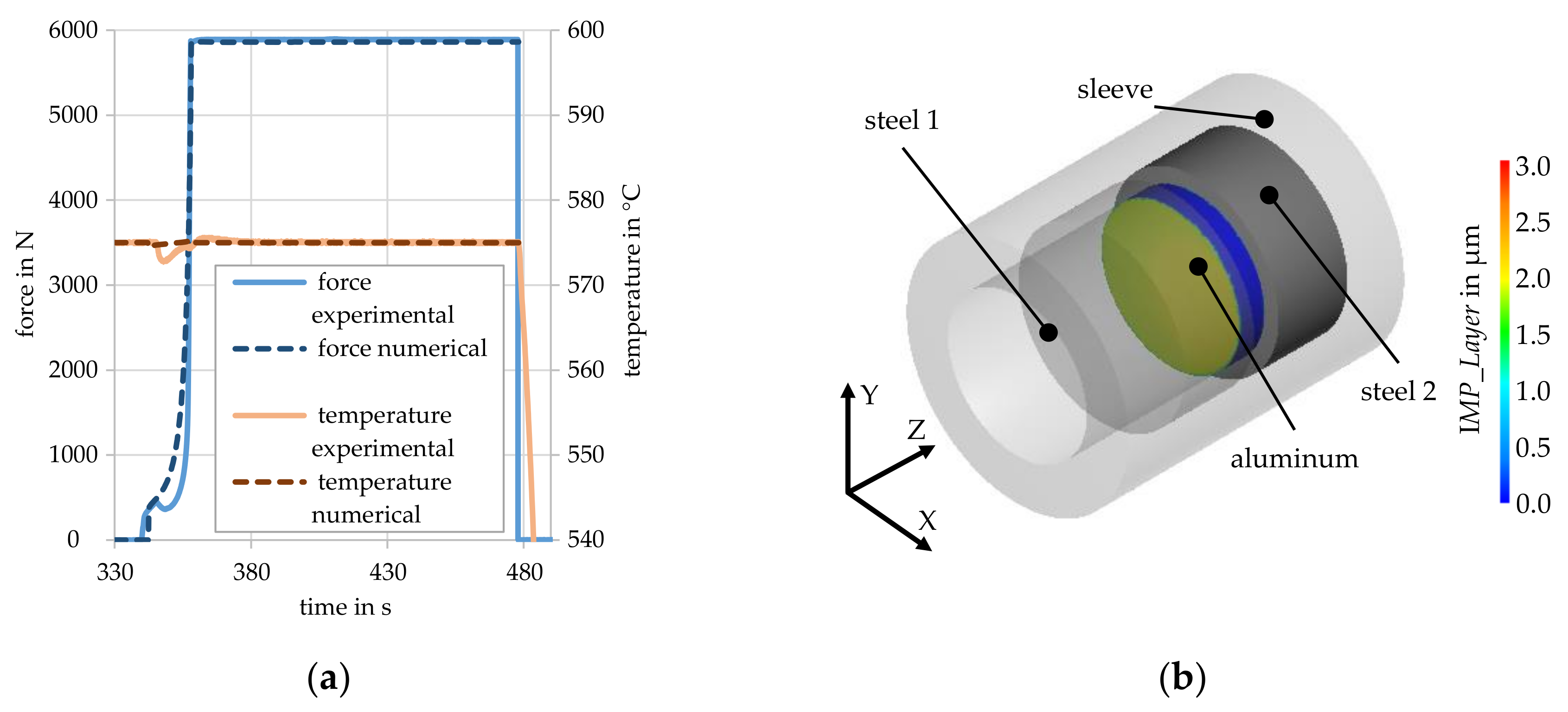
3.3. Validation of the Subroutine
4. Conclusions and Outlook
- As expected, the growth of intermetallic phases in the joint zone of EN AW-6082 and 20MnCr5 is time-dependent. By calculating the intermetallic phase seam width using the Einstein–Smoluchowski equation, a good agreement with the experimental data was achieved.
- With rising temperature, the phase seam width and the apparent diffusion coefficient increase.
- The force showed no significant effect on the phase formation in the investigated range.
- The SEM images indicated the presence of up to three different intermetallic phases in the joining zone. This was confirmed by EDS and nanoindentation measurements. At temperatures above 560 °C or times above 120 s, the formation of different intermetallic phases was observed.
- Due to the high aluminum content and the hardness determined in the EDS and nanoindentation analysis, the presence of the phases FeAl2, Fe2Al5 or FeAl3 would be possible, but could not be clearly proven. To confirm this assumption, further electron probe micro analysis (EPMA) and X-ray diffraction (XRD) investigations are to be carried out. In future work, the usability of the subroutine for the co-extrusion process will be tested and validated based on experimental investigations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sierra, G.; Peyre, P.; Deschaux-Beaume, F.; Stuart, D.; Fras, G. Steel to aluminium key-hole laser welding. Mater. Sci. Eng. A 2007, 447, 197–208. [Google Scholar] [CrossRef]
- Watanabe, T.; Takayama, H.; Yanagisawa, A. Joining of aluminum to steel by friction stir welding. J. Mater. Process. Technol. 2006, 342–349. [Google Scholar] [CrossRef]
- Ashfaq, M.; Sajja, N.; Khalid Rafi, H.; Prasad Rao, K. Improving strength of stainless steel/aluminum alloy friction welds by modifying faying surface design. JMEPEG 2013, 22, 376–383. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Kosch, K.-G. Development of the heating and forming strategy in compound forging of hybrid steel-aluminum parts. Mat. Werkstofftech. 2011, 42, 973–978. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Klose, C.; Chugreev, A.; Heimes, N.; Thürer, S.E.; Uhe, J. A numerical study on co-extrusion to produce coaxial aluminum-steel compounds with longitudinal weld seams. Metals 2018, 8, 717. [Google Scholar] [CrossRef] [Green Version]
- Ogura, T.; Ueda, K.; Saito, Y.; Hirose, A. Nanoindentation measurement of interfacial reaction layers in 6000 series aluminum alloys and steel dissimilar metal joints with alloying elements. Mater. Trans. 2011, 52, 979–984. [Google Scholar] [CrossRef] [Green Version]
- Ryabov, V.R. Welding of aluminum alloys to steels. Weld. Surf. Rev. 1998, 9, 1–139. [Google Scholar]
- Agudo, L.; Jank, N.; Wagner, J.; Schmaranzer, C.; Arenholz, E.; Bruckner, J.; Hackl, H.; Pyzalla, A. Investigation of microstructure and mechanical properties of steel-aluminium joints produced by metal arc joining. Steel Res. Int. 2008, 79, 530–535. [Google Scholar] [CrossRef]
- Springer, H.; Kostka, A.; Payton, E.J.; Raabe, D.; Kaysser-Pyzalla, A.; Eggeler, G. On the formation and growth of intermetallic phases during interdiffusion between low-carbon steel and aluminum alloys. Acta Mater. 2011, 59, 1586–1600. [Google Scholar] [CrossRef]
- Yamamoto, N.; Tkahashi, M.; Aritoshi, M.; Ikeuchi, K. Effect of intermetallic compound layer on bond strength of friction-welded interface of commercially pure aluminum to mild steel. Q. J. Jpn. Weld. Soc. 2005, 23, 622–627. [Google Scholar] [CrossRef]
- Kimapong, K.; Watanabe, T. Lap joint of A5083 aluminum alloy and SS400 steel by friction stir welding. Mater. Trans. 2005, 46, 835–841. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, M.; Çöl, M.; Acet, M. Interface properties of aluminum/steel friction-welded components. Mater. Charact. 2003, 49, 421–429. [Google Scholar] [CrossRef]
- Fukumoto, S.; Tsubakino, H.; Okita, K.; Aritoshi, M.; Tomita, T. Static joint strength of friction welded joint between aluminium alloys and stainless steel. Weld. Int. 2000, 14, 89–93. [Google Scholar] [CrossRef]
- Herbst, S.; Dovletoglou, C.N.; Nürnberger, F. Method for semi-automated measurement and statistical evaluation of iron aluminum intermetallic compound layer thickness and morphology. Metallogr. Microstruct. Anal. 2017, 6, 367–374. [Google Scholar] [CrossRef] [Green Version]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.-C. Nanoindentation, 3rd ed.; Springer: New York, NY, USA, 2011; pp. 21–37. [Google Scholar]
- Heumann, T. Diffusion in Metallen. Grundlagen, Theorie, Vorgänge in Reinmetallen und Legierungen, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 4–13. [Google Scholar]
- Rummel, G.; Zumkley, T.; Eggersmann, M.; Freitag, K.; Mehrer, H. Diffusion of implanted 3d-transition elements in aluminium part II: Pressure dependence. diffusion implantierter 3d-Übergangselemente in aluminium. Teil II: Druckabhängigkeit. Z. Met. 1995, 95b, 131–140. [Google Scholar]
- Rummel, G.; Zumkley, T.; Eggersmann, M.; Freitag, K.; Mehrer, H. Diffusion of implanted 3d-transition elements in aluminium part I: Temperature dependence. diffusion implantierter 3d-Übergangselemente in aluminium. Teil I: Temperaturabhängigkeit. Z. Met. 1995, 95a, 122–130. [Google Scholar]
- Massalski, T.B.; Okamoto, H. Binary alloy phase diagrams. In American Society for Metals; ASM International: Novelty, OH, USA, 1990. [Google Scholar]
- Behrens, B.-A.; Klose, C.; Thürer, S.E.; Heimes, N.; Uhe, J. Numerical modeling of the development of intermetallic layers between aluminium and steel during co-extrusion. AIP Conf. Proc. 2019, 2113, 040029. [Google Scholar]
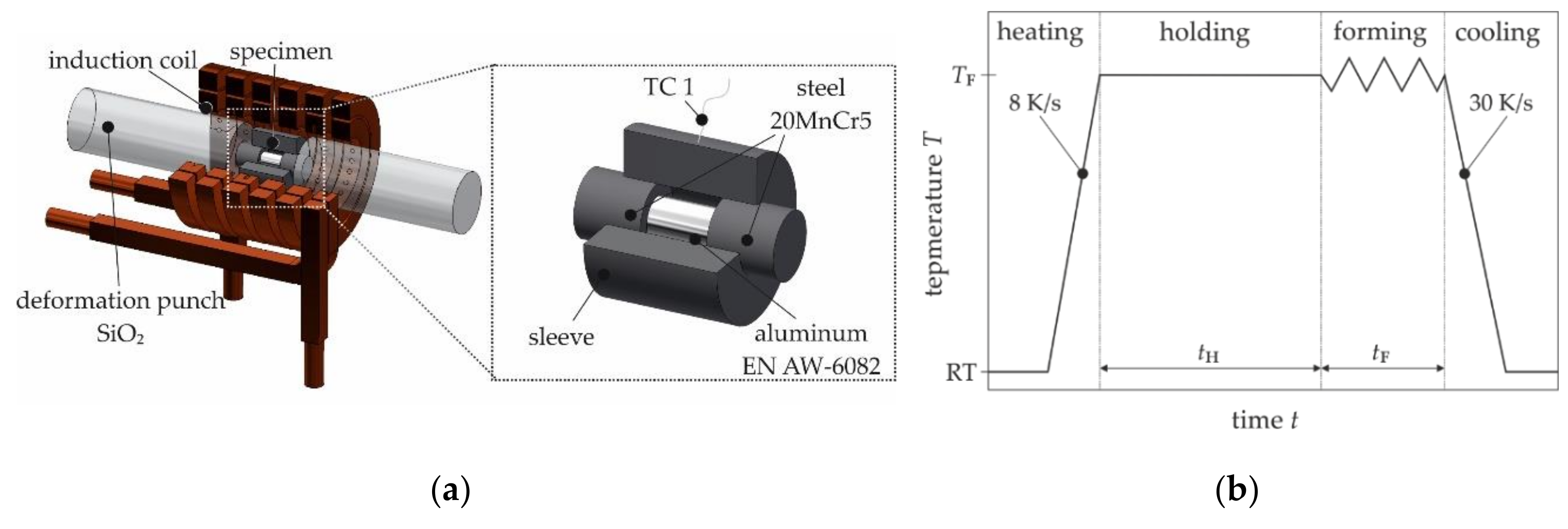


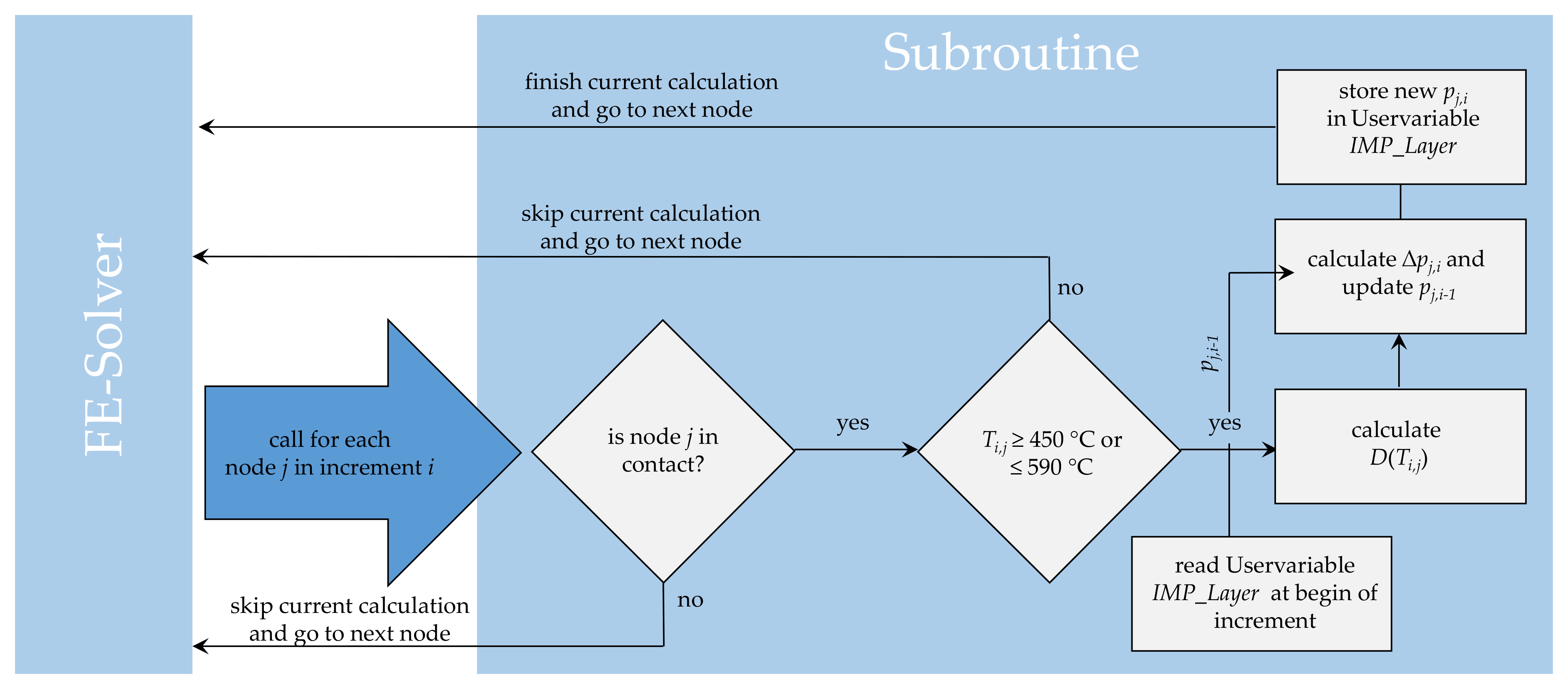

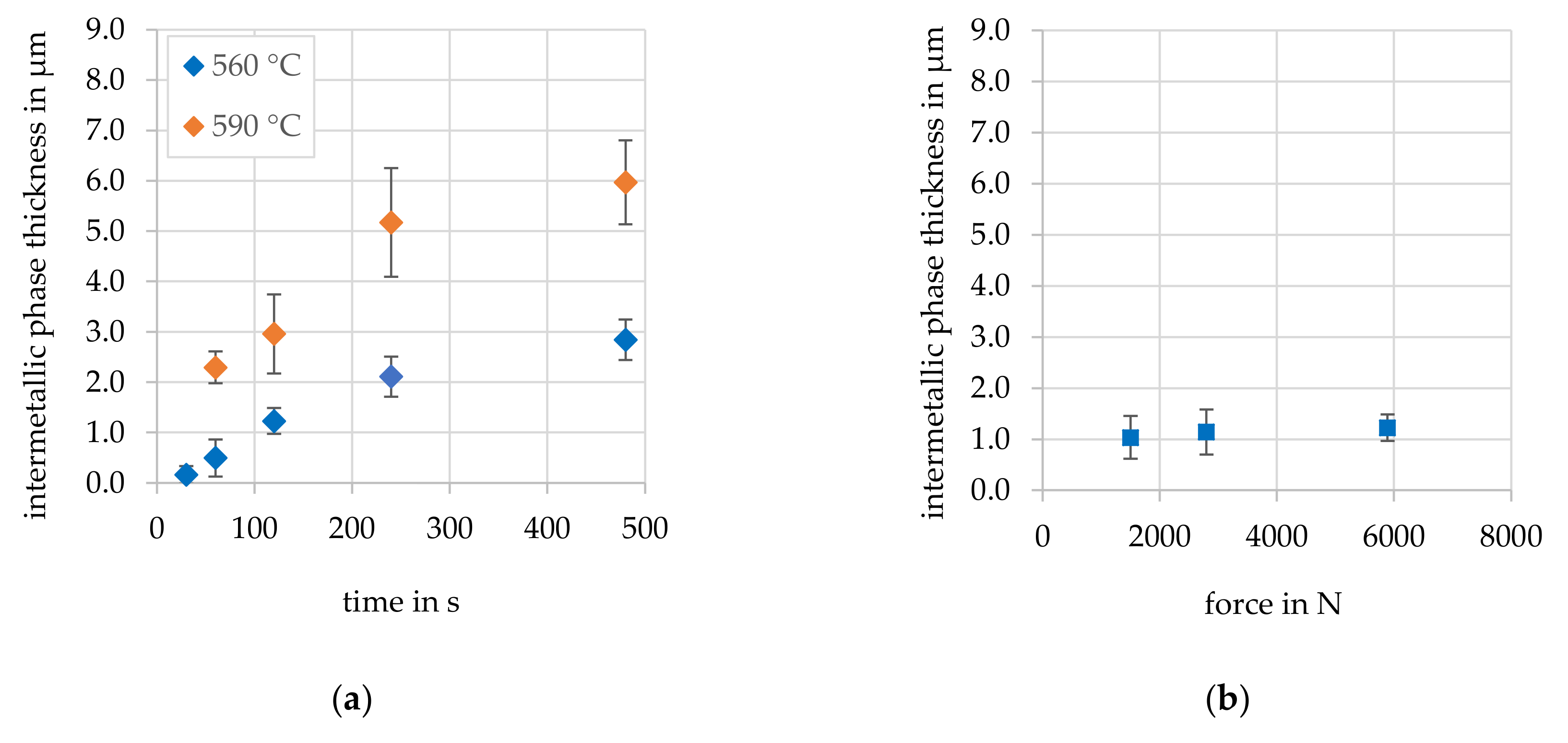
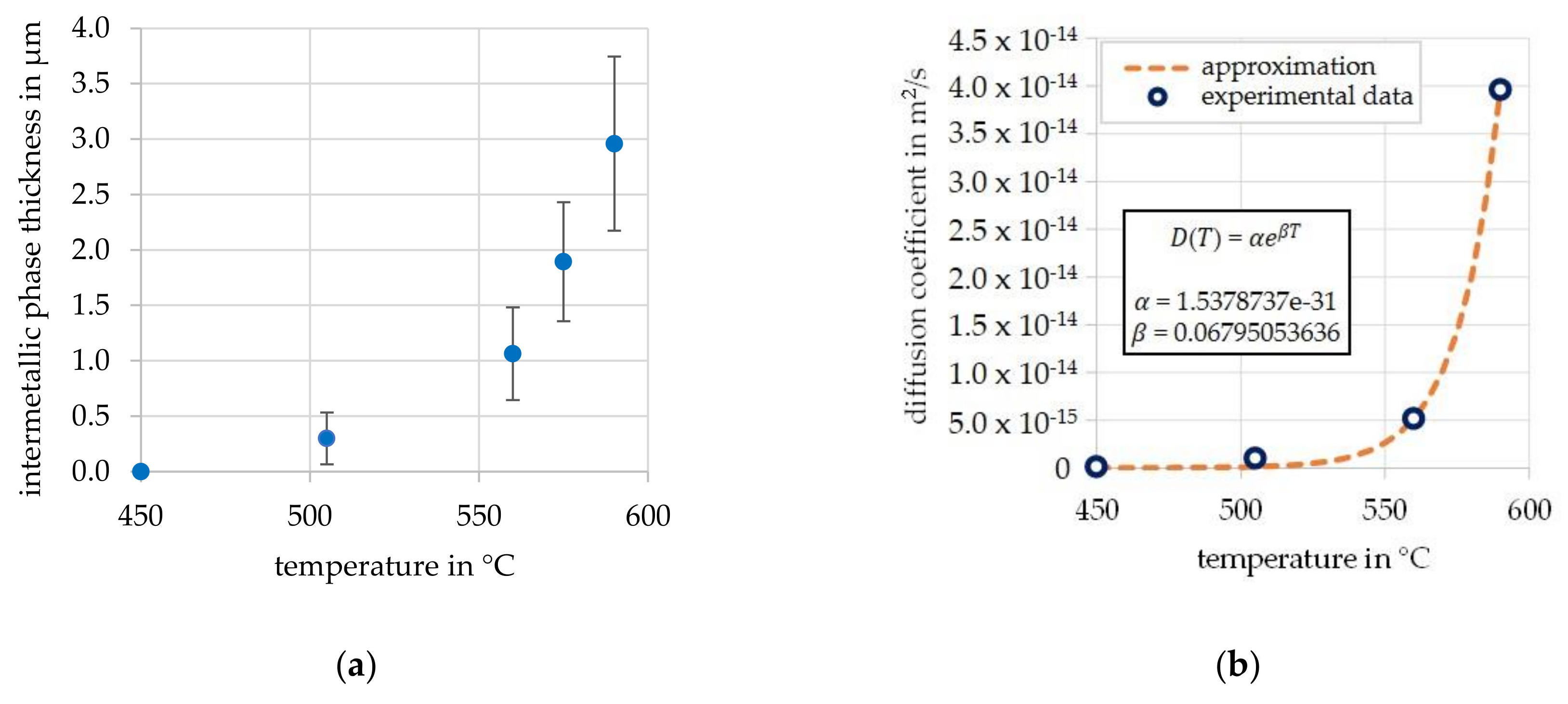


| Test Series | Temperature TF in °C | Forming Time tF in s | Force F in N |
|---|---|---|---|
| Reference variant | 560 | 120 | 5890 |
| Temperature variation | 450, 505, 560, 590 | 120 | 5890 |
| Time variation 1 | 560 | 30, 60, 120, 240, 480 | 5890 |
| Time variation 2 | 590 | 60, 120, 240, 480 | 5890 |
| Force variation | 560 | 120 | 1500, 2797, 5890 |
| Validation | 575 | 120 | 5890 |
| Material | Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti |
|---|---|---|---|---|---|---|---|---|
| EN AW-6082 | 1.11 ± 0.0295 | 0.19 ± 0.0349 | 0.0349 ± 0.001 | 0.438 ± 0.006 | 0.656 ± 0.027 | 0.0352 ± 0.001 | 0.0169 ± 0.002 | 0.0186 ± 0.002 |
| Material | C | Si | Mn | Cr | S |
|---|---|---|---|---|---|
| 20MnCr5 | 0.22 ± 0.02 | 0.21 ± 0.01 | 1.10 ± 0.02 | 1.01 ± 0.0109 | 0.0131 ± 0.0007 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behrens, B.-A.; Maier, H.J.; Klose, C.; Wester, H.; Thürer, S.E.; Heimes, N.; Uhe, J. Characterization and Modeling of Intermetallic Phase Formation during the Joining of Aluminum and Steel in Analogy to Co-Extrusion. Metals 2020, 10, 1582. https://doi.org/10.3390/met10121582
Behrens B-A, Maier HJ, Klose C, Wester H, Thürer SE, Heimes N, Uhe J. Characterization and Modeling of Intermetallic Phase Formation during the Joining of Aluminum and Steel in Analogy to Co-Extrusion. Metals. 2020; 10(12):1582. https://doi.org/10.3390/met10121582
Chicago/Turabian StyleBehrens, Bernd-Arno, Hans Jürgen Maier, Christian Klose, Hendrik Wester, Susanne Elisabeth Thürer, Norman Heimes, and Johanna Uhe. 2020. "Characterization and Modeling of Intermetallic Phase Formation during the Joining of Aluminum and Steel in Analogy to Co-Extrusion" Metals 10, no. 12: 1582. https://doi.org/10.3390/met10121582
APA StyleBehrens, B.-A., Maier, H. J., Klose, C., Wester, H., Thürer, S. E., Heimes, N., & Uhe, J. (2020). Characterization and Modeling of Intermetallic Phase Formation during the Joining of Aluminum and Steel in Analogy to Co-Extrusion. Metals, 10(12), 1582. https://doi.org/10.3390/met10121582






