Self-Diffusion in Liquid Copper, Silver, and Gold
Abstract
1. Introduction
2. Theory
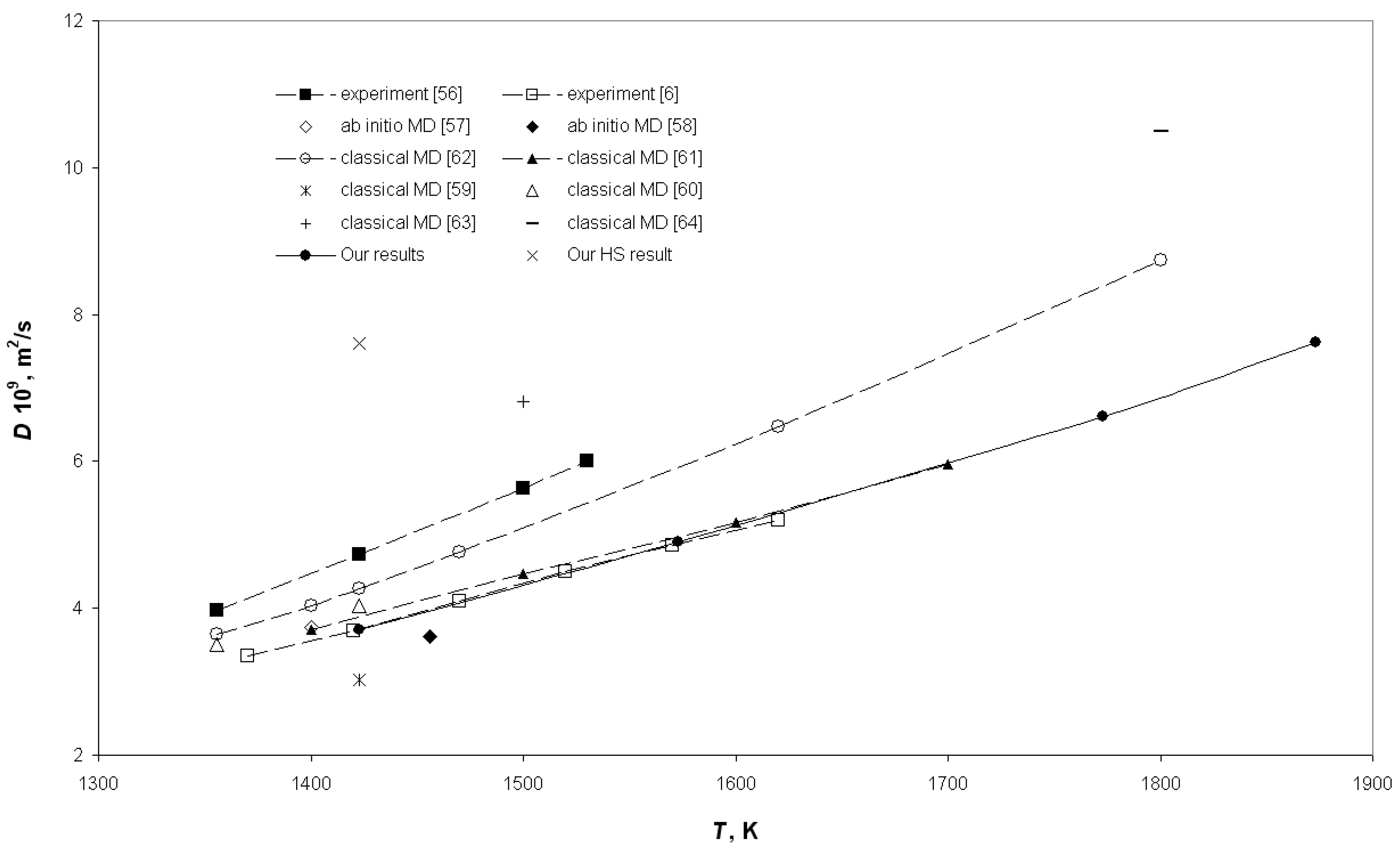
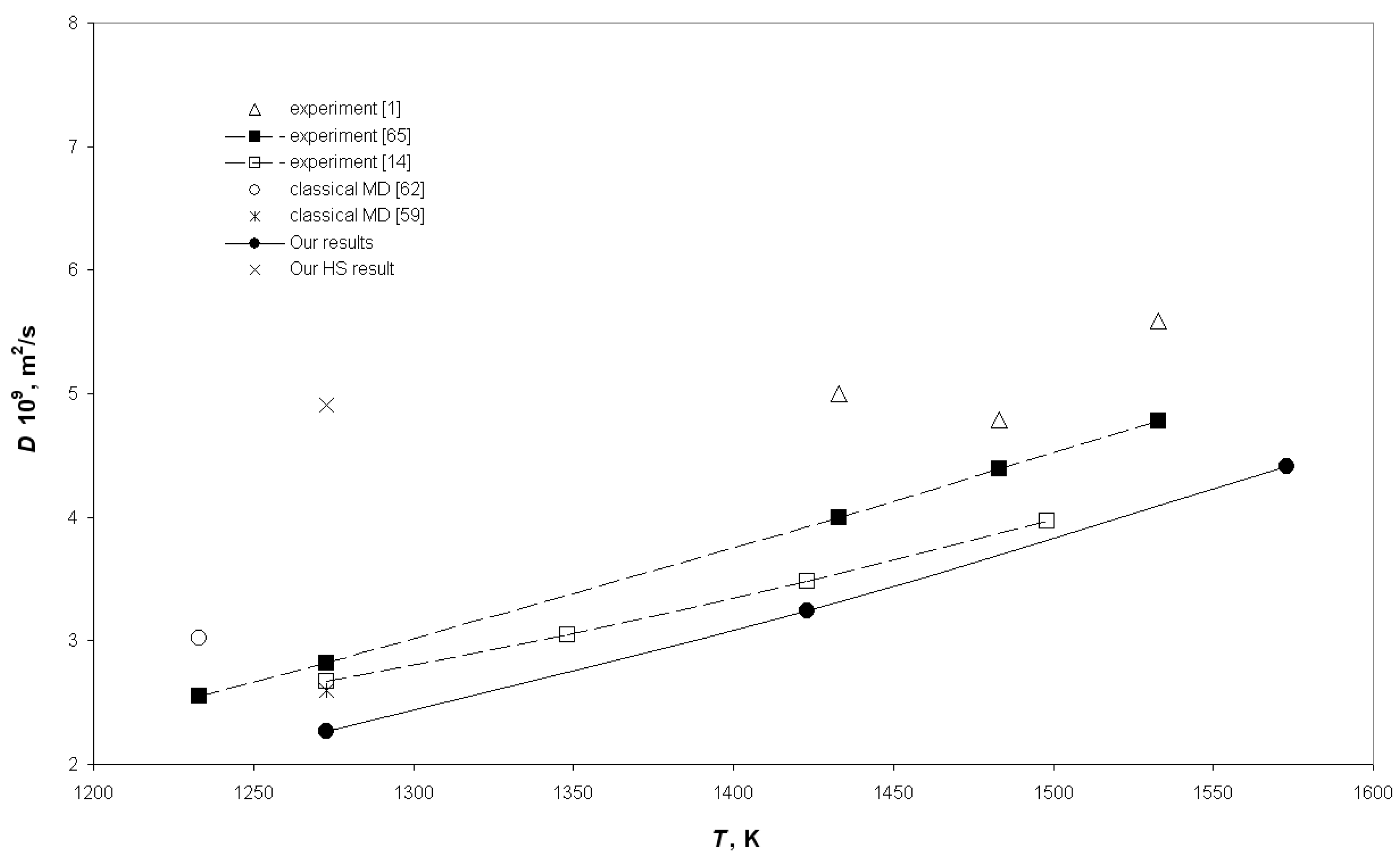
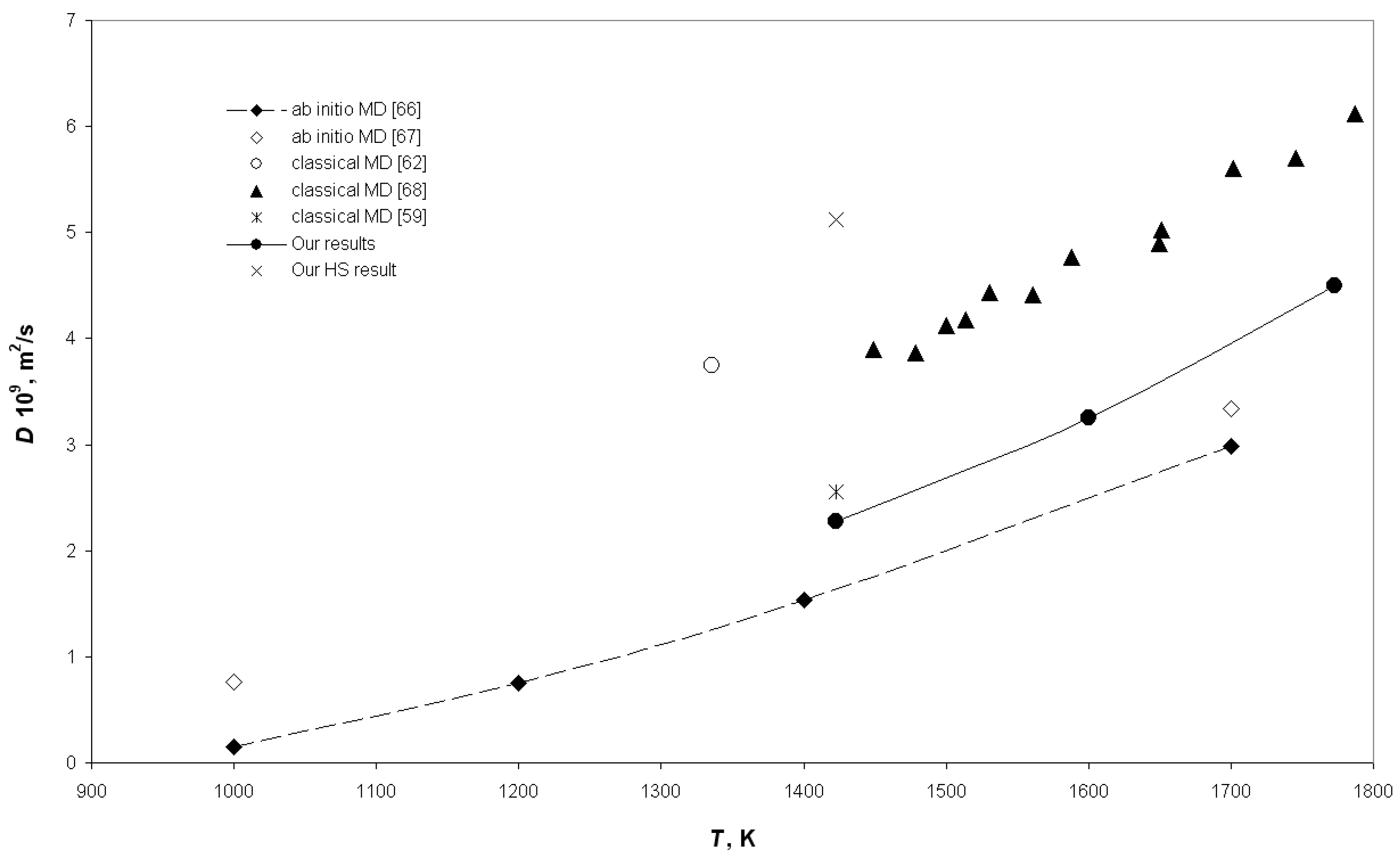
3. Results and Discussion
4. Conclusions
Funding
Conflicts of Interest
References
- Itami, T.; Mizuno, A.; Aoki, H.; Arai, Y.; Goto, K.; Amano, S.; Tateiwa, N.; Kaneko, M.; Fukazawa, T.; Nakamura, R.; et al. The study of self-diffusion and mutual-diffusion of liquid Cu-Ag alloys. J. Jpn. Soc. Microgravity Appl. 2000, 17, 64–69. [Google Scholar]
- Masaki, T.; Fukazawa, T.; Matsumoto, S.; Itami, T.; Yoda, S. Measurements of diffusion coefficients of metallic melt under microgravity—Current status of the development of shear cell technique towards JEM on ISS. Meas. Sci. Technol. 2005, 16, 327–335. [Google Scholar] [CrossRef]
- Mathiak, G.; Plescher, E.; Willnecker, R. Liquid metal diffusion experiments in microgravity—Vibrational effects. Meas. Sci. Technol. 2005, 16, 336–344. [Google Scholar] [CrossRef]
- Cahoon, J.R.; Jiao, Y.; Tandon, K.; Chaturvedi, M. Interdiffusion in liquid tin. J. Phase Equilibria Diffus. 2006, 27, 325–332. [Google Scholar] [CrossRef]
- Meyer, A.; Stüber, S.; Holland-Moritz, D.; Heinen, O.; Unruh, T. Determination of self-diffusion coefficients by quasielastic neutron scattering measurements of levitated Ni droplets. Phys. Rev. B 2008, 77, 092201. [Google Scholar] [CrossRef]
- Meyer, A. Self-diffusion in liquid copper as seen by quasielastic neutron scattering. Phys. Rev. B 2010, 81, 012102. [Google Scholar] [CrossRef]
- Bartsch, A.; Rätzke, K.; Meyer, A.; Faupel, F. Dynamic Arrest in Multicomponent Glass-Forming Alloys. Phys. Rev. Lett. 2010, 104, 195901. [Google Scholar] [CrossRef]
- Porth, C.B.; Cahoon, J.R. Interdiffusion of Bi in Liquid Sn. J. Phase Equilibria Diffus. 2010, 31, 149–156. [Google Scholar] [CrossRef]
- Lee, N.; Cahoon, J.R. Interdiffusion of Copper and Iron in Liquid Aluminum. J. Phase Equilibria Diffus. 2011, 32, 226–234. [Google Scholar] [CrossRef]
- Brillo, J.; Pommrich, A.I.; Meyer, A. Relation between Self-Diffusion and Viscosity in Dense Liquids: New Experimental Results from Electrostatic Levitation. Phys. Rev. Lett. 2011, 107, 165902. [Google Scholar] [CrossRef]
- Weis, H.; Unruh, T.; Meyer, A. The measurement of self-diffusion coefficients in liquid germanium using quasielastic neutron scattering. High Temp. High Press. 2013, 42, 39–47. [Google Scholar]
- Pommrich, A.I.; Unruh, T.; Meyer, A. Self-diffusion of 3d transition metals in liquid silicon alloys. High Temp. High Press. 2013, 42, 49–55. [Google Scholar]
- Geng, Y.; Zhu, C.; Zhang, B. A sliding cell technique for diffusion measurements in liquid metals. AIP Adv. 2014, 4, 037102. [Google Scholar] [CrossRef]
- Engelhardt, M.; Meyer, A.; Yang, F.; Simeoni, G.; Kargl, F. Self and Chemical Diffusion in Liquid Al-Ag. Defect Diffus. Forum 2016, 367, 157–166. [Google Scholar] [CrossRef]
- Basuki, S.W.; Yang, F.; Gill, E.; Rätzke, K.; Meyer, A.; Faupel, F. Atomic dynamics in Zr-based glass forming alloys near the liquidus temperature. Phys. Rev. B 2017, 95, 024301. [Google Scholar] [CrossRef]
- Zhong, L.; Hu, J.; Geng, Y.; Zhu, C.; Zhang, B. A multi-slice sliding cell technique for diffusion measurements in liquid metals. Rev. Sci. Instruments 2017, 88, 93905. [Google Scholar] [CrossRef]
- Xiong, L.H.; Wang, X.D.; Cao, Q.P.; Zhang, D.X.; Xie, H.L.; Xiao, T.Q.; Jiang, J.Z. Composition- and temperature-dependent liquid structures in Al–Cu alloys: An ab initio molecular dynamics and X-ray diffraction study. J. Phys. Condens. Matter 2017, 29, 035101. [Google Scholar] [CrossRef]
- Belova, I.; Heuskin, D.; Sondermann, E.; Ignatzi, B.; Kargl, F.; Murch, G.E.; Meyer, A. Combined interdiffusion and self-diffusion analysis in Al-Cu liquid diffusion couple. Scr. Mater. 2018, 143, 40–43. [Google Scholar] [CrossRef]
- Sondermann, E.; Jakse, N.; Binder, K.; Mielke, A.; Heuskin, D.; Kargl, F.; Meyer, A. Concentration dependence of interdiffusion in aluminum-rich Al-Cu melts. Phys. Rev. B 2019, 99, 024204. [Google Scholar] [CrossRef]
- Weis, H.; Kargl, F.; Kolbe, M.; Koza, M.M.; Unruh, T.; Meyer, A. Self- and interdiffusion in dilute liquid germanium-based alloys. J. Phys. Condens. Matter 2019, 31, 455101. [Google Scholar] [CrossRef]
- Rao, R.V.G.; Bhattacharyya, M. Partial structures of compound-forming liquid gold–caesium alloy. A model potential approach. Phys. Status Solidi 1987, 140, 51–61. [Google Scholar] [CrossRef]
- Venkatesh, R.; Rao, R. Total and partial structure factors, compressibility, diffusion coefficients and other associated properties of an Ag-Se semiconducting alloy. J. Mol. Struct. 1996, 361, 283–288. [Google Scholar] [CrossRef]
- Anusionwu, B.C.; Akinlade, O.; Hussain, L.A. A Theoretical Study of Structure and Ordering in Pb-Bi Molten Alloys. Phys. Chem. Liq. 1997, 34, 1–13. [Google Scholar] [CrossRef]
- Venkatesh, R.; Mishra, R.K.; Rao, R.V.G. Structural, thermodynamic and other associated properties of partially ordered Ag-In alloy. Phys. Status Solidi 2003, 240, 549–560. [Google Scholar] [CrossRef]
- Grosdidier, B.; Gasser, J.-G. Ordering potential in liquid Al–Ge alloys structure and thermodynamics. Intermetallics 2003, 11, 1253–1258. [Google Scholar] [CrossRef]
- Grosdidier, B.; Osman, S.M.; Ben Abdellah, A. Liquid gallium-lead mixture spinodal, binodal, and excess thermodynamic properties. Phys. Rev. B 2008, 78, 024205. [Google Scholar] [CrossRef]
- Dubinin, N.; Filippov, V.; Malkhanova, O.; Vatolin, N. Structure factors of binary liquid metal alloys within the square-well model. Cent. Eur. J. Phys. 2009, 7, 584–590. [Google Scholar] [CrossRef]
- Osman, S.M.; Grosdidier, B.; Ali, I.; Ben Abdellah, A. Liquid gallium-lead mixture phase diagram, surface tension near the critical mixing point, and prewetting transition. Phys. Rev. E 2013, 87, 062103. [Google Scholar] [CrossRef]
- Dubinin, N.; Filippov, V.; Yuryev, A.; Vatolin, N. Excess entropy of mixing for binary square-well fluid in the mean spherical approximation: Application to liquid alkali-metal alloys. J. Non-Cryst. Solids 2014, 401, 101–104. [Google Scholar] [CrossRef]
- Yu, Y.-X.; Han, M.-H.; Gao, G.-H. Self-diffusion in a fluid of square-well spheres. Phys. Chem. Chem. Phys. 2001, 3, 437–443. [Google Scholar] [CrossRef]
- Krekelberg, W.P.; Mittal, J.; Ganesan, V.; Truskett, T.M. How short-range attractions impact the structural order, self-diffusivity, and viscosity of a fluid. J. Chem. Phys. 2007, 127, 044502. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, R.; Khanna, K. Self-diffusion coefficients of dense fluid for a square-well fluid. J. Mol. Liq. 2007, 136, 156–160. [Google Scholar] [CrossRef]
- Ryltsev, R.E.; Chtchelkatchev, N.M.; Ryzhov, V.N. Superfragile Glassy Dynamics of a One-Component System with Isotropic Potential: Competition of Diffusion and Frustration. Phys. Rev. Lett. 2013, 110, 025701. [Google Scholar] [CrossRef] [PubMed]
- Ryltsev, R.E.; Klumov, B.; Chtchelkatchev, N. Self-assembly of the decagonal quasicrystalline order in simple three-dimensional systems. Soft Matter 2015, 11, 6991–6998. [Google Scholar] [CrossRef] [PubMed]
- Ryltsev, R.E.; Chtchelkatchev, N. Universal self-assembly of one-component three-dimensional dodecagonal quasicrystals. Soft Matter 2017, 13, 5076–5082. [Google Scholar] [CrossRef]
- Torres-Carbajal, A.; Trejos, V.M.; Collazo, L.A.N. Self-diffusion coefficient of the square-well fluid from molecular dynamics simulations within the constant force approach. J. Chem. Phys. 2018, 149, 144501. [Google Scholar] [CrossRef]
- Davydov, A.G.; Tkachev, N. Features of the dimerization equilibrium in square-well fluids. J. Mol. Liq. 2019, 275, 91–99. [Google Scholar] [CrossRef]
- Fomin, Y. Anomalously high heat capacity of core-softened liquids. Phys. Chem. Liq. 2017, 57, 67–74. [Google Scholar] [CrossRef]
- Tsiok, E.; Fomin, Y.D.; Ryzhov, V.N. The effect of confinement on the solid–liquid transition in a core-softened potential system. Physica A 2020, 550, 124521. [Google Scholar] [CrossRef]
- Fomin, Y. A comparison of dynamic properties of a core-softened system of particles across glass transition, melting and random tiling formation. Phys. Chem. Liq. 2019, 58, 290–301. [Google Scholar] [CrossRef]
- Dubinin, N.; Filippov, V.; Vatolin, N. Structure and thermodynamics of the one- and two-component square-well fluid. J. Non-Cryst. Solids 2007, 353, 1798–1801. [Google Scholar] [CrossRef]
- Ornstein, L.S.; Zernice, F. Interference of rontgen rays. Proc. Acad. Sci. 1914, 17, 793. [Google Scholar]
- Lebowitz, J.L.; Percus, J.K. Mean Spherical Model for Lattice Gases with Extended Hard Cores and Continuum Fluids. Phys. Rev. 1966, 144, 251–258. [Google Scholar] [CrossRef]
- Helfand, E. Theory of the Molecular Friction Constant. Phys. Fluids 1961, 4, 681–691. [Google Scholar] [CrossRef]
- Davis, H.T. Contribution to the Friction Coefficient from Time Correlations between Hard and Soft Molecular Interactions. J. Chem. Phys. 1967, 46, 4043–4047. [Google Scholar] [CrossRef]
- Dubinin, N.E. Self-diffusion coefficients of liquid alkali metals described by the square-well model within the mean spherical approximation. Indian J. Pure Appl. Phys. 2015, 53, 392–394. [Google Scholar]
- Dubinin, N.E. The SW-MSA Calculation of Self-Diffusion Coefficients in Liquid Lithium and Rubidium. Acta Phys. Pol. A 2016, 129, 310–312. [Google Scholar] [CrossRef]
- Dubinin, N.E. Square-well self-diffusion coefficients in liquid binary alloys of alkali metals within the mean spherical approximation. J. Alloys Compd. 2019, 803, 1100–1104. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. (In German) [Google Scholar] [CrossRef]
- Croxton, C.A. Liquid State Physics—A Statistical Mechanical Introduction; Cambridge University Press: Cambridge, UK, 1974. [Google Scholar]
- Iida, T.; Guthrie, R.I.L. The Physical Properties of Liquid Metals; Clarendon Press: Oxford, UK, 1988. [Google Scholar]
- Longuet-Higgins, H.; Valleau, J. Transport coefficients of dense fluids of molecules interacting according to a square well potential. Mol. Phys. 1958, 1, 284–294. [Google Scholar] [CrossRef]
- Wertheim, M.S. Exact Solution of the Percus-Yevick Integral Equation for Hard Spheres. Phys. Rev. Lett. 1963, 10, 321–323. [Google Scholar] [CrossRef]
- Thiele, E. Equation of State for Hard Spheres. J. Chem. Phys. 1963, 39, 474–479. [Google Scholar] [CrossRef]
- Waseda, Y. The Structure of Non-Crystalline Materials; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Henderson, J.; Yang, L. Self-diffusion of copper in molten copper. Trans. Met. Soc. AIME 1961, 221, 72. [Google Scholar]
- Mitrokhin, Y. Comparison of simulations of liquid metals by classical and ab initio molecular dynamics. Comput. Mater. Sci. 2006, 36, 189–193. [Google Scholar] [CrossRef]
- Liu, D.; Qin, J.; Gu, T. The structure of liquid Mg–Cu binary alloys. J. Non-Cryst. Solids 2010, 356, 1587–1592. [Google Scholar] [CrossRef]
- Alemany, M.M.G.; Rey, C.; Gallego, L.J. Transport coefficients of liquid transition metals: A computer simulation study using the embedded atom model. J. Chem. Phys. 1998, 109, 5175–5176. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, H.F.; Qin, F.X.; Hu, Z.Q. Molecular dynamics study of atomic transport properties in rapidly cooling liquid copper. J. Chem. Phys. 2004, 120, 1826–1831. [Google Scholar] [CrossRef]
- Han, X.; Chen, M.; Lu, Y.J. Transport Properties of Undercooled Liquid Copper: A Molecular Dynamics Study. Int. J. Thermophys. 2008, 29, 1408–1421. [Google Scholar] [CrossRef]
- Mei, J.; Davenport, J.W. Molecular-dynamics study of self-diffusion in liquid transition metals. Phys. Rev. B 1990, 42, 9682–9684. [Google Scholar] [CrossRef]
- Cheng, H.; Lü, Y.J.; Chen, M. Interdiffusion in liquid Al–Cu and Ni–Cu alloys. J. Chem. Phys. 2009, 131, 044502. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, L.; Fang, T. Demixing behaviour in binary Cu-Co melt. Phys. Chem. Liq. 2013, 51, 687–694. [Google Scholar] [CrossRef]
- Leak, V.G.; Swalin, R.A. Trans. Met. Soc. AIME 1964, 230, 426. Available online: https://scholar.google.com/scholar_lookup?title=&journal=Trans.%20TMS-AIME&volume=230&pages=426-30&publication_year=1964&author=Leak%2CV.%20G.&author=Swalin%2CR.%20A (accessed on 8 October 2020).
- Pasturel, A.; Tasci, E.S.; Sluiter, M.H.F.; Jakse, N. Structural and dynamic evolution in liquid Au-Si eutectic alloy byabinitiomolecular dynamics. Phys. Rev. B 2010, 81, 40202. [Google Scholar] [CrossRef]
- Peng, H.-L.; Voigtmann, T.; Kolland, G.; Kobatake, H.; Brillo, J. Structural and dynamical properties of liquid Al-Au alloys. Phys. Rev. B 2015, 92, 184201. [Google Scholar] [CrossRef]
- Bogicevic, A.; Hansen, L.B.; Lundqvist, B.I. Simulations of atomic structure, dynamics, and self-diffusion in liquid Au. Phys. Rev. E 1997, 55, 5535–5545. [Google Scholar] [CrossRef]
| Metal | = 1273 K | = 1423 K | = 1573 K | = 1773 K | = 1873 K |
|---|---|---|---|---|---|
| Cu | - | 7970 | 7860 | 7690 | 7620 |
| Ag | 9270 | 9120 | 8980 | - | - |
| Au | - | 17,200 | 17,100 | 16,900 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubinin, N. Self-Diffusion in Liquid Copper, Silver, and Gold. Metals 2020, 10, 1651. https://doi.org/10.3390/met10121651
Dubinin N. Self-Diffusion in Liquid Copper, Silver, and Gold. Metals. 2020; 10(12):1651. https://doi.org/10.3390/met10121651
Chicago/Turabian StyleDubinin, Nikolay. 2020. "Self-Diffusion in Liquid Copper, Silver, and Gold" Metals 10, no. 12: 1651. https://doi.org/10.3390/met10121651
APA StyleDubinin, N. (2020). Self-Diffusion in Liquid Copper, Silver, and Gold. Metals, 10(12), 1651. https://doi.org/10.3390/met10121651




