Silicon Steel Strip Profile Control Technology for Six-High Cold Rolling Mill with Small Work Roll Radius
Abstract
1. Introduction
2. Methods and Materials
2.1. Bending Terms
2.2. Flattening between Work Roll and Strip
2.3. Flattening between Stacked Rolls
2.4. Rolling Pressure Resulting from Strip Elastic–Plastic Deformation
2.5. Model Calculation Flow
2.6. Model Parameters
2.7. Model Calculation Accuracy Verification
3. Analysis of Calculation Results
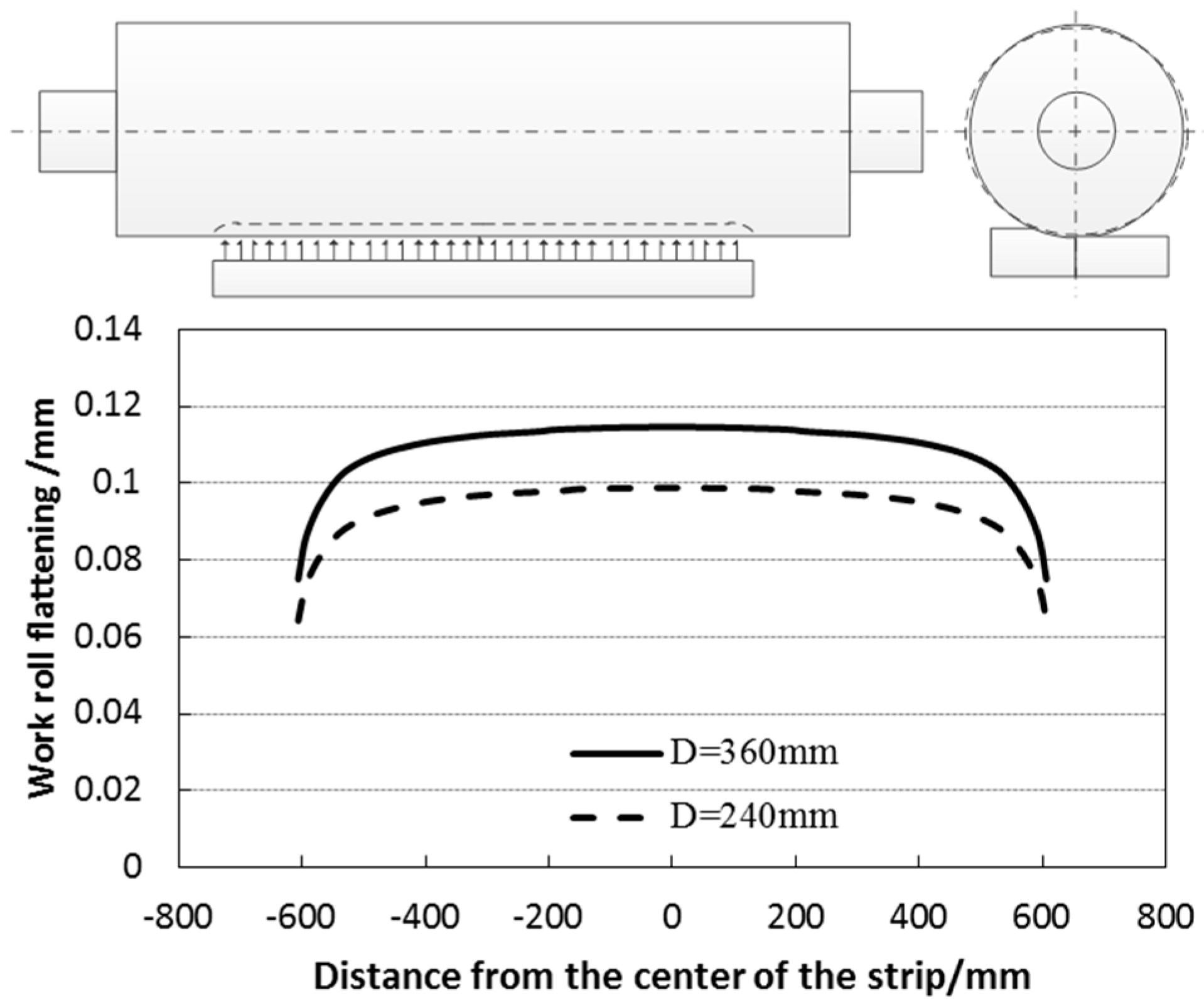
3.1. Calculation of Roll Flattening Deformation
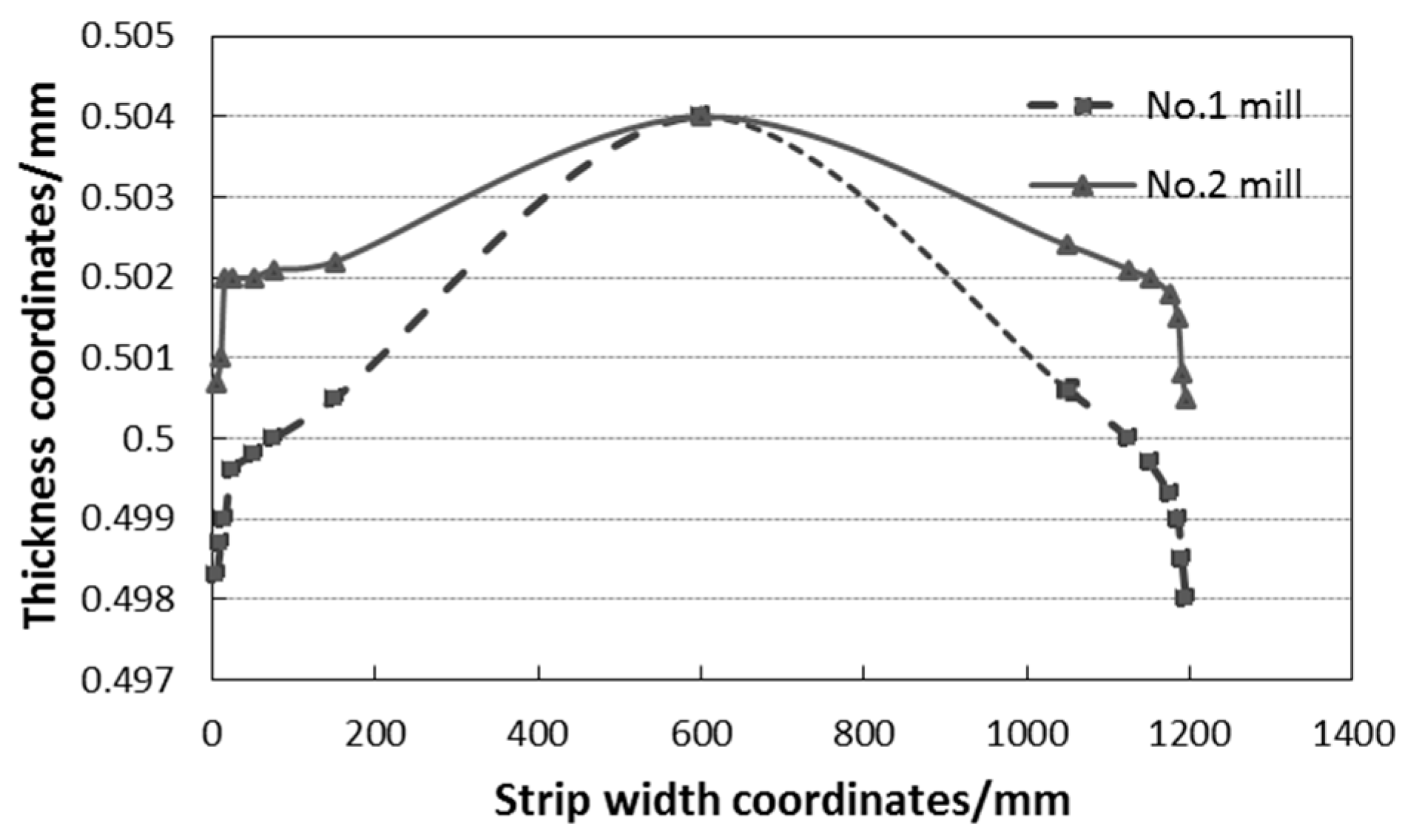
3.2. Calculation of Cross-Sectional Profile of Strip
4. Industrial Application
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xia, S.Z.; Kang, L.Y.; Wang, L.Q. Developments in the production of grain-oriented electrical steel. J. Magn. Magn. Mater. 2008, 320, 3229–3233. [Google Scholar] [CrossRef]
- Yao, H.C.; He, R.A.; Shao, J.; Zhang, J.Y.; Zhao, S.H. Edge drop and high spot control of hot-rolled non-oriented electrical steel strip by taper roll shifting strategy. Ironmak. Steelmak. 2018, 1–7. [Google Scholar] [CrossRef]
- Ma, X.B.; Wang, D.C.; Liu, H.M.; Wen, C.C.; Zhou, Y. Large concave roll technology for hot rolled silicon steel. Ironmak. Steelmak. 2018, 45, 66–75. [Google Scholar] [CrossRef]
- Zhao, J.W.; Wang, X.C.; Yang, Q.; Wang, Q.N.; Liu, C.; Song, G.Y. High Precision Shape Model and Presetting Strategy for Strip Hot Rolling. J. Mater. Process. Technol. 2018, 265, 99–111. [Google Scholar] [CrossRef]
- Wang, X.C.; Yang, Q.; Sun, Y.Z. Rectangular section control technology for silicon steel rolling. J. Iron Steel Res. Int. 2015, 22, 185–191. [Google Scholar] [CrossRef]
- Ma, X.B.; Wang, D.C.; Liu, H.M. Coupling mechanism of control on strip profile and flatness in single stand universal crown reversible rolling mill. Steel Res. Int. 2017, 88, 1600495–1600505. [Google Scholar] [CrossRef]
- Cao, J.G.; Chai, X.T.; Li, Y.L.; Kong, N.; Jia, S.H.; Zeng, W. Integrated design of roll contours for strip edge drop and crown control in tandem cold rolling mills. J. Mater. Process. Technol. 2018, 252, 432–439. [Google Scholar] [CrossRef]
- Sun, W.Q.; Yang, Q.; Shao, J.; He, A.R.; Li, M.X. Edge drop control technique of silicon steel for UCM tandem cold rolling mills. J. Univ. Sci. Technol. Beijing 2010, 32, 1340–1345. [Google Scholar] [CrossRef]
- Liu, Y.J.; Ma, J.J.; Zhao, Y.P.; Wang, L.B.; Zhang, G.Z.; Shang, G.P. Edge Wave Control Strategy Caused by Edge Drop Control During UCMW Cold Tandem Mill. J. Iron Steel Res. 2012, 24, 114–119. [Google Scholar]
- Zhang, Q.D.; Bai, J.; Xu, L.J.; Gu, H.Z.; Jin, G. Study and Improvement of Mill Type of 1550 Tandem Cold Mill in Baosteel. Iron Steel 2009, 44, 67–82. [Google Scholar]
- Zhang, Y.; Yang, Q.; Shao, J.; Du, X.Z.; Wang, X.C. Edge drop control using sinusoidal tapered work roll on a UCMW mill. J. Univ. Sci. Technol. Beijing 2009, 31, 1611–1615. [Google Scholar] [CrossRef]
- Lee, J.S.; Shin, T.J.; Yoon, S.J.; Hwang, S.M. Prediction of Steady-State Strip Profile in Flat Rolling. Steel Res. Int. 2016, 87, 930–940. [Google Scholar] [CrossRef]
- Minton, J.J.; Cawthorn, C.J.; Brambley, E.J. Asymptotic analysis of asymmetric thin sheet rolling. Int. J. Mech. Sci. 2016, 113, 36–48. [Google Scholar] [CrossRef]
- Hacquin, A.; Montmitonnet, P.; Guillerault, J.P. A three-dimensional semi-analytical model of rolling stand deformation with finite element validation. Eur. J. Mech. A Solids 1998, 17, 79–106. [Google Scholar] [CrossRef]
- Yuan, Z.W.; Xiao, H.; Xie, H.B. Practice of improving roll deformation theory in strip rolling process based on boundary integral equation method. Metall. Mater. Trans. A 2014, 45, 1019–1026. [Google Scholar] [CrossRef]
- Pawelski, O.; Teutsch, H. A mathematical model for computing the distribution of loads and thickness in the width direction of a strip rolled in four-high cold-rolling mills. Eng. Fract. Mech. 1985, 21, 853–859. [Google Scholar] [CrossRef]
- Wang, T.; Huang, Q.X.; Xiao, H.; Qi, X.D. Modification of roll flattening analytical model based on the plane assumption. Chin. J. Mech. Eng. 2018, 31, 46–53. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Wei, D.; Tieu, A.K. Analysis of cold rolling of ultra-thin strip. J. Mater. Process. Technol. 2009, 209, 4584–4589. [Google Scholar] [CrossRef]
- Le, H.R.; Sutcliffe, M.P.F. Robust model for rolling of thin strip and foil. Int. J. Mech. Sci. 2001, 43, 1405–1419. [Google Scholar] [CrossRef]
- Chen, S.X.; Li, W.G.; Liu, X.H. Calculation of rolling pressure distribution and force based on improved Karman equation for hot strip mill. Int. J. Mech. Sci. 2014, 89, 256–263. [Google Scholar] [CrossRef]
- Cawthorn, C.J.; Minton, J.J.; Brambley, E.J. Asymptotic analysis of cold sandwich rolling. Int. J. Mech. Sci. 2016, 106, 184–193. [Google Scholar] [CrossRef]
- Shigaki, Y.; Nakhoul, R.; Montmitonnet, P. Numerical treatments of slipping/no-slip zones in cold rolling of thin sheets with heavy roll deformation. Lubricants 2015, 3, 113–131. [Google Scholar] [CrossRef]











| Parameters | Value |
|---|---|
| Backup roll length/mm | 1420 |
| Backup roll neck diameter/mm | 690 |
| Work roll length/mm | 1420 |
| The distance between two bending points of work roll/mm | 2150 |
| Intermediate roll length/mm | 1445 (Chamfer 50) |
| The distance between two bending points of intermediate roll/mm | 2800 |
| Parameters | Value |
|---|---|
| Entry/exit thickness/mm | 2.200/1.360 |
| Reduction/% | 32.0 |
| Work roll bending force/kN | 120 |
| Intermediate roll bending force/kN | 150 |
| Before/after tension/MPa | 20/118 |
| Intermediate roll shifting value/mm | 20 |
| Strip width/mm | 1230 |
| Steel Grade | Width | Entry/Exit Thickness |
|---|---|---|
| 50SW800 | 1230 mm | 2.5/0.5 mm |
| C | Si | Mn | Al | P | S |
|---|---|---|---|---|---|
| 0.003 | 0.85 | 0.25 | 0.33 | 0.03 | 0.0045 |
| Iron Loss P15/50 (≤W/kg) | Magnetic Induction B50 (≥T) | Number of Reverse Bending in Rolling Direction | Residual Curvature (mm) |
|---|---|---|---|
| 8 | 1.55 | ≥2 | ≤35 |
| Work Roll Contour | No.1 mill | No.2 mill |
|---|---|---|
| Curve A | 7.8 μm | 9 μm |
| Curve B | 5.5 μm | 7.9 μm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Shao, J.; Wang, X.; Yang, Q.; Feng, X. Silicon Steel Strip Profile Control Technology for Six-High Cold Rolling Mill with Small Work Roll Radius. Metals 2020, 10, 401. https://doi.org/10.3390/met10030401
He H, Shao J, Wang X, Yang Q, Feng X. Silicon Steel Strip Profile Control Technology for Six-High Cold Rolling Mill with Small Work Roll Radius. Metals. 2020; 10(3):401. https://doi.org/10.3390/met10030401
Chicago/Turabian StyleHe, Hainan, Jian Shao, Xiaochen Wang, Quan Yang, and Xiawei Feng. 2020. "Silicon Steel Strip Profile Control Technology for Six-High Cold Rolling Mill with Small Work Roll Radius" Metals 10, no. 3: 401. https://doi.org/10.3390/met10030401
APA StyleHe, H., Shao, J., Wang, X., Yang, Q., & Feng, X. (2020). Silicon Steel Strip Profile Control Technology for Six-High Cold Rolling Mill with Small Work Roll Radius. Metals, 10(3), 401. https://doi.org/10.3390/met10030401




