Flow-Stress Model of 300M Steel for Multi-Pass Compression
Abstract
:1. Introduction
2. Materials and Experiments
2.1. Materials
2.2. Multi-Pass Compression Experiments
3. Results
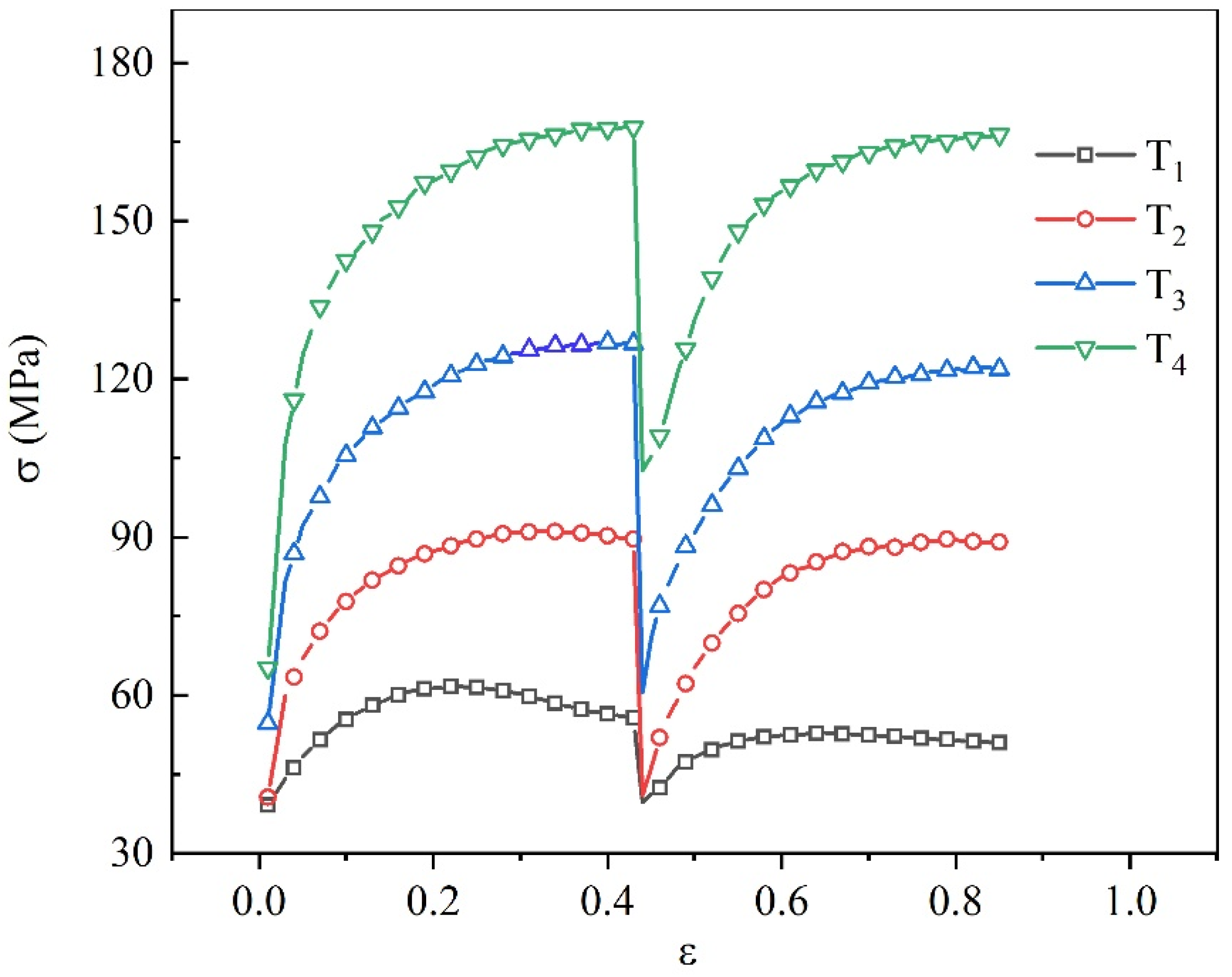
3.1. Influence of Strain Rate
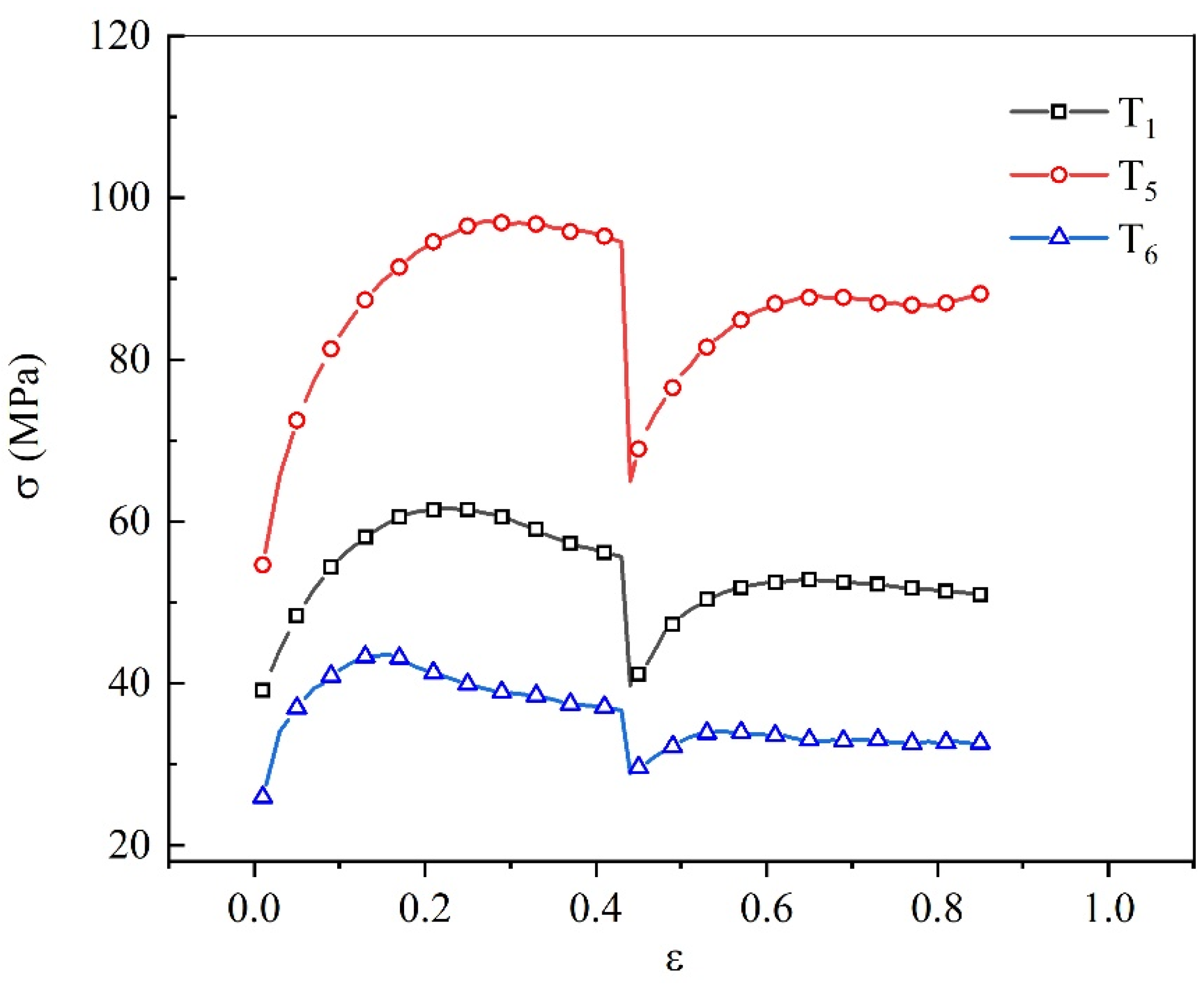
3.2. Influence of Temperature
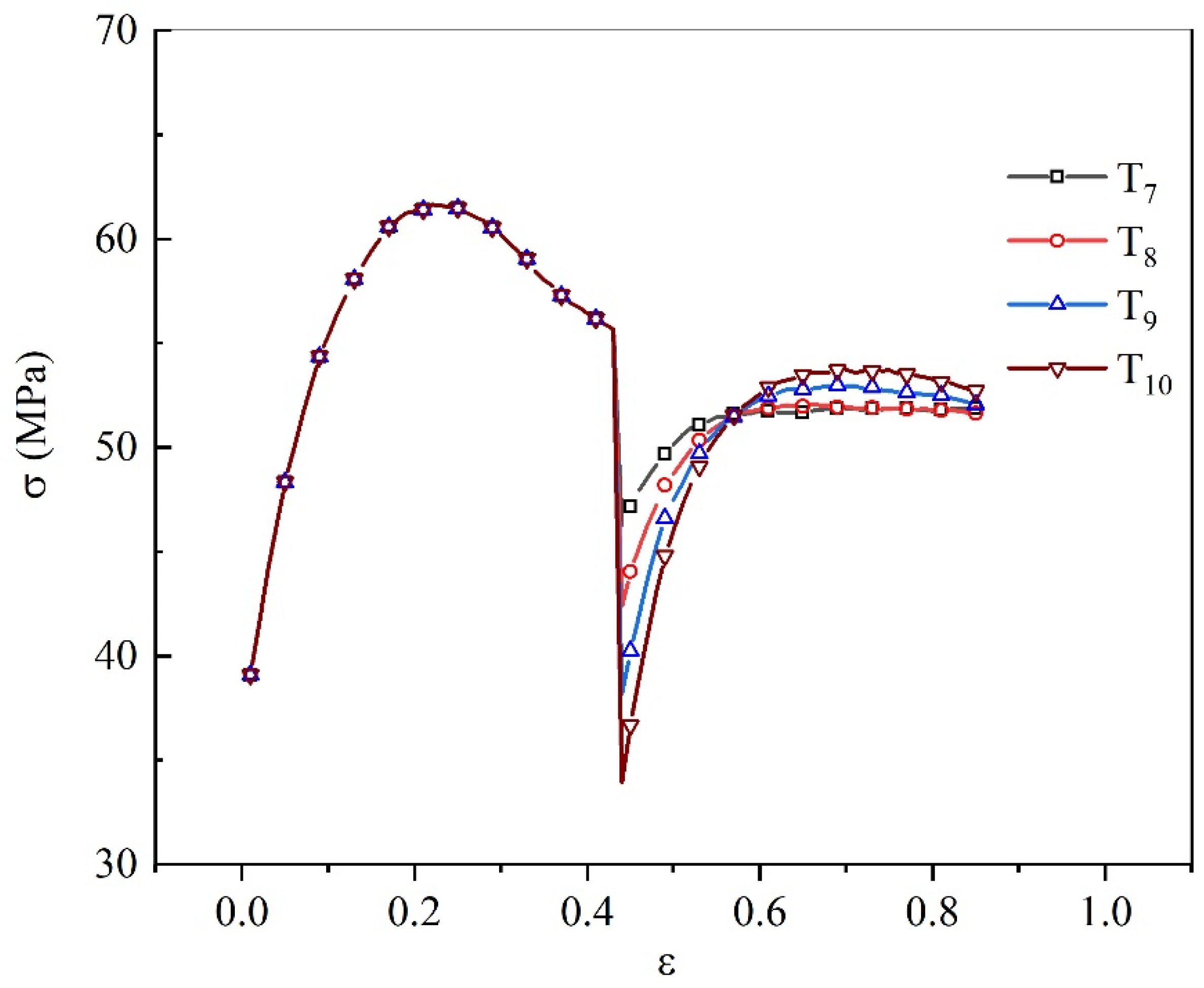
3.3. Influence of Inter-Pass Holding Time
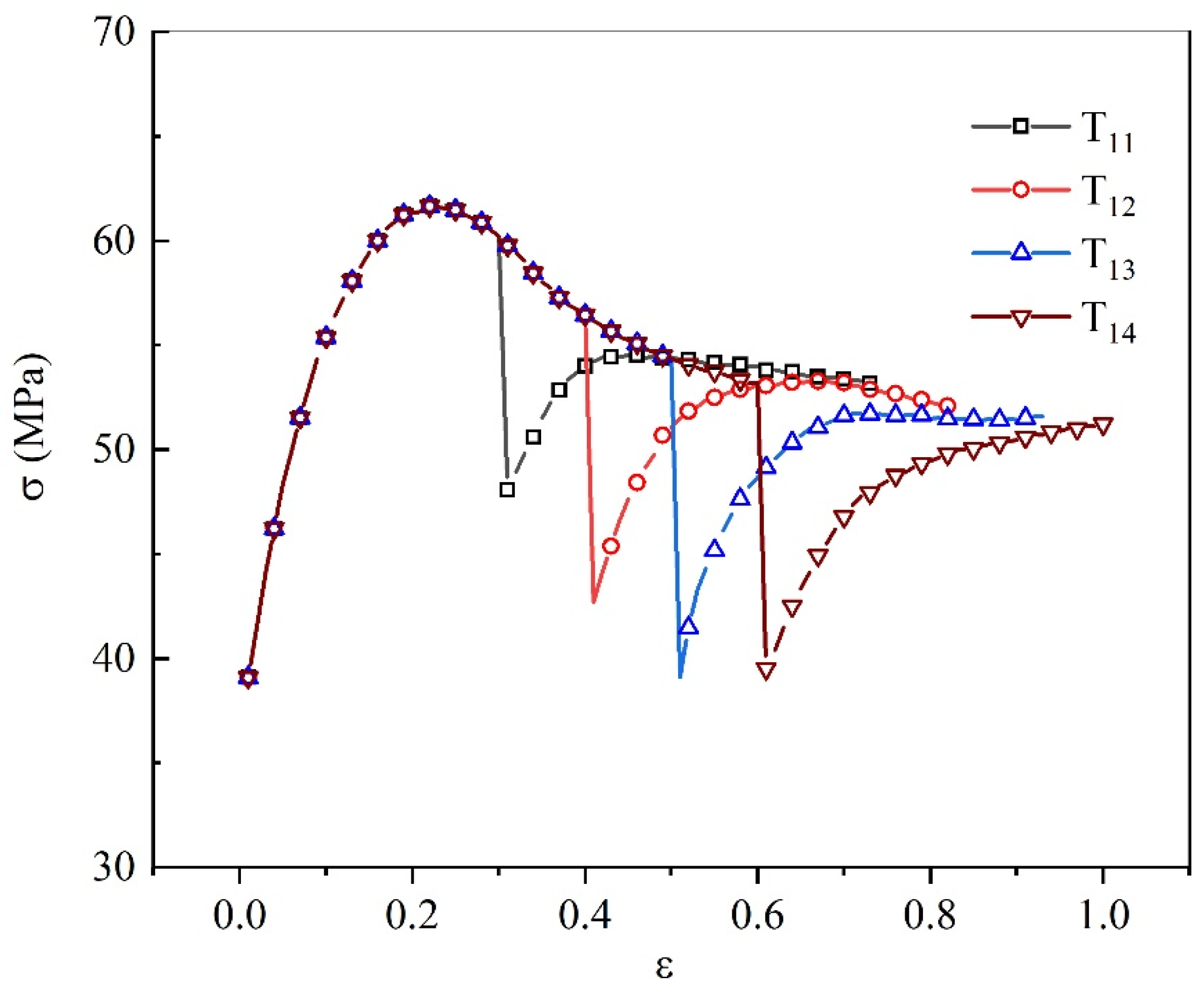
3.4. Influence of Interrupt Strain
3.5. Influence of Total Pass Number
4. Discussion
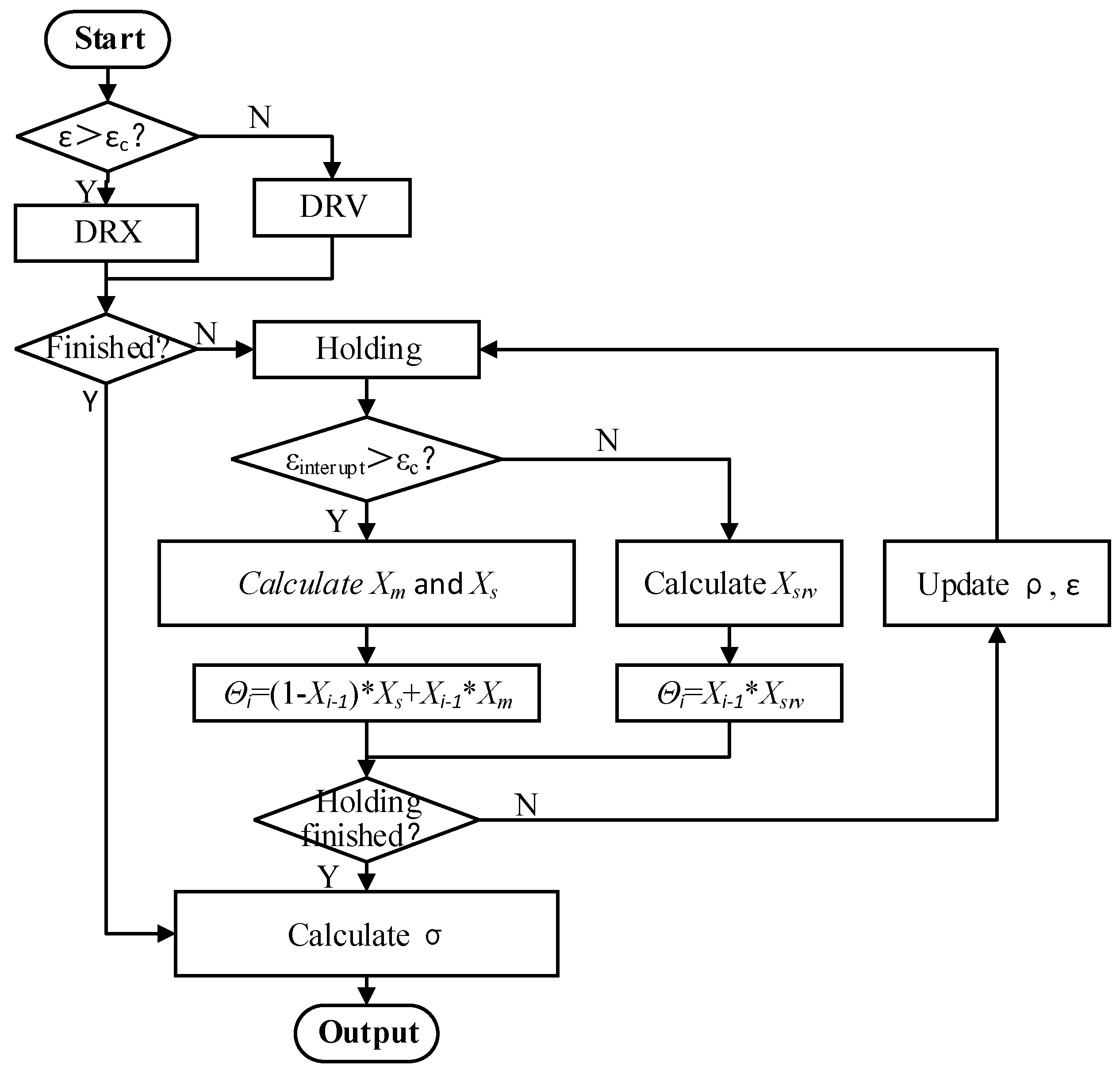
4.1. The Flow-Stress Model
4.2. Parameter Identification
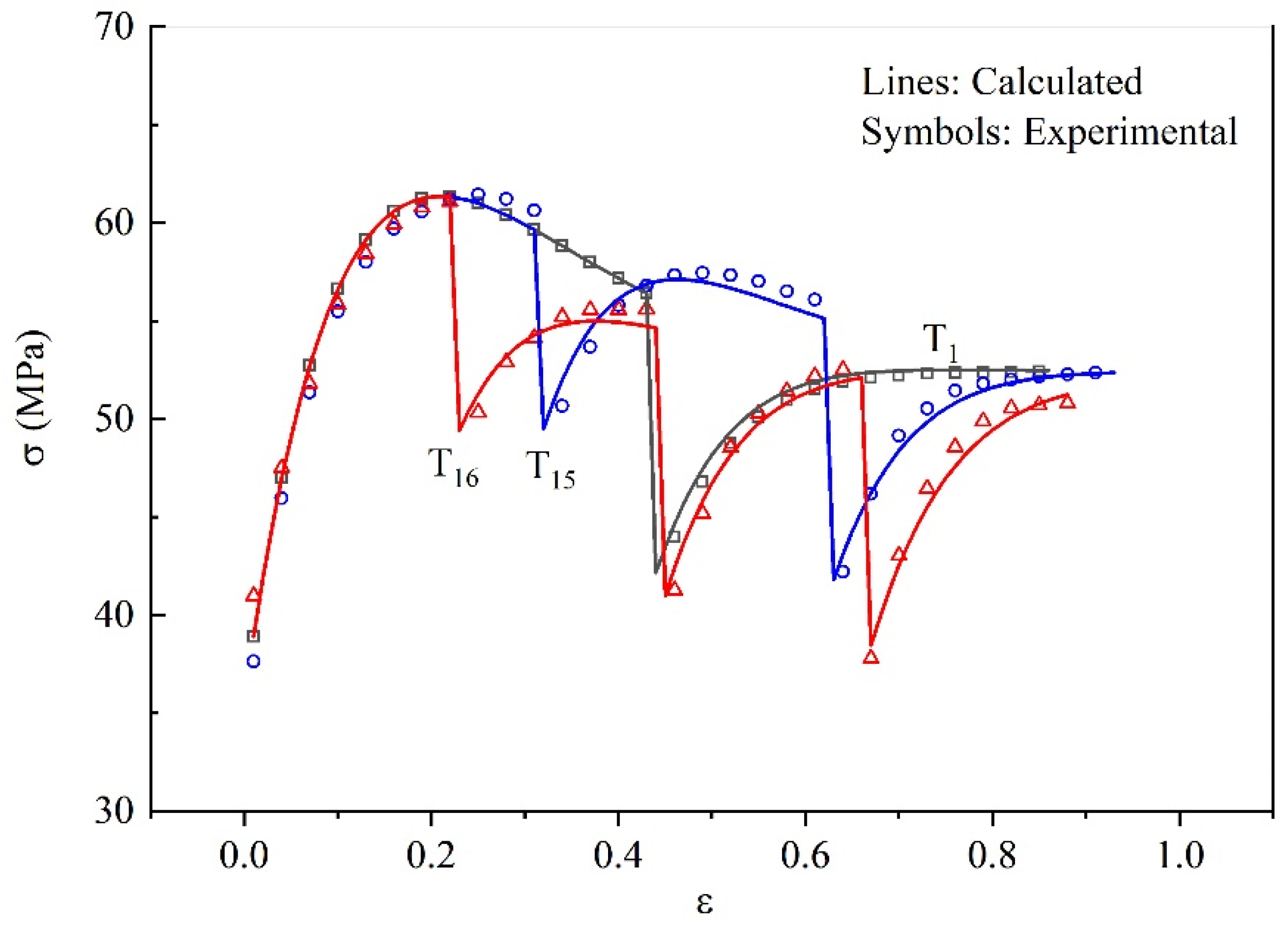
4.3. Comparison and Validation
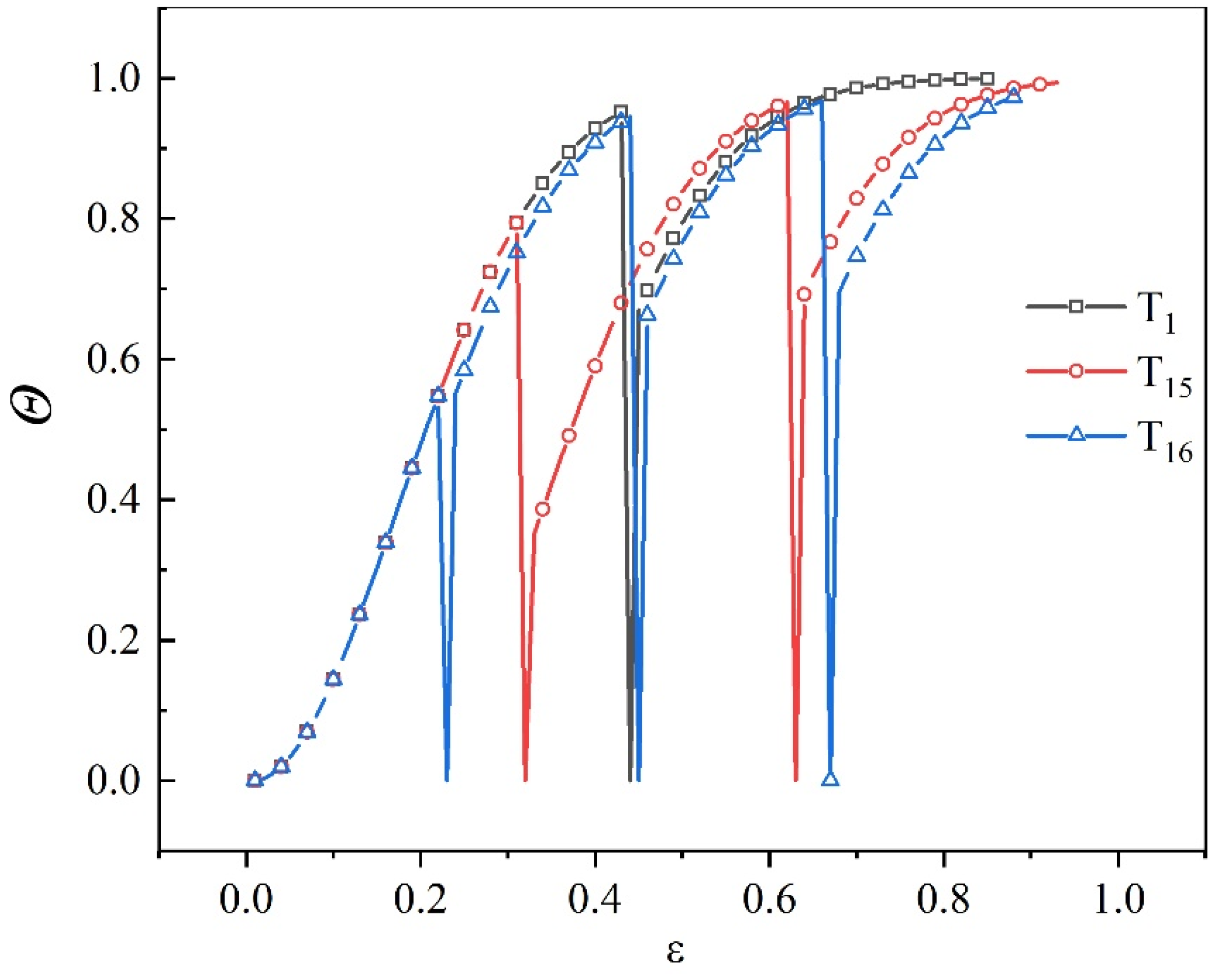
4.4. Analysis of the Softening Fraction
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, G.L.; Zhang, Y.J.; Wu, S.W. Characterization of hot deformation behaviour of Nb-Ti microalloyed high strength steel. J. S. Afr. I. Min. Metall. 2019, 119, 503–508. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, K. Evolution of Dynamic Recrystallization in 5CrNiMoV Steel during Hot Forming. Adv. Mater. Sci. Eng. 2020, 2020, 4732683. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Xu, W.; Wang, S. A cellular automaton coupled FEA model for hot deformation behavior of AZ61 magnesium alloys. J. Alloy Compd. 2020, 816, 152562. [Google Scholar] [CrossRef]
- Gong, B.; Duan, X.W.; Liu, J.S. A physically based constitutive model of As-forged 34CrNiMo6 steel and processing maps for hot working. Vacuum 2018, 155, 345–357. [Google Scholar] [CrossRef]
- Guo, L.; Wang, F.; Zhen, P. A novel unified model predicting flow stress and grain size evolutions during hot working of non-uniform as-cast 42CrMo billets. Chin. J. Aeronaut. 2019, 32, 531–545. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, Q.; Zhang, X. Avrami Kinetic-Based Constitutive Relationship for Armco-Type Pure Iron in Hot Deformation. Metals 2019, 9, 365. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Liu, D.; Wang, J. Characterization of hot deformation behavior of 30Si2MnCrMoVE low-alloying ultra-high-strength steel by constitutive equations and processing maps. J. Iron Steel Res. Int. 2020, in press. [Google Scholar] [CrossRef]
- Chen, F.; Wang, H.; Zhu, H. High-temperature deformation mechanisms and physical-based constitutive modeling of ultra-supercritical rotor steel. J. Manuf. Process. 2019, 38, 223–234. [Google Scholar] [CrossRef]
- Safara, N.; Engberg, G.; Ågren, J. Modeling Microstructure Evolution in a Martensitic Stainless Steel Subjected to Hot Working Using a Physically Based Model. Metall. Mater. Trans. A 2019, 50, 1480–1488. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.; Zhou, Y.; Weng, H. Constitutive behavior of 4343/4A60 aluminum alloy at multi-pass hot deformation. Strength Mater. 2017, 49, 83–92. [Google Scholar] [CrossRef]
- Beltran, O.; Huang, K.; Logé, R.E. A mean field model of dynamic and post-dynamic recrystallization predicting kinetics, grain size and flow stress. Comp. Mater. Sci. 2015, 102, 293–303. [Google Scholar] [CrossRef]
- Guan, Y.; Chen, Q.; Ma, J. A study on recrystallization behavior of low carbon bainitic steel during multi-pass deformation. Appl. Mech. Mater. 2012, 217–219, 471–475. [Google Scholar] [CrossRef]
- Cho, H.E.; Hammi, Y.; Bowman, A.L. A unified static and dynamic recrystallization Internal State Variable (ISV) constitutive model coupled with grain size evolution for metals and mineral aggregates. Int. J. Plast. 2019, 112, 123–157. [Google Scholar] [CrossRef]
- Yanagida, A.; Yanagimoto, J. Formularization of softening fractions and related kinetics for static recrystallization using inverse analysis of double compression test. Mater. Sci. Eng. A 2008, 487, 510–517. [Google Scholar] [CrossRef]
- Puchi-Cabrera, E.S.; Staia, M.H.; Guérin, J.D. An experimental analysis and modeling of the work-softening transient due to dynamic recrystallization. Int. J. Plast. 2014, 54, 113–131. [Google Scholar] [CrossRef]
- Puchi-Cabrera, E.S.; Guerin, J.D.; Barbera-Sosa, J.G. Incremental constitutive description of SAE 5120 steel deformed under hot-working conditions. Int. J. Mech. Sci. 2017, 133, 619–630. [Google Scholar] [CrossRef]
- Lin, J.; Liu, Y.; Farrugia, D.C.J. Development of dislocation-based unified material model for simulating microstructure evolution in multipass hot rolling. Philos. Mag. 2005, 85, 1967–1987. [Google Scholar] [CrossRef]
- Chen, R.; Guo, P.; Zheng, Z. Dislocation Based Flow Stress Model of 300M Steel in Isothermal Compression Process. Materials 2018, 11, 972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, P.; Deng, L.; Wang, X.Y. Modelling of dynamic recrystallization kinetics of 300M steel at high strain rates during hot deformation. Sci. China Technol. Sci. 2019, 62, 1–11. [Google Scholar] [CrossRef]
- Zhao, M.; Huang, L.; Zeng, R. In-situ observations and modeling of static recrystallization in 300M steel. Mater. Sci. Eng. A 2019, 765, 138300. [Google Scholar] [CrossRef]
- Zhao, M.; Huang, L.; Zeng, R. In-situ observations and modeling of metadynamic recrystallization in 300M steel. Mater. Charact. 2020, 159, 109997. [Google Scholar] [CrossRef]
- Zeng, R.; Huang, L.; Li, J. Quantification of multiple softening processes occurring during multi-stage thermoforming of high-strength steel. Int. J. Plast. 2019, 120, 64–87. [Google Scholar] [CrossRef]
- Chen, R.; Xiao, H.; Wang, M. Hot Workability of 300M Steel Investigated by In Situ and Ex Situ Compression Tests. Metals 2019, 9, 880. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Zheng, Z.; Li, N. In-situ investigation of phase transformation behaviors of 300M steel in continuous cooling process. Mater. Charact. 2018, 144, 400–410. [Google Scholar] [CrossRef]
- Liu, J.; Edberg, J.; Tan, M.J. Finite element modelling of superplastic-like forming using a dislocation density-based model for AA5083. Model. Simul. Mater. Sci. Eng. 2013, 21, 25006–25028. [Google Scholar] [CrossRef]




| No. | Tc (°C) | (1) | |||
|---|---|---|---|---|---|
| T1 | 1050 | 0.01 | 0.43 | 30 | 0.43 |
| T2 | 1050 | 0.1 | 0.43 | 30 | 0.43 |
| T3 | 1050 | 1 | 0.43 | 30 | 0.43 |
| T4 | 1050 | 10 | 0.43 | 30 | 0.43 |
| T5 | 950 | 0.01 | 0.43 | 30 | 0.43 |
| T6 | 1150 | 0.01 | 0.43 | 30 | 0.43 |
| T7 | 1050 | 0.01 | 0.43 | 1 | 0.43 |
| T8 | 1050 | 0.01 | 0.43 | 10 | 0.43 |
| T9 | 1050 | 0.01 | 0.43 | 120 | 0.43 |
| T10 | 1050 | 0.01 | 0.43 | 600 | 0.43 |
| T11 | 1050 | 0.01 | 0.3 | 30 | 0.6 |
| T12 | 1050 | 0.01 | 0.4 | 30 | 0.5 |
| T13 | 1050 | 0.01 | 0.5 | 30 | 0.4 |
| T14 | 1050 | 0.01 | 0.6 | 30 | 0.3 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 57.3 | |||||
| 19.3 | |||||
| 7.79 | |||||
| 2.31 | |||||
| 0.172 | |||||
| n | 1.95 | ||||
| 1.21 | 0.132 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Zeng, J.; Yao, G.; Feng, F. Flow-Stress Model of 300M Steel for Multi-Pass Compression. Metals 2020, 10, 438. https://doi.org/10.3390/met10040438
Chen R, Zeng J, Yao G, Feng F. Flow-Stress Model of 300M Steel for Multi-Pass Compression. Metals. 2020; 10(4):438. https://doi.org/10.3390/met10040438
Chicago/Turabian StyleChen, Rongchuang, Jiao Zeng, Guichuan Yao, and Fei Feng. 2020. "Flow-Stress Model of 300M Steel for Multi-Pass Compression" Metals 10, no. 4: 438. https://doi.org/10.3390/met10040438
APA StyleChen, R., Zeng, J., Yao, G., & Feng, F. (2020). Flow-Stress Model of 300M Steel for Multi-Pass Compression. Metals, 10(4), 438. https://doi.org/10.3390/met10040438






