Simulation of Ultrasonic Induced Cavitation and Acoustic Streaming in Liquid and Solidifying Aluminum
Abstract
:1. Introduction
2. Numerical Modeling
2.1. General
2.2. Fluid
2.3. Physics
2.4. Geometry and Movement
2.5. Time Step Definition
3. Results
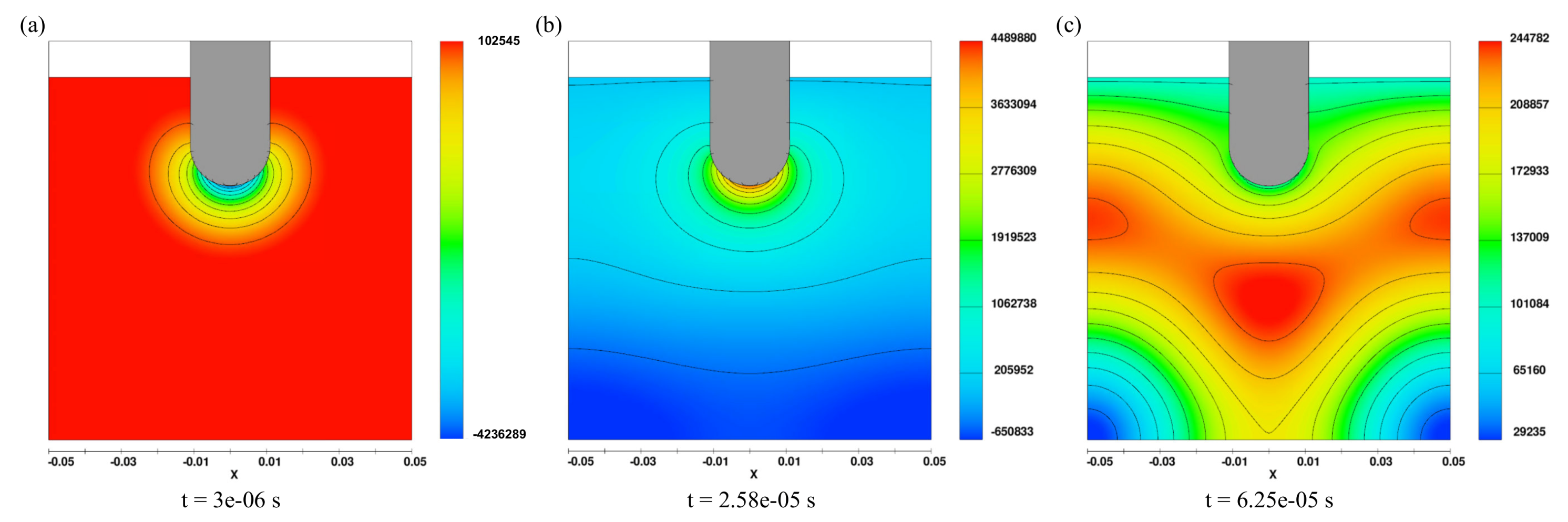
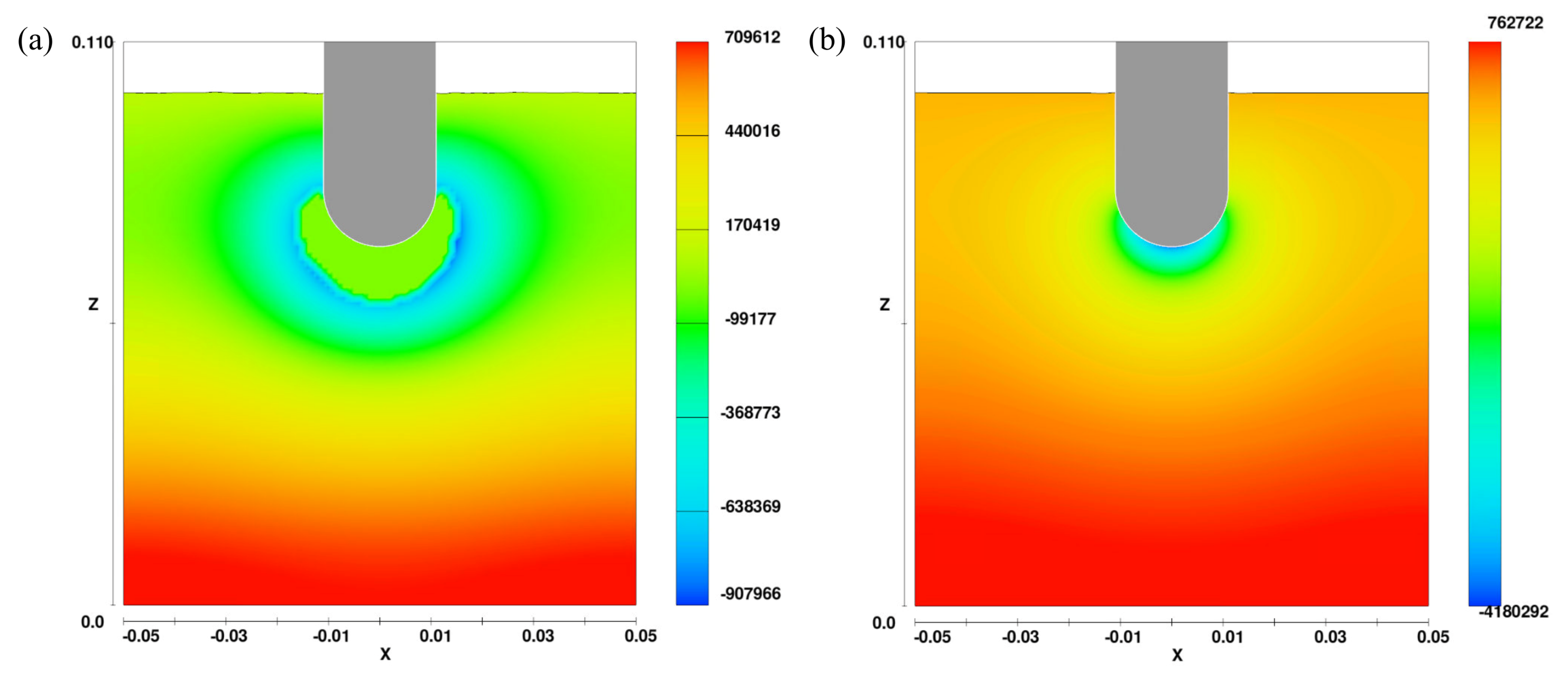
3.1. Acoustic Pressure Wave Propagation
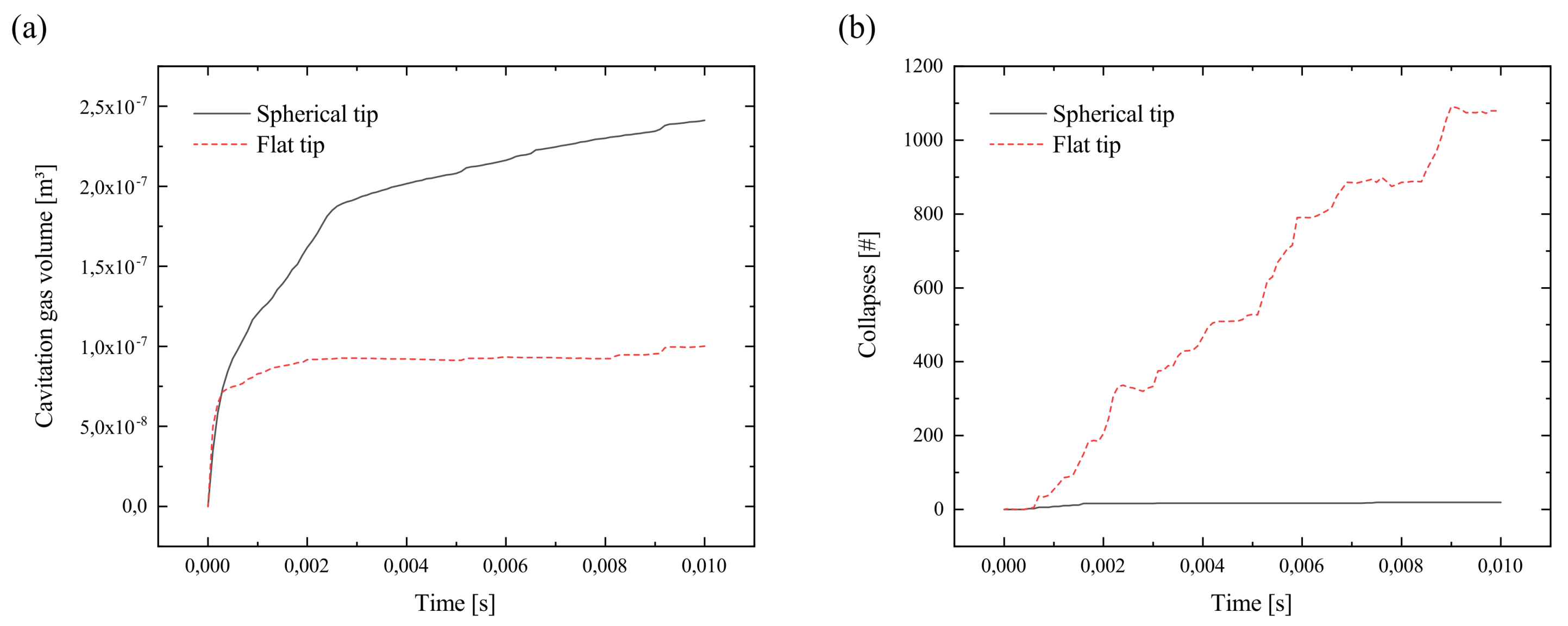
3.2. Cavitation Development
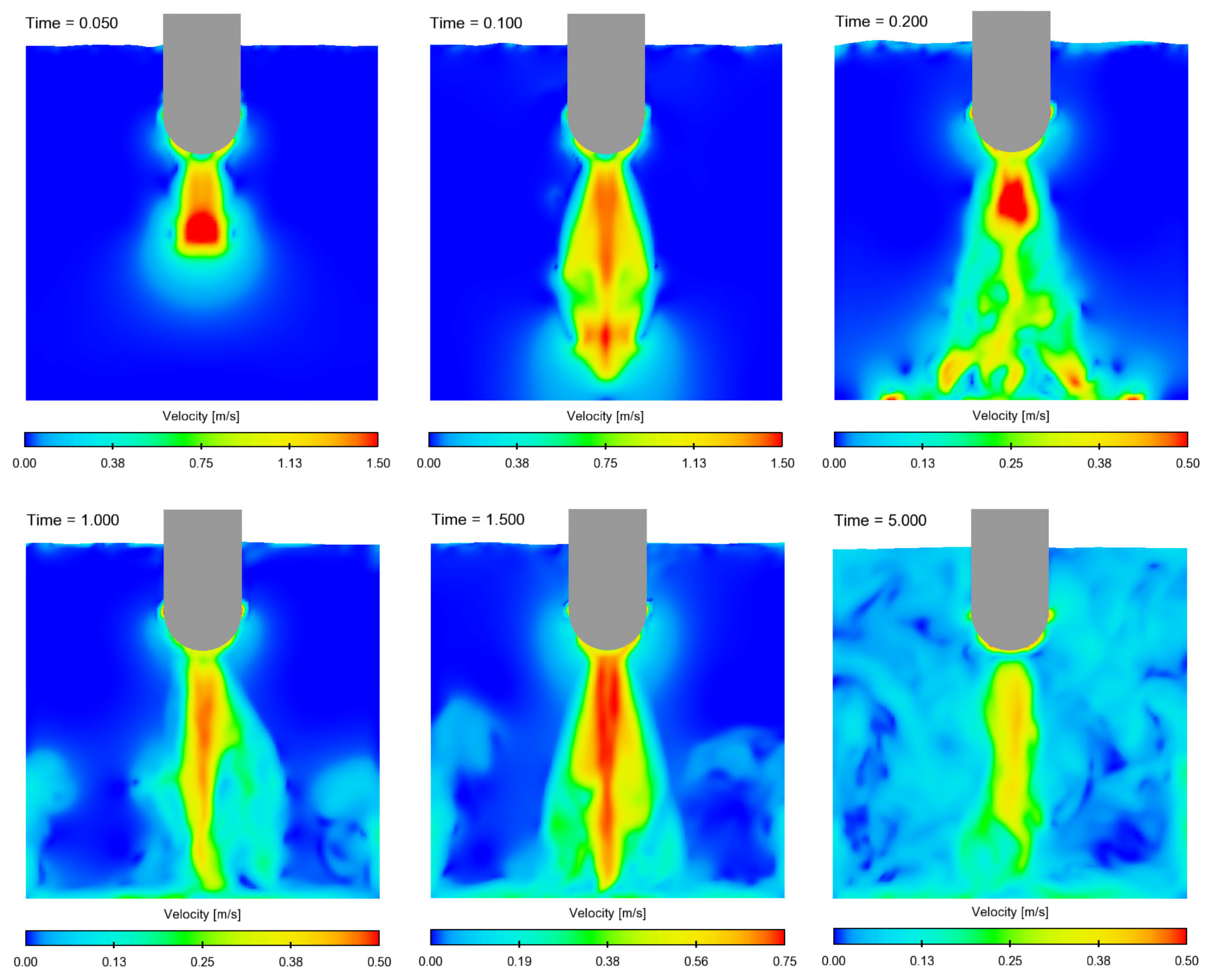
3.3. Acoustic Streaming
3.3.1. Development and Propagation
3.3.2. Cavitation and Mass Transport
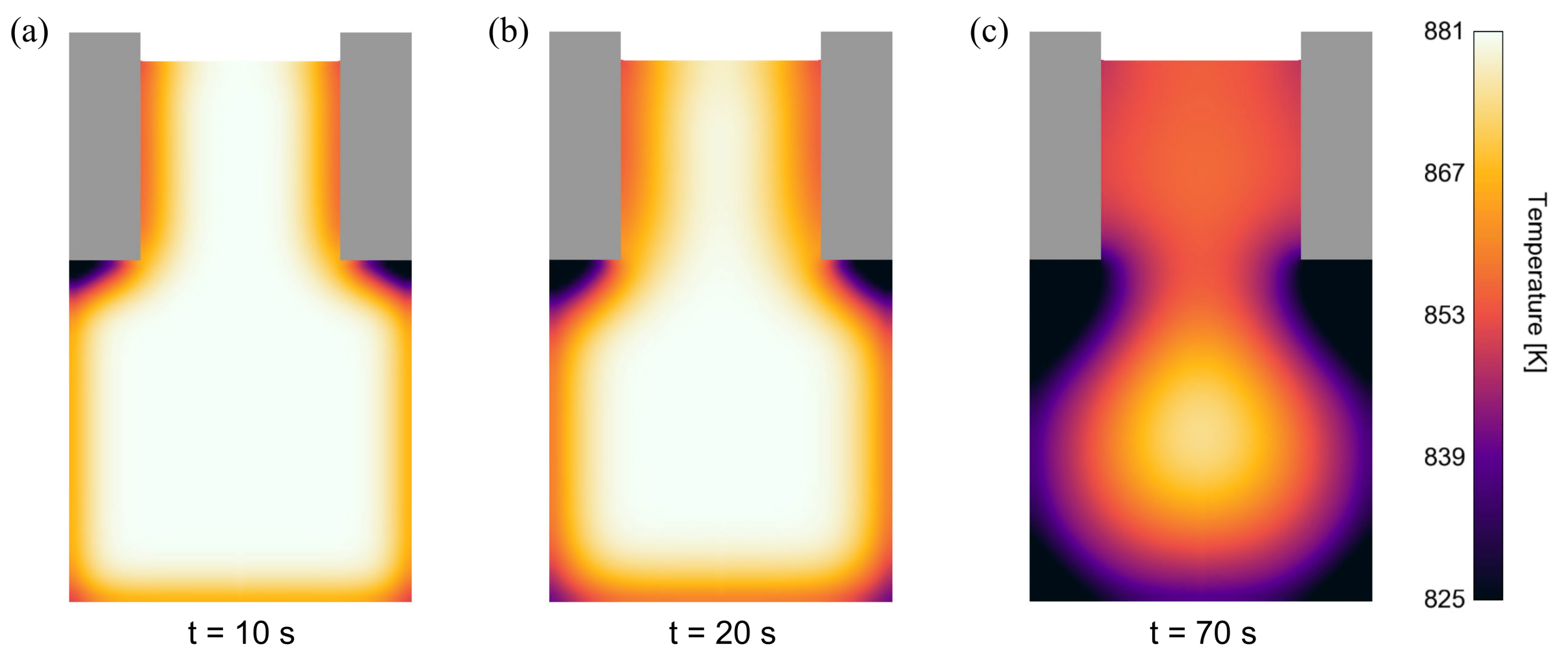
3.3.3. Solidification and Heat Transport
4. Discussion
4.1. Acoustic Pressure Wave Propagation
4.2. Cavitation Development
4.3. Acoustic Streaming
4.4. FLOW-3D
5. Summary
- The simulation tool can predict the development and distribution of pressure waves in a fluid, induced through a modeled radiator.
- Based on this, the development of the cavitation zone below and around the radiator tip can be calculated. Furthermore, information about cavitation intensity is provided. The results are consistent with the theoretical descriptions and demonstrated experimental behaviour of cavitation of previous investigations. With growing distance from the radiator surface, the pressure oscillations fall below the cavitation threshold, and most cavities are not able to survive in these regions. Furthermore, a shielding effect on acoustic field, proceeding from the cavitation zone, is measurable. However, for more accurate results, the used model may require adjustment for the application case of UST.
- Rapidly changing pressure conditions lead to calculated acoustic streaming, consistent with the qualitative descriptions and circumstances leading to acoustic streaming. Furthermore, the results are in good agreement and have the same order of magnitude as the results of other studies and experimental PIV-measurements.
- The influence of acoustic streaming on the cavitation can be calculated as well as particle transport and, for example, heat and mass transfer during solidification.
- The simulation tool is able to create a three-dimensional prediction of cavitation and acoustic streaming. The possibility of producing two- and three-dimensional results is a great advantage for analyzing, developing, and adjusting upcoming ultrasonic systems (e.g., different radiator geometries and properties).
- All parameters for the fluid and vessel geometries (as well as the ultrasonic system) are easily changeable and thus allow for preinvestigations into the influence of frequency, amplitude, etc., on the process and different fluids.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AMC | Aluminum matrix composites |
| CCC | Commercial CFD-Code |
| CFD | Computational fluid dynamics |
| GMO | General moving object |
| PIV | Particle image velocimetry |
| UST | Ultrasonic treatment |
References
- Eskin, G.; Eskin, D. Ultrasonic Treatment of Light Alloy Melts, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Meek, T.; Han, Q. Ultrasonic Processing of Materials; Technical Report; U.S. Department of Energy—Energy Efficiency and Renewable Energy: Washington, DC, USA, 2006. [Google Scholar]
- Eskin, G. Influence of cavitation treatment of melts on the processes of nucleation and growth of crystals during solidification of ingots and castings from light alloys. Ultrason. Sonochem. 1994, 1, S59–S63. [Google Scholar] [CrossRef]
- Eskin, G. Broad prospects for commercial application of the ultrasonic (cavitation) melt treatment of light alloys. Ultrason. Sonochem. 2001, 8, 319–325. [Google Scholar] [CrossRef]
- Xu, W.; Tzanakis, I.; Srirangam, P.; Mirihanage, W.; Eskin, D.; Bodey, A.; Lee, P. Synchrotron quantification of ultrasound cavitation and bubble dynamics in Al–10Cu melts. Ultrason. Sonochem. 2016, 31, 355–361. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, H.; Yu, S.; Li, Y.; Gong, L. Effect of ultrasonic treatment on microstructures of hypereutectic AlSi alloy. J. Mater. Process. Technol. 2008, 208, 330–335. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, Y.; Cheng, X.; Chen, G.; Dai, Q. High-energy ultrasonic field effects on the microstructure and mechanical behaviors of A356 alloy. J. Alloy. Compd. 2009, 470, 168–172. [Google Scholar] [CrossRef]
- Huang, H.; Xu, Y.; Da, S.; Han, Y.; Jun, W.; Sun, B. Effect of ultrasonic melt treatment on structure refinement of solidified high purity aluminum. Trans. Nonferrous Met. Soc. China 2014, 24, 2414–2419. [Google Scholar] [CrossRef]
- Wang, F.; Eskin, D.; Connolley, T.; Mi, J. Effect of ultrasonic melt treatment on the refinement of primary Al 3 Ti intermetallic in an Al–0.4 Ti alloy. J. Cryst. Growth 2016, 435, 24–30. [Google Scholar] [CrossRef] [Green Version]
- Eskin, D. Ultrasonic processing of molten and solidifying aluminium alloys: Overview and outlook. Mater. Sci. Technol. 2017, 33, 636–645. [Google Scholar] [CrossRef] [Green Version]
- Tuan, N.; Puga, H.; Barbosa, J.; Pinto, A. Grain refinement of Al-Mg-Sc alloy by ultrasonic treatment. Met. Mater. Int. 2015, 21, 72–78. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Dargusch, M.; Qian, M.; Eskin, D.; StJohn, D. The role of ultrasonic treatment in refining the as-cast grain structure during the solidification of an Al–2Cu alloy. J. Cryst. Growth 2014, 408, 119–124. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Kateryna, S.; Li, T. Effect of ultrasonic treatment on formation of iron-containing intermetallic compounds in Al-Si alloys. China Foundry 2016, 13, 316–321. [Google Scholar] [CrossRef]
- Youn, J.; Kim, Y. Nucleation enhancement of Al alloys by high intensity ultrasound. Jpn. J. Appl. Phys. 2009, 48, 07GM14. [Google Scholar] [CrossRef]
- Huang, H.; Shu, D.; Zeng, J.; Bian, F.; Fu, Y.; Wang, J.; Sun, B. In situ small angle X-ray scattering investigation of ultrasound induced nucleation in a metallic alloy melt. Scr. Mater. 2015, 106, 21–25. [Google Scholar] [CrossRef]
- Atamanenko, T.; Eskin, D.; Zhang, L.; Katgerman, L. Criteria of grain refinement induced by ultrasonic melt treatment of aluminum alloys containing Zr and Ti. Metall. Mater. Trans. A 2010, 41, 2056–2066. [Google Scholar] [CrossRef] [Green Version]
- Shu, D.; Sun, B.; Mi, J.; Grant, P. A high-speed imaging and modeling study of dendrite fragmentation caused by ultrasonic cavitation. Metall. Mater. Trans. A 2012, 43, 3755–3766. [Google Scholar] [CrossRef]
- Supponen, O.; Kobel, P.; Obreschkow, D.; Farhat, M. The inner world of a collapsing bubble. Phys. Fluids 2015, 27, 091113. [Google Scholar] [CrossRef]
- Chow, R.; Blindt, R.; Chivers, R.; Povey, M. The sonocrystallisation of ice in sucrose solutions: Primary and secondary nucleation. Ultrasonics 2003, 41, 595–604. [Google Scholar] [CrossRef]
- Wang, S.; Kang, J.; Zhang, X.; Guo, Z. Dendrites fragmentation induced by oscillating cavitation bubbles in ultrasound field. Ultrasonics 2017, 83, 26–32. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, D.; Xuan, Y.; Nastac, L. An experimental and modeling investigation of aluminum-based alloys and nanocomposites processed by ultrasonic cavitation processing. Appl. Acoust. 2016, 103, 226–231. [Google Scholar] [CrossRef]
- Eskin, G. Cavitation mechanism of ultrasonic melt degassing. Ultrason. Sonochem. 1995, 2, S137–S141. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Jian, X.; Meek, T.; Han, Q. Degassing of molten aluminum A356 alloy using ultrasonic vibration. Mater. Lett. 2004, 58, 3669–3673. [Google Scholar] [CrossRef]
- Xu, H.; Meek, T.; Han, Q. Effects of ultrasonic field and vacuum on degassing of molten aluminum alloy. Mater. Lett. 2007, 61, 1246–1250. [Google Scholar] [CrossRef]
- Puga, H.; Teixeira, J.; Barbosa, J.; Seabra, E.; Ribeiro, S.; Prokic, M. The combined effect of melt stirring and ultrasonic agitation on the degassing efficiency of AlSi9Cu3 alloy. Mater. Lett. 2009, 63, 2089–2092. [Google Scholar] [CrossRef]
- Eskin, D.; Alba-Baena, N.; Pabel, T.; da Silva, M. Ultrasonic degassing of aluminium alloys: Basic studies and practical implementation. Mater. Sci. Technol. 2014, 31, 79–84. [Google Scholar] [CrossRef]
- Haghayeghi, R.; Kapranos, P. The effect of processing parameters on ultrasonic degassing efficiency. Mater. Lett. 2014, 116, 399–401. [Google Scholar] [CrossRef]
- Xu, H.; Han, Q.; Meek, T. Effects of ultrasonic vibration on degassing of aluminum alloys. Mater. Sci. Eng. A 2008, 473, 96–104. [Google Scholar] [CrossRef]
- Abramov, O. Action of high intensity ultrasound on solidifying metal. Ultrasonics 1987, 25, 73–82. [Google Scholar] [CrossRef]
- Nowak, T.; Thiemann, A.; Holsteyns, F.; Lippert, A.; Mettin, R. Messung der akustisch induzierten Strömungen mit und ohne Kavitation. In Proceedings of the DAGA 2011, Düsseldorf, Germany, 21–24 March 2011; pp. 923–924. [Google Scholar]
- Eskin, G. Principles of ultrasonic treatment: Application for light alloy melts. Adv. Perform. Mater. 1997, 4, 223–232. [Google Scholar] [CrossRef]
- Puga, H.; Costa, S.; Barbosa, J.; Ribeiro, S.; Prokic, M. Influence of ultrasonic melt treatment on microstructure and mechanical properties of AlSi9Cu3 alloy. J. Mater. Process. Technol. 2011, 211, 1729–1735. [Google Scholar] [CrossRef] [Green Version]
- Jung, J.; Lee, S.; Lee, J.; Cho, Y.; Kim, S.; Yoon, W. Improved mechanical properties of near-eutectic Al-Si piston alloy through ultrasonic melt treatment. Mater. Sci. Eng. A 2016, 669, 187–195. [Google Scholar] [CrossRef]
- Eskin, D. Ultrasonic melt processing: Achievements and challenges. Mater. Sci. Forum 2015, 828–829, 112–118. [Google Scholar] [CrossRef] [Green Version]
- Trujillo, F.; Knoerzer, K. CFD modelling of the acoustic streaming induced by an ultrasonic horn reactor. In Proceedings of the Seventh International Conference on CFD in the Minerals and Process Industries, Melbourne, Australia, 9–11 December 2009. [Google Scholar]
- Louisnard, O. A viable method to predict acoustic streaming in presence of cavitation. Ultrason. Sonochem. 2017, 35, 518–524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Kang, J.; Wang, S.; Ma, J.; Huang, T. The effect of ultrasonic processing on solidification microstructure and heat transfer in stainless steel melt. Ultrason. Sonochem. 2015, 27, 307–315. [Google Scholar] [CrossRef] [PubMed]
- Schenker, M.; Eskin, M.P.D.; Boersma, B. PIV quantification of the flow induced by an ultrasonic horn and numerical modeling of the flow and related processing times. Ultrason. Sonochem. 2012, 20, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Ishiwata, Y.; Komarov, S.; Takeda, Y. Investigation of acoustic streaming in aluminum melts axposed to high-intensity ultrasonic irradiation. In ICAA13 Pittsburgh; Springer International Publishing: Cham, Switzerland, 2012; pp. 183–188. [Google Scholar]
- Tzanakis, I.; Lebon, G.; Eskin, D.; Hyde, M.; Grant, P. Investigation of acoustic streaming and cavitation intensity in water as an analogue for liquid metal. In Proceedings of the 10th International Synmposium on Cavitation, Baltimore, MD, USA, 14–16 May 2018. [Google Scholar]
- Lebon, B.; Tzanakis, I.; Pericleous, K.; Eskin, D. Numerical modelling of the ultrasonic treatment of aluminium melts: An overview of recent advances. Materials 2019, 12, 3262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rubinette, D.; Weiss, D.; Müller, J.; Wahlen, A. Numerical modeling and validation concept for acoustic streaming induced by ultrasonic treatment. In Proceedings of the Comsol Conference 2016, Munich, Germany, 12–14 October 2016. [Google Scholar]
- Sajjadi, B.; Raman, A.; Ibrahim, S. Influence of ultrasound power on acoustic streaming and micro-bubbles formations in a low frequency sono-reactor: Mathematical and 3D computational simulation. Ultrason. Sonochem. 2015, 24, 193–203. [Google Scholar] [CrossRef]
- Lebon, G.; Tzanakis, I.; Djambazov, G.; Pericleous, K.; Eskin, D. Numerical modelling of ultrasonic waves in a bubbly Newtonian liquid using a high-order acoustic cavitation model. Ultrason. Sonochem. 2017, 37, 660–668. [Google Scholar] [CrossRef]
- Žnidarčič, A.; Mettin, R.; Dular, M. Modeling cavitation in a rapidly changing pressure field—Application to a small ultrasonic horn. Ultrason. Sonochem. 2015, 22, 482–492. [Google Scholar] [CrossRef]
- Mottyll, S.; Skoda, R. Numerical 3D flow simulation of ultrasonic horns with attached cavitation structures and assessment of flow aggressiveness and cavitation erosion sensitive wall zones. Ultrason. Sonochem. 2016, 31, 570–589. [Google Scholar] [CrossRef]
- Wang, G.; Croaker, P.; Dargusch, M.; McGuckin, D.; StJohn, D. Simulation of convective flow and thermal conditions during ultrasonic treatment of an Al-2Cu alloy. Comput. Mater. Sci. 2017, 134, 116–125. [Google Scholar] [CrossRef]
- Riedel, E.; Horn, I.; Stein, N.; Stein, H.; Bähr, R.; Scharf, S. Ultrasonic treatment: A clean technology that supports sustainability in casting processes. Procedia CIRP 2019, 80, 101–107. [Google Scholar] [CrossRef]
- Dahlem, O.; Reisse, J.; Halloin, V. The radially vibrating horn: A scaling-up possibility for sonochemical reactions. Chem. Eng. Sci. 1999, 54, 2829–2838. [Google Scholar] [CrossRef]
- Kumar, A.; Kumaresan, T.; Pandit, A.; Joshi, J. Characterization of flow phenomena induced by ultrasonic horn. Chem. Eng. Sci. 2006, 61, 7410–7420. [Google Scholar] [CrossRef]
- Klima, J.; Friasferrer, A.; Gonzalezgarcia, J.; Ludvik, J.; Saez, V.; Iniesta, J. Optimisation of 20 kHz sonoreactor geometry on the basis of numerical simulation of local ultrasonic intensity and qualitative comparison with experimental results. Ultrason. Sonochem. 2007, 14, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Nastac, L. Mathematical modeling of the solidification structure evolution in the presence of ultrasonic stirring. Metall. Mater. Trans. B 2011, 42, 1297–1305. [Google Scholar] [CrossRef]
- Jamshidi, R.; Pohl, B.; Peuker, U.; Brenner, G. Numerical investigation of sonochemical reactors considering the effect of inhomogeneous bubble clouds on ultrasonic wave propagation. Chem. Eng. J. 2012, 189–190, 364–375. [Google Scholar] [CrossRef]
- Xu, Z.; Yasuda, K.; Koda, S. Numerical simulation of liquid velocity distribution in a sonochemical reactor. Ultrason. Sonochem. 2013, 20, 452–459. [Google Scholar] [CrossRef]
- Jamshidi, R. Modeling and Numerical Investigation of Acoustic Cavitation with Applications in Sonochemistry. Ph.D. Thesis, Clausthal University of Technology, Clausthal-Zellerfeld, Germany, 2013. [Google Scholar]
- Jamshidi, R.; Brenner, G. An Euler-Lagrange method considering bubble radial dynamics for modeling sonochemical reactors. Ultrason. Sonochem. 2014, 21, 154–161. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Nastac, L. Numerical modeling of the dispersion of ceramic nanoparticles during ultrasonic processing of aluminum-based nanocomposites. J. Mater. Res. Technol. 2014, 3, 296–302. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.; Zhang, X.; Wang, S.; Ma, J.; Huang, T. The comparison of ultrasonic effects in different metal melts. Ultrasonics 2015, 57, 11–17. [Google Scholar] [CrossRef]
- Lebon, G.; Pericleous, K.; Tzanakis, I.; Eskin, D. Application of the “Full Cavitation Model” to the fundamental study of cavitation in liquid metal processing. IOP Conf. Ser. Mater. Sci. Eng. 2015, 72, 052050. [Google Scholar] [CrossRef]
- Jamshidi, R.; Rossi, D.; Saffari, N.; Gavriilidis, A.; Mazzei, L. Investigation of the effect of ultrasound parameters on continuous sonocrystallization in a millifluidic device. Cryst. Growth Des. 2016, 16, 4607–4619. [Google Scholar] [CrossRef]
- Lebon, G.; Pericleous, K.; Tzanakis, I.; Eskin, D. A model of cavitation for the treatment of a moving liquid metal volume. In Advances in the Science and Engineering of Casting Solidification; Springer Nature: Cham, Switzerland, 2016. [Google Scholar]
- Wang, S.; Kang, J.; Guo, Z.; Lee, T.; Zhang, X.; Wang, Q.; Deng, C.; Mi, J. In situ high speed imaging study and modelling of the fatigue fragmentation of dendritic structures in ultrasonic fields. Acta Mater. 2019, 165, 388–397. [Google Scholar] [CrossRef]
- Rahimi, M.; Movahedirad, S.; Shahhosseini, S. CFD study of the flow pattern in an ultrasonic horn reactor: Introducing a realistic vibrating boundary condition. Ultrason. Sonochem. 2017, 35, 359–374. [Google Scholar] [CrossRef]
- Sajjadi, B.; Asgharzadehahmadi, S.; Asaithambi, P.; Raman, A.; Parthasarathy, R. Investigation of mass transfer intensification under power ultrasound irradiation using 3D computational simulation: A comparative analysis. Ultrason. Sonochem. 2017, 34, 504–518. [Google Scholar] [CrossRef]
- Lebon, G.; Tzanakis, I.; Pericleous, K.; Eskin, D. Experimental and numerical investigation of acoustic pressures in different liquids. Ultrason. Sonochem. 2018, 42, 411–421. [Google Scholar] [CrossRef]
- Fang, Y.; Yamamoto, T.; Komarov, S. Cavitation and acoustic streaming generated by different sonotrode tips. Ultrason. Sonochem. 2018, 48, 79–87. [Google Scholar] [CrossRef]
- Lebon, G.; Tzanakis, I.; Pericleous, K.; Eskin, D.; Grant, P. Ultrasonic liquid metal processing: The essential role of cavitation bubbles in controlling acoustic streaming. Ultrason. Sonochem. 2019, 55, 243–255. [Google Scholar] [CrossRef]
- Lebon, G.; Salloum-Abou-Jaoude, G.; Eskin, D.; Tzanakis, I.; Pericleous, K.; Jarry, P. Numerical modelling of acoustic streaming during the ultrasonic melt treatment of direct-chill (DC) casting. Ultrason. Sonochem. 2019, 54, 171–182. [Google Scholar] [CrossRef]
- Komarov, S.; Yamamoto, T. Role of acoustic streaming in formation of unsteady flow in billet sump during ultrasonic DC casting of aluminum alloys. Materials 2019, 12, 3532. [Google Scholar] [CrossRef] [Green Version]
- FLOW-3D v11.2 Users Manual; Flow Science, Inc.: Santa Fe, NM, USA, 2017.
- Brethour, J. Improved Generalized Minimal Residual (GMRES) Solver in FLOW-3D—How It Works and When to Use It; Flow Science, Inc.: Santa Fe, NM, USA, 2009. [Google Scholar]
- Von Böckh, P.; Stripf, M. Technische Thermodynamik; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Tzanakis, I.; Lebon, G.; Eskin, D.; Pericleous, K. Investigation of the factors influencing cavitation intensity during the ultrasonic treatment of molten aluminium. Mater. Des. 2016, 90, 979–983. [Google Scholar] [CrossRef]
- Tzanakis, I.; Lebon, G.; Eskin, D.; Pericleous, K. Characterisation of the ultrasonic acoustic spectrum and pressure field in aluminium melt with an advanced cavitometer. J. Mater. Process. Technol. 2016, 229, 582–586. [Google Scholar] [CrossRef] [Green Version]












| Author(s) | Year | Fluid/Alloy | Software | AP/WP | C | AS | S | Reference |
|---|---|---|---|---|---|---|---|---|
| Dahlem et al. | 1999 | Water | Sysnoise /Fluent CFD | X | X | [49] | ||
| Kumar et al. | 2006 | Water | Other CFD-Code | X | [50] | |||
| Klima et al. | 2007 | Water | FEM LAB 3.1 | X | [51] | |||
| Trujillo & Knoerzer | 2009 | Unclear | COMSOL Multiphysics | X | [35] | |||
| Nastac | 2011 | Aluminum (A356) | Other CFD-Code | X | X | X | [52] | |
| Shu et al. | 2012 | Succinonitril | COMSOL Multiphysics | X | [17] | |||
| Jamshidi et al. | 2012 | Water | COMSOL Multiphysics | X | X | [53] | ||
| Ishiwata et al. | 2012 | Aluminum | Other CFD-Code | X | [39] | |||
| Schenker et al. | 2012 | Water | Fluent | X | [38] | |||
| Xu et al. | 2013 | Water | COMSOL Multiphysics | X | X | [54] | ||
| Jamshidi | 2013 | Water | COMSOL Multiphysics | X | [55] | |||
| Huang et al. | 2014 | Pure aluminum | COMSOL Multiphysics | X | [8] | |||
| Jamshidi et al. | 2014 | Water | FVM-Code | X | X | [56] | ||
| Zhang & Nastac | 2014 | Aluminum (6061) | ANSYS Fluent | X | [57] | |||
| Kang et al. | 2015 | Water/aluminum/steel | ANSYS Fluent | X | X | [58] | ||
| Sajjadi et al. | 2015 | Water | ANSYS Fluent | X | X | [43] | ||
| Zhang et al. | 2015 | Stainless steel | ANSYS Fluent | X | X | [37] | ||
| Sajjadi et al. | 2015 | Water | Other CFD-Code | X | X | X | [43] | |
| Lebon et al. | 2015 | Water/aluminum | Other CFD-Code | X | X | [59] | ||
| Žnidarčič | 2015 | Water | ANSYS Fluent | X | [45] | |||
| Jamshidi et al. | 2016 | Adipic acid | Other code | X | X | X | [60] | |
| Lebon et al. | 2016 | Water/aluminum | Other CFD-Code | X | X | [61] | ||
| Wang et al. | 2016 | Succinonitril | Other code | X | [62] | |||
| Mottyll & Skoda | 2016 | Water | ANSYS ICEM CFD | X | [46] | |||
| Jia et al. | 2016 | Aluminum (A356) | ANSYS Fluent | X | [21] | |||
| Rubinette et al. | 2016 | Aluminum/water | COMSOL Multiphysics | X | [42] | |||
| Rahimi et al. | 2017 | Water | Other CFD-Code | X | X | X | [63] | |
| Lebon et al. | 2017 | Aluminum | Other code | X | [44] | |||
| Wang et al. | 2017 | Aluminum (AlCu2) | ProCAST (FEM) | X | X | [47] | ||
| Louisnard | 2017 | Water | COMSOL | X | [36] | |||
| Sajjadi et al. | 2017 | Water/glycerol | ANSYS Fluent | X | x | [64] | ||
| Lebon et al. | 2018 | Water/aluminum a.o. | Other code | X | [65] | |||
| Fang et al. | 2018 | Water | OpenFOAM | X | X | [66] | ||
| Tzanakis et al. | 2018 | Water | OpenFOAM | X | [40] | |||
| Lebon et al. | 2019 | Water/aluminum | OpenFOAM | X | X | [67] | ||
| Lebon et al. | 2019 | Aluminum | OpenFOAM | X | X | X | [68] | |
| Lebon et al. | 2019 | Aluminum | OpenFOAM | X | X | X | [41] | |
| Riedel et al. | 2019 | Aluminum (A356) | FLOW-3D | X | X | [48] | ||
| Komarov & Yamamoto | 2019 | Water/aluminum (AlSi17) | Other code | X | X | [69] |
| Parameter | A356 | Unit |
|---|---|---|
| Density | 2437 | kg/ |
| Viscosity | 0.0019 | kg/m/s |
| Specific heat | 1074 | J/kg/K |
| Thermal conductivity | 86.9 | W/m/K |
| Liquidus temperature | 881.15 | K |
| Solidus temperature | 825.55 | K |
| Speed of sound | 4600 | m/s |
| Compressibility | 1.94 | 1/Pa |
| Surface tension | 0.871 | kg/ |
| Model | Parameter | A356 | Unit |
|---|---|---|---|
| Bubble and phase change | Gamma | 1.4 | Without unit |
| with adiabatic bubble and | Pressure | 101,325 | Pa |
| dynamic nucleation | |||
| Cavitation with empirical | Cavitation pressure | 0 | Pa |
| model for cavitation control | (Cavitation threshold) | ||
| active model for voids and | Surface tension coeff. | 0.871 | kg/ |
| activated cavitation | Density of cav. bubbles | 0.025 | kg/ |
| potential model | Cav. production coeff. | 0.02 | Without unit |
| Cav. dissipation coeff. | 0.01 | Without unit | |
| Surface tension model with | Surface tension coeff. | 0.871 | kg/ |
| explicit numerical | Temperature dependence | 0 | kg//K |
| approximation for surface | Contact angle | 90 | Degrees(s) |
| tension pressure |
| Parameter | Value | Unit |
|---|---|---|
| Gas pressure p | 101,325 | Pa |
| Universal gas constant | 8314.41 | J/(kmol K) |
| Temperature T | 973.15 | K |
| Molar mass M () | 2.016 | kg/kmol |
| Simulation | Maximum Time Step [s] |
|---|---|
| Pressure | |
| Cavitation | |
| Acoustic Streaming | |
| UST + solidification |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riedel, E.; Liepe, M.; Scharf, S. Simulation of Ultrasonic Induced Cavitation and Acoustic Streaming in Liquid and Solidifying Aluminum. Metals 2020, 10, 476. https://doi.org/10.3390/met10040476
Riedel E, Liepe M, Scharf S. Simulation of Ultrasonic Induced Cavitation and Acoustic Streaming in Liquid and Solidifying Aluminum. Metals. 2020; 10(4):476. https://doi.org/10.3390/met10040476
Chicago/Turabian StyleRiedel, Eric, Martin Liepe, and Stefan Scharf. 2020. "Simulation of Ultrasonic Induced Cavitation and Acoustic Streaming in Liquid and Solidifying Aluminum" Metals 10, no. 4: 476. https://doi.org/10.3390/met10040476
APA StyleRiedel, E., Liepe, M., & Scharf, S. (2020). Simulation of Ultrasonic Induced Cavitation and Acoustic Streaming in Liquid and Solidifying Aluminum. Metals, 10(4), 476. https://doi.org/10.3390/met10040476




