A Comparison of Strengthening Mechanisms of Austenitic Fe-13Mn-1.3C Steel in Warm and Cold High-Pressure Torsion
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. A Comparison of the Microstructures Produced by HPT-Processing at Room Temperature and 400 °C
3.2. The Effect of Post-Deformation Anneal at Temperature 400 °C on Microstructure of the HPT-Processed Specimens
3.3. X-Rays Observations
3.4. Microhardness Test
4. Discussion
5. Conclusions
- Twin boundaries induced by cold HPT possess high thermal stability. HPT deformation at room temperature is associated with the formation of a dense net of twinning-assisted boundaries and high dislocation density and is not accompanied with any phase transformations. These twin boundaries stay untransformed after post-deformation annealing at temperature 400 °C.
- In high pressure-torsion, twinning for the first time has been experimentally confirmed as a high-temperature deformation mechanism. The increase in deformation temperature from 23 °C up to 400 °C decreases the activity of mechanical twinning, but twin lamellae are experimentally observed even at a deformation temperature of 400 °C.
- In high-pressure torsion at 400 °C, the synergetic effect of high temperature and severe plastic deformation on microstructure and phase composition of Hadfield steel has been confirmed for the first time. High-temperature severe plastic deformation drives austenite decomposition and provides a formation of multiphase (austenite, ferrite, carbides) microstructure, whilst separate effects of high temperature anneal (400 °C), high pressure torsion or their gradual application (cold HPT + annealing at 400 °C) is not accompanied with any phase transformations.
- A complex effect of the HPT-driven nucleation of the nanoscale precipitates (carbides and ferrite), along with deformation-induced defects (dislocations, twin boundaries, low-angle boundaries, shear bands) in high-temperature deformation provides high microhardness values, which are similar to twin-assisted hardening in cold HPT.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Watanabe, T. Grain boundary engineering: Historical perspective and future prospects. J. Mater. Sci. 2011, 46, 4095–4115. [Google Scholar] [CrossRef]
- Liu, T.; Xia, S.; Du, D.; Bai, Q.; Zhang, L.; Lu, Y. Grain boundary engineering of large-size 316 stainless steel via warm-rolling for improving resistance to intergranular attack. Mater. Lett. 2019, 234, 201–204. [Google Scholar] [CrossRef]
- Glezer, A.M.; Shurygina, N.A.; Blinova, E.N.; Permyakova, I.E.; Firstov, S.A. Approach to the theoretical strength of Ti-Ni-Cu alloy nanocrystals by grain boundary design. J. Mater. Sci. Technol. 2015, 31, 91–96. [Google Scholar] [CrossRef]
- Song, S.-H.; Zhao, Y.; Cui, Y.; Sun, J.; Si, H.; Li, J.-Q. Effect of grain boundary character distribution and grain boundary phosphorus segregation on the brittleness of an interstitial-free steel. Mater. Lett. 2016, 182, 328–331. [Google Scholar] [CrossRef]
- Randle, V. Grain boundary engineering: An overview after 25 years. Mater. Sci. Technol. 2010, 26, 253–261. [Google Scholar] [CrossRef]
- Emeis, F.; Peterlechner, M.; Divinski, S.V.; Wilde, G. Grain boundary engineering parameters for ultrafine grained microstructures: Proof of principles by a systematic composition variation in the Cu-Ni system. Acta Mater. 2018, 150, 262–272. [Google Scholar] [CrossRef]
- Sauvage, X.; Wilde, G.; Divinski, S.V.; Horita, Z.; Valiev, R.Z. Grain boundaries in ultrafine grained materials processed by severe plastic deformation and related phenomena. Mater. Sci. Eng. A 2012, 540, 1–12. [Google Scholar] [CrossRef]
- Langdon, T.G. Twenty-five years of ultrafine-grained materials: Achieving exceptional properties through grain refinement. Acta Mater. 2013, 61, 7035–7059. [Google Scholar] [CrossRef]
- Zhilyaev, A.P.; Langdon, T.G. Using high-pressure torsion for metal processing: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 893–979. [Google Scholar] [CrossRef]
- Ivanisenko, Y.; Valiev, R.Z.; Fecht, H.-J. Grain boundary statistics in nano-structured iron produced by high pressure torsion. Mater. Sci. Eng. A 2005, 390, 159–165. [Google Scholar] [CrossRef]
- Astafurova, E.G.; Dobatkin, S.V.; Naydenkin, E.V.; Shagalina, S.V.; Zakharova, G.G.; Ivanov, Y.F. Structural and phase transformations in nanostructured 0.1% C-Mn-V-Ti steel during cold deformation by high pressure torsion and subsequent heating. Nanotechnol. Russ. 2009, 4, 109–120. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Estrin, Y.; Horita, Z.; Langdon, T.G.; Zehetbauer, M.J. Producing bulk ultrafine-grained materials by severe plastic deformation. J. Mater. 2006, 58, 33–39. [Google Scholar] [CrossRef]
- Zhang, X.; Misra, A. Superior thermal stability of coherent twin boundaries in nanotwinned metals. Scr. Mater. 2012, 66, 860–865. [Google Scholar] [CrossRef]
- Wang, S.J.; Jozaghi, T.; Karaman, I.; Arroyave, R.; Chumlyakov, Y.I. Hierarchical evolution and thermal stability of microstructure with deformation twins in 316 stainless steel. Mater. Sci. Eng. A 2017, 694, 121–131. [Google Scholar] [CrossRef]
- De Cooman, B.C.; Estrin, Y.; Kim, S.K. Twinning-induced plasticity (TWIP) steels. Acta Mater. 2018, 142, 283–362. [Google Scholar] [CrossRef]
- Randle, V. Twinning-related grain boundary engineering. Acta Mater. 2004, 52, 4067–4081. [Google Scholar] [CrossRef]
- Wang, H.T.; Tao, N.R.; Lu, K. Strengthening an austenitic Fe–Mn steel using nanotwinned austenitic grains. Acta Mater. 2012, 60, 4027–4040. [Google Scholar] [CrossRef]
- Vercammen, S.; Blanpain, B.; De Cooman, B.C.; Wollants, P. Cold rolling behaviour of an austenitic Fe–30Mn–3Al–3Si TWIP-steel: The importance of deformation twinning. Acta Mater. 2004, 52, 2005–2012. [Google Scholar] [CrossRef]
- Christian, J.W.; Mahajan, S. Deformation twinning. Prog. Mater. Sci. 1995, 39, 1–157. [Google Scholar] [CrossRef]
- Niewczas, M. Dislocations and twinning in face centered cubic crystals. In Dislocations in Solids; Nabarro, F., Hirth, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 263–364. [Google Scholar]
- Astafurova, E.G.; Kireeva, I.V.; Chumlyakov, Y.I.; Maier, H.J.; Sehitoglu, H. The influence of orientation and aluminium content on the deformation mechanisms of Hadfield steel single crystals. Int. J. Mat. Res. 2007, 98, 144–149. [Google Scholar] [CrossRef]
- Chumlyakov, Y.I.; Kireeva, I.V.; Sehitoglu, H.; Litvinova, E.I.; Zaharova, E.G.; Luzginova, N.V. High-strength single crystals of austenitic stainless steel with nitrogen content: Mechanisms of deformation and fracture. Mater. Sci. Forum 1999, 318, 395–400. [Google Scholar] [CrossRef]
- Bouaziz, O.; Scott, C.P.; Petitgand, G. Nanostructured steel with high work-hardening by the exploitation of the thermal stability of mechanically induced twins. Scr. Mater. 2009, 60, 714–716. [Google Scholar] [CrossRef]
- Kim, J.G.; Enikeev, N.A.; Abramova, M.M.; Park, B.H.; Valiev, R.Z.; Kim, H.S. Effect of initial grain size on the microstructure and mechanical properties of high-pressure torsion processed twinning-induced plasticity steels. Mater. Sci. Eng. A 2017, 682, 164–167. [Google Scholar] [CrossRef]
- Kim, J.G.; Enikeev, N.A.; Seol, J.B.; Abramova, M.M.; Karavaeva, M.V.; Valiev, R.Z.; Park, C.G.; Kim, H.S. Superior strength and multiple strengthening mechanisms in nanocrystalline TWIP steel. Sci. Rep. 2018, 8, 11200. [Google Scholar] [CrossRef] [PubMed]
- Matoso, M.; Figueiredo, R.B.; Kawasaki, M.; Santos, D.B.; Langdon, T.G. Processing a twinning-induced plasticity steel by high-pressure torsion. Scr. Mater. 2012, 67, 649–652. [Google Scholar] [CrossRef]
- Astafurova, E.G.; Tukeeva, M.S.; Zakharova, G.G.; Melnikov, E.V.; Maier, H.J. The role of twinning on microstructure and mechanical response of severely deformed single crystals of high-manganese austenitic steel. Mater. Charact. 2011, 62, 588–592. [Google Scholar] [CrossRef]
- Astafurova, E.G.; Tukeeva, M.S.; Maier, G.G.; Melnikov, E.V.; Maier, H.J. Microstructure and mechanical response of single-crystalline high-manganese austenitic steels under high-pressure torsion: The effect of stacking-fault energy. Mater. Sci. Eng. A 2014, 604, 166–175. [Google Scholar] [CrossRef]
- Teplov, V.A.; Korshunov, L.G.; Shabashov, V.A.; Kuznetsov, R.I.; Pilyugin, V.P.; Tupitsa, D.I. Structure transformations in high-manganese austenite steels upon deformation by shear under pressure. Phys. Met. Metall. 1988, 66, 563–571. (In Russian) [Google Scholar]
- Abramova, M.M.; Enikeev, N.A.; Kim, J.G.; Valiev, R.Z.; Karavaeva, M.V.; Kim, H.S. Structural and phase transformation in a TWIP steel subjected to high pressure torsion. Mater. Lett. 2016, 166, 321–324. [Google Scholar] [CrossRef]
- Park, B.H.; Um, H.Y.; Kim, J.G.; Jeong, H.Y.; Lee, S.; Kim, H.S. Large deformation of twin-induced plasticity steels under high-pressure torsion. Met. Mater. Int. 2016, 22, 1003–1008. [Google Scholar] [CrossRef]
- Timokhina, I.B.; Medvedev, A.; Lapovok, R. Severe plastic deformation of a TWIP steel. Mat. Sci. Eng. A 2014, 593, 163–169. [Google Scholar] [CrossRef]
- Derby, J.J.; Yeckel, A. Heat transfer analysis and design for bulk crystal growth: Perspectives of the Bridgman method. In Bulk Crystal Growth: Growth Mechanisms and Dynamics; Rudolph, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 793–843. [Google Scholar]
- Zuidema, B.K.; Subramanyam, D.K.; Leslie, W.C. Effect of aluminium on the work hardening and wear resistance of Hadfield manganese steel. Metall. Trans. A 1987, 18, 1629–1639. [Google Scholar] [CrossRef]
- Chumlyakov, Y.I.; Kireeva, I.V.; Litvinova, E.I.; Zaharova, E.G.; Luzginova, N.V.; Sehitoglu, H.; Karaman, I. Strain hardening in single crystals of Hadfield steel. Phys. Met. Metall. 2000, 90, S1–S17. [Google Scholar]
- Karaman, I.; Sehitoglu, H.; Gall, K.; Chumlyakov, Y.I.; Maier, H.J. Deformation of single crystal Hadfield steel by twinning and slip. Acta Mater. 2000, 48, 1345–1359. [Google Scholar] [CrossRef]
- Randle, V. Mechanism of twinning-induced grain boundary engineering in low stacking-fault energy materials. Acta Mater. 1999, 47, 4187–4196. [Google Scholar] [CrossRef]
- Straumal, B.B.; Mazilkin, A.A.; Baretzky, B.; Schütz, G.; Rabkin, E.; Valiev, R.Z. Accelerated diffusion and phase transformations in CoCu alloys driven by the severe plastic deformation. Mater. Trans. 2012, 53, 63–71. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C.P.; Cugy, P.; Barbier, D. High manganese austenitic twinning induced plasticity steels: A review of the microstructure properties relationships. Curr. Opin. Solid State Mater. Sci. 2011, 15, 141–168. [Google Scholar] [CrossRef]
- Zhou, P.; Liang, Z.Y.; Liu, R.D.; Huang, M.X. Evolution of dislocations and twins in a strong and ductile nanotwinned steel. Acta Mater. 2016, 111, 96–107. [Google Scholar] [CrossRef]
- De Cooman, B.C. High Mn TWIP steel and medium Mn steel. In Automotive Steels: Design, Metallurgy, Processing and Applications; Rana, R., Singh, S.B., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 317–385. [Google Scholar]
- Kim, H.-S.; Suh, D.-W.; Kim, N.-J. Fe–Al–Mn–C lightweight structural alloys: A review on the microstructures and mechanical properties. Sci. Technol. Adv. Mater. 2013, 14, 14205:1–14205:11. [Google Scholar] [CrossRef]
- Kusakin, P.; Belyakov, A.; Haase, C.; Kaibyshev, R. Molodov, D.A. Microstructure evolution and strengthening mechanisms of Fe–23Mn–0.3C–1.5Al TWIP steel during cold rolling. Mater. Sci. Eng. A 2014, 617, 52–60. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C. Effect of grain and twin boundaries on the hardening mechanisms of twinning-induced plasticity steels. Scr. Mater. 2008, 58, 484–487. [Google Scholar] [CrossRef]
- Rittel, D.; Roman, I. Tensile deformation of coarse-grained cast austenitic manganese steels. Mater. Sci. Eng. A 1989, 110, 77–87. [Google Scholar] [CrossRef]
- Gladman, T. Precipitation hardening in metals. Mater. Sci. Technol. 1999, 15, 30–36. [Google Scholar] [CrossRef]
- Wang, Z.W.; Wang, Y.B.; Liao, X.Z.; Zhao, Y.H. Influence of stacking fault energy on deformation mechanism and dislocation storage capacity in ultrafine-grained materials. Scr. Mater. 2009, 60, 52–55. [Google Scholar] [CrossRef]
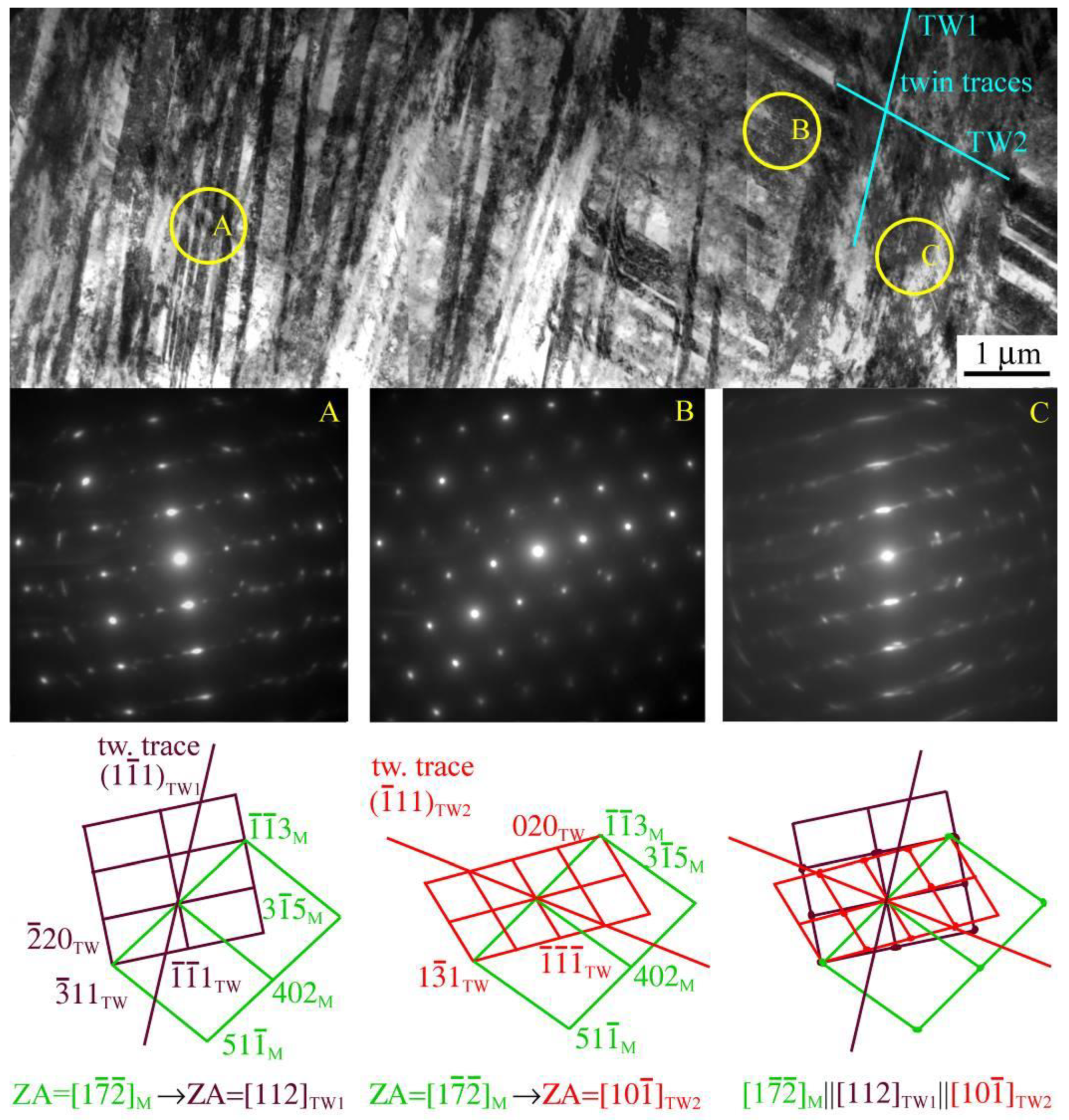
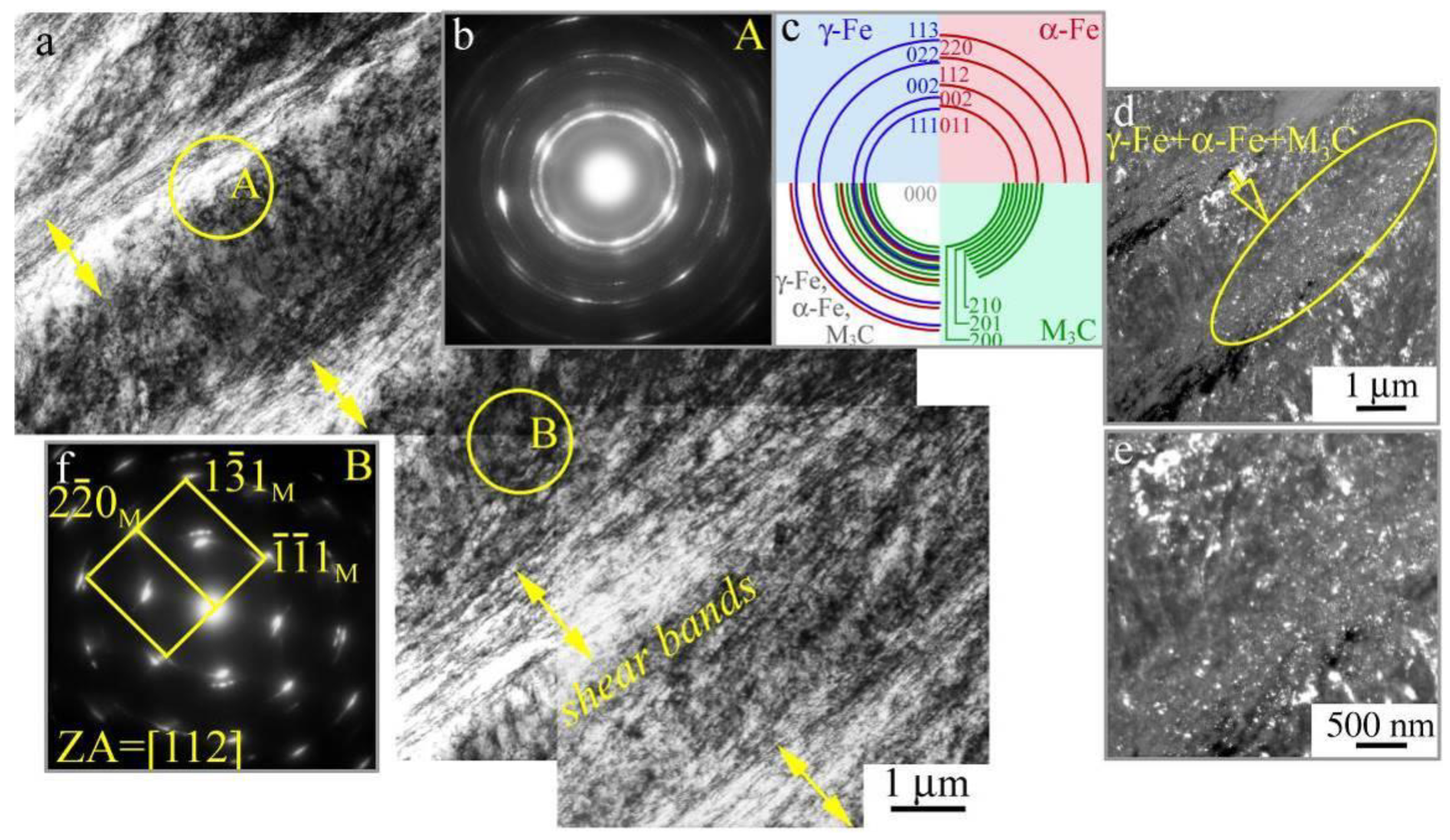



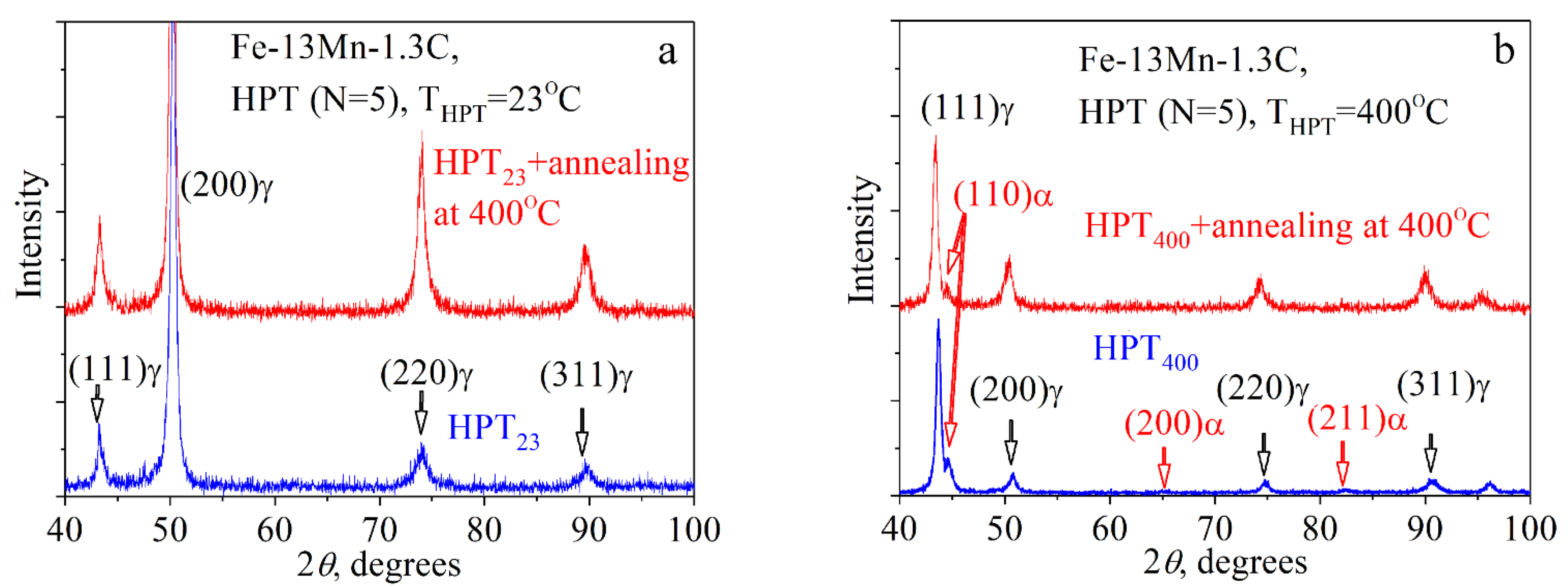
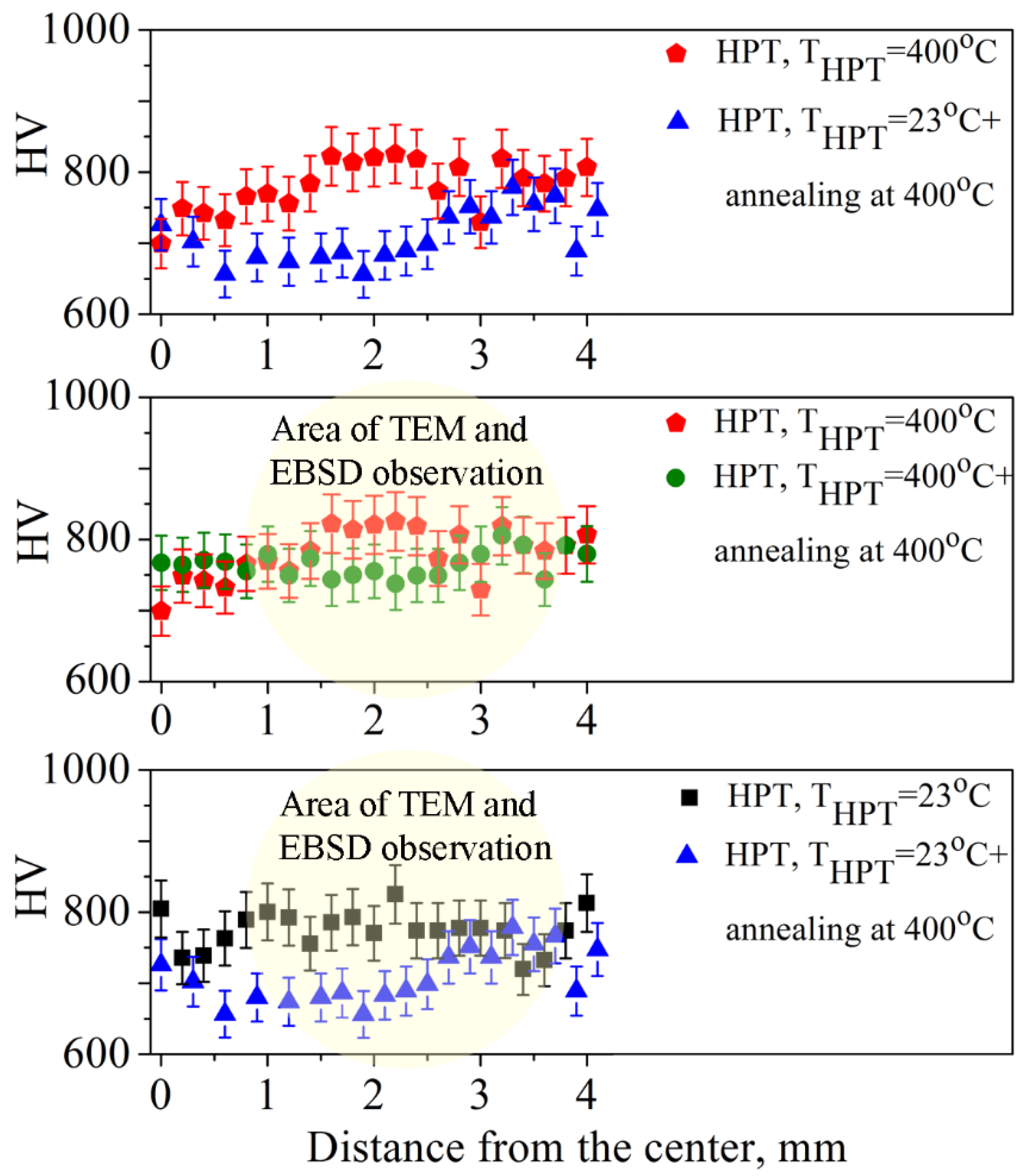

| State | a (nm) | Dhkl (nm) | Δd/d·10−4 | ρdis·1014 (m−2) |
|---|---|---|---|---|
| HPT23 | 0.3620 | 15 | 18.4 | 17 |
| HPT23 + 400 °C | 0.3621 | 14 | 14.2 | 14 |
| HPT400 | 0.3607 | 26 | 20.7 | 11 |
| HPT400 + 400 °C | 0.3609 | 25 | 16.5 | 7 |
| State | Phase Composition * | Mechanism of Deformation * | VTW, % |
|---|---|---|---|
| HPT23 | austenite, ε-phase | twinning, dislocation slip, shear bands, γ-ε transformation | ≈40 |
| HPT23 + 400 °C | austenite, ε-phase | - | ≈40 |
| HPT400 | austenite, α′-phase, ε-phaseM3C | slip, shear bands, twinning, γ-ε transformation, γ-α transformation, particle strengthening | ≈20 |
| HPT400 + 400 °C | austenite, α′-phase, ε-phase M3C | - | ≈20 |
| State | σSS, MPa | σGB, MPa | σTB, MPa | σρ, MPa | σPS, MPa | HV Experiment | σ *, GPa |
|---|---|---|---|---|---|---|---|
| HPT23 | 450 | - | 420 | 480–1080 | - | 780 | 2600 |
| HPT23+ 400 °C | 450 | - | 420 | 430–980 | - | 760 | 2530 |
| HPT400 | 290 | 1400 | 100 | 390–870 | 130 | 820 | 2730 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maier, G.G.; Astafurova, E.G. A Comparison of Strengthening Mechanisms of Austenitic Fe-13Mn-1.3C Steel in Warm and Cold High-Pressure Torsion. Metals 2020, 10, 493. https://doi.org/10.3390/met10040493
Maier GG, Astafurova EG. A Comparison of Strengthening Mechanisms of Austenitic Fe-13Mn-1.3C Steel in Warm and Cold High-Pressure Torsion. Metals. 2020; 10(4):493. https://doi.org/10.3390/met10040493
Chicago/Turabian StyleMaier, Galina G., and Elena G. Astafurova. 2020. "A Comparison of Strengthening Mechanisms of Austenitic Fe-13Mn-1.3C Steel in Warm and Cold High-Pressure Torsion" Metals 10, no. 4: 493. https://doi.org/10.3390/met10040493
APA StyleMaier, G. G., & Astafurova, E. G. (2020). A Comparison of Strengthening Mechanisms of Austenitic Fe-13Mn-1.3C Steel in Warm and Cold High-Pressure Torsion. Metals, 10(4), 493. https://doi.org/10.3390/met10040493





