Assessment of Internal Stresses Using Dislocation Dipole Heights in Cyclically Deformed [001] Copper Single Crystals
Abstract
1. Introduction
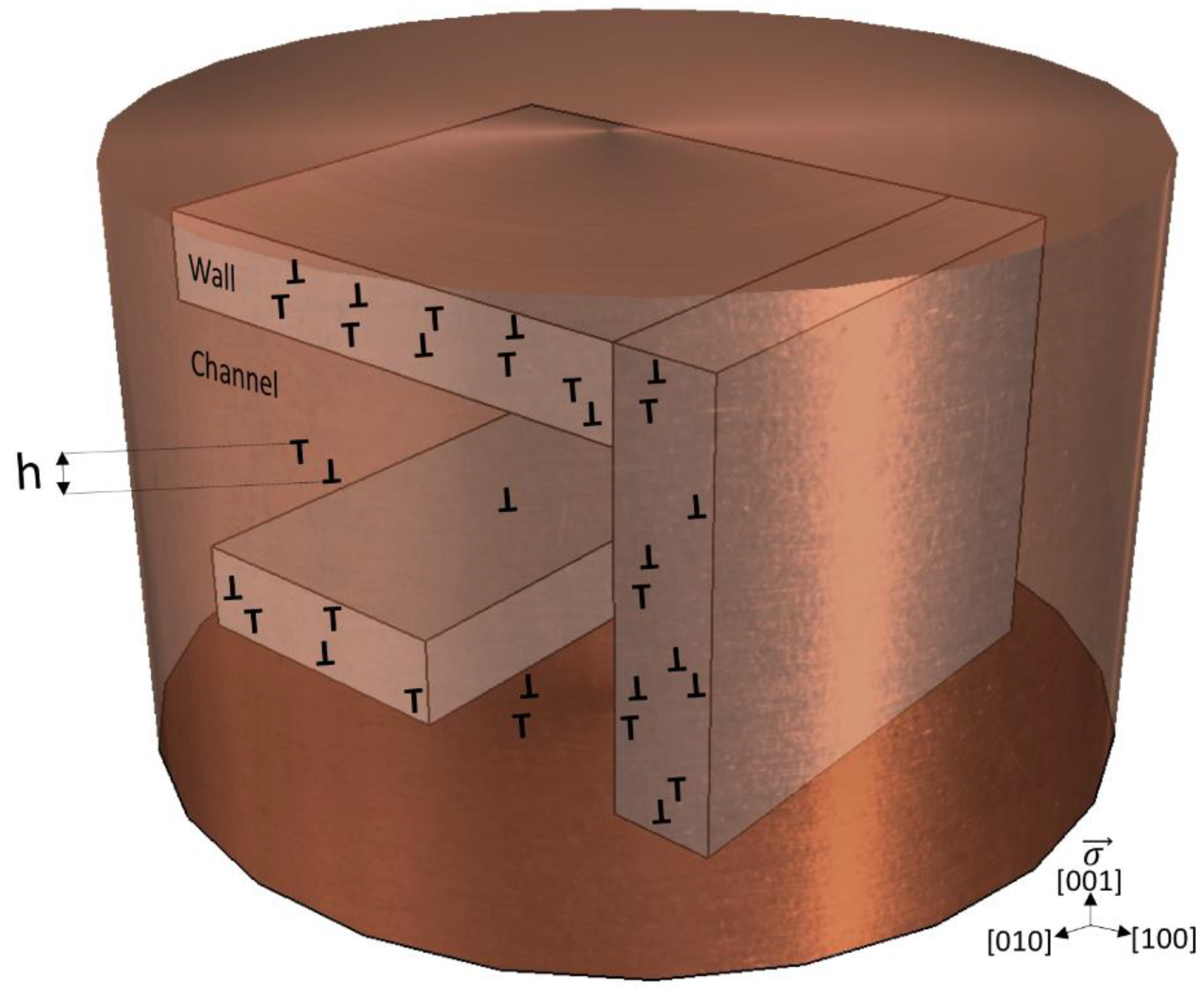
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fujii, T.; Kajita, T.; Miyazawa, T.; Arai, S. Characterization of dislocation microstructures in cyclically deformed [001] copper single crystals using high voltage scanning transmission electron microscopy. Mater. Charact. 2018, 136, 206–211. [Google Scholar] [CrossRef]
- Wang, Z.; Gong, B.; Wang, Z. Cyclic deformation behavior and dislocation structures of [001] copper single crystals—II. Characteristics of dislocation structures. Acta Mater. 1997, 45, 1379–1391. [Google Scholar] [CrossRef]
- Gong, B.; Wang, Z.; Wang, Z. Cyclic deformation behavior and dislocation structures of [001] copper single crystals—I cyclic stress-strain response and surface feature. Acta Mater. 1997, 45, 1365–1377. [Google Scholar] [CrossRef]
- Li, P.; Li, S.X.; Wang, Z.G.; Zhang, Z.F. Fundamental factors on formation mechanism of dislocation arrangements in cyclically deformed fcc single crystals. Prog. Mater. Sci. 2011, 56, 328–377. [Google Scholar] [CrossRef]
- Charsley, P.; Kuhlmann-wilsdorf, D. Configuration of {100} dislocation walls formed during fatigue. Philos. Mag. A. 1981, 44, 1351–1361. [Google Scholar] [CrossRef]
- Jin, N.Y.; Winter, A.T. Dislocation structures in cyclically deformed [001] copper crystals. Acta Metall. 1984, 32, 1173–1176. [Google Scholar] [CrossRef]
- Levine, L.E.; Stoudt, M.R.; Creuziger, A.; Phan, T.Q.; Ruqing, X.; Kassner, M.E. Basis for the Bauschinger effect in copper single crystals: Changes in the long-range internal stress with reverse deformation. J. Mater. Sci. 2019, 54, 6579–6585. [Google Scholar] [CrossRef]
- Kassner, M.E.; Geantil, P.; Levine, L.E. Long range internal stresses in single-phase crystalline materials. Int. J. Plast. 2013, 45, 44–60. [Google Scholar] [CrossRef]
- Sauzay, M.; Kubin, L.P. Scaling laws for dislocation microstructures in monotonic and cyclic deformation of fcc metals. Prog. Mater. Sci. 2011, 56, 725–784. [Google Scholar] [CrossRef]
- Kassner, M.E.; Wall, M.A.; Delos-Reyes, M.A. Microstructure and mechanisms of cyclic deformation of aluminum single crystals at 77 K. Metall. Mater. Trans. A 1997, 28, 595–609. [Google Scholar] [CrossRef]
- Kassner, M.E.; Wall, M.A. Microstructure and mechanisms of cyclic deformation in aluminum single crystals at 77 K: Part II. Edge dislocation dipole heights. Metall. Mater. Trans. A 1999, 30, 777–779. [Google Scholar] [CrossRef]
- Kassner, M.E.; Wall, M.A.; Delos-Reyes, M.A. Primary and secondary dislocation dipole heights in cyclically deformed copper single crystals. Mater. Sci. Eng. A 2001, 317, 28–31. [Google Scholar] [CrossRef]
- Kassner, M.E.; Pérez-Prado, M.T.; Vecchio, K.S.; Wall, M.A. Determination of internal stresses in cyclically deformed copper single crystals using convergent-beam electron diffraction and dislocation dipole separation measurements. Acta Mater. 2000, 48, 4247–4254. [Google Scholar] [CrossRef]
- Antonopoulos, J.G.; Winter, A.T. Weak-beam study of dislocation structures in fatigued copper. Philos. Mag. 1976, 33, 87–95. [Google Scholar] [CrossRef]
- Tippelt, B.; Breitschneider, J.; Hähner, P. The Dislocation Microstructure of Cyclically Deformed Nickel Single Crystals at Different Temperatures. Phys. Status Solidi 1997, 163, 11–26. [Google Scholar] [CrossRef]
- Essmann, U.; Mughrabi, H. Annihilation of dislocations during tensile and cyclic deformation and limits of dislocation densities. Philos. Mag. A 1979, 40, 731–756. [Google Scholar] [CrossRef]
- Mughrabi, H. Dislocation wall and cell structures and long-range internal stresses in deformed metal crystals. Acta Metall. 1983, 31, 1367–1379. [Google Scholar] [CrossRef]
- Mughrabi, H. A two-parameter description of heterogeneous dislocation distributions in deformed metal crystals. Mater. Sci. Eng. 1987, 85, 15–31. [Google Scholar] [CrossRef]
- Brown, L.M. A discussion of the structure and behaviour of dipole walls in cyclic plasticity. Philos. Mag. 2004, 84, 2501–2520. [Google Scholar] [CrossRef]
- Kassner, M.E.; Pollard, J.; Evangelista, E.; Cerri, E. Restoration mechanisms in large-strain deformation of high purity aluminum at ambient temperature and the determination of the existence of ‘steady-state’. Acta Metall. Mater. 1994, 42, 3223–3230. [Google Scholar] [CrossRef]
- Kassner, M.E.; McQueen, H.J.; Pollard, J.; Evangelista, E.; Cerri, E. Restoration mechanisms in large-strain deformation of high purity aluminum at ambient temperature. Scripta Metall. Mater. 1994, 31, 1331–1336. [Google Scholar] [CrossRef]
- Ham, R.K. The determination of dislocation densities in thin films. Philos. Mag. 1961, 6, 1183–1184. [Google Scholar] [CrossRef]
- Orowan, E. Causes and effects of internal stresses. Internal Stresses and Fatigue in MetalsRassweiler, G.M., Grube, W.L., Eds.; General Motors SymposiumElsevier: Amsterdam, The Netherlands, 1959; pp. 59–80. [Google Scholar]
- Sleeswyk, A.W.; James, M.R.; Plantinga, D.H.; Maathuis, W.S.T. Reversible strain in cyclic plastic deformation. Acta Metall. 1978, 26, 1265–1271. [Google Scholar] [CrossRef]
- Scattergood, R.O.; Bacon, D.J. The Orowan mechanism in anisotropic crystals. Philos. Mag. 1975, 31, 179–198. [Google Scholar] [CrossRef]
- Veyssiere, P.; Chiu, Y.L. Equilibrium and passing properties of dislocation dipoles. Philos. Mag. 2007, 87, 3351–3372. [Google Scholar] [CrossRef]
- Fultz, B.; Howe, J. Transmission Electron Microscopy and Diffractometry of Materials, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2013; p. 344. [Google Scholar]
- Sauzay, M.; Dupuy, L. Internal Stresses in Deformation-Induced Microstructures; XXIV ICTAM: Montreal, QC, Canada, 2016. [Google Scholar]
- Neumann, P.D. The interactions between dislocations and dislocation dipoles. Acta Metall. 1971, 19, 1233–1241. [Google Scholar] [CrossRef]
- Neumann, P.D. Constitutive Equations in Plasticity; Argon, A.S., Ashby, M.F., Eds.; MIT Press: Cambridge, UK, 1975. [Google Scholar]
- Haasen, P. Physical Metallurgy; Cambridge Press: London, UK, 1978; p. 116. [Google Scholar]
- Brown, L.M. A dipole model for the cross-slip of screw dislocations in FCC metals. Philos. Mag. A. 2002, 82, 1691–1711. [Google Scholar] [CrossRef]
- Forwood, C.T.; Humble, P. Dislocartion dipoles in elastically anisotropic crystals. Aust. J. Phys. 1970, 23, 697–718. [Google Scholar] [CrossRef][Green Version]
- Wintner, E.; Karnthaler, H.P. The study of dipoles in Cu-Al alloys using weak-beam electron microscopy. Philos. Mag. 1977, 36, 1317–1329. [Google Scholar] [CrossRef]
- Levine, L.E.; Larson, B.C.; Yang, W.; Kassner, M.E.; Tischler, J.Z.; Delos-Reyes, M.A.; Fields, R.J. X-ray microbeam measurements of individual cell elastic strains in deformed single crystal copper. Nat. Mater. 2006, 5, 619–622. [Google Scholar]


| This Study (Cu) | Cu [13] | Al [11] | Ni [15] | |||||
|---|---|---|---|---|---|---|---|---|
| Labyrinth Walls | Labyrinth Channels | Dipole Bundles (Veins) | Channels | Dipole Bundles (Veins) | Channels | PSB Walls | PSB Channels | |
| Maximum Dipole Height (nm) | 4.3 | 4 | 15 | 12 | 31 | 32 | 6 | 7.1 |
| Dipole Stress for hmax (MPa) | 270 (h = 4.15) | 52 (h = 13.5) | 16 (h = 31.5) | 186.6 (h = 6.55) | ||||
| Applied Resolved Shear Stress (MPa) | 112 | 19 | 20 | 50 | ||||
| saturation | half of saturation stress | pre-saturation | saturation | |||||
| τd/τa (for hmax) | 2.4 | 2.7 | 0.8 | 3.7 | ||||
| Slip | polyslip | single slip | single slip | single slip | ||||
| SFE mJ/m2 [31,32,33,34] | 60 | 60 | 200 | 90 | ||||
| T/Tm | 0.22 | 0.22 | 0.12 | 0.17 | ||||
| Strain Amplitude | 0.40% | Plastic only = 0.125% | Plastic only = 0.12% | 0.40% | ||||
| Strain Rate | 2 × 10−3 | 2.5 × 10−3 | 2 × 10−4 | 10−3 | ||||
| Number of Cycles | 157 | 200 | 560 | - | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ermagan, R.; Sauzay, M.; Kassner, M.E. Assessment of Internal Stresses Using Dislocation Dipole Heights in Cyclically Deformed [001] Copper Single Crystals. Metals 2020, 10, 512. https://doi.org/10.3390/met10040512
Ermagan R, Sauzay M, Kassner ME. Assessment of Internal Stresses Using Dislocation Dipole Heights in Cyclically Deformed [001] Copper Single Crystals. Metals. 2020; 10(4):512. https://doi.org/10.3390/met10040512
Chicago/Turabian StyleErmagan, Roya, Maxime Sauzay, and Michael Ernest Kassner. 2020. "Assessment of Internal Stresses Using Dislocation Dipole Heights in Cyclically Deformed [001] Copper Single Crystals" Metals 10, no. 4: 512. https://doi.org/10.3390/met10040512
APA StyleErmagan, R., Sauzay, M., & Kassner, M. E. (2020). Assessment of Internal Stresses Using Dislocation Dipole Heights in Cyclically Deformed [001] Copper Single Crystals. Metals, 10(4), 512. https://doi.org/10.3390/met10040512







