Abstract
The addition of B can inhibit the precipitation of σ phases at the grain boundary to improve the hot workability and corrosion resistance for super austenitic stainless steel with high Cr and Mo content. This study focused on the interaction between B and Mo at the Fe–Cr(111)/Cr2O3(0001) interface and its effect on interfacial adhesion by employing the first-principles method, especially the effect of B on the segregation behavior of Mo. The most stable O-terminated Fe/Cr2O3 interface was chosen as the basic configuration. The segregation energy and the work of separation were calculated for the metal/chromia interface with Fe–Cr as the substrate. It has been demonstrated that B can promote the diffusion of Mo atoms into the oxide layer to increase the content of Mo in the passive film. In addition, the interfacial adhesion is higher at the most segregated sites. However, it is more difficult for two or more Mo atoms than a single Mo atom to diffuse into the oxide part with the effect of B, indicating that B can only improve the Mo content of the passive film to a small extent. The electronic properties were also further discussed to analyze the interactions and the binding characters between doped atoms and their surrounding atoms and to explain the underlying reasons for the variation of interfacial adhesion.
1. Introduction
Super austenitic stainless steel, possessing the austenitic microstructure with a face-centered cubic crystal structure, has been extensively applied in harsh service conditions such as seawater, oilfields, cooling water systems, flue gases, chemical applications, and nuclear reactions [1,2,3] due to its excellent corrosion resistance. In general, a high content of Cr and Mo assures its unique corrosion resistance. Particularly, the addition of Mo can significantly heighten the resistance to pitting and crevice corrosion in a reductive and chloride environment. Nonetheless, higher Cr and Mo content is likely to induce precipitation of the brittle second phases such as sigma, chi, and laves phase [4,5,6], which deteriorates the hot workability and corrosion resistance. Fortunately, B atoms are easier to segregate at grain boundaries, suppressing the precipitation of the second phases. Bai et al. clarified the inhibition effect of B on the σ phase [7]. Besides, it has been demonstrated experimentally that B can elevate the content of Mo oxide in the passive film [8], which improves pitting corrosion resistance. The compactness and composition of the passivation film and its adhesion with the substrate can affect the corrosion resistance of stainless steel to some extent. Thus, it is worthwhile to study the effects of the added microelement B on the metal/chromia interface.
Currently, there have been many theoretical studies on metal/oxide interfaces [9,10,11,12,13,14]. The structure and properties of such heterogeneous interfaces can significantly affect the performance of materials, and they even play a decisive role in some special properties such as corrosion resistance and high-temperature oxidation resistance. Stainless steel is a typical example, with a dense protective passivation film formed on its surface. Dong et al. investigated the segregation behavior of different alloying additives of the Fe/Cr2O3 interface and their effects on the interfacial adhesive strength [15], which can provide theoretical guidance for the chemical composition design of austenitic heat-resistant stainless steels. However, the substrate was pure iron, the composition of which was inconsistent with the actual austenitic stainless steel enriched in Fe, Cr, and Ni. Kamiya et al. carried out ab initio calculations of electronic structures and carrier transport properties for ZnO–metal interfaces and revealed the nature of the interfaces [16]. First-principles calculations can describe the interactions among atoms in detail and obtain some information like the interfacial atomic coordination, bonding nature, and electronic structures, which compensates for such disadvantages in experiments.
In our previous work [17], the effect of B on the segregation of Mo at grain boundaries was studied by first-principles calculations. The results showed that B can restrain the segregation of Mo at grain boundaries to reduce the precipitation of the σ phase. However, the effects of B on Mo at the metal/oxide interface have not been discussed yet. Moreover, the effects of B on the composition of the passive film and the interfacial adhesion play a significant role in corrosion resistance. In addition, it is hard to observe the effect of B on the diffusion of Mo by means of existing characterization methods. Therefore, in this work, first-principles calculations were adopted to study the segregation behavior and the interfacial adhesion of the Fe–Cr/Cr2O3 interface and to explore the reason for this from the perspective of charge interaction.
2. Computational Details
The first-principles calculations based on density functional theory (DFT) [18,19,20] were implemented with the Vienna Ab initio Simulation Package (VASP) [21,22]. The Perdew–Burke–Ernzehof (PBE) [23] generalized gradient approximation (GGA) [24] was adopted to describe electronic exchange and correlation effects. The interaction between valence electrons and ion cores was represented by projector-augmented wave pseudopotentials (PAW) [25,26]. The kinetic energy cutoff was 400 eV, and the Brillouin zone was sampled by a 5 × 3 × 1 Γ-centered k-points mesh following the Monkhorst–Pack method [27]. As for magnetism of the paramagnetic austenitic phase γ–Fe, there are different ways to deal with the directions of the magnetic moments, including disregard [28,29,30], setting spin according to the ferromagnetic phase [31], and adopting the disordered local moments model [32,33,34]. Spin polarization was not adopted in this study. Unless otherwise stated, the convergence criteria of all optimizations were 10−4 eV and 0.01 eV/Å−1 for electronic and ionic relaxations, respectively.
To verify the rationality of calculation parameters chosen in this paper and to build interface models for the next step, the lattice constants of face-centered-cubic (fcc) Fe and rhombohedral corundum structure Cr2O3 were calculated. The obtained crystal lattice constants were a = b = c = 3.45 Å and a = b = 5.06 Å, c = 13.85 Å, respectively, in good agreement with the calculated [29,31,35] and experimental values [36,37,38,39] (within 5% difference). Then, the interface structures were built with optimized unit cells.
The segregation energy and the ideal work of separation can be utilized to investigate the diffusion behavior of impurity atoms and their effects on interfacial adhesion. All these definitions are depicted in more detail below.
The formation energy of impurity atoms can be defined as [40,41,42]:
where and represent the doped and the substituted atoms, respectively, and and correspond to the number of and atoms, respectively; and refer to the total energy of the interface structure with and without impurity atoms, respectively; and denote the total energies of per and atom in their bulk states, respectively.
The segregation energy of one doped state can be defined as [41,42]:
where and represent the impurity formation energy of doped atom(s) at possible segregation sites (interface, near the interface, passive film and other transition positions) and in the substrate, respectively. The segregation energy reflects the tendency of the impurity atom to migrate from substrate to other sites. A negative value suggests that it is energetically favorable for the impurity atom to segregate to this state. In addition, a more negative value means a stronger tendency of segregation.
The ideal work of separation is the energy required for an interface to separate into two free surfaces regardless of deformation, which can be obtained by Equation (3) [43,44,45]:
where is the cross-sectional area of the interface; is the total energy of interface system, while ( is or ) corresponds to the total energy of slab kept in vacuum with the other one replaced. The higher the value indicates better interfacial binding.
3. Results and Discussion
3.1. Interface Structures
For modeling a heterogeneous interface, it is necessary to determine the basic orientation relation and other fine details, such as misfit dislocation, atomic stoichiometry, and atomic coordination of the interface. Here, the close-packed direction of Fe(111)/[10] parallel to that of Cr2O3(0001)/[110] was chosen as the crystalline orientation on the basis of the similar fcc–metal/hcp–oxide interfaces [46,47,48,49,50]. The Cr2O3 slab has three termination types: O-rich, stoichiometric, and Cr-rich. In this simulation, the stoichiometric O-terminated metal/chromia interface was adopted, as this interface has lower formation energy than the other two kinds of stoichiometric Cr-terminated interfaces [49]. While the average lattice parameters of Fe slab and Cr2O3 slab were employed as interface lattice constants, the lattice mismatch is less than 0.05%. The lattice mismatch can be computed as [45] 1 − [2A/(A1 + A2)], where A is the interface area, and A1 and A2 are the area of Fe and Cr2O3 supercells corresponding to the interface. As A2 is larger than A1, the Fe part and the oxide part near the interface are under tension and compression, respectively. The stress caused by lattice mismatch can weaken the interface.
According to the relative positions of the interfacial Fe atom with respect to the Cr2O3 slab, there are five types of interface models, as shown in Figure 1. An Fe atom on the top of the Cr1-site, Cr2-site, Cr3-site, and O-site, and an Fe vacancy on the top of O-site of the O-terminated interface, are labeled in Figure 1 as topCr1, topCr2, topCr3, topO, and topV, respectively. The atomic coordination of topO and topV are almost the same, the only difference being that the Fe atom is replaced by an Fe vacancy. All the heterogeneous interfaces were composed of a Fe(111) slab with seven Fe atomic layers and a Cr2O3(0001) slab with four sets of O–Cr–O and Cr–O–Cr alternate-stacking atomic layers. A 12 Å vacuum was set perpendicular to the Cr2O3(0001) surface, which was used to avoid the interaction of periodic slabs in this order. The top two layers of the metal-substrate part were kept fixed at their initial bulk positions to mimic a semi-infinite bulk crystal.
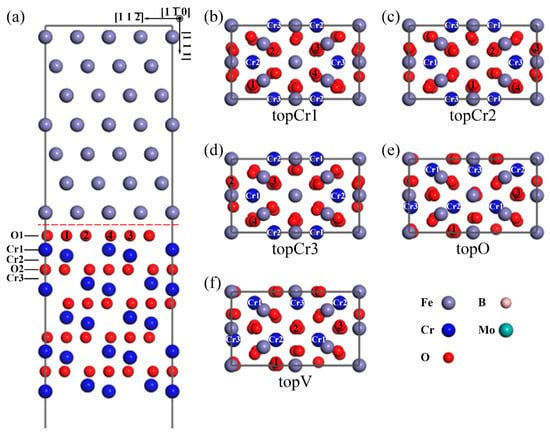
Figure 1.
The atomic structures of the O-terminated Fe(111)/Cr2O3(0001) interface models. A side view of (a) the O-terminated topCr1 interface. The top view of the O-terminated interfaces with five different interfacial atomic coordination: (b) topCr1 with an Fe atom on top of Cr1 site; (c) topCr2 with an Fe atom on top of Cr2 site; (d) topCr3 with an Fe atom on top of Cr3 site; (e) topO with an Fe atom on top of O1 site; (f) topV with an Fe vacancy on top of O1 site. (The only difference of the e and f plots is that there is no gray Fe atom on the middle red O atom at the topV interface. For clarity, only the interfacial Fe layer of the top view is shown. Unless otherwise stated, the gray spheres correspond to the Fe atoms, the blue spheres represent the Cr ions, the smaller red spheres are the O ions, the smaller pink spheres represent the B atoms, and the larger cyan spheres are the Mo atoms.).
The work of separation and the interface energy [51,52] were then calculated to assess the adhesion strength and the stability of interfaces, respectively. The can be expressed as:
where is the total energy of the interface; and represent the energy of the Fe and Cr2O3 surfaces, respectively; and are the total energy of bulk Fe and Cr2O3 in their formula unit, respectively; and x and y correspond to the number of unit cells in the interface. The lower values means the better thermodynamic stability of an interface. The results of and for different O-terminated interfaces are shown in Figure 2. The topCr1 construction has the highest work of separation (2.25 J·m−2), while there are fewer differences among the other four. The interface energy of the topV structure (6.33 J·m−2) is around 2.5 times the value of the others, which is much larger than the difference in work of separation. This suggests that vacancy defects can significantly reduce the stability of the interface rather than greatly weaken the interfacial adhesion strength. It will take a lot of computation time to study the segregation behavior of all interface configurations, so it was necessary to choose one typical case. As the highest and the lowest , the topCr1 interface model was chosen as the structure in focus for the following discussion.
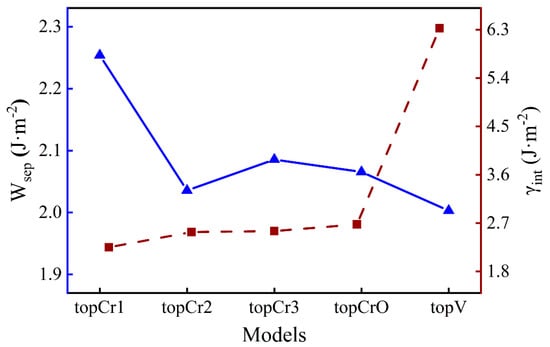
Figure 2.
The work of separation and the interface energy for Fe/Cr2O3 systems.
3.2. Diffusion Behavior of B Atom
In order to make the simulation closer to the actual composition of super austenitic stainless steel, 13 Cr atoms replaced Fe atoms in the Fe–Cr substrate as uniformly as possible. From Figure 3, the Cr atoms are uniformly distributed, and are neither adjacent to the interface nor clustered. According to one previous study [53], B was placed in interstitial sites of γ–Fe to explore the effect of alloying on the behavior of B and S at the grain boundary. We computed the formation energy of B in Fe or Cr2O3 bulk, as shown in Table 1. According to the most energetically favorable sites, we placed B in the octahedral interstitial sites of fcc–Fe and the substitutional sites of the oxide, respectively, to study its segregation behavior.
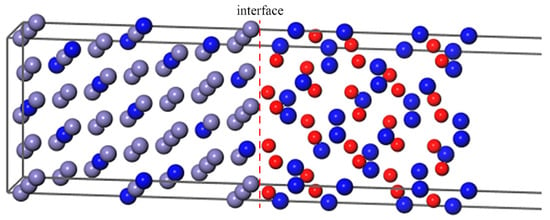
Figure 3.
The Fe–Cr(111)/Cr2O3(0001) interface with Cr atoms distributing uniformly.

Table 1.
The formation energy of a B atom in Fe or Cr2O3 bulk. (The subscript “int” represents B in an octahedral interstitial site, and the “sub” indicates B at a substitutional site. The subscripts “sub_O” and “sub_Cr” mean that B replaces the O atom or the Cr atom in Cr2O3 bulk, respectively.).
Then, a B atom was introduced in different interstitial sites to study its diffusion behavior, as shown in Figure 4, where numbers 1–7 denote the different diffusion positions of the B atom. A Mo atom or two atoms substitute the Fe atoms in the substrate labeled Mo/2Mo, respectively; this can be used to study the diffusion of B with different Mo content. As can be seen from Figure 5 and Figure 7, the segregation energy of a single B atom at the most stable position is −0.67 eV, while that of a single Mo atom is −0.10 eV. Owing to the greater negative segregation energy and the smaller atomic radius of B, it is reasonable to believe that the B atom diffuses faster than the Mo atom to affect the migration of Mo. Therefore, the diffusion of B was first studied to determine the most favorable sites, when B and Mo were added together. Following that, the effect of B on the segregation behavior of Mo, which is hard to migrate, was analyzed, as described in the following section.
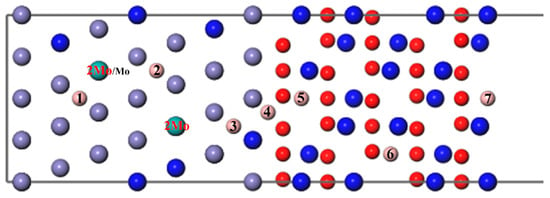
Figure 4.
The different diffusion sites of a B atom at the Fe–Cr/Cr2O3 interface with varying Mo content.
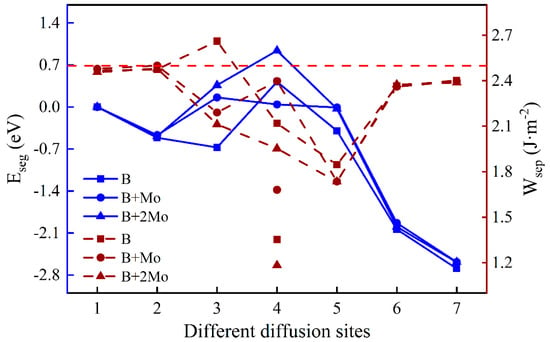
Figure 5.
The segregation energy and the work of separation of different diffusion sites for a B atom with varying Mo content. (The left and right ordinates reflect the values of and , respectively. The blue solid lines and crimson dashed lines indicate the values of and with different diffusion sites, respectively. The labels of the symbols mean the effect of the element after “+” on the other one before “+”. Points under the lines stand for the work of separation between the B layer and the substrate part, and corresponding on-line points represent that of the B layer and the oxide part. Unless otherwise specified, the red dashed line corresponds to the contrast value of the work of separation without dopant atoms.).
To understand the segregation behavior of B with varying Mo content and its effect on interfacial adhesion, the segregation energy, and the work of separation are illustrated in Figure 5. The lowest segregation energy of a single B is −0.67 eV in the Fe–Cr substrate portion near the interface (Site 3), while those with one Mo atom and two Mo atoms are −0.47 eV and −0.49 eV, respectively. It is beneficial for a single B atom to diffuse a position near the interface in the substrate, mainly because the Fe–Cr part near the interface is under tension, while the corresponding oxide part is under compression. Obviously, the addition of Mo can suppress the diffusion of B atom, and the most stable site of B has changed from the vicinity of the interface (Site 3) to the substrate (Site 2). The of the Fe–Cr/Cr2O3 interface without impurity atoms is around 2.50 J·m-2. By comparison, the addition of B weakens interfacial adhesion in almost all cases, even if the substrate contains Mo additive distributed uniformly, except when a single B atom is located in the substrate near the interface. The work of separation increases when B is at the interface with a Mo atom (2.40 J·m−2 and 1.68 J·m−2), mainly due to the higher surface energy of the substrate after interface fracture. Moreover, the work of separation between the B layer and the oxide is much greater than that of this layer and the Fe–Cr substrate, implying that the B atom has stronger interactions with O atoms than with Fe or Cr atoms when a B atom is at the interface.
3.3. The Effect of B on the Segregation of Mo
The most energy-favorable sites of the B atom have been defined, and the larger Mo atom has been shown to have an inhibition effect on B atom migration. The B atom, in turn, can also have an effect on the segregation of the Mo atom. Mo can play a different role in the interfacial adhesion at different diffusion sites, either weakening or strengthening them, and the Mo content in the passive film plays a significant role in corrosion resistance. The interfacial adhesion and the composition of the passive film can affect the properties of stainless steel. The effect of B on the diffusion of Mo and the variation of interfacial adhesion were further explored in the following discussion to explain the experimental phenomenon.
3.3.1. The Segregation Behavior of a Mo Atom
As shown in Figure 6, we introduced a Mo atom with a B atom located at the most stable site, where numbers 1–6 indicate the different diffusion substitutional sites of Mo. The mass fraction of a Mo atom in the substrate is about 3.07%. The segregation behavior and the interfacial adhesion of the interface with a Mo atom at different sites can be assessed by the segregation energy and the work of separation, respectively, as shown in Figure 7. From Figure 7, it can be seen that the values of a Mo atom with B are more negative than that without B. Furthermore, the segregation energy of Mo from the substrate (Site 1) to the interface (Site 3) becomes gradually more negative, indicating that Mo can spontaneously segregate to the interface (Site 3) under the effect of B. However, the negative
at the next diffusion site (−0.44 eV) is suddenly greater than the value at the interface (−0.68 eV), which is metastable and prone to segregate to Site 5. The reason for this may be that the Mo atom in the oxide layer near the interface causes a larger distortion of its adjacent atoms and it is difficult to accommodate a larger atom under compression. The lowest Eseg value is about −0.97 eV at Site 5 in the middle of the Cr2O3 oxide, and the value of the surface site becomes positive. It shows that the Mo atom in the middle of the oxide layer is most stable. Above all, the addition of B contributes to the segregation of Mo, which can raise the Mo content in the Cr2O3 oxide layer.
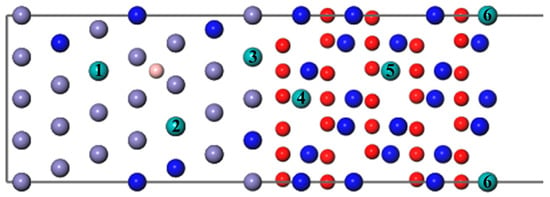
Figure 6.
The different diffusion sites of a Mo atom at the Fe–Cr/Cr2O3 interface with and without the B atom.
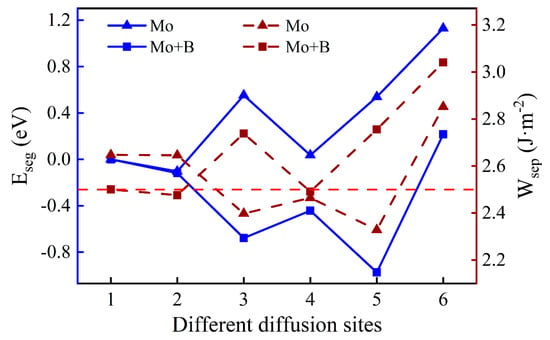
Figure 7.
The segregation energy and the work of separation of different diffusion sites for a Mo atom with and without B.
When the Mo atom is in the substrate (Sites 1 or 2), the values of with B are lower than that without B, which suggests that the presence of B can reduce the interfacial adhesion. However, when the Mo atom migrates to the interface or into the oxide layer, the opposite is true. The metastable segregation site of the Mo atom (Site 4) has the lowest = 2.49 J·m−2, which is slightly weaker than the pure Fe–Cr/Cr2O3 interfacial adhesion. Fortunately, the Mo atom is favorable to the performance of interfacial bonding at the most stable position, and its work of separation is 2.76 J·m−2. The better interfacial adhesion means that the passivation film is not easily separated from the substrate, which is beneficial to the corrosion resistance of stainless steel.
3.3.2. The Segregation Behavior of Two Mo Atoms
One Mo atom added in the interface is inconsistent with the actual composition of super austenitic stainless steel. Consequently, the number of Mo atoms was added so that the mass fraction increased to 6.06%. The diffusion sites of two atoms are shown in Figure 8 and the calculation results of two Mo atoms are shown in Figure 9. The values of two single Mo atoms for different segregation sites are basically positive, except for Site 5, implying that two Mo atoms are more difficult to segregate into the oxide. The presence of B reduces the segregation energy to a negative value, and it becomes more and more negative from the substrate (Site 1) to the interface (Site 3). The effect of B on the segregation of two Mo atoms is similar to that of a single Mo atom. However, the lowest was recorded at the interface (−0.84 eV) instead of in the oxide layer, indicating that the most stable position has changed and the two Mo atoms are more likely to segregate to the interface rather than to the oxide layer. According to the segregation behavior of a single Mo atom and two Mo atoms, the addition of B can promote the diffusion of Mo into the oxide layer, but will only increase the Mo content in the passivation film to a small extent.
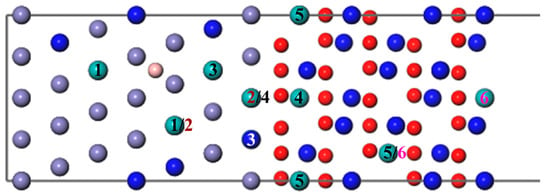
Figure 8.
The different diffusion sites of two Mo atoms at the Fe–Cr/Cr2O3 interface with and without B. (The labels 1–6 represent different diffusion sites of two atoms. The same number means a diffusion site, and the Mo atom represented by the white Number 3 is behind the blue Cr atom, which cannot be seen.).
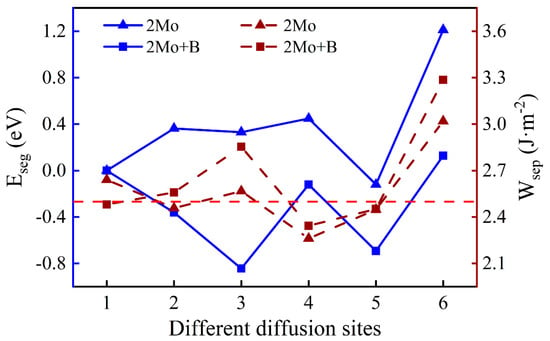
Figure 9.
The segregation energy and the work of separation of different diffusion sites for two Mo atoms with and without B.
There is a minor difference in the work of separation values with and without B. Similarly, the work of separation without B is higher when the two Mo atoms are uniformly distributed in the substrate (Site 1). However, the interface containing B has higher work of separation with Mo at other sites. At the interface, the largest work of separation is 2.85 J·m−2 at the most stable site, which indicates that the interface has a higher adhesion. When Mo atoms are in the oxide layer excluding the surface, interfacial bonding is weakened. That is likely because Mo atoms in the oxide near the interface cause greater interfacial stress.
3.4. Interface Electronic Structure
The charge density describes the distribution of valence electrons, which can mirror general bonding situations and the strength of atomic interactions. The electron localization function (ELF) can easily reveal types of bonding and the distribution of lone electron pairs. The value of ELF is limited between “0” and “1”, where “1” signifies complete electron localization and “0” corresponds to complete electron delocalization or no-electron domain [54,55,56]. The value ELF = 0.5 represents electron gas-like pair probability. Therefore, charge density and ELF were computed to explore the atomic interactions and electronic bonding properties. The computed results near the interface are shown in Figure 10, which can be divided into three situations: A single B atom at the interface, a Mo atom in the middle of the oxide, and two Mo atoms near the interface in the substrate with B added.
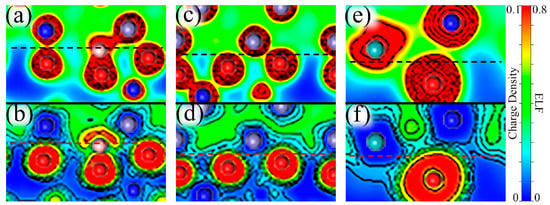
Figure 10.
Charge densities and the electron localization functions (ELFs) near the Fe–Cr/Cr2O3 interface. (a,c,e) depict the charge densities near the interface with a single B atom (Site 4), a Mo atom + a B atom (Site 5), and two Mo atoms + a B atom (Site 3), respectively. (b,d,f) describe the corresponding ELFs. These graphs do not represent the real size of the atoms, but only reflects the electronic characteristics. The gray atoms are Fe, the blue atoms represent Cr, the smaller red atoms are O, the smaller pink atoms correspond to B and the larger cyan atoms are Mo. The location of the interface is marked by dashed lines.
With B at the interface, we can see from Figure 10a that in terms of charge density between B and O atoms they share charges and have a strong interaction. Furthermore, Figure 10b shows a localization domain between B and O atoms, which suggests that the binding of B–O is dominantly covalent. However, it should be noted that the lone pair electrons of the B atom on the outside of the B–O bond have an adverse effect on the binding between B and interfacial metal atoms. This also explains why B has a better binding with the oxide layer than with the substrate. Similarly, we can further analyze the effects on electronic properties for the addition of Mo. When a Mo atom is in the middle of the passive film, we can see from Figure 10c that with the Mo atom far away from the interface, the Fe and O atoms near the interface are more closely bound, mainly because the distortion caused by the distant Mo atom can be relieved by the surface and only affects the interface slightly. Figure 10d shows two different regions between interfacial Fe and O atoms, a delocalization region around the Fe atom, and a localized domain surrounding the O atom, which reveals ionic bonds between Fe–O. The asymmetric ELF around Fe shows the directionality of the bonds, indicating that Fe–O bonds are somewhat covalent. When two Mo atoms are segregated at the interface, the interfacial Mo atom migrates closer to the oxide layer than the same-layer metal atoms, which is reflected in Figure 10e. The characteristics of Cr–O and Mo–O bonds are similar to Fe–O bonds, but their covalency is stronger, which can be seen in Figure 10f.
4. Conclusions
We investigated the interaction between B and Mo at the Fe–Cr(111)/Cr2O3(0001) interface through first-principles calculations. The most stable interface is topCr1, where one Fe atom is on top of the Cr1 site at the interface, and then Cr atoms were added into the Fe substrate part of this interface, which was chosen as the basic configuration to explore the effects of B and Mo additives. According to the calculated segregation energies, it is found that neither a single Mo atom nor two Mo atoms can easily diffuse into the oxide layer. However, the results show that B can promote the segregation of Mo into the Cr2O3 oxide to increase the Mo content in the passive film, and that the most stable interface structure has better interfacial adhesion under the combined effect of B and Mo. Therefore, the addition of B can not only inhibit the precipitation of second phases, but also improve the adhesion between the substrate and the passive film and the Mo content in the oxide layer. All these effects of B can improve the corrosion resistance of super austenitic stainless steel. Analyses of the electronic properties reveal the bonding characteristics and the strength of atomic interactions. The interfacial B atom has a weak interaction with the substrate and is harmful to the interfacial adhesion. The Cr–O and Mo–O bonds are both ionic and covalent, and the addition of a Mo atom can cause greater distortion, which has a significant effect on the interfacial adhesion.
Author Contributions
Data collection, Y.Z.; data analysis, Y.Z. and N.D.; writing—original draft preparation, Y.Z.; writing—review and editing, C.Z.; literature search, Y.Z. and C.Z.; formal analysis, Y.Z. and Y.L.; figures Y.Z. and Z.L.; visualization, Z.L.; study design, C.Z., P.H., and J.W.; software Z.Z.; funding acquisition, Z.Z., N.D., P.H. and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the National Natural Science Foundation of China (Grants No.51871159, No.U1860204, No.51801133), the Natural Science Foundation of Shanxi Province (Grants No.201801D221125, No.201901D111103, No.201901D111109), and Opening Project of PCOSS, Xiamen University (No. 201928).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Olsson, J.; Wasielewska, W. Applications and experience with a Superaustenitic 7Mo stainless steel in hostile environments. Mater. Corros. 1997, 48, 791–798. [Google Scholar] [CrossRef]
- Kim, S.J.; Hong, S.G. A study on pitting initiation mechanism of super-austenitic stainless steel weld in chloride environment. J. Mater. Res. 2016, 31, 1–7. [Google Scholar] [CrossRef]
- Dong, Y.Q.; Jiang, B.T.; Xu, D.K.; Jiang, C.Y.; Li, Q.; Gu, T.Y. Severe microbiologically influenced corrosion of S32654 super austenitic stainless steel by acid producing bacterium Acidithiobacillus caldus SM-1. Bioelectrochemistry 2018, 123, 34–44. [Google Scholar] [CrossRef]
- Heino, S. Role of Mo and W during sensitization of superaustenitic stainless steel—crystallography and composition of precipitates. Metall. Mater. Trans. A 2000, 31, 1893–1905. [Google Scholar] [CrossRef]
- Heino, S.; Karlsson, B. Cyclic deformation and fatigue behaviour of 7Mo–0.5N superaustenitic stainless steel-tress-strain relations and fatigue life. Acta Mater. 2001, 49, 339–351. [Google Scholar] [CrossRef]
- Koutsoukis, T.; Redjaïmia, A.; Fourlaris, G. Phase transformations and mechanical properties in heat treated superaustenitic stainless steels. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2013, 561, 477–485. [Google Scholar] [CrossRef]
- Bai, J.G.; Cui, Y.S.; Wang, J.; Dong, N.; Qurashi, M.S.; Wei, H.R.; Yang, Y.C.; Han, P.D. Effect of boron addition on the precipitation behavior of S31254. Metals 2018, 8, 497. [Google Scholar] [CrossRef]
- Qurashi, M.S.; Cui, Y.S.; Wang, J.; Dong, N.; Bai, J.G.; Wu, Y.C.; Han, P.D. Corrosion resistance and passivation behavior of b-containing S31254 stainless steel in a low pH medium. Int. J. Electrochem. Sci. 2019, 14, 10642–10656. [Google Scholar] [CrossRef]
- Carling, K.M.; Carter, E.A. Effects of segregating elements on the adhesive strength and structure of the α-Al2O3/β-NiAl interface. Acta Mater. 2017, 55, 2791–2803. [Google Scholar] [CrossRef]
- Shi, S.Q.; Tanaka, S.; Kohyama, M. First-Principles investigation of the atomic and electronic structures of α-Al2O3 (0001)/Ni(111) interfaces. J. Am. Ceram. Soc. 2007, 90, 2429–2440. [Google Scholar] [CrossRef]
- Hou, P.Y. Segregation phenomena at thermally grown Al2O3/Alloy interfaces. Ann. Rev. Mater. Res. 2008, 38, 275–298. [Google Scholar] [CrossRef]
- Punkkinen, M.P.J.; Kokko, K.; Levämäki, H.; Ropo, M.; Lu, S.; Delczeg, L.; Zhang, H.L.; Delczeg-Czirjak, E.K.; Johansson, B.; Vitos, L. Adhesion of the iron–chromium oxide interface from first-principles theory. J. Phys. Condens. Matter 2013, 25, 495501. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Smith, J.; Evans, A. First principles assessment of metal/oxide interface adhesion. Appl. Phys. Lett. 2008, 92, 141918. [Google Scholar] [CrossRef]
- Lan, G.Q.; Jiang, Y.; Yi, D.Q.; Liu, S.J. Theoretical prediction of impurity effects on the internally oxidized metal/oxide interface: The case study of S on Cu/Al2O3. Phys. Chem. Chem. Phys. 2012, 14, 11178–11184. [Google Scholar] [CrossRef] [PubMed]
- Dong, N.; Zhang, C.L.; Liu, H.; Fan, G.W.; Fang, X.D.; Han, P.D. Effects of different alloying additives X (X=Si, Al, V, Ti, Mo, W, Nb, Y) on the adhesive behavior of Fe/Cr2O3 interfaces: A first-principles study. Comput. Mater. Sci. 2015, 109, 293–299. [Google Scholar] [CrossRef]
- Kamiya, T.; Tajima, K.; Nomura, K.; Yanagi, H.; Hosono, H. Interface electronic structures of zinc oxide and metals: First-principle study. Phys. Status Solidi A Appl. Mat. 2008, 205, 1929–1933. [Google Scholar] [CrossRef]
- Li, J.G.; Zhang, C.L.; Xu, L.; Zhang, Z.X.; Dong, N.; Liu, Y.; Wang, J.; Zhang, Y.L.; Ling, L.X.; Han, P.D. Effects of B on the segregation of Mo at the Fe-Cr-NiΣ5(210) grain boundary. Physica B 2019, 568, 25–30. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Jones, R.O. Density functional calculations for atoms, molecules and clusters. Phys. Scr. 1980, 21, 394–401. [Google Scholar] [CrossRef]
- Jones, R.O.; Gunnarsson, O. The density functional formalism, its applications and prospects. Rev. Mod. Phys. 1989, 61, 689–746. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1966, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.L.; Wu, P.; Chen, S.; Zhang, S.; Chen, N.; Huai, X.L. First principles calculation of boron diffusion in fcc-Fe. Curr. Appl. Phys. 2018, 18, 1108–1112. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, Y.K.; Soon, A. The austenite/ɛ martensite interface: A first-principles investigation of the fcc Fe(111)/hcp Fe(0001) system. Appl. Surf. Sci. 2012, 258, 9977–9981. [Google Scholar] [CrossRef]
- Leonov, I.; Poteryaev, A.I.; Anisimov, V.I.; Vollhardt, D. Calculated phonon spectra of paramagnetic iron at the α-γ Phase transition. Phys. Rev. B 2011, 85, 020401. [Google Scholar] [CrossRef]
- Jiang, D.E.; Carter, E.A. Carbon dissolution and diffusion in ferrite and austenite from first principles. Phys. Rev. B 2003, 67, 214103. [Google Scholar] [CrossRef]
- Zhang, H.L.; Al-Zoubi, N.; Johansson, B.; Vitos, L. Alloying effects on the elastic parameters of ferromagnetic and paramagnetic Fe from first-principles theory. J. Appl. Phys. 2011, 110, 073707. [Google Scholar] [CrossRef]
- Okatov, S.V.; Kuznetsov, A.R.; Gornostyrev, Y.N.; Urtsev, V.N.; Katsnelson, M.I. Effect of magnetic state on γ-α transition in iron: First-principle calculations of the Bain transformation path. Phys. Rev. B 2008, 79, 094111. [Google Scholar] [CrossRef]
- Ai-Zoubi, N.; Johansson, B.; Nilson, G.; Vitos, L. The Bain path of paramagnetic Fe-Cr based alloys. J. Appl. Phys. 2011, 110, 366–373. [Google Scholar]
- Rohrbach, A.; Hafner, J.; Kresse, G. Ab initio study of the (0001) surfaces of hematite and chromia: Influence of strong electronic correlations. Phys. Rev. B 2004, 70, 125426. [Google Scholar] [CrossRef]
- Onink, M.; Brakman, C.M.; Tichelaar, F.D.; Mittemeijer, E.J.; Van der Zwaag, S.; Root, J.H.; Konyer, N.B. The lattice parameters of austenite and ferrite in Fe-C alloys as functions of carbon concentration and temperature. Scr. Metall. Mater. 1993, 29, 1011–1016. [Google Scholar] [CrossRef]
- Mazur, J. Lattice parameters of martensite and of austenite. Nature 1950, 166, 828. [Google Scholar] [CrossRef]
- Di Cerbo, R.K.; Seybolt, A.U. Lattice parameters of the α-Fe2O3-Cr2O3 solid solution. J. Am. Ceram. Soc. 2006, 42, 430–431. [Google Scholar] [CrossRef]
- Finger, L.W.; Hazen, R.M. Crystal structure and isothermal compression of Fe2O3, Cr2O3, and V2O3 to 50 Kbars. J. Appl. Phys. 1980, 51, 5362–5367. [Google Scholar] [CrossRef]
- Peng, M.M.; Lai, W.S. Interaction between vacancies and the α-Fe/Y2O3 interface: A first-principles study. Nucl. Instrum. Methods B 2015, 352, 67–71. [Google Scholar] [CrossRef]
- Liu, S.Y.; Shang, J.X.; Wang, F.H.; Zhang, Y. Surface segregation of Si and its effect on oxygen adsorption on a γ-TiAl(111) surface from first principles. J. Phys.-Condes. Matter 2009, 21, 225005. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.P.; Zhao, S.J. First principles study of Al and Ni segregation to the α-Fe/Cu (100) coherent interface and their effects on the interfacial cohesion. Comput. Mater. Sci. 2012, 63, 329–335. [Google Scholar] [CrossRef]
- Batirev, I.G.; Alavi, A.; Finnis, M.W.; Deutsch, T. First-principles calculations of the ideal cleavage energy of Bulk Niobium(111)/α-Alumina (0001) interfaces. Phys. Rev. Lett. 1999, 82, 1510–1513. [Google Scholar] [CrossRef]
- Adams, J.B.; Hector Jr, L.G.; Siegel, D.J.; Yu, H.; Zhong, J. Adhesion, lubrication and wear on the atomic scale. Surf. Interface Anal. 2001, 31, 619–626. [Google Scholar] [CrossRef]
- Johnson, D.F.; Carter, E.A. Bonding and adhesion at the SiC/Fe interface. J. Phys. Chem. A 2009, 113, 4367–4373. [Google Scholar] [CrossRef]
- Sasaki, T.; Mizoguchi, T.; Matsunaga, K.; Tanaka, S.; Yamamoto, T.; Kohyama, M.; Ikuhara, Y. HRTEM and EELS characterization of atomic and electronic structures in Cu/α-Al2O3 interfaces. Appl. Surf. Sci. 2005, 241, 87–90. [Google Scholar] [CrossRef]
- Xiao, M.X.; Zhao, M.L.; Lang, X.Y.; Zhu, Y.F.; Jiang, Q. Improvement of electromigration reliability and diffusion of Cu films using coherent Cu(111)/Cr2O3(0001) interfaces. Chem. Phys. Lett. 2012, 542, 85–88. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.P.; Zhang, C.L.; Dong, N.; Lan, A.D.; Li, H.F.; Dong, H.B.; Han, P.D. Effects of aluminum diffusion on the adhesive behavior of the Ni(111)/Cr2O3(0001) interface: First principle study. Comput. Mater. Sci. 2013, 78, 116–122. [Google Scholar]
- Lan, G.Q.; Wang, Y.R.; Jiang, Y.; Zhou, H.M.; Yi, D.Q. Effects of rare-earth dopants on the thermally grown Al2O3/Ni(Al) interface: The first-principles prediction. J. Mater. Sci. 2014, 49, 2640–2646. [Google Scholar] [CrossRef]
- Zhang, W.; Smith, J.R.; Evans, A.G. The connection between ab initio calculations and interface adhesion measurements on metal/oxide systems: Ni/Al2O3 and Cu/Al2O3. Acta Mater. 2002, 50, 3803–3816. [Google Scholar] [CrossRef]
- Liu, W.; Li, J.C.; Zheng, W.T.; Jiang, Q. NiAl(110)/Cr(110) interface: A density functional theory study. Phys. Rev. B 2006, 73, 205421. [Google Scholar] [CrossRef]
- Yuge, K.; Kishida, K.; Inui, H.; Koizumi, Y.; Hagihara, K.; Nakano, T. Cr segregation at C11b/C40 interface in MoSi2-based alloys: A first-principles study. Intermetallics 2013, 42, 165–169. [Google Scholar] [CrossRef]
- Li, Y.P.; Han, C.; Zhang, C.L.; Jia, K.; Han, P.D.; Wu, X.L. Effects of alloying on the behavior of B and S at ∑5 (210) grain boundary in γ-Fe. Comp. Mater. Sci. 2016, 115, 170–176. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Shetty, S.; Pal, S.; Kanhere, D.G. A study of electronic and bonding properties of Sn doped Lin clusters and aluminum based binary clusters through electron localization function. J. Chem. Phys. 2003, 118, 7288–7296. [Google Scholar] [CrossRef]
- Saha, D.; Mahapatra, S. Theoretical insights on the electro-thermal transport properties of monolayer MoS2 with line defects. J. Appl. Phys. 2016, 119, 134304. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).