A Physics-Based Mean-Field Model for Ferrite Recovery and Recrystallization

Abstract

An original mean field model for the nucleation and the growth of new recrystallized grains during annealing treatments of deformed, low-carbon ferritic steels is proposed in this paper. The model was calibrated on two steels extensively studied in the literature under both isothermal annealing and continuous heating schedules. It permits one to predict not only recrystallization kinetics but also advanced microstructural features (such as dislocation density, dislocation cell size and grain size) during complex heat treatments. Once calibrated, the model was applied to the case of a third ferrite/pearlite steel and was shown to accurately capture the effect of cold-rolling ratio on the recrystallization kinetics.

1. Introduction

Recovery and recrystallization lead to important changes in the microstructure of deformed ferrite during the annealing of cold-rolled steels. Both phenomena are governed by the same driving force; i.e., the decrease in the elastic energy due to deformation-induced defects, such as dislocations in the deformed microstructure. Recovery and recrystallization, hence, compete for the same driving force during the annealing process and both can strongly affect the morphogenesis of the ferrite/austenite microstructure in the intercritical range, which is a key and current concern for steelmakers [1,2,3,4,5,6,7]. Indeed, the resulting sizes, morphologies and topologies of the phases govern, for instance, the tensile and damaging properties of advanced dual-phase steels [8,9,10].

The recrystallization of austenite at high temperatures has been the subject of numerous works due to its industrial significance for the production of micro-alloyed, thermo-mechanical control processed (TMCP) steels [11,12,13]. The recrystallization of deformed ferrite during annealing, after cold-rolling, has been less studied. Existing works in the literature on this topic led to two kinds of models. The first kind corresponds to mean-field approaches, aiming mainly at calculating the recrystallization kinetics. Such models are reasonably able to capture the growth process of the newly recrystallized grains by thermally-activated motion of high angle grain boundaries. On the contrary, the nucleation process is rarely accounted for, as it requires describing the simultaneous evolution of a dislocation structure (density, cells, subgrains) and a nucleation rate. A typical example of such a model is that proposed by Li et al. [14] to predict the recrystallization kinetics during continuous annealing at constant heating rate assuming the validity of the Johnson–Mehl–Avrami–Kolmogorov (JMAK) equations during infinitesimal small isothermal steps.

$$\mathrm{X}=1-\exp (-\frac{\mathrm{n}}{{\mathsf{\beta }}^{\mathrm{n}}}{{\displaystyle \int }}_{{\mathrm{T}}^{*}}^{\mathrm{T}}{\mathrm{b}}_0\exp (-\frac{\mathrm{Q}}{\mathrm{RT}}){(\mathrm{T}-{\mathrm{T}}^{*})}^{\mathrm{n}-1}\mathrm{dT})$$

(1)

In this expression, X is the recrystallized fraction as a function of temperature T, β is the constant heating rate, R is the gas constant, Q is the apparent activation enthalpy of the growth process, n is a parameter describing the nature of the nucleation process, b₀ is a calibration parameter and T* is the temperature for the start of the recrystallization process. The reported values of n for the recrystallization of cold-rolled steels, are generally small (lower than 3), indicating that nucleation is inhomogeneous (n = 1.7, Zhu et al. [15]; n = 1, Huang et al. [16]; and n = 1.7, Kulakov et al. [4]). In addition, the activation energies are generally higher than the values expected for grain-boundary self-diffusion in alpha iron (125 kJ∙mol⁻¹ up to 170 kJ∙mol⁻¹ according to [17] or 148 kJ∙mol⁻¹ according to [18]) and those for bulk diffusion (285 kJ∙mol⁻¹ up to 330 kJ∙mol⁻¹ according to [17]), suggesting that the mobility of the interface could be controlled by substitutional elements (Q = 350 kJ∙mol⁻¹ for Huang et al. [16] for instance). However, the predicting-ability of such a framework remains limited insofar as the temperature of the start of recrystallization, T*, is in fact a complex function of β. This function must also be calibrated for each steel and for each initial deformation state. Moreover, Liu et al. [19] have highlighted that the recrystallization process can show two stages, the first one controlled by both nucleation and growth and the second by the growth only (saturation of nucleation site). The independent modeling of both mechanisms is thus of the greatest interest for capturing such fine features.

The second group of models corresponds to full-field approaches able to reproduce the microstructural evolution of a representative elementary volume (REV). These models which include vertex, Monte Carlo Potts and phase-field [15,20] approaches and cellular automata [2,21], can predict the recrystallization start temperature, kinetics and final microstructures but require large Central Processing Unit (CPU) resources. They also lack versality as the local field describing the initial REV must be reparametrized for each steel studied.

In this paper, we propose an original mean-field model for both recovery and recrystallization, and the interaction between the two processes. Dislocation recovery has been modeled based on Friedel’s seminal work. Recrystallization kinetics were predicted by a new model merging a nucleation model adapted from Zurob et al. [11,12] and a growth model based on interface-controlled growth, similar to the one used by Sinclair et al. [18]. Hence, our new model predicts the evolutions of dislocation structures, and the nucleation of new recrystallized grains and their growth. In that sense, the model is physics-based, is sufficiently flexible to describe any thermal treatments (isothermal, multistep, continuous heating) and any initial microstructure states (deformed ferritic grains) and can be considered as CPU efficient.

2. Materials and Methods

For the sake of demonstration, the parameters and mobility functions were calibrated to best reproduce experimental trends observed for two cold-rolled ferrite-pearlite steels that have been extensively described in the literature. The steels were chosen with low fractions of pearlite to minimize the possible interactions between phases. Both isothermal and continuous heating conditions were examined to calibrate the model over a wide range of temperatures. The first steel (steel A) has been studied by Huang et al. [16] and is a Fe-0.06C-1.86Mn-0.155Mo (wt.%) steel which has been cold-reduced by 55% with a hot-rolled grain size of 6µm and a pearlite fraction of 11%. The heat treatment (isothermal holding at 600, 650, 680 and 710 °C and continuous heating at 1 and 10 °C/s) has been performed using a Gleeble device and the recrystallisation fraction was measured by conventional techniques; i.e., using a combination of hardness measurements and direct microstructure observations. Using the available data, the dislocation density in the deformed state has been estimated to be around 2.7 × 10¹⁵ m.m⁻³ using the micromechanical model of Bouaziz et al. for cold-rolled ferritic-steels [22]. The second steel (steel B) has been studied by Zhu et al. [15] and is a Fe–0.11C–1.86Mn-0.16Si–0.34Cr (wt.%) steel which was cold-reduced 50% with a hot-rolled grain size of 2.8 µm and containing 5% pearlite. The experimental heat treatments consisted of isothermal holding at 600, 625 or 650 °C and continuous heating at 1 or 10 °C/s (all the details have not been given in the original publication). The density of dislocation in the deformed state has been estimated to be 1.7 × 10¹⁵ m.m⁻³. In the last part of this paper, the model will also be applied to the steel studied by Moreno et al. (steel C) [7,23]. The purpose is to demonstrate that it is able to capture the effect of cold-reduction ratio on recrystallization kinetics. The recrystallization kinetics in this last work were measured using an original method developed by our group but which still needs some improvements. This new method cannot be considered well established for the time-being. This is the reason why we have not used these data to calibrate the model, and instead to show its ability to capture complex interactions between recovery and recrystallization in the second part of this paper.

The main characteristics of the steels used to calibrate and to assess the model are summarized in

Table 1. Compositions (wt.%) and microstructural states before cold-rolling of the ferrite-pearlite studied steels.

Steel	Ref.	C	Mn	Mo	Si	Cr	Pearlite Fraction (%)	Ferrite Grain Size (µm)	Cold-Rolling Ratio (%)
Steel A	[16]	0.06	1.86	0.155	-	-	11	6	55
Steel B	[15]	0.11	1.86	-	0.16	0.34	5	2.8	50
Steel C	[7,23]	0.1	1.9	-	0.2	0.2	16	8	30/61

. It should be emphasized that the three studied steels present almost the same nominal Mn content.

3. Modeling Approach

Most models of recrystallization estimate the driving force, G, for the growth of new grains based on the stored energy in the deformed structure [24]. This stored energy is directly proportional to the density of dislocations ρ:

$$\mathrm{G}=\frac{1}{2}\mathsf{\mu }{\mathrm{b}}^2\mathsf{\rho }$$

(2)

where µ is the shear modulus and b the Burgers vector. The estimation of the dislocation density during annealing, which is controlled by recovery, is thus a prerequisite to modeling recrystallization.

3.1. Recovery

Different equations are proposed in the literature to model the evolution of the dislocation density ρ as a function of time t and temperature T [25]. The model developed by Verdier et al. [26] for Al-Mg alloys was able to reproduce some observed trends in ferritic steels but not it did not lead to a perfect agreement with the experimental data (e.g., data of Moreno et al. [23]). For this reason, we could not justify the use of the complex model of Verdier et al. and reverted to the original relaxation model of Friedel et al. [27]:

$$\frac{\mathrm{d}\mathsf{\rho }}{\mathrm{dt}}=-\mathrm{Kexp}\left(\frac{-{\mathrm{U}}_0+\mathrm{V}\mathsf{\alpha }\mathrm{M}\mathsf{\mu }\mathrm{b}\sqrt{\mathsf{\rho }}}{\mathrm{kT}}\right)\frac{2\sqrt{\mathsf{\rho }}}{\mathsf{\alpha }\mathrm{M}\mathsf{\mu }\mathrm{b}}$$

(3)

The parameters of the forest hardening equations were set as follows: α = 0.15, M = 3, b = 2.5 × 10⁻¹⁰ m. The model of Ghosh and Olson [28] was employed for the evolution of the elastic constants as a function of the temperature. U₀, V and K have been considered as calibration parameters. In the absence of experimental data on steels A and B, the parameters have been adjusted to best reproduce the recovery process under isothermal conditions at 450 and 550 °C but also during continuous annealing (3 and 30 °C∙s⁻¹) of steel C [7]. In those particular cases, the data have been obtained via the Williamson–Hall method applied on in situ high energy X-ray experiments on synchrotron beamlines. The parameters were set to U₀ = 180 kJ∙mol⁻¹, V = 30 b³ and K = 10¹³ Pa. These values are consistent with those found in the literature, particularly for the activation energy, U₀, which is a fraction of the one for bulk iron diffusion (2/3) as discussed above. It could be consistent with a pipe diffusion process (150 kJ∙mol⁻¹ or 174 kJ∙mol⁻¹ for dislocation core diffusion according Stechneur and Nes [17,29]) or grain-boundary diffusion processes. The activation volumes are also similar to the ones proposed by Verdier et al. (about 40 b³ in Al at 120 °C) [26] and by Zurob et al. (35 b³ in austenite at high temperature) [12] even if the comparison is not straightforward.

3.2. Recrystallization

For the recrystallisation part, the proposed modeling is largely adapted from Zurob et al. [12,13]. It first describes the nucleation rate considering that only the largest subgrains can evolve into a new recrystallized grain according to the SIBM theory (strain induced boundary migration). The probability of this nucleation event depends on a critical radius r_c, calculated according the Bailey–Hirsch criterion. Contrary to the simplifying choice of Sinclair et al. [18] and Zhu et al. [15] who have considered a fixed number of sites, this approach permits a physics-based description of the start of recrystallization and avoids the arbitrary determination of recrystallization start temperature, T*.

The first step of the model consists of calculating the subgrain size in non-recrystallized ferrite, which is a byproduct of the recovery mechanism. In the studied steel, the typical radius of the subgrains is of the order of a micrometer. Zurob et al. [12] assumed that their mean radius was governed by the rate at which the low angle boundaries migrates when the migration process is controlled by the climb of extrinsic dislocations [30]:

$$\langle \mathrm{r}\left(\mathrm{t}\right)\rangle ={\mathrm{r}}_0+{{\displaystyle \int }}_0^{\mathrm{t}}\frac{2}{\mathrm{L}}{\mathrm{D}}_{\mathrm{Fe}}\left(\mathrm{T}\right)\sin \mathrm{h}\left({\mathrm{K}}_{\mathrm{ad}}\frac{{\mathsf{\alpha }\mathrm{M}\mathsf{\mu }\mathrm{b}}^3}{\mathrm{kT}}\right)\mathrm{dt}$$

(4)

where r₀ is the initial mean radius of the subgrains inherited from the cold-rolling process and K_ad is a calibration parameter. T is given in K in all subsequent equations. D_Fe is the bulk self-diffusion of ferromagnetic bcc iron. In this work we used the value proposed by Stechneur et al. (in m²∙s⁻¹) [17]:

$${\mathrm{D}}_{\mathrm{Fe}}\left(\mathrm{T}\right)=6.0\times {10}^{-4}\exp (-\frac{\mathrm{285,000}}{\mathrm{RT}})$$

(5)

The same activation energy was employed by Nes [29] (280 kJ∙mol⁻¹) and was suggested for ferromagnetic ferrite by Kučera [31] (292 kJ∙mol⁻¹). The whole model is extremely sensitive to the choice of this diffusion coefficient which in fact controls the nucleation process.

The critical radius for nucleation r_c is given by:

$${\mathrm{r}}_{\mathrm{c}}=\frac{2\mathsf{\gamma }}{\frac{1}{2}\mathsf{\Delta }{\mathsf{\rho }\mathsf{\mu }\mathrm{b}}^2}$$

(6)

where γ is the interfacial energy of the bulging grain boundary, and Δρ the difference in dislocation density across the moving boundary. This is the size that a subgrain must reach to possibly become a new grain. For the sake of simplicity, we can assume that the new grains are defect-free, meaning that Δρ = ρ. As the density of dislocations decreases during the thermal treatment, the driving force for recrystallization decreases while the critical radius increases as per Equation (6).

The main innovation brought by Zurob et al. [12] is to introduce the subgrain size distribution around the mean value, <r>. Such a distribution follows the Rayleigh law [32,33]. Hence the fraction of subgrain having a size greater than the critical radius r_c is given by:

$$\mathrm{f}\left(\mathrm{t}\right)={{\displaystyle \int }}_{\frac{{\mathrm{r}}_{\mathrm{c}}}{\langle \mathrm{r}\rangle }}^{+\infty }\frac{\mathsf{\pi }}{2}\frac{\mathrm{r}}{\langle \mathrm{r}\rangle }\exp \left(-\frac{\mathsf{\pi }}{4}{\left(\frac{\mathrm{r}}{\langle \mathrm{r}\rangle }\right)}^2\right)\mathrm{d}\left(\frac{\mathrm{r}}{\langle \mathrm{r}\rangle }\right)=\exp \left(-\frac{\mathsf{\pi }}{4}{\left(\frac{{\mathrm{r}}_{\mathrm{c}}}{\langle \mathrm{r}\rangle }\right)}^2\right)$$

(7)

If the critical radius is twice higher than the mean subgrain size, then the probability to find a cell larger than this critical value is less than 5%. In contrast, if the mean subgrain size is equal to the critical size, the probability increases up to 46%. Zurob et al. [12] established that the increase in the number of the active nuclei, N is directly proportional to the increase in f. According the experimental observations of Lefevre-Schlick et al. on pure iron [34], nucleation sites are mainly located on deformed ferrite grain boundaries and the most favorable sites are triple junctions. A rough estimate of nucleation sites on a triple junction is given by:

$$N_0=\frac{\delta }{D^2{r}_C}$$

(8)

where δ is a calibration parameter representing the viable proportion of nucleation sites on triple junctions. The shape of deformed grains and their increased surface area per unit induced by cold-rolling have not been considered in this model, as the preferred nucleation sites are the sole triple junctions. However, this contribution could be added in the next version to refine, possibly, the description of the nucleation sites.

In low carbon steels, Senuma et al. [35] have observed that the nucleation rate is limited when recrystallization reaches about 10%. These two-stage kinetics were also extensively studied by Liu et al. [19] in HSLA steels. Liu et al. showed that recrystallization occurs first by nucleation and growth of new grains and after a certain time by growth only. The transition between the two modes depends on the steel, the temperature and the cold-rolling ratio. The optical observations provided by Huang et al. at 650 °C, suggest that these results also apply to the steels being modelled in this work. The measurements of recrystallized grain density after 3 and 60 min are almost similar (about 5 × 10¹⁵ m⁻³). This value is of the same order of magnitude as the values retained by Zhu et al. (6.25 × 10¹⁵ m⁻³) for their phase-field simulations and those obtained by Sinclair et al. (5 × 10¹⁴ m⁻³). This observation corresponds in fact to a rapid exhaustion of the possible nucleation sites.

The two-stage kinetics cannot be described by the function, Fn, considered originally by Zurob et al. to account for the impingement of the austenite nuclei. This is partly due to the fact that the nucleation sites in the present ferritic steels are often isolated and independent. As a consequence, it has been chosen to express the nucleation rate using a saturating law:

$$\frac{\mathrm{dN}}{\mathrm{dt}}=\frac{\mathrm{df}}{\mathrm{dt}}{\mathrm{N}}_0\left(1-\frac{\mathrm{N}}{{\mathrm{N}}_0}\right)$$

(9)

Once the nucleation rate is known, the extended recrystallized volume X_ext corresponds to the number of active nuclei multiplied by the mean volume of the recrystallized grains whose mean size is $\overline{\mathrm{R}}$:

$${\mathrm{X}}_{\mathrm{ext}}={\mathrm{N}\frac{4}{3}\pi \overline{\mathrm{R}}}^3$$

(10)

The evolution of the radius R of a given independent grain is governed by a mobility equation:

$$\frac{\mathrm{dR}}{\mathrm{dt}}{=\mathrm{M}}_{\mathrm{HAB}}\mathrm{G}$$

(11)

with M_HAB being the mobility of the high angle boundary (HAB) and G the driving force of recrystallization; i.e., the energy stored in dislocation structures, given by Equation (2).

As the new recrystallized grains are formed progressively over time, a size distribution is obtained. To avoid the tedious calculation of the evolution of the distribution function, only the mean radius $\overline{\mathrm{R}}$ of the size distribution was tracked. At a given time step, the mean must account concomitantly for the increases of the radii of previously nucleated grains, and the contributions due to the radii of the newly nucleated ones. These new grains will of course contribute to slow down the evolution of the mean radius $\overline{\mathrm{R}}$. This leads to the expression:

$$\frac{\mathrm{d}\overline{\mathrm{R}}}{\mathrm{dt}}={\mathrm{M}}_{\mathrm{HAB}}\mathrm{G}+\frac{\mathrm{dN}}{\mathrm{Ndt}}({\mathrm{r}}_c-\overline{\mathrm{R}})$$

(12)

The increase in mean radius $\overline{\mathrm{R}}$ can be then integrated step by step, assuming that the initial grain size of the first nucleated grains is r_c. Finally, the recrystallized fraction X is given according the extended volume theory [18,36]:

$$\mathrm{X}=1-\exp \left(-{\mathrm{X}}_{\mathrm{ext}}\right)$$

(13)

3.3. Calibration of the Model

The model parameters have been adjusted accounting for the available data on steels A and B to best reproduce the experimental recrystallization kinetics. As the studied steels are rather similar, a common set of calibration parameters that works reasonably for both steels has been used instead of favoring a perfect adjustment with different parameters for each steel. Only the mobility equation, which is known to be highly sensitive to the chemical composition, has been adjusted separately on each dataset.

The initial subgrain size was set to r₀ = 0.2 µm, in accordance with the SEM (scanning electron microscopy) observations of Moreno et al. [7] on a similar steel (steel C). The grain boundary energy, γ, was set to 600 mJ∙m⁻² as suggested by Sinclair et al. [18] for ferritic steels and close to the value proposed by Zhu et al. [15] (800 mJ∙m⁻²). Accounting for the volume driving force available in steels A and B leads to a critical nucleus radius of about 0.8 µm, which is consistent with the experimental observations of Moreno et al. [7] on steel C. K_ad was set to 0.23 to obtain a reasonable agreement with the experimental data and to reproduce the early saturation of nucleation sites, as observed by Senuma et al. [35]. These values are close to the ones used by Rehman [13] for austenitic steels. δ has been fixed to 5% for studied steels in order to impose a realistic number of nucleation sites. As discussed above, the resulting values for N₀, as given by Equation (8), are in good agreement with the experimental observations.

Another important calibration parameter is the HAB (high angle grain-boundary) interface mobility M_HAB. Figure 1 shows a comparison between the thermally activated models for the mobility of high angle grain boundaries, as found in literature, and the values proposed to best fit the kinetics of the two steels studied here. For pure iron, Hillert proposed an expression based on grain-growth in alpha ferrite [37]. The equations proposed by Zheng et al. [2] and those calculated based on the Turnbull mobility [12,18] of pure iron lead to mobilities of the similar order of magnitude. The parameters in the Turnbull function were calculated using the activation energy for iron self-diffusion at grain boundaries given by Sinclair et al. [18]. However, the latter mobility values are probably relevant for pure iron but are too high for the studied steels. In fact, Turnbull’s model does not account for attachment kinetics, so it is necessarily an over-estimate. If solutes are present (Mn in particular), the kinetics would be much slower. That is the reason why Zhu et al. [20] proposed far lower mobility values for steel B with higher activation energy (360 kJ∙mol⁻¹) which is similar to the value retained by Huang et al. [16] for their JMAK modeling (350 kJ∙mol⁻¹). To obtain the best adjustments for studied steels A and B, we have considered the following mobility equations for the steels studied by Huang et al. and Zhu et al. respectively:

$${\mathrm{M}}_{\mathrm{HAB}}=\frac{4.85\times {10}^8}{\mathrm{T}}\exp (-\frac{\mathrm{350,000}}{\mathrm{RT}}) \text{Huang et al.} \left(\mathrm{steel\; A}\right)$$

(14)

$${\mathrm{M}}_{\mathrm{HAB}}=\frac{1.39\times {10}^8}{\mathrm{T}}\exp (-\frac{\mathrm{350,000}}{\mathrm{RT}}) \text{Zhu et al.} \left(\mathrm{steel\; B}\right)$$

(15)

It should be noted that Zheng et al. conducted their isothermal holding experiments at high temperatures above 700 °C where all the models are in fact equivalent.

4. Results and Discussions

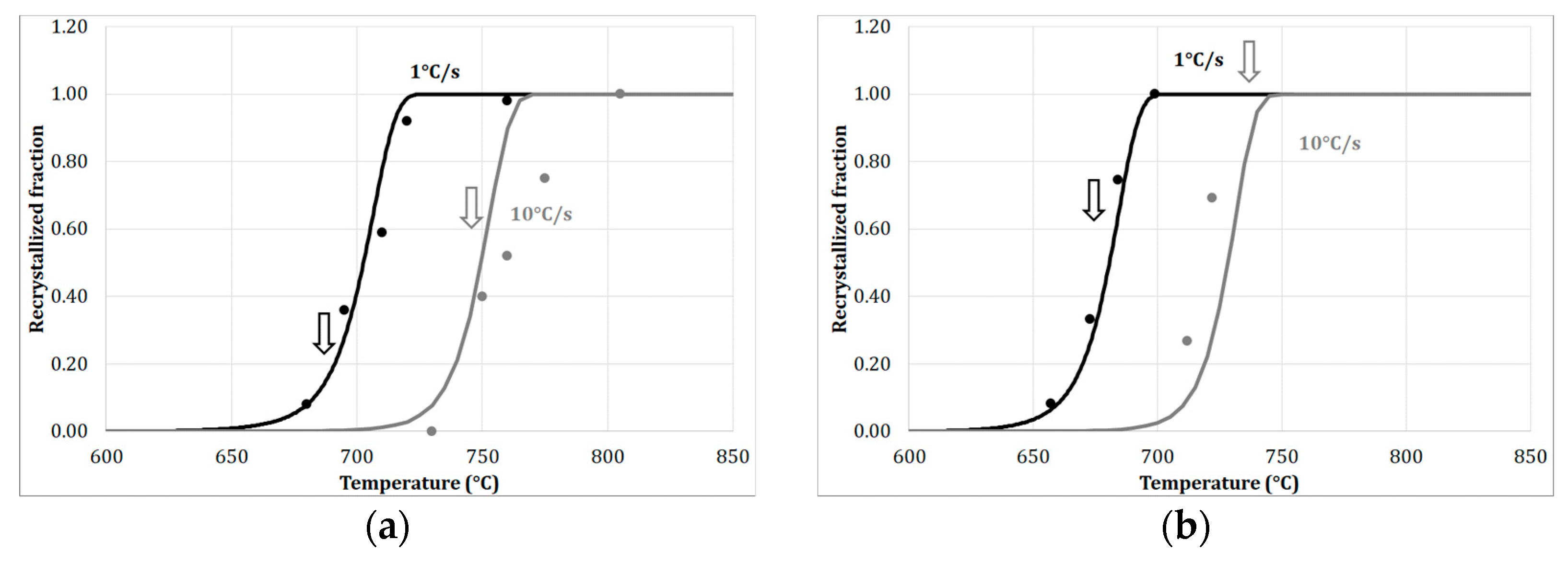
4.1. Results of the Calibration Procedure

The results of the model are compared with the recrystallization kinetics determined during the continuous heating at different rates in Figure 2a,b and isothermal annealing at different temperatures in Figure 2e,f for both steels, A and B. The previous equations were solved explicitly. The integration time step was chosen to provide a result insensitive to the step size (integration step time = 0.5 s). The calculations are in that sense CPU efficient and can be performed using a very basic solver (calculation time <1 s for any thermal treatment with the considered step time). The calibration procedure leads to an excellent agreement between the experimental and calculated results with a single set of adjustable parameters. Only the mobility equation (M_HAB) has to be adapted for each steel.

Figure 2c,d shows the density of active nuclei during the continuous heating of both studied steels. As expected, the majority of nuclei become active before half of recrystallization is achieved. The arrows in Figure 2a,b represent the time at which 80% of nuclei are already active. The model thus permits predicting, unambiguously, the nucleation and growth stages. As shown by [19], recrystallization occurs in two stages, the first characterized by the concomitance of nucleation and growth and the second by the sole growth of recrystallized grains. However, the transition between these two stages is hardly revealed by the study of the sole kinetics in the present cases.

The mean diameter predicted by the model for the isothermal heat treatment studied by Huang et al. is 11.5 µm at the end of the recrystallization. This value is in good agreement with the grain size measured experimentally (between 6.3 and 8.9 µm) as the values calculated by the models correspond to growth without impingement (cf. Equation (12)).

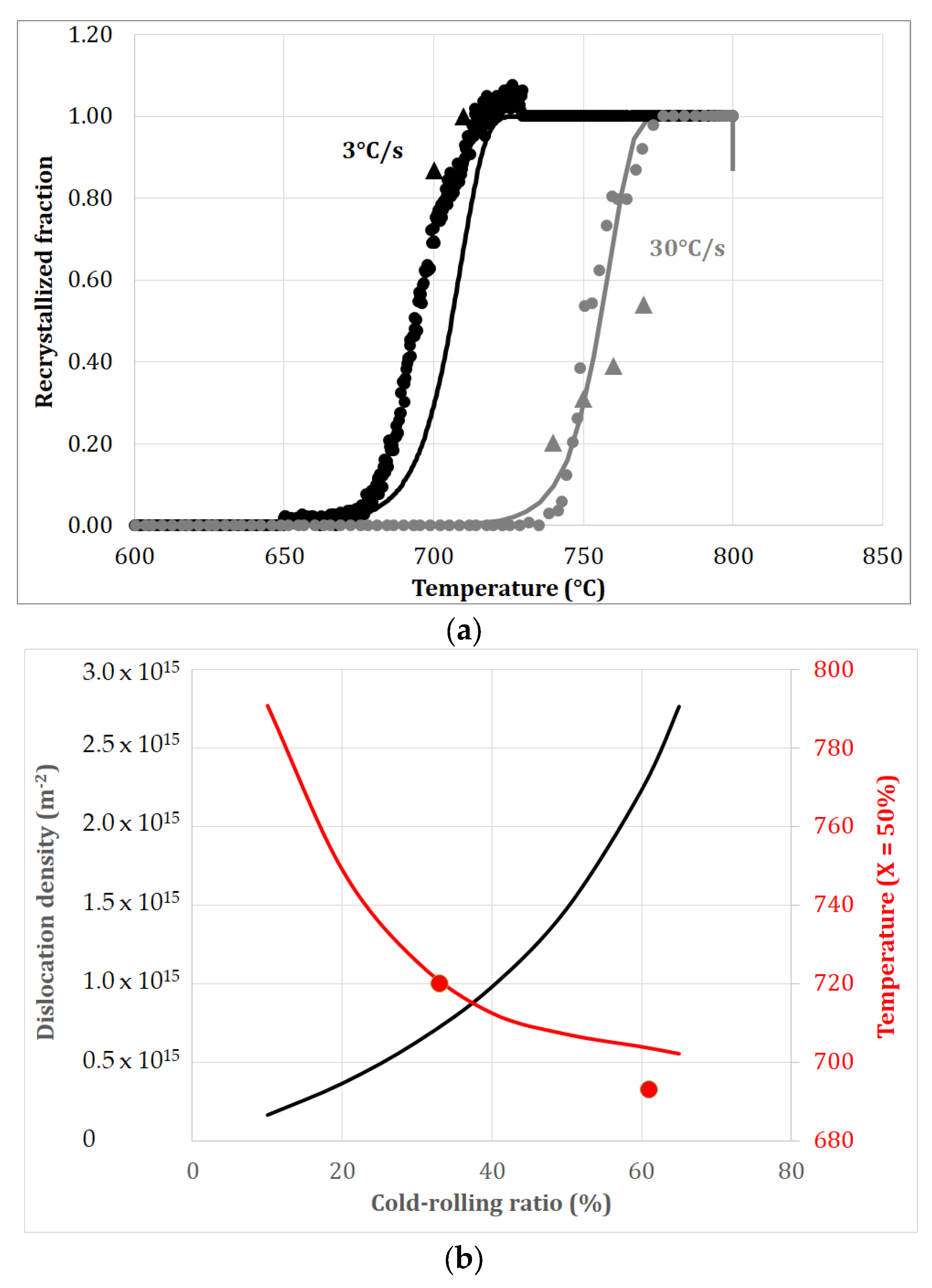
4.2. Effect of the Cold-Rolling Ratio

The model was then applied to the continuous heating experiments conducted by Moreno et al. on Fe-0.1C-1.9Mn-0.2Cr-0.2Si (steel C). Those data were not used to calibrate the model, since the kinetics were measured by high energy x-ray diffraction (HEXRD) and a new peak counting procedure, which cannot be considered as a reference and an absolute method to measure the recrystallized fraction. All the details about this original and exploratory method have been published elsewhere [7,23]. Steel C is similar to the steel studied by Zhu et al. except that the initial grain size is about 8 µm and the pearlite fraction was estimated to 16%. As a consequence, mobility (Equation (15)) calibrated on Zhu et al.’s data was used again. In the following, we will consider only the recrystallization process in the ferritic matrix. After 61% of cold-rolling, according to the work-hardening model of Bouaziz et al. [22], the density of dislocations was estimated to be 2.3 × 10¹⁵ m.m⁻³. Figure 3a shows the measured and calculated recrystallization kinetics for the studied steel at two heating rates (10 and 30 °C∙s⁻¹ respectively). Without any additional calibration, except the reasonable choice of the mobility equation, the results of the model are in excellent agreement with the experimental data (HEXRD and conventional microscopy).

The recrystallization kinetics has also been studied in steel C after a lower cold-rolling ratio. It appears that the onset of recrystallization is delayed by 30 °C (about 3 s at 10 °C∙s⁻¹) as the density of dislocations is reduced in ferrite, leading to a lower driving force for recrystallization. This phenomenon is well captured by the model, as shown in Figure 3b. The figure shows the evolution of the density of dislocations in the ferritic matrix of the studied steel predicted by the model of Bouaziz et al. [22] as a function of the cold-rolling ratio and the corresponding temperatures for 50% recrystallization (X = 50%) for a continuous heating of 10 °C∙s⁻¹. The red circles correspond to the experimental data obtained by High Energy X-Ray Diffraction (HEXRD). This simulation shows that the trend is not linear and that the model predicts a minimum temperature for recrystallization to occur in the studied continuous heating conditions.

5. Conclusions

This paper proposes an original mean field model for the recrystallization of deformed, low-carbon ferritic steels during annealing treatments. Such a model is of the greatest relevance for the prediction of further phase transformation kinetics (austenite transformation) and for the prediction of the final mechanical properties of annealed steels (recrystallized fraction and grain size).

It is based on detailed modeling of the nucleation and growth of new recrystallized grains, using as a driving force the energy stored during the prior cold-rolling process. These processes are thus correlated to the recovery state of deformed grains (density of dislocations and subgrain structure).

The main novelties of our approach are the following:

• The nucleation process in ferrite. The model inspired from previous works on austenite has been integrally adapted to the case of ferritic steels. It permits efficiently predicting the start of the recrystallization on a physical basis (SIBM theory) and avoiding the use of empirical T* functions.
• The modeling of the mean grain size considering both interface mobility and nucleation rate of small grains at the critical size. In most of recrystallization models, only the growth process is considered.
• The calibration of the mobility of interfaces (subgrains and recrystallized grains) on the results from different sources. This procedure highlights the key role played by the composition of the alloy on the kinetics (Mn content in the considered cases).

The coupling between recovery and recrystallization in a mean field approach is not a novelty in itself, as it has been conducted in the case of austenite by Zurob et al. To our best knowledge, this is however, the first time that a full coupling has been proposed for ferrite.

The calibration of the model has been conducted using the data available on three similar steels studied in the literature. The recovery kinetics and the microstructural values have been adjusted mainly on steel C, while recrystallization kinetics were reproduced from steels A and B. The model is very sensitive to the choice of the mobility functions introduced to describe the growth of sub-grains and recrystallized grains.

It must finally be highlighted that:

• Contrary to empirical models, it permits predicting the recrystallization start temperature, the microstructure state (grain and subgrain size) and the nucleation rate all along any complex temperature schedule.
• It accounts for the two-stage kinetics of recrystallization of ferritic microstructures observed experimentally with a regime controlled by the nucleation and a regime controlled by the growth only, even if not revealed obviously by the global kinetics.
• The model is sensitive to the chemical composition of the steel based on the mobility equation and to its deformed microstructure (initial grain size, cold-rolling ratio). It still needs to be improved to explicitly elucidate the composition dependence of the mobility of the HAB and to account for nucleation sites other than triple junctions and consider flatten deformed grains.
• The model is highly versatile, as it is CPU efficient and it permits conducting easy sensitivity analysis of processing conditions, compositions and microstructural parameters (resulting from the upstream process).
• As this model has been developed via an industrial collaboration, there is also no doubt that it could be useful for the steel industry for their product/process developments