Optimization of the Schedule for the Whole Process in Hot Strip Manufacturing
Abstract
:1. Introduction
2. Modeling of Energy Multi-Objective Function
2.1. Multi-Objective Function Design
2.2. Mathematical Models
2.2.1. Heating Energy Objective Function
2.2.2. Rolling Energy Objective Function
2.2.3. Temperature Model
2.3. Constraints Conditions
2.3.1. Process Requirements Constraints
2.3.2. Equipment Capacity Constraint
3. Optimization Algorithm and Calculation Procedure
3.1. Differential Evolution Algorithm
3.2. Calculation Procedure
4. Analysis and Discussion
4.1. Plant Description
4.2. Analysis and Discussion
4.2.1. Analysis of Single Objective Function
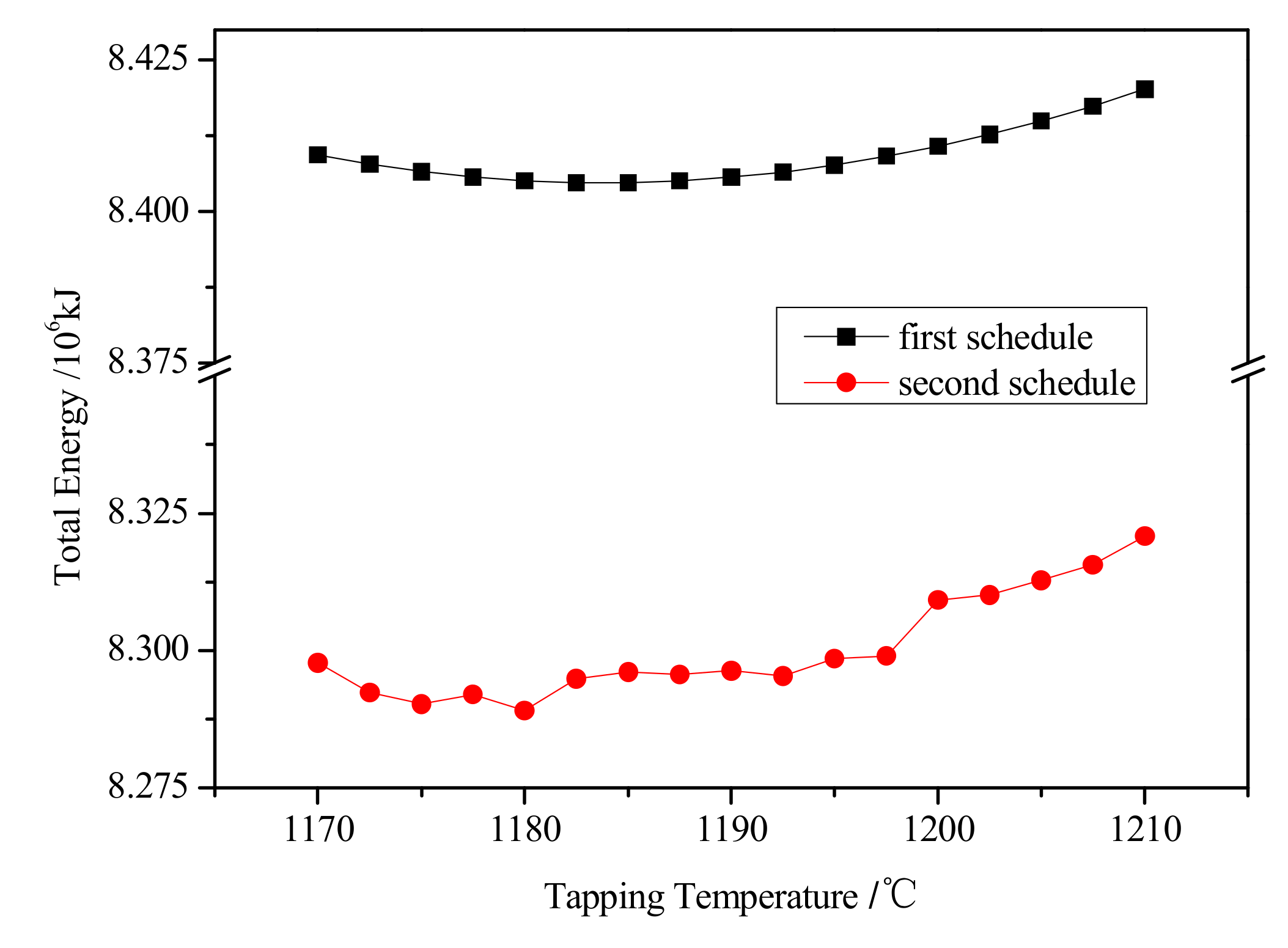
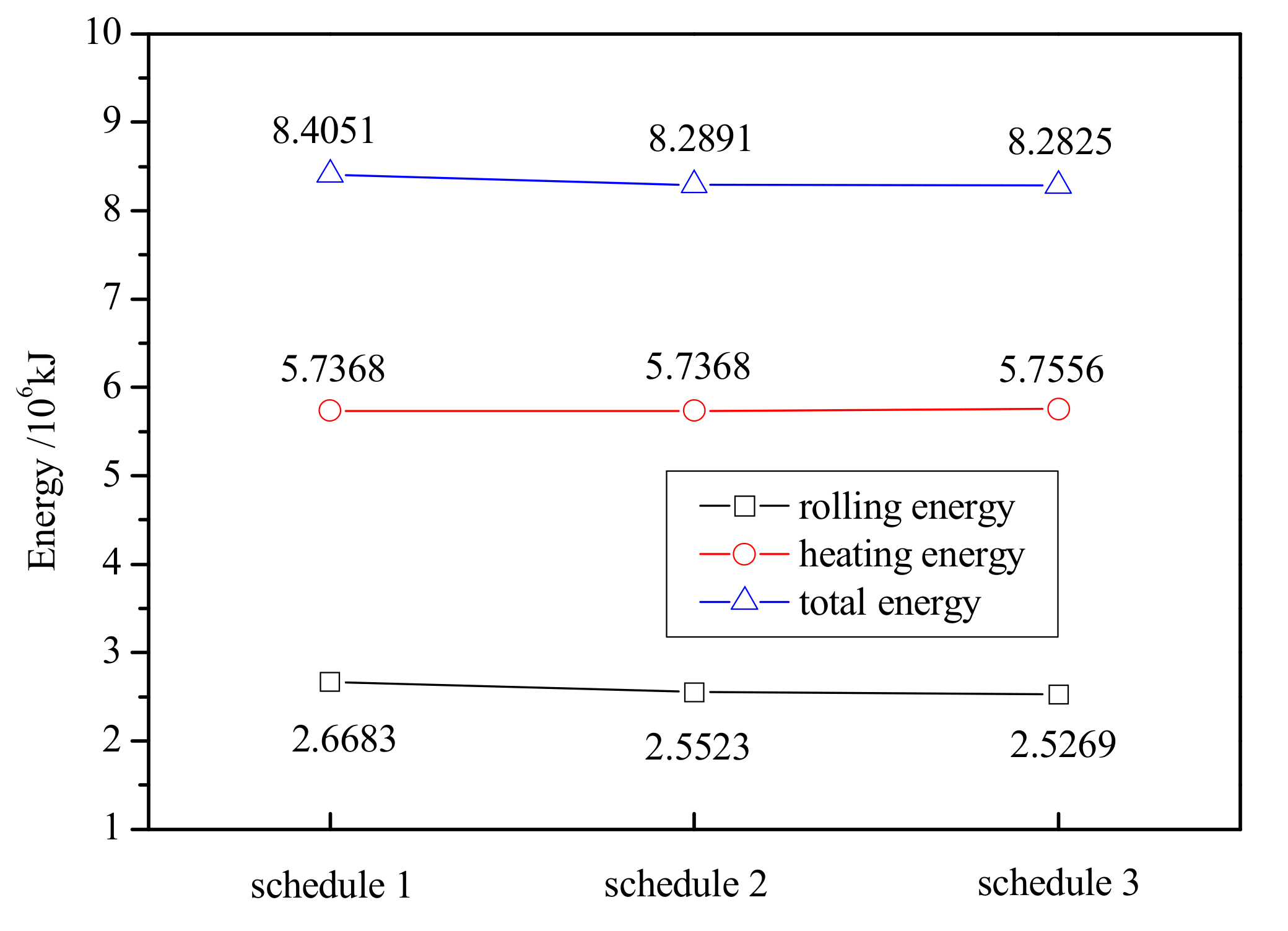
4.2.2. Analysis of Multi-Objective Function
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
| Symbol List | ||||
| Abbreviations | Instructions | Unit | Value | Position |
| Heating energy consumption | kJ | - | Equation (1) | |
| Drive motors energy consumption | kJ | - | Equation (1) | |
| Total pass number | - | - | Equation (1) | |
| Pass number of rough rolling | - | - | Equation (1) | |
| Pass number of finishing rolling | - | - | Equation (1) | |
| Mass of the slab | kg | - | Equation (2) | |
| Specific heat capacity of the slab | J/(kg·K) | - | Equation (2) | |
| Charging temperature of the slab | K | - | Equation (2) | |
| Tapping temperature of the slab | K | - | Equation (2) | |
| Energy conversion efficiency coefficient | - | - | Equation (2) | |
| Rolling power of the drive motor | kW | - | Equation (3) | |
| Rolling time during the strip through the roll | s | - | Equation (3) | |
| Rolling torque of the drive motor | N·M | - | Equation (4) | |
| Rotational speed of the drive motor | rad/min | - | Equation (4) | |
| Rolling force | kN | - | Equation (5) | |
| Arm coefficient | mm | - | Equation (5) | |
| Contact arc length | mm | - | Equation (5) | |
| Additional torque of the drive motor | N·M | - | Equation (5) | |
| Width of the rolling strip | mm | - | Equation (6) | |
| Influence coefficient of tension | - | - | Equation (6) | |
| Deformation resistance of the rolling strip | MPa | - | Equation (6) | |
| Basic deformation resistance of the rolling strip | MPa | - | Equation (7) | |
| Deformation temperature of the rolling strip | K | - | Equation (7) | |
| Deformation velocity of the rolling strip | s−1 | - | Equation (7) | |
| True strain of the rolling strip | - | - | Equation (7) | |
| Influence coefficient of stress state | - | - | Equation (8) | |
| Ambient temperature | K | 300 | Equation (9) | |
| Temperature change caused by ambient | K | - | Equation (9) | |
| Temperature change caused by water cooling | K | - | Equation (9) | |
| Temperature change caused by deformation | K | - | Equation (9) | |
| Temperature change caused by friction | K | - | Equation (9) | |
| Temperature change caused by conduction | K | - | Equation (9) | |
| Equivalent emissivity | - | 0.8 | Equation (10) | |
| Density of the strip | kg/m3 | 7850 | Equation (10) | |
| Heat transfer time | s | Equation (10) | ||
| Forced convection heat transfer coefficient | W/(m2·K) | - | Equation (11) | |
| Deformation efficiency coefficient | - | 0.50 | Equation (12) | |
| friction efficiency coefficient | - | 0.65 | Equation (13) | |
| speed difference between the work roll and strip | m/s | - | Equation (13) | |
| Contact heat flow coefficient of the work roll | - | 0.70 | Equation (14) | |
| Heat conduction coefficient of the strip | W/m·K | Equation (14) | ||
| Temperature of the work roll | K | - | Equation (14) | |
| Minimum reliable thickness | mm | - | Equation (17) | |
| Diameter of the work roll | mm | - | Equation (18) | |
| Maximum thickness ratio of pass i | % | - | Equation (19) | |
| Bite angle | - | - | Equation (20) | |
| Reduction | - | - | Equation (20) | |
| Friction angle | - | - | Equation (20) | |
| Friction coefficient | - | 0.3 | Equation (20) | |
| Maximum rolling force | kN | - | Equation (21) | |
| Maximum rolling power of drive motors | kW | - | Equation (22) | |
| Maximum torque of drive motors | N·M | - | Equation (23) | |
| Maximum rotational speed of drive motors | rad/min | - | Equation (24) | |
References
- Sun, J.; Peng, W.; Ding, J.G.; Li, X.; Zhang, D.H. Key Intelligent Technology of Steel Strip Production through Process. Metals 2018, 8, 597. [Google Scholar] [CrossRef] [Green Version]
- Boom, R. The discussions of best heating technology of rolling furnace. Ironamk. Steelmak. 2014, 41, 647–652. [Google Scholar] [CrossRef]
- Wang, Z.B.; Zhao, B.; Zhang, S.J. The discussions of best heating technology of rolling furnace. Beijing Energy Metall. Ind. 2008, 5, 8. [Google Scholar]
- Steinboeck, A.; Wild, D.; Kiefer, T. A fast simulation method for 1D heat conduction. Math. Comput. Simulat. 2011, 82, 392–403. [Google Scholar] [CrossRef]
- Kim, J.G.; Huh, K.Y.; Kim, I.T. Three-dimensional analysis of the walking beam type reheating furnace in hot strip mills. Numer. Heat Transf. 2000, 38, 589–609. [Google Scholar]
- Kim, M.A. Heat transfer model for the analysis of transient heating of the slab in a direct-fired walking beam type reheating furnace. Int. J. Heat Mass Transf. 2007, 50, 3740–3748. [Google Scholar] [CrossRef]
- Miao, C.; Kai, Y.; Liu, Y.F. Inverse estimation of transient heat flux to slab surface. J. Iron Steel Res. 2012, 19, 13–18. [Google Scholar]
- Suzuki, M.; Katsuki, K.; Imura, J.I. Simultaneous optimization of slab permutation scheduling and heat controlling for a reheating furnace. J. Process Control 2014, 24, 225–238. [Google Scholar] [CrossRef]
- Emadi, A.; Saboonchi, A.; Taheri, M. Heating characteristics of billet in a walking hearth type reheating furnace. Appl. Therm. Eng. 2014, 63, 396–405. [Google Scholar] [CrossRef]
- Morgado, T.; Coelho, P.J.; Talukdar, P. Assessment of uniform temperature assumption in zoning on the numerical simulation of a walking beam reheating furnace. Appl. Therm. Eng. 2015, 76, 496–508. [Google Scholar] [CrossRef]
- Han, S.H.; Baek, S.W.; Kim, M.Y. Transient radiative heating characteristics of slabs in a walking beam type reheating furnace. Int. J. Heat Mass Transf. 2009, 52, 1005–1011. [Google Scholar] [CrossRef]
- Casal, J.M.; Porteiro, J.; Miguez, J.L. New methodology for CFD three-dimensional simulation of a walking-beam type reheating furnace in steady state. Appl. Therm. Eng. 2015, 86, 69–80. [Google Scholar] [CrossRef]
- Depree, N.; Sneyd, J.; Taylor, S. Development and validation of models for annealing furnace control from heat transfer fundamentals. Comput. Chem. Eng. 2010, 34, 1849–1853. [Google Scholar] [CrossRef]
- Feliu, B.V.; Rivas, P.R.; Castillo, G.F.J. Simple fractional order controller combined with a Smith predictor for temperature control in a steel slab reheating furnace. Int. J. Control Autom. Syst. 2013, 11, 533–544. [Google Scholar] [CrossRef]
- Wang, W.; Li, H.X.; Zhang, J. A hybrid approach for supervisory control of furnace temperature. Control Eng. Pract. 2003, 11, 1325–1334. [Google Scholar] [CrossRef]
- Wang, Y.J.; Huang, J.W.; Su, C.; Li, H.G. Furnace thermal efficiency modeling using an improved convolution neural network based on parameter-adaptive mnemonic enhancement optimization. Appl. Therm. Eng. 2019, 149, 332–343. [Google Scholar] [CrossRef]
- Prieler, R.; Mayrhofer, M.; Gaber, C.; Gerhardter, H.; Schluckner, C.; Landfahrer, M.; Eichhorn-Gruber, M.; Schwabegger, G.; Hochenauer, C. CFD-based optimization of a transient heating process in a natural gas fired furnace using neural networks and genetic algorithms. Appl. Therm. Eng. 2018, 138, 217–234. [Google Scholar] [CrossRef]
- Jiang, X.; Hu, X.L.; Liu, X.H.; Wang, G.D. Application of compound equal load distribution method in rough rolling schedule. J. Iron Steel Res. 2006, 18, 26–29. [Google Scholar]
- Shen, X.G.; Han, N.; Shen, H.Y. Application of synergetic artificial intelligence to the scheduling in the finishing train of hot strip mills. J. Mater. Process. Technol. 1996, 60, 405–408. [Google Scholar]
- Li, H.J.; Wang, G.D.; Xu, J.Z. Optimization of draft schedules with variable metric hybrid genetic algorithm during hot strip rolling. J. Iron Steel Res. Int. 2007, 19, 33–36. [Google Scholar]
- Li, W.G.; Liu, C.; Bian, H.; Liu, X.H. Optimization calculation strategy of load distribution for hot strip mills. J. Iron Steel Res. 2017, 29, 391–396. [Google Scholar]
- Jia, S.J.; Li, W.G.; Liu, X.H.; Du, B. Multi-objective load distribution optimization for hot strip mills. J. Iron Steel Res. Int. 2013, 20, 27–32. [Google Scholar] [CrossRef]
- Li, H.J.; Xu, J.Z.; Wang, G.D. Improvement on conventional load distribution algorithm in hot tandem mills. J. Iron Steel Res. Int. 2007, 14, 36–41. [Google Scholar] [CrossRef]
- Li, W.G.; Liu, X.H.; Guo, Z.H. Multi-objective optimization for draft scheduling of hot strip mill. J. Cent. South Univ. 2012, 19, 3069–3078. [Google Scholar] [CrossRef]
- Qi, X.D.; Wang, T.; Xiao, H. Optimization of pass schedule in hot strip rolling. J. Iron Steel Res. Int. 2012, 19, 25–28. [Google Scholar] [CrossRef]
- Pan, Q.K.; Gao, L.; Wang, L. A multi-objective hot-rolling scheduling problem in the compact strip production. Appl. Math. Model. 2019, 73, 327–348. [Google Scholar] [CrossRef]
- Peng, W.; Liu, Z.Y.; Yang, X.L.; Zhang, D.H. Optimization of temperature and force adaptation algorithm in hot strip mill. J. Iron Steel Res. Int. 2014, 21, 300–305. [Google Scholar] [CrossRef]
- Liu, E.Y.; Peng, L.G.; Yuan, G. Advanced run-out table cooling technology based on ultra-fast cooling and laminar cooling in hot strip mill. J. Cent. South Univ. 2012, 19, 1341–1345. [Google Scholar] [CrossRef]
- Stone, M.D. Rolling of thin strip. Iron Steel Eng. 1953, 30, 61–65. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution-A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Space, TR-95-012; International Computer Science Institute: Berkeley, CA, USA, 1995. [Google Scholar]
- Price, K.; Storn, R.; Lampinen, J. Differential Evolution-A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Peng, W.; Zhang, D.H.; Zhao, D.W. Application of parabolic velocity field for the deformation analysis in hot tandem rolling. Int. J. Adv. Manuf. Technol. 2017, 91, 2233–2243. [Google Scholar] [CrossRef]
- Qi, K.M.; Ding, H. Material Forming Technology; Metallurgical industry press: Beijing, China, 2013. [Google Scholar]
- Ginzburg, V.B.; Ballas, R. Fundamentals of Flat Rolling Manufacturing Engineering and Materials Processing; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]








| Parameter | R | F1 | F2 | F3 | F4 | F5 | F6 | F7 |
|---|---|---|---|---|---|---|---|---|
| Roll Diameter/mm | 1100 | 800 | 800 | 800 | 800 | 700 | 700 | 700 |
| Max Rolling Force/kN | 40,000 | 40,000 | 40,000 | 40,000 | 40,000 | 34,000 | 34,000 | 34,000 |
| Max Torque/(kN·m) | 4300 | 2000 | 2000 | 2000 | 1500 | 1500 | 1200 | 1200 |
| Max Motor Power/kW | 7500×2 | 8000 | 8000 | 8000 | 8000 | 8000 | 7500 | 7500 |
| Max Motor Speed (rad s/−1) | 700 | 450 | 450 | 450 | 450 | 450 | 600 | 600 |
| Coefficient | a1 | a2 | a3 | a4 | a5 | a6 | a7 |
|---|---|---|---|---|---|---|---|
| Value | 5.0 | −0.0588 | 0.12828 | −0.041 | 1.3 | 0.41 | 2.80 |
| Parameter | R | F1 | F2 | F3 | F4 | F5 | F6 | F7 |
|---|---|---|---|---|---|---|---|---|
| Thickness Ratio Range *1/% | 60% | 40–50% | 35–45% | 30–40% | 25–35% | 25–35% | 20–30% | 10–20% |
| Max Bite Angle *2/° | 18.30 | 18.47 | 18.74 | 19.25 | 20.59 | 17.30 | 17.72 | 18.16 |
| Min Thickness *3/mm | 55.62 | 56.68 | 58.29 | 61.47 | 70.25 | 36.18 | 37.94 | 39.83 |
| Pass | R1 | R2 | R3 | R4 | R5 | F1 | F2 | F3 | F4 | F5 | F6 | F7 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Thickness/mm | 145.0 | 103.0 | 72.0 | 48.0 | 33.0 | 16.65 | 9.44 | 5.69 | 3.90 | 2.92 | 2.33 | 2.00 |
| Thickness ratio/% | 27.50 | 28.97 | 30.10 | 33.33 | 31.25 | 49.55 | 43.30 | 39.72 | 31.46 | 25.13 | 20.21 | 14.16 |
| Velocity m/s | 2.5 | 3.0 | 3.5 | 3.6 | 4.0 | 1.20 | 2.12 | 3.51 | 5.13 | 6.85 | 8.58 | 10.00 |
| Parameter | schedule | R1 | R2 | R3 | R4 | R5 | F1 | F2 | F3 | F4 | F5 | F6 | F7 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Thickness/mm | 1 | 145.0 | 103.0 | 72.0 | 48.0 | 33.0 | 16.65 | 9.44 | 5.69 | 3.90 | 2.92 | 2.33 | 2.00 |
| 2 | 153.0 | 112.7 | 84.41 | 60.48 | 39.19 | 19.91 | 11.04 | 6.66 | 4.43 | 3.16 | 2.47 | 2.00 | |
| 3 | 151.5 | 114.7 | 85.8 | 60.7 | 39.3 | 19.8 | 10.9 | 6.64 | 4.40 | 3.13 | 2.43 | 2.00 | |
| Velocity/m/s | 1 | 2.50 | 3.00 | 3.50 | 3.60 | 4.00 | 1.20 | 2.12 | 3.51 | 5.13 | 6.85 | 8.58 | 10.00 |
| 2 | 2.50 | 3.00 | 3.50 | 3.60 | 4.00 | 1.00 | 1.81 | 3.00 | 4.52 | 6.32 | 8.09 | 10.00 | |
| 3 | 2.50 | 3.00 | 3.50 | 3.60 | 4.00 | 1.01 | 1.83 | 3.01 | 4.54 | 6.39 | 8.23 | 10.00 | |
| Force/kN | 1 | 21,608 | 21,718 | 21,716 | 23,462 | 23,249 | 26,950 | 24,071 | 23,724 | 19,960 | 15,296 | 13,491 | 9970 |
| 2 | 18,578 | 20,042 | 18,426 | 20,138 | 26,002 | 25,072 | 23,243 | 21,825 | 19,674 | 16,306 | 13,432 | 13,343 | |
| 3 | 19,077 | 18,363 | 18,471 | 20,774 | 25,874 | 25,263 | 23,196 | 21,370 | 19,680 | 16,531 | 13,781 | 12,022 | |
| Temperature/°C | 1 | 1142.8 | 1133.8 | 1121.0 | 1099.1 | 1050.3 | 1015.1 | 993.4 | 971.1 | 947.6 | 924.6 | 901.8 | 880.1 |
| 2 | 1143.2 | 1135.1 | 1124.6 | 1108.6 | 1073.4 | 1037.8 | 1016.2 | 993.2 | 969.7 | 946.2 | 922.9 | 899.7 | |
| 3 | 1145.0 | 1136.9 | 1126.6 | 1110.9 | 1075.6 | 1040.0 | 1018.3 | 995.4 | 971.6 | 948.0 | 924.5 | 901.4 | |
| Power/kW | 1 | 13,122 | 13,551 | 13,331 | 12,739 | 11,044 | 4440 | 4777 | 5831 | 5306 | 4628 | 4290 | 3036 |
| 2 | 10,541 | 12,329 | 10,948 | 11,031 | 14,450 | 3729 | 4307 | 4873 | 4972 | 4942 | 4195 | 4565 | |
| 3 | 10,954 | 10,825 | 11,057 | 11,599 | 14,369 | 3798 | 4322 | 4730 | 4989 | 5070 | 4389 | 3965 | |
| Energy/×106 kJ | 1 | 0.051 | 0.061 | 0.074 | 0.103 | 0.117 | 0.311 | 0.334 | 0.408 | 0.371 | 0.324 | 0.300 | 0.213 |
| 2 | 0.039 | 0.051 | 0.052 | 0.071 | 0.129 | 0.261 | 0.302 | 0.341 | 0.348 | 0.346 | 0.294 | 0.320 | |
| 3 | 0.041 | 0.044 | 0.052 | 0.074 | 0.128 | 0.266 | 0.303 | 0.331 | 0.349 | 0.355 | 0.307 | 0.278 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, W.; Ma, J.; Chen, X.; Ji, Y.; Sun, J.; Ding, J.; Zhang, D. Optimization of the Schedule for the Whole Process in Hot Strip Manufacturing. Metals 2020, 10, 717. https://doi.org/10.3390/met10060717
Peng W, Ma J, Chen X, Ji Y, Sun J, Ding J, Zhang D. Optimization of the Schedule for the Whole Process in Hot Strip Manufacturing. Metals. 2020; 10(6):717. https://doi.org/10.3390/met10060717
Chicago/Turabian StylePeng, Wen, Jianyang Ma, Xiaorui Chen, Yafeng Ji, Jie Sun, Jinggou Ding, and Dianhua Zhang. 2020. "Optimization of the Schedule for the Whole Process in Hot Strip Manufacturing" Metals 10, no. 6: 717. https://doi.org/10.3390/met10060717
APA StylePeng, W., Ma, J., Chen, X., Ji, Y., Sun, J., Ding, J., & Zhang, D. (2020). Optimization of the Schedule for the Whole Process in Hot Strip Manufacturing. Metals, 10(6), 717. https://doi.org/10.3390/met10060717





