Early Stages of Plastic Deformation in Low and High SFE Pure Metals

Abstract

Severe plastic deformation (SPD) techniques are known to promote exceptional mechanical properties due to their ability to induce significant grain and cell size refinement. Cell and grain refinement are driven by continuous newly introduced dislocations and their evolution can be followed at the earliest stages of plastic deformation. Pure metals are the most appropriate to study the early deformation processes as they can only strengthen by dislocation rearrangement and cell-to-grain evolution. However, pure metals harden also depend on texture evolution and on the metal stacking fault energy (SFE). Low SFE metals (i.e., copper) strengthen by plastic deformation not only by dislocation rearrangements but also by twinning formation within the grains. While, high SFE metals, (i.e., aluminium) strengthen predominantly by dislocation accumulation and rearrangement with plastic strain. Thence, in the present study, the early stages of plastic deformation were characterized by transmission electron microscopy on pure low SFE Oxygen-Free High Conductivity (OFHC) 99.99% pure Cu and on a high SFE 6N-Al. To induce an almost continuous rise from very-low to low plastic deformation, the two pure metals were subjected to high-pressure torsion (HPT). The resulting strengthening mechanisms were modelled by microstructure quantitative analyses carried out on TEM and then validated through nanoindentation measurements.

1. Introduction

The improved mechanical tensile, fatigue, and ductile properties yield by ultrafine-grained (UFG) metallic materials and alloys compared to the conventional grained counterparts are well-known within the scientific community [1]. Different technological methods were developed in the last three decades to obtain UFG metals and alloys.

In particular, two diametrically distant approaches are able to get similar, if not same, mechanical properties. The first of them is a top-down approach by which a bulk metallic material is plastically forced to deform and refine the grain structure accordingly. Among the most effective and well-developed such top-down techniques the severe plastic deformation (SPD) methods are the ones showing the most promising and technologically reliable ones [2,3,4,5,6,7,8,9,10]. Several SPD techniques were successfully developed so far, these include high-pressure torsion (HPT), equal-channel angular pressing (ECAP), accumulative roll-bonding (ARB), accumulative press-bonding (APB), cyclic extrusion-compression (CEC), twist extrusion (TE), friction stir processing (FSP), repetitive corrugation and straightening (RCS), high-pressure sliding (HPS) ([4,5,6,7] and references therein). A second approach start from powder metallic materials which are compacted to get UFG bulk alloys, and it is called bottom-up approach [11,12].

Especially when using the top-down approach, the physical principles behind the SPD-driven UFG formation can be properly described by using pure metals. In fact, under SPD pure metals can only be strengthened by dislocation motion and rearrangement. Tangled dislocations (TDs) can then be induced to entangle and reorganize to form boundary structures (both low-angle, i.e., cell, and high-angle, i.e., grain). With this regard, the strengthening mechanisms induced within the pure metal microstructure can be related to the metal stacking fault energy (SFE). The SFE can thus identified at least two types of pure metals, the ones with low-SFE, and others with high-SFE. Pure copper is a good example of low-SFE metal, while aluminum is an example of high-SFE. Copper has an SFE ≅ 70 mJm⁻² [13,14], while aluminum has an SFE ≅ 165 mJm⁻² [15].

In the present study, both pure Cu and Al were used to study the early stages of plastic deformation with the aim of determining the microstructure evolution on which is based the formation of cell boundaries (low-angle boundaries, LABs), grain boundaries (high-angle boundaries, HABs). The role of twinning formation, due to the low-SFE, in pure copper was also addressed.

To properly follow the earlier stages of plastic deformation induced in both the pure metals a SPD suitable technique was necessary. With this respect, the HPT was essentially among the few that allowed to strain the metallic materials for strain levels as low as ε_eq = 0.02. Moreover, by HPT an almost continuous range of strain levels can be induced by simply limiting the number fraction of plunger rotation under the applied pressure. This because HPT is able to generate progressive plastic deformation levels which depend on the arc of rotation and on the location of the disc. That is, for a given rotation the strain level varies almost continuously form the disc center, where it is minimum, to the disc periphery, where it is at its maximum.

Thus, for the present study, the two meaningful parameters are the number fraction of revolution and the location of the disc, from center to periphery. Since, the imposed strain chiefly depends on the distance from the center of the disc, the microstructure modifications imposed by HPT are greatly inhomogeneous but progressive.

As for the induced microstructure modifications with cumulative straining during SPD, a number of published works [16,17,18] recognized that the UFG formation proceeds starting from TD and dense dislocation walls (having very low-angle boundaries). These are continuously introduced in the material and eventually induced to rearrange and thus form cell structures (LABs). These are eventually induced to rise their misorientation angle to eventually become grain boundaries (HABs).

In this study, the role of twinning formation, in pure copper, and the LABs, and HABs evolution, in both pure copper and pure aluminum, to the microstructure evolution driven by the early stages of plastic deformation by HPT was addressed by electron microscopy technique (TEM). The microstructure-based strengthening model was modelled and compared to nanoindentation hardness measurements. To this purpose, an Oxygen-Free High Conductivity (OFHC) 99.99% pure Cu and a 99.9999% Al (6N-Al) were used.

2. Experimental Procedures and Method

2.1. The Pure Metals

OFHC 99.99% pure copper rod with 10 mm diameter were annealed at 673 K for 1 h, followed by cooling in the turned off furnace (cooling time of 8 h). The chemical composition of the 99.99% purity Cu is as follows (wt.% × 1000): 4.4(Ag + Pb + S), 1.5Fe, 0.5O, 0.4P, 0.2Cd, 0.9 others, 99992 Cu. The 6 N-Al (purity of 99.9999%) was annealed at 655 K for 1 h.

2.2. High-Pressure Torsion (HPT) Details

Discs of 10 mm in diameter and 1.0 mm-thick of annealed OFHC Cu and 6N-Al were HPT under quasi-constrained conditions at room temperature. This way, material outflow during straining was avoided. Quite low and low strain levels were induced to get a discrete close range of plastic deformation into the two pure metals. The strain levels here tested are reported in

Table 1. Equivalent strain ε_eq obtained by the different HPT experimental parameters for Oxygen-Free High Conductivity (OFHC) Cu and 6N-Al; ε_eq calculated by rotation angle, θ°, number of turns, N, distance to disc center, r (mm) using Equation (2).

OFHC Cu	εeq = 0.40 20; 1/18; 2;	εeq = 0.91 45; 1/8; 2;	εeq = 1.21 60; 1/6; 2;
6N-Al	εeq = 0.02 5; 1/120; 0.3;	εeq = 0.05 15; 1/45; 0.3;	εeq = 0.10 15; 1/45; 0.6;

for both Cu and Al. These were from ε_eq = 0.02 to 0.24, in 6N-Al, and from ε_eq = 0.40 to 1.21, in OFHC Cu.

Figure 1 shows a schematic representation of the location from which TEM discs were extracted to describe the microstructure modifications induced by the HPT strain levels reported in Table 1.

HPT strain deformation was given by dω/ω, being ω the angular rotation around the disc center. Since in the present case the disc thickness does not dependent on the rotation angle ω = 2πN, the resulting HPT shear strain, γ, was calculated according to Equation (1) [4]:

γ = 2πNr/t

(1)

where r is the distance from the disc center, ranging from 0 to the disc radius, R, and t is the disc thickness. For low HPT strains, γ, the resulting vön Mises strain is [4,19], Equation (2):

$${\epsilon }_{eq}=\frac{\gamma }{\sqrt{3}}=\frac{2\pi Nr}{t\sqrt{3}}$$

(2)

HPT was carried out by depressing the vertical anvils to a depth of 0.05 mm into the 1 mm-thick HPT discs. Torsion strain was exerted by rotating the upper anvil at a low rotation speed of 0.7 rpm, corresponding to a rotation of ~4° s⁻¹, under a pressure of 2.0 GPa. This anvil pressure allowed to avoid any possibility of disc slipping during rotational motion under HPT. According to Equation (2) the different strain levels, ε_eq, inspected by TEM according to Table 1 were obtained by extracting the TEM discs at given radial distance from the HPT disc center.

2.3. TEM Sample Preparation and Method

TEM discs were extracted from the middle height of the HPT discs. To avoid any possible artefact during sample preparation, the ~1 mm-thick HPT discs were prepared for TEM inspections by chemical and electro-chemical means down to a thickness of 200 µm. OFHC Cu was thinned using a solution of 30% of phosphoric acid 20% ethylic alcohol in 50% distilled water at room temperature and a voltage of 12 V. Final thinning to electron transparency was performed by Gatan Inc. precision ion-milling (PIPS) (Pleasanton, CA, USA) working with low dual incident beam (2° respect to the disc surface). The low incidence of the Argon beam was selected to minimize the possible artefacts coming from the disc preparation (i.e., to minimize the dislocations possibly introduced during the ion-milling process). The 6N-Al was thinned using a solution consisting of 15% HCl₄, 15% C₃H₃(OH)₃, and 70% methanol and then electro-chemically polished to electron transparency by double-jet with a solution of 1/3 nitric acid and 2/3 methanol working at 238 K and V = 12 V.

TEM inspections were carried out in a Philips^TM C-20^® (Amsterdam, The Netherlands) working at 200 keV with a double-tilt specimen holder equipped with a liquid-nitrogen cooling stage. Two-beam excitation conditions were selected for most of the TEM observation and dislocation characterizations. All the inspections of Al and Cu were carried out along the {110} crystallographic planes. Dislocation density, ρ_disl., was quantitatively evaluated by stereological methods, such as the Ham’s interception method [20]. Thence, ρ_disl. was calculated through the count of interception points between the mesh and the existing dislocations, n_disl, in the TEM micrographs. This was evaluated by ρ_disl. = 2n_disl/(l_mesht_TEM), were, l_mesh is the total length of the mesh, and t_TEM is the thickness of the TEM foil. Crystal thickness, t_TEM, was determined through the diffracted beam intensity variation under dual beam conditions, using converged electron beam diffraction (CBED) patterns. This way, by plotting the linear interpolation of data points in a S²/n_fringes² vs. n_fringes⁻² graph, where S is the fringes spacing, and n_fringes the number of counted fringes, t_TEM⁻² was determined at y-axis line intercept. Cell (LAB) and grain boundary (HAB) misorientation were measured by Kikuchi band patterns. The misorientation angle measurement procedure by Kikuchi pattern on TEM is fully described elsewhere in previous published works by this author [10,21,22]. The misorientation across the detected boundaries was measured from at least 100 g per experimental condition in both Al and Cu.

2.4. Nanoindentation Measurement Details

Nanoindentation measurements were performed at same HPT location of the ones used for the TEM inspections. Sample preparation followed the same procedures used to polish the TEM discs prior final thinning to electron transparency.

A Hysitron Inc. Triboscope UBI-1^® (Minneapolis, MN, USA) was used. Calibration procedures were followed according to [23]. A trapezoidal load function of 5 s loading, 15 s at the set load, and 5 s unloading was used, with a set load, P_Max = 10 mN, and at a constant loading rate of 0.25 mN/s. Series of 8 × 8 individual measurements spaced 250 µm apart were carried out for each experimental condition.

Data analysis was performed according to the Oliver–Pharr model [24]. Thence, hardness, H, was evaluated as H = P_Max/A, with A = K_indh_c² being the contact area, K_ind an indenter tip dependent coefficient (24.56 for Berkovich tip [25]), h_c the contact depth related to the maximum penetration depth, h_m, which is h_c = h_m-χP_Max/S, χ = 0.75 for Berkovich tip [24] and S the material stiffness. Stiffness was measured through the unloading slope at the maximum penetration depth, h_m, being S = Bm(h_m-h_r)^m−1, where B is the unloading curve intercept at P = 0, m is the unloading slope, and h_r is the residual depth (the permanent plastic penetration depth on unloading). By using the Oliver–Pharr method, the reduced elastic modulus is E_r = [(π/4)^0.5/β]·[S/(A)^0.5], where β = 1.034 for Berkovich tips [24]. Thence, H = 0.041·P_Max/h_c² and E_r = 0.173·S/h_c.

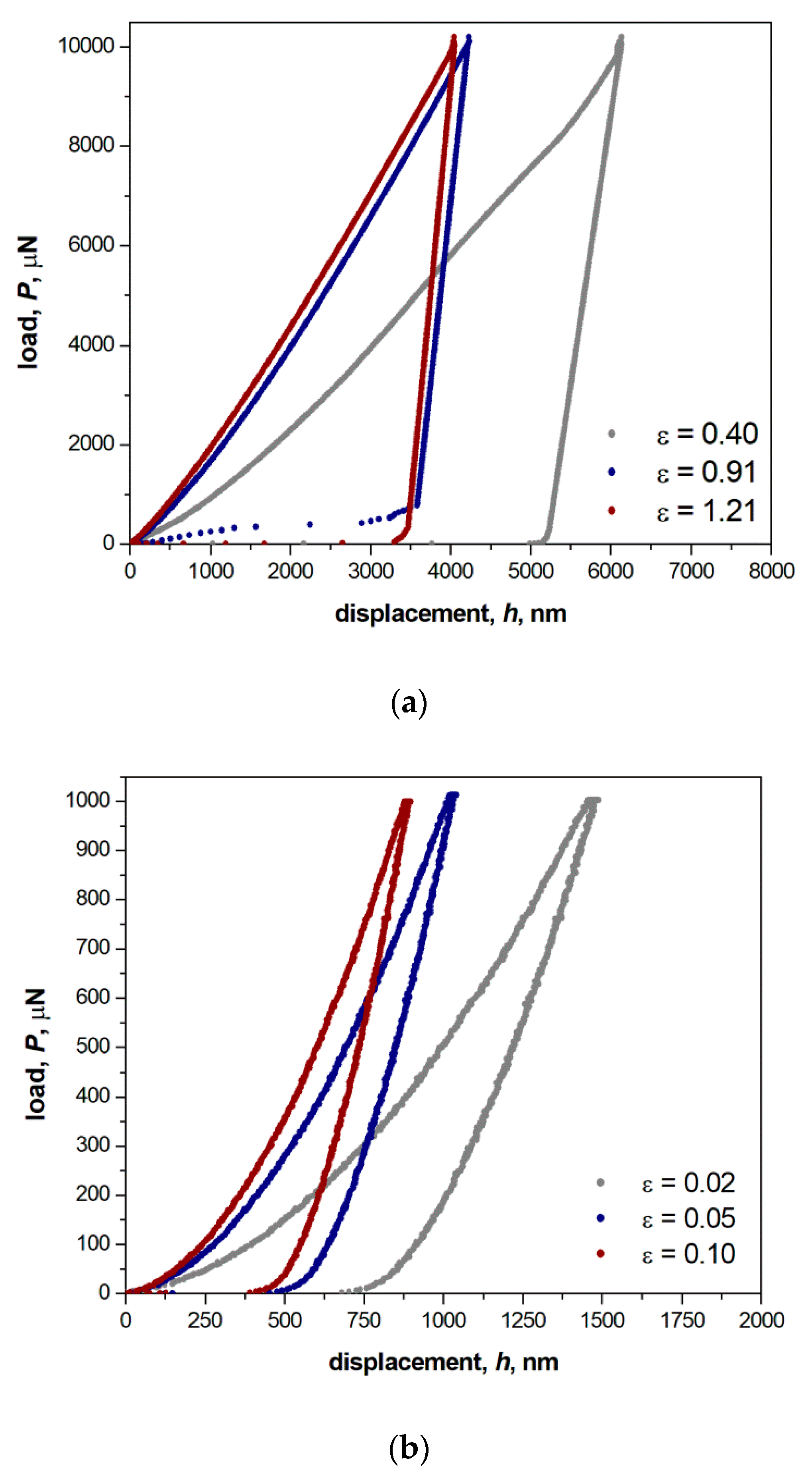
3. Experimental Results

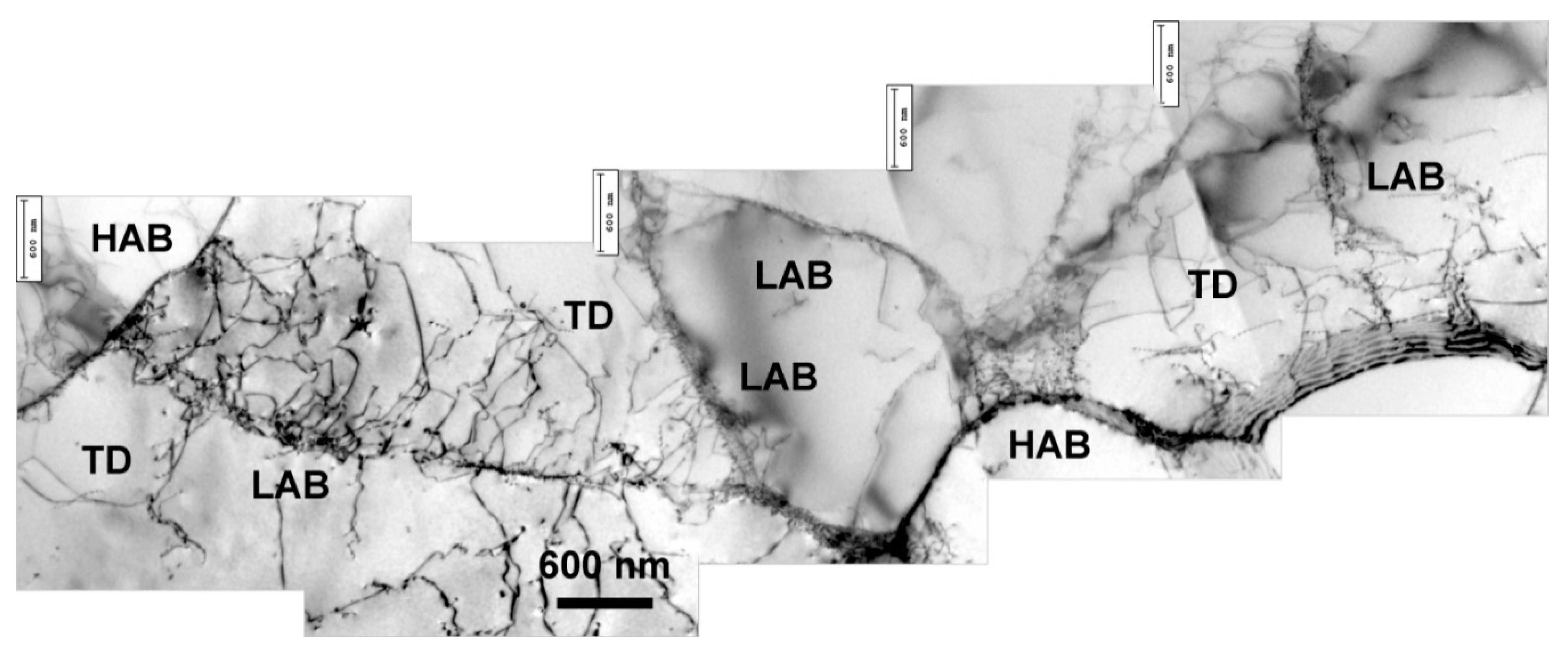
3.1. Microstructure

The microstructure evolution induced by HPT in OFHC 99.99% pure Cu and 6N-Al is shown in Figure 2, which reports strain levels of ε_eq = 0.40, 0.91, and 1.21 for Cu, and in Figure 3, reporting the microstructure after ε_eq = 0.02, 0.05, and 0.10 for Al.

In the case of copper, twins were formed from a HPT strain level of ε_eq = 0.91. From this HPT strain level Cu started to refine its grain structure through significant formation of grain boundaries (HABs). At the same time, twins started to cumulate within the refining grains. Thus, Cu microstructure initially started to deform by formation of statistically stored dislocations (SSD) and by geometrically necessary dislocations (GND) (ε_eq = 0.40, Figure 2a). Eventually, at ε_eq = 0.91 both SSDs and GNDs were promoted to form the first cell boundaries (LABs) and new grain boundaries (HABs) (Figure 2b). At this strain level twins started to form. That is, from ε_eq = 0.91 two strengthening mechanisms are activated at the same time, twin and grain boundary mechanisms. Thence, the strain level ε_eq = 0.91 can be considered a threshold-like strain limit to initiate a microstructure twin strengthening. At strain levels above it, ε_eq = 1.21, the pure copper plastically deformed under HPT straining by further generating new GNDs and by refining the grain structure (Figure 2c). Moreover, Figure 2c also shows the formation of dislocation pile-up. This, in turns, is responsible for the generation of lattice distortion on both sides of the cell wall that evolves together with the twins. These twins nucleated at grain boundaries to extend within the grain.

The formation of these twins is responsible for the development of sharp grain boundaries, which in turns implies a substantial stress relief in the boundary surrounding areas.

The microstructure evolution of the 6N-Al proceeds by the initial formation and then evolution of the TDs (ε_eq = 0.05, Figure 3a)). The density of the TD, ρ_TD, is initially quite low. Anyway, this is induced to rise steadily already at ε_eq = 0.05 (Figure 3b). Whenever cell boundaries and then grain boundaries are formed out of the TDs, their density start to slightly decrease (Figure 3c). The quantitative evaluation of the ρ_TD is reported in

Table 2. Tangled dislocation density, ρ_TD, calculated by quantitative TEM analysis at the different HPT strain levels for OFHC Cu and 6N-Al.

OFHC Cu	εeq ρTD, 1014 m−2	0.40 3.50 ± 0.30	0.91 1.30 ± 0.20	1.21 0.90 ± 0.20
6N-Al	εeq ρTD, 1014 m−2	0.02 0.03 ± 0.01	0.05 1.80 ± 0.20	0.10 0.60 ± 0.10

. In particular, Figure 3b clearly shows the formation of the first LABs, while at ε_eq = 0.10 (Figure 3c), some grain boundaries (HABs) were also detected. This in turns means that the minimum necessary strain to induce the formation of cell, and eventually grain boundaries, that is the initiation of microstructure refining process induced by the plastic deformation, can be identified as ε_eq ≅ 0.05.

Thus, it resulted that at ε_eq = 0.05 TDs start to rearrange and to group to a certain crystallographic orientation, forming a cell wall (LAB). By cumulating the shear deformation, even if at the earliest levels (ε_eq < 0.10) LABs are induced to evolve into cell boundaries, and eventually to grain boundaries (HABs).

In the case of OFHC pure Cu, the dislocation density, ρ_TD, continuously decreased with cumulative straining. In particular, at the strain level by which twins started to form, (ε_eq = 0.91), ρ_TD reduced by one-third respect to the tangled dislocation density measured at the strain level where no new grain boundaries were generated by HPT, (ε_eq = 0.40). As soon as grain boundary started to be promoted by the HPT, and twinning grains were formed, the tangled dislocation density reduction trend was found to slow down. On the other hand, the fraction of twinned grains at ε_eq = 0.91 and ε_eq = 1.21 was 3.0 ± 0.5%, and 14 ± 2%, respectively. The mean spacing of twins did not changed significantly from ε_eq = 0.91 to 1.21, being λ_T = 27 ± 3 and λ_T = 30 ± 5 nm, respectively.

Mean grain, d_g, and cell size, d_cell, evolution with cumulative HPT straining, were measured by TEM in the OFHC pure Cu. Grain, and especially cell size reduced steadily from ε_eq = 0.40 to 1.21. These data are reported in

Table 3. Nanoindentation hardness, H, of OFHC Cu and 6N-Al at the different experimental HPT conditions. The mean cell and grain size of OFHC Cu are also reported.

OFHC Cu	εeq	0.40	0.91	1.21
	H, MPa	780 ± 60	980 ± 60	1060 ± 60
	dg, µm	19 ± 1	14.5 ± 0.5	10.6 ± 0.5
	dcell, nm	1100 ± 100	760 ± 50	540 ± 50
6N-Al	εeq	0.02	0.05	0.10
	H, MPa	75 ± 5	170 ± 10	210 ± 10

. Thus, from the initial annealed state, where d_g = 28 µm, grain size reduced to 19 µm at ε_eq = 0.40, and to ~11 µm at ε_eq = 1.21. Correspondingly, cell size reduced from an initial mean value d_cell = 1100 nm, at ε_eq = 0.40, to 540 nm, at ε_eq = 1.21.

3.2. Nanoindentation Hardness, H

In order to describe the strengthening evolution of the two pure metals with cumulative HPT straining, nanoindentation hardness, H, measurements were performed. Figure 4 shows representative nanoindentation load–displacement curves, P–h (with a fixed load P = 10 mN) of OFHC Cu and 6N-Al. For Cu, nanoindentation curves refer to ε_eq = 0.40, 0.91, and 1.21, while for Al curves refer to ε_eq = 0.02, 0.05, and 0.10.

As expected, the penetration depth, h_c, reduced with cumulative straining. In particular, for Cu, the unloading slope of the P–h slightly increased from the minimum detected strain of ε_eq = 0.40 to ε_eq = 0.91. This is due to the reduced Young’s modulus, E_r, which slightly increased from a strain of ε_eq = 0.91. This in turns implies that the occurrence of twinning formation within the grains affects the elastic response of pure Cu. On the other hand, as reported in Table 3, H steadily increased from the minimum, ε_eq = 0.40, to ε_eq = 1.21.

In the case of Al the hardness increased from ε_eq = 0.02 to 0.05, and it appeared to significantly slowdown from ε_eq = 0.05 to 0.10 (Table 3). This is believed to be due to the detected formation of LABs, and some HABs, from TDs, which was found to occur at ε_eq = 0.05. That is, Al started to be hardened by the effect of the TDs continuously introduced by the HPT shear for strain levels ε_eq < 0.05. At ε_eq = 0.05, the strengthening mechanism changed from TDs to TDs, LABs, and to a much lesser extent also by HABs.

4. Discussion

4.1. Case of OFHC 99.99% Pure Copper

Dislocation formation, in form of statistically stored dislocations (SSDs), and geometrically necessary dislocations (GNDs), and twin formation with cumulative straining are the two key mechanisms of microstructure strengthening in OFHC 99.99% pure Cu. Under plastic deformation, the newly introduced dislocations are induced to slide, and deformation twinning can be activated. Both microstructure modifications account to accommodate the imposed plastic strain [26]. The mean factors governing these microstructure modifications can be identified as the material stacking fault energy (SFE), the grain size, d_g, and crystallographic orientation (texture) [27,28,29]. Whenever twinned grains have a proper crystallographic orientation respect to the external load, multiple twinning systems are activated, leading to twin–twin intersection phenomena. These, in turn, become a further strengthening mechanism for the twinned metallic material [30,31].

Thence, in low SFE metals the reduced dislocation mobility make the twinning deformation a necessary-like mechanism for the microstructure rearrangement driven by the applied external load. In the present study, this necessary-like microstructure mechanism of twinning formation under HPT was found to occur for a strain level as low as ε_eq = 0.91. For lower strain levels, the microstructure strengthened only by formation and evolution of SSDs, GNDs, cell walls, and eventually some HABs. Thence, the role of the SSDs and GNDs referring to the continuous process of cell and grain refinement induced by the HPT deformation was twofold. On one side, it was a microstructure source of active line defects able to thickening the newly generated boundaries (cells or grains). On another side, it contributed to rise the boundary misorientation angle to promote the formation of new grain boundaries from the earlier formed cell boundaries. That is, a boundary misorientation continuous increment to promote LABs to HABs.

The OFHC Cu strengthening with cumulative HPT straining was modelled starting from the observed and quantified features acting in the deformed microstructure. These contributions were the dislocations and LABs introduced by HPT for strain levels ε_eq < 0.40. From this strain, the occurrence of twins make the metal strengthening to be described not any longer only by dislocations and LABs, but also by HABs, and twinning. Thence, the following relationship was proposed to model the OFHC Cu strengthening, Equation (3) [32,33]:

σ_y = σ₀ + σ_disl. + σ_HP + σ_TB

(3)

where σ₀, σ_disl. is the stress due to SSDs and GNDs, σ_HP is the stress given by the Hall–Petch relationship applied to the grains, σ_TB is the stress due to the twins (twin boundaries, TB).

The dislocation contribution is the linear combination of the SSDs and of the GNDs strengthening, and they are both directly dependent on the related densities. In particular, SSDs do form very low-angle and low-angle boundaries under plastic deformation, and thus their density is expressed as, Equation (4) [10]:

ρ_SSD = fρ_wall + (1 − f)ρ_TD

(4)

where f is the fraction of the SSDs that do contribute to the wall (boundary) formation, ρ_wall is the density of the formed walls, and ρ_TD represents the density of the dislocations existing in the cell and grain interiors that did not form boundaries (i.e., TD). According to [34] the value of f can be determined as f = 1 − (1 − λ_wall/d_cell)³, λ_wall and d_cell being the mean wall (cell boundary) thickness and cell size, respectively.

Thence, the dislocation strengthening contribution, σ_disl., can be calculated as, Equation (5):

σ_disl. = MαGb[fρ_wall + (1 − f)ρ_TD + ρ_GND]^0.5

(5)

where M = 3.06 is the Taylor factor, α = 0.33, G = 48.2 GPa is the shear modulus of pure copper, and b = 0.256 nm is the copper Burgers vector [35].

Onset of twinning occurs whenever the slip stress reaches the minimum necessary strain to activate the twinning. The present results showed that the minimum necessary strain level to initiate the twin formation was ε_eq = 0.91. Thence, according to Meyers et al. [26], twins yield a further strengthening contribution given by their boundaries (TB), σ_TB. This strengthening contribution is of the same type of Hall–Petch for grains, with K_TB = 0.28 MPa·m^1/2 that is σ_TB = K_TB·d_g^−1/2.

Thus, by taking into account the actual fraction of twinned grains, f_twin, the following strengthening model was here proposed, Equation (6):

σ_y = σ₀ + MαGb{[fρ_wall + (1 − f)ρ_TD + ρ_GND]^1/2 + [(f_twin·K_TB + (1 − f_twin)·K_HP]d_g^−1/2}

(6)

Dislocation density, namely ρ_wall, ρ_TD, ρ_GND, and fraction of wall boundaries, f, were determined by TEM stereology analyses (ASM EN-112). These data are reported in

Table 4. Dislocation density and dislocation wall volume fraction, f, for OFHC Cu at ε_eq = 0.40, 0.91, and 1.21; Tangled dislocation density, ρ_TD, for 6N-Al at ε_eq = 0.02, 0.05, and 0.10.

Material	Dislocation Data Measured by TEM	εeq = 0.40	εeq = 0.91	εeq = 1.21
OFHC Cu	ρwall, 1012 m−2	105 ± 10	130 ± 20	165 ± 20
	f (wall), 10−2	4	6	7
	ρTD, 1012 m−2	25 ± 5	35 ± 5	40 ± 5
	ρGND, 1012 m−2	95 ± 5	110 ± 5	120 ± 10
	-	εeq = 0.02	εeq = 0.05	εeq = 0.10
6N-Al	ρTD, 1012 m−2	3 ± 1	180 ± 20	60 ± 10

.

The present approach founds a number of scientific support given by previously published works and models proposed for different pure metals and alloys. These include studies by Mughrabi using a composite-like model [36], and several other modified models used to adapt the Mughrabi composite-like model to different metals and alloys [37,38,39,40]. Anyhow, the innovative aspect of the present findings is that the present approach is applied to model the earlier stages of plastic deformation in pure metals, such copper.

The strengthening obtained by Equation (6) was compared to the OFHC Cu stress derived from the experimental nanoindentation hardness measurements.

Thus, using χ = H^nanoind/σ_y = 3.5 [41] as multiplicative factor between the measured hardness, H^nanoind, and the metal yield stress, σ_y, the microstructure model described by Equation (6) showed quite a good agreement. These data are reported in Table 4. Thus, the model of Equation (6) is able to determine which microstructure features contribute to the pure Cu strengthening during the earlier stages of HPT plastic deformation.

4.2. Case of 6N-Al

In materials with medium to high SFE, as the 6N-Al used here, both SSDs and GNDs started to develop since the early stages of plastic deformation. The role of GNDs is to accommodate the shear strain gradients throughout the microstructure. SSDs are formed by tangled dislocation random trapped under uniform localized deformation. These newly introduced dislocations easily slide by cross slip and thence LABs and HABs are induced to form with cumulative strain. The mechanism of boundary formation is ultimately driven by a mutual trapping, rearrangement, and annihilation process of the TDs (chiefly being of GND type) [42].

Hardness rising trend with cumulative strain was found to slow down starting from ε_eq > 0.05. This is likely to be due to the high dislocation mobility that is favored by the ultrahigh purity and the high stacking fault energy. The newly formed grain boundaries start acting as dislocation sinks, as when the grain sizes are large, the dislocations can accumulate in the interior of grains and form dislocation cells.

Thus, the hardness results suggest a direct correlation between the minimum necessary strain to initiate cell boundaries (LABs) formation and the hardness trend of increment with cumulative straining. In fact, at ε_eq = 0.05 the density of TDs, ρ_TD, started to slightly reduce (Table 2). Due to the high SFE of high-purity aluminum, microstructural evolution occurs by TD rearrangement at low levels and low deformation rates under HPT, as high strain levels are needed to achieve microstructural homogeneity. In particular, due to the specific strain path induced by HPT, the vast majority of dislocations, if not all of them, are GNDs [43].

To model the pure aluminum strengthening driven by the earlier stages of HPT deformation, the following relationship was here proposed, Equation (7):

σ_y = σ₀ + σ_d = σ₀ + σ_TD + (σ_VLAB + σ_LAB + σ_GB)

(7)

where σ₀ = 10 MPa is the frictional stress of pure Al, σ_d the strengthening factor given by all the existing dislocations, that is σ_TD due to the TDs, σ_VLAB the contribution form the cell boundaries with misorientation angle within 2° (very-low angle boundaries, VLABs), and σ_LAB and σ_GAB the contributions coming from the cell (LAB) and grain (HAB) boundaries, respectively. This strengthening model was first introduced by Hansen [17] and later adapted by Cabibbo in [10].

According to the TEM observations, for strain levels ε_eq < 0.05, the yield stress is given only by the TDs, and Equation (7) reduced to Equation(8):

σ_y|ε<0.05 = σ₀ + σ_TD

(8)

On the other hand, for ε_eq > 0.05, Equation (7) can be rewritten as, Equation (9):

σ_{y|ε=0.05−0.10} = σ₀ + σ_TD + (σ_VLAB + σ_LAB)

(9)

According to [44], σ_TD, that as above outlined essentially coincides with the GNDs (ρ_{TD ≅} ρ_GND), can be calculated as, Equation (10):

σ_TD = MαGbρ_TD^0.5

(10)

where M = 2.94 is the Taylor factor [45], α is a fitting constant ranging from 0.2 to 0.3, and usually agreed to be 0.24 [45], G = 26 GPa is the shear modulus of aluminum, and b = 0.286 is the aluminum Burgers vector.

Since at low strain levels, i.e., ε_eq < 0.10 the detected volume fraction of the cell boundaries was quite low, and that of the grain boundaries was even lower, the strengthening contribution of these could be estimated by taking into account the mean dislocation density forming those boundaries. Thus, σ_VLAB + σ_LAB = σ_VLAB + _LAB = MαGbρ_VLAB + _LAB^0.5, and ρ_VLAB + _LAB is the average dislocation density that form the very-low angle and low-angle boundaries. These can be considered together, since in the early stages of formation of cell boundaries from TDs, the misorientation angle was found to be within 8°, with a large fraction around 2–6° misorientation angles.

In the present case, for low strain levels, the newly formed boundaries are rather scattered and have mostly low misorientation angles formed by few dislocations. Thus, to evaluate the cell boundary contribution the approach drawn by Qiao and co-workers [46] was here taken into account, Equation (11):

σ_VLAB+LAB = (α′GbS/4.365)ρ_VLAB+_LAB

(11)

where α′ = 2 [46], S is the average distance between the boundary dislocations. This relationship holds for low angle boundaries and this why the approach of Equation (9) was used.

According to [47], the strengthening contribution by the few grain boundaries formed at 0.05 < ε_eq < 0.10, was modelled as, Equation (12):

$${\sigma }_{HAB}=\left(\frac{{\alpha }^{\prime }Gb}{4.365}\right)\frac{b{\rho }_{HAB}}{arctg\left(\raisebox{1ex}{$b$}\!\left/ \!\raisebox{-1ex}{$S$}\right.\right)}$$

(12)

Thus, Equations (8) and (9) can be rewritten as, Equations (13) and (14):

σ_y|ε<0.05 = σ₀ + MαGbρ_TD^0.5

(13)

$${\sigma }_{y|\epsilon =0.0-0.10}={\sigma }_0+M\alpha \mathit{Gb}{{\rho }_{\mathit{TD}}}^{0.5}+({\alpha }^{\prime }\mathit{GbS}/4.365){\rho }_{\mathit{VLAB}+\mathit{LAB}}+\left(\frac{{\alpha }^{\prime }Gb}{4.365}\right)\frac{b{\rho }_{HAB}}{arctg\left(\raisebox{1ex}{$b$}\!\left/ \!\raisebox{-1ex}{$S$}\right.\right)}$$

(14)

The average distance S of, respectively, the LAB, Equation (11), and HAB, (Equation (12)), was evaluated by TEM inspections. The 6N-Al yield stress as determined by the Equation (13) and Equation (14), for the lower strain levels, i.e., ε_eq < 0.10, is listed in the

Table 5. Yield stress, σ_y, as calculated according to Equation (6) for OFHC Cu, and individual microstructure contributions (σ_TD, σ_VLAB+LAB, and σ_HAB) as determined by Equations (13) and (14) for 6N-Al. The yield stress as determined by the nanoindentation hardness measurements, H, using χ = 3.5 as multiplicative factor are reported for comparison. σ_y^model refers to the microstructure model, σ_y^nanoind refers to the values determined from the nanoindentation measurements.

Material	Yield Stress, MPa	εeq = 0.40	εeq = 0.91	εeq = 1.21
OFHC Cu	σymodel, MPa	217	237	256
	σynanoind, MPa	223	280	303
		εeq = 0.02	εeq = 0.05	εeq = 0.10
6N-Al	σTD, MPa	9	22	15
	σVLAB+LAB, MPa	-	5	14
	σHAB, MPa	-	-	11
	σymodel, MPa	19	37	50
	σynanoind, MPa	21	49	60

.

A good agreement between the modelled 6N-Al strengthening with HPT and the measured nanoindentation hardness was obtained for the three strain levels here considered, ε_eq = 0.02, 0.05, and 0.10. Data are reported in Table 5. It resulted that the good agreement was found by using the same multiplicative factor, χ = 3.5, between nanoindentation hardness, H^nanoind, and yield stress. In particular, in OFHC Cu the yield stress determined by the microstructure model of Equation (6), σ_y^model, deviated from the values obtained by the nanoindentation measurements, σ_y^nanoind, by 18% at the most. On the other hand, in 6N-Al the microstructure based strengthening model of Equations (13) and (14) underestimated the metal yield stress as determined by nanoindentation by a few percent at the lowest strain level (ε_eq = 0.02). The largest difference between the σ_y^model and the σ_y^nanoind was found at the strain level at which TDs started to form LABs, cell boundaries ((ε_eq = 0.05). Anyhow, the agreement between σ_y^model and σ_y^nanoind was reasonably good.

Finally, Figure 5 shows a montage of TEM micrographs documenting the process of LAB and HAB formation from TDs which was able to successfully model the microstructure strengthening induced by the early stages of plastic deformation in HPT 6N-Al.

5. Conclusions

The early stages of plastic deformation by HPT on pure copper and pure aluminum were characterized by TEM and nanoindentation A OFHC 99.99 pure Cu was subjected to shear strain up to ε_eq = 1.21, while a 6N-Al was plastically deformed for quite low shear strains, up to ε_eq = 0.10.

The following major findings can be outlined.

• A minimum necessary strain level to induce the formation of LABs and eventually HABs was identified for both copper and aluminum, and it was found to be ε_eq = 0.05 for the 6N-Al, and ε_eq < 0.40 for the OFHC Cu.
• In OFHC Cu a low cut-off strain level of ε_eq = 0.91 was identified as the minimum necessary strain to induce twin formation within the grains.
• A microstructure based strengthening model was proposed and applied for both the pure metals. In the case of aluminum, the strengthening contribution came from the tangled dislocations (TDs) which were promoted to form LABs and eventually HABs with cumulative HPT straining. In the case of copper, being a low SFE metal, statistically stored dislocations (SSDs), geometrically necessary dislocations (GNDs), dislocation walls (DWs), and grain boundaries contributed to the metal strengthening before the occurrence of twin that was promoted by the cumulative straining from ε_eq = 0.91. Beyond this strain, twin boundaries started to act as further strengthening contribution for the HPT OFHC Cu.
• Both microstructure-based models were directly compared to the metal stress obtained by the nanoindentation hardness measurements at the different experimental conditions here tested. Quite a good agreement was found by setting the multiplicative factor between the measured hardness and the resulting metal yield stress, H_V/σ_y, χ = 3.5.