On Glass Forming Ability of Bulk Metallic Glasses by Relating the Internal Friction Peak Value
Abstract
:1. Introduction
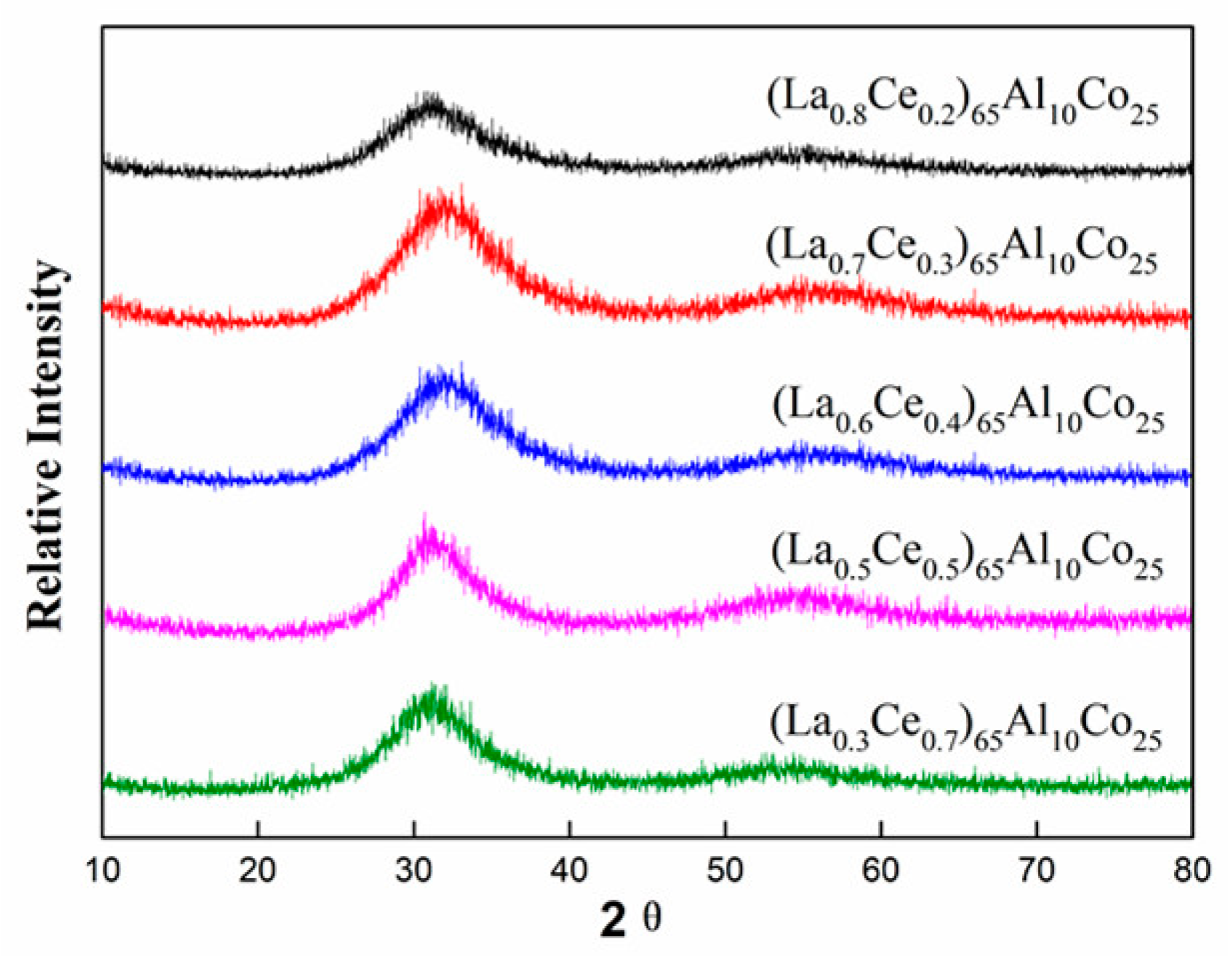
2. Experimental Procedure
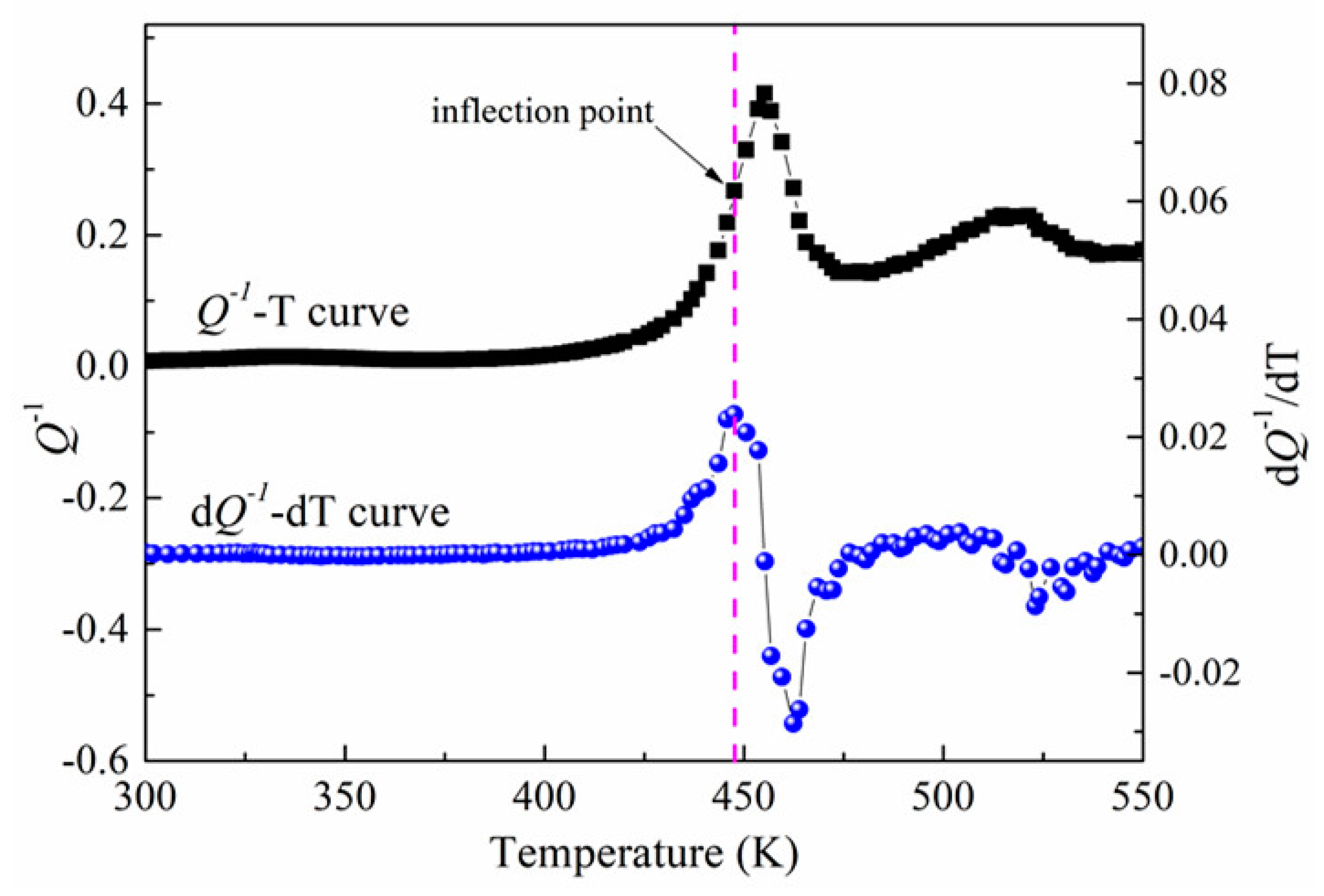
3. Results
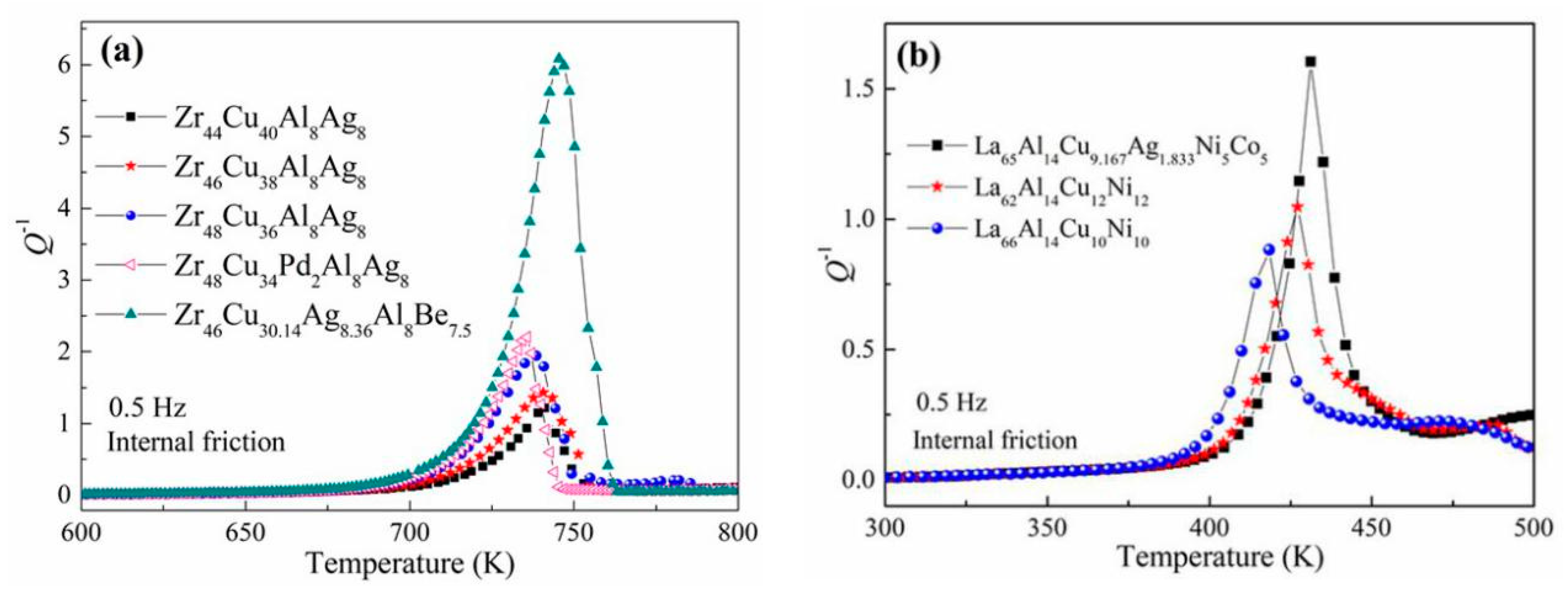
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, L.T.; Ge, T.S. Nonlinear internal friction in Mn-Cu Martensite. Phys. Status Solidi A 1988, 105, 447–453. [Google Scholar] [CrossRef]
- Khonik, V.A.; Spivak, L.V. On the nature of low temperature internal friction peaks in metallic glasses. Acta Mater. 1996, 44, 367–381. [Google Scholar] [CrossRef]
- Sinning, H.R. Low-frequency internal friction of metallic glasses near Tg-A critigue of the use of the torsion pendulum. J. Non-Cryst. Solids 1989, 110, 195–202. [Google Scholar] [CrossRef]
- He, Y.H.; Li, X.G. A new type of internal-friction peak of metallic glasses near Tg. Phys. Status Solidi A 1987, 99, 115–120. [Google Scholar]
- Barmatz, M.; Chen, H.S. Youngs modulus and internal-friction in metallic glass alloys from 1.5 to 300K. Phys. Rev. B 1974, 9, 4073–4083. [Google Scholar] [CrossRef]
- Hiki, Y.; Tanahashi, M.; Takeuchi, S. Stabilization of metallic glass studied by internal friction measurement. J. Non-Cryst. Solids 2008, 354, 1780–1785. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, X.F.; Meng, L.Z.; Guo, J.; Ma, Y.B.; Meng, X.J.; Bian, B.C.; Zhao, R.G.; Zu, F.Q. Analysis of β relaxation using internal friction measurement and mechanical testing for a LaCe-based bulk metallic glass. J. Non-Cryst. Solids 2019, 525, 119670. [Google Scholar] [CrossRef]
- Jung, I.C.; Kang, D.G.; De Cooman, B.C. Impulse Excitation Internal Friction Study of Dislocation and Point Defect Interactions in Ultra-Low Carbon Bake-Hardenable Steel. Metall. Mater. Trans. A 2014, 45, 1962–1978. [Google Scholar] [CrossRef] [Green Version]
- Fang, Q.F.; Ge, T.S. Low temperature internal friction peaks associated with the interaction between dislocations and point defects in dilute aluminium-magnesium solid solutions. Acta Metall. Mater. 1990, 38, 419–424. [Google Scholar] [CrossRef]
- Sun, M.; Wang, X.P.; Wang, L.; Wang, H.; Jiang, W.B.; Liu, W.; Hao, T.; Gao, R.; Gao, Y.X.; Zhang, T.; et al. High-temperature order-disorder phase transition in Fe-18Ga alloy evaluated by internal friction method. J. Alloys Compd. 2018, 750, 669–676. [Google Scholar] [CrossRef]
- Wu, Y.X.; Hao, T.; Sun, M.; Jiang, W.B.; Wang, X.P.; Fang, Q.F.; Liu, X.B.; Li, Y.F.; Xue, F. Internal friction study on precipitation/dissolution of Mn-Ni-Si phase in aged RPV model steel. Matter. Lett. 2020, 269, 127668. [Google Scholar] [CrossRef]
- Khonik, V.; Kobelev, N. Metallic Glasses: A New Approach to the Understanding of the Defect Structure and Physical Properties. Metals 2019, 9, 605. [Google Scholar] [CrossRef] [Green Version]
- Nemilov, S.V. The review of possible interrelations between ionic conductivity, internal friction and the viscosity of glasses and glass forming melts within the framework of Maxwell equations. J. Non-Cryst. Solids 2011, 357, 1243–1263. [Google Scholar] [CrossRef]
- Qiao, J.C.; Ren, T.P.; Lyu, G.J.; Zhang, L.; Zhang, H.F.; Pelletier, J.M.; Yao, Y. Physical mechanism of internal friction behavior of beta-type bulk metallic glass composites. Mater. Sci. Eng. A 2019, 739, 193–197. [Google Scholar] [CrossRef]
- Hockicko, P.; Mizerakova, J.; Munoz, F. The internal friction of lithium and sodium borophosphate glasses. J. Non-Cryst. Solids 2018, 498, 194–198. [Google Scholar] [CrossRef]
- Fursova, Y.V.; Khonik, V.A. Viscoelastic infralow-frequency internal friction as a result of irreversible structural relaxation of a metallic glass. Philos. Mag. A 2000, 80, 1855–1865. [Google Scholar] [CrossRef]
- Tan, M.; He, Y.Z. Internal friction behaviour of metallic glass Cu70Ti30 during structural relaxation and crystallization. J. Non-Cryst. Solids 1988, 105, 155–161. [Google Scholar]
- Liu, C.R.; Pineda, E.; Crespo, D.; Qiao, J.C.; Evenson, Z.; Ruta, B. Sub-Tg relaxation times of the alpha process in metallic glasses. J. Non-Cryst. Solids 2017, 471, 322–327. [Google Scholar] [CrossRef] [Green Version]
- Ding, H.L.; Xie, Z.M.; Fang, Q.F.; Zhang, T.; Cheng, Z.J.; Zhuang, Z.; Wang, X.P.; Liu, C.S. Determination of the DBTT of nanoscale ZrC doped W alloys through amplitude-dependent internalfriction technique. Mater. Sci. Eng. A 2018, 716, 268–273. [Google Scholar] [CrossRef]
- Morito, N.; Egami, T. Internal-friction and reversible structure relaxation in the metallic-glass Fe32Ni36Cr14P12B6. Acta Metall. 1984, 32, 603–613. [Google Scholar] [CrossRef]
- Morito, N.; Egami, T. Correlation of the shear modulus and internal-friction in the reversible structural relaxation of a glassy metal. J. Non-Cryst. Solids 1984, 61–62, 973–978. [Google Scholar] [CrossRef]
- Yang, K.W.; Jia, E.G.; Shui, J.P.; Zhu, Z.G. Crystallization study of amorphous Pd43Ni10CU27P20 alloy by internal friction measurement. Phys. Status Solidi A 2007, 204, 3297–3304. [Google Scholar] [CrossRef]
- Zhang, B.; Zu, F.Q.; Zhen, K.; Shui, J.P.; Wen, P. Internal friction behaviours in Zr57Al10Ni12.4Cu15.6Nb5 bulk metallic glass. J. Phys. D Condens. Matter 2002, 14, 7461–7470. [Google Scholar] [CrossRef]
- Inoue, A.; Zhang, T.; Masumoto, T. Glass-forming ability of alloys. J. Non-Cryst. Solids 1993, 156, 473–480. [Google Scholar] [CrossRef]
- Turnbull, D. Under what conditions can a glass be formed. Contemp. Phys. 1969, 10, 473. [Google Scholar] [CrossRef]
- Lu, Z.P.; Liu, C.T. A new glass-forming ability criterion for bulk metallic glasses. Acta Mater. 2002, 50, 3501–3512. [Google Scholar] [CrossRef]
- Wang, L.F.; Zhang, Q.D.; Cui, X.; Zu, F.Q. An empirical criterion for predicting the glass-forming ability of amorphous alloys based on electrical transport properties. J. Non-Cryst. Solids 2015, 419, 51–57. [Google Scholar] [CrossRef]
- Long, Z.L.; Wei, H.Q.; Ding, Y.H.; Zhang, P.; Xie, G.Q.; Inoue, A. A new criterion for predicting the glass-forming ability of bulk metallic glasses. J. Alloys Compd. 2009, 475, 207–219. [Google Scholar] [CrossRef]
- Lou, H.B.; Wang, X.D.; Xu, F.; Ding, S.Q.; Cao, Q.P.; Hono, K.; Jiang, J.Z. 73 mm-diameter bulk metallic glass rod by copper mould casting. Appl. Phys. Lett. 2011, 99, 051910. [Google Scholar] [CrossRef]
- Luo, Q.; Wang, W.H. Rare earth based bulk metallic glasses. J. Non-Cryst. Solids 2009, 355, 759–775. [Google Scholar] [CrossRef]
- Jiang, Q.K.; Zhang, G.Q.; Yang, L.; Wang, X.D.; Saksl, K.; Franz, H.; Wunderlich, R.; Fecht, H.; Jiang, J.Z. La-based bulk metallic glasses with critical diameter up to 30 mm. Acta Mater. 2007, 55, 4409–4418. [Google Scholar] [CrossRef]
- Li, R.; Pang, S.J.; Ma, C.L.; Zhang, T. Influence of similar atom substitution on glass formation in (La–Ce)–Al–Co bulk metallic glasses. Acta Mater. 2007, 55, 3719–3726. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.N.; Qiao, J.C.; Hao, Q.; Chen, Y.H.; Yao, Y.; Crespo, D.; Pelletier, J.M. Dynamic Mechanical Relaxation in LaCe-Based Metallic Glasses: Influence of the Chemical Composition. Metals 2019, 9, 1013. [Google Scholar] [CrossRef] [Green Version]
- Qiao, J.C.; Wang, Q.; Pelletier, J.M.; Kato, H.; Casalini, R.; Crespo, D.; Pineda, E.; Yao, Y.; Yang, Y. Structural heterogeneities and mechanical behavior of amorphous alloys. Prog. Mater. Sci. 2019, 104, 250–329. [Google Scholar] [CrossRef]
- Cui, X.; Zu, F.Q.; Wang, L.F.; Wang, Z.Z.; Li, X.Y.; Huang, Z.Y. A method for determining the crystallization temperature in studying internal friction behaviors of bulk metallic glasses. J. Non-Cryst. Solids 2013, 366, 59–63. [Google Scholar] [CrossRef]
- Yu, H.B.; Wang, W.H.; Bai, H.Y.; Samwer, K. The β-relaxation in metallic glasses. Natl. Sci. Rev. 2014, 1, 429–461. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Lu, J.; Gu, F.J.; Xu, H.; Dong, Y.D. Isothermal internal friction behaviour of a Zr based bulk metallic glass with large supercooled liquid region. J. Phys. D Appl. Phys. 2006, 39, 2851–2855. [Google Scholar] [CrossRef]
- Busch, R.; Masuhr, A.; Johnson, W.L. Thermodynamics and kinetics of Zr-Ti-Cu-Ni-Be bulk metallic glass forming liquids. Mater. Sci. Eng. A 2001, 304–306, 97–102. [Google Scholar] [CrossRef]
- Qiao, J.C.; Wang, Y.J.; Pelletier, J.M.; Keer, L.M.; Fine, M.E.; Yao, Y. Characteristics of stress relaxation kinetics of La60Ni15Al25 bulk metallic glass. Acta Mater. 2015, 98, 43–50. [Google Scholar] [CrossRef] [Green Version]
- Qiao, J.C.; Wang, Y.J.; Zhao, L.Z.; Dai, L.H.; Crespo, D.; Pelletier, J.M.; Keer, L.M.; Yao, Y. Transition from stress-driven to thermally activated stress relaxation in metallic glasses. Phys. Rev. B 2016, 94, 104203. [Google Scholar] [CrossRef] [Green Version]
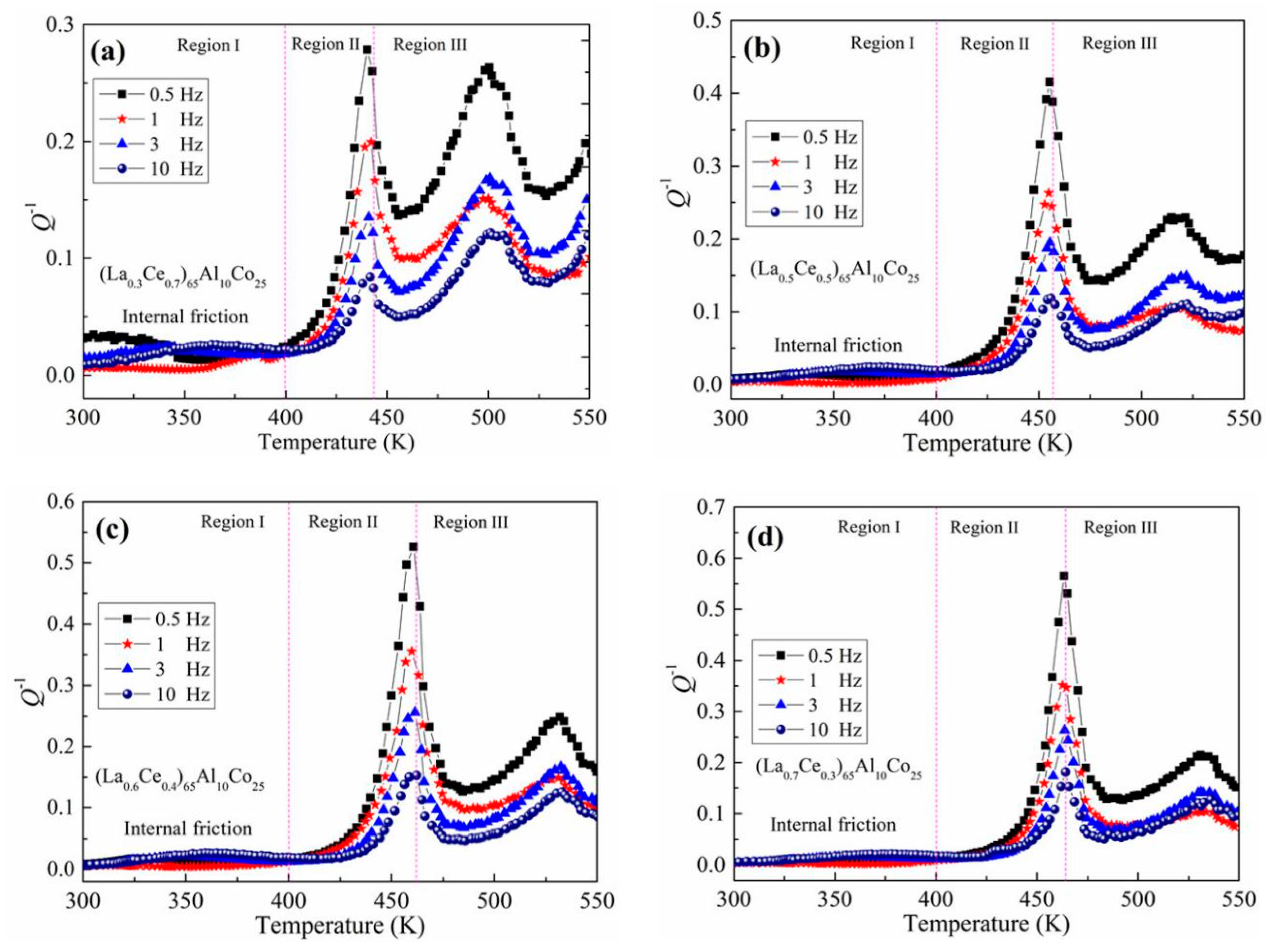


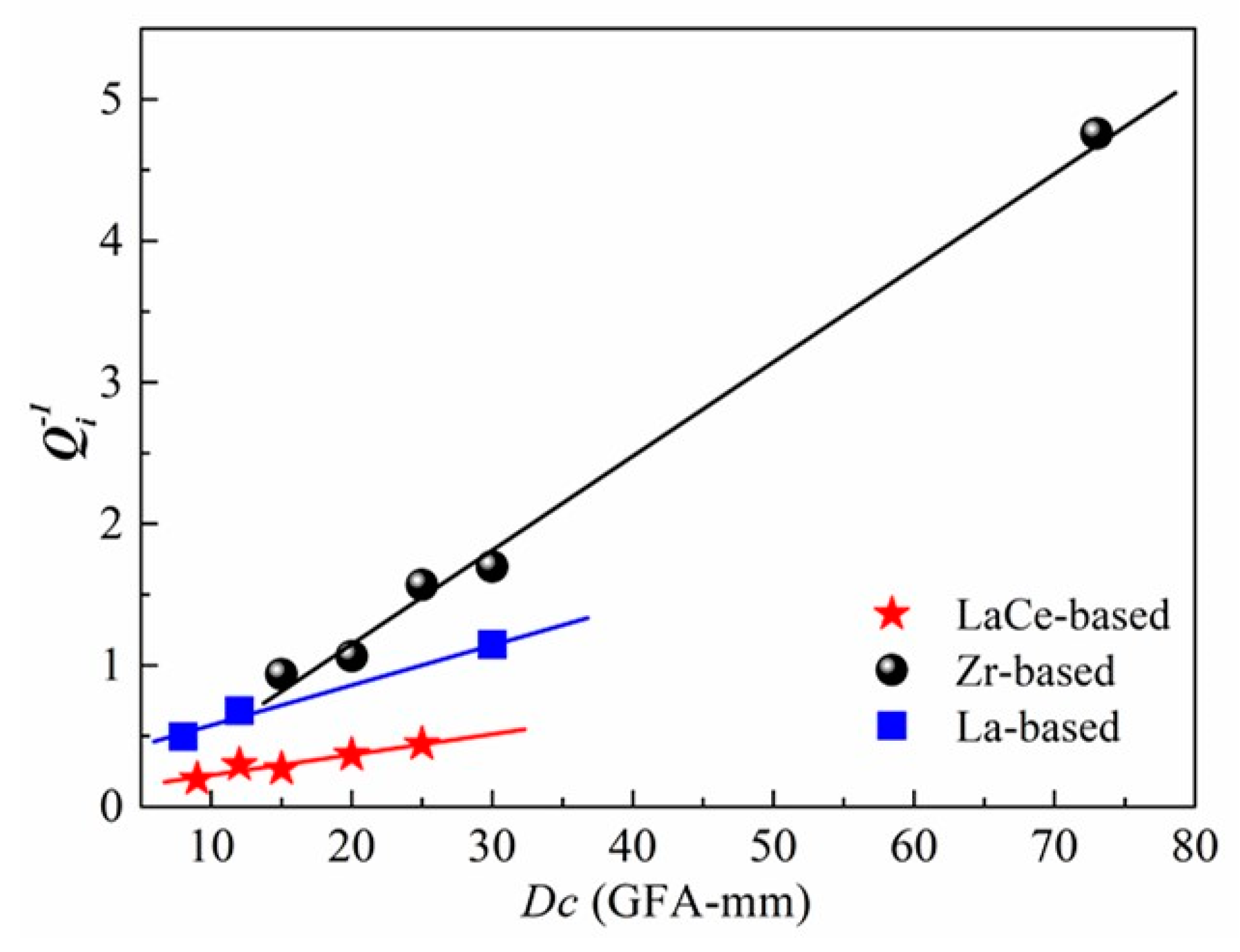
| BMG Composition | Dc (mm) [32] | Tg (K) [32] | Tx (K) [32] | ΔTx (K) [32] | Trg [32] | Γ [32] | Qp−1 | Qi−1 |
|---|---|---|---|---|---|---|---|---|
| (La0.3Ce0.7)65Al10Co25 | 9 | 416 | 436 | 20 | 0.54 | 0.365 | 0.28 | 0.19 |
| (La0.5Ce0.5)65Al10Co25 | 15 | 427 | 453 | 26 | 0.55 | 0.376 | 0.42 | 0.27 |
| (La0.6Ce0.4)65Al10Co25 | 20 | 437 | 467 | 30 | 0.52 | 0.367 | 0.53 | 0.37 |
| (La0.7Ce0.3)65Al10Co25 | 25 | 437 | 472 | 35 | 0.51 | 0.367 | 0.56 | 0.44 |
| (La0.8Ce0.2)65Al10Co25 | 12 | 439 | 476 | 37 | 0.50 | 0.364 | 0.51 | 0.29 |
| BMG Composition | Dc (mm) | Q−1p | Q−1i |
|---|---|---|---|
| Zr44Cu40Al8Ag8 | 15 [28] | 1.215 | 0.937 |
| Zr46Cu38Al8Ag8 | 20 [28] | 1.428 | 1.064 |
| Zr48Cu36Al8Ag8 | 25 [28] | 1.943 | 1.569 |
| Zr48Cu34Pd2Al8Ag8 | 30 [28] | 2.202 | 1.697 |
| Zr46Cu30.14Ag8.36Al8Be7.5 | 73 [29] | 6.081 | 4.758 |
| La66Al14Cu10Ni10 | 8 [30] | 0.883 | 0.495 |
| La62Al14Cu12Ni12 | 12 [28] | 1.046 | 0.677 |
| La65Al14Cu9.167Ag1.833Ni5Co5 | 30 [31] | 1.604 | 1.146 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Cui, X.; Du, Z.; Zu, F.; Li, J.; Bian, B.; Xu, K.; Zhang, X. On Glass Forming Ability of Bulk Metallic Glasses by Relating the Internal Friction Peak Value. Metals 2020, 10, 767. https://doi.org/10.3390/met10060767
Zhang X, Cui X, Du Z, Zu F, Li J, Bian B, Xu K, Zhang X. On Glass Forming Ability of Bulk Metallic Glasses by Relating the Internal Friction Peak Value. Metals. 2020; 10(6):767. https://doi.org/10.3390/met10060767
Chicago/Turabian StyleZhang, Xianfeng, Xiao Cui, Zhuotong Du, Fangqiu Zu, Jinjing Li, Bingchuan Bian, Kuilong Xu, and Xinyao Zhang. 2020. "On Glass Forming Ability of Bulk Metallic Glasses by Relating the Internal Friction Peak Value" Metals 10, no. 6: 767. https://doi.org/10.3390/met10060767
APA StyleZhang, X., Cui, X., Du, Z., Zu, F., Li, J., Bian, B., Xu, K., & Zhang, X. (2020). On Glass Forming Ability of Bulk Metallic Glasses by Relating the Internal Friction Peak Value. Metals, 10(6), 767. https://doi.org/10.3390/met10060767




