SteBLife, a New Approach for the Accelerated Generation of Metallic Materials’ Fatigue Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
- SAE 1045 (C45E) Steel
- SAE 4140 (42CrMo4) Steel
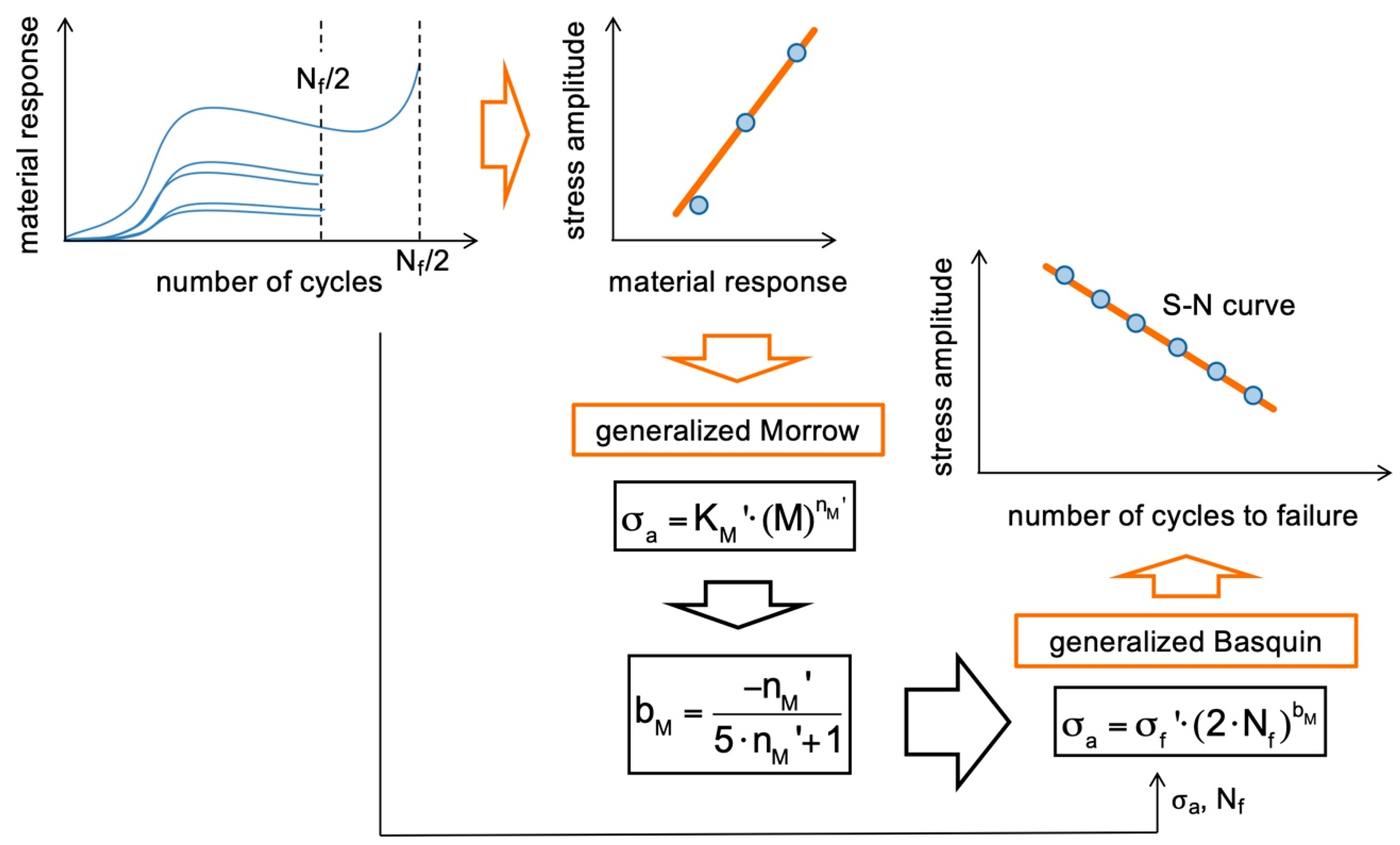
2.2. Fatigue Life Calculation Method SteBLife
2.3. Measurement Technology
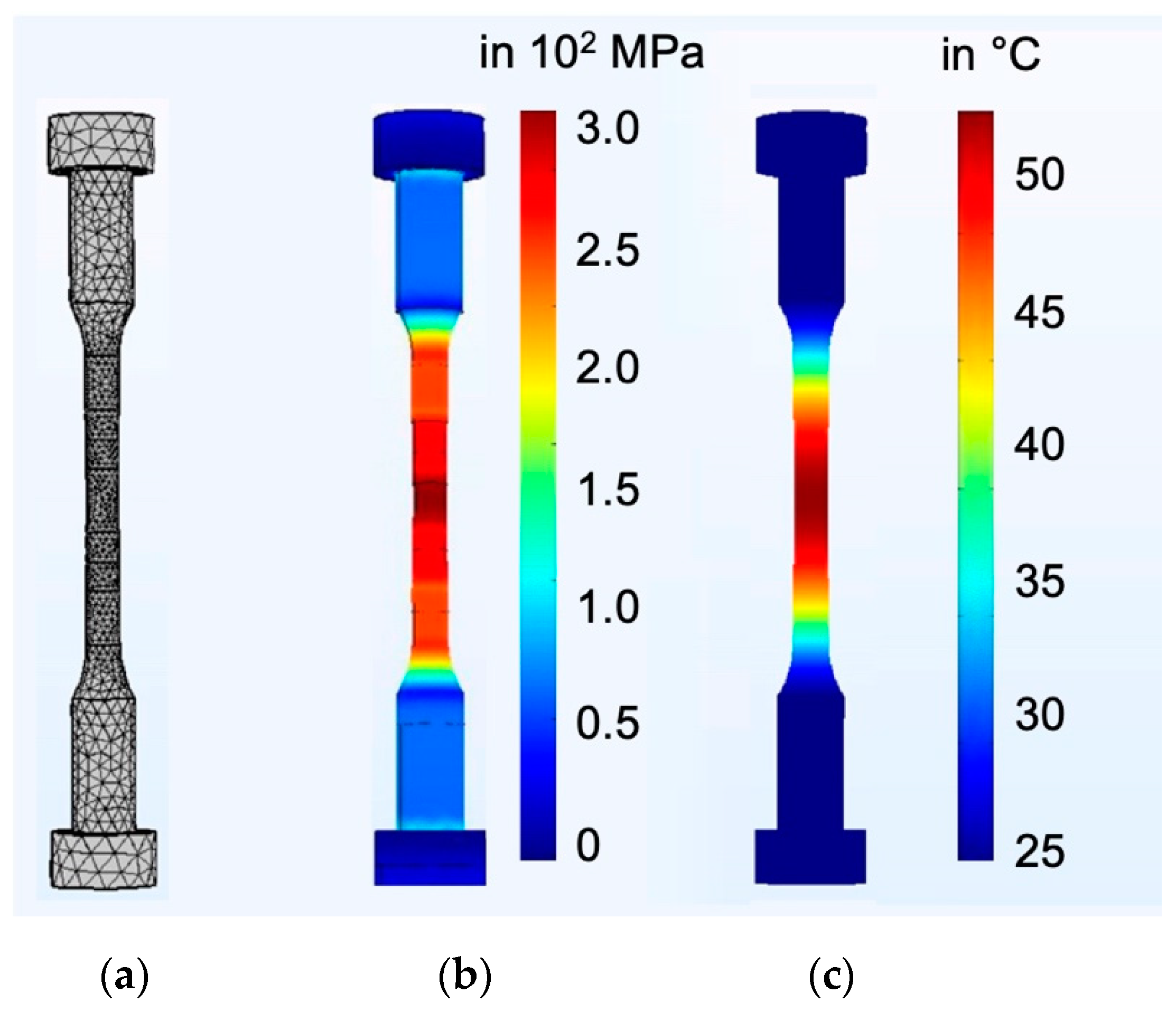
2.3.1. Fatigue Testing System
2.3.2. Temperature Measurements
2.3.3. Magnetic-Based Measurements
3. Results and Discussion
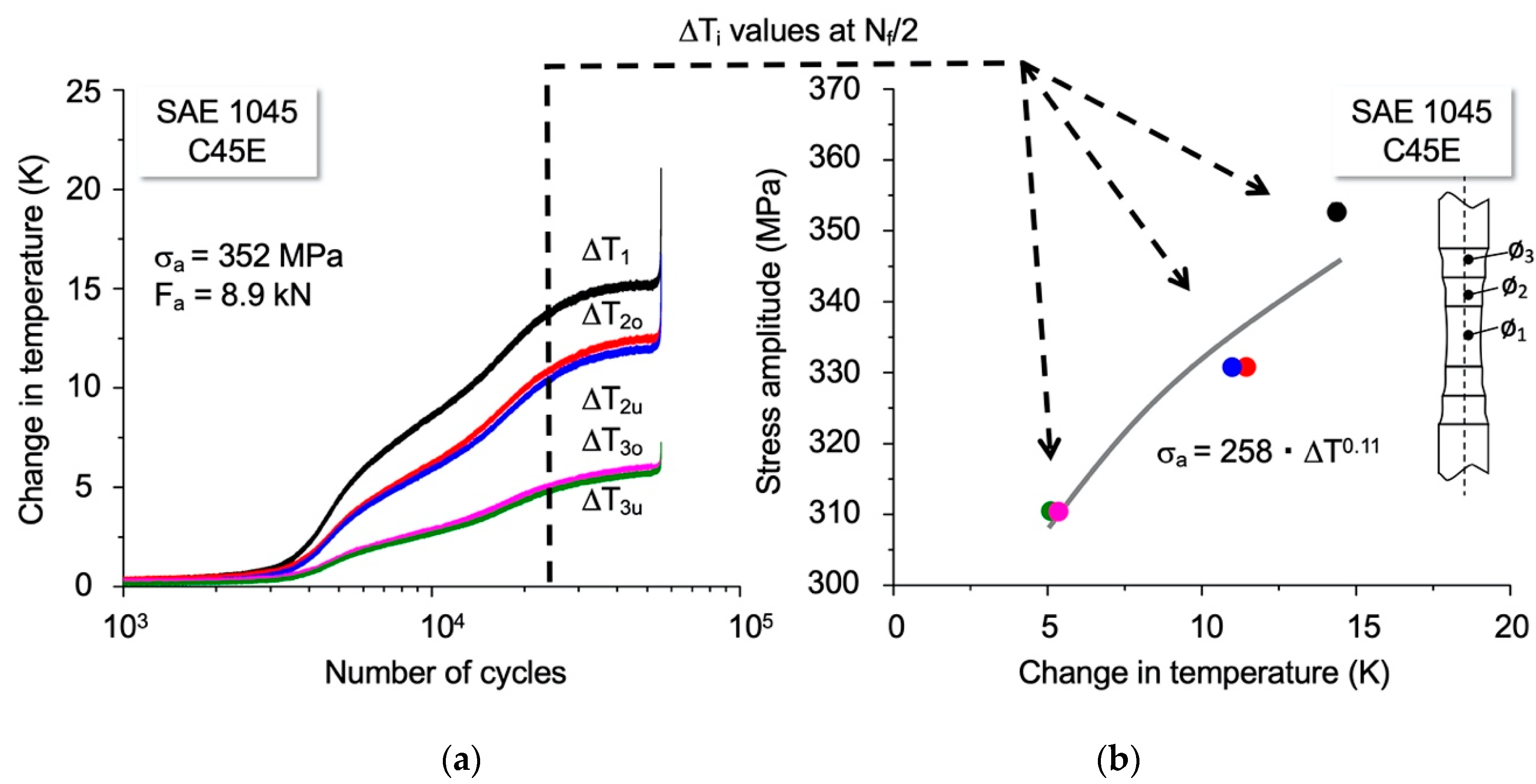
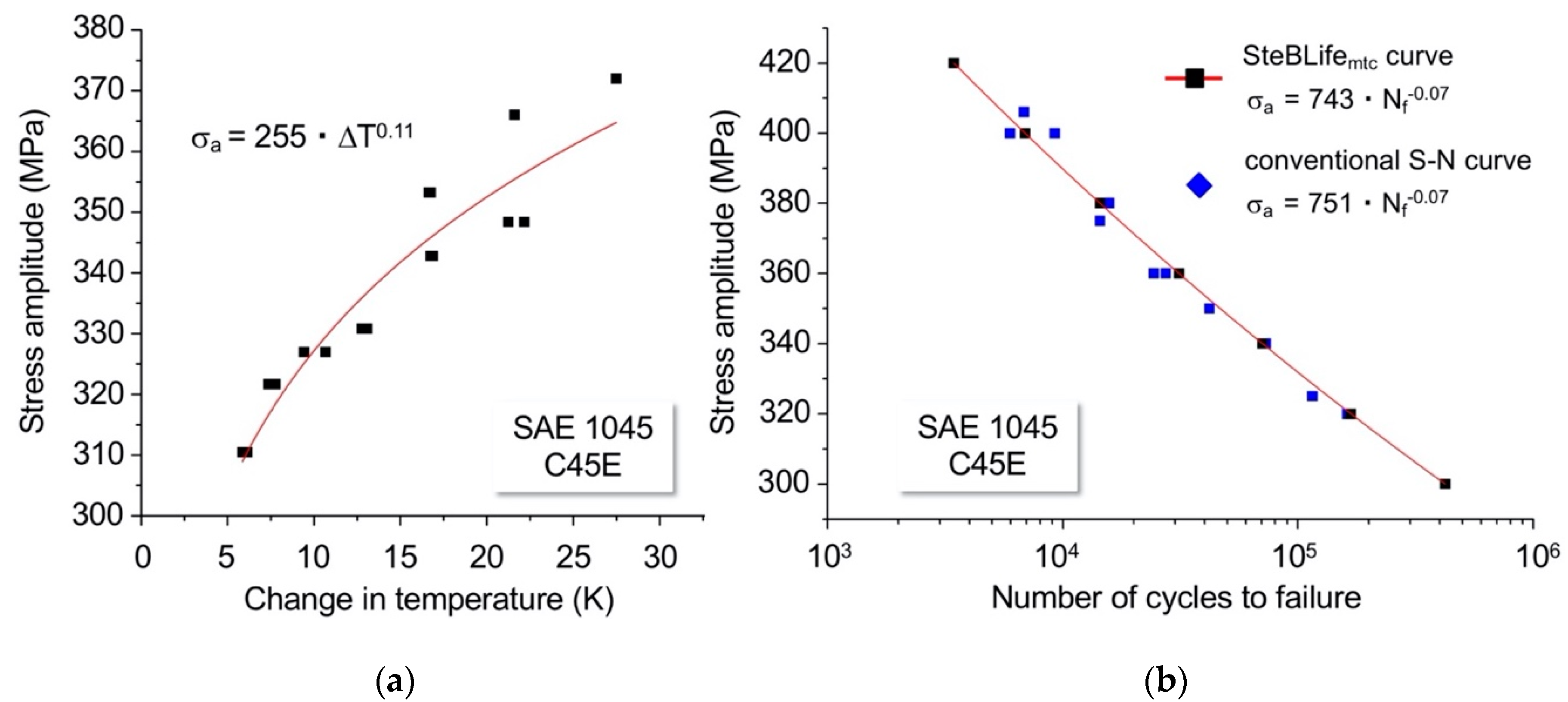
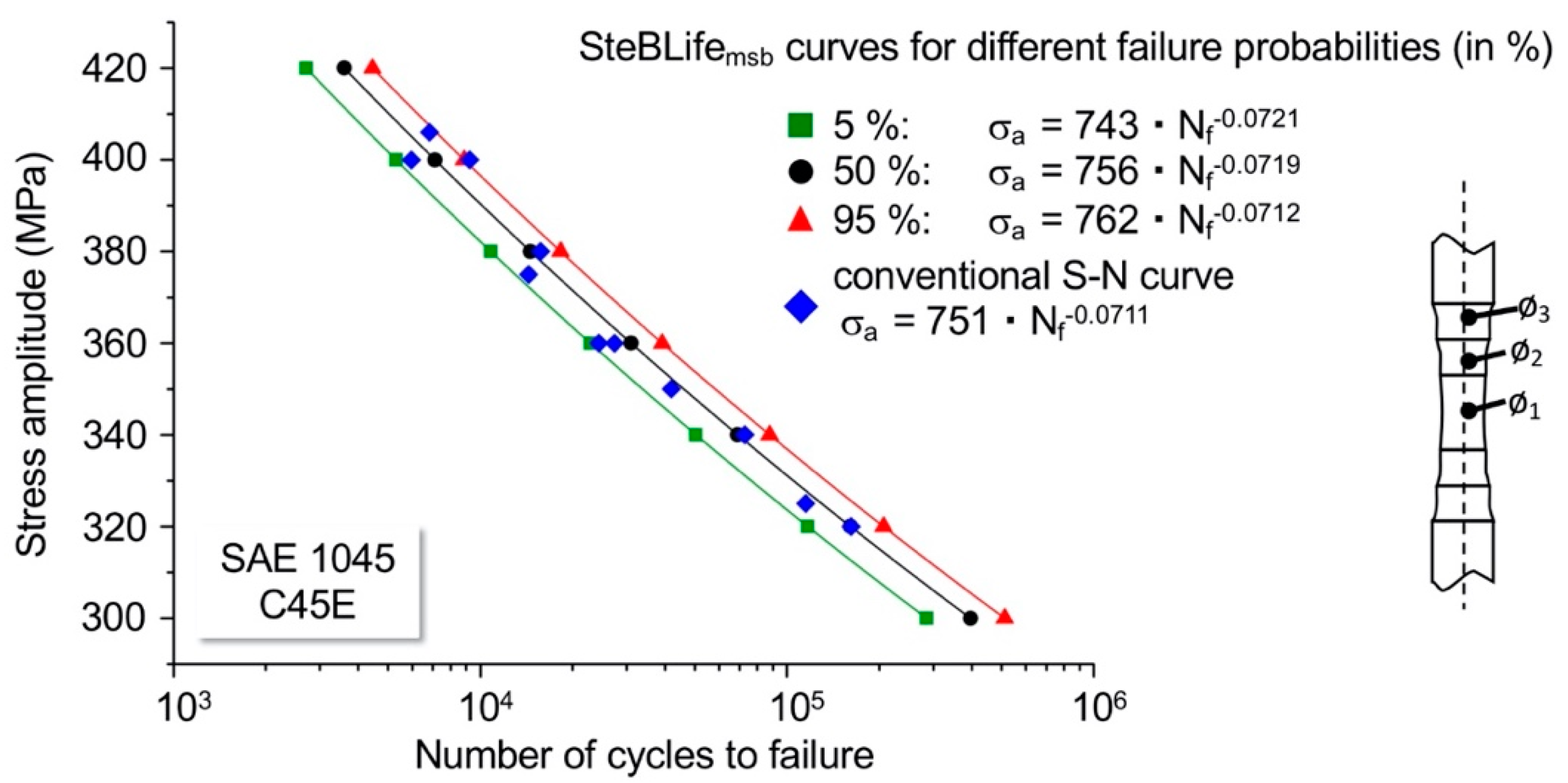
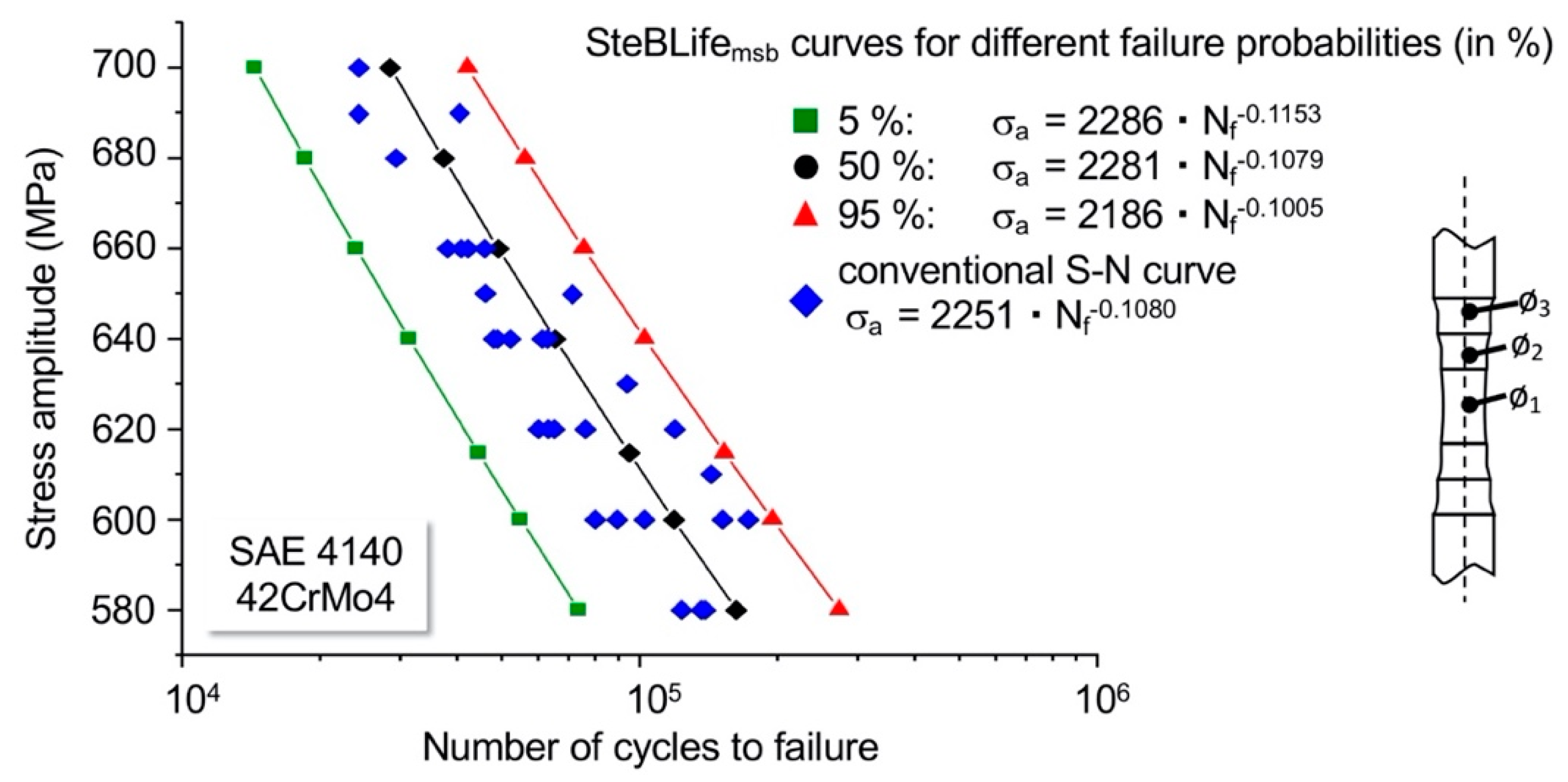
3.1. Temperature-Based Calculations
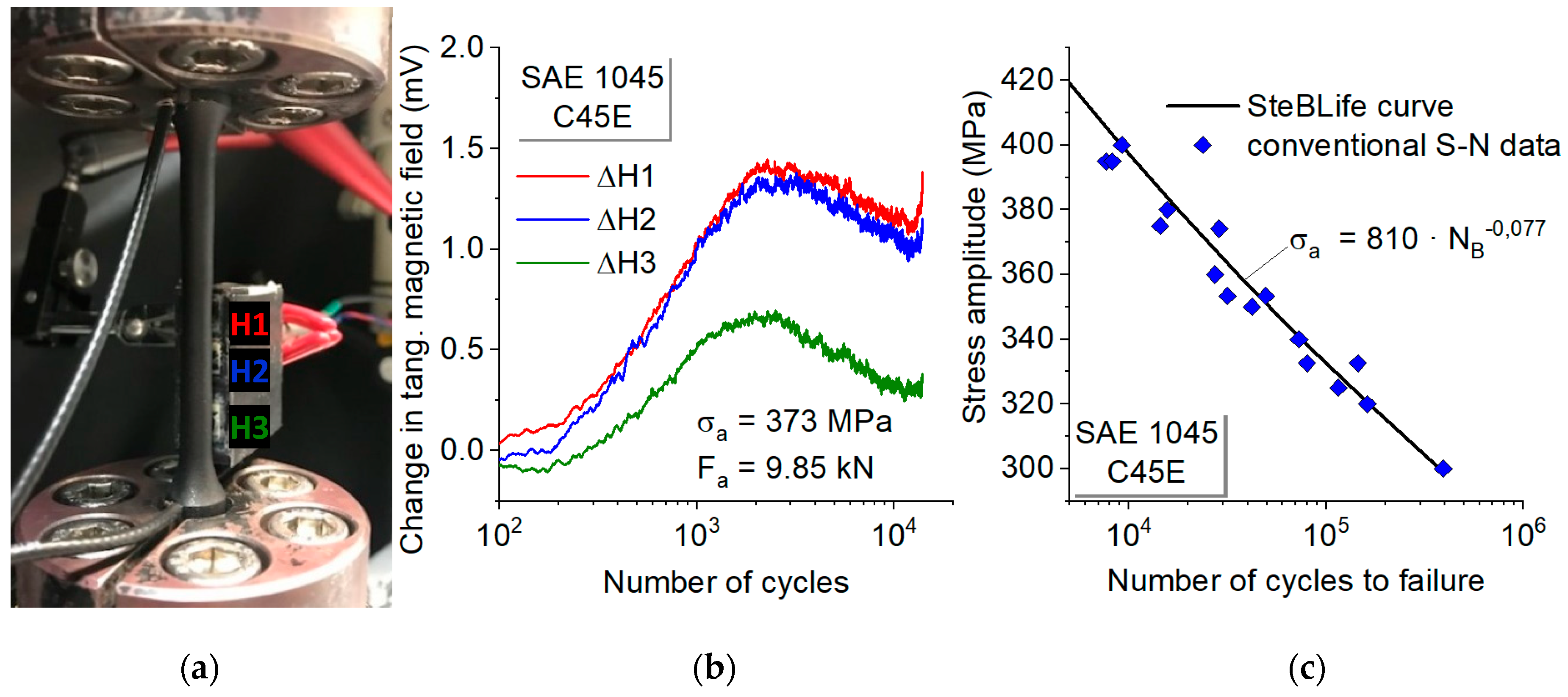
3.2. Magnetic-Based Calculations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Berger, C.; Eulitz, K.G.; Heuler, P.; Kotte, K.L.; Naundorf, H.; Schütz, W.; Sonsino, C.M.; Wimmer, A.; Zenner, H. Betriebsfestigkeit in Germany—An overview. Int. J. Fatigue 2002, 24, 603–625. [Google Scholar] [CrossRef]
- Seeger, T.; Heuler, P. Generalized application of Neuber’ s rule. J. Test. Eval. 1980, 8, 199–204. [Google Scholar]
- Haibach, E. Betriebsfestigkeit: Verfahren und Daten zur Bauteilberechnung (Structural integrity: Methods and Data for Component Calculation); Springer-Verlag: Berlin/Heidelberg, Germany, 2006; ISBN 9783540293637. (In German) [Google Scholar]
- Müller, A.; Grubisic, V. Simulation and measurement of complex, multi-axial, dynamic stress states on vehicle axle components. Rep. Appl. Meas. 1995, 9, 5–10. [Google Scholar]
- Radaj, D.; Sonsino, C.M.; Fricke, W. Fatigue Assessment of Welded Joints by Local Approaches, 2nd ed.; Woodhead Publishing: Sawston, UK, 2006. [Google Scholar]
- Grubisic, V.; Sonsino, C.M. Betriebsfeste Bemessung von Stahlkonstruktionen im Anlagenbau (Design against operational strength of steel constructions for plants). Materwiss. Werksttech. 1995, 26, 416–424. (In German) [Google Scholar] [CrossRef]
- Pawliczek, R.; Rozumek, D. The effect of mean load for S355J0 steel with increased strength. Metal (Basel) 2020, 10, 209. [Google Scholar] [CrossRef] [Green Version]
- Gassner, E.; Lowak, H. Bedeutung der Unregelmäßigkeit Gauß’scher Zufallsfolgen fur die Betriebsfestigkeit (Significance of irregularity of Gaussian random sequences on Fatigue). Materwiss. Werksttech. 1978, 9, 246–256. (In German) [Google Scholar] [CrossRef]
- Palmgren, A. Die Lebensdauer von Kugellagern. (The life of roller bearings). Z. Des. Ver. Dtsch. Ing. 1924, 68, 339–341. (In German) [Google Scholar]
- Miner, M. Cumulative damage in fatigue. J. Appl. Mech. 1945, 3, 159–164. [Google Scholar]
- Neuber, H. Theory of stress concentration for shear-strained prismatical bodies with arbitrary nonlinear stress-strain Law. J. Appl. Mech. 1961, 28, 544–550. [Google Scholar] [CrossRef]
- Schütz, W.; Zenner, H. Schadensakkumulationshypothesen zur Lebensdauervorhersage bei schwingender Beanspruchung. Teil 1—Ein kritischer Uberblick (Cumulative damage theories for the prediction of fatigue life—Part 1). Materwiss. Werksttech. 1973, 4, 25–33. (In German) [Google Scholar] [CrossRef]
- Schütz, W.; Zenner, H. Schadensakkumulationshypothesen zur Lebensdauervorhersage bei schwingender Beanspruchung. Teil 2—Ein kritischer Überblick (Cumulative damage theories for the prediction of fatigue life—Part 2). Materwiss. Werksttech. 1973, 4, 97–102. (In German) [Google Scholar] [CrossRef]
- Radaj, D.; Vormwald, M. Advanced Methods of Fatigue Assessment; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Laue, S.; Bomas, H.; Mayr, P. Vergleichende untersuchungen zur anrisslebensdauervorhersage gekerbter proben mit dem örtlichen konzept und dem nennspannungskonzept am beispiel des stahls Cm15 (Comparative investigations on service life assessment of notched specimens based on the local). Materwiss. Werksttech. 2004, 35, 135–142. (In German) [Google Scholar] [CrossRef]
- Christ, H.-J. Ermüdungsverhalten Metallischer Werkstoffe (Fatigue Behaviour of Metallic Materials); Wiley-VCH: Weinheim, Germany, 1998. (In German) [Google Scholar]
- Basquin, O.H. The exponential law of endurance. Am. Soc. Test. Mater. 1910, 10, 625–630. [Google Scholar]
- Ricotta, M. Simple expressions to estimate the Manson-Coffin curves of ductile cast irons. Int. J. Fatigue 2015, 78, 38–45. [Google Scholar] [CrossRef]
- ASTM International. Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S–N) and Strain-Life (ε–N) Fatigue Data: ASTM E739-91; ASTM International: West Conshohocken, PA, USA, 2004; Volume 3, pp. 658–664. [Google Scholar]
- Boller, C.; Seeger, T. Materials Data for Cyclic Loading; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Goto, M. Scatter in small crack propagation and fatigue behaviour in carbon steels. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 795–809. [Google Scholar] [CrossRef]
- Blacha, L.; Karolczuk, A.; Bański, R.; Stasiuk, P. Application of the weakest link analysis to the area of fatigue design of steel welded joints. Eng. Fail. Anal. 2013, 35, 665–677. [Google Scholar] [CrossRef]
- Wu, H.; Bill, T.; Teng, Z.J.; Pramanik, S.; Hoyer, K.P.; Schaper, M.; Starke, P. Characterization of the fatigue behaviour for SAE 1045 steel without and with load-free sequences based on non-destructive, X-ray diffraction and transmission electron microscopic investigations. Mater. Sci. Eng. A 2020. Accepted for publication. [Google Scholar] [CrossRef]
- Starke, P.; Bäumchen, A.; Wu, H. SteBLife—A new short-time procedure for the calculation of S-N curves and failure probabilities. Mater. Test. 2018, 60, 121–127. [Google Scholar] [CrossRef]
- Starke, P.; Wu, H. Use of non-destructive testing methods in a new one-specimen test strategy for the estimation of fatigue data. Int. J. Fatigue 2018, 111, 177–185. [Google Scholar] [CrossRef]
- Starke, P. StressLifetc—NDT-related assessment of the fatigue life of metallic materials. Mater. Test. 2019, 61, 297–303. [Google Scholar] [CrossRef]
- Wu, H.; Bäumchen, A.; Engel, A.; Acosta, R.; Boller, C.; Starke, P. SteBLife—A new short-time procedure for the evaluation of fatigue data. Int. J. Fatigue 2019, 124, 82–88. [Google Scholar] [CrossRef]
- Weber, F.; Acosta, R.; Eyrisch, T.; Hielscher, T.; Magin, M.; Starke, P. Influence of processing parameters on the fatigue life time of specimens made from quenched and tempered steel SAE 4140H. Mater. Test. 2019, 61, 842–850. [Google Scholar] [CrossRef]
- Starke, P.; Eifler, D.; Boller, C. Fatigue assessment of metallic materials beyond strain measurement. Int. J. Fatigue 2016, 82, 274–279. [Google Scholar] [CrossRef]
- Starke, P.; Walther, F.; Eifler, D. New fatigue life calculation method for quenched and tempered steel SAE 4140. Mater. Sci. Eng. A 2009, 523, 246–252. [Google Scholar] [CrossRef]
- Acosta, R.; Boller, C.; Starke, P.; Jamrozy, M.; Knyazeva, M.; Walther, F.; Heckmann, K.; Sievers, J.; Weihe, S.; Schopf, T. Non-destructive testing derived parameters for microstructure- based residual service life assessment of aging metallic materials in nuclear engineering. Mater. Test. 2019, 61, 1029–1038. [Google Scholar] [CrossRef]
- Morrow, J. Cyclic plastic strain energy and fatigue of metals. In Internal Friction, Damping, and Cyclic Plasticity; Lazan, B.J., Ed.; ASTM International: West Conshohocken, PA, USA, 1965; pp. 45–87. ISBN 978-0-8031-5995-2. [Google Scholar]
- Starke, P.; Wu, H.; Boller, C. SteBLife—The enhanced short-time evaluation procedure for materials fatigue data generation. Mater. Sci. Forum 2019, 941, 2395–2400. [Google Scholar] [CrossRef]
- Maletta, C.; Bruno, L.; Corigliano, P.; Crupi, V.; Guglielmino, E. Crack-tip thermal and mechanical hysteresis in shape memory alloys under fatigue loading. Mater. Sci. Eng. A 2014, 616, 281–287. [Google Scholar] [CrossRef]
- Sangid, M.D. The physics of fatigue crack initiation. Int. J. Fatigue 2013, 57, 58–72. [Google Scholar] [CrossRef]
- Hall, E.H. On a new action of the magnet on electric currents. Am. J. Math. 1879, 2, 287–292. [Google Scholar] [CrossRef]
- Karplus, R.; Luttinger, J.M. Hall effect in ferromagnetics. Phys. Rev. 1954, 95, 1154–1160. [Google Scholar] [CrossRef]



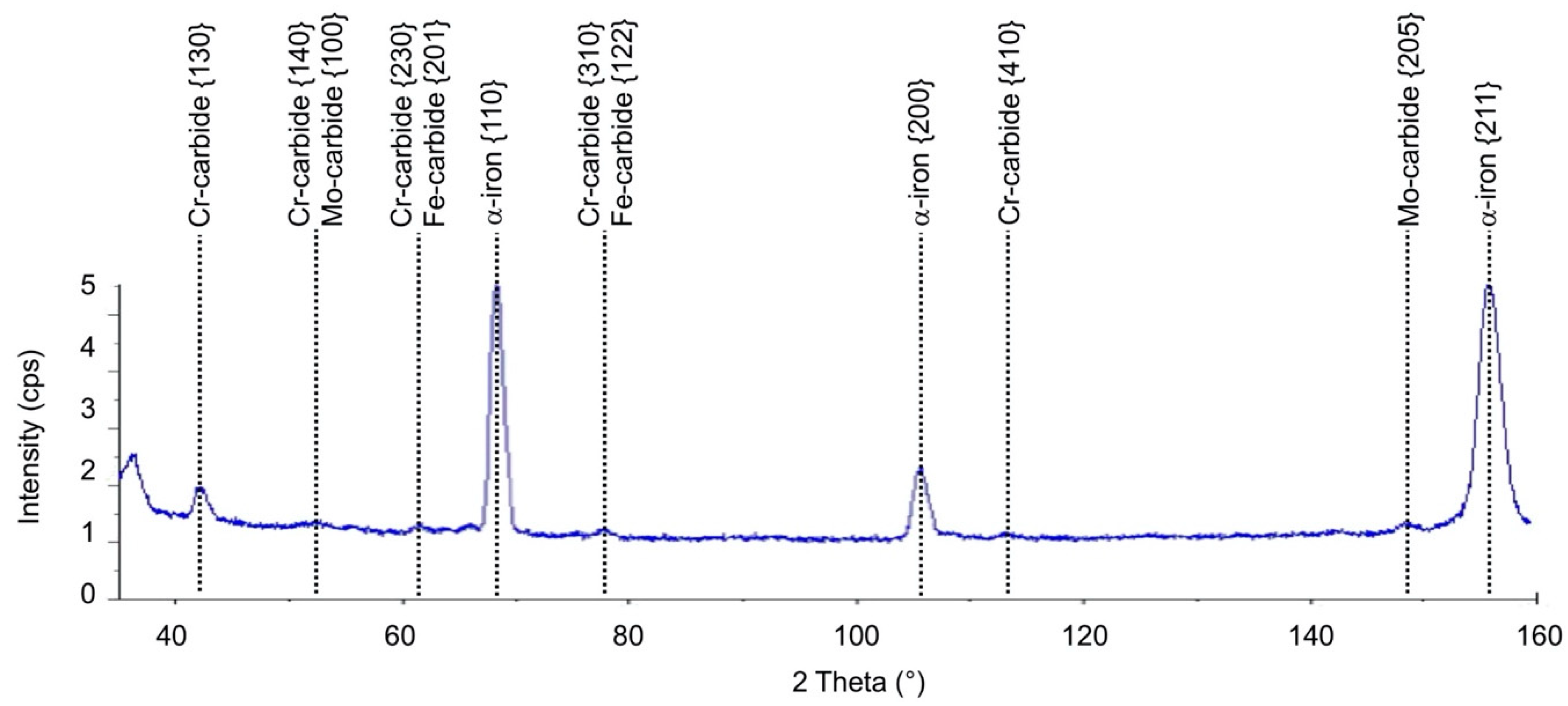



| (wt %) | C | Si | Mn | P | S | Cr | Mo | Ni | |
|---|---|---|---|---|---|---|---|---|---|
| DIN−standard | Min | 0.42 | - | 0.50 | - | - | - | - | - |
| Max. | 0.50 | 0.40 | 0.80 | 0.030 | 0.035 | 0.40 | 0.100 | 0.40 | |
| Certificate | 0.47 | 0.23 | 0.72 | 0.012 | 0.013 | 0.67 | 0.014 | 0.07 | |
| Rm (MPa) | Rp0.2 (MPa) | E (GPa) | A (%) | HV10 | KCU (Jm cm−2) |
|---|---|---|---|---|---|
| 710 | 413 | 204.5 | 23.5 | 218 | 56 |
| (wt %) | C | Si | Mn | P | S | Cr | Mo | Ni | |
|---|---|---|---|---|---|---|---|---|---|
| DIN-standard | Min. | 0.38 | - | 0.60 | - | 0.020 | 0.90 | 0.15 | - |
| Max. | 0.45 | 0.4 | 0.99 | 0.025 | 0.035 | 1.20 | 0.30 | - | |
| Certificate | 0.40 | 0.26 | 0.74 | 0.02 | 0.02 | 1.07 | 0.18 | 0.09 | |
| Rm (MPa) | Rp0.2 (MPa) | E (GPa) | A (%) | Z (%) | HV10 |
|---|---|---|---|---|---|
| 1051 | 960 | 208 | 16 | 55 | 345 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acosta, R.; Wu, H.; Sridaran Venkat, R.; Weber, F.; Tenkamp, J.; Walther, F.; Starke, P. SteBLife, a New Approach for the Accelerated Generation of Metallic Materials’ Fatigue Data. Metals 2020, 10, 798. https://doi.org/10.3390/met10060798
Acosta R, Wu H, Sridaran Venkat R, Weber F, Tenkamp J, Walther F, Starke P. SteBLife, a New Approach for the Accelerated Generation of Metallic Materials’ Fatigue Data. Metals. 2020; 10(6):798. https://doi.org/10.3390/met10060798
Chicago/Turabian StyleAcosta, Ruth, Haoran Wu, Ramanan Sridaran Venkat, Fabian Weber, Jochen Tenkamp, Frank Walther, and Peter Starke. 2020. "SteBLife, a New Approach for the Accelerated Generation of Metallic Materials’ Fatigue Data" Metals 10, no. 6: 798. https://doi.org/10.3390/met10060798
APA StyleAcosta, R., Wu, H., Sridaran Venkat, R., Weber, F., Tenkamp, J., Walther, F., & Starke, P. (2020). SteBLife, a New Approach for the Accelerated Generation of Metallic Materials’ Fatigue Data. Metals, 10(6), 798. https://doi.org/10.3390/met10060798








