Precipitation Versus Partitioning Kinetics during the Quenching of Low-Carbon Martensitic Steels
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Material Characterization
3.2. Carbon Kinetics Simulations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kömi, J.; Karjalainen, P.; Porter, D. Direct-Quenched Structural Steels. Encycl. Iron Steel Alloy 2016, 1109–1125. [Google Scholar]
- Bhadeshia, H.K.D.H.; Honeycombe, R.W.K. Steels: Microstructure and Properties, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Krauss, G. Martensite in steel: Strength and structure. Mater. Sci. Eng. A 2002, 273–275, 40–57. [Google Scholar] [CrossRef]
- Pereloma, E.; Edmonds, D. Phase Transformations in Steels; Elsevier Science & Technology: London, UK, 2012; ISBN 9781845699710. [Google Scholar]
- Babu, S.R.; Nyyssönen, T.; Jaskari, M.; Järvenpää, A.; Davis, T.P.; Pallaspuro, S.; Kömi, J.; Porter, D. Observations on the relationship between crystal orientation and the level of auto-tempering in an as-quenched martensitic steel. Metals 2019, 9, 1255. [Google Scholar] [CrossRef] [Green Version]
- Hutchinson, B.; Hagström, J.; Karlsson, O.; Lindell, D.; Tornberg, M.; Lindberg, F.; Thuvander, M. Microstructures and hardness of as-quenched martensites (0.1–0.5%C). Acta Mater. 2011, 59, 5845–5858. [Google Scholar] [CrossRef]
- Speer, J.; Matlock, D.K.; De Cooman, B.C.; Schroth, J.G. Carbon partitioning into austenite after martensite transformation. Acta Mater. 2003, 51, 2611–2622. [Google Scholar] [CrossRef]
- Matsuda, H.; Mizuno, R.; Funakawa, Y.; Seto, K.; Matsuoka, S.; Tanaka, Y. Effects of auto-tempering behaviour of martensite on mechanical properties of ultra high strength steel sheets. J. Alloy. Compd. 2013, 577, S661–S667. [Google Scholar] [CrossRef]
- Takaki, S.; Akama, D.; Tsuchiyama, T. Quantitative Evaluation of Auto-Tempering During Quenching. NETSUSHORI 2017, 56, 340–344. [Google Scholar]
- Babu, S.R.; Jaskari, M.; Järvenpää, A.; Porter, D. The effect of hot-mounting on the microstructure of an As-Quenched auto-tempered low-carbon martensitic steel. Metals 2019, 9, 550. [Google Scholar] [CrossRef] [Green Version]
- Babu, S.R.; Davis, T.P.; Haas, T.; Jarvenpää, A.; Kömi, J.; Porter, D. Image Processing Tool Quantifying Auto-Tempered Carbides in As-Quenched Low Carbon Martensitic Steels. Metals 2020, 10, 171. [Google Scholar] [CrossRef] [Green Version]
- Borgenstam, A.; Höglund, L.; Ågren, J.; Engström, A. DICTRA, a tool for simulation of diffusional transformations in alloys. J. Phase Equilibria 2000, 21, 269–280. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, K.; Sterner, G.; Mason, P. Modeling Precipitation Kinetics During Heat Treatment with Calphad-Based Tools. J. Mater. Eng. Perform. 2014, 23, 4193–4196. [Google Scholar] [CrossRef]
- Ramesh Babu, S.; Ivanov, D.; Porter, D. Influence of Microsegregation on the Onset of the Martensitic Transformation. ISIJ Int. 2018, 59, 169–175. [Google Scholar] [CrossRef]
- Klinger, M.; Jäger, A. Crystallographic Tool Box (CrysTBox): Automated tools for transmission electron microscopists and crystallographers. J. Appl. Cryst. 2015, 48, 2012–2018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andersson, J.O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad Comput. Coupling Phase Diagr. 2002, 26, 273–312. [Google Scholar]
- Garcia, J.; Lindwall, G.; Prat, O.; Frisk, K. Kinetics of formation of graded layers on cemented carbides: Experimental investigations and DICTRA simulations. Int. J. Refract. Met. Hard Mater. 2011, 29, 256–259. [Google Scholar] [CrossRef]
- Kashchiev, D. Nucleation: Basic Theory with Applications; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Russell, K.C. Nucleation in solids: The induction and steady state effects. Adv. Colloid Interface Sci. 1980, 13, 205–318. [Google Scholar] [CrossRef]
- Thermo-Calc, Version 2019b. In Precipitation Module (TC-PRISMA) User Guide; Thermo-Calc Software AB: Solna, Sweden, 2019.
- Chen, Q.; Jeppsson, J.; Ågren, J. Analytical treatment of diffusion during precipitate growth in multicomponent systems. Acta Mater. 2008, 56, 1890–1896. [Google Scholar] [CrossRef]
- Prat, O.; García, J.; Rojas, D.; Sanhueza, J.P.; Camurri, C. Study of nucleation, growth and coarsening of precipitates in a novel 9%Cr heat resistant steel: Experimental and modeling. Mater. Chem. Phys. 2014, 143, 754–764. [Google Scholar] [CrossRef]
- Morsdorf, L.; Tasan, C.C.; Ponge, D.; Raabe, D. Acta Materialia 3D structural and atomic-scale analysis of lath martensite: Effect of the transformation sequence. Acta Mater. 2015, 95, 366–377. [Google Scholar] [CrossRef]
- Morsdorf, L.; Jeannin, O.; Barbier, D.; Mitsuhara, M.; Raabe, D.; Tasan, C.C. Acta Materialia Multiple mechanisms of lath martensite plasticity. Acta Mater. 2016, 121, 202–214. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Carbon content of retained austenite in quenched steels. Met. Sci. 1983, 17, 151–152. [Google Scholar] [CrossRef]
- Sarikaya, M.; Thomas, G.; Steeds, J.W.; Barnard, S.J.; Smith, G.D.W. Solute Element Partitioning and Austenite Stabilization in Steels. In Proceedings of the International Conference on Solid to Solid Phase Transformations, H.I Aaronson, TMS, Warrendale, PA, USA, 1982; pp. 1421–1425. [Google Scholar]
- Santofimia, M.J.; Speer, J.G.; Clarke, A.J.; Zhao, L.; Sietsma, J. Influence of interface mobility on the evolution of austenite–martensite grain assemblies during annealing. Acta Mater. 2009, 57, 4548–4557. [Google Scholar] [CrossRef] [Green Version]
- Hillert, M.; Höglund, L.; Ågren, J. Escape of carbon from ferrite plates in austenite. Acta Met. Mater. 1993, 41, 1951–1957. [Google Scholar] [CrossRef]
- Jang, J.H.; Bhadeshia, H.K.D.H.; Suh, D.-W. Solubility of carbon in tetragonal ferrite in equilibrium with austenite. Scr. Mater. 2013, 68, 195–198. [Google Scholar] [CrossRef]
- Zener, C. Kinetics of the decomposition of austenite. Trans. Met. Soc. Aime 1946, 167, 550–595. [Google Scholar]
- Morito, S.; Nishikawa, J.; Maki, T. Dislocation Density within Lath Martensite in Fe-C and Fe-Ni Alloys. ISIJ Int. 2003, 43, 1475–1477. [Google Scholar] [CrossRef] [Green Version]
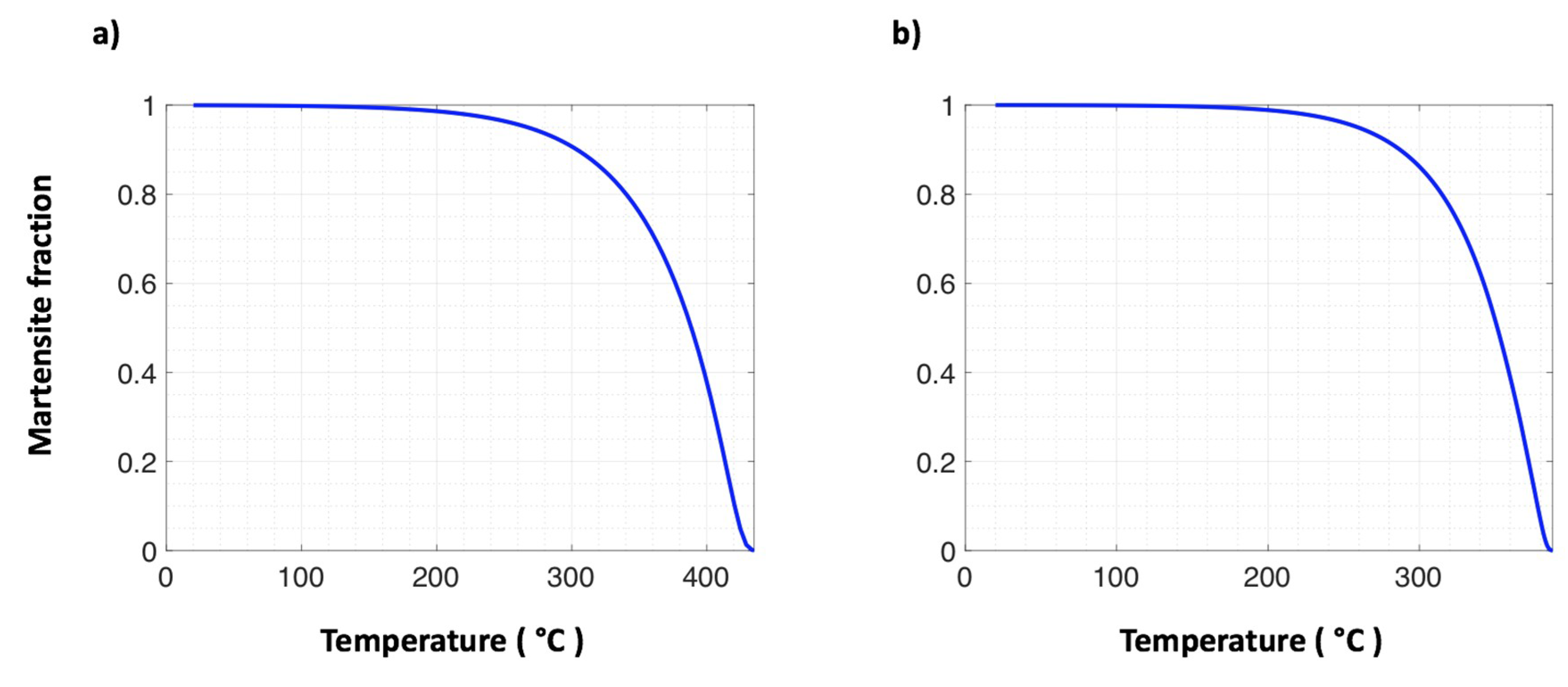




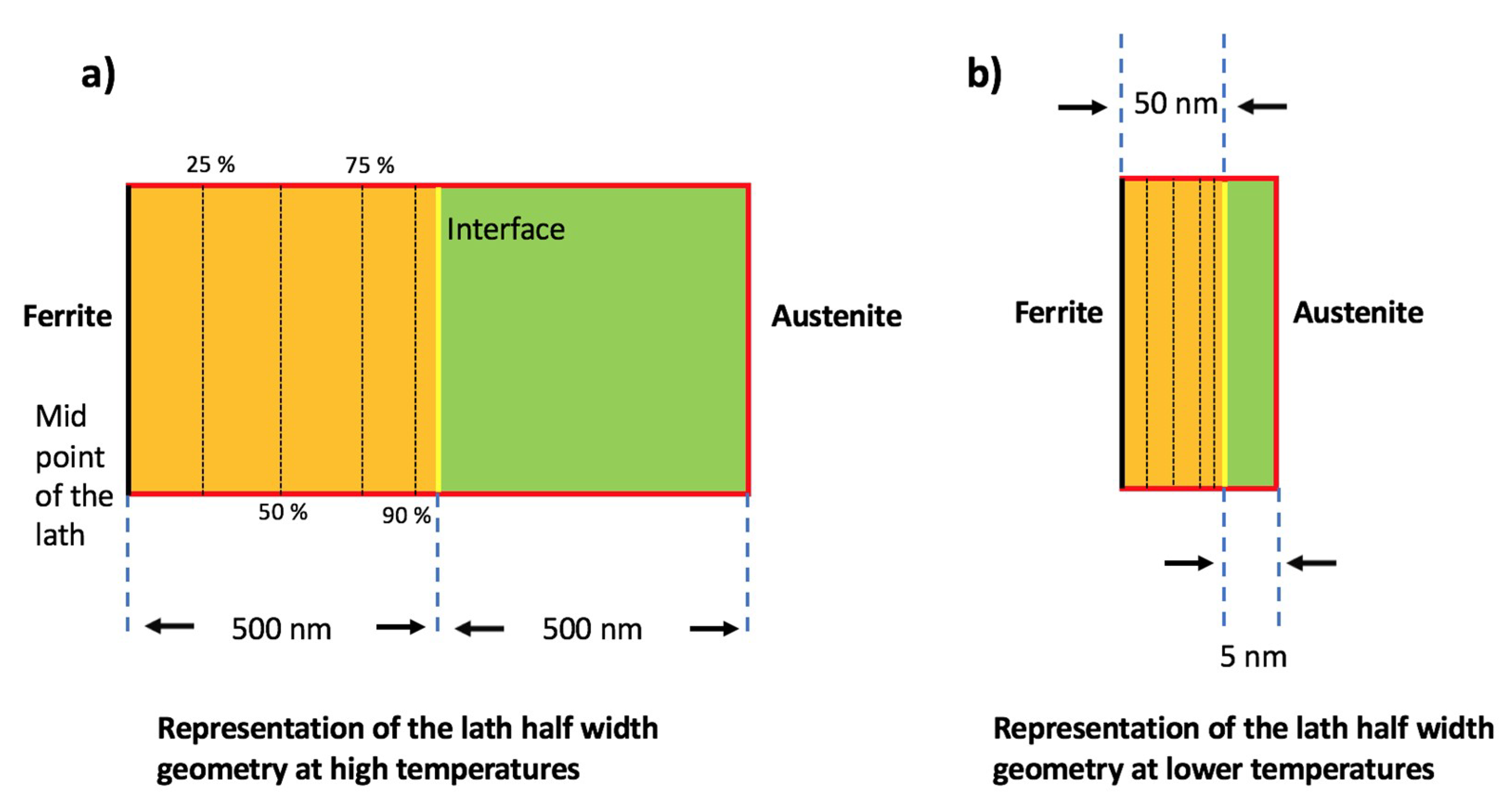
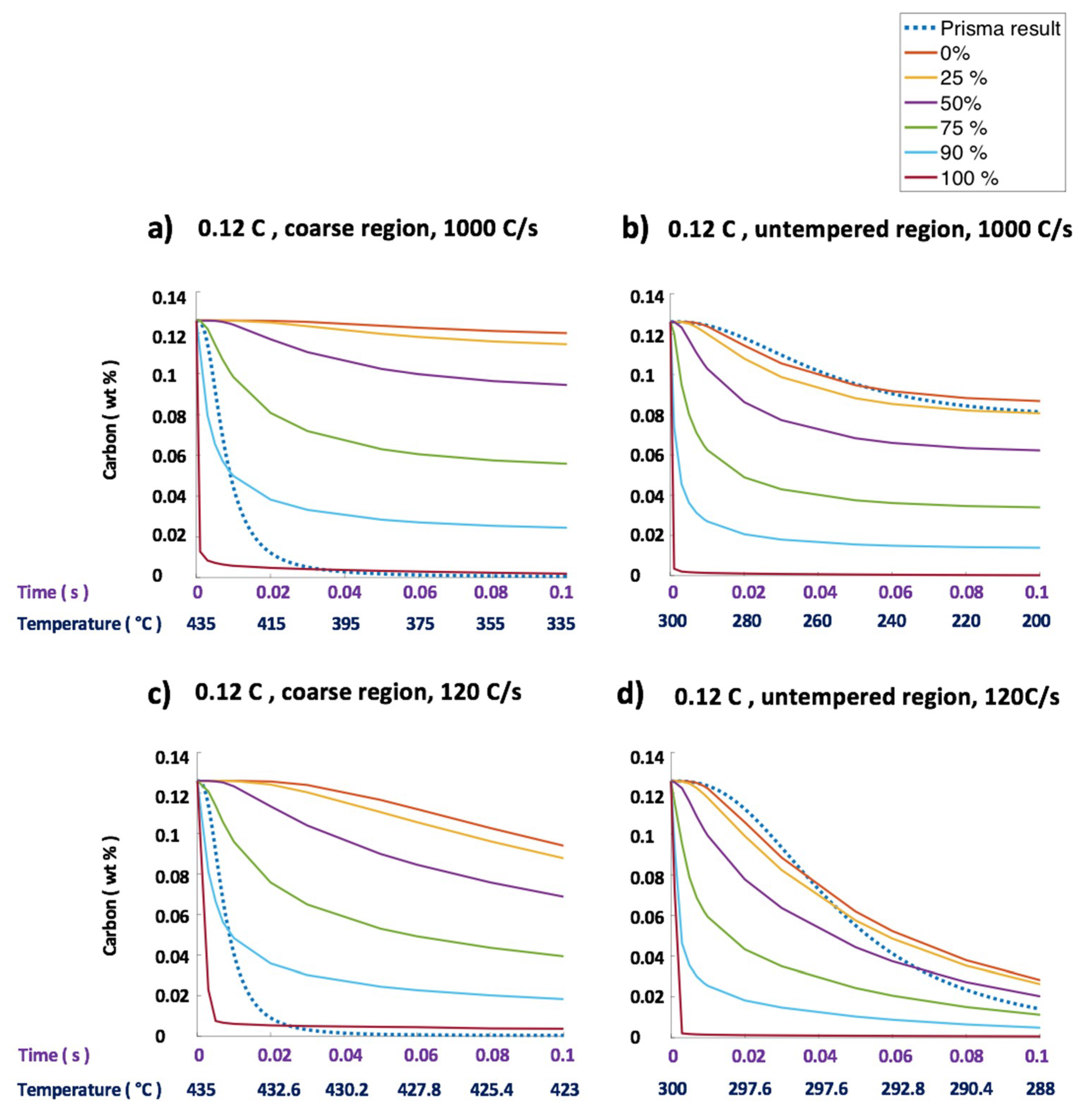
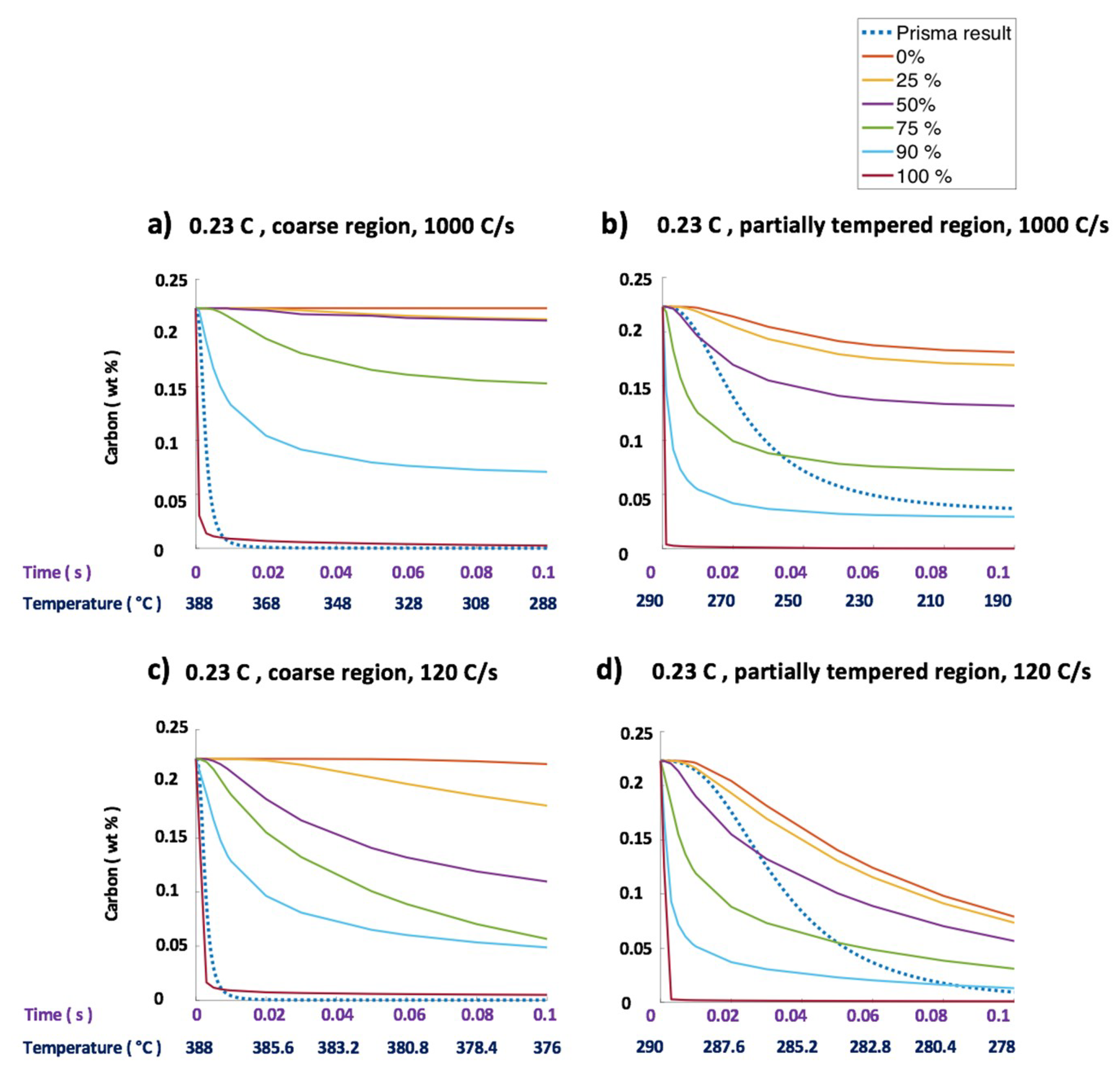
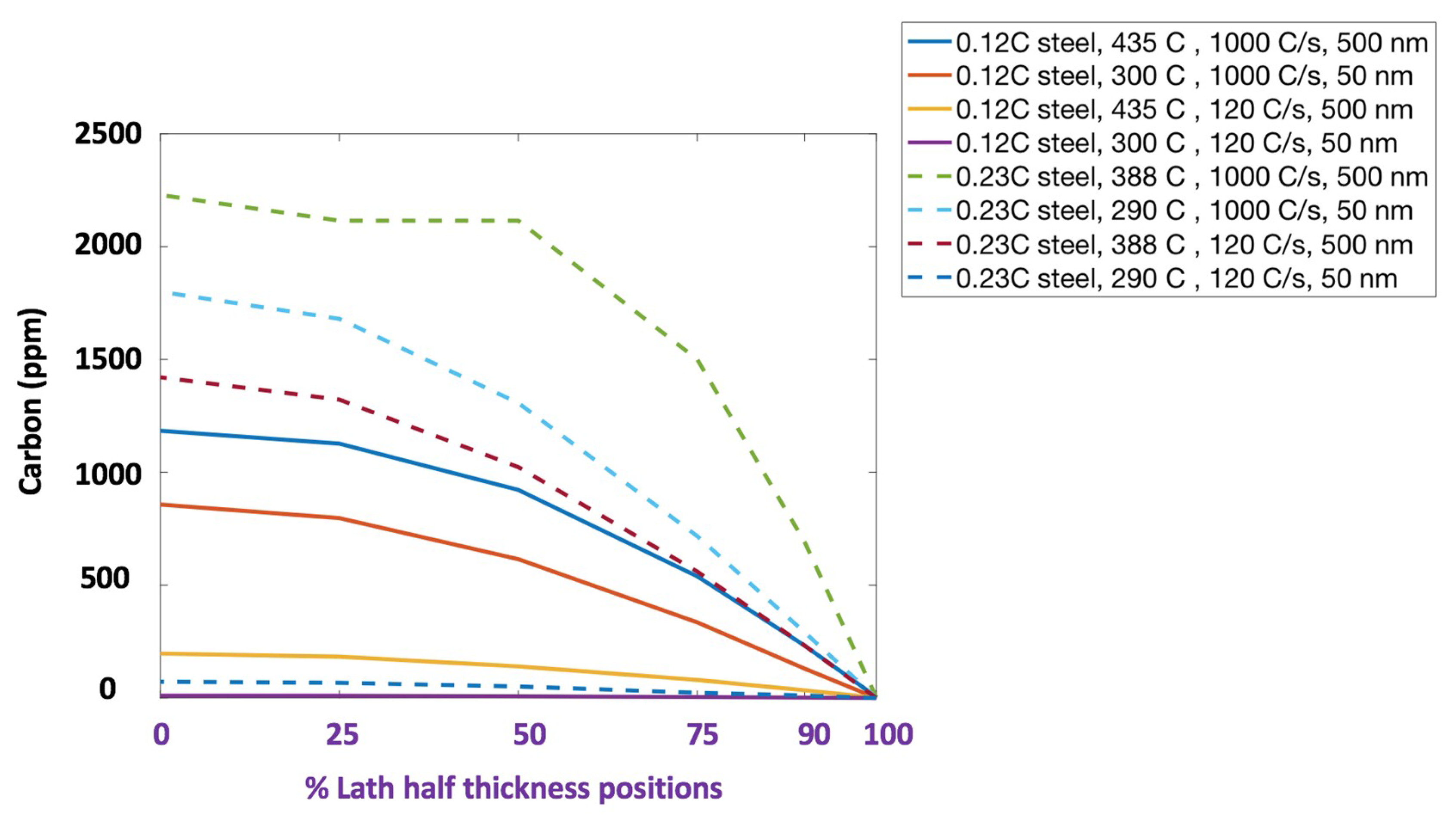


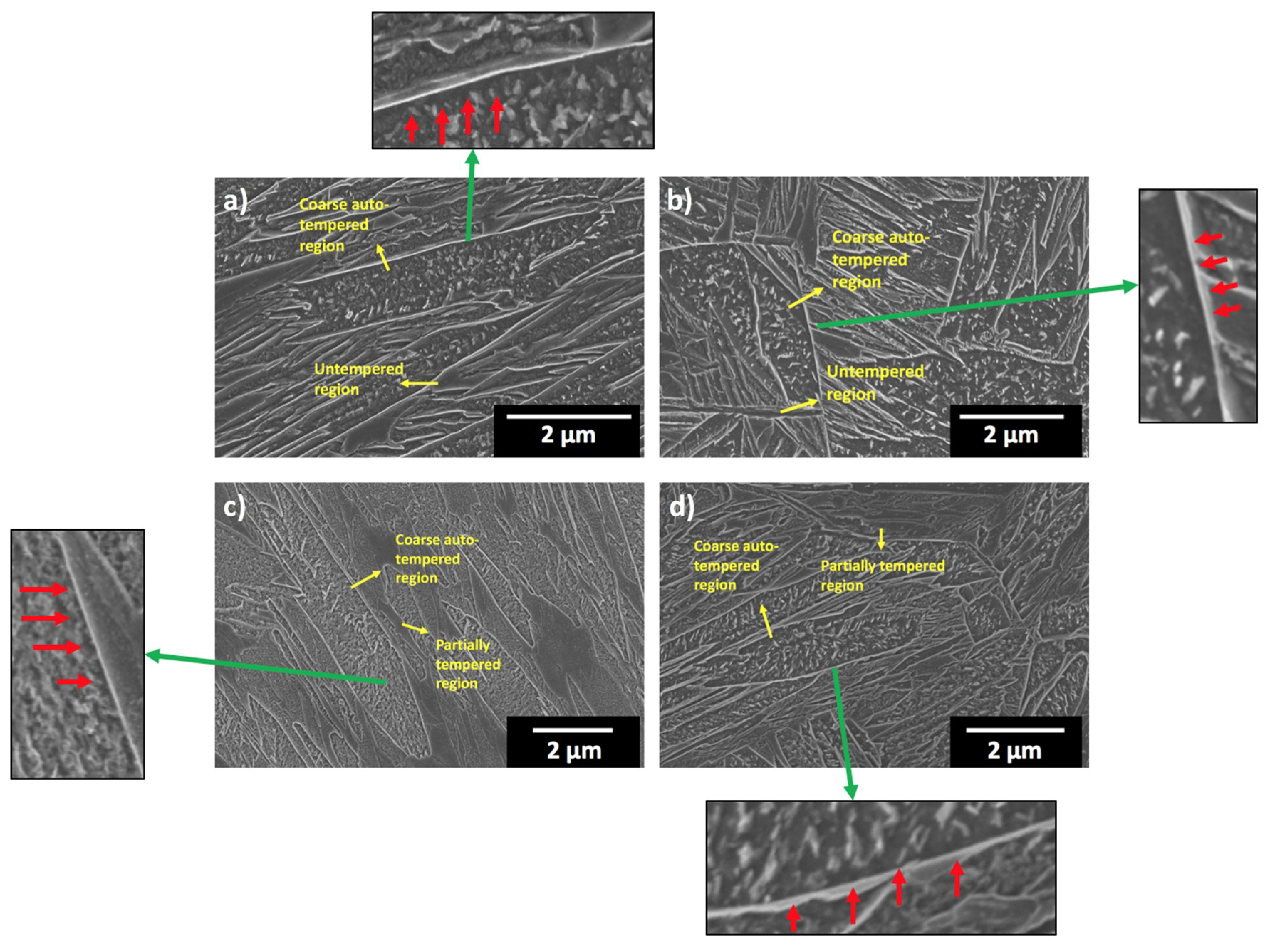
| Steel Code | C | Mn | Si | Cr | Ni | Ti | V | Al | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 0.12C | 0.126 | 1.66 | 0.72 | 0.27 | 0.038 | 0.027 | 0.047 | 0.054 | Bal. |
| 0.23C | 0.223 | 1.26 | 0.42 | 0.25 | 0.044 | 0.019 | 0.043 | 0.058 | Bal. |
| Alloy | 500 nm Ferrite Half-Thickness | 50 nm Ferrite Half-Thickness |
|---|---|---|
| Lath Formation Temperature (°C) | Lath Formation Temperature (°C) | |
| 0.12C steel | 435 | 300 |
| 0.23C steel | 388 | 290 |
| Steel Code | 0.12C | 0.23C | ||
| Lath Formation Temperature, °C | 434 °C | 300 °C | 388 °C | 290 °C |
| 1000 °C/s | 4.3 | n.a. | 0 | 343.5 |
| 120 °C/s | 0 | n.a. | 0 | 0 |
| Steel Code | 0.12C | 0.23C | ||||||
| Cooling rate (C/s) | 120 | 1000 | 120 | 1000 | ||||
| Lath formation temperature (°C) | 435 | 300 | 435 | 300 | 388 | 290 | 388 | 290 |
| Minimum austenite half-width (nm) | 70 | 5 | 35 | 5 | 55 | 5 | 20 | 5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramesh Babu, S.; Jaskari, M.; Jarvenpää, A.; Davis, T.P.; Kömi, J.; Porter, D. Precipitation Versus Partitioning Kinetics during the Quenching of Low-Carbon Martensitic Steels. Metals 2020, 10, 850. https://doi.org/10.3390/met10070850
Ramesh Babu S, Jaskari M, Jarvenpää A, Davis TP, Kömi J, Porter D. Precipitation Versus Partitioning Kinetics during the Quenching of Low-Carbon Martensitic Steels. Metals. 2020; 10(7):850. https://doi.org/10.3390/met10070850
Chicago/Turabian StyleRamesh Babu, Shashank, Matias Jaskari, Antti Jarvenpää, Thomas Paul Davis, Jukka Kömi, and David Porter. 2020. "Precipitation Versus Partitioning Kinetics during the Quenching of Low-Carbon Martensitic Steels" Metals 10, no. 7: 850. https://doi.org/10.3390/met10070850
APA StyleRamesh Babu, S., Jaskari, M., Jarvenpää, A., Davis, T. P., Kömi, J., & Porter, D. (2020). Precipitation Versus Partitioning Kinetics during the Quenching of Low-Carbon Martensitic Steels. Metals, 10(7), 850. https://doi.org/10.3390/met10070850





