On Numerical Simulation of Casting in New Foundries: Dynamic Process Simulations
Abstract
:1. Introduction
2. Dynamic Simulation Framework
- ➢
- The initial mould filling and primary thermal boundary conditions are modelled using the results of either thermal-CFD melt delivery simulation or thermal boundary assumptions.
- ➢
- The initial geometry of the main domain (i.e., mould, starting head) and its discretization are defined and initial system matrices are assembled.
- ➢
- The initial time steps/iterations are solved (using a thermal-mechanical simulation) and based on the casting speed the billet domain coordinates are updated.
- ➢
- The new discretized grid and its boundaries are adapted by adding a single/multiple layer ‘element-block’ based on the evolution of the domain in vertical direction (including updating coordinates and accounting for shrinkage and thermal deformation).
- ➢
- The solver is re-started and the system matrices are modified/appended while the input energy is distributed amongst the newly generated grid.
- ➢
- Thermal time history results (from previous time steps) are mapped to the updated grid and thermal boundaries are updated.
- ➢
- The energy balance (thermal energy) is achieved through the energy sink/source concept and the previous converged solution is used as a first step for a newly updated domain.
- ➢
- The simulation scheme continues with the new discretised grid, till the next evolution step is triggered.
- ◾
- Pure experimental methods where results of experimental trials are used (and sometimes extrapolated) for Heat Transfer Coefficient (HTC) calculations using a set of process conditions (water flow rates, billet surface temperatures, etc.).
- ◾
- Analytical-experimental technique where analytical and empirical parameters are fitted using results of carefully designed experimental trials.
- ◾
- Numerical techniques based on CFD simulation where bubble dynamics and flow regimes are considered using multi-phase fluid techniques.
- ◾
- Hybrid numerical-analytical-experimental techniques where analytical techniques (using experimentally fitted parameters) are used to enhance the multi-phase CFD simulation for HTC calculation. The accuracy and agility of these hybrid techniques can be improved with the help of Machine-Learning (ML) and Artificial Intelligence (AI) for data fitting and extrapolation.
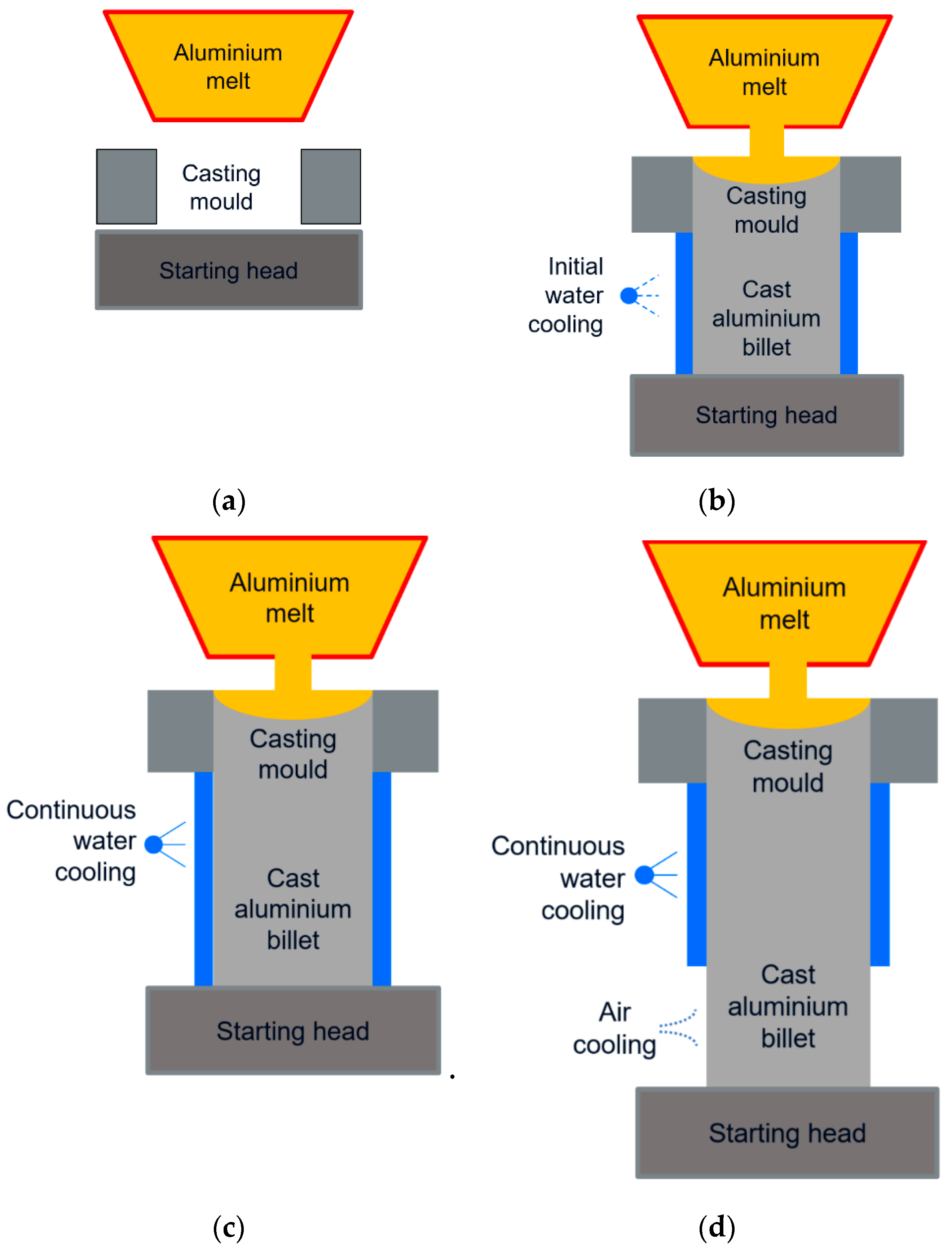
3. Dynamic Casting Simulation
- ➢
- The initial thermal boundaries and cooling rates are defined using the results of either CFD filling simulations or analytical-experimental thermal boundary assumptions.
- ➢
- The initial geometry of the main domain (i.e., starting head, mold) and its discretization are carried out where the boundaries are defined and initial system matrices are assembled.
- ➢
- The FE solver’s initiation time steps/iterations are carried out (using both thermal and mechanical solvers) and nodal coordinates for the billet domain are updated.
- ➢
- New mesh block is appended based on the evolution of the billet domain (with casting speed) and the domain discretized grid is modified and adapted for shrinkage and thermal deformation changes.
- ➢
- The solver global system matrices are updated and the material/thermal input energies are distributed amongst the newly generated mesh block.
- ➢
- The mapping process is carried out at new boundaries by adapting time history results (from previous time steps).
- ➢
- The thermal energy balance is reached through a manual/automated energy sink/source scheme and the previous converged solution is used as a first step for a newly updated domain.
- ➢
- The FE simulation continues with the new mesh/boundaries till the next evolution step is triggered.
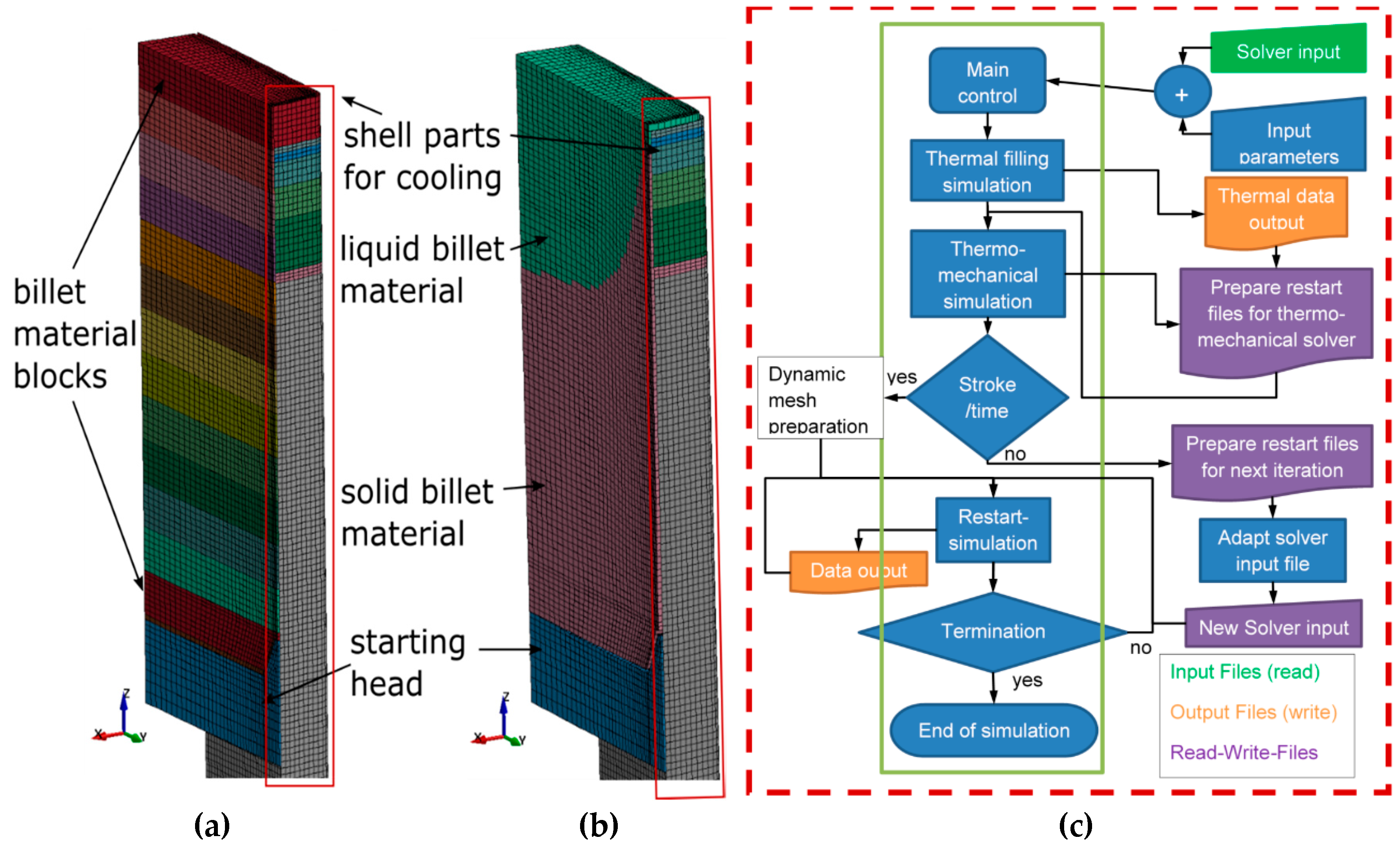
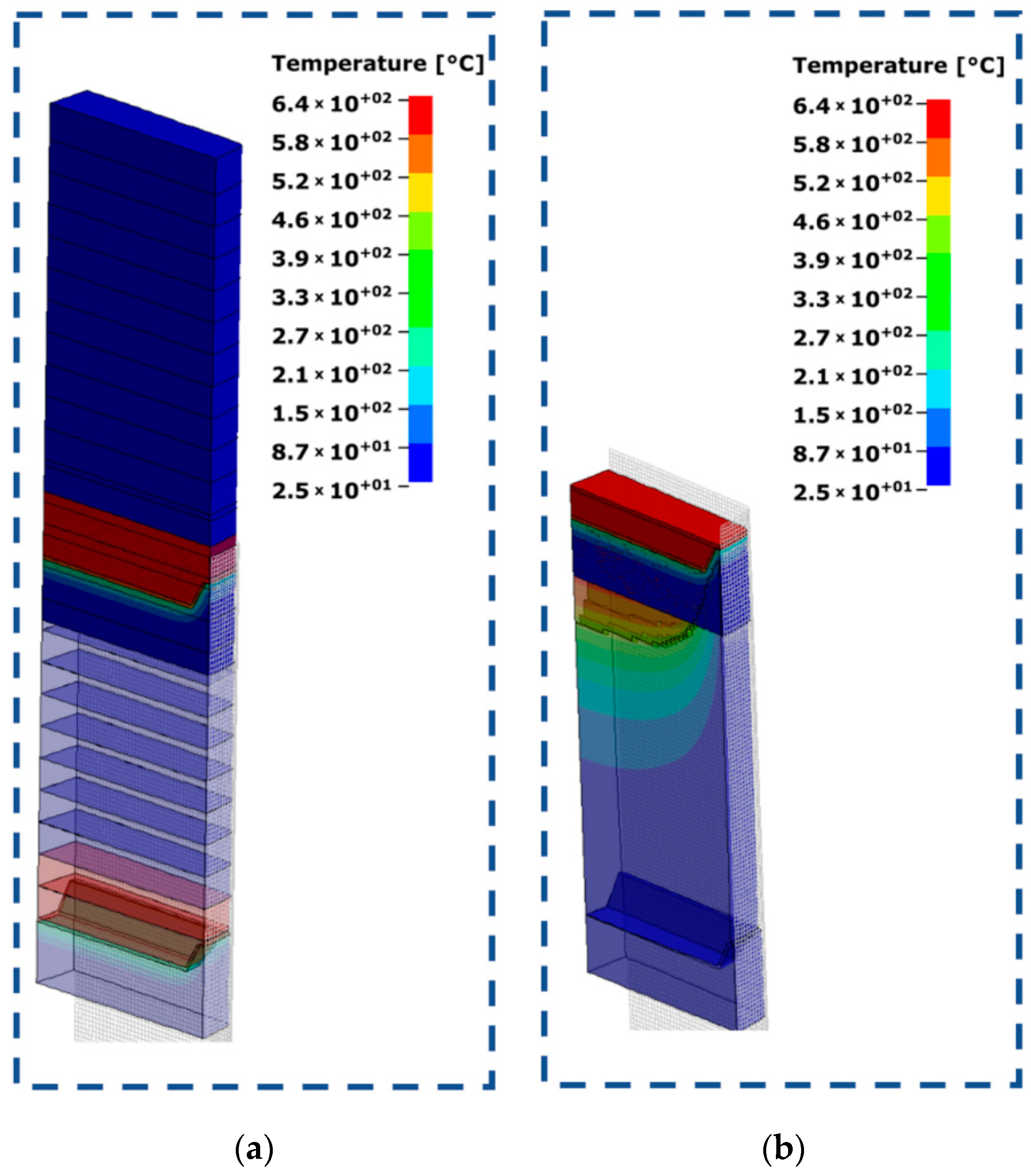
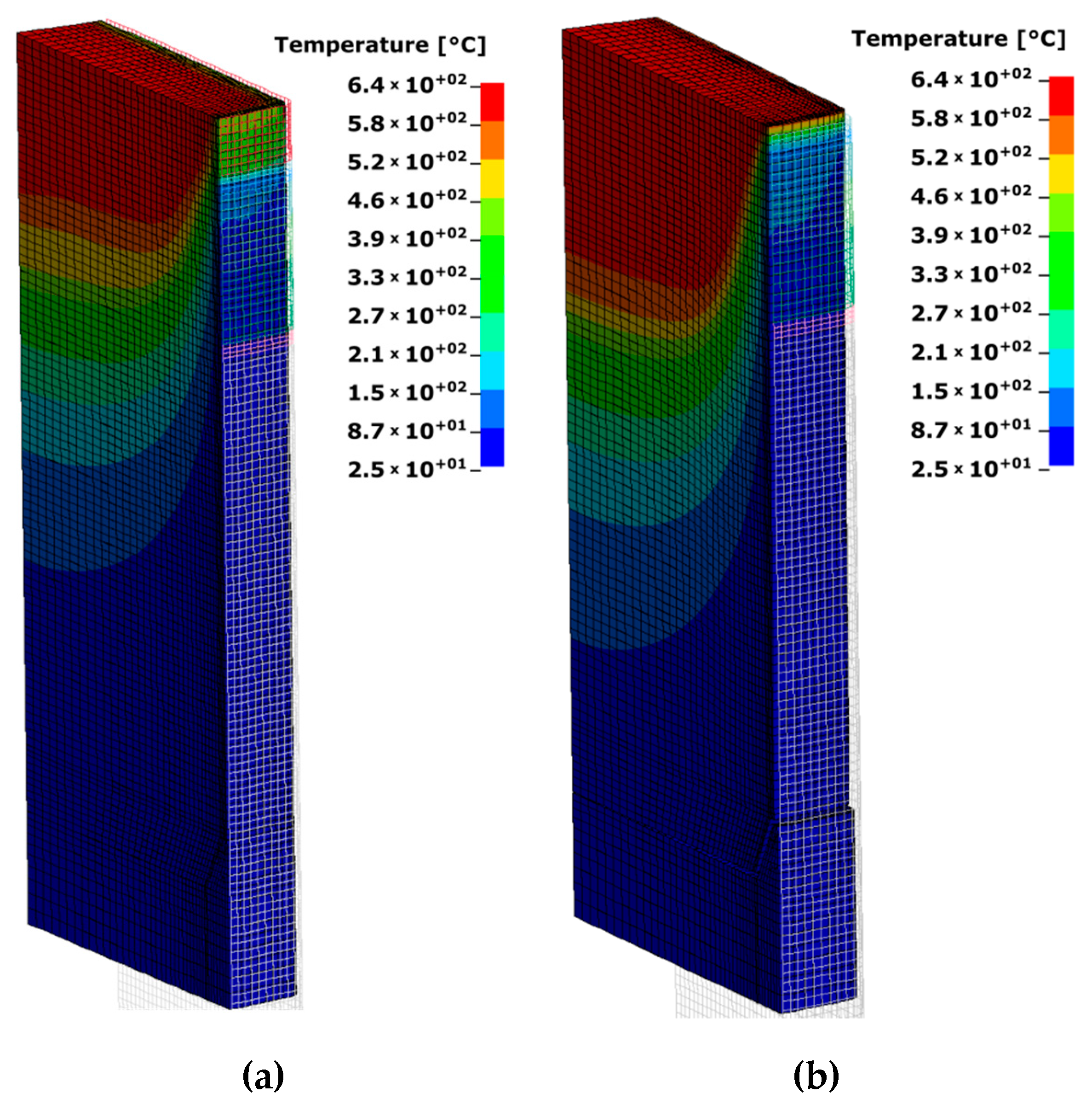
4. Industrial Case Study
- ➢
- For the conventional technique, all element blocks (and their contact elements) already exist in the domain from the start of the simulation.
- ➢
- New mesh blocks are individual parts for the conventional BT which are attached to rest of the domain using contact elements while for DMT elements are added to the already existing billet domain.
- ➢
- Since new blocks are individual parts in BT, the contact elements need to be setup at the start of simulation to enable heat conductance and mechanical contact during simulation.
- ➢
- Activated element blocks in conventional BT consist of 3 layers of elements (to limit the CPU time) compared to higher-resolution single layer of element insertions for the DMT.
5. Computational Performance
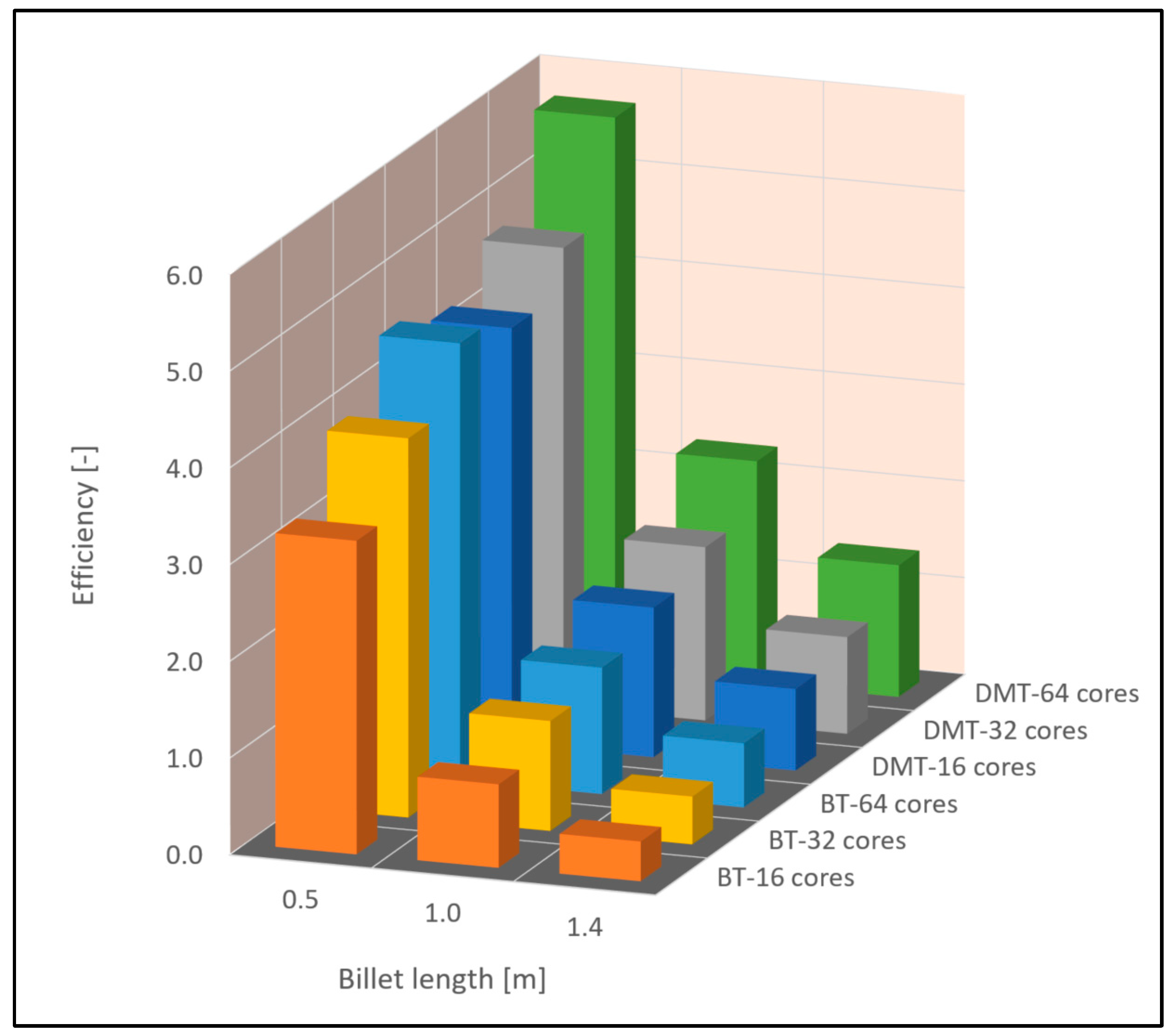
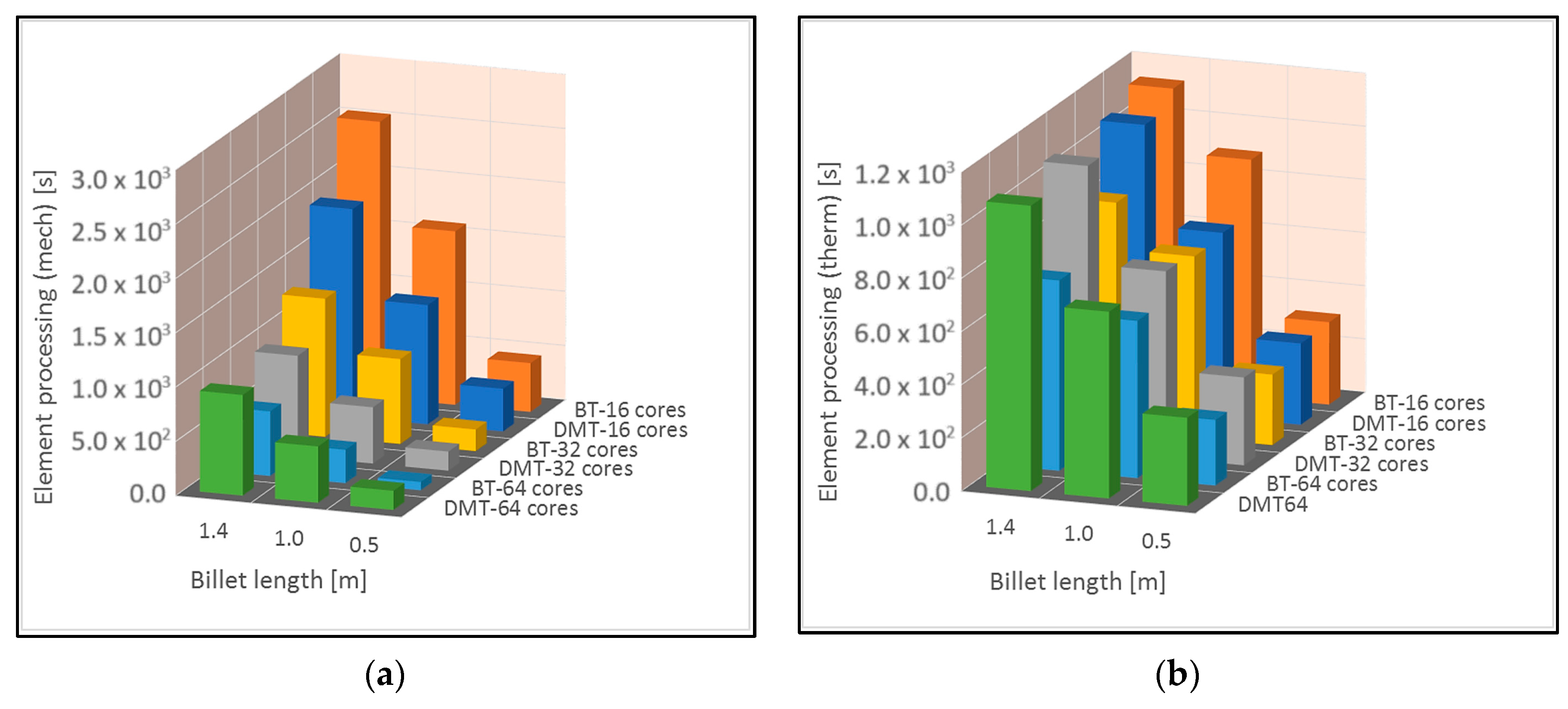
5.1. Computational Efficiency and CPU Timing
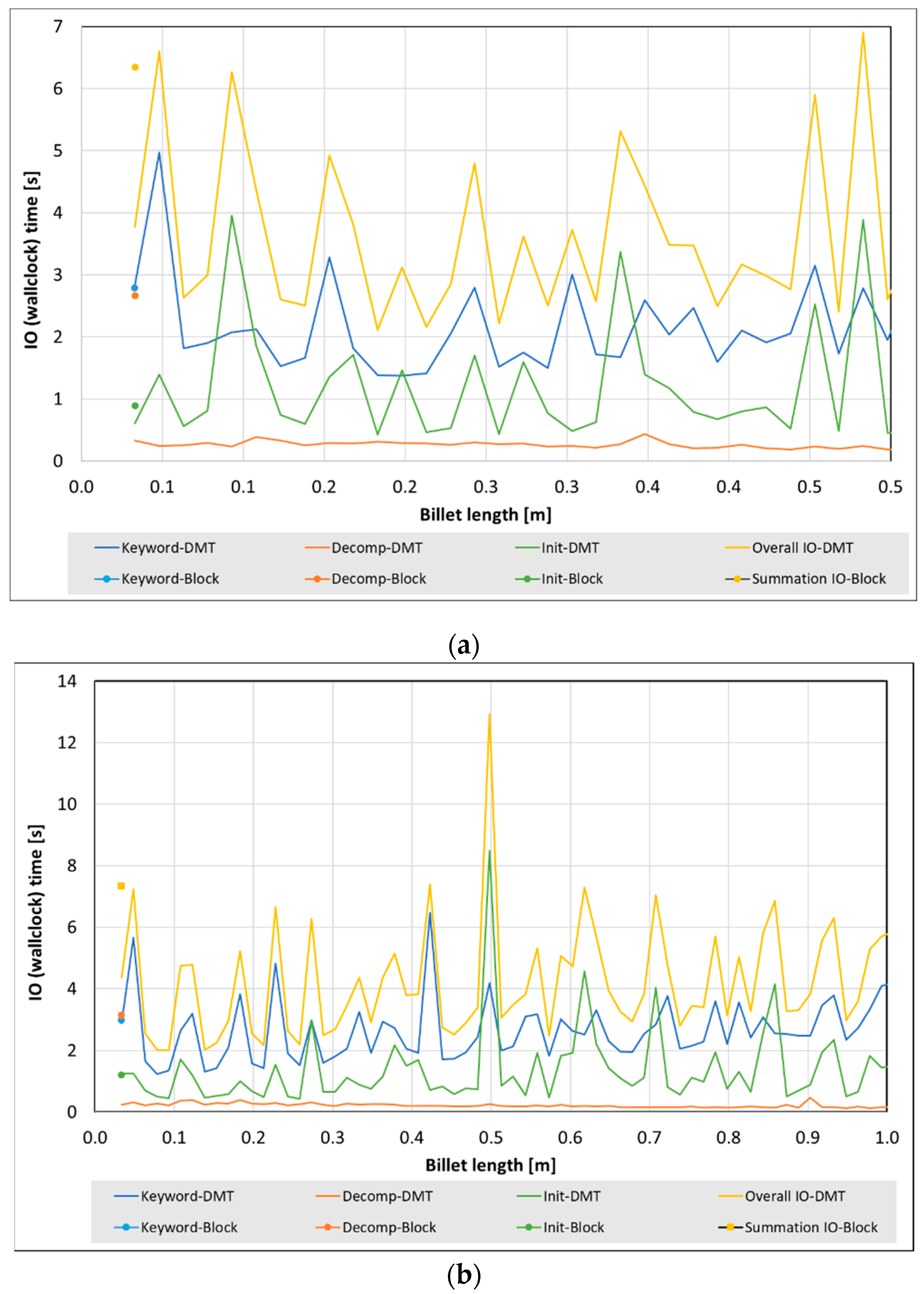
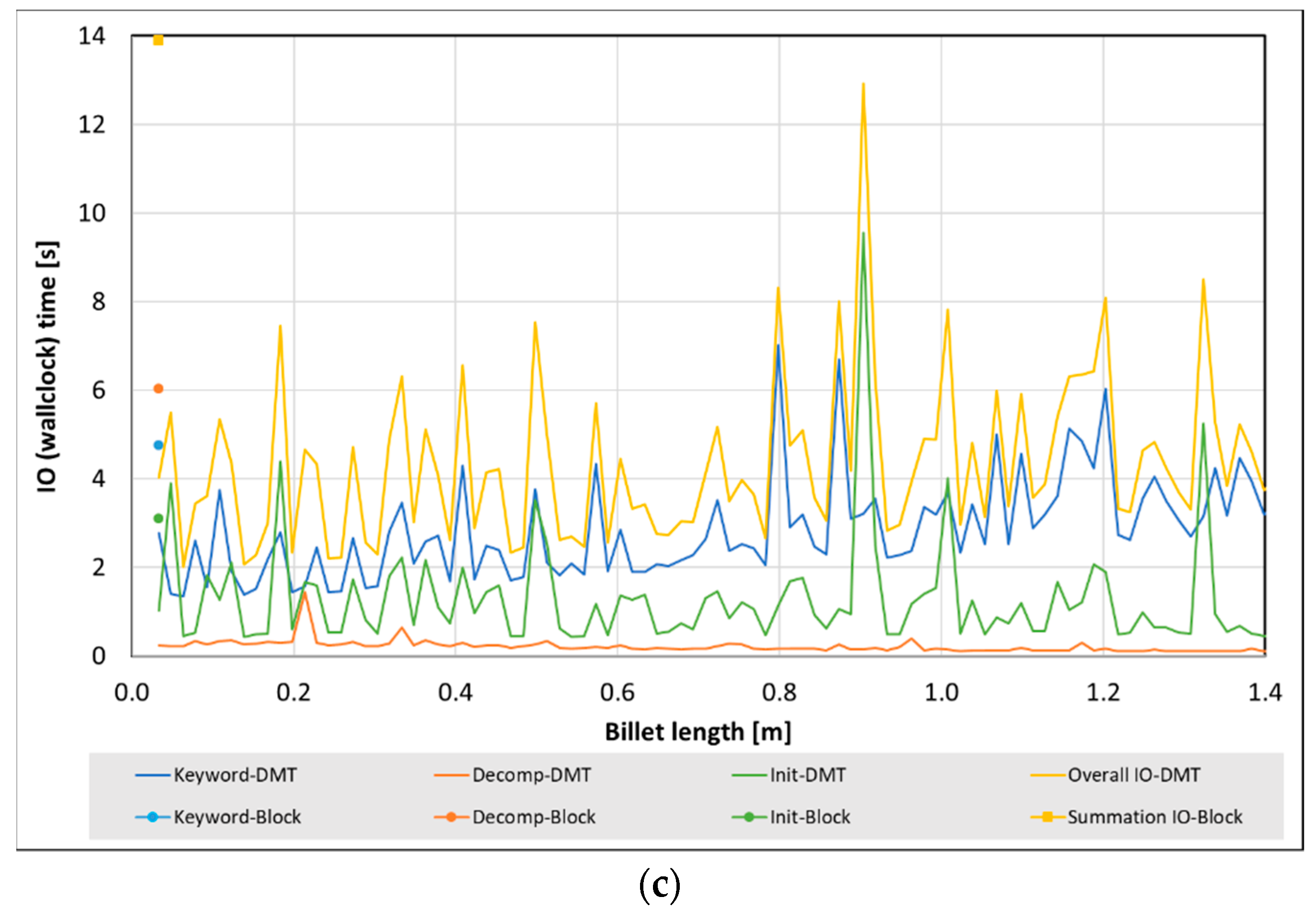
5.2. Computational Resources and Memory
6. Discussion
- ➢
- Overall computation time (including CPU and IO times) are meaningfully lower for the proposed DMT compared to the conventional activation technique.
- ➢
- The overall IO time for DMT with many solver restarts and repeated matrices’ assemblies is higher than the conventional technique (with single start of the solver). However, the total simulation wall clock time for DMT is significantly lower than the conventional technique due to the fact that the CPU computational time is generally more than two orders of magnitude larger than IO times for real-size casting applications.
- ➢
- Considering today’s efficient existing partitioning and parallel processing routines implemented in commercial software, the IO times for decomposition of the numerical domain shows a steady trend over the different billet lengths. This means that with a carefully chosen number of computational nodes (e.g., based on the size of the final domain), the computing resources can be optimised for a manageable overall simulation time.
- ➢
- The implementation of the technique and its flexibility towards enhancing commercial software capabilities for dynamic systems would inspire the use of the technique in simulation of modern foundry processes.
- ➢
- Although the thermal-mechanical simulation of casting processes will provide a valuable source of information for foundry processes, the link to melt delivery and filling simulation would enhance the optimisation capabilities of these simulations. Hence, the next development step for the proposed technique is to establish a sound numerical link to pre-solidified melt flow and filling simulations.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, J.-E.; Yeo, T.-J.; Oh, K.H.; Yoon, J.-K.; Yoon, U.-S. Prediction of cracks in continuously cast steel beam blank through fully coupled analysis of fluid flow, heat transfer, and deformation behavior of a solidifying shell. Met. Mater. Trans. A 2000, 31, 225–237. [Google Scholar] [CrossRef]
- Koric, S.; Hibbeler, L.; Liu, R.; Thomas, B.G. Multiphysics Model of Metal Solidification on the Continuum Level. Numer. Heat Transf. Part B Fundam. 2010, 58, 371–392. [Google Scholar] [CrossRef]
- Zappulla, M.L.; Cho, S.-M.; Koric, S.; Lee, H.-J.; Kim, S.-H.; Thomas, B.G. Multiphysics modeling of continuous casting of stainless steel. J. Mater. Process. Technol. 2020, 278, 116469. [Google Scholar] [CrossRef]
- Brötz, S.; Horr, A. Framework for progressive adaption of FE mesh to simulate generative manufacturing processes. Manuf. Lett. 2020, 24, 52–55. [Google Scholar] [CrossRef]
- Montevecchi, F.; Venturini, G.; Scippa, A.; Campatelli, G. Finite Element Modelling of Wire-arc-additive-manufacturing Process. Procedia Cirp 2016, 55, 109–114. [Google Scholar] [CrossRef] [Green Version]
- Keller, N.; Neugebauer, F.; Xu, H.; Ploshikhin, V. Thermo-mechanical Simulation of Additive Layer Manufacturing of Titanium Aerospace structures. In Proceedings of the EURO LIGHTMAT, Bremen, Germany, 3–5 September 2013. [Google Scholar]
- Keller, N.; Ploshikhin, V. New Method for fast predictions of residual stress and distortion of AM parts. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 4–6 August 2014. [Google Scholar]
- Lindwall, A.L.J.; Lindgren, L.E. Thermal FE-simulation of PBF using adaptive meshing and time stepping. In Proceedings of the Simulation for Additive Manufacturing, Munich, Germany, 11–13 October 2017. [Google Scholar]
- Lundback, A.; Lindgren, L.E. Modelling of metal deposition. Finite Elem. Anal. Des. 2011, 47, 1169–1177. [Google Scholar] [CrossRef]
- Simunovic, S.; Nycz, A.; Noakes, M.W.; Chin, C.; Oancea, V. Metal Big Area Additive Manufacturing: Process Modeling and Validation. In Proceedings of the Science in the Age of Experience, Chicago, IL, USA, 15–18 May 2017. [Google Scholar]
- Tripathy, S.; Chin, C.; Oancea, V.; London, T.; Ankalkhope, U. Process Modeling and Validation of Powder Bed Metal Additive Manufacturing. In Proceedings of the NAFEMS World Congress, Stockholm, Sweden, 11–14 June 2017. [Google Scholar]
- Brötz, S.; Scheiblhofer, S. Prozesssimulation Drahtbasierter Additiver Fertigungsverfahren; NAFEMS Online-Magazin: Munich, Germany, 2019; Volume 50, pp. 81–88. [Google Scholar]
- Ludwig, O.; Marco, A. State of the Art in Modelling of Continuous Casting. In Proceeding of the 6th European Conference on Continuous Casting, Riccione, Italy, 4–6 June 2008. [Google Scholar]
- Panagiotis, M. Modeling metal deposition in heat transfer analyses of additive manufacturing processes. Finite Elem. Anal. Des. 2014, 86, 51–60. [Google Scholar]
- Claus, S.; Bigot, S.; Kerfriden, P. CutFEM Method for Stefan—Signorini Problems with Application in Pulsed Laser Ablation. SIAM J. Sci. Comput. 2018, 40, B1444–B1469. [Google Scholar] [CrossRef]
- Bastian, P.; Engwer, C. An unfitted finite element method using discontinuous Galerkin. Int. J. Numer. Methods Eng. 2009, 79, 1557–1576. [Google Scholar] [CrossRef]
- Fausty, J.; Bozzolo, N.; Muñoz, D.P.; Bernacki, M. A novel level-set finite element formulation for grain growth with heterogeneous grain boundary energies. Mater. Des. 2018, 160, 578–590. [Google Scholar] [CrossRef]
- Horr, A. Computational Evolving Technique for Casting Process of Alloys. Math. Probl. Eng. 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Horr, A.M. Integrated material process simulation for lightweight metal products. CMEM 2015 2015, 1, 201–212. [Google Scholar] [CrossRef] [Green Version]
- Jäger, S.; Horr, A.M.; Scheiblhofer, S. Thermal evolution effects on solidification process during continuous casting. In Proceedings of the 6th Decennial International Conference on Solidification Processing, Old Windsor, UK; 2017; Volume 2017, pp. 675–678. [Google Scholar]
- Horr, A.M.; Kronsteiner, J.; Muhlstatter, C. Recent Advances in Aluminium Casting Simulation: Evolving Domains & Dynamic Meshing. In Proceedings of the Aluminium 2000 Conference, Verona, Italy, 20–24 June 2017. [Google Scholar]
- Horr, A. Thermal Energy Approach for Aluminium Process Simulations: Source-Capacity Technique. Mater. Today Proc. 2019, 10, 263–270. [Google Scholar] [CrossRef]
- Horr, A. On Analytical Concepts of Novel Multi-Resolution Casting Simulations. In Proceedings of the IOP Conference Series: Materials Science and Engineering; 5th Inter. Symposium on Cutting Edge of Computer Simulation of Solidification, Casting and Refining, Salzburg, Austria, 17–21 June 2019; Volume 529, p. 012055. [Google Scholar] [CrossRef]
- Horr, A.M. Notes on New Physical & Hybrid Modelling Trends for Material Process Simulations. In Proceedings of the IOP conference Series, 4th International Conference on Applied Physics, Simulation and Computing, Rome, Italy, 23–25 May 2020. [Google Scholar]
- Chen, J.C. Correlation for Boiling Heat Transfer to Saturated Fluids in Convective Flow. Ind. Eng. Chem. Process. Des. Dev. 1966, 5, 322–329. [Google Scholar] [CrossRef] [Green Version]
- Mühlstätter, C.; Jäger, S. CFD zur Abbildung von Effekten in der Leichtmetallherstellung. In Proceedings of the 13. Cadfem ANSYS Simulation Conference Austria, Linz, Austria, 24–25 April 2018. [Google Scholar]
- Wagner, S.; Affenzeller, M. HeuristicLab: A Generic and Extensible Optimization Environment. Adapt. Nat. Comput. Algorithms 2005, 538–541. [Google Scholar] [CrossRef]




| Melt Temperature [°C] | Billet Width [m] | Billet Thickness [m] | Casting Speed [m s−1] | Cooling Water Temperature [°C] | HTC- Air Cooling [kW m−2 K−1] | HTC- Water Cooling [kW m−2 K−1] |
|---|---|---|---|---|---|---|
| 630 | 1.24 | 0.3 | 0.01 | 20 | 1.5 (average) | 11 (average) |
| Scenario No. | Billet Length [m] | No. of Elements | CPU Time DMT [s] | CPU Time BT [s] | IO Time DMT [s] | IO Time BT [s] | CPU Ratio DMT/BT |
|---|---|---|---|---|---|---|---|
| S1 | 0.5 | 27,189 | 16,345 | 20,581 | 78.62 | 6.90 | 79% |
| S2 | 1 | 41,357 | 45,577 | 77,387 | 179.18 | 7.02 | 59% |
| S3 | 1.4 | 59,573 | 84,545 | 163,063 | 271.84 | 13.77 | 52% |
| CPU Name | No. of Sockets | Cores per Socket | Total Memory [MB] | Communication Between Nodes | Parallelization Scheme | LS-DYNA Release | Accuracy |
|---|---|---|---|---|---|---|---|
| Intel Xeon E5-2687W v4 | 2 | 8 | 65,536 | InfiniBand | Platform MPI 08.02.00.00 [10060] | MPP R8.1.0 | Double precision |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horr, A.M.; Kronsteiner, J. On Numerical Simulation of Casting in New Foundries: Dynamic Process Simulations. Metals 2020, 10, 886. https://doi.org/10.3390/met10070886
Horr AM, Kronsteiner J. On Numerical Simulation of Casting in New Foundries: Dynamic Process Simulations. Metals. 2020; 10(7):886. https://doi.org/10.3390/met10070886
Chicago/Turabian StyleHorr, Amir M., and Johannes Kronsteiner. 2020. "On Numerical Simulation of Casting in New Foundries: Dynamic Process Simulations" Metals 10, no. 7: 886. https://doi.org/10.3390/met10070886
APA StyleHorr, A. M., & Kronsteiner, J. (2020). On Numerical Simulation of Casting in New Foundries: Dynamic Process Simulations. Metals, 10(7), 886. https://doi.org/10.3390/met10070886







