Analysis of Forming Parameters Involved in Plastic Deformation of 441 Ferritic Stainless Steel Tubes
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
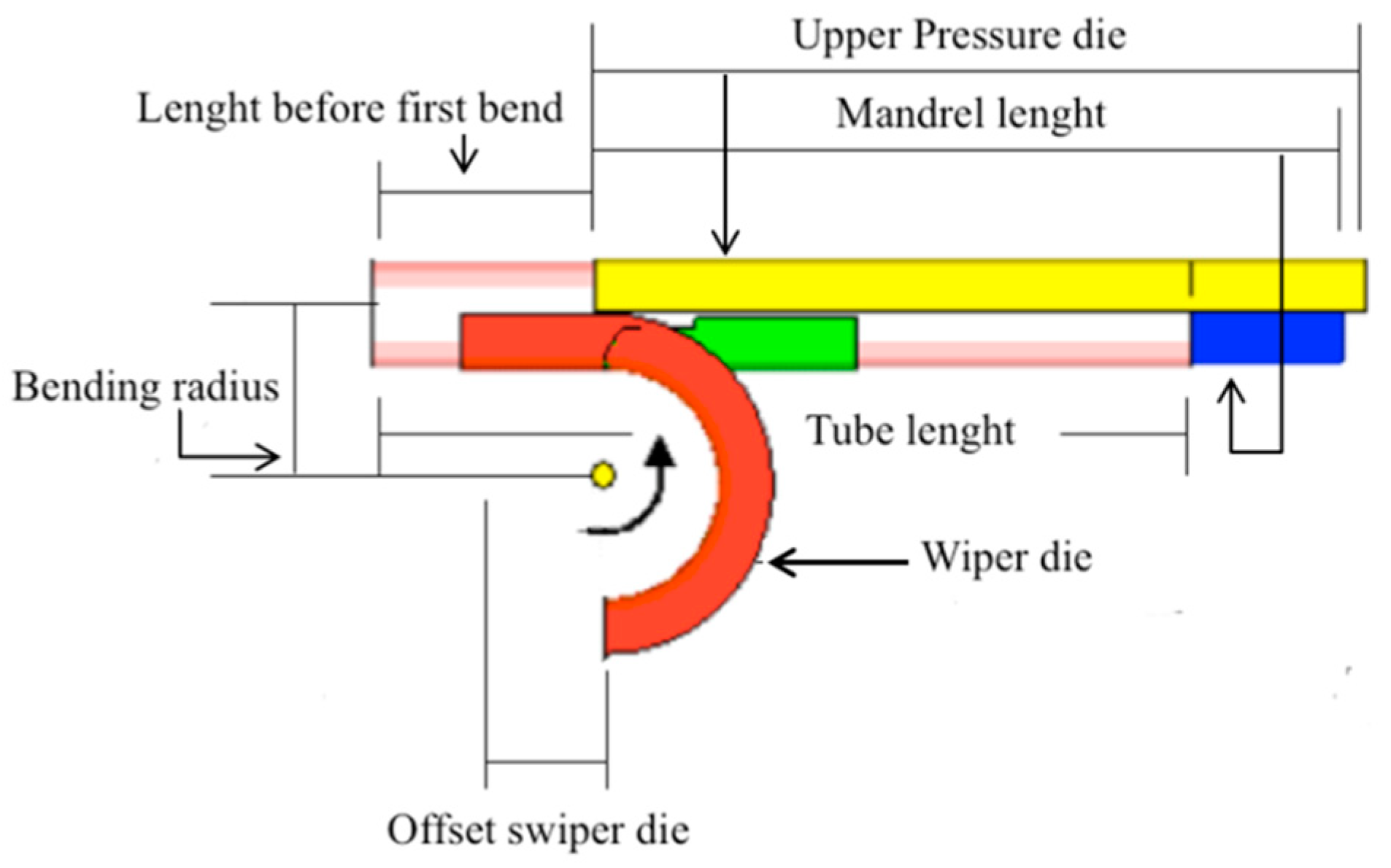
2.3. Model
- bending radius;
- bending angle;
- rotational speed;
- bending temperature.
3. Results and Discussion
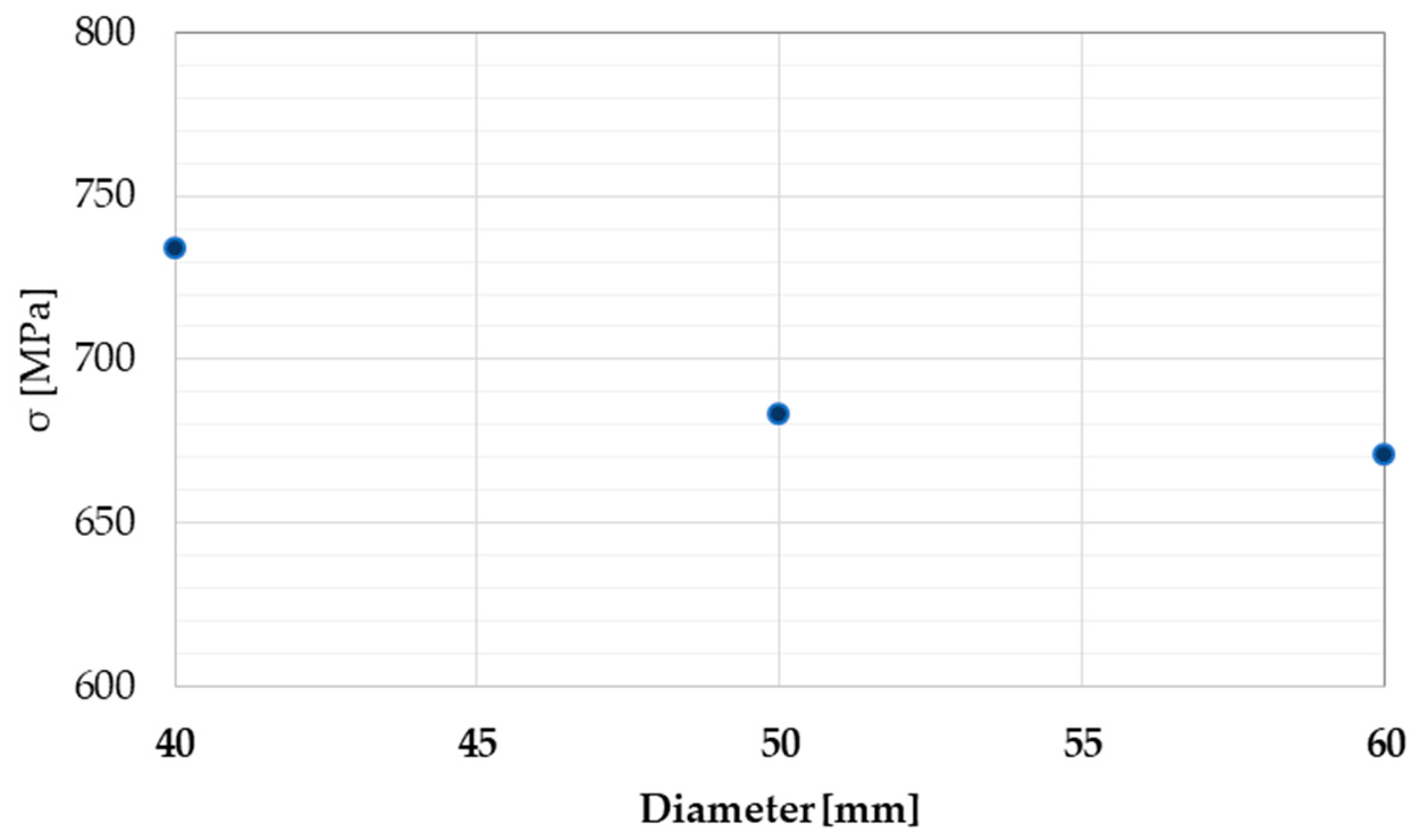
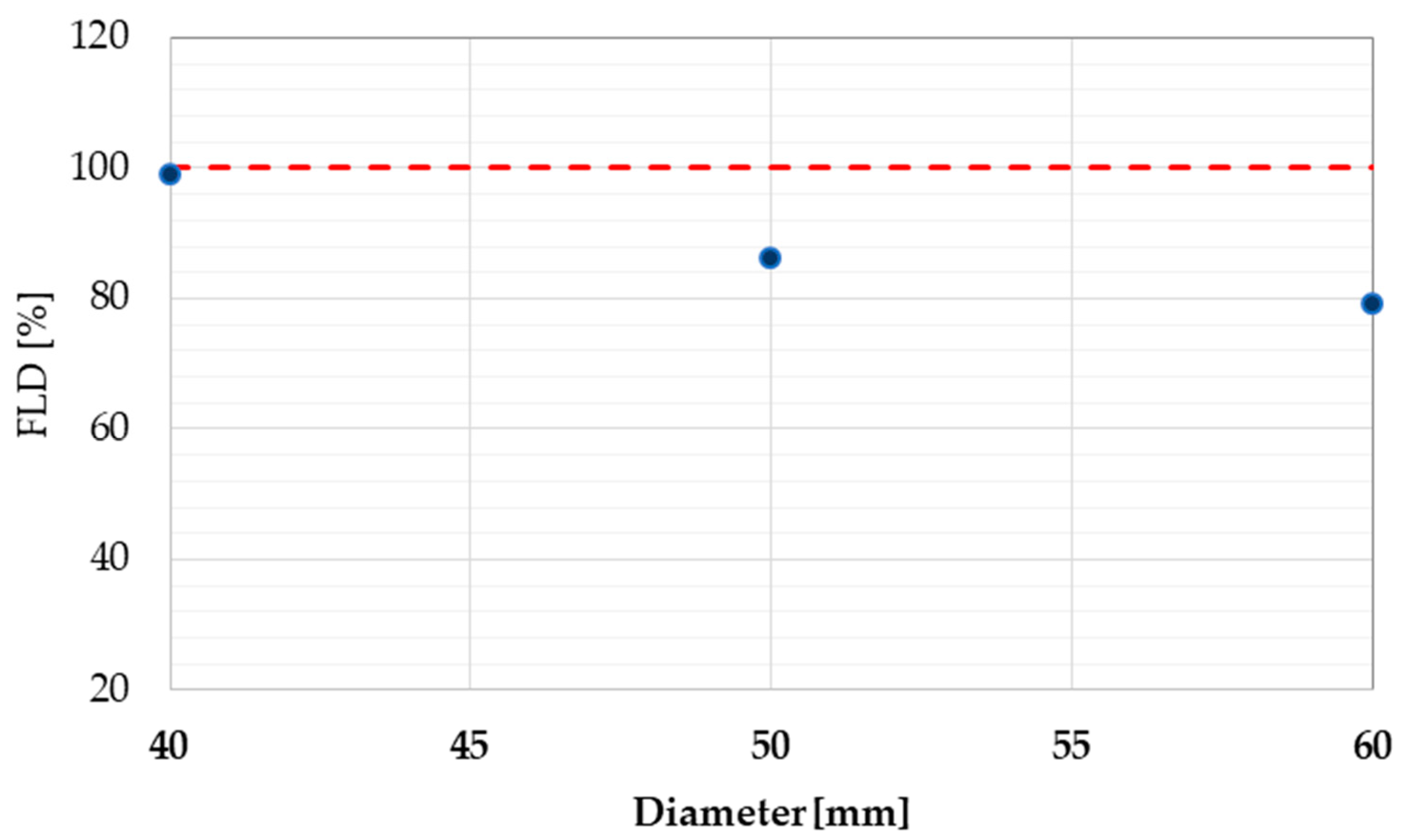
3.1. Effect of Tube Diameter
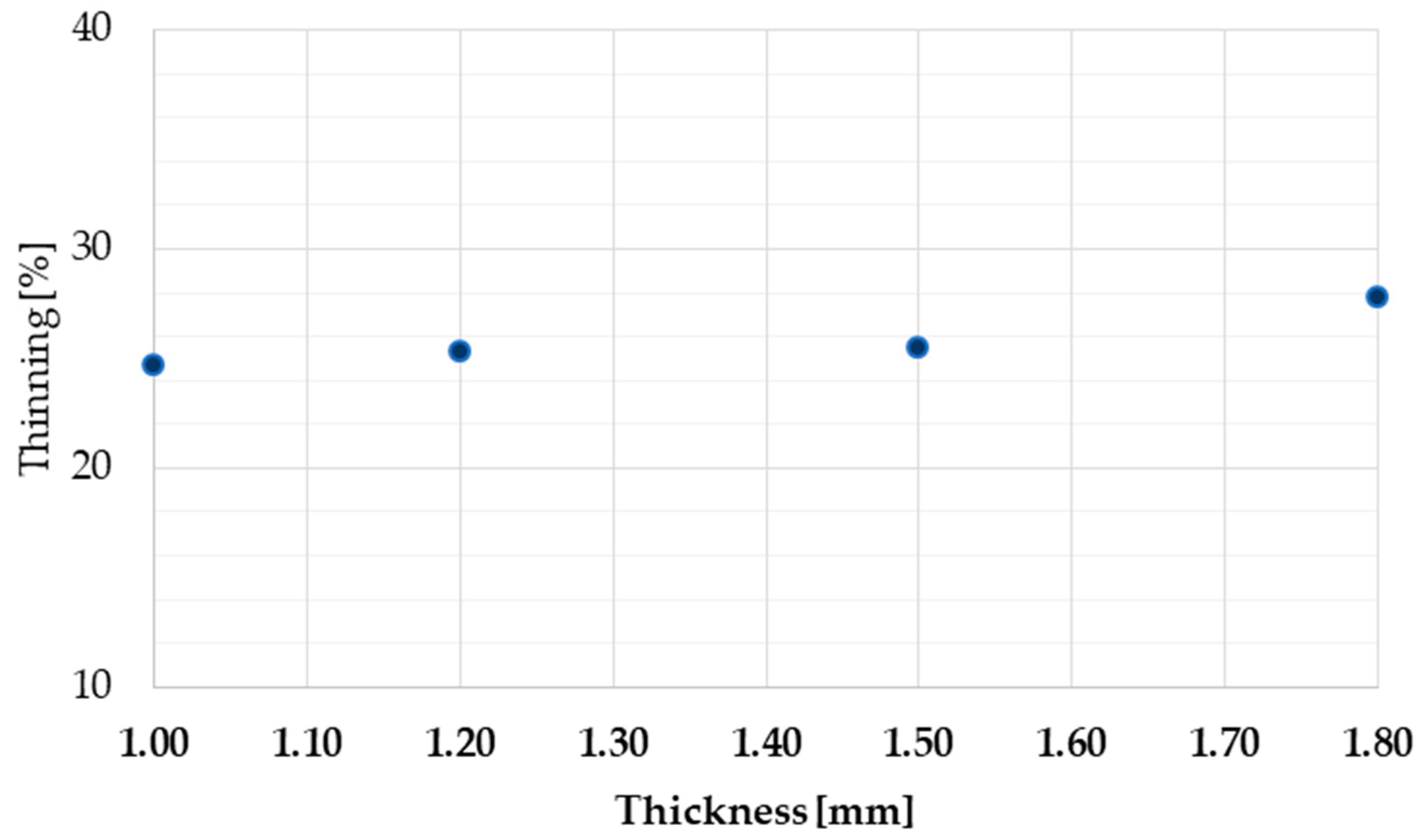
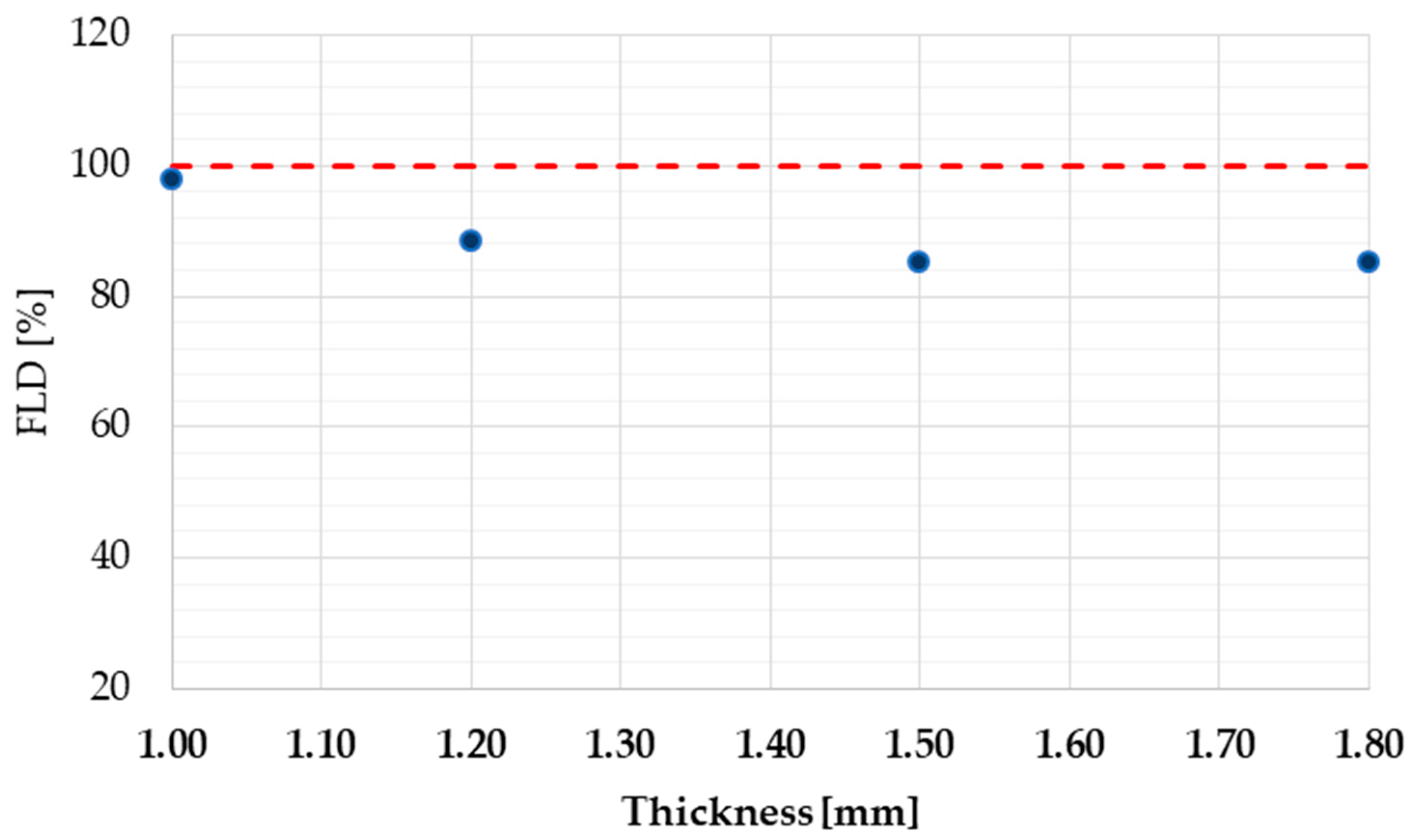
3.2. Tubes Thickness Effect
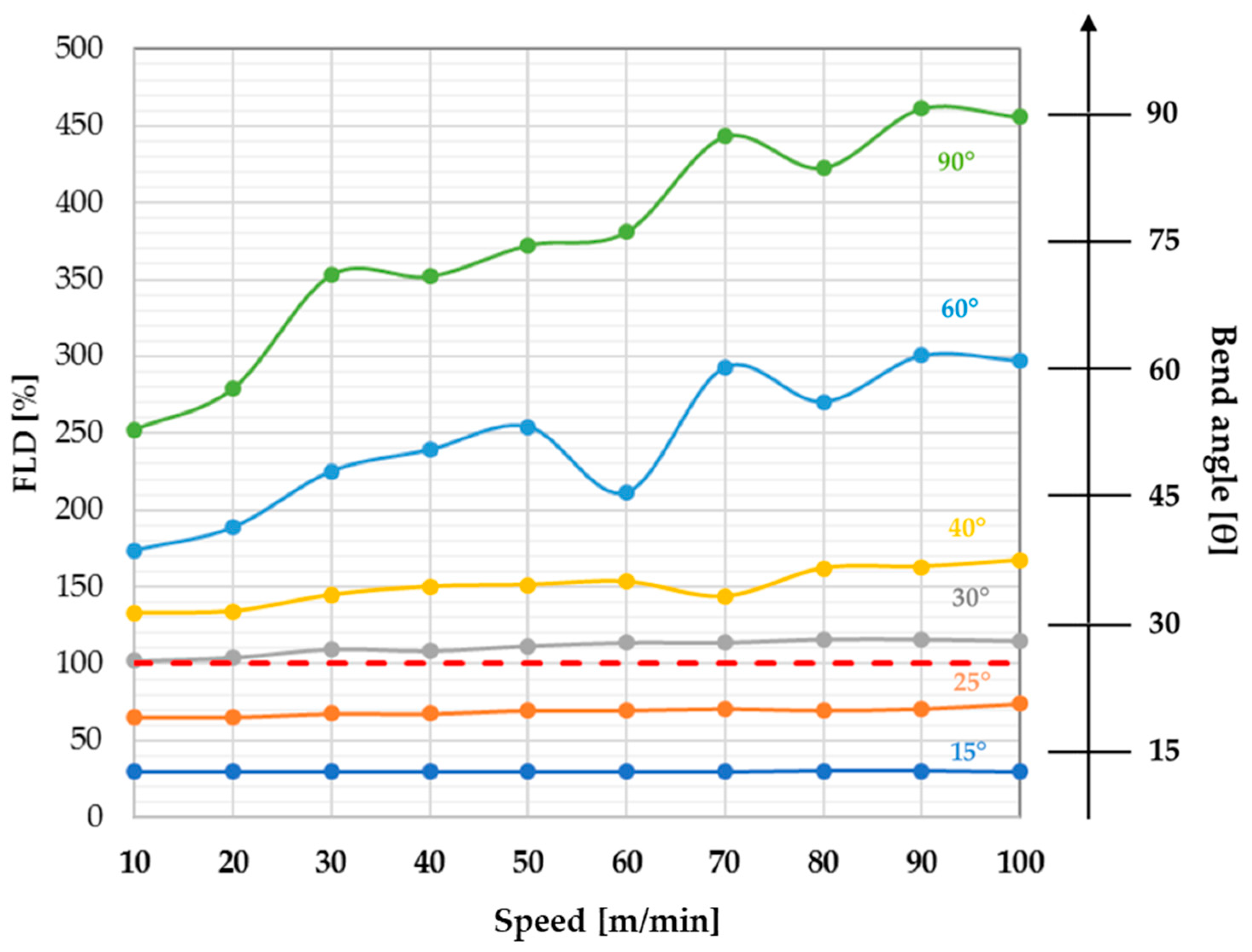
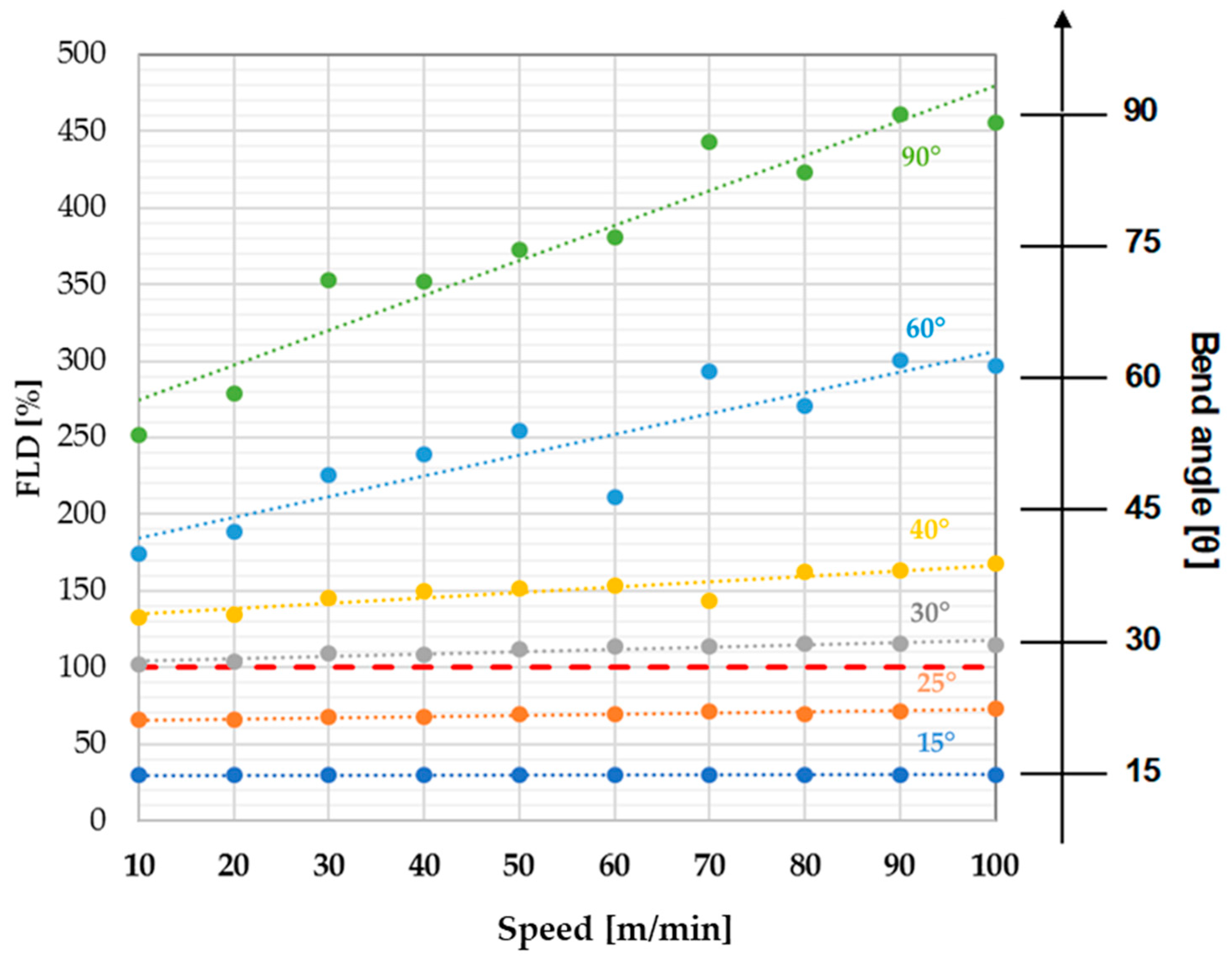
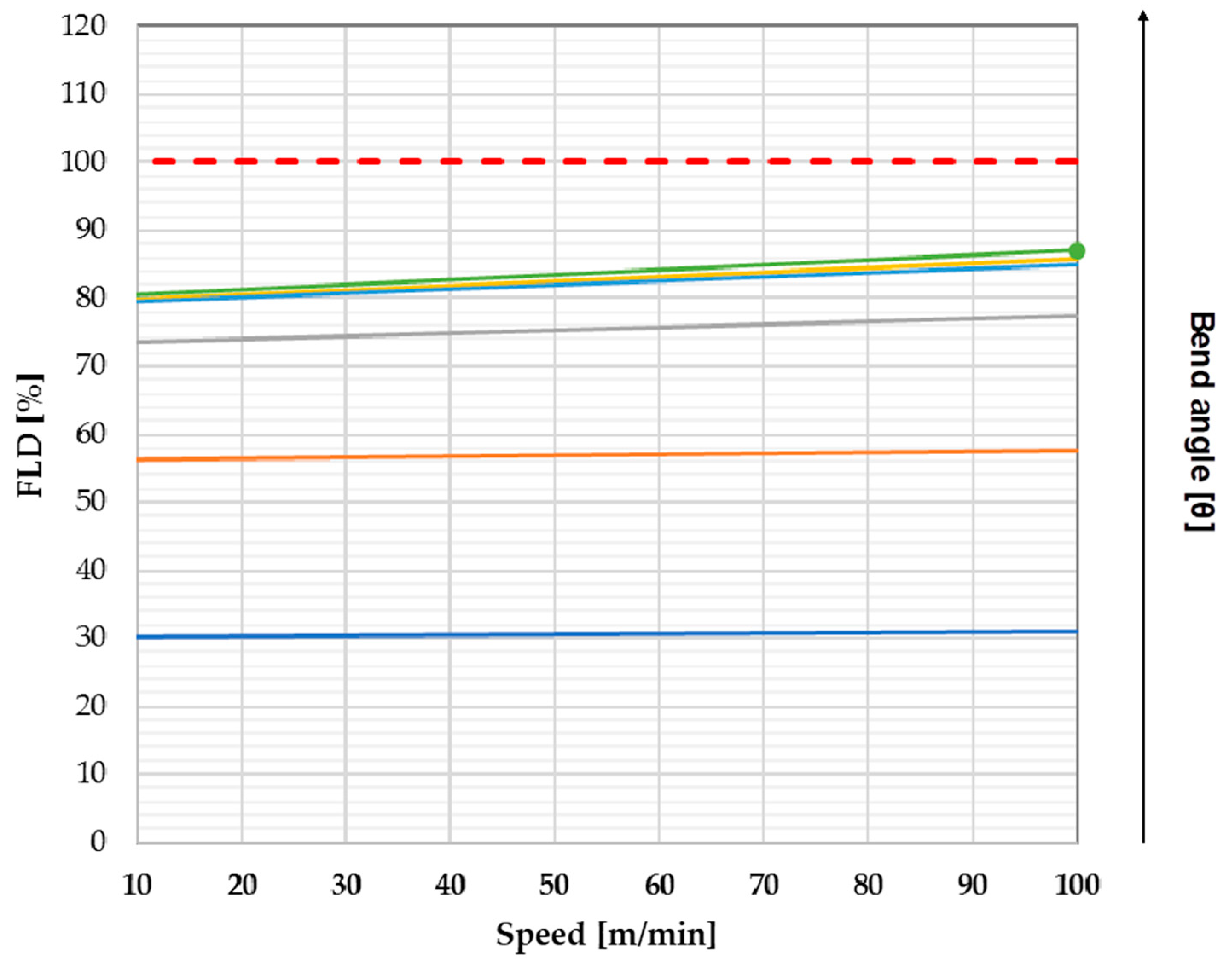
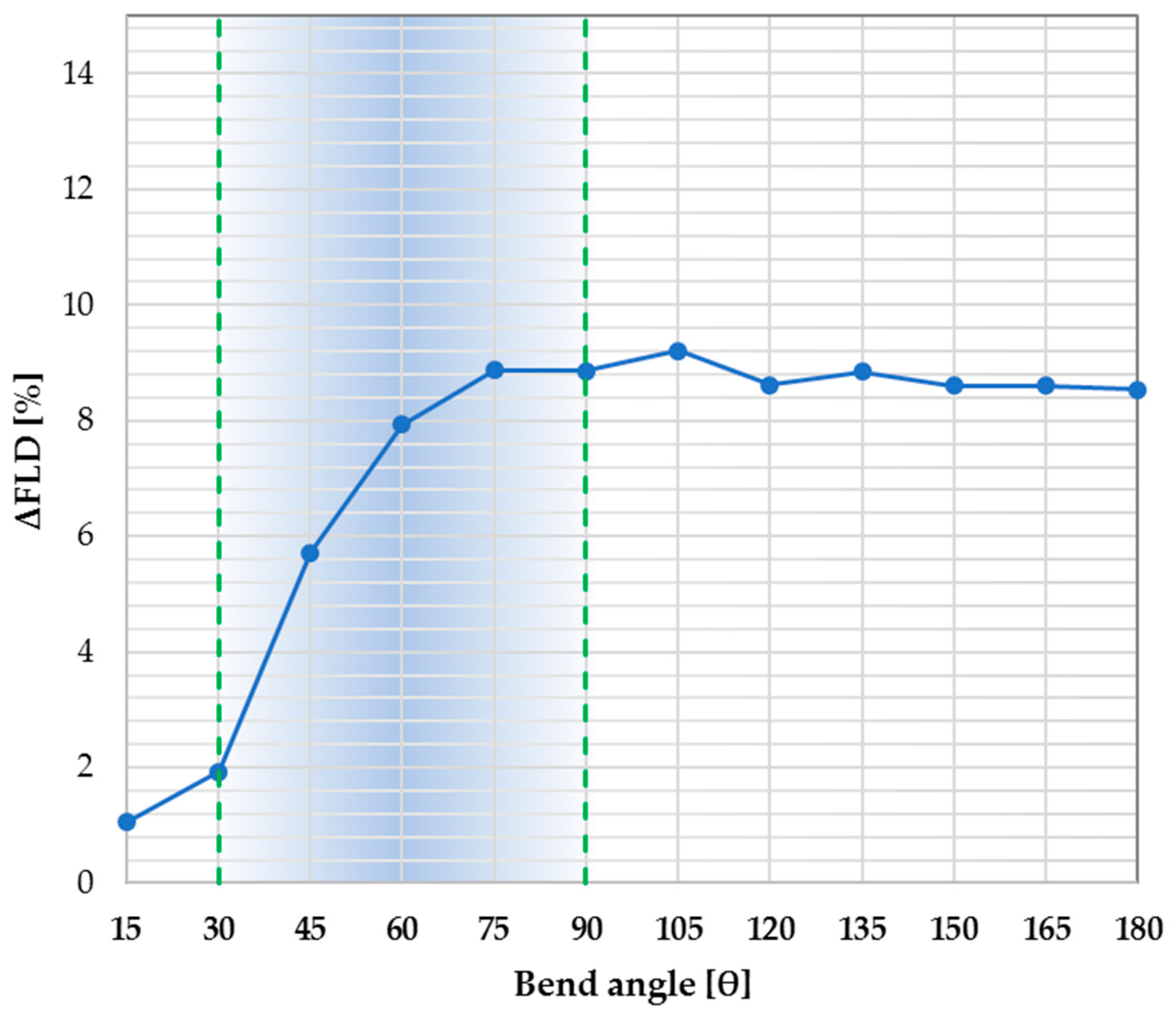
3.3. Speed and Bend Angle Effects
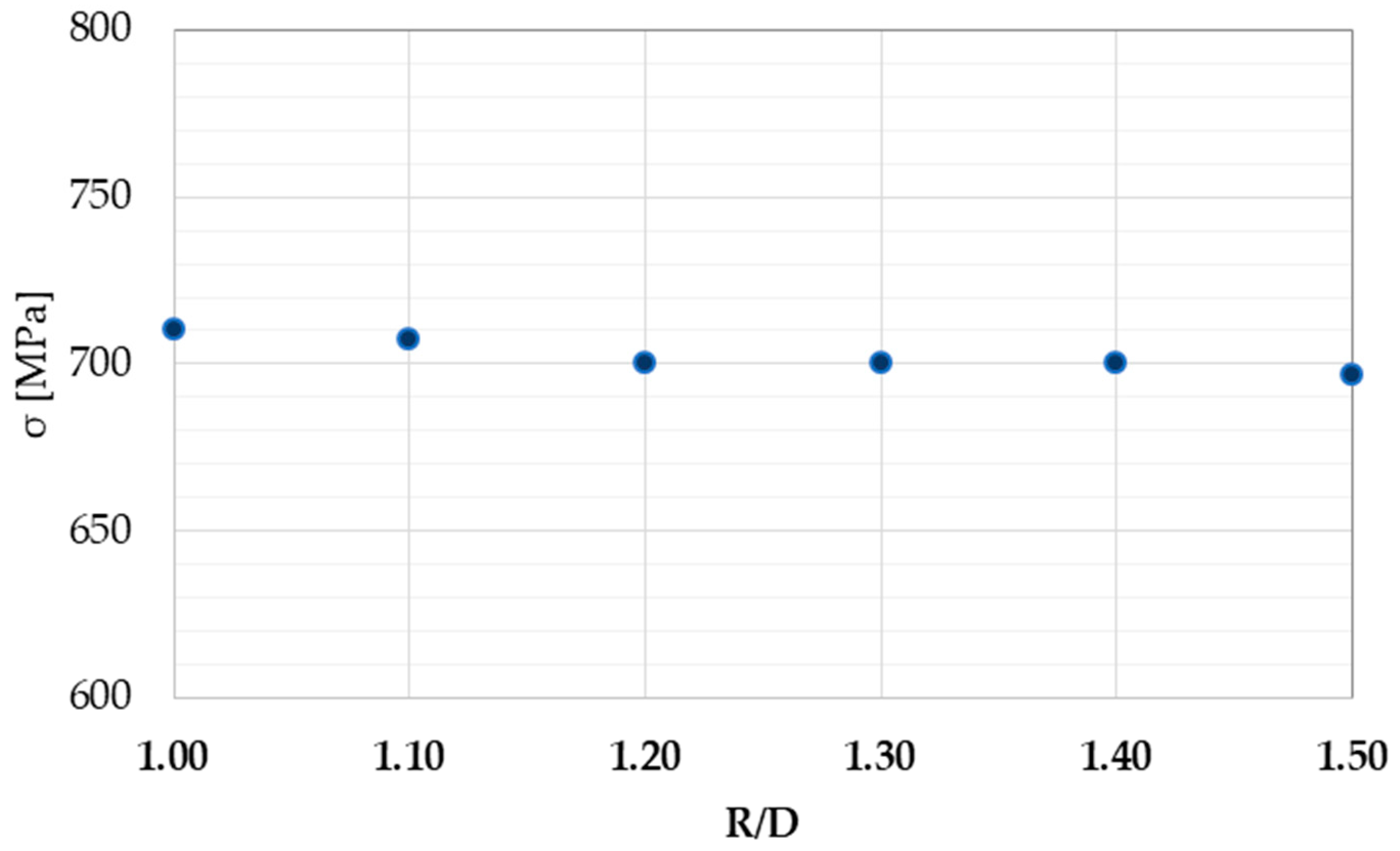
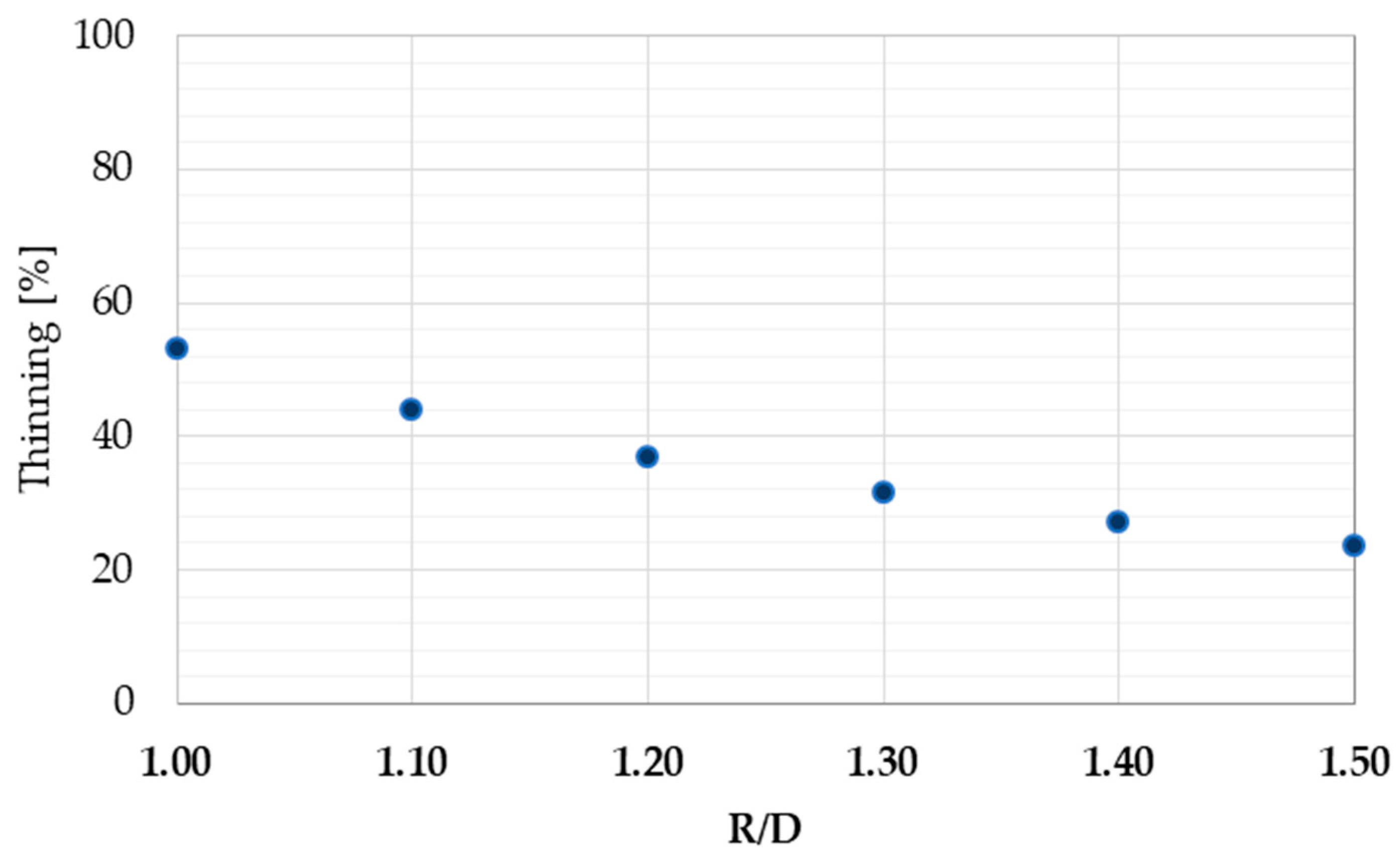
3.4. R/D Effect
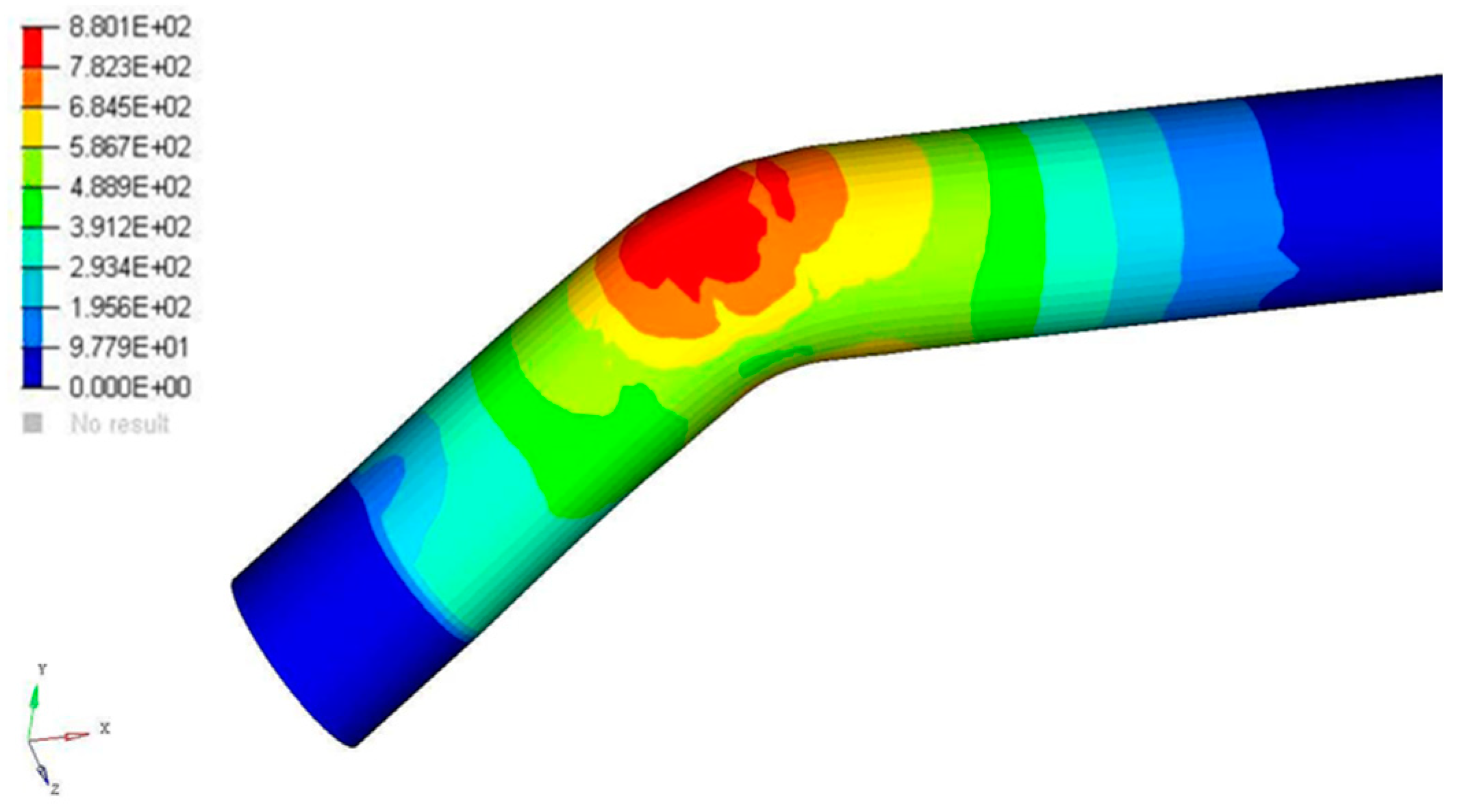
3.5. Experimental Validation
4. Conclusions
- Pipe diameter effect on forming: If the same parameters are considered and the R/D ratio between the radius and diameter is kept constant, an increase in the diameter size (in the typical automotive range) will result in a −9% variation in terms of internal stresses, evaluated according to the von Mises criterion. The thinning of the tube will decrease by −4%, and the feasibility characteristics of the process will improve; in fact, the percentage reaching the formability limit will drop by −20%. The diameter size choice appears therefore to be a key issue in terms of process feasibility. In this sense, the reported approach is a useful tool aimed to properly design, also in quantitative terms, the forming process for different pipe sizes.
- Pipe thickness effect on forming: It is reported that a pipe thickness increase implies more safety for the bending process. In fact, keeping the operating conditions constant, the increase from a thickness of 1.0 mm to a thickness of 1.8 mm will lead to a reduction in the internal stresses of the −6% f, −3% for thinning and −13% in FLD.
- The combined study of bending angle and speed has shown how the simulation has incorrect results when the tube collapses. In non-breaking conditions, the speed has relevant importance in terms of feasibility in the range of the bending angle 30°–90°.
- The simulations show the R/D ratio as the most important parameter in the bending process. An increase in it from 1.0 to 1.5 entails a 30% reduction in thinning and a 60% increase in the bending process success.
Author Contributions
Funding
Conflicts of Interest
References
- Marshall, P. Austenitic Stainless Steels: Microstructure and Mechanical Properties; Elsevier Applied Science Publisher: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Di Schino, A. Manufacturing and application of stainless steels. Metals 2020, 10, 327. [Google Scholar] [CrossRef]
- Liu, W.; Lian, J.; Munstermann, S.; Zeng, C.; Fang, X. Prediction of crack formation in the progressive folding of square tubes during dynamic axial crushing. Int. J. Mech. Sci. 2020, 176, 105534. [Google Scholar] [CrossRef]
- Corradi, M.; Osofero, A.I.; Borri, A. Repair and Reinforcement of Historic Timber Structures with Stainless Steel—A Review. Metals 2019, 9, 106. [Google Scholar] [CrossRef]
- Gedge, G. Structural uses of stainless steel—Buildings and civil engineering. J. Constr. Steel Res. 2008, 64, 1194–1198. [Google Scholar] [CrossRef]
- Di Schino, A. Analysis of heat treatment effect on microstructural features evolution in a micro-alloyed martensitic steel. Acta Met. Slovaca 2016, 22, 266–270. [Google Scholar] [CrossRef]
- Sharma, D.K.; Filipponi, M.; Di Schino, A.; Rossi, F.; Castaldi, J. Corrosion behavior of high temperature fuel cells: Issues for materials selection. Metalurgija 2019, 58, 347–351. [Google Scholar]
- Gennari, C.; Lago, M.; Bogre, B.; Meszaros, I.; Calliari, I.; Pezzato, L. Microstructural and corrosion properties of cold rolled laser welded UNS S32750 duplex stainless steel. Metals 2018, 8, 1074. [Google Scholar] [CrossRef]
- Fava, A.; Montanari, R.; Varone, A. Mechanical spectroscopy investigation of point defect-driven phenomena in a Chromium martensitic steel. Metals 2018, 8, 870. [Google Scholar] [CrossRef]
- Di Schino, A.; Kenny, J.M.; Abbruzzese, G. Analysis of the recrystallization and grain growth processes in AISI 316 stainless steel. J. Mat. Sci. 2002, 37, 5291–5298. [Google Scholar] [CrossRef]
- Di Schino, A.; Testani, C. Corrosion behavior and mechanical properties of AISI 316 stainless steel clad Q235 plate. Metals 2020, 10, 552. [Google Scholar] [CrossRef]
- Rufini, R.; Di Pietro, O.; Di Schino, A. Predictive simulation of plastic processing of welded stainless steel pipes. Metals 2018, 8, 519. [Google Scholar] [CrossRef]
- Di Schino, A.; Valentini, L.; Kenny, J.M.; Gerbig, Y.; Ahmed, I.; Hefke, H. Wear resistance of high-nitrogen austenitic stainless steel coated with nitrogenated amorphous carbon films. Surf. Coat. Technol. 2002, 161, 224–231. [Google Scholar] [CrossRef]
- Di Schino, A.; Di Nunzio, P.E.; Turconi, G.L. Microstructure evolution during tempering of martensite in medium carbon steel. Mater. Sci. Forum 2007, 558, 1435–1441. [Google Scholar]
- Di Schino, A.; Alleva, L.; Guagnelli, M. Microstructure evolution during quenching and tempering of martensite in a medium C steel. Mater. Sci. Forum 2012, 715–716, 860–865. [Google Scholar]
- Zitelli, C.; Folgarait, P.; Di Schino, A. Laser powder bed fusion of stainless steel grades: A review. Metals 2019, 9, 731. [Google Scholar] [CrossRef]
- Mancini, S.; Langellotto, L.; Di Nunzio, P.E.; Zitelli, C.; Di Schino, A. Defect reduction and quality optimisation by modelling plastic deformation and metallurgical evolution in ferritic stainless steels. Metals 2020, 10, 186. [Google Scholar] [CrossRef]
- Gardner, L. The use of stainless steel in structures. Prog. Struct. Eng. Mat. 2005, 7, 45–55. [Google Scholar] [CrossRef]
- Mulidran, P.; Siser, M.; Slota, J.; Spisak, E.; Sleziak, T. Numerical Prediction of Forming Car Body Parts with Emphasis on Springback. Metals 2018, 8, 60435. [Google Scholar] [CrossRef]
- Mei, Z.; Khun, G.; He, Y. Advances and trends in plastic forming technologies for welded tubes. Chin. J. Aeron. 2016, 29, 305–315. [Google Scholar]
- Oliveira, M.C.; Fernandes, J.B. Modelling and simulation of sheet metals forming processes. Metals 2019, 9, 1356. [Google Scholar] [CrossRef]
- Cherouat, A.; Borouchaki, H.; Zhang, J. Simulation of Sheet Metal Forming Processes Using a Fully Rheological-Damage Constitutive Model Coupling and a Specific 3D Remeshing Method. Metals 2018, 8, 991. [Google Scholar] [CrossRef]
- Bong, H.J.; Barlat, F.; Lee, M.; Ahn, D.C. The forming limit diagram of ferritic stainless steel sheets: Experiments and modeling. Int. J. Mech. Sci. 2012, 64, 1–10. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y. The inverse parameter identification of Hill’48 yield function for small-sized tube combining response surface methodology and three-point bending. J. Mat. Res. 2017, 32, 2343–2351. [Google Scholar] [CrossRef]
- Lehmberg, A.; Suderkoetter, C.; Glaesner, T.; Brokmeier, H.G. Forming behavior of stainless steel sheets at different material thicknesses. Mater. Sci. Eng. 2019, 651, 012082. [Google Scholar]
- Scott, T.; Kotadia, H. Microstructural evolution of 316L austenitic stainless steel during in-situ biaxial deformation and annealing. Mat. Chat. 2020, 163, 110288. [Google Scholar]
- He, Y.; Heng, L.; Zhiyoing, Z.; Mei, Z.; Jing, L.; Guangjun, L. Advances and Trends on Tube Bending Forming Technologies. Chin. J. Aeron. 2012, 25, 1–12. [Google Scholar]
- Wu, W.Y.; Zhang, P.; Zeng, X.Q.; Li, J.; Yao, S.S.; Luo, A.A. Bendability tubes using a rotary draw bender. Mater. Sci. Eng. A 2008, 486, 596–601. [Google Scholar] [CrossRef]
- Liu, K.X.; Liu, Y.L.; Yang, H.; Zhao, G.Y. Experimental study on cross-section distortion of thin-walled rectangular tube by rotary draw bending. Int. J. Mater. Prod. Technol. 2011, 42, 110–120. [Google Scholar] [CrossRef]
- Liu, K.X.; Liu, Y.L.; Yang, H. Experimental study on the effect of dies on wall thickness distribution in NC bending of thin-walled rectangular tube. Int. J. Mater. Prod. Technol. 2013, 68, 1867–1874. [Google Scholar]
- Tang, N. Plastic-deformation analysis in tube bending. Int. J. Pres. Vessels. Pip. 2000, 77, 751–759. [Google Scholar] [CrossRef]
- Al-Qureshi, H.; Russo, A. Spring-back and residual stresses in bending of thin-walled tubes. Mater. Des. 2002, 23, 217–222. [Google Scholar] [CrossRef]
- Chen, J.; Ding, J.; Bai, X. In-plane strain solution of stress and defects of tube bending with exponential hardening law. Mech. Based Des. Struct. Mach. Int. J. 2012, 40, 257–276. [Google Scholar]
- Li, H.; Yang, H.; Song, F.F.; Zhan, M.; Li, G.J. Spring-back characterization and behaviors of high-strength tube in cold rotary draw bending. J. Mater. Process. Technol. 2012, 212, 1973–1987. [Google Scholar] [CrossRef]
- Jeong, H.S.; Ha, M.Y.; Cho, J.R. Theoretical and FE analysis for fine tube bending to predict spring-back. Int. J. Precis. Eng. Manuf. 2012, 13, 2143–2148. [Google Scholar] [CrossRef]
- Liu, J.; Tang, C.; Ning, R. Deformation calculation of cross section based on virtual force in thin-walled tube bending process. Chin. J. Mech. Eng. 2009, 22, 696–701. [Google Scholar] [CrossRef]
- Li, H.; Yang, H.; Yan, J.; Zhan, M. Numerical study on deformation behaviors of thin-walled tube NC bending with large diameter and small bending radius. Comput. Mat. Sci. 2009, 45, 921–934. [Google Scholar] [CrossRef]
- Napoli, G.; Di Schino, A.; Paura, M.; Vela, T. Colouring titanium alloys by anodic oxidation. Metalurgija 2018, 57, 111–113. [Google Scholar]
- Di Schino, A.; Di Nunzio, P. Metallurgical aspects related to contact fatigue phenomena in steels for back up rolling. Acta Metall. Slovaca 2017, 23, 62–71. [Google Scholar] [CrossRef]
- Di Schino, A. Analysis of phase transformation in high strength low alloyed steels. Metalurgija 2017, 56, 349–352. [Google Scholar]
- Wang, S.; Wei, K.; Li, J.; Liu, Y.; Huang, Z.; Mao, Q.; Li, Y. Enhanced tensile properties of 316L stainless steel processed by a novel ultrasonic resonance plastic deformation technique. Mater. Lett. 2019, 236, 342–345. [Google Scholar] [CrossRef]
- Kaushal, M.; Joshi, Y.M. Three-dimensional yielding in anisotropic materials: Validation of Hill’s criterion. Soft Matter 2019, 15, 4915–4920. [Google Scholar] [CrossRef] [PubMed]
- Cazacu, O.; Revil-Baudard, B.; Chandola, N. Yield criteria for anisotropic polycrystals. In Plasticity-Damage Couplings: From Single Crystal to Polycrystalline Materials. Solid Mechanics and Its Applications; Springer International Publishing: Cham, Switzerland, 2019; volume 253. [Google Scholar]
- Lumelskyj, D.; Rojek, J.; Tkocz, M. Numerical simulations of Nakazima formability tests with prediction of failure. Appl. Mech. 2015, 60, 184–194. [Google Scholar]
- Yang, T.B.; Yu, Z.Q.; Xu, C.B.; Li, S.H. Numerical analysis for forming limit of welded tube in hydroforming. J. Shanghai Jiaotong Univ. 2011, 45, 6–10. [Google Scholar]




| Steel Grade | C | Cr | Ni | Mo | Ti+Nb | Fe |
|---|---|---|---|---|---|---|
| 441 | 0.02–0.04 | 17.5–18.5 | − | − | 0.55% | Balance |
| Steel Grade | Tube Diameter [mm] | Tube Thickness [mm] |
|---|---|---|
| 441 | 40; 45; 50; 55; 60 | 1.0; 1.2; 1.5; 1.8 |
| Density | Young Modulus | Poisson Ratio | Lankford Value | Strain Hardening |
|---|---|---|---|---|
| 210,000.0 | 0.30 | 1.30–1.40 | 0.20–0.25 |
| Mandrel [mm] | Upper Pressure Die [mm] | Offset Swiper Die [mm] | Bending Radius [mm] |
|---|---|---|---|
| 750 | 750 | 100 | 100 |
| Rotational Velocity [rad/sec] | Bending Radius [mm] | Temperature [°C] | Bend Angle [ϑ] |
|---|---|---|---|
| 1.6235 | 100.0 | 25.0 | 90 |
| Angle | Thickness (mm) | ||||||
|---|---|---|---|---|---|---|---|
| Specimen n° 1 | Specimen n° 2 | Specimen n° 3 | Specimen n° 4 | Specimen n° 5 | Specimen n° 6 | MeanValue | |
| 0° | 1.169 | 1.200 | 1.180 | 1.124 | 1.250 | 1.235 | 1.193 |
| 22.5° | 1.003 | 1.019 | 1.026 | 1.023 | 1.123 | 1.101 | 1.049 |
| 45° | 0.982 | 0.993 | 1.002 | 1.058 | 1.157 | 1.016 | 1.035 |
| 67.5° | 1.086 | 1.016 | 1.050 | 1.029 | 1.166 | 1.052 | 1.067 |
| 90° | 1.200 | 1.180 | 1.180 | 1.152 | 1.149 | 1.161 | 1.166 |
| Measurement Angle | Simulation Thickness [mm] | Sample Mean Thickness [mm] | ∆Thickness [mm] | Percentage Variation [%] |
|---|---|---|---|---|
| 0° | 1.168 | 1.193 | −0.025 | −2.10 |
| 22.5° | 1.014 | 1.049 | −0.035 | −3.35 |
| 45° | 0.876 | 1.035 | −0.159 | −15.34 |
| 67.5° | 0.892 | 1.067 | −0.175 | −16.36 |
| 90° | 1.171 | 1.170 | 0.001 | 0.06 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Pietro, O.; Napoli, G.; Gaggiotti, M.; Marini, R.; Di Schino, A. Analysis of Forming Parameters Involved in Plastic Deformation of 441 Ferritic Stainless Steel Tubes. Metals 2020, 10, 1013. https://doi.org/10.3390/met10081013
Di Pietro O, Napoli G, Gaggiotti M, Marini R, Di Schino A. Analysis of Forming Parameters Involved in Plastic Deformation of 441 Ferritic Stainless Steel Tubes. Metals. 2020; 10(8):1013. https://doi.org/10.3390/met10081013
Chicago/Turabian StyleDi Pietro, Orlando, Giuseppe Napoli, Matteo Gaggiotti, Roberto Marini, and Andrea Di Schino. 2020. "Analysis of Forming Parameters Involved in Plastic Deformation of 441 Ferritic Stainless Steel Tubes" Metals 10, no. 8: 1013. https://doi.org/10.3390/met10081013
APA StyleDi Pietro, O., Napoli, G., Gaggiotti, M., Marini, R., & Di Schino, A. (2020). Analysis of Forming Parameters Involved in Plastic Deformation of 441 Ferritic Stainless Steel Tubes. Metals, 10(8), 1013. https://doi.org/10.3390/met10081013






