Numerical Simulation of Latent Heat of Solidification for Low Pressure Casting of Aluminum Alloy Wheels
Abstract
:1. Introduction
2. Process and Numerical Methods
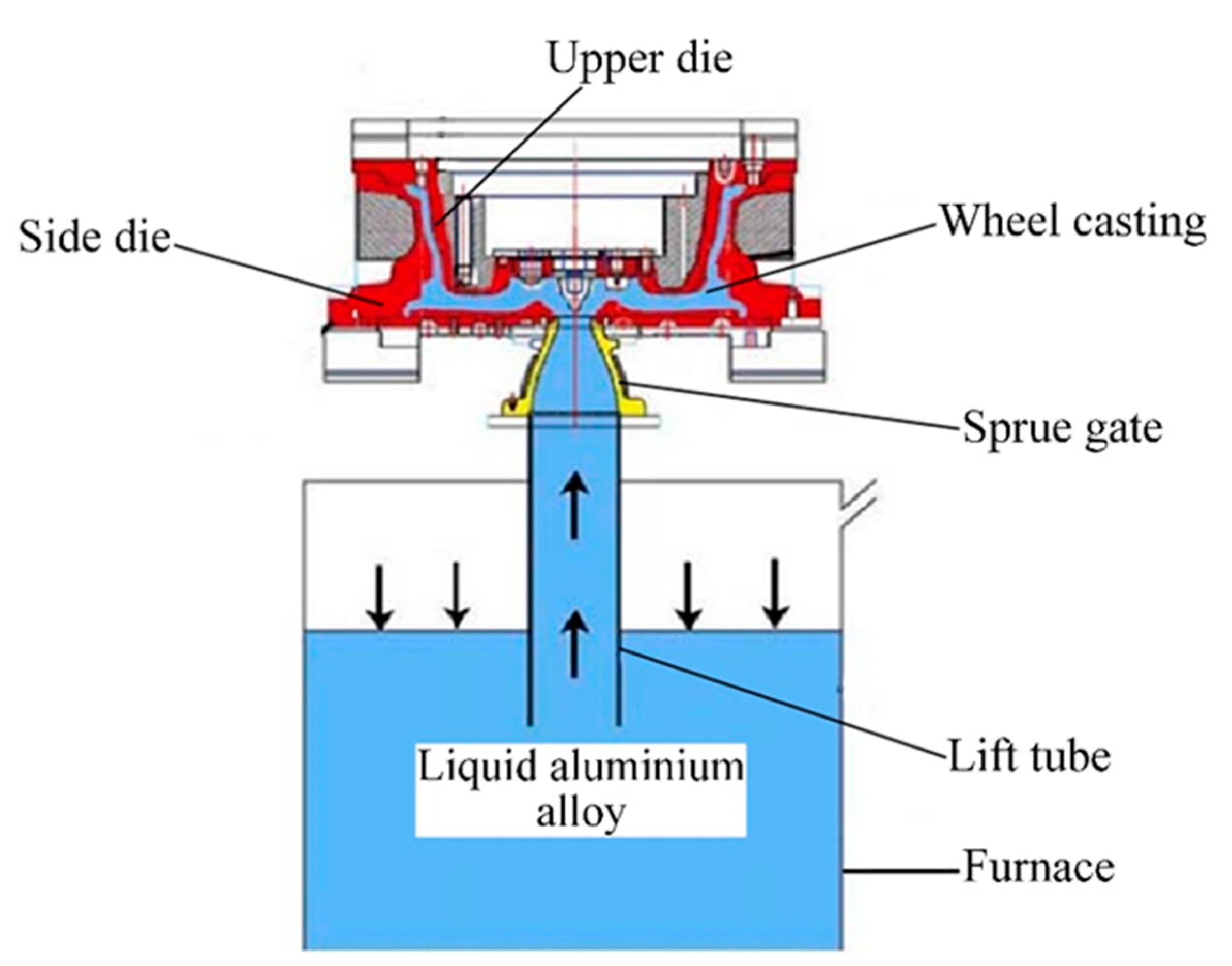
2.1. Wheel Casting Process
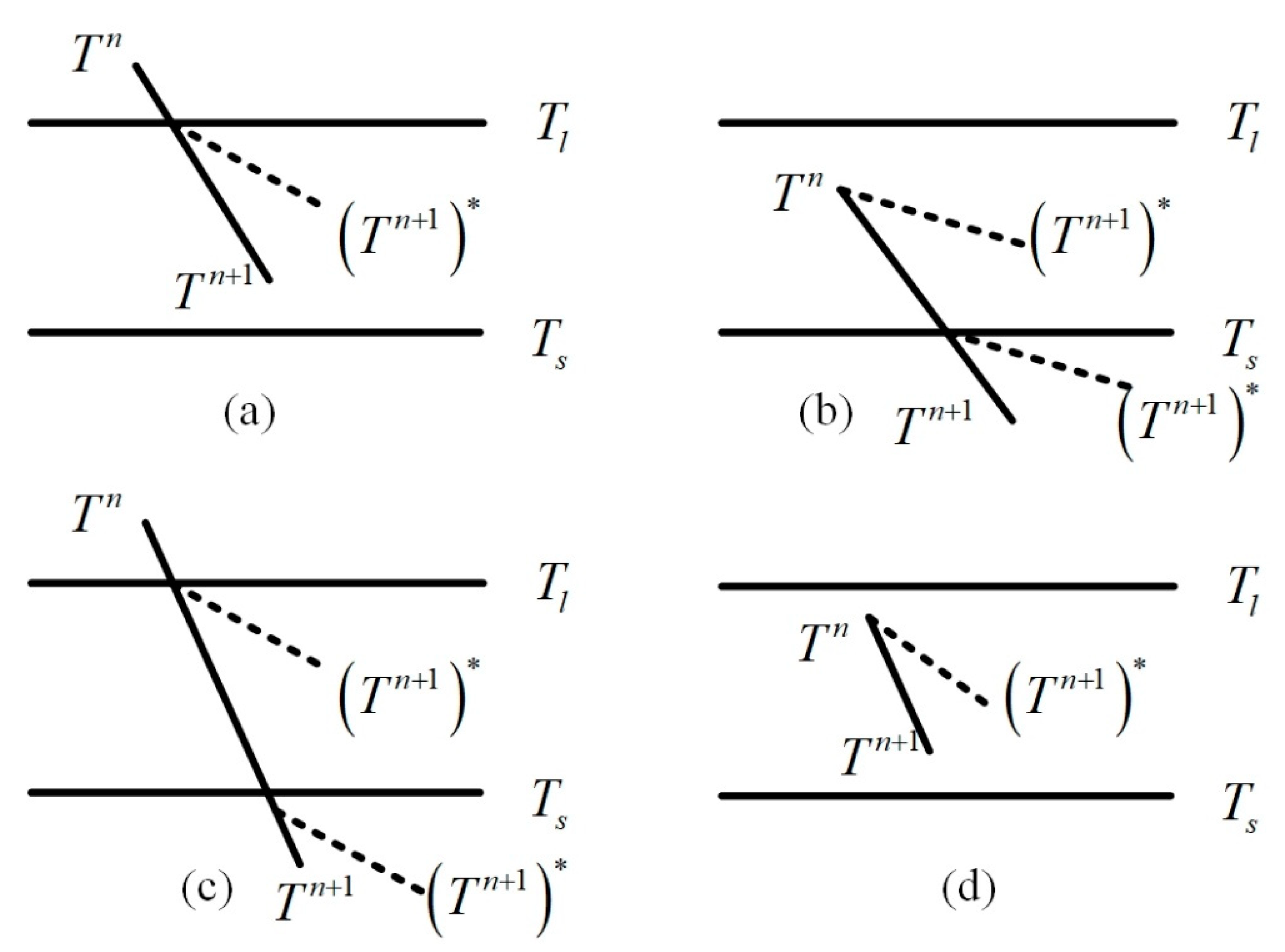
2.2. Different Numerical Methods of Latent Heat of Solidification
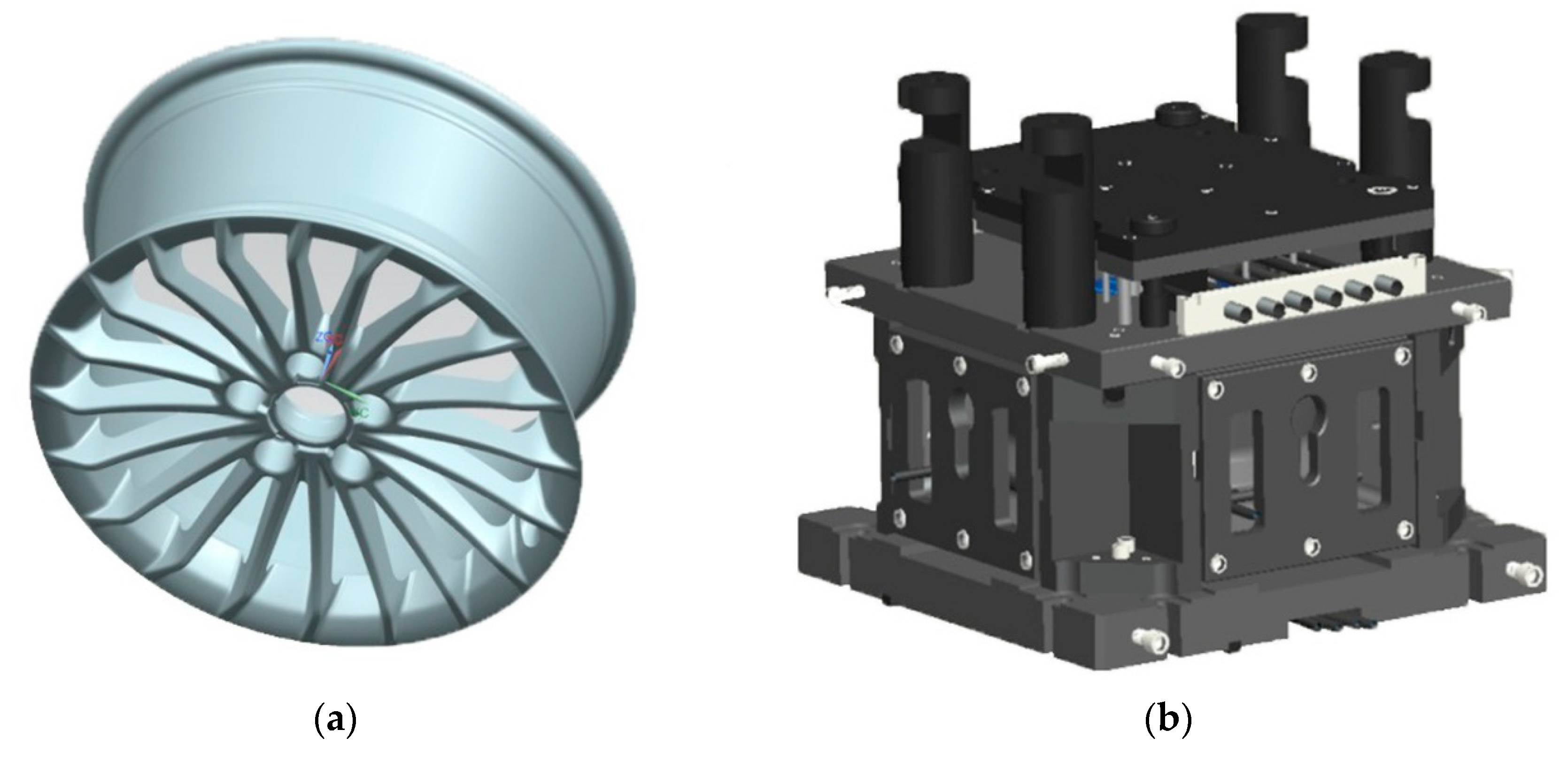
2.3. Finite Element Analysis
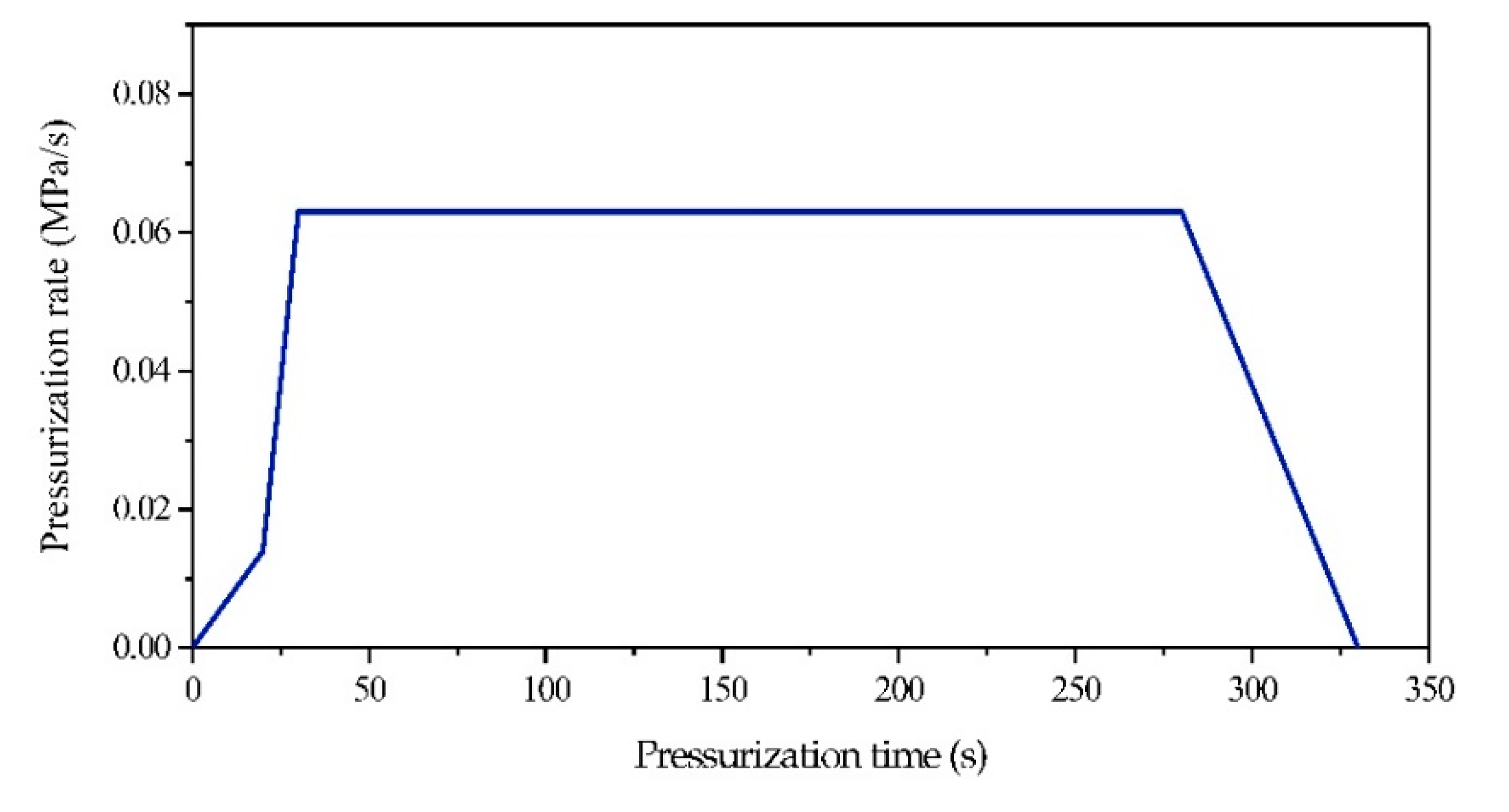
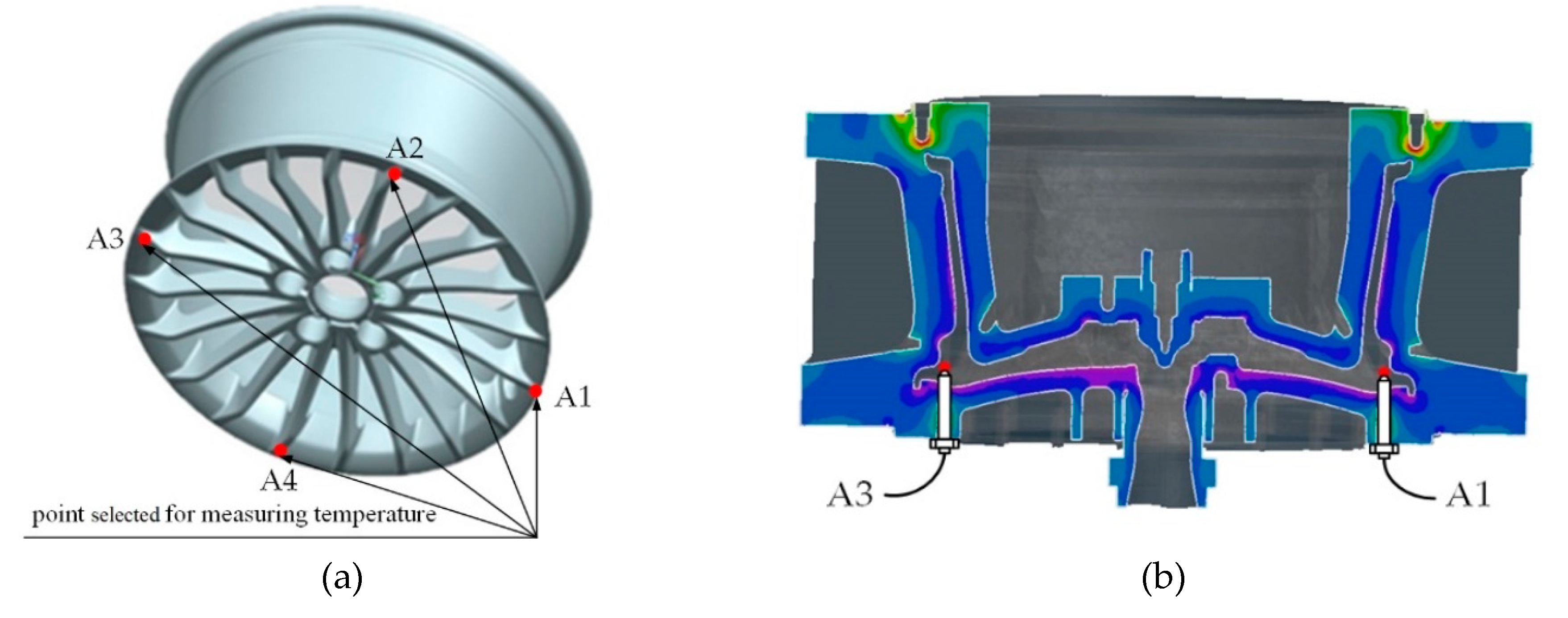
3. Plant Trial
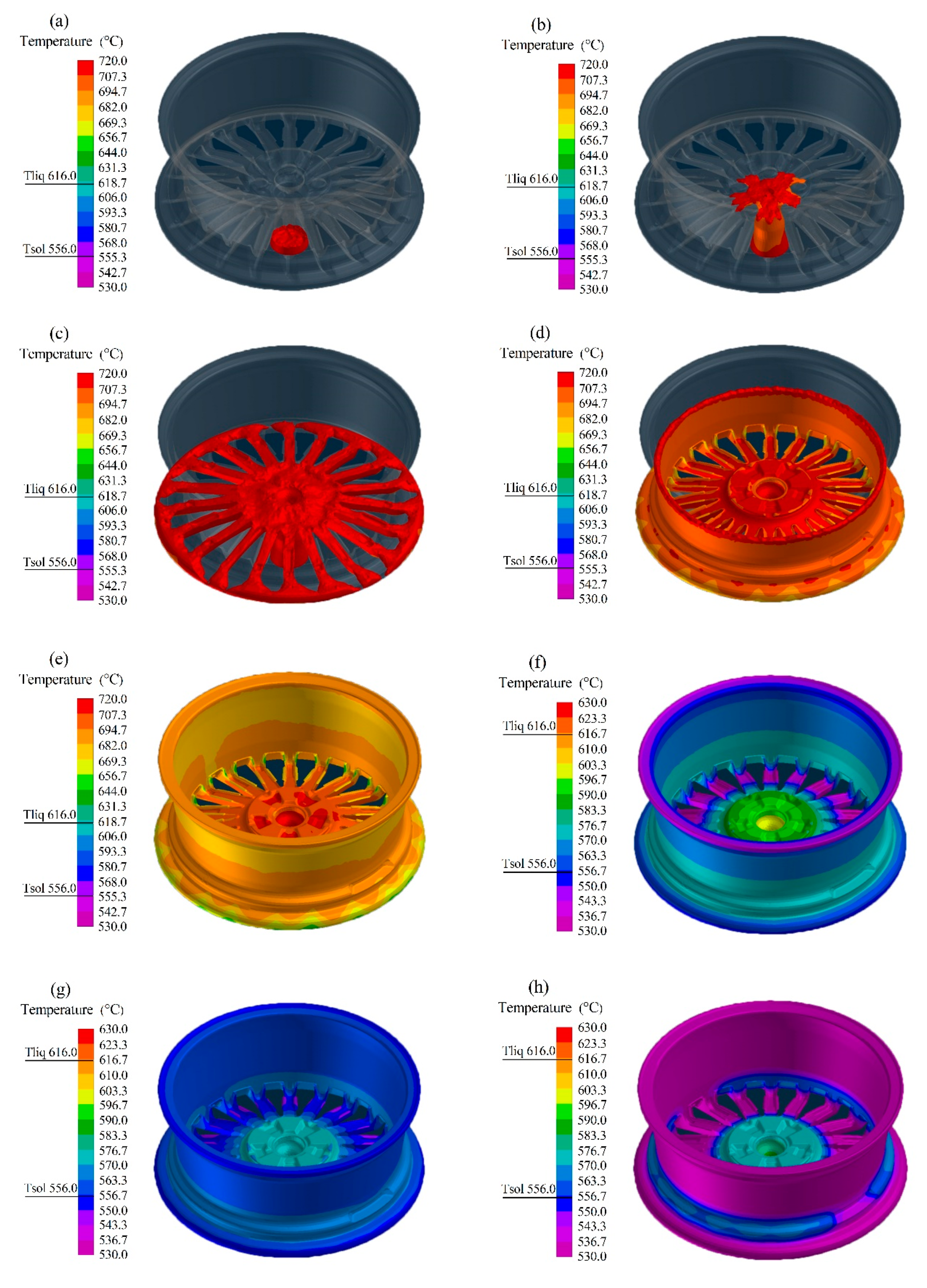
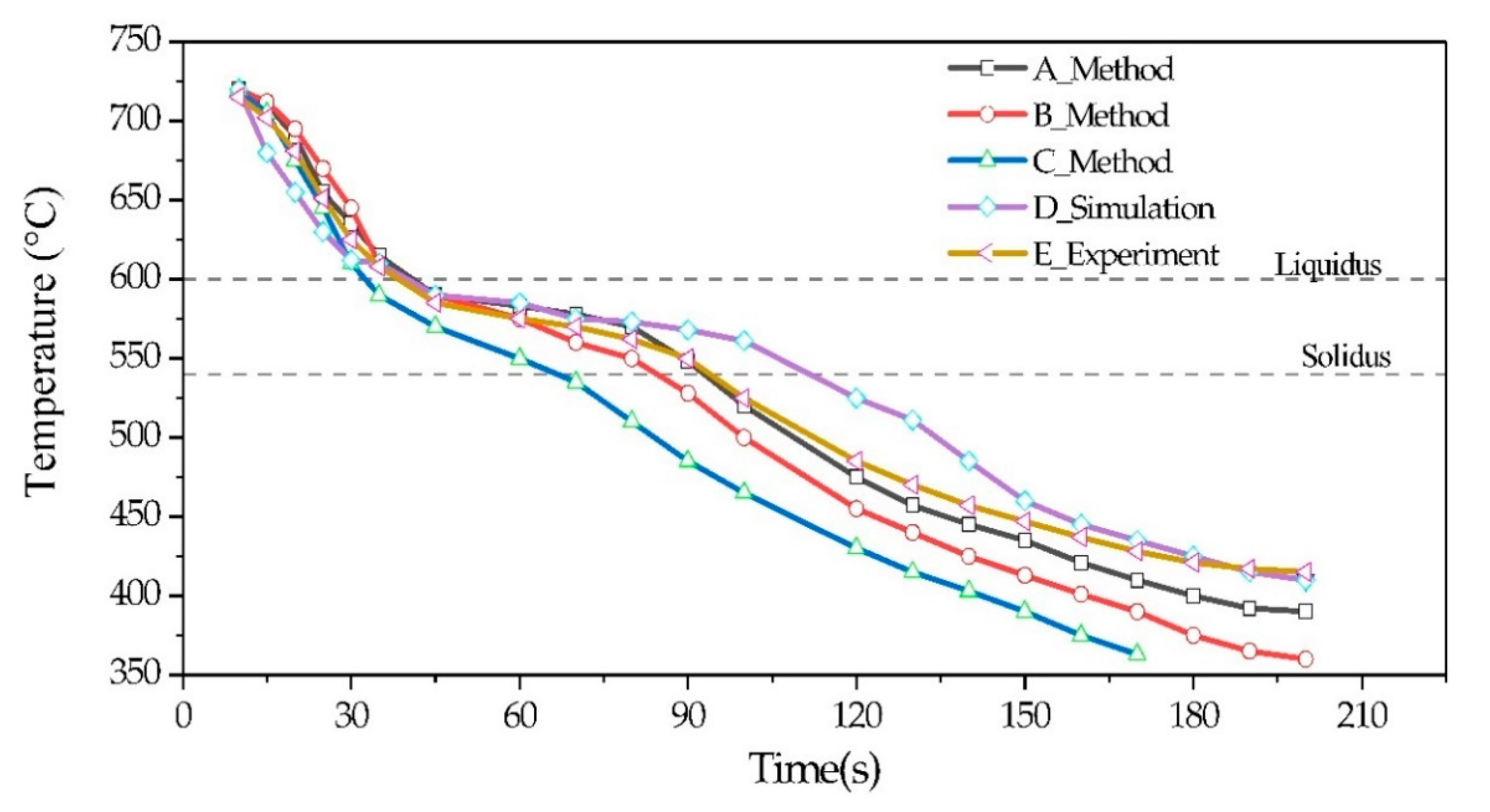
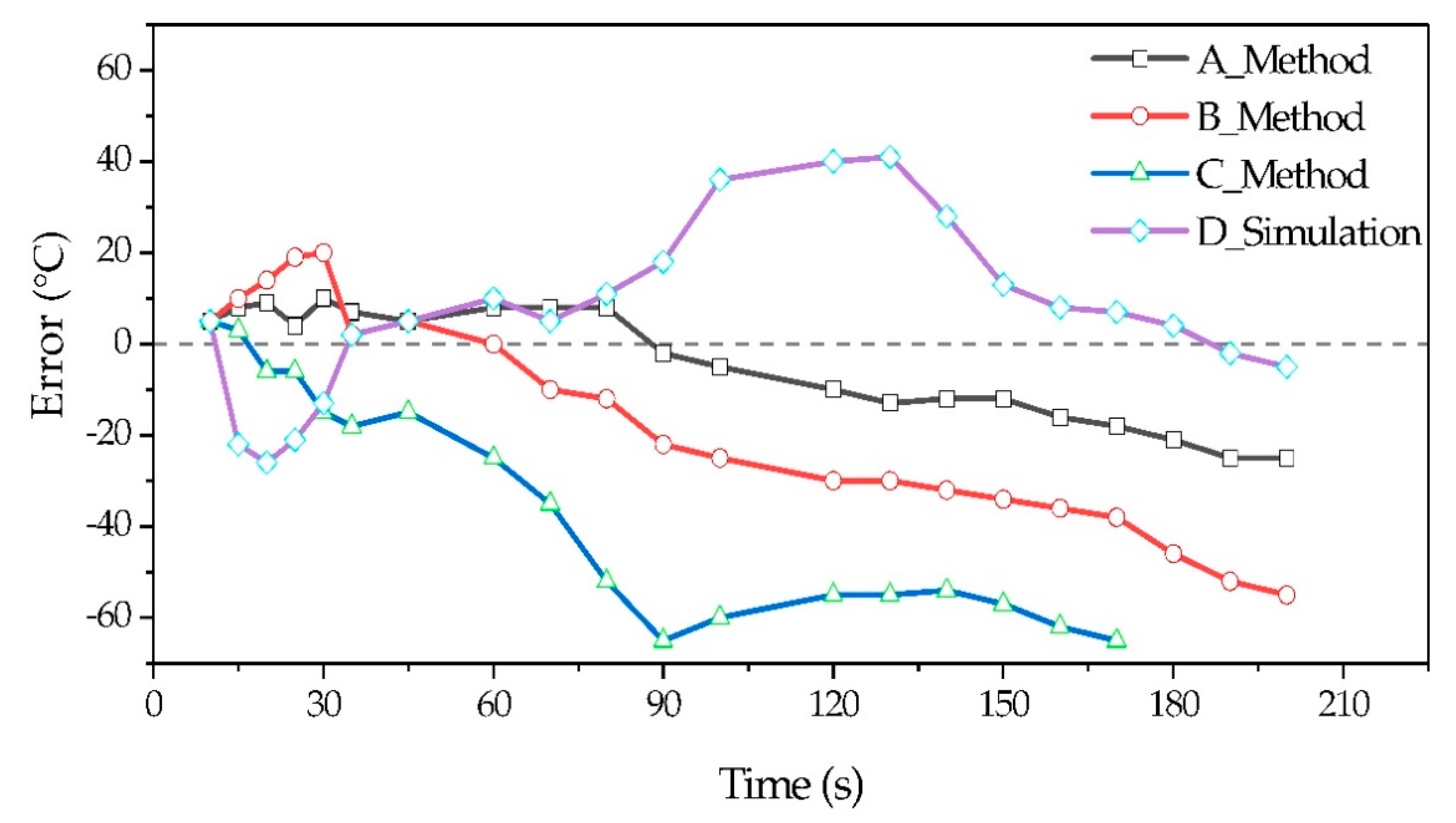
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eray, E.; Ozen, G.; Çaglar, Y. Determination of Acceptable Quality Limit for Casting of A356 Aluminium Alloy: Supplier’s Quality Index (SQI). Metals 2019, 9, 957–971. [Google Scholar]
- Thompson, S.; Cockcroft, S.L.; Wells, M.A. Advanced light metals casting development: Solidification of aluminium alloy A356. Mater. Sci. Technol. 2004, 20, 194–200. [Google Scholar] [CrossRef]
- Uludag, M.; Çetin, R.; Dispinar, D.; Tiryakioglu, M. Characterization of the effect of Melt Treatments on Melt Quality in Al-7wt %Si-Mg Alloys. Metals 2017, 7, 157. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.D.; Cockcroft, S.L. Modeling of microporosity formation in A356 aluminum alloy casting. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2006, 37, 1075–1085. [Google Scholar] [CrossRef]
- Loizaga, A.; Niklas, A.; Fernandez, A.I. Thermal analysis applied to estimation of solidification kinetics of Al–Si aluminium alloys. Int. J. Cast Met. Res. 2009, 22, 345–352. [Google Scholar] [CrossRef] [Green Version]
- Carina, M.; Osvaldo, F.; Olga, G. Fluidity of Sn-based eutectic solder alloys. J. Mater. Sci. Mater. Electron. 2015, 26, 9478–9483. [Google Scholar]
- Zhang, A. Determination of the interfacial heat transfer coefficient at the metal-sand mold interface in low pressure sand casting. Exp. Therm. Fluid Sci. 2017, 88, 472–482. [Google Scholar] [CrossRef]
- Pan, A.; Wang, J.; Zhang, X. Prediction of Melting Temperature and Latent Heat for Low-melting Metal PCMs. Rare Met. Mater. Eng. 2016, 45, 874–880. [Google Scholar] [CrossRef]
- Jin, X.; Huo, H.Y.; Shi, X. Comparison of two numerical heat transfer models for phase change material board. Appl. Therm.Eng. 2018, 128, 1331–1339. [Google Scholar] [CrossRef]
- Sun, Y.C.; Zheng, H.L.; Zhang, N. A Modified Method of Latent Heat Release during Al-Si Alloy Solidification. ISIJ Int. 2010, 50, 1875–1887. [Google Scholar] [CrossRef] [Green Version]
- Reilly, C.; Duan, J.; Yao, L. Process Modeling of Low-Pressure Die Casting of Aluminum Alloy Automotive Wheels. JOM 2013, 65, 1111–1121. [Google Scholar] [CrossRef]
- Tavakoli, R. Smooth modeling of solidification based on the latent heat evolution approach. Int. J. Adv. Manuf. Technol. 2017, 88, 3041–3052. [Google Scholar] [CrossRef]
- Wang, K.Y. Estimation of heat transfer coefficient and phase transformation latent heat by modified pattern search method. Int. Commun. Heat Mass Transf. 2015, 68, 14–19. [Google Scholar] [CrossRef]
- Qin, X.Y.; Su, Y.; Chen, J. Finite element analysis for die casting parameters in high-pressure die casting process. China Found. 2019, 16, 272–276. [Google Scholar] [CrossRef] [Green Version]
- Han, Z.Q.; Zhu, W.; Liu, B.C. A thermomechanical finite element model for simulating the solidification process of squeeze casting. Int. J. Cast Met. Res. 2009, 22, 119–122. [Google Scholar] [CrossRef]
- Wang, D.; Li, N.; Luo, M. One visualization simulation operation system for distal femoral fracture. Medicine 2017, 96, e7770. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Luo, S.; Zhu, M. Numerical Simulation of Dendritic Growth of Continuously Cast High Carbon Steel. Metall. Mater. Trans. A 2015, 46, 396–406. [Google Scholar] [CrossRef]
- Pan, F.; Steve, C.; Daan, M. Examination and Simulation of Silicon Macrosegregation in A356 Wheel Casting. Metals 2018, 8, 503–516. [Google Scholar]
- Bakhtiyarov, S.I.; Overfelt, R.A.; Teodorescu, S.G. Electrical and thermal conductivity of A319 and A356 aluminum alloys. J. Mater. Sci. 2001, 36, 4643–4648. [Google Scholar] [CrossRef]

| No. | Model Application Conditions | Calculation Formula after Temperature Rise |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
| Material | Properties | Value | Unit |
|---|---|---|---|
| A356 | Thermal conductivity of solid | 70 | W/m/K |
| Thermal conductivity of liquid | 159.6 | W/m/K | |
| Specific heat | 1150 | J/kg/K | |
| Latent heat | 397,500 | J/kg | |
| Density of solid | 2685 | Kg/m3 | |
| Density of liquid | 2540 | Kg/m3 | |
| Viscosity of the liquid | 0.0014 | Kg/m/s | |
| Partition coefficient of Si | 0.13 | - | |
| Partition coefficient of Mg | 0.48 | - | |
| steel-H13 | Density | 7800 | Kg/m3 |
| Specific heat | 460 | J/kg/K | |
| Thermal conductivity | 24.4 | W/m/K |
| Temperature (°C) | 25 | 107 | 200 | 340 | 400 | 579 | 700 |
|---|---|---|---|---|---|---|---|
| Thermal Conductivity [] | 159.6 | - | 168.2 | - | 229.3 | - | 103.7 |
| Enthalpy (J) | - | 7.3 × 108 | - | 1.43 × 108 | - | 1.69 × 108 | - |
| Temperature (°C) | 100 | 200 | 300 | 500 | 700 |
|---|---|---|---|---|---|
| Thermal Conductivity [] | 20.1 | 20.2 | 22.7 | 23.4 | 24.3 |
| Specific heat [] | 468.2 | 525.5 | 560.4 | 612.3 | 685.5 |
| Sampling Time(s) | A1 (°C) | A2 (°C) | A3 (°C) | A4 (°C) | A Mean (°C) |
|---|---|---|---|---|---|
| 5 | 727 | 732 | 730 | 735 | 731 |
| 10 | 711 | 716 | 715 | 718 | 715 |
| 15 | 700 | 702 | 702 | 704 | 702 |
| 20 | 676 | 680 | 683 | 685 | 681 |
| 25 | 647 | 651 | 650 | 656 | 651 |
| 30 | 621 | 625 | 625 | 629 | 625 |
| 40 | 606 | 607 | 607 | 612 | 608 |
| 50 | 581 | 583 | 588 | 588 | 585 |
| 60 | 578 | 579 | 580 | 583 | 580 |
| 70 | 575 | 574 | 574 | 577 | 575 |
| 80 | 568 | 570 | 572 | 570 | 570 |
| 90 | 559 | 563 | 562 | 564 | 562 |
| 100 | 551 | 553 | 548 | 548 | 550 |
| 110 | 520 | 526 | 526 | 528 | 525 |
| 120 | 483 | 485 | 487 | 485 | 485 |
| 130 | 471 | 473 | 469 | 467 | 470 |
| 140 | 459 | 460 | 456 | 453 | 457 |
| 150 | 447 | 450 | 445 | 446 | 447 |
| 160 | 436 | 440 | 435 | 437 | 437 |
| 170 | 429 | 431 | 426 | 426 | 428 |
| 180 | 421 | 420 | 420 | 423 | 421 |
| 190 | 419 | 417 | 416 | 416 | 417 |
| 200 | 417 | 416 | 414 | 413 | 415 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Q.; Xiao, Y.; Zhang, T.; Zhu, P.; Ma, W.; Liu, J. Numerical Simulation of Latent Heat of Solidification for Low Pressure Casting of Aluminum Alloy Wheels. Metals 2020, 10, 1024. https://doi.org/10.3390/met10081024
Zheng Q, Xiao Y, Zhang T, Zhu P, Ma W, Liu J. Numerical Simulation of Latent Heat of Solidification for Low Pressure Casting of Aluminum Alloy Wheels. Metals. 2020; 10(8):1024. https://doi.org/10.3390/met10081024
Chicago/Turabian StyleZheng, Qingchun, Yinhong Xiao, Tao Zhang, Peihao Zhu, Wenpeng Ma, and Jingna Liu. 2020. "Numerical Simulation of Latent Heat of Solidification for Low Pressure Casting of Aluminum Alloy Wheels" Metals 10, no. 8: 1024. https://doi.org/10.3390/met10081024
APA StyleZheng, Q., Xiao, Y., Zhang, T., Zhu, P., Ma, W., & Liu, J. (2020). Numerical Simulation of Latent Heat of Solidification for Low Pressure Casting of Aluminum Alloy Wheels. Metals, 10(8), 1024. https://doi.org/10.3390/met10081024





