Cluster-Related Phenomena in the Properties and Transformations of Transition Metal-Based Glassy Alloys
Abstract
:1. Introduction
2. Cluster Formation and Their Influence on Properties
2.1. Origin and Role of Cluster Formation and Glass-Forming Tendency in Supercooled Metallic Liquids
2.2. Some Structural and Bonding Aspects of the Investigated Glass-Forming Melts and the Relaxation Mechanism during Supercooling
2.3. Temperature Dependence of Viscosity and Cluster Formation Tendency in Supercooled Liquids
2.4. Compositional Effects as Cluster Manifestation in Thermal and Magnetic Properties of Fe(TM)-B Glasses
- I.
- am-FeB → α-Fe + am’-Fe75B25 (composition of the remaining amorphous phase)
- II.
- am’-Fe75B25 → Fe3B
- III.
- Fe3B → α-Fe + Fe2B.
2.5. Cluster Manifestation in the Host Metal Replacement
- a.
- Affinity of T metals to the metalloid (the differences can be inferred from the appropriate heat of formation between the T elements and Fe-borides, respectively);
- b.
- An additional source of cluster formation is the already discussed entrapment of γ-type phase reminiscences.
2.6. Fluctuating Exchange Interaction in Fe-B Glasses, Induced by Third Metallic Element Additions
2.7. Cluster Manifestation (as γ-Phase Reminiscence) in the Enthalpy and Curie Temperature Relaxation of Fe- and Fe-Ni-Based Glasses Metallurgical Approach to the Interpretation
2.8. Irreversible and Reversible Enthalpy and TCam Relaxation
2.9. Irreversible and Reversible TCam Shift
- -
- ΔTCam between the thick and thin Fe40Ni40 (SiB)20 samples slowly decreases during the repeated heat treatments and measurements. In the thinner samples, relaxation is more rapid, and an irreversible TCam increase in both types of samples can be detected during the measuring runs.
- -
- ΔTCam arises partially from the measurement process (an irreversible increase when heating the samples for the TCam determination). This phenomenon is known as “self-relaxation”, which is especially detectable when TCam is high. This is typically the case for the Fe40Ni40(SiB)20 samples.
- -
- -
- A similar irreversible TCam increase was detected for other FeNiB samples with various Ni-contents during the first measuring run or in the initial period of isothermal heat treatments (see Figure 15).
2.10. Imprint of the γ ↔ α Allotropic Transition as Background of the TCam Shift in Fe(Ni) Glasses during Liquid Quenching and Subsequent Isothermal Heat Treatments
2.11. Irreversible TCam Changes in Fe(Ni)-Based Samples
2.12. Curie Temperature Shift Induced by Low Temperature Storage
2.13. Stress Level Change during Cryo-Treatments
- -
- Stable structural features are formed in the samples due to low temperature storage. These features also modify the response of the samples during the consecutive heat treatments.
- -
- The LN treated samples exhibit much higher atomic mobility during the first period of isothermal heat treatments. The response of the individual physical properties of the samples to the LN treatment is highly composition-dependent.
2.14. Cluster-Phenomena in the Mechanism of the Amorphous-Nanocrystalline Transformation
2.15. Mechanism of Hydrogen Absorption and Related Cluster Phenomena in TM-Based Glasses
- ⮚
- The manifestation of a H-induced stress state in amorphous, and nanocrystalline alloys, (interaction between the dissolved H-atoms and the quenched-in cluster structure in TM-based glasses).
- ⮚
- H-induced micro-phase separation in TM-based metallic glasses.
2.16. Possible Model for the Metallurgical Description of the Origin of H Trapping Sites in Fe-Based Glasses
2.17. Influence of H Absorption on the Curie Temperature: Combined Effects Arising from Simultaneous H Absorption–Desorption and Self-Relaxation during the Tcam Measurement
2.18. The Role of H Absorption in Ni-Containing Glasses (Combined Compositional Effects)
2.19. Micro-Phase Separation in the Amorphous State
3. Summary
- -
- An extraordinary concentration dependence of TCam and μFe in binary Fe-B glasses: in contrast to the expected increase of TCam and μFe with decreasing metalloid content, an opposite tendency is observed in binary Fe-B glasses, which hints to an increasing fraction of quenched-in fcc environments in the as-quenched samples. This is the consequence of a local decrease of interatomic distances between Fe-Fe atoms, which can be inferred from the Bethe–Slater correlation. As a consequence, TCam increases during the first period of structural relaxation due to the fcc → bcc rearrangements on a short-range order scale. When Fe is partially replaced by Ni (5 at.%) in hypo-eutectic FeB, this tendency is modified by the magnetic moment of the Ni atoms.
- -
- The quenched-in fcc-like environments (γ-reminiscence) give a significant contribution to the relaxation and crystallization enthalpy (ΔHcryst). An increasing contribution to the total crystallization enthalpy (ΔHcryst) can be detected in the hypo-eutectic concentration range of Fe-B glasses, which is supported by the quenching-rate dependence of the irreversible heat of relaxation and the crystallization enthalpy (ΔHcryst).
- -
- The tendency of γ (fcc) entrapment is even more pronounced for TCam, and the enthalpy relaxation of various Fe(Ni)-based glasses (quenching-rate dependence of TCam) indicates that less-relaxed structures contain an increasing number of fcc-like clusters with decreasing strength of the net ferromagnetic coupling in the as-quenched state.
- -
- Other well-known relaxation types are a reversible TCam shift (inverse relation between the temperature of TCam in FeNi-based systems) and the role of cryogenic treatment on the direction of the TCam shift. These observations were successfully explained assuming the co-existence of fcc and bcc cluster types in Fe(Ni)- based glasses.
- -
- Low temperature treatments at 77 K result in stable structural features in the samples, which can be explained by a non-diffusive mechanism, similar as is it well known for residual austenite formation in steel metallurgy. It can be regarded as completion of glass transition, whereby additional fcc clusters are formed via non-diffusive, stress-induced, cluster-level transformations, in which cooperative atomic displacements are involved.
- -
- The significance of cluster phenomena is proposed in the mechanism of the initial (nucleation) stage of the amorphous-nanocrystalline transformation in FINEMET-type precursors. It is demonstrated that not solely nanocrystalline grain dimensions but also the special nucleation process plays a significant role in the development of magnetic ultrasoftness in this alloy. Eutectoid decomposition (annihilation) of γ (fcc-like) clusters leads to α-Fe (nanograin) nucleation. The separation of Cu atoms outside the α-Fe grains is the consequence of the insolubility of Cu atoms in the bcc α-Fe nuclei.
- -
- The interaction between the glassy matrix and dissolved hydrogen has been studied during absorption–desorption cycles. The H-induced cluster formation tendency depends on the thermodynamic driving force for H dissolution. Like several chemical properties of metallic glasses, the ability of hydrogen absorption is also inherited from the metallic host. As a result, the solubility of hydrogen is strongly restricted in endothermic types of dissolution reactions. In spite of this, indirect effects (the change in physical properties) can be large, arising mainly from the resulting change in the stress level. Consequently, stress-sensitive properties like coercivity (Hc), permeability (μr) saturation magnetostriction (λs) or the anisotropy (K) change significantly during H charging or discharging. This effect is mostly restricted to the residence time of H atoms in the glassy matrix, i.e., the property changes are reversible. The presence of fcc-type clusters contributes to the activity of hydrogen. When these clusters are eliminated by heat treatment, the properties will be insensitive to H dissolution, i.e., the preferential H trapping sites in the as-quenched Fe-based glasses are coupled with the quenched-in fcc clusters.
- -
- We revealed the role of absorbed H atoms on the sign of ΔTCam in Fe-based glasses. The interpretation of the results is based on the Bethe–Slater concept, which was originally developed for understanding the correlation between atomic distances and the strength, as well as the sign of exchange interaction in 3d transition metals.
- -
- H-induced micro-phase separation as a sterically extended form of cluster formation has been detected in several metallic glasses, which consist of metallic components exhibiting exothermic and endothermic dissolution enthalpies during H dissolution. In such (ternary) alloys, repeated absorption–desorption cycles result in micro-phase separation in the amorphous state, whereby local concentration fluctuations of the components develop as a consequence of the relative hydride phase stability of the individual components (described by the hydride phase Ellingham diagram) in the crystalline phases.
- -
- In-situ resistivity measurements show that such phase separations are irreversible, which also suggests that this atomic mechanism may be related to poisoning and deterioration of the H storage capacity of these alloys. The same process is considered to be responsible for the volume activation in several H storage absorber alloys.
Author Contributions
Funding
Conflicts of Interest
References
- Andres, R.; Averback, R.S.; Brown, W.; Brus, L.; Goddard, W.; Kaldor, A.; Louie, S.; Moscovits, M.; Peercy, P.; Riley, S. Research opportunities on clusters and cluster-assembled materials-A Department of Energy, Council on Materials Science Panel Report. J. Mater. Res. 1989, 4, 704–736. [Google Scholar] [CrossRef]
- Siegel, R.W. Cluster Assembly of Nanophase Materials. In Materials Science and Technology; Cahn, R.W., Haasen, P., Kramer, E.J., Eds.; VCH Verlag GmbH: Weinheim, Germany, 1991; pp. 585–627. [Google Scholar]
- Gleiter, H. Nanostructured materials: Basic concepts and microstructure. Acta Mater. 2000, 48, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Siegel, R.W. Nanostructured materials -mind over matter. Nanostruct. Mater. 1993, 3, 1–18. [Google Scholar] [CrossRef]
- Kappes, M.M.; Schumacher, E.J. Metal Clusters: Between the Individual and Collectivity. Z. Phys. Chem. 1988, 156, 23–40. [Google Scholar] [CrossRef]
- Goldstein, A.; Echer, C.; Alivisatos, A. Melting in Semiconductor Nanocrystals. Science 1992, 256, 1425–1427. [Google Scholar] [CrossRef]
- Gates, B.C.; Guczi, L.; Knözinger, H. Metal Clusters in Catalysis; Elsevier Science Publisher: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Veprek, S.; Jilek, M. Super- and ultrahard nanacomposite coatings: Generic concept for their preparation, properties and industrial applications. Vacuum 2002, 67, 443–449. [Google Scholar] [CrossRef]
- Siegel, R.W.; Eastman, J.A. Synthesis, Characterization, and Properties of Nanophase Ceramics. In Material Research Society Symposia Proceedings; McCandlish, L.E., Polk, D.E., Siegel, R.W., Kear, B.H., Eds.; Cambridge University Press: San Diego, CA, USA, 1989; pp. 3–14. [Google Scholar]
- Turnbull, D. Metastable structures in metallurgy. Metall. Trans. B 1981, 12, 217–230. [Google Scholar] [CrossRef]
- Kauzmann, W. The Nature of the Glassy State and the Behavior of Liquids at Low Temperatures. Chem. Rev. 1948, 43, 219–256. [Google Scholar] [CrossRef]
- Bakai, A.S. The polycluster concept of amorphous solids. In Glassy Metals III: Amorphization Techniques, Catalysis, Electronic and Ionic Structure; Beck, H.G.H.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 209–255. [Google Scholar]
- Noskova, N.I.; Vildanova, N.F.; Potapov, A.P.; Glazer, A.A. The structure and properties of Fe-Co-Si-B and Fe-Si-B amorphous alloys. In Proceedings of the 12th European Crystallographic Meeting, Sverdlovsk, Russia, 20–29 August 1989; pp. 301–309. [Google Scholar]
- Hirotsu, Y.; Uehara, M.; Ueno, M. Microcrystalline domains in amorphous Pd77.5Cu6Si16.5 alloys studied by high-resolution electron microscopy. J. Appl. Phys. 1986, 59, 3081–3086. [Google Scholar] [CrossRef]
- Gaskell, P.H. High resolution electron microscopy of amorphous alloys. In Proceedings of the 4th International Conference on Rapidly Quenched Metals, Sendai, Japan, 24–28 August 1981; Gakkai, N.K., Ed.; Japan Institute of Metals: Sendai, Japan, 1981; pp. 439–442. [Google Scholar]
- Piller, J.; Haasen, P. Atom probe field ion microscopy of a FeNiB glass. Acta Metall. 1982, 30, 1–8. [Google Scholar] [CrossRef]
- Greer, A.L. Thermodynamics of undercooled liquids. J. Less Common Met. 1988, 145, 131–144. [Google Scholar] [CrossRef]
- Battezzati, L.; Garrone, E. On the approximation of the free energy of undercooled glass-forming metallic melts. Z. Metallkd. 1984, 75, 305–310. [Google Scholar]
- Dubey, K.; Ramachandrarao, P. On the free energy change accompanying crystallisation of undercooled melts. Acta Metall. 1984, 32, 91–96. [Google Scholar] [CrossRef]
- Jones, D.; Chadwick, G. The experimental determination of the kinetics of solid-liquid interfaces in transparent materials using temperature-gradient zone migration. Philos. Mag. A 1971, 24, 1327–1345. [Google Scholar] [CrossRef]
- Angell, C.A.; Ngai, K.L.; McKenna, G.B.; McMillan, P.F.; Martin, S.W. Relaxation in glassforming liquids and amorphous solids. J. Appl. Phys. 2000, 88, 3113–3157. [Google Scholar] [CrossRef] [Green Version]
- Luborsky, F.E. Applications-oriented magnetic properties. In Amorphous Metallic Alloys; Luborsky, F.E., Ed.; Butterworth-Heinemann: London, UK, 1983; pp. 360–380. [Google Scholar]
- Krebs, H. Electrical conductivity and chemical bonding in crystalline, glassy and liquid phases. J. Non-Cryst. Solids 1969, 1, 455–473. [Google Scholar] [CrossRef]
- Zielinski, P.G.; Matyja, H. Influence of liquid structure on glass forming tendency. In Proceedings of the 2nd International Conference on Rapidly Quenched Metals, Cambridge, MA, USA, 17–19 November 1975; Grant, N.J., Giessen, B.C., Eds.; Massachusetts Institute of Technology: Cambridge, MA, USA, 1975; pp. 237–248. [Google Scholar]
- Sommer, F. Association model for the description of the thermodynamic functions of liquid alloys. I.-Basic concepts. Z. Metallkd. 1982, 73, 72–76. [Google Scholar]
- Inoue, A. Bulk amorphous alloys. In Non-Equilibrium Processing of Materials; Suryanarayana, C., Ed.; Pergamon Materials: New York, NY, USA, 1999; pp. 375–415. [Google Scholar]
- Predel, B. Thermodynamic Stability of Amorphous Alloys. Key Eng. Mater. 1990, 40, 17–38. [Google Scholar] [CrossRef]
- Finney, J. Random packings and the structure of simple liquids. I. The geometry of random close packing. Proc. R. Soc. A Math. Phys. Sci. 1970, 319, 479–493. [Google Scholar]
- Pauling, L. The Nature of the Chemical Bond; Cornell University Press Ithaca: New York, NY, USA, 1960. [Google Scholar]
- Miedema, A.R.; De Boer, F.R.; De Chatel, P.F. Empirical description of the role of electronegativity in alloy formation. J. Phys. F Met. Phys. 1973, 3, 1558–1576. [Google Scholar] [CrossRef]
- Hermann, H.; Mattern, N.; Matz, W. Magnetic and structural properties of rapidly quenched iron–boron metallic glasses. Phys. Stat. Sol. B 1987, 140, 581–588. [Google Scholar] [CrossRef]
- Dubois, J.-M. Topological instability of metallic lattices and glass formation. J. Less Common Met. 1988, 145, 309–326. [Google Scholar] [CrossRef]
- Frank, F.C. Supercooling of liquids. Proc. R. Soc. A Math. Phys. Sci. 1952, 215, 43–46. [Google Scholar]
- Angell, C.A. Structural instability and relaxation in liquid and glassy phases near the fragile liquid limit. J. Non-Cryst. Solids 1988, 102, 205–221. [Google Scholar] [CrossRef]
- Kholodenko, A.L.; Douglas, J.F. Generalized Stokes-Einstein equation for spherical particle suspensions. Phys. Rev. E 1995, 51, 1081. [Google Scholar] [CrossRef]
- DeBenedetti, P.G.; Stillinger, F.H. Supercooled liquids and the glass transition. Nature 2001, 410, 259. [Google Scholar] [CrossRef]
- Debenedetti, P.G. Metastable Liquids: Concepts and Principles; Princeton University Press: Princeton, NJ, USA, 1996. [Google Scholar]
- Köster, U.; Janlewing, R. Fragility parameter and nanocrystallization of metallic glasses. Mater. Sci. Eng. A 2004, 375, 223–226. [Google Scholar] [CrossRef]
- Johari, G.P. Intrinsic mobility of molecular glasses. J. Chem. Phys. 1973, 58, 1766–1770. [Google Scholar] [CrossRef]
- Ediger, M.D. Spatially heterogeneous dynamics in supercooled liquids. Annu. Rev. Phys. Chem. 2000, 51, 99–128. [Google Scholar] [CrossRef] [Green Version]
- Popel, P.; Sidorov, V. Microheterogeneity of liquid metallic solutions and its influence on the structure and properties of rapidly quenched alloys. Mater. Sci. Eng. A 1997, 226, 237–244. [Google Scholar] [CrossRef]
- Mel’Cuk, A.I.; Ramos, R.A.; Gould, H.; Klein, W.; Mountain, R.D. Long-Lived Structures in Fragile Glass-Forming Liquids. Phys. Rev. Lett. 1995, 75, 2522–2525. [Google Scholar] [CrossRef]
- Casalini, R.; Ngai, K.L. Structural dependence of fast relaxation in glass-forming substances and correlation with the stretch exponent of the slow structural α-relaxation. J. Non-Cryst. Solids 2001, 293, 318–326. [Google Scholar] [CrossRef]
- Teoh, W.; Teoh, N.; Arajs, S. Electrical Resistivity and Crystallization of Amorphous Metglas 2826 and Metglas 2826A. In Amorphous Magnetism II; Levy, R.A., Hasegawa, R., Eds.; Springer: Boston, MA, USA, 1977; pp. 327–333. [Google Scholar]
- Rao, K.V. Electrical transport properties. In Amorphous Metallic Alloys; Luborsky, F.E., Ed.; Butterworth-Heinemann: London, UK, 1983; pp. 401–431. [Google Scholar]
- Mizutani, U. Electronic structure and electron transport properties of liquid metals, amorphous metals and quasicrystals. In Introduction to the Electron Theory of Metals; Cambridge University Press: Cambridge, UK, 2001; pp. 451–515. [Google Scholar]
- Vincze, I.; Boudreaux, D.; Tegze, M. Short-range order in Fe-B metallic glass alloys. Phys. Rev. B 1979, 19, 4896–4900. [Google Scholar] [CrossRef]
- Gaskell, P.H. Similarities and differences between dense-random-packed, stereochemically defined and polytetrahedral models for amorphous alloys. In Proceedings of the 4th International Conference on Rapidly Quenched Metals, Sendai, Japan, 24–28 August 1981; Japan Institute of Metals: Sendai, Japan, 1981; pp. 247–252. [Google Scholar]
- Dimitrov, V. Theory of fluidity of liquids, glass transition, and melting. J. Non-Cryst. Solids 2006, 352, 216–231. [Google Scholar] [CrossRef]
- Lovas, A.; Kiss, L.; Sommer, F. Hardness and thermal stability of Fe-Cr-metalloid glasses. J. Non-Cryst. Solids 1995, 192, 608–611. [Google Scholar] [CrossRef]
- Kemény, T.; Vincze, I.; Fogarassy, B.; Arajs, S. Structure and crystallization of Fe-B metallic glasses. Phys. Rev. B 1979, 20, 476–488. [Google Scholar] [CrossRef]
- Totten, G.E.; Colas, R. Encyclopedia of Iron, Steel, and Their Alloys; CRC Press: London, UK, 2016. [Google Scholar]
- Potocky, L.; Novak, L.; Kisdi, K.E.; Lovas, A.; Takacs, J. Temperature dependence of the coercive force of amorphous Fe-B alloys. Acta Phys. Slov. 1979, 29, 281–287. [Google Scholar]
- Lovas, A.; Kisdi-Koszo, E.; Potocký, L.; Novak, L. Effect of processing conditions on physical properties of transition metal-metalloid metallic glasses. J. Mater. Sci. 1987, 22, 1535–1546. [Google Scholar] [CrossRef]
- O’Handley, R.C. Fundamental magnetic properties. In Amorphous Metallic Alloys; Luborsky, F.E., Ed.; Butterworth-Heinemann: London, UK, 1983; pp. 257–282. [Google Scholar]
- Leslie, W.C.; Hornbogen, E. Physical metallurgy of steels. In Physical Metallurgy, 4th ed.; Cahn, R.W., Haasen, P., Eds.; North-Holland: Oxford, UK, 1996; pp. 1555–1620. [Google Scholar]
- Kokosza, A.; Pacyna, J. Effect of retained austenite on the fracture toughness of tempered tool steel. Arch. Mater. Sci. Eng. 2008, 31, 87–92. [Google Scholar]
- Rzepski, J.; Quivy, A.; Calvayrac, Y.; Bigot, J.; Chevalier, J.P. Retained γFe in nominality amorphous ferrous soft magnetic glasses. J. Non-Cryst. Solids 1984, 63, 419–423. [Google Scholar] [CrossRef]
- Lovas, A.; Kisdi-Koszó, É.; Varga, L.; Kovác, J. Structural memory effects in rapidly quenched iron-boron-based glassy alloys. Key Eng. Mater. 1993, 81, 607–612. [Google Scholar] [CrossRef]
- Bán, K.; Kováč, J.; Novák, L. The study of Curie point shifts in Fe (Ni)-based glasses induced by hydrogen absorption and low temperature storage. In Proceedings of the 13th International Conference on Rapidly Quenched and Metastable Materials, Dresden, Germany, 24–29 August 2008; p. 012013. [Google Scholar]
- Hasegawa, R.; Ray, R. Iron-boron metallic glasses. J. Appl. Phys. 1978, 49, 4174–4179. [Google Scholar] [CrossRef]
- Wohlfarth, E.P. Itinerant electron model of magnetic properties. In Amorphous Metallic Alloys; Luborsky, F.E., Ed.; Butterworth-Heinemann: London, UK, 1983; pp. 283–299. [Google Scholar]
- Jiles, D. Introduction to magnetism and magnetic materials; CRC Press: New York, NY, USA, 2015. [Google Scholar]
- Konczos, G.; Kisdi-Koszó, É.; Lovas, A.; Kajcsos, Z.; Potocký, L.; Daniel-Szabó, J.; Kováč, J.; Novák, L. Correlation between magnetic properties and density of Fe-TB (T= W, Cr) glassy alloys. J. Magn. Magn. Mater. 1984, 41, 121–124. [Google Scholar] [CrossRef]
- Lovas, A. New approach to the phenomenology of amorphous curie-point relaxation. Acta Phys. Pol. A 2010, 118, 770. [Google Scholar] [CrossRef]
- Lovas, A.; Kisdi-Koszó, É.; Konczos, G.; Potocký, L.; Vértesy, G. Casting of ferromagnetic amorphous ribbons for electronic and electrotechnical applications. Philos. Mag. B 1990, 61, 549–565. [Google Scholar] [CrossRef]
- Cohen, M.H.; Grest, G. Liquid-glass transition, a free-volume approach. Phys. Rev. B 1979, 20, 1077–1098. [Google Scholar] [CrossRef]
- Egami, T. Magnetic amorphous alloys: Physics and technological applications. Rep. Prog. Phys. 1984, 47, 1601–1640. [Google Scholar] [CrossRef]
- Von Goldbeck, O.K. Iron—Platinum Fe—Pt. In IRON—Binary Phase Diagrams; Springer: Berlin/Heidelberg, Germany, 1982; pp. 91–94. [Google Scholar]
- Swartzendruber, L.; Itkin, V.; Alcock, C. The Fe-Ni (iron-nickel) system. J. Phase Equilib. 1991, 12, 288–312. [Google Scholar] [CrossRef]
- Greer, A.L. Structural relaxation and atomic transport in amorphous alloys. In Rapidly Solidified Alloys: Processes-Structures-Properties-Applications; Liebermann, H.H., Ed.; Marcel Dekker, Inc.: New York, NY, USA, 1993; p. 269. [Google Scholar]
- Hasegawa, R.; O’Handley, R. Soft magnetic properties of metallic glasses—Recent developments. J. Appl. Phys. 1979, 50, 1551–1556. [Google Scholar] [CrossRef]
- Hasegawa, R. Soft magnetic properties of metallic glasses. J. Magn. Magn. Mater. 1984, 41, 79–85. [Google Scholar] [CrossRef]
- Ström-Olsen, J.; Brüning, R.; Altounian, Z.; Ryan, D. Structural relaxation in metallic glasses. J. Less Common. Met. 1988, 145, 327–338. [Google Scholar] [CrossRef]
- Van den Beukel, A. On the kinetics of structural relaxation in metallic glasses. Key Eng. Mater. 1993, 81, 3–16. [Google Scholar] [CrossRef]
- Sun, Y.; Peng, S.-X.; Yang, Q.; Zhang, F.; Yang, M.-H.; Wang, C.-Z.; Ho, K.-M.; Yu, H.-B. Predicting Complex Relaxation Processes in Metallic Glass. Phys. Rev. Lett. 2019, 123, 105701. [Google Scholar] [CrossRef] [Green Version]
- Berthier, L.; Biroli, G. Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 2011, 83, 587–645. [Google Scholar] [CrossRef]
- Egami, T. Structural relaxation in amorphous alloys-compositional short range ordering. Mater. Res. Bull. 1978, 13, 557–562. [Google Scholar] [CrossRef]
- Tarnoczi, T. Effect of antiferromagnetically coupled species on Curie temperature during relaxation of metallic glasses. Mater. Sci. Eng. A 1991, 133, 200–203. [Google Scholar] [CrossRef]
- Greer, A. Effect of quench rate on the structural relaxation of a metallic glass. J. Mater. Sci. 1982, 17, 1117–1124. [Google Scholar] [CrossRef]
- Gránásy, L.; Lovas, A. The influence of technological conditions on the Curie point relaxation of Fe25Ni55B10Si10 metallic glasses. J. Magn. Magn. Mater. 1984, 41, 113–115. [Google Scholar] [CrossRef]
- Bán, K.; Lovas, A.; Kovác, J.; Novák, L. Cluster manifestations in Fe and Fe-Ni based glassy alloys during their Curie tempera ture relaxation. In Proceedings of the 23rd International Colloquium of Advanced Manufacturing and Repair Technologies in Vehicle Industry, Kollm, Germany, 10–12 May 2006; pp. 67–72. [Google Scholar]
- Pickles, A.; Sucksmith, W. A magnetic study of the two-phase iron-nickel alloys. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1940, 175, 331–344. [Google Scholar]
- Kaufman, L.; Cohen, M. The martensitic transformation in the iron-nickel system. JOM 1956, 8, 1393–1401. [Google Scholar] [CrossRef]
- Lagarec, K.; Rancourt, D.; Bose, S.; Sanyal, B.; Dunlap, R. Observation of a composition-controlled high-moment/low-moment transition in the face centered cubic Fe–Ni system: Invar effect is an expansion, not a contraction. J. Magn. Magn. Mater. 2001, 236, 107–130. [Google Scholar] [CrossRef]
- Varga, B.; Kovac, J. Study of alpha-gamma transformation in two-phase iron-nickel alloys by thermomagnetic measurements. Mater. Sci. Forum 2001, 373, 285–288. [Google Scholar] [CrossRef]
- Lovas, A.; Novák, L.; Kovac, J.; Balla, S. Similarities and differences between the glass forming mechanism in polymers and metallic liquids. Open Macromol. J. 2010, 4, 37–43. [Google Scholar]
- Herlach, D.M. Solidification from undercooled melts. Mater. Sci. Eng. A 1997, 226, 348–356. [Google Scholar] [CrossRef]
- Cacciamani, G.; De Keyzer, J.; Ferro, R.; Klotz, U.E.; Lacaze, J.; Wollants, P. Critical evaluation of the Fe–Ni, Fe–Ti and Fe–Ni–Ti alloy systems. Intermetallics 2006, 14, 1312–1325. [Google Scholar] [CrossRef] [Green Version]
- Bán, K.; Kovac, J.; Novak, L.; Lovas, A. New effects in amorphous Curie-temperature relaxation. Acta Electron. Inform. 2002, 38, 248–251. [Google Scholar]
- Zaichenko, S.; Roth, S.; Glezer, A. Influence of the internal stresses relaxation on magnetic properties of Finemet-type amorphous alloy. J. Magn. Magn. Mater. 2003, 258, 571–573. [Google Scholar] [CrossRef]
- Zaichenko, S.; Perov, N.; Glezer, A.; Gan’shina, E.; Kachalov, V.; Calvo-Dalborg, M.; Dalborg, U. Low-temperature irreversible structural relaxation of amorphous metallic alloys. J. Magn. Magn. Mater. 2000, 215, 297–299. [Google Scholar] [CrossRef]
- Chen, H. Kinetics of low temperature structural relaxation in two (Fe-Ni)-based metallic glasses. J. Appl. Phys. 1981, 52, 1868–1870. [Google Scholar] [CrossRef]
- Ramamurty, U.; Lee, M.; Basu, J.; Li, Y. Embrittlement of a bulk metallic glass due to low-temperature annealing. Scripta Mater. 2002, 47, 107–111. [Google Scholar] [CrossRef] [Green Version]
- Ketov, S.; Sun, Y.; Nachum, S.; Lu, Z.; Checchi, A.; Beraldin, A.; Bai, H.; Wang, W.; Louzguine-Luzgin, D.; Carpenter, M. Rejuvenation of metallic glasses by non-affine thermal strain. Nature 2015, 524, 200–203. [Google Scholar] [CrossRef] [Green Version]
- Lovas, A.; Bán, K.; Kováč, J.; Zagyi, B. New effects and interpretation of amorphous Curie point relaxation in FeNi-based metallic glasses. Czech. J. Phys. 2004, 54, 89–92. [Google Scholar] [CrossRef]
- Bán, K.; Lovas, A.; Kováč, J. Cryogenic effects in the amorphous Curie temperature shift of Fe-based glassy alloys. Czech. J. Phys. 2004, 54, 141–144. [Google Scholar] [CrossRef]
- Kovac, J.; Vehovszky, B.; Novak, L.; Lovas, A. Viscous phenomena in magnetic and thermal properties of Fe-Ni-based glasses induced by cryo-treatments. IEEE Trans. Magn. 2010, 46, 353–356. [Google Scholar] [CrossRef]
- Makino, A.; Inoue, A.; Masumoto, T. Nanocrystalline soft magnetic Fe–M–B (M=Zr, Hf, Nb) alloys produced by crystallization of amorphous phase. Mater. Trans. JIM 1995, 36, 924–938. [Google Scholar] [CrossRef] [Green Version]
- Lu, K. Nanocrystalline metals crystallized from amorphous solids: Nanocrystallization, structure, and properties. Mater. Sci. Eng. R 1996, 16, 161–221. [Google Scholar] [CrossRef]
- Scott, M.G. Crystallization. In Amorphous Metallic Alloys; Luborsky, F.E., Ed.; Butterworth-Heinemann: Oxford, UK, 1983; pp. 144–168. [Google Scholar]
- Lu, K.; Wang, Y.Z.; Wei, W.D.; Li, Y.Y. Electrical resistivity of nanocrystalline Ni-P alloys. In Advances in Cryogenic Materials; Fickett, F.R., Reed, R.P., Eds.; Plenum Press: New York, NY, USA, 1992; Volume 38, pp. 285–292. [Google Scholar]
- Herzer, G. Nanocrystalline soft magnetic alloys. In Handbook of Magnetic Materials; Buschow, K.H.J., Ed.; Elsevier: London, UK, 1997; Volume 10, pp. 415–462. [Google Scholar]
- Lovas, A.; Kiss, L.; Varga, B.; Kamasa, P.; Balogh, I.; Bakonyi, I. Survey of magnetic properties during and after amorphous-nanocrystalline transformation. J. Phys. IV France 1998, 8, 291–298. [Google Scholar] [CrossRef]
- Yamauchi, K.; Yoshizawa, Y. Recent development of nanocrystalline soft magnetic alloys. Nanostruct. Mater. 1995, 6, 247–254. [Google Scholar] [CrossRef]
- Yoshizawa, Y.; Yamauchi, K. Effects of magnetic field annealing on magnetic properties in ultrafine crystalline Fe-Cu-Nb-Si-B alloys. IEEE Trans. Magn. 1989, 25. [Google Scholar] [CrossRef]
- Ayers, J.; Harris, V.; Sprague, J.; Elam, W.; Jones, H. A model for nucleation of nanocrystals in the soft magnetic alloy Fe73. 5Nb3Cu1Si13. 5B9. Nanostruct. Mater. 1997, 9, 391–396. [Google Scholar] [CrossRef]
- Müller, M.; Mattern, N.; Illgen, L. The Influence of the Si/B content on the microstructure and on the magnetic properties of magnetically soft nanocrystalline FeBSi--CuNb alloys. Z. Metallkd. 1991, 82, 895–901. [Google Scholar]
- Hono, K.; Zhang, Y.; Inoue, A.; Sakurai, T. Atom probe studies of nanocrystalline microstructural evolution in some amorphous alloys. Mater. Trans. JIM 1995, 36, 909–917. [Google Scholar] [CrossRef] [Green Version]
- Hono, K.; Hiraga, K.; Wang, Q.; Inoue, A.; Sakurai, T. The microstructure evolution of a Fe73.5Si13.5B9Nb3Cu1 nanocrystalline soft magnetic material. Acta Metall. Mater. 1992, 40, 2137–2147. [Google Scholar] [CrossRef]
- Dai, J.; Wang, Y.G.; Yang, L.; Xia, G.T.; Zeng, Q.S.; Lou, H.B. Thermal dependence of structural and magnetic properties in an amorphous Fe-Si-B-Cu alloy. J. Alloys Compd. 2017, 695, 1266–1270. [Google Scholar] [CrossRef]
- Varga, B.; Lovas, A.; Ye, F.; Gu, X.; Lu, K. Pressure dependence of nanocrystallization in amorphous Fe86B14 and Fe85Cu1B14 alloys. Mater. Sci. Eng. A 2000, 286, 193–196. [Google Scholar] [CrossRef]
- Kisdi-Koszó, É.; Lovas, A. Clustering in amorphous alloys and Its connection with the nanocrystalline state. Key Eng. Mater. 1993, 81, 209–214. [Google Scholar] [CrossRef]
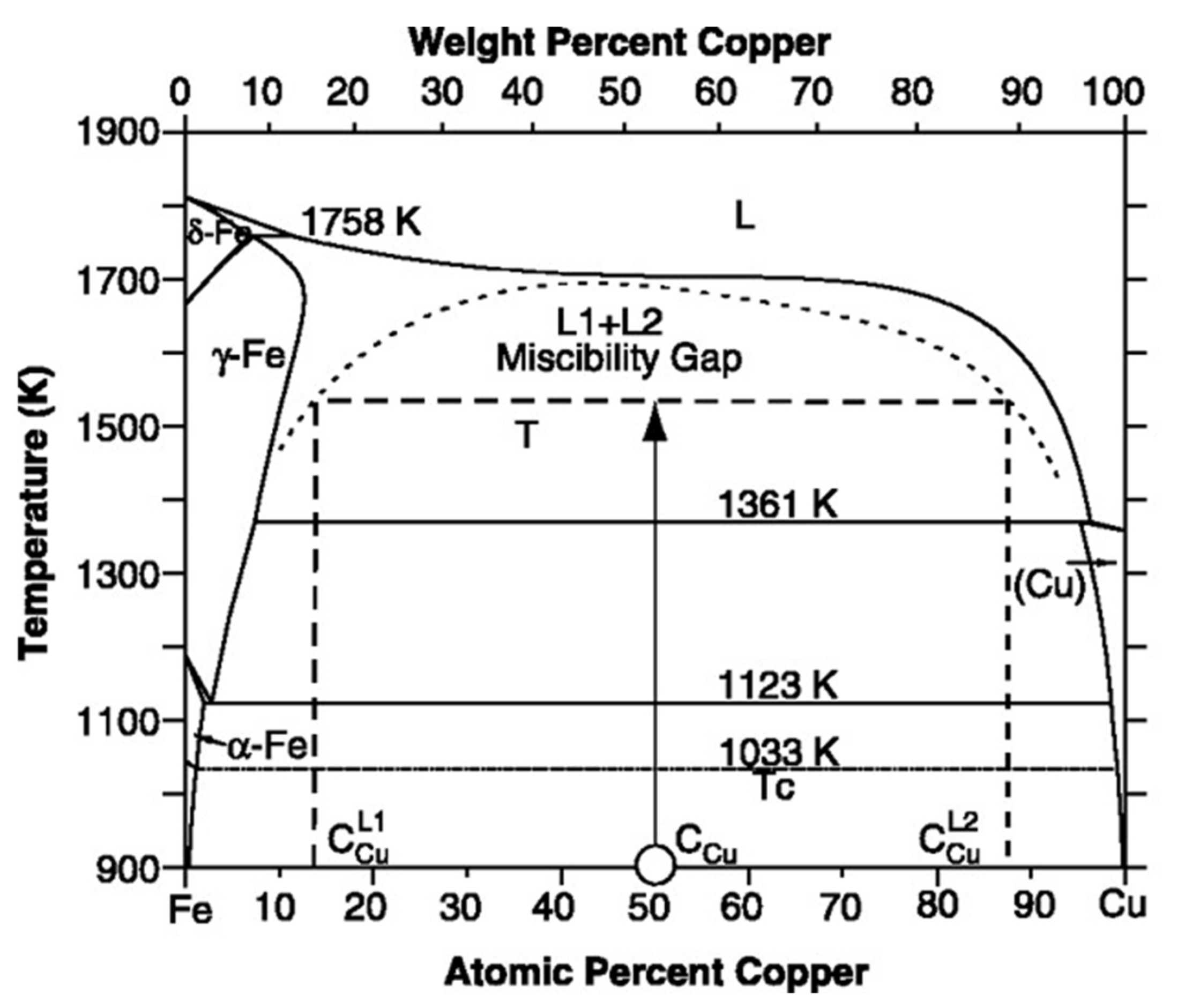
- Chen, Y.; Liu, F.; Yang, G.; Xu, X.Q.; Zhou, Y.H. Rapid solidification of bulk undercooled hypoperitectic Fe–Cu alloy. J. Alloys Compd. 2007, 427, L1–L5. [Google Scholar] [CrossRef]
- Hoselitz, K. The saturation magnetization of some substituted Fe-Si-B metallic glasses. J. Magn. Magn. Mater. 1982, 26, 106–108. [Google Scholar] [CrossRef]
- Lovas, A.; Kiss, L.; Balogh, I. Saturation magnetization and amorphous Curie point changes during the early stage of amorphous–nanocrystalline transformation of a FINEMET-type alloy. J. Magn. Magn. Mater. 2000, 215, 463–465. [Google Scholar] [CrossRef]
- Lovas, A.; Varga, B.; Kiss, L.F.; Nakonechna, L.; Kalincsák, Z. The evolution of soft magnetic properties and the related density change during amorphous–nanocrystalline transformation. J. Magn. Magn. Mater. 2003, 254–255, 489–491. [Google Scholar] [CrossRef]
- Fast, J.D. Thermodynamics and phase relations. In Interaction of Metals and Gases Philips Technical Library; Eichenauer, W., Ed.; Red Globe Press: London, UK, 1965; Volume 1. [Google Scholar]
- Fukai, Y. Hydrogen in alloys. In The Metal-Hydrogen System; Fukai, Y., Ed.; Springer: Berlin, Germany, 2005; Volume 21, pp. 55–90. [Google Scholar]
- Aoki, K.; Kamachi, M.; Masumoto, T. Thermodynamics of hydrogen absorption in amorphous Zr-Ni alloys. J. Non-Cryst. Solids 1984, 61, 679–684. [Google Scholar] [CrossRef]
- Novák, L.; Lovas, A.; Kiss, L. Change in soft magnetic properties of Fe-based metallic glasses during hydrogen absorption and desorption. J. Appl. Phys. 2005, 98, 043904–043905. [Google Scholar] [CrossRef]
- Novák, L.; Kisdi-Koszó, E.; Duhaj, P. Influence of hydrogenation-dehydrogenation on the magnetic properties of amorphous and nanocrystalline FINEMET alloys. In Proceedings of the 9th International Conference on Rapidly Quenched and Metastable Materials, Bratislava, Slovakia, 25–30 August 1996; pp. 216–219. [Google Scholar]
- Zehringer, R.; Oelhafen, P.; Güntherodt, H.-J.; Yamada, Y.; Mizutani, U. Electronic structure of hydrogenated amorphous Ni-Zr alloys. Mater. Sci. Eng. 1988, 99, 253–256. [Google Scholar] [CrossRef]
- Manchester, F.; Khatamian, D. Mechanisms for activation of intermetallic hydrogen absorbers. Mater. Sci. Forum 1988, 31, 261–296. [Google Scholar] [CrossRef]
- Völkl, J.; Alefeld, G. Diffusion of hydrogen in metals. In Hydrogen in Metals I- Basic Properties; Völkl, G.A., Ed.; Springer: Berlin, Germany, 1978; Volume 28, pp. 321–348. [Google Scholar]
- Novák, L.; Ziman, J.; Kovalaková, M.; Kladivová, M. Hydrogen diffusion in amorphous FeCrB ribbons. Acta Electrotech. Inform. 2012, 12, 72–75. [Google Scholar] [CrossRef]
- Kladivová, M.; Ziman, J.; Novák, L.; Kovalaková, M. Hydrogen diffusion and strain distribution in amorphous Fe-based ribbons. Acta Electrotech. Inform. 2013, 13, 65–69. [Google Scholar] [CrossRef]
- Koval’aková, M.; Novák, L.; Lovas, A.; Kováč, J. Study of influence of chromium admixture on hydrogenation and dehydrogenation of FeB amorphous ribbons. Czech. J. Phys. 2004, 54, 149–152. [Google Scholar] [CrossRef]
- Garaguly, J. Investigation of Hydrogen Absorption-Desorption in Amorphous Alloys via In-Situ Resistance Measurements. Ph.D. Thesis, BME Faculty of Transportation Engineering, MTA Institute for solid State Physics and Optics, Budapest University of Technology and Economics, Budapest, Hungary, 1998. [Google Scholar]
- Novák, L.; Stančáková, A.; Lovas, A.; Bán, K. Hydrogen induced changes of magnetic properties during amorphous-nanocrystalline transformation. Czech. J. Phys. 2004, 54, 201–204. [Google Scholar] [CrossRef]
- Sharma, S.; Banerjee, S.; Jain, A.K. Some correlations for diffusion in amorphous alloys. J. Mater. Res. 1989, 4, 603–606. [Google Scholar] [CrossRef]
- Novák, L.; Bán, K.; Kováč, J.; Lovas, A. Curie temperature changes of Fe-based glassy alloys, induced by electrochemical hydrogen-charging and subsequent discharging. J. Magn. Magn. Mater. 2006, 304, e669–e671. [Google Scholar] [CrossRef]
- Pál, Z.; Lovas, A. Anomalous concentration dependence of amorphous curie temperature and the thermopower in ternary Fe-Cr-B glasses. Acta Phys. Pol. A 2008, 113, 139–142. [Google Scholar] [CrossRef]
- Gerling, R.; Schimansky, F.; Wagner, R. Two-stage embrittlement of amorphous Fe40Ni40P20 resulting from a loss of free volume and phase separation. Acta Metall. 1988, 36, 575–583. [Google Scholar] [CrossRef]
- Huizer, E.; Van Den Beukel, A. Reversible and irreversible length changes in amorphous Fe40Ni40B20 during structural relaxation. Acta Metall. 1987, 35, 2843–2850. [Google Scholar] [CrossRef]
- Russew, K.; Stojanova, L.; Lovas, A.; Konzcos, G. Viscous flow, thermal expansion and phase separation of Fe40Ni40Si6B14 amorphous alloy. Mater. Sci. Eng. A 1991, 133, 532–534. [Google Scholar] [CrossRef]
- Nagy, I.; Bakonyi, I.; Lovas, A.; Tóth-Kádár, E.; Tompa, K.; Hossó, M.; Cziraki, A.; Fogarassy, B. Hydrogen sorption and hydrogen-induced phase separation in a nearly equiatomic Ni-Zr amorphous alloy. J. Less Common. Met. 1991, 167, 283–303. [Google Scholar] [CrossRef]
- Garaguly, J.; Lovas, A.; Cziráki, Á.; Reybold, M.; Takács, J.; Wetzig, K. Reversible and irreversible hydrogen absorption in Ni67- xCuxZr33 glasses monitored by in situ resistivity measurements. Mater. Sci. Eng. A 1997, 226, 938–942. [Google Scholar] [CrossRef]
- Harris, J.; Curtin, W.; Tenhover, M. Universal features of hydrogen absorption in amorphous transition-metal alloys. Phys. Rev. B 1987, 36, 5784–5797. [Google Scholar] [CrossRef]
- Buschow, K.; Bouten, P.; Miedema, A. Hydrides formed from intermetallic compounds of two transition metals: A special class of ternary alloys. Rep. Prog. Phys. 1982, 45, 937–1039. [Google Scholar] [CrossRef]
- Yamada, Y.; Tanaka, K. Electrical resistivity change during hydrogen charging and subsequent heating in Zr–Ni alloy glasses. Trans. JIM 1986, 27, 409–415. [Google Scholar] [CrossRef] [Green Version]
- Tóth, J.; Garaguly, J.; Tompa, K.; Lovas, A.; Varga, L. Hydrogen uptake monitored by resistance change in amorphous Zr33Ni67 alloy. Int. J. Hydrogen Energy 1996, 21, 1039–1040. [Google Scholar] [CrossRef]













































| Annealings | Ms (emu/g) 12 K | Ms (emu/g) 300 K | Hc (mOe) 12 K | Hc (mOe) 300 K |
|---|---|---|---|---|
| as-quenched | 153.1 | 131.3 | - | 102 |
| 400 °C/0.5 h | 154.6 | 135.0 | 83 | 36.6 |
| 450 °C/15 min | 155.1 | 135.5 | 154 | 36.8 |
| 525 °C/4 min | 159.4 | 138.2 | 165.5 | 67.2 |
| 525 °C/1 h | 145.9 | 134.1 | 67.2 | <20 |
| Ionic | Metallic | Covalent | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LiH −176 | |||||||||||||||||
| NaH −117 | MgH2 −75 | (AlH3)x | |||||||||||||||
| KH −117 | CaH2 −176 | ScH2 −201 | TiH2 −126 | VH −59 | CrH 17 | MnH −17 | FeH +34 | CoH +34 | NiH +17 | CuH 21 | GaH6 | GeH4 | AsH3 | ||||
| RbH −109 | SrH2 −188 | YH2 −226 | ZrH2 −163 | NbH −75 | MoH +17 | TcH +50 | RuH +67 | RhH +38 | PdH −38 | InH3 | SnH4 | SbH3 | TeH2 | ||||
| CsH −100 | BaH2 −176 | LaH2 −209 | HfH2 −134 | TaH2 −59 | WH +42 | ReH +92 | OsH +84 | IrH +67 | PtH +17 | T1H3 | PbH4 | BiH3 | PoH2 | ||||
| (Re)H3 | PrH2 −209 | NdH2 −209 | SmH2 −222 | GdH2 −201 | ErH2 −226 | ||||||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lovas, A.; Ramasamy, P.; Szabó, A.; Kováč, J.; Novák, L.; Eckert, J. Cluster-Related Phenomena in the Properties and Transformations of Transition Metal-Based Glassy Alloys. Metals 2020, 10, 1025. https://doi.org/10.3390/met10081025
Lovas A, Ramasamy P, Szabó A, Kováč J, Novák L, Eckert J. Cluster-Related Phenomena in the Properties and Transformations of Transition Metal-Based Glassy Alloys. Metals. 2020; 10(8):1025. https://doi.org/10.3390/met10081025
Chicago/Turabian StyleLovas, Antal, Parthiban Ramasamy, Attila Szabó, Jozef Kováč, Ladislav Novák, and Jürgen Eckert. 2020. "Cluster-Related Phenomena in the Properties and Transformations of Transition Metal-Based Glassy Alloys" Metals 10, no. 8: 1025. https://doi.org/10.3390/met10081025
APA StyleLovas, A., Ramasamy, P., Szabó, A., Kováč, J., Novák, L., & Eckert, J. (2020). Cluster-Related Phenomena in the Properties and Transformations of Transition Metal-Based Glassy Alloys. Metals, 10(8), 1025. https://doi.org/10.3390/met10081025





