Review of Non-Classical Features of Deformation Twinning in hcp Metals and Their Description by Disconnection Mechanisms
Abstract
:1. Introduction
2. Dislocations and Disconnections
2.1. Crystal Dislocation Versus Twin Boundary Dislocation
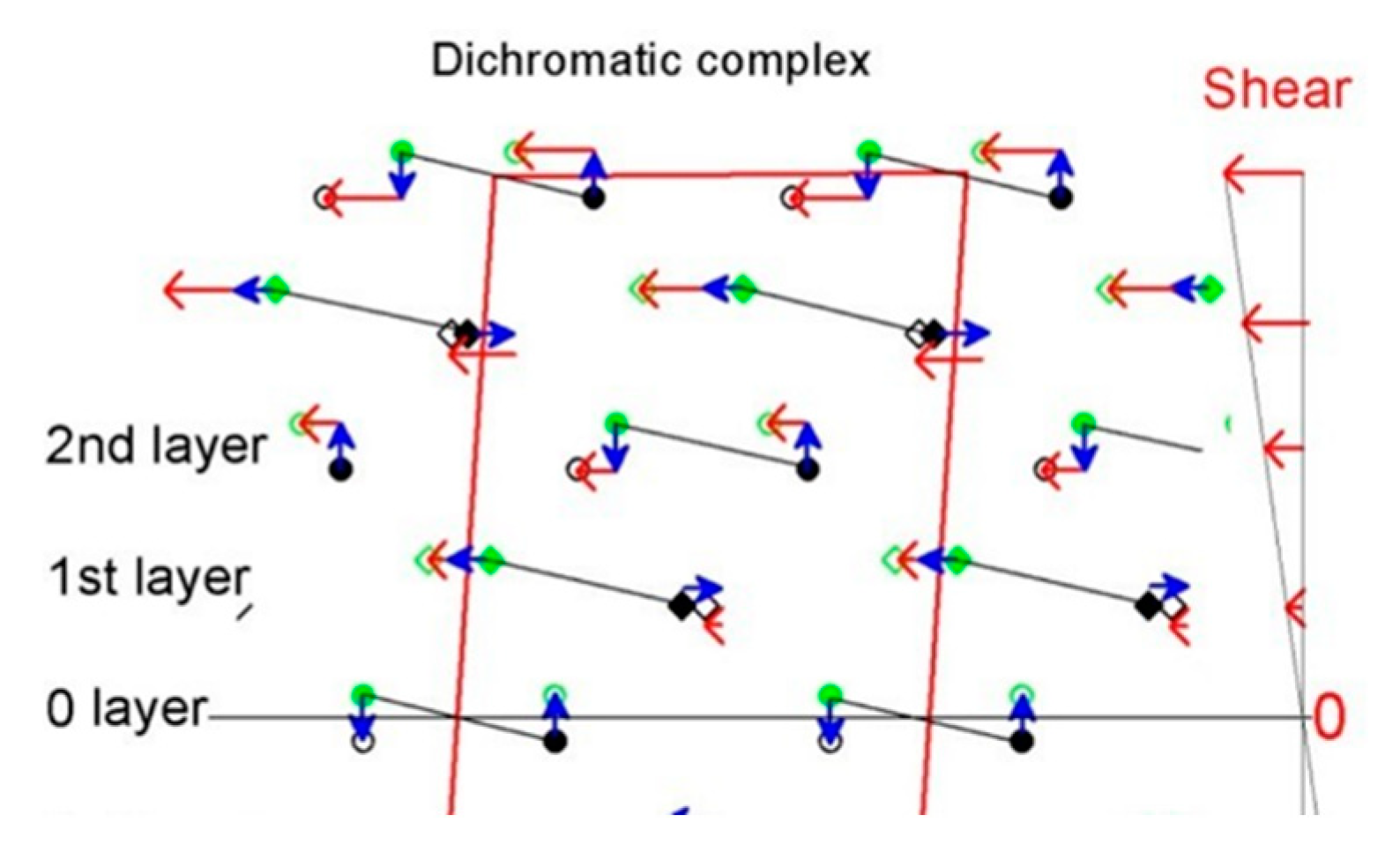
2.2. Description of Disconnections
2.3. Sources of Disconnections
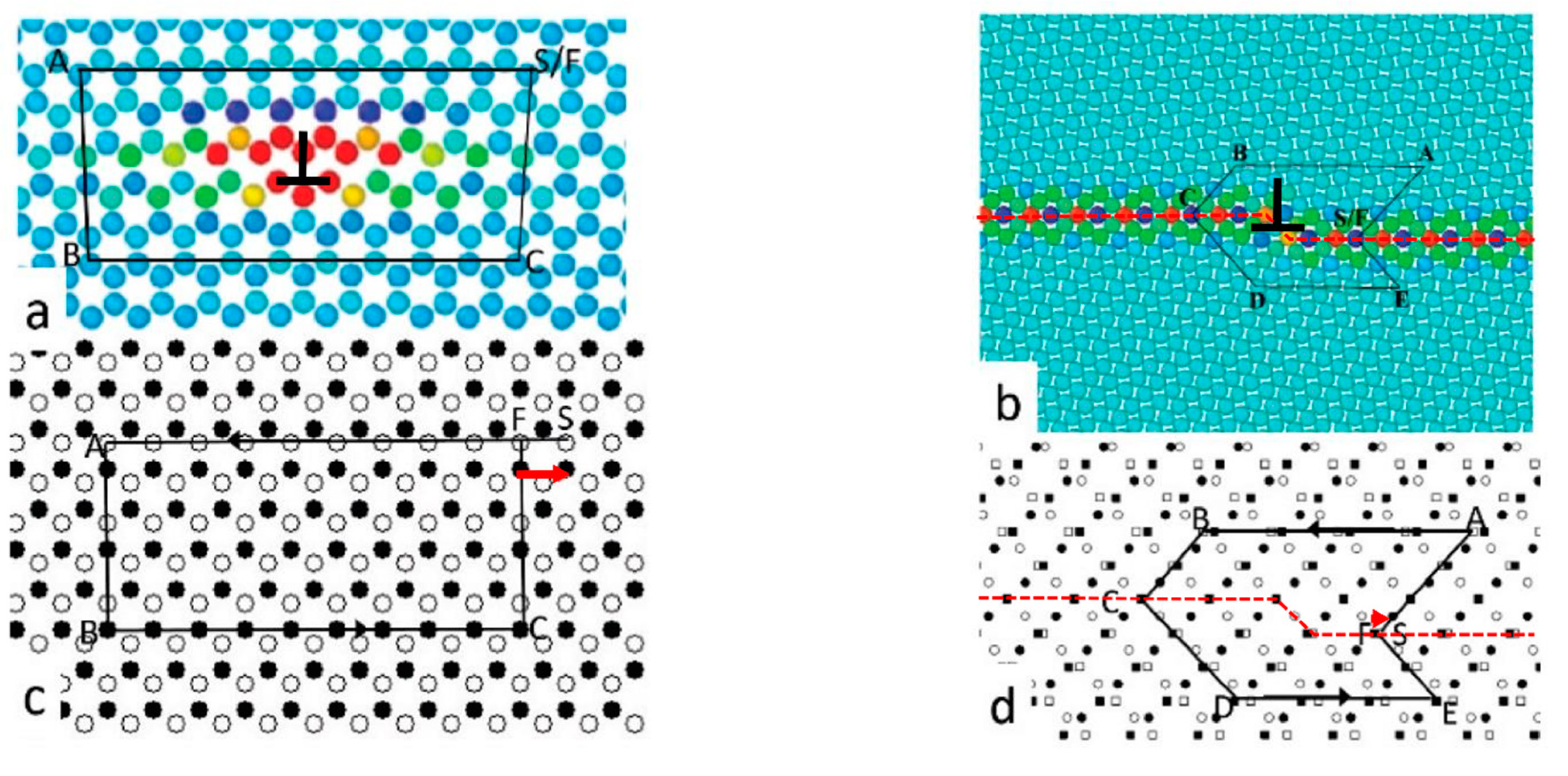
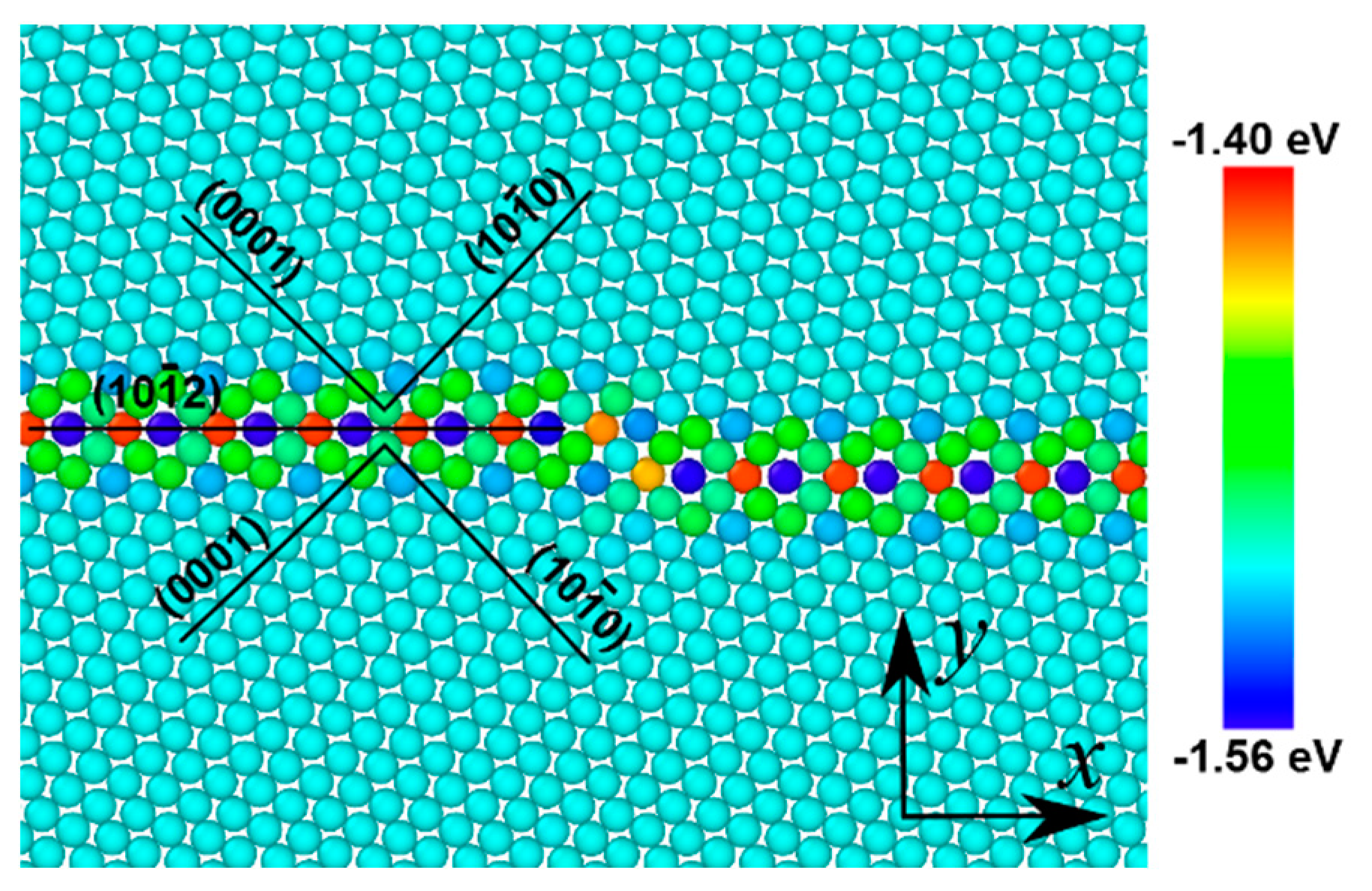
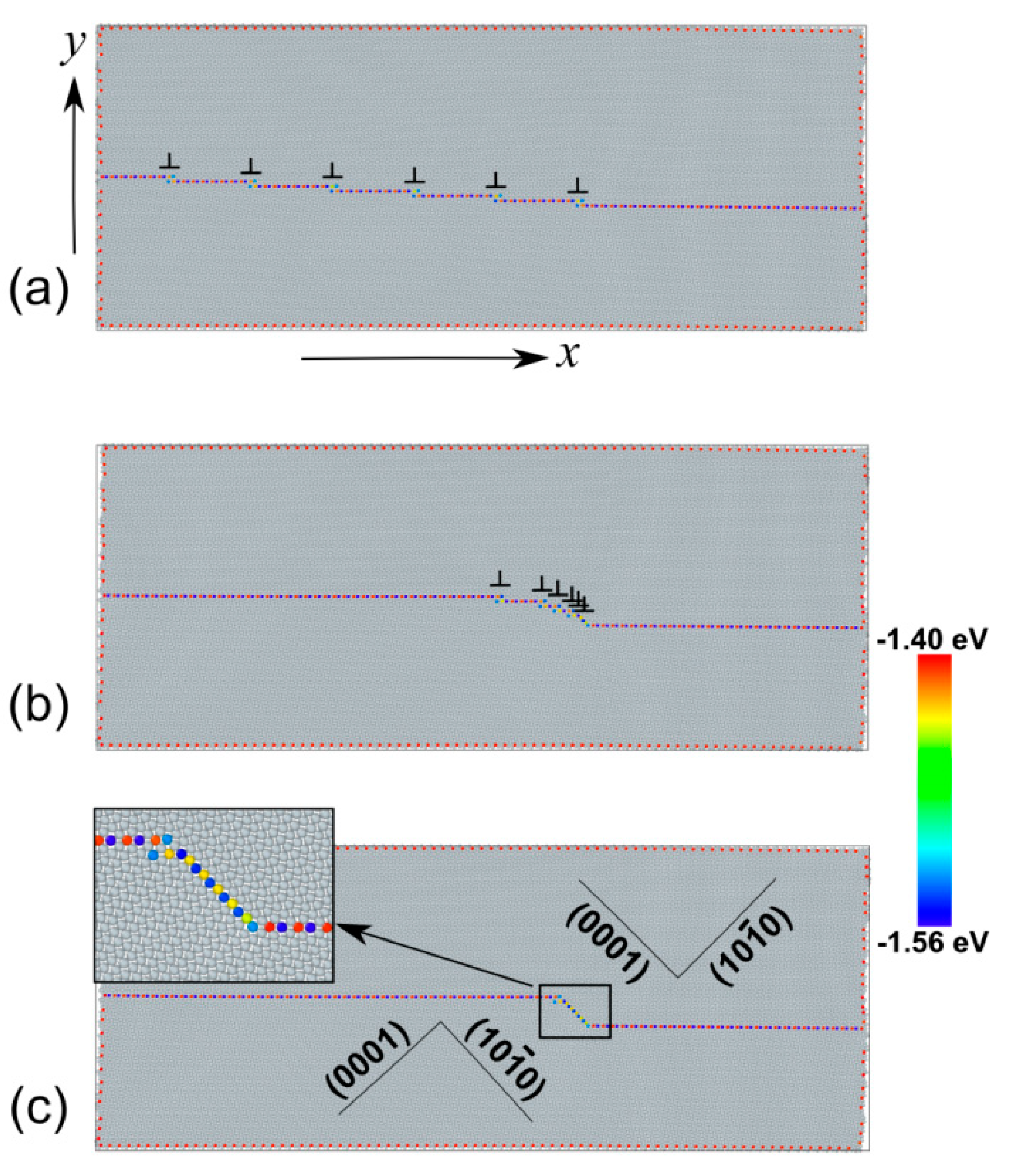
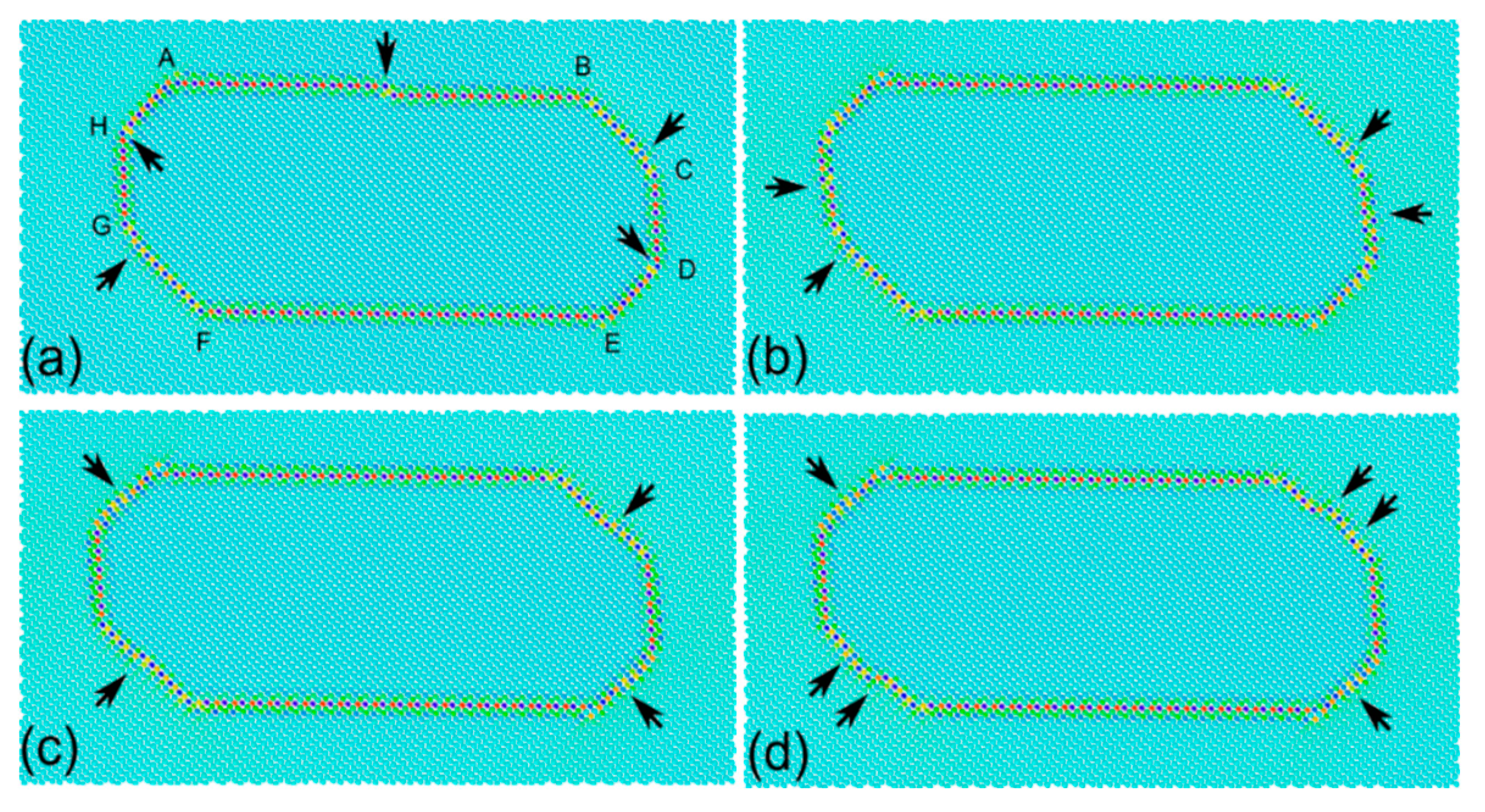
3. Faceting of Twin Boundaries
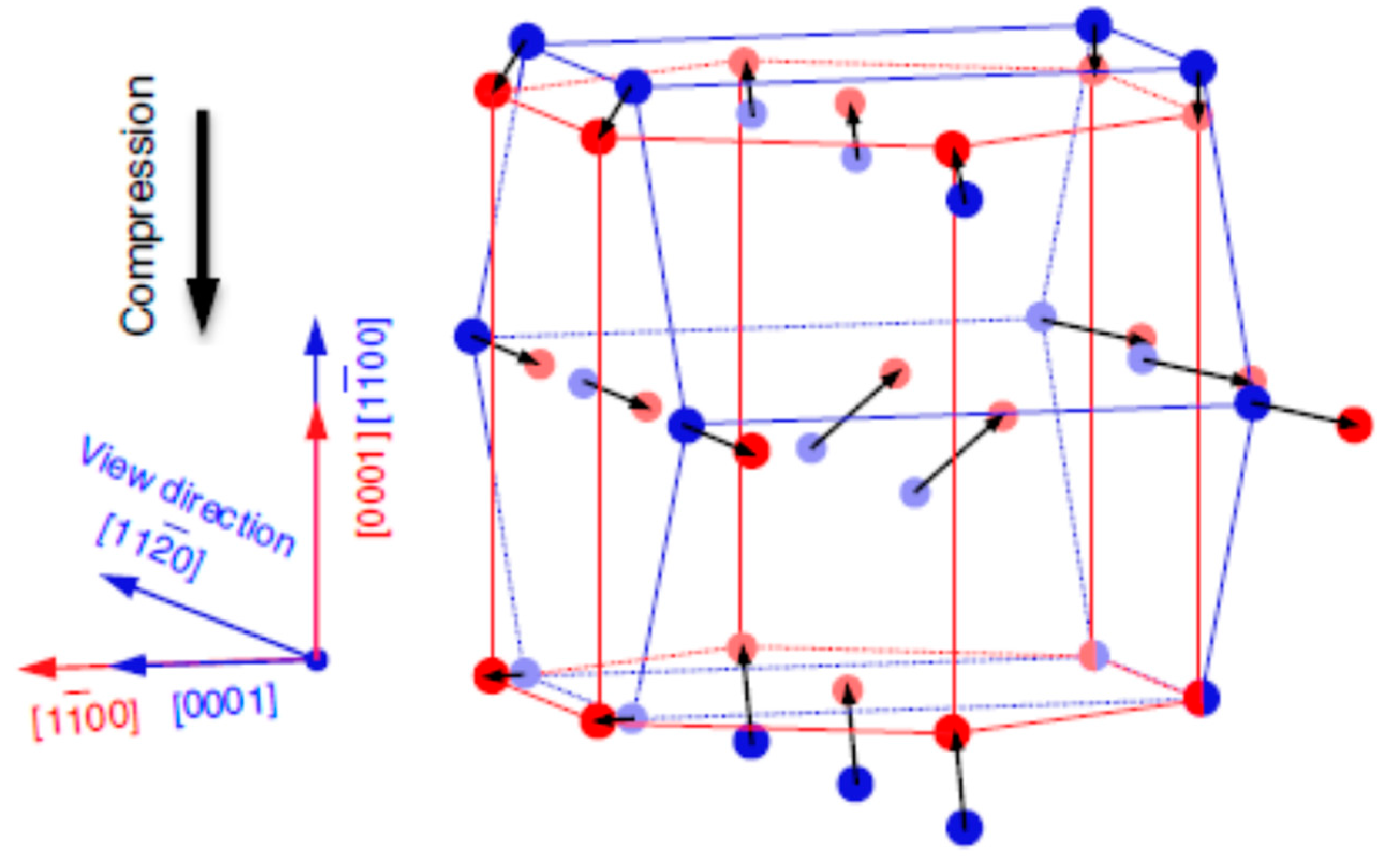
4. The {1012} Deformation Twinning
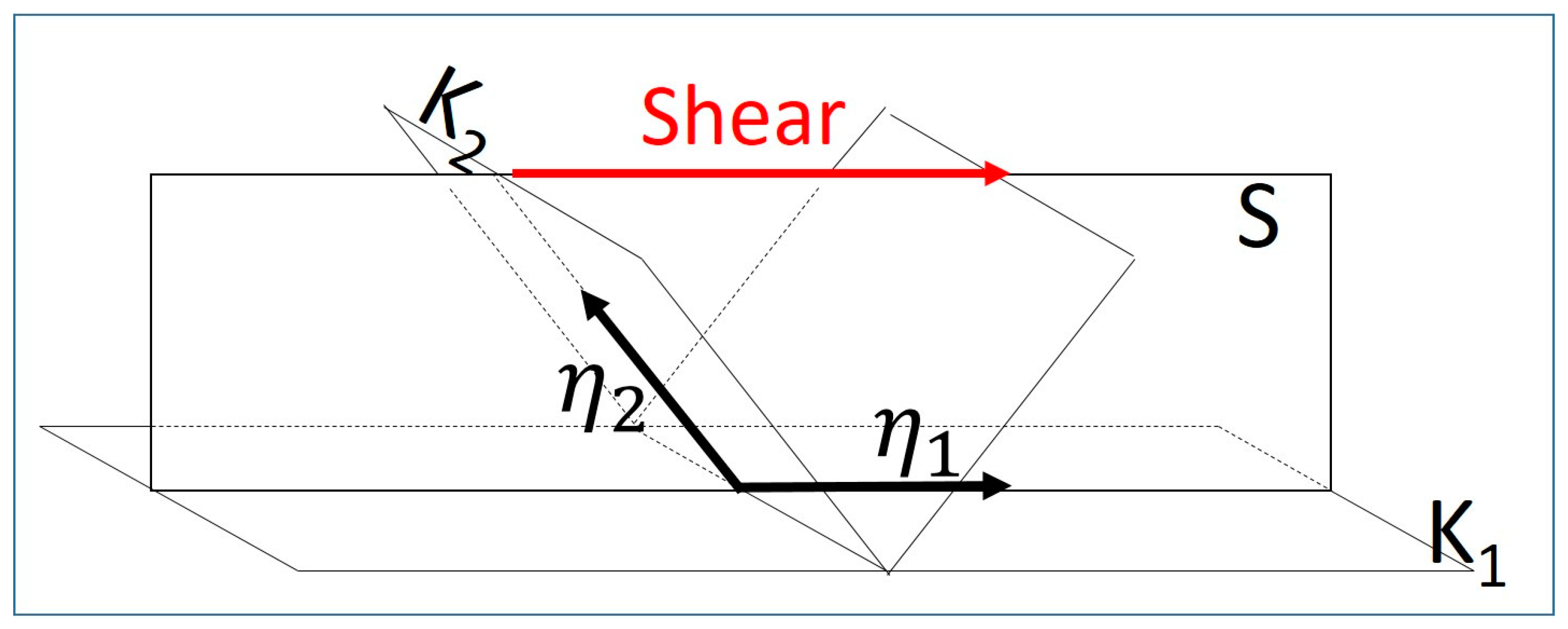
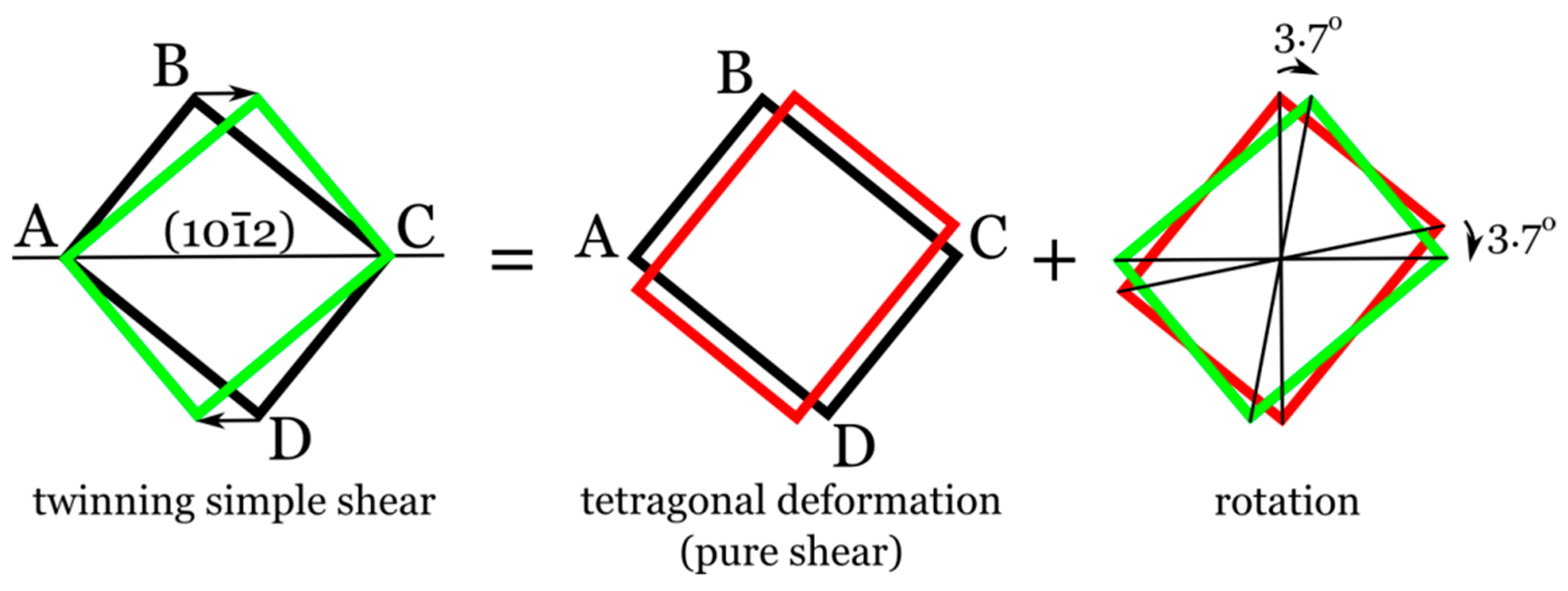
4.1. Twinning Shear of {1012} Twin Mode
4.2. Non-Schmid Behavior
5. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Cahn, R.W. Twinned crystals. Adv. Phys. 1954, 3, 363–445. [Google Scholar] [CrossRef]
- Christian, J.W. The Theory of Transformations in Metals and Alloys; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Bilby, B.A.; Crocker, A.G. The theory of the crystallography of deformation twinning. Proc. R. Soc. A 1965, 288, 240–255. [Google Scholar]
- Bevis, M.; Crocker, A.G. Twinning shears in lattices. Proc. R. Soc. A 1968, 304, 123–134. [Google Scholar]
- Bevis, M.; Crocker, A.G. Twinning modes in lattices. Proc. R. Soc. A 1969, 313, 509–529. [Google Scholar]
- Yoo, M.H.; Lee, J.K. Deformation twinning in h.c.p. metals and alloys. Philos. Mag. A 1991, 63, 987–1000. [Google Scholar] [CrossRef]
- Christian, J.W.; Mahajan, S. Deformation twinning. Prog. Mater. Sci. 1995, 3, 1–157. [Google Scholar] [CrossRef]
- Hardouin Duparc, O.B.M. A review of some elements for the history of mechanical twinning centred on its German origins until Otto Mügge’s K1 and K2 invariant plane notations. J. Mater. Sci. 2017, 52, 4182–4196. [Google Scholar] [CrossRef]
- Ericksen, J.L. On correlating two theories of twinning. Arch. Ration. Mech. Anal. 2000, 153, 261–289. [Google Scholar] [CrossRef]
- Barrett, C.D.; El Kadiri, H. Impact of deformation faceting on {1012} {1011} and {1013} embryonic twin nucleation in hcp metals. Acta Mater. 2014, 70, 137–161. [Google Scholar] [CrossRef]
- Barrett, C.D.; El Kadiri, H. Fundamentals of mobile tilt grain boundary faceting. Scr. Mater. 2014, 84, 15–18. [Google Scholar]
- Ostapovets, A.; Gröger, R. Twinning disconnections and basal–prismatic twin boundary in Mg. Model. Simul. Mater. Sci. Eng. 2014, 22, 025015. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, X.Y.; Wang, Y.C.; Ren, Y.; Tan, L.; Liu, Q. Structural characterization of {1011} twin boundaries in deformed cobalt. Mater. Character. 2016, 116, 44–47. [Google Scholar] [CrossRef]
- Tu, J.; Zhang, X.Y.; Zhou, Z.M.; Huang, C. Structural characterization of {1012} twin tip in deformed magnesium alloy. Mater. Character. 2015, 110, 39–43. [Google Scholar] [CrossRef]
- Ostapovets, A.; Gornakova, A.S. On faceting of {1011} and {1012} twin boundaries in hcp metals. Mater. Lett. 2019, 247, 99–101. [Google Scholar] [CrossRef]
- Braisaz, T.; Ruterana, P.; Nouet, G.; Serra, A.; Karakostas, T.; Kehagias, T. HREM Study of the (1012) twin and defects analysis in deformed polycrystaline alpha-Titanium. Philos. Mag. Lett. 1996, 74, 331–338. [Google Scholar] [CrossRef]
- Wang, S.; Gong, M.; Mc Cabe, R.; Capolungo, L.; Wang, J.; Tomé, C.N. Characteristic boundaries associated with three-dimensional twins in hexagonal metals. Sci. Adv. 2020, 6, eaaz2600. [Google Scholar] [CrossRef]
- Xu, B.; Capolungo, L.; Rodney, D. On the importance of prismatic/basal interfaces in the growth of {1012} Twins in hexagonal close packed crystals. Scr. Mater. 2013, 68, 901–904. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.J.; Chen, Y.J.; Walmsley, J.C.; Mathins, R.H.; Dumoulin, S.; Roven, H.J. Faceted interfacial structure of {1011} twins in Ti formed during equal channel angular pressing. Scr. Mater. 2010, 62, 443–446. [Google Scholar] [CrossRef] [Green Version]
- Pond, R.C. Line defects in interfaces. In Dislocations in Solids; Nabarro, F.N.R., Ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1989; Volume 8, pp. 1–66. [Google Scholar]
- Hirth, J.P. Dislocations, steps and disconnections at interfaces. J. Phys. Chem. Solids 1994, 55, 985–989. [Google Scholar] [CrossRef]
- Capolungo, L.; Beyerlein, I.J. Nucleation and stability of twins in hcp metals. Phys. Rev. B 2008, 78, 024117. [Google Scholar] [CrossRef]
- Wang, J.; Hirth, J.P.; Tomé, C.N. (1102) Twinning nucleation mechanisms in hexagonal-close-packed crystals. Acta Mater. 2009, 57, 5521–5530. [Google Scholar] [CrossRef]
- Wang, J.; Beyerlein, I.J.; Hirth, J.P. Nucleation of elementary {1101} and {1103} twinning dislocations at a twin boundary in hexagonal close-packed crystals. Modelling Simul. Mater. Sci. Eng. 2012, 20, 024001. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; McCabe, R.J.; Tomé, C.N. Effect of microstructure on the nucleation of deformation twins in polycrystalline high-purity magnesium: A multi-scale modeling study. J. Mech. Phys. Solids 2011, 59, 988–1003. [Google Scholar] [CrossRef]
- Barrett, C.D.; El Kadiri, H.; Tschopp, M.A. Breakdown of the Schmid law in homogeneous and heterogeneous nucleation events of slip and twinning in magnesium. J. Mech. Phys. Solids 2012, 60, 2084–2099. [Google Scholar] [CrossRef]
- Godet, S.; Jiang, L.; Luo, A.A.; Jonas, J.J. Use of Schmid factors to select extension twin variants in extruded magnesium alloy tubes. Scr. Mater. 2006, 55, 1055–1058. [Google Scholar] [CrossRef]
- Li, B.; Zhang, X.Y. Twinning with zero twinning shear. Scr. Mater. 2016, 125, 73–79. [Google Scholar] [CrossRef]
- Serra, A.; Bacon, D.J. A new model for {1102} twin growth in hcp metals. Philos. Mag. 1996, 73, 333–343. [Google Scholar] [CrossRef]
- Li, B.; Ma, E. Atomic Shuffling Dominated Mechanism for Deformation Twinning in Magnesium. Phys. Rev. Lett. 2009, 103, 035503. [Google Scholar] [CrossRef]
- Khater, H.A.; Serra, A.; Pond, R.C.; Hirth, J.P. The disconnection mechanism of coupled migration and shear at grain boundaries. Acta Mater. 2012, 60, 2007–2020. [Google Scholar] [CrossRef]
- Khater, H.A.; Serra, A.; Pond, R.C. Atomic shearing and shuffling accompanying the motion of twinning disconnections in Zirconium. Philos. Mag. 2013, 93, 1279–1298. [Google Scholar] [CrossRef]
- El Kadiri, H.; Barrett, C.D.; Tschopp, M.A. The candidacy of shuffle and shear during compound twinning in hexagonal close-packed structures. Acta Mater. 2013, 61, 7646–7659. [Google Scholar] [CrossRef] [Green Version]
- Pond, R.C.; Hirth, J.P.; Serra, A.; Bacon, D.J. Atomic displacements accompanying deformation twinning: Shears and shuffles. Mater. Res. Lett. 2016, 4, 185–190. [Google Scholar] [CrossRef] [Green Version]
- Capolungo, L.; Beyerlein, I.J.; Tomé, C.N. Slip-assisted twin growth in hexagonal close-packed metals. Scr. Mater. 2009, 60, 32–35. [Google Scholar] [CrossRef]
- Lay, S.; Nouet, G. Interaction of slip dislocations with the (0112) twin interface in zinc. Philos. Mag. 1994, 70, 1027–1044. [Google Scholar] [CrossRef]
- Lay, S.; Nouet, G. HREM study of the (0112) twin interface in zinc. Philos. Mag. 1994, 70, 261–275. [Google Scholar] [CrossRef]
- Lay, S.; Nouet, G. Morphology of (0112) twins in zinc and related interfacial defects. Philos. Mag. 1995, 72, 603–617. [Google Scholar] [CrossRef]
- Kvashin, N.; García-Müller, P.L.; Anento, N.; Serra, A. Atomic processes of the shear-coupled migration of {112} twins and vicinal grain boundaries in bcc-Fe. Phys. Rev. Mater. 2020, 4, 073604. [Google Scholar] [CrossRef]
- Combe, N.; Mompiou, F.; Legros, M. Heterogeneous disconnection nucleation mechanisms during grain boundary migration. Phys. Rev. Mater. 2019, 3, 060601. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Huang, H.C. Shockley partial dislocations to twin: Another formation mechanism and generic driving force. Appl. Phys. Lett. 2004, 85, 5983. [Google Scholar] [CrossRef]
- Narayan, J.; Zhu, V. Self-thickening, cross-slip deformation twinning model. Appl. Phys. Lett. 2008, 92, 151908. [Google Scholar] [CrossRef] [Green Version]
- Marian, J.; Cai, W.; Bulatov, V.V. Dynamic transitions from smooth to rough to twinning in dislocation motion. Nat. Mater. 2004, 3, 158. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Zhang, X.Y.; Ren, Y.; Tu, J.; Liu, Q. Interfacial structure of {1012} twin tip in deformed magnesium alloy. Scr. Mater. 2014, 90–91, 41–44. [Google Scholar] [CrossRef]
- Tu, J.; Zhang, S. On the {1012} twinning growth mechanism in hexagonal close-packed metals. Mater. Des. 2016, 96, 143–149. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Li, B.; Wu, X.L.; Zhu, Y.T.; Ma, Q.; Liu, Q.; Wang, P.T.; Horstemeyer, M.F. Twin boundaries showing very large deviations from the twinning plane. Scr. Mater. 2012, 67, 862–865. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.Y.; Li, B.; Tu, J.; Sun, Q.; Liu, Q. Non-classical twinning behavior in dynamically deformed Co. Mater. Res. Lett. 2015, 3, 142. [Google Scholar] [CrossRef]
- Ostapovets, A.; Buršík, J.; Gröger, R. Deformation due to migration of faceted {1012} twin boundaries in magnesium and cobalt. Philos. Mag. 2015, 95, 4106–4117. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L.; Tomé, C.N.; Mao, S.X.; Gong, S.K. Twinning and De-twinning via Glide and Climb of Twinning Dislocations along Serrated Coherent Twin Boundaries in Hexagonal-close-packed Metals. Mater. Res. Lett. 2013, 1, 81–88. [Google Scholar] [CrossRef]
- Braisaz, T.; Ruterana, P.; Nouet, G. Twin tip defects related to the nucleation and growth mechanisms of the twin (1012) in zinc characterized by high-resolution electron microscopy. Philos. Mag. A 1997, 76, 1. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, X.Y.; Yin, R.S.; Ren, Y.; Tan, L. Structural characterization of {1013} twin boundaries in deformed cobalt. Scr. Mater. 2015, 108, 109–112. [Google Scholar] [CrossRef]
- Zhang, J.; Xi, G.; Wan, X. {1011} twin boundary showing very large deviation from the theoretical one in deformed magnesium alloy. Mater. Charact. 2017, 132, 280–283. [Google Scholar] [CrossRef]
- Ostapovets, A.; Serra, A. Characterization of the matrix–twin interface of a (1012) twin during growth. Philos. Mag. 2014, 94, 2827–2839. [Google Scholar] [CrossRef]
- He, Y.; Li, B.; Wang, C.; Mao, S.X. Direct observation of dual-step twinning nucleationin hexagonal close-packed crystals. Nat. Commun. 2020, 11, 2483. [Google Scholar] [CrossRef] [PubMed]
- Pond, R.C.; Hirth, J.P. Topological model of type II deformation twinning. Acta Mater. 2018, 151, 229–242. [Google Scholar] [CrossRef]
- Pond, R.C.; Hirth, J.P.; Knowles, K.M. Topological model of type-II deformation twinning in NiTi martensite. Philos. Mag. 2019, 99, 1619–1632. [Google Scholar] [CrossRef]
- Liu, Y.; Li, N.; Shao, S.; Gong, M.Y.; Wang, J.; McCabe, R.J.; Jiang, Y.; Tomé, C.N. Characterizing the boundary lateral to the shear direction of deformation twins in magnesium. Nat. Commun. 2016, 7, 11577. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, P.Z.; Gong, M.Y.; McCabe, R.J.; Wang, J.; Tomé, C.N. Three-dimensional character of the deformation twin in magnesium. Nat. Commun. 2019, 10, 3308. [Google Scholar] [CrossRef]
- Zu, Q.; Tang, X.Z.; Xu, S.; Guo, Y.F. Atomistic study of nucleation and migration of the basal/prismatic interfaces in Mg single crystals. Acta Mater. 2017, 130, 310–318. [Google Scholar] [CrossRef] [Green Version]
- Lay, S.; Ayed, P.; Nouet, G. A study of (0112) twin deviating from exact orientation in magnesium. Acta Metall. Mater. 1992, 40, 2351–2359. [Google Scholar] [CrossRef]
- Molnar, P.; Jager, A.; Lejcek, P. Twin nucleation at grain boundaries in Mg–3 wt.% Al–1 wt.% Zn alloy processed by equal channel angular pressing. Scr. Mater. 2012, 67, 467–470. [Google Scholar] [CrossRef]
- El Kadiri, H.; Kapil, J.; Oppedal, A.L.; Hector, L.G., Jr.; Agnew, S.R.; Cherkaoui, M.; Vogel, S.C. The effect of twin–twin interactions on the nucleation and propagation of {1012} twinning in magnesium. Acta Mater. 2013, 61, 3549–3563. [Google Scholar] [CrossRef]
- Liu, B.Y.; Wang, J.; Li, B.; Lu, L.; Zhang, X.Y.; Shan, Z.W.; Li, J.; Jia, C.L.; Sun, J.; Ma, E. Twinning-like lattice reorientation without a crystallographic twinning plane. Nat. Commun. 2014, 5, 3297. [Google Scholar] [CrossRef] [Green Version]
- Molodov, K.D.; Al-Samman, T.; Molodov, D.A.; Korte-Kerzel, S. On the twinning shear of {1012} twins in magnesium–Experimental determination and formal description. Acta Mater. 2017, 134, 267–273. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Li, B.; Sun, Q. On the “twinning shear” measured from line deflection. Scr. Mater. 2019, 159, 133–136. [Google Scholar] [CrossRef]
- Li, B.; Zhang, X.Y. Global strain generated by shuffling-dominated {1012}〈1011〉 twinning. Scr. Mater. 2014, 71, 45–48. [Google Scholar] [CrossRef]
- Li, B.Y.; Wan, L.; Wang, J.; Ma, E.; Shan, Z.W. Terrace-like morphology of the boundary created through basal prismatic transformation in magnesium. Scr. Mater. 2015, 100, 86–89. [Google Scholar] [CrossRef] [Green Version]
- Ostapovets, A.; Molnár, P. On the relationship between the “shuffling-dominated” and “shear-dominated” mechanisms for twinning in magnesium. Scr. Mater. 2013, 69, 287–290. [Google Scholar] [CrossRef]
- Zheng, Q.-S.; He, Q.C.; Curnier, A. Simple shear decomposition of the deformation gradient. Acta Mech. 2000, 140, 131–147. [Google Scholar] [CrossRef]
- Namakian, R.; Voyiadjis, G.Z. An atomic displacive model for {1012}〈1011〉 twinning in hexagonal close packed metals with the emphasis on the role of partial stacking faults in formation of {1012} twins. Acta Mater. 2018, 150, 381–393. [Google Scholar] [CrossRef]
- Ostapovets, A.; Molnár, P.; Gröger, R. IOP Conference. Ser. Mater. Sci. Eng. 2014, 63, 012134. [Google Scholar]
- Le Lann, A.; Dubertret, A. Model for {1012} Twins in H.C.P. Metals. Phys. Stat. Solids (A) 1979, 51, 497–507. [Google Scholar]
- Schmid, E. Neuere Untersuchungen an Metallkristallen. In Proceedings of the International Congress for Applied Mechanics, Delft, The Netherlands, 22–26 April 1924; pp. 342–353. [Google Scholar]
- Schmid, E.; Boas, W. Kristallplastizität mit besonderer Berücksichtigung der Metalle; Springer: Berlin, Germany, 1935. [Google Scholar]
- Duesbery, M.S.; Vitek, V. Plastic anisotropy in bcc transition metals. Acta Mater. 1998, 46, 1481–1492. [Google Scholar] [CrossRef]
- Gröger, R.; Vitek, V. Stress dependence of the Peierls barrier of 1/2<111> screw dislocations in bcc metals. Acta Mater. 2013, 61, 6362–6371. [Google Scholar] [CrossRef]
- Ito, K.; Vitek, V. Atomistic study of non-Schmid effects in the plastic yielding of bcc metals. Philos. Mag. 2001, 81, 1387–1407. [Google Scholar] [CrossRef]
- Bolton, C.J.; Taylor, G. Anomalous slip in high-purity niobiumsingle crystals deformed at 77 K in tension. Philos. Mag. 1972, 26, 1359–1376. [Google Scholar] [CrossRef]
- Gröger, R.; Chlup, Z.; Kuběna, I.; Kruml, T. Slip activity in molybdenum single crystals compressed at 77 K. Philos. Mag. 2018, 98, 2749–2768. [Google Scholar] [CrossRef]
- Paidar, V.; Pope, D.P.; Vitek, V. A theory of the anomalous yield behaviour in L12 ordered alloys. Acta Metall. 1984, 258, 29–32. [Google Scholar]
- Qin, Q.; Bassani, J.L. Non-Schmid yield behavior in single crystals. J. Mech. Phys. Solids 1992, 40, 813–833. [Google Scholar] [CrossRef]
- Ostapovets, A.; Vatazhuk, O. Non-Schmid behavior of extended dislocations in computer simulations of magnesium. Comput. Mater. Sci. 2018, 142, 261–267. [Google Scholar] [CrossRef]
- Barnett, M.R.; Keshavarz, Z.; Beer, A.G.; Ma, X. Non-Schmid behaviour during secondary twinning in a polycrystalline magnesium alloy. Acta Mater. 2008, 56, 5–15. [Google Scholar] [CrossRef]
- Martin, E.; Capolungo, L.; Jiang, L.; Jonas, J.J. Variant selection during secondary twinning in Mg-3%Al. Acta Mater. 2010, 58, 3970–3983. [Google Scholar] [CrossRef]
- Capolungo, L.; Marshall, P.E.; McCabe, R.J.; Beyerlein, I.J.; Tomé, C.N. Nucleation and growth of twins in Zr: A statistical study. Acta Mater. 2009, 57, 6047–6056. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Y.; Eisenlohr, P.; Bieler, T.R.; Crimp, M.A.; Mason, D.E. Twin Nucleation by Slip Transfer across Grain Boundaries in Commercial Purity Titanium. Met. Mater. Trans. A 2010, 41, 421. [Google Scholar] [CrossRef]
- Cayron, C. Hard-sphere displacive model of extension twinning in magnesium. Mater. Des. 2017, 119, 361–375. [Google Scholar] [CrossRef] [Green Version]
- Kana, T.; Ostapovets, A.; Paidar, V. The matrix–twin transition in a perfect Mg crystal: Ab initio study. Int. J. Plast. 2018, 108, 186–200. [Google Scholar] [CrossRef]
- Kumar, A.; Wang, J.; Tomé, C.N. First-principles study of energy and atomic solubility of twinning-associated boundaries in hexagonal metals. Acta Mater. 2015, 85, 144–154. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.Y.; Adams, J.B.; Ercolessi, F.; Moriarty, J.A. EAM potential for magnesium from quantum mechanical forces. Model. Simul. Mater. Sci. Eng. 1996, 4, 293–303. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.; Liu, C.; Gao, Y.; Jiang, S.; Chen, Z. A rotation-shear model on the atomic motion during {1012} twinning in magnesium alloys. Mater. Lett. 2016, 165, 185–188. [Google Scholar] [CrossRef]




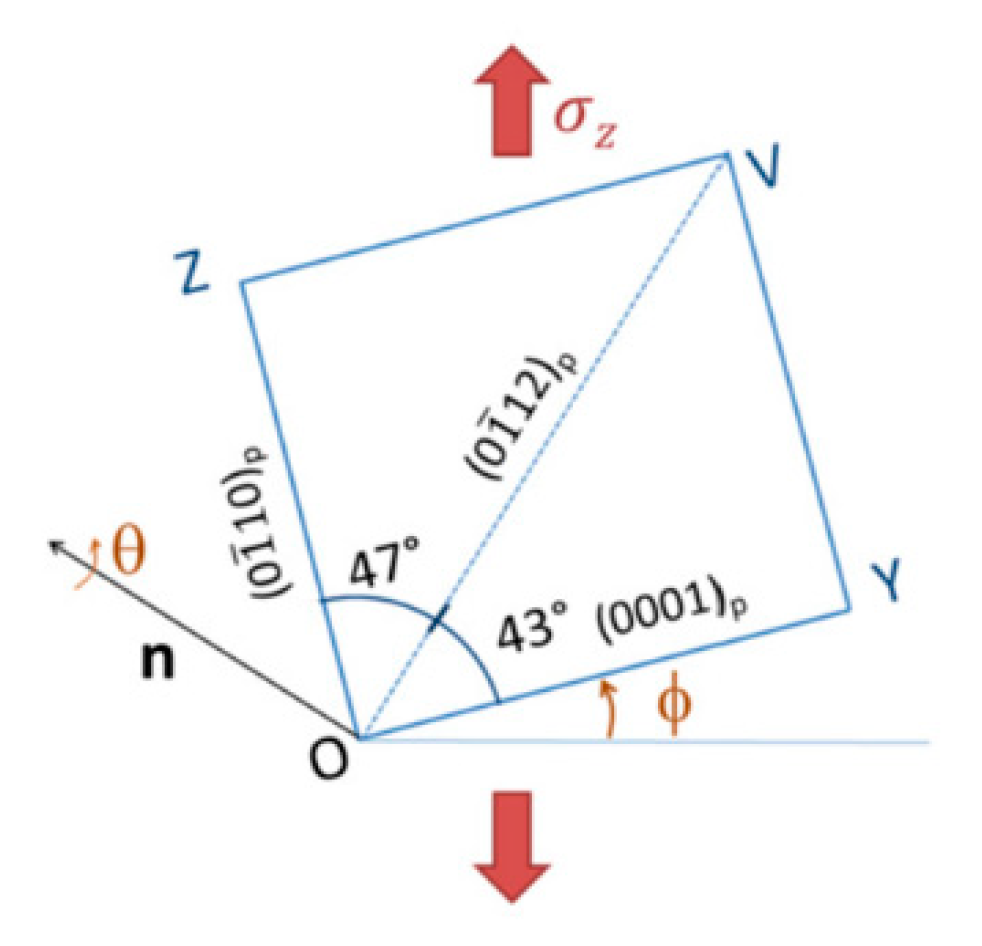

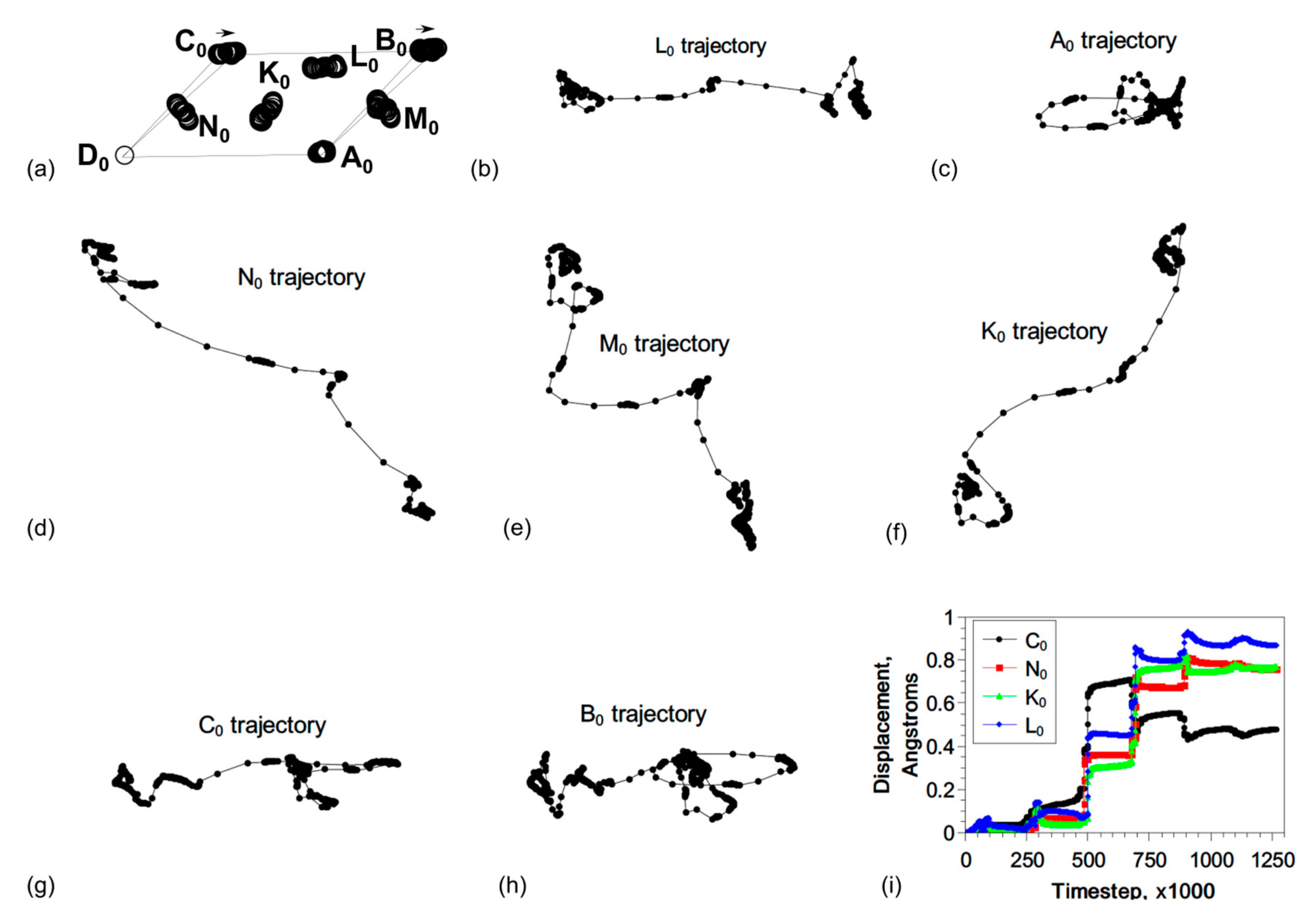
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ostapovets, A.; Serra, A. Review of Non-Classical Features of Deformation Twinning in hcp Metals and Their Description by Disconnection Mechanisms. Metals 2020, 10, 1134. https://doi.org/10.3390/met10091134
Ostapovets A, Serra A. Review of Non-Classical Features of Deformation Twinning in hcp Metals and Their Description by Disconnection Mechanisms. Metals. 2020; 10(9):1134. https://doi.org/10.3390/met10091134
Chicago/Turabian StyleOstapovets, Andriy, and Anna Serra. 2020. "Review of Non-Classical Features of Deformation Twinning in hcp Metals and Their Description by Disconnection Mechanisms" Metals 10, no. 9: 1134. https://doi.org/10.3390/met10091134
APA StyleOstapovets, A., & Serra, A. (2020). Review of Non-Classical Features of Deformation Twinning in hcp Metals and Their Description by Disconnection Mechanisms. Metals, 10(9), 1134. https://doi.org/10.3390/met10091134





