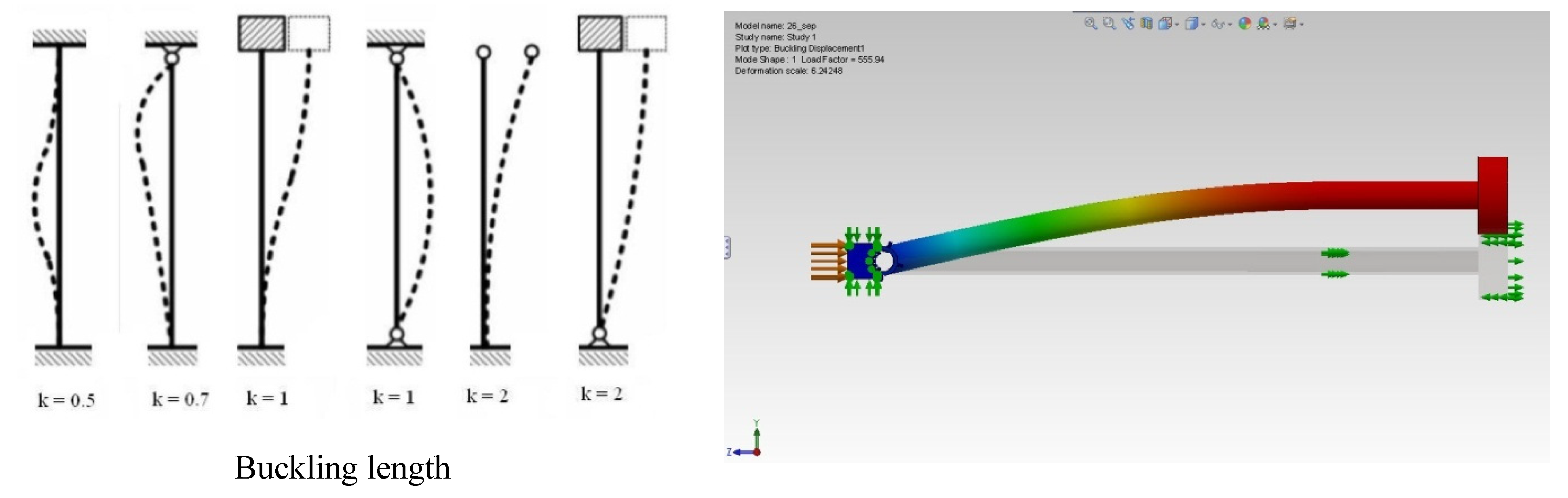
1. Introduction
It is a fact that a structural element subjected to a central compression (axial) load will have the bearing capacity directly proportional with the minimum value of the axial moment of inertia relative to the axes of the reference system of the section. During the stages, this fact may show a tendency to create structures with significant slenderness-ratio factors, but these types of elements can become unstable because of the manifestation of the phenomenon of loss of stability of the elastic equilibrium shape, i.e., buckling [
1,
2,
3].
Hydraulic cylinders are commonly mass-produced using traditional metals. High-strength steels are used for the production of the rod and the cylinder tube, whereas the pistons are generally made of aluminum. The core aspects of the hydraulic cylinder design are described by [
4,
5,
6], whose manuals offer guidelines for designing such components effectively. These manuals present a complete scenario of problems and targets that need to be considered when designing the actuator, e.g., buckling analysis, strain and stress analyses, sealing performance and autofrettage investigations.
Buckling strength is a key component for hydraulic cylinders. Leonhard Euler’s equation of buckling—as in elastic instability of structures—is still generally used in engineering practice. Euler’s method is appropriate to analyze linearly elastic slender structures. However, it has demonstrated an incapability to predict critical loads for structures of smaller slenderness with nonlinear behavior of material and imperfections of geometry and load [
7].
In 2005, [
8] assessed buckling instability by making an allowance for initial misalignment as an imperfection in the rod–cylinder tube intersection. The research defined the influence of the misalignment angle and friction coefficient on the buckling load by both numeric and experimental approaches.
Baragetti et al. [
9,
10] presented numeric models to analyze the buckling behavior of a double-acting cylinder. In the research, analytical and experimental models were used to study the influence of the friction coefficient, the geometric imperfections between the piston and rod–cylinder connections and the weight of the oil. A mathematical formulation, which accounts for the parameters previously introduced, was given and compared to experimental data. The pressure distribution acting on the wear rings was assumed in [
10] to be triangular. This profile was probably suggested due to the fact that one of the sides of the seal is subject to zero pressure. However, the results of [
11] show that the pressure profile along the contact zone remains fundamentally constant rather than triangular. In the case of rectangular seals with rounded edges, the pressure distribution exhibits lateral bumps for a frictionless contact whose values may be computed with the analytical approach presented in [
12]. Therefore, the initial hypothesis of the pressure distribution considered between the seal and the piston-rod of a hydraulic actuator influences the wear of the seals and the leakage of the actuator.
In 2010, Morelli [
13] presented experimental results on buckling occurrence for a telescopic actuator. Several pieces of research [
14,
15] studied stroke and cushioning devices to reduce the piston-rod kinetic energy during motion. They formulated a mathematical model of hydraulic circuits to study the supply pressure influence and alternative solutions were evaluated.
With respect to the material aspects, thin-walled composite cylinders have been researched for mechanical applications such as pressure vessels [
16,
17,
18,
19] and components that support energy absorption [
20,
21,
22,
23]. These components were gotten by filament winding, which is done by coupling an inner liner with an outer composite laminate.
The likelihood of using composite materials for hydraulic actuators seem to be inadequate; in fact, little contributions are evident [
24,
25,
26,
27]. In [
24], the study presented an experimental test of hydraulic actuators on static and fatigue cyclic pressurization and, also other areas relating to wear. In [
25,
27], a methodology was presented for designing the cylinder tube and the rod in composites of a hydraulic actuator and the analytical results and the experimental data are compared. In [
26], the feasibility of a hydraulic cylinder in composites is investigated by using numeric FEM analyses. Static analyses are exploited to examine the stress and the strain field caused by oil pressure. In addition, the buckling occurrence of the rod is analyzed. Optimization techniques have been applied to cylinder composite stacking sequence and shape in order to increase the critical buckling load. In [
27], a hydraulic actuator made up of composites was applied to a telescopic hydraulic cylinder where the weight reduction obtained was approximately 96% compared to the cylinder in steel.
Recently, Fragassa et al. refer to the state of deformation occurred as a result of a given calculation scheme, the convergence of results being verified by means specific to resistive tensometry—the object of study is represented by the telescopic structure of the arm itself, focusing on areas of transition between sections (sliding pads). Measuring deformations were used to validate different design assumptions and to investigate the presence of local instability process, which is not predictable using only theoretical formulations [
28].
In 2017, Pavlovic et al. dealt with the phenomenon of buckling at the global level of the telescopic arm of the machine, as a direct result of changing the geometric characteristics of the section of telescopic sections, by reducing the thickness of metal sheets, with direct implication on the stability of the structure itself. The paper highlighted the fact that the linear buckling techniques showed that critical loads and corresponding buckling modes were higher than the most extreme working conditions [
29].
This paper aims to be a starting point in the approach—by means of the numeric algorithms based on the finite element method—of stability issues concerning slender structures subjected to axial compression. The high degree of complexity of the application demands a careful study with regard to the set of conditions initially established as input parameters.
The need to carry out this study is justified by the analysis of a technical accident caused by the manifestation of buckling failure of a hydraulic cylinder that is equipped in a self-lifting platform (
Figure A1).
4. Results
The results of the nonlinear analysis for the piston–cylinder assembly are shown in
Figure 17:
Regardless of the software application used, finding solutions to an analysis problem with the help of FEM involves solving several equations simultaneously, there are two major families of solving methods: the direct method, which uses numeric algorithms such as inverse matrix, LU decomposition, Gauss–Jordon, respectively iterative methods, in which approximate calculation techniques are used for finding a solution, the calculation sequence being repeated until the required degree of convergence is obtained.
In this case, we opt for the study with direct resolution algorithm DSS (direct sparse solver), given that the implicit iterative algorithms for solving FEPlus (finite-element plus), are more suitable for linear analysis.
After several simulation attempts, the maximum degree of accuracy of the solutions (including the absence of error messages) is obtained for the Crisfield–Riks control method for numeric simulation (incremental arc length control method), respectively for the Newton iterative calculation method—Raphson (NR) (
Figure 18).
In the case of nonlinear analysis, the system of equations to be solved at the generic moment
is of the form:
where:
R and F represents matrices of the vectors of the external loads applied in the nodes of the structure and, respectively matrices of the vectors of the internal efforts at the level of the nodes;
The need to use an iterative method is given by the dependence of the value of the matrix
on the matrix of the movements of the nodes of the network
at a given moment. Thus, the simplified form of a calculation step (rank i iteration) can be represented by the set of relations:
where:
The Newton–Raphson method of iterative calculation is represented schematically in
Figure 19, in ordinate being represented the external loads and in abscissa the displacements; notice the reestimation of the Jacobian matrix terms for each iteration performed within the given calculation step
The use of the nonlinear solving algorithm is mainly due to the amplitude of the structural deformations, not being able to ignore the changes of the terms of the stiffness matrix with the increase of the load; in the case of state-of-the-art applications, the presence of a dedicated nonlinear calculation (large displacement formulation) option is noted, taking into account the large deformations of the studied structure, a variant valid when using solid meshing or shell discretization.
Table 2 below shows the comparative values of the study results, as follows:
By means of structural modeling at the main arm articulated structure level, one can see that the critical buckling load was exceeded several times in the circumstances in which the accident occurred; the loading scheme for this case study can only be presumed (
Figure 20 and
Figure 21).
5. Conclusions
The problem that led to the collapse of the articulated platform was the hydraulic device failure as a result of the occurrence of the buckling phenomenon for the mentioned rod.
Following the study, a certain degree of dispersion of the results has been noticed in the use of various software applications and working environment/working platforms used (Ansys, Solidworks for Windows, Salome-Mecca, OpenFoam, Code Aster for Linux). As a rule of thumb, at least two approaching methods should be used for comparison purposes.
For the studied case, the highest accuracy rank of the result (having referenced the traditional analytical solutions) was obtained for the latest generation of commercial software applications. Significant steps were made also for the open-source software with regard to the nonlinear analysis algorithms based on the finite element method. However, the lack of dedicated implementation programs (support schemes and complex loading schemes) and the lack of rich options in terms of solver settings were felt.
However, for the methodology applied in this article, it is worth noting the reduced spreading character of the estimated values for the critical buckling load, which confirms the validity of the obtained parameter and also the importance of support scheme modeling for the various cases considered, with direct implications on the accuracy of the output study parameters.
The article is limited to the detailed treatment of the phenomenon of loss of elastic equilibrium (buckling), at the level of the actuator rod that achieves the positioning of one of the component sections of the telescopic structure, a leading phenomenon to technical collapse from the general point of view of the structure. This approach is made starting from the behavior of the material from which the rod is made, with the mechanical properties and with the presented metallographic structure.
The occurrence of the undesirable phenomenon for the extension of the hydraulic actuator rod to a value lower than the maximum, with the inevitable displacement of the failure area by losing the elastic equilibrium from “Euler buckling” to the post-elastic or plastic buckling area, is due to the modification of the characteristic parameter “buckling length”, a parameter that depends on the effective support scheme of the rod at the moment of entry into operation of the studied failure mechanism.
Thus, the study showed a significant convergence of the results obtained in parallel with traditional calculation relations (giving up quasi-empirical calculation formulas of Tetmajer–Jasinski type in favor of the general Johnson relationship), respectively treatment by calculation with the finite element method (linear and nonlinear approach). The set of results naturally leads to the recommendation to modify the working parameters of the safety elements from the hydraulic actuation scheme of the hydraulic actuators in order to avoid reaching the working pressures that would generate the appearance of critical compression forces from the buckling phenomenon at the level of the actuating rod of the element in question. The convergence of the obtained solution is confirmed by the set of output parameters shown in
Table 2, which thus validates the calculation methods studied.
Author Contributions
Conceptualization, V.F. and L.R.; methodology, V.F.; software, S.M.; validation, L.R., V.F.; formal analysis, S.M.; investigation, V.F., L.R., D.C.M. and A.G.; resources, A.B.; data curation, S.M., V.F.; writing—original draft preparation, V.F.; writing—review and editing, A.B.; visualization, S.M.; supervision, L.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Deutsch, I. The Strength of Materials; Didactic and Pedagogic Publishing House: Bucharest, Romania, 1979. [Google Scholar]
- Ungureanu, I.; Ispas, B.; Constantinescu, E. The Strength of Materials; The Institute of Civil Engineering: Bucharest, Romania, 1981; Volume 2. [Google Scholar]
- Andreescu, I.; Mocanu, Ş. Compendium of the Strength of Materials; Matrix Rom: Bucharest, Romania, 2005. [Google Scholar]
- Hunt, T.; Vaughan, N. The Hydraulic Handbook, 9th ed.; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Speich, H.; Bucciarelli, A. Manuale di Oleodinamica: Principi, Componenti, Circuiti, Applicazioni; Tecniche Nuove: Milan, Italy, 2002. [Google Scholar]
- Vullo, V. Circular cylinders and pressure vessels. In Stress Analysis and Design; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Evaldas, N. Buckling strength of hydraulic cylinders—An engineering approach and finite element analysis. Mechanika 2016, 22, 474–477. [Google Scholar]
- Gamez-Montero, P.J.; Salazar, E.; Castilla, R.; Khamashta, M.; Codina, E. Misalignment effects on the load capacity of a hydraulic cylinder. Int. J. Mech. Sci. 2005, 51, 105–113. [Google Scholar] [CrossRef]
- Baragetti, S.; Terranova, A. Bending behaviour of double-acting hydraulic actuator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2001, 215, 607–619. [Google Scholar] [CrossRef]
- Baragetti, S.; Villa, F. Effects of geometrical clearances, supports friction, and wear rings on hydraulic actuators bending behavior. Math. Probl. Eng. 2016. [Google Scholar] [CrossRef]
- Field, G.J.; Nau, B.S. An experimental study of reciprocating rubber seals. In Proceedings of the IMechE Symposium on Elastohydrodynamic Lubrication; Institution of Mechanical Engineers: London, UK, 1972; pp. 29–36. [Google Scholar]
- Strozzi, A.; Bertocchi, E.; Mantovani, S.; Giacopini, M.; Baldini, A. Analytical evaluation of the peak contact pressure in a rectangular elastomeric seal with rounded edges. J. Strain Anal. Eng. Des. 2016, 51, 304–317. [Google Scholar] [CrossRef]
- Morelli, P. On the Buckling Behaviour of Telescopic Hydraulic Cylinders, Key Engineering Materials; Trans Tech Publications: Red Hook, NY, USA, 2010; Volume 417, pp. 281–284. [Google Scholar]
- Lie, T.; Chapple, P.J.; Tilley, D.G. Actuator cushion performance simulation and test results. In Proceedings of the Bath Workshop on Power Transmission and Motion Control (PTMC 2000), Bath, UK, 15–18 September 2000; pp. 187–198. [Google Scholar]
- Schwartz, C.; De Negri, V.J.; Climaco, J.V. Modeling and analysis of an auto-adjustable stroke end cushioning device for hydraulic cylinders. J. Braz. Soc. Mech. Sci. Eng. 2005, 27, 415–425. [Google Scholar] [CrossRef]
- Lifshitz, J.M.; Dayan, H. Filament-wound pressure vessel with thick metal liner. Compos. Struct. 1995, 32, 313–323. [Google Scholar] [CrossRef]
- Chapelle, D.; Perreux, D. Optimal design of type 3 hydrogen vessel: Part I—Analytic modelling of the cylindrical section. Int. J. Hydrogen Energy 2006, 31, 627–638. [Google Scholar] [CrossRef]
- Comond, C.; Perreux, D.; Thiebaud, F.; Weber, M. Methodology to improve the lifetime of type III HP tank with a steel liner. Int. J. Hydrogen Energy 2009, 34, 3077–3090. [Google Scholar] [CrossRef]
- Gay, D.; Hoa, S.V.; Tsai, S.W. Composite Materials: Design and Applications, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Bragohain, M.K. Composite Structures Design, Mechanics, Analysis, Manufacturing and Testing; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Thesken, C.; Murthy, P.L.N.; Phoenix, S.L.; Greene, N.; Palko, J.L.; Eldridge, J.; Sutter, J.; Saulsberry, R.; Beeson, H. A Theoretical Investigation of Composite Overwrapped Pressure Vessel (COPV) Mechanics Applied to NASA Full-Scale Tests. Technical Memorandum. 2009. Available online: https://ntrs.nasa.gov/citations/20090037028 (accessed on 8 April 2020).
- Lanzi, L.; Castelletti, L.M.L.; Anghileri, M. Multi-objective optimization of composite absorber shape under crashworthiness requirements. Compos. Struct. 2004, 65, 433–441. [Google Scholar] [CrossRef]
- Bisagni, C.; Di Pietro, G.; Fraschini, L.; Terletti, D. Progressive crushing of fiber-reinforced composite structural components of a Formula One racing car. Compos. Struct. 2005, 68, 491–503. [Google Scholar] [CrossRef]
- Otte, B.; Stelling, O.; Müller, C. High-Pressure Lightweight Hydraulic Fully Composite Piston Accumulators. In Proceedings of the 8th International Fluid Power Conference, Dresden, Germany, 26–28 March 2012. [Google Scholar]
- Solazzi, L. Feasibility study of hydraulic cylinder subject to high pressure made of aluminum alloy and composite material. Compos. Struct. 2019, 209, 739–746. [Google Scholar] [CrossRef]
- Solazzi, L. Design and experimental tests on hydraulic actuator made of composite material. Compos. Struct. 2020, 232. [Google Scholar] [CrossRef]
- Solazzi, L.; Bunoli, A. Telescopic Hydraulic Cylinder Made of Composite Material. Appl. Compos. Mater. 2019, 26, 1189–1206. [Google Scholar] [CrossRef]
- Fragassa, C.; Minak, G.; Pavlovic, A. Measuring deformations in the telescopic boom under static and dynamic load conditions. Facta Univ. Ser. Mech. Eng. 2020, 18, 315–328. [Google Scholar] [CrossRef]
- Pavlovic, A.; Fragassa, C.; Minak, G. Buckling analysis of telescopic boom: Theoretical and numerical verification of sliding pads. Tehnički Vjesnik 2017, 24, 729–735. [Google Scholar] [CrossRef]
Figure 1.
Position of the platform after the accident.
Figure 2.
Buckled element. (a) General structure view; (b) actuator area; (c) actuator rod.
Figure 3.
State of the material. (a) In the contraction area; (b) in the stretched area.
Figure 4.
Section in the affected area: 1—maximum and 2—minimum thickness zones.
Figure 5.
Collected samples from affected and unaffected areas of the rod.
Figure 6.
Metallographic structures. (a) With cold deformation; (b) with plastic deformation.
Figure 7.
Actuator-rod parameters.
Figure 8.
Detail of key position.
Figure 9.
Johnson’s Parabola.
Figure 10.
Hydraulic cylinder-rod solid model assembly, SolidWorks V 2014, Dassault Systèmes, Vélizy-Villacoublay, France.
Figure 11.
Deformed shape of the rod/buckling length output parameters.
Figure 12.
Buckling safety factor (load factor); Euler buckling output parameters.
Figure 13.
Buckling safety factor (load factor), nonlinear study output parameters.
Figure 14.
Piston rod–cylinder solid model assembly, SolidWorks 2014, Dassault Systèmes.
Figure 15.
Deformed shape and buckling safety factor—output parameters.
Figure 16.
Computational scheme (a) and buckling length—input (b)/output (c) parameters.
Figure 17.
Buckling safety factor (load factor), the nonlinear study of the assembly—output parameters.
Figure 18.
Nonlinear analysis settings.
Figure 19.
N–R method of iterative calculation.
Figure 20.
Beam internal forces/axial loads values. (a) Structure–beam internal forces; (b) detail of beam internal forces.
Figure 21.
Boundary conditions for the loading scheme diagram—input parameters, AxisVM 9, InterCad, Budapest, Hungary.
Table 2.
Values obtained by different methods.
| Method Used | Critical Buckling Load (kN) | Hydraulic Fluid Pressure in the Cylinder Chamber (bar) |
|---|
| Euler | 609.60 | 114.50 |
| Johnson | 593.80 | 111.51 |
| Nonlinear modeling FEM—piston-rod | 555.94 | 104.40 |
| Nonlinear modeling FEM—piston-rod and cylinder assembly | 586.99 | 110.24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).