Modeling Air Aspiration in Steel Continuous Casting Slide-Gate Nozzles
Abstract
:1. Introduction
2. Previous Models
3. New 1-D Pressure Energy Model
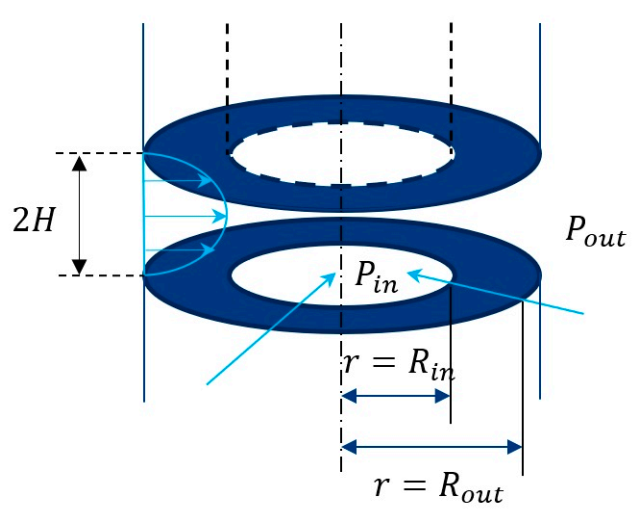
3.1. Model Geometry: Slide-Gate System
3.2. Model Methodology: 1-D Pressure Energy Model for Multiphase Flow
| Point ⑩ (mold level) | (6) | |
| Point (top of port outlet) | (7) | |
| Point (SEN, same height to Point 9) | (8) | |
| Point (SEN, outlet of tapered part) | (9) | |
| Point (SEN, inlet of tapered part) | (10) | |
| Point (just below slide-gate) | (11) | |
| Point (just above slide-gate) | (12) | |
| Point (inlet of UTN) | (13) | |
| Point (bottom of tundish) | (14) | |
| Point (tundish level) | (15) |
| (16) | |
| (17) | |
| (18) | |
| (19) | |
| (20) | |
| (21) | |
| (22) | |
| (23) | |
| (24) | |
| (25) | |
| (26) | |
| (27) |
3.3. Pressure Loss Calculation
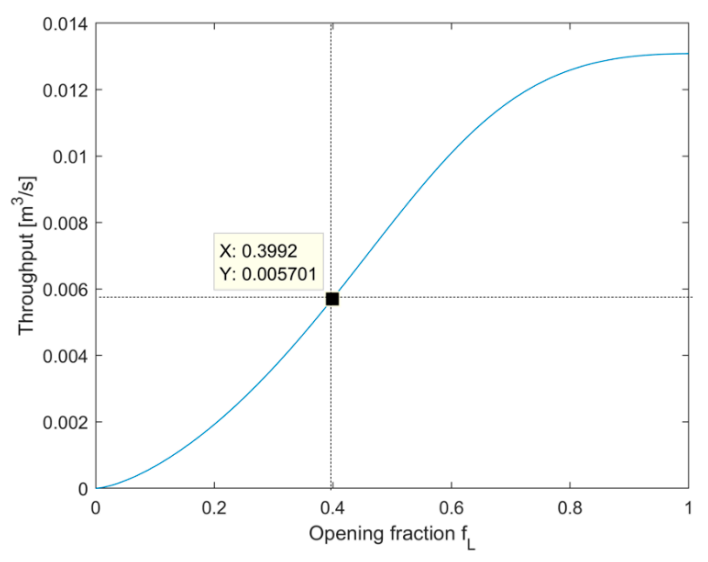
3.4. Throughput and Velocity Calculation
3.5. Gas Aspiration Model
3.6. Inclusion Formation Model
3.7. Dynamic Clogging Model
- (1)
- calculate the required slide-gate opening to achieve a target throughput.
- (2)
- estimate the pressure distribution for these conditions.
- (3)
- calculate the air aspirated based on the local pressure difference between inside and outside of the refractory wall, (), and the thickness of a postulated gap.
- (4)
- calculate the mass of oxides formed based on the reaction rate of alumina with the aspirated oxygen.
- (5)
- deposit the alumina at the selected site of the clog and update the additional pressure loss for the new clogged geometry.
- (6)
- move to the next time step and repeat steps 1 to 5 until the slide-gate opening reaches 100% or the deposit size is fully-clogged.
4. 3-D Computational Model of Nozzle Flow and Pressure
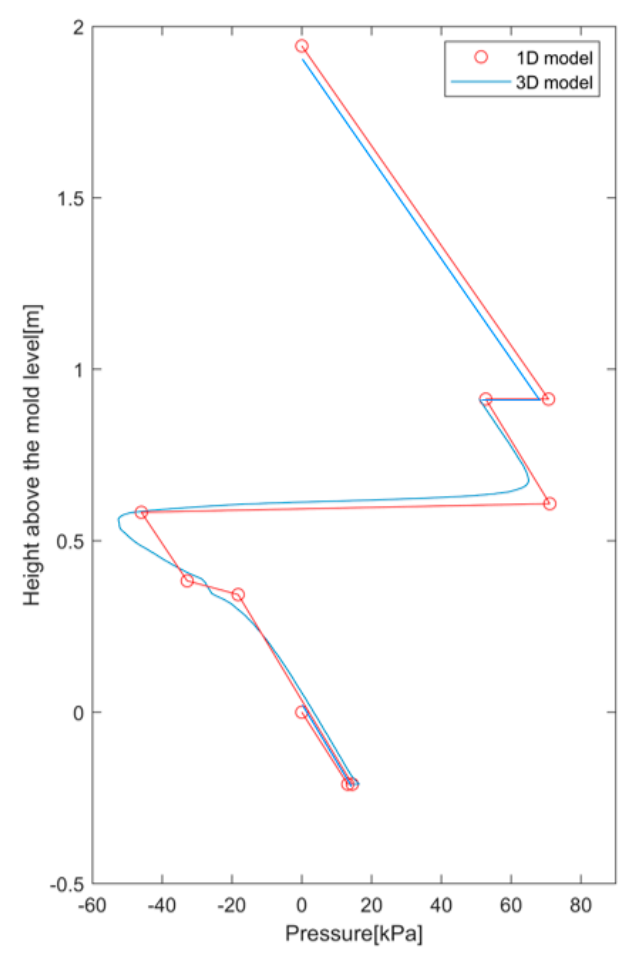
5. 1-D Model Verification with 3-D Computational Model
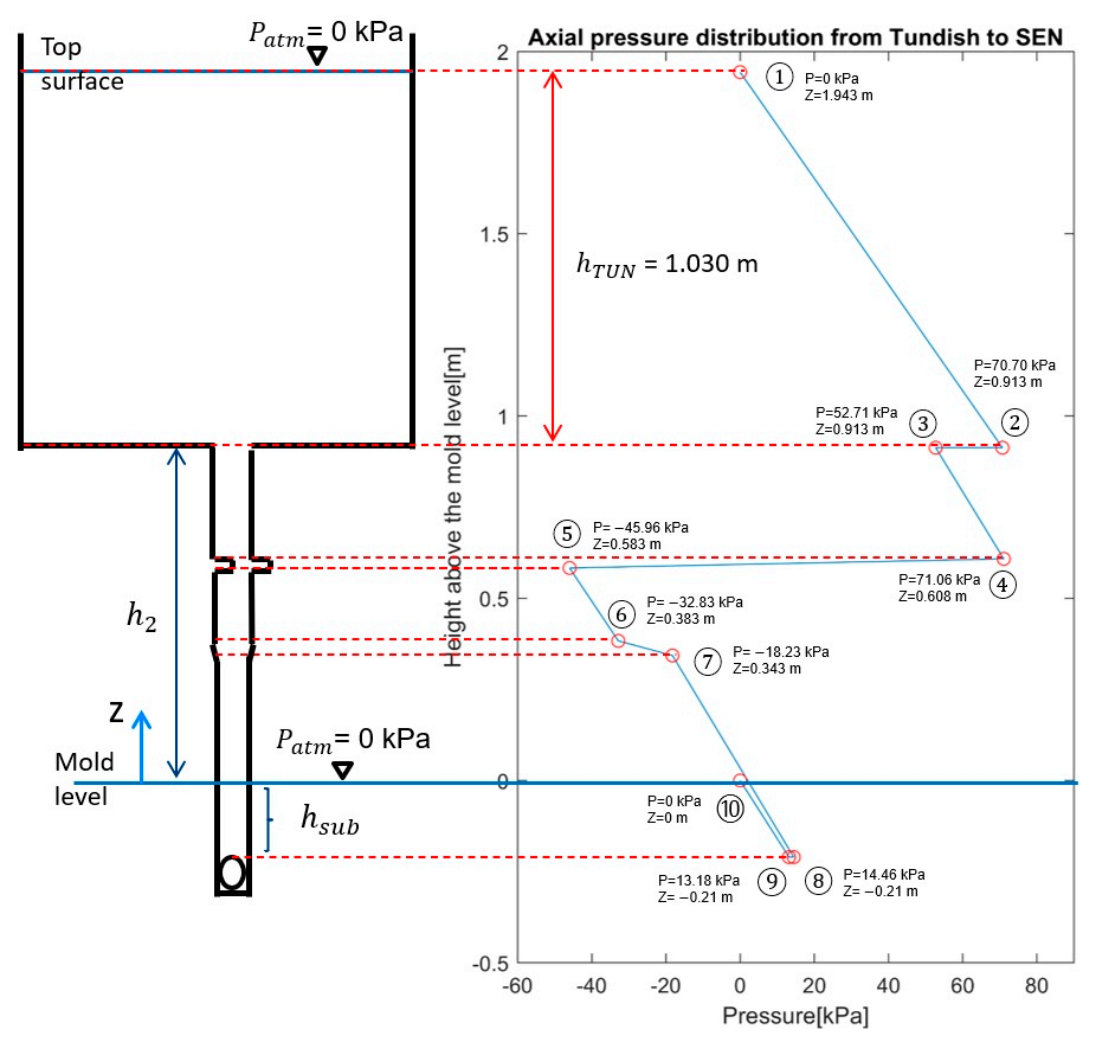
6. Model Validation with Plant Measurements
7. Parametric Studies
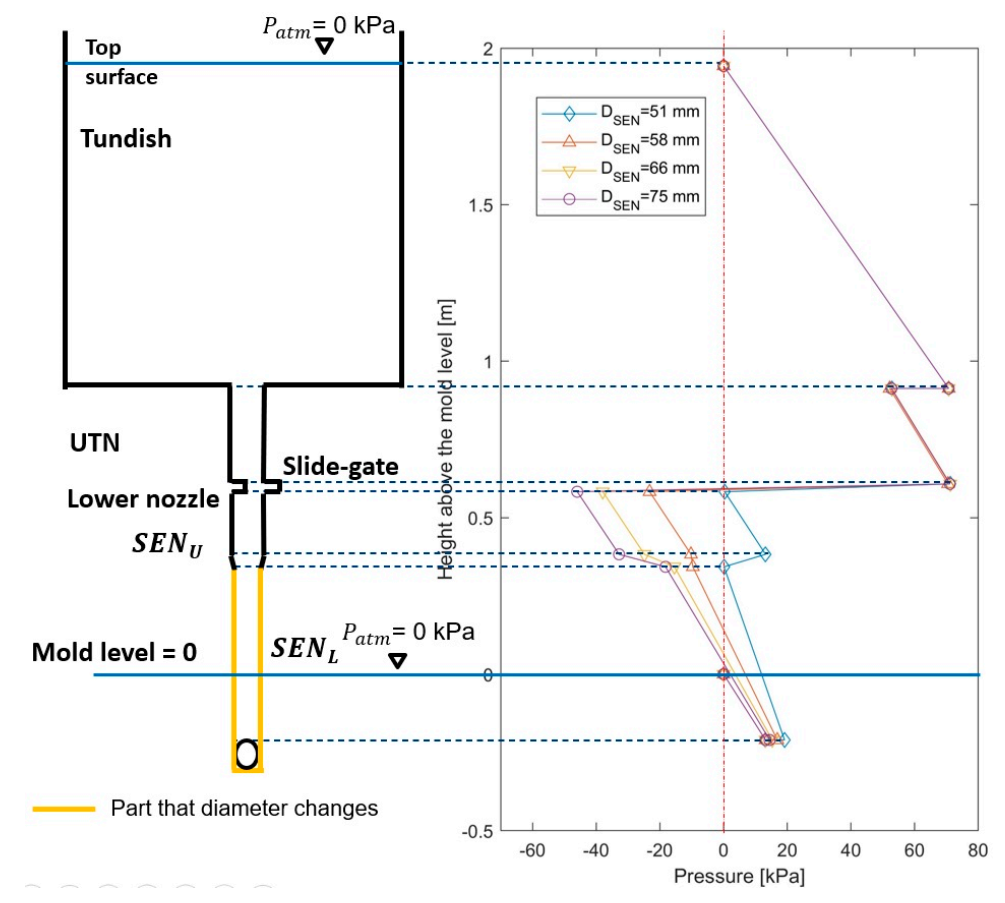
7.1. Effect of SEN Lower Diameter
7.2. Effect of Overall Nozzle Diameter
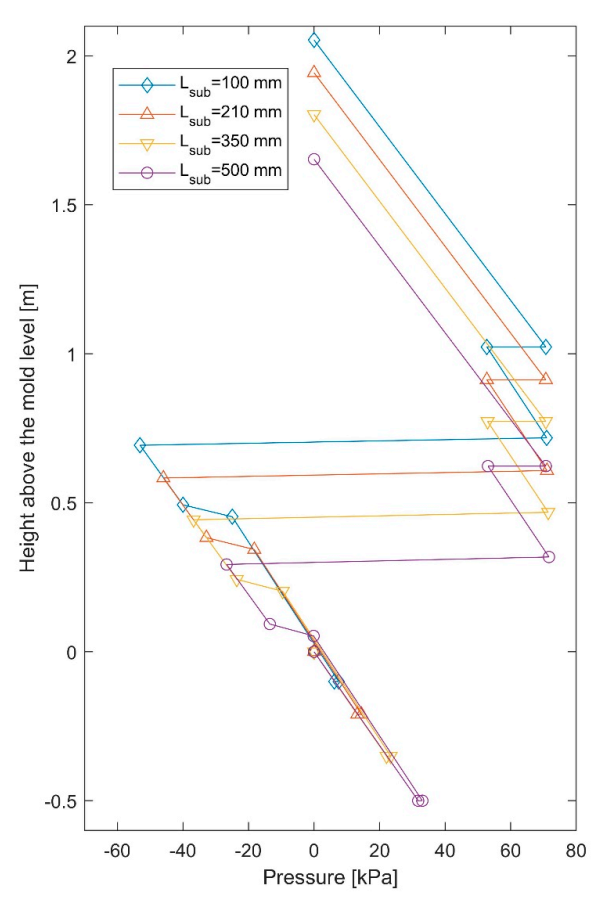
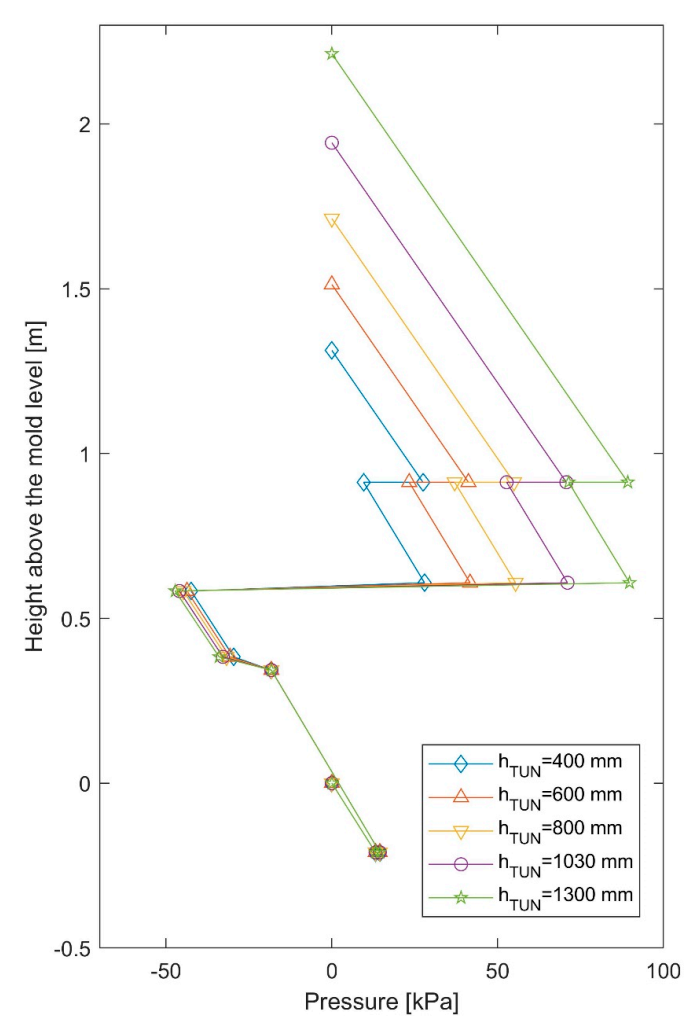
7.3. Effect of Submergence Depth and Tundish Level
8. Estimation of Air Aspiration, Reoxidation, and Transient Clogging
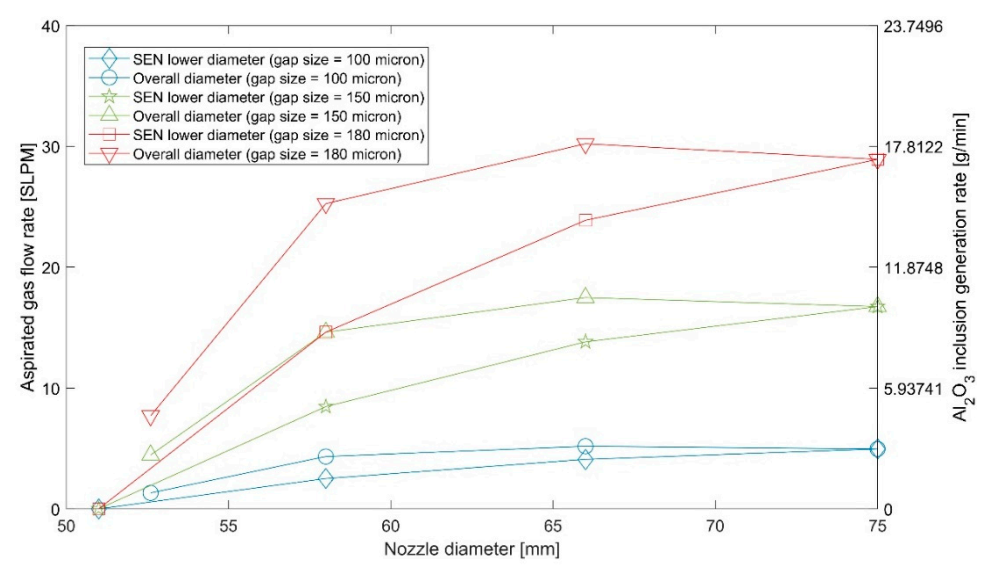
8.1. Estimation of Aspirated Gas Flow Rate and Reaction Rate of Generated Alumina
8.2. Static and Dynamic Estimation of Clogging Shutdown Time
9. Discussion
10. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Rackers, K.; Thomas, B. Clogging in continuous casting nozzles. In Proceedings of the 78th Steelmaking Conference, Nashville, TN, USA, 2–5 April 1995; Volume 78, pp. 723–734. [Google Scholar]
- Yokoya, S.; Takagi, S.; Souma, H.; Iguchi, M.; Asako, Y.; Hara, S. Prevention of air suction from the contact-part between sliding gate and immersion nozzle. ISIJ Int. 1998, 38, 1346–1352. [Google Scholar] [CrossRef]
- Bai, H.; Thomas, B.G. Effects of clogging, argon injection, and continuous casting conditions on flow and air aspiration in submerged entry nozzles. Metall. Mater. Trans. B 2001, 32, 707–722. [Google Scholar] [CrossRef]
- Savolainen, J.; Rousu, A.; Fabritius, T.; Mattila, O.; Sulasalmi, P. Modelling of Pressure Distribution inside the SEN in a Stopper-rod controlled System. Steel Res. Int. 2010, 81, 980–986. [Google Scholar] [CrossRef]
- Zhang, L.; Thomas, B.G. Inclusions in continuous casting of steel. In Proceedings of the XXIV National Steelmaking Symposium, Morelia, Mich, Mexico, 26–28 November 2003; pp. 138–183. [Google Scholar]
- Janis, D.; Karasev, A.; Inoue, R.; Jönsson, P.G. A Study of Cluster Characteristics in Liquid Stainless Steel and in a Clogged Nozzle. Steel Res. Int. 2015, 86, 1271–1278. [Google Scholar] [CrossRef]
- Mohammadi-Ghaleni, M.; Asle Zaeem, M.; Smith, J.D.; O’Malley, R. Comparison of CFD Simulations with Experimental Measurements of Nozzle Clogging in Continuous Casting of Steels. Metall. Mater. Trans. B 2016, 47, 3384–3393. [Google Scholar] [CrossRef]
- Yang, H.; Vanka, S.P.; Thomas, B.G. Modeling Argon Gas Behavior in Continuous Casting of Steel. JOM 2018, 70, 2148–2156. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Zuo, X. Flow Transport and Inclusion Motion in Steel Continuous-Casting Mold under Submerged Entry Nozzle Clogging Condition. Metall. Mater. Trans. B 2008, 39, 534–550. [Google Scholar] [CrossRef]
- Thomas, B.G. Modeling of continuous casting defects related to mold fluid flow. Iron Steel Technol. 2006, 3, 127. [Google Scholar]
- Hibbeler, L.C.; Thomas, B.G. Mold slag entrainment mechanisms in continuous casting molds. Iron Steel Technol. 2013, 10, 121–136. [Google Scholar]
- Cho, S.-M.; Kim, S.-H.; Chaudhary, R.; Thomas, G.B.; Shin, H.-J.; Choi, W.-R.; Kim, S.-K. Effect of Nozzle Clogging on Surface Flow and Vortex Formation in the Continuous Casting Mold. In Proceedings of the AISTech 2011, Indianapolis, IN, USA, 2–5 May 2011. [Google Scholar]
- Murakami, Y.; Kodama, S.; Konuma, S. Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. I: Basic fatigue mechanism and evaluation of correlation between the fatigue fracture stress and the size and location of non-metallic inclusions. Int. J. Fatigue 1989, 11, 291–298. [Google Scholar] [CrossRef]
- Wilson, A.D. The Influence of Inclusions on the Toughness and Fatigue Properties of A516-70 Steel. J. Eng. Mater. Technol. 1979, 101, 265. [Google Scholar] [CrossRef]
- Zhang, L.; Aoki, J.; Thomas, B.G. Inclusion removal by bubble flotation in a continuous casting mold. Metall. Mater. Trans. B 2006, 37, 361–379. [Google Scholar] [CrossRef]
- Wang, L.; Lee, H.G.; Hayes, P. Modelling of air ingress and pressure distribution in ladle shroud system for continuous casting of steel. Steel Res. 1995, 66, 279–286. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Q.; Yang, S.; Chen, Z.; Li, J.; Jiang, Z. Advances in Ladle Shroud as A Functional Device in Tundish Metallurgy: A Review. ISIJ Int. 2019, 59, 1167–1177. [Google Scholar] [CrossRef] [Green Version]
- Ishiguro, K.; Iguchi, M. Model Experiment on the Behavior of Argon Gas in Immersion Nozzle. ISIJ Int. 2003, 43, 663–670. [Google Scholar] [CrossRef]
- Kato, T.; Hara, M.; Muto, A.; Hiraki, S.; Kawamoto, M. Fluid Flow Behavior in Submerged Entry Nozzle of Continuous Casting. ISIJ Int. 2007, 47, 840–846. [Google Scholar] [CrossRef] [Green Version]
- Timmel, K.; Shevchenko, N.; Röder, M.; Anderhuber, M.; Gardin, P.; Eckert, S.; Gerbeth, G. Visualization of Liquid Metal Two-phase Flows in a Physical Model of the Continuous Casting Process of Steel. Metall. Trans. B 2015, 46, 700–710. [Google Scholar] [CrossRef]
- POSCO. Method For Continuous Casting to Prevent AirAspiration in Slide Gate. Korea Patent KR 1020040039502, 2004. [Google Scholar]
- SMS Siemag LLC. Method and Apparatus for Testing the Integrity of A Shroud Seal on A Ladle for A Continuous Casting Installation. U.S. Patent US007628952B2, 4 May 2007. [Google Scholar]
- Liu, R.; Thomas, B.G.; Sengupta, J.; Chung, S.D.; Trinh, M. Measurements of Molten Steel Surface Velocity and Effect of Stopper-rod Movement on Transient Multiphase Fluid Flow in Continuous Casting. ISIJ Int. 2014, 54, 2314–2323. [Google Scholar] [CrossRef] [Green Version]
- Majidi, S.H.; Beckermann, C. Effect of pouring conditions and gating system design on air entrainment during mold filling. Int. J. Metalcast. 2019, 13, 255–272. [Google Scholar] [CrossRef]
- Prakash, M.; Cleary, P.W.; Grandfield, J.; Rohan, P.; Nguyen, V. Optimisation of ingot casting wheel design using SPH simulations. Prog. Comput. Fluid Dyn. 2007, 7, 101–110. [Google Scholar] [CrossRef]
- Suzuki, M.; Yamaoka, Y.; Kubo, N.; Suzuki, M. Oxidation of molten steel by the air permeated through a refractory tube. ISIJ Int. 2002, 42, 248–256. [Google Scholar] [CrossRef] [Green Version]
- Moody, L.F. Friction factors for pipe flow. Trans. ASME 1944, 66, 671–684. [Google Scholar]
- Churchill, S.W. Empirical expressions for the shear stress in turbulent flow in commercial pipe. AlChE J. 1973, 19, 375–376. [Google Scholar] [CrossRef]
- Colebrook, C.F.; Blench, T.; Chatley, H.; Essex, E.; Finniecome, J.; Lacey, G.; Williamson, J.; Macdonald, G. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 12, 393–422. [Google Scholar] [CrossRef]
- Todreas, N.E.; Kazimi, M.S. Nuclear Systems: Thermal Hydraulic Fundamentals; CRC Press: Boca Raton, FL, USA, 2012; Volume 1. [Google Scholar]
- Erhard, P.; Etling, D.; Muller, U.; Riedel, U.; Sreenivasan, K.; Warnatz, J. Prandtl-Essentials of Fluid Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Volume 158. [Google Scholar]
- White, F.M. Fluid Mechanics, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Brater, E.F.; King, H.W. Handbook of Hydraulics for the Solution of Hydraulic Engineering Problems; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Valve, C. Flow of Fluids through Valves, Fittings and Pipe TP-410 Metric; Vervante: Lindon, UT, USA, 1999. [Google Scholar]
- Thomas, B.G.; Huang, X.; Sussman, R.C. Simulation of Argon Gas Flow Effects in a Continuous Slab Caster. Metall. Mater. Trans. B 1994, 25, 527–547. [Google Scholar] [CrossRef]
- Liu, R.; Thomas, B.G.; Forman, B.; Yin, H. Transient turbulent flow simulation with water model validation and application to slide gate dithering. In Proceedings of the AISTech 2012, Atlanta, GA, USA, 7–10 May 2012. [Google Scholar]
- Armaly, B.F.; Durst, F.; Pereira, J.; Schönung, B. Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 1983, 127, 473–496. [Google Scholar] [CrossRef]
- Biswas, G.; Breuer, M.; Durst, F. Backward-facing step flows for various expansion ratios at low and moderate Reynolds numbers. J. Fluids Eng. 2004, 126, 362–374. [Google Scholar] [CrossRef]
- Lima, R.C.; Andrade, C.R.; Zaparoli, E.L. Numerical study of three recirculation zones in the unilateral sudden expansion flow. Int. Commun. Heat Mass Transfer 2008, 35, 1053–1060. [Google Scholar] [CrossRef]
- Gutiérrez, E.; Barreto, J.d.J.; Garcia-Hernandez, S.; Morales, R.; González-Solorzano, M.G. Decrease of Nozzle Clogging through Fluid Flow Control. Metals 2020, 10, 1420. [Google Scholar] [CrossRef]
- Barati, H.; Wu, M.; Kharicha, A.; Ludwig, A. A transient model for nozzle clogging. Powder Technol. 2018, 329, 181–198. [Google Scholar] [CrossRef]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- White, F.M.; Corfield, I. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 2006; Volume 3. [Google Scholar]
- Clauser, F.H. Turbulent boundary layers in adverse pressure gradients. J. Aeronaut. Sci. 2012, 21, 91–108. [Google Scholar] [CrossRef]
- Nikuradse, J. Strömungsgesetze in Rauhen Rohren ForschHft. Ver. Dt. Ing 1933, 361. [Google Scholar]
- Kojola, N.; Ekerot, S.; Jönsson, P. Pilot plant study of clogging rates in low carbon and stainless steel grades. Ironmak. Steelmak. 2011, 38, 81–89. [Google Scholar] [CrossRef]









| Dimension | Value |
|---|---|
| UTN bore diameter, (mm) | 80 |
| UTN length (mm) | 255 |
| Upper plate thickness (mm) | 50 |
| Upper plate bore diameter, (mm) | 80 |
| Slide-gate thickness (mm) | 25 |
| Slide-gate bore diameter, (mm) | 80 |
| Slide-gate orientation (deg.) | 90 |
| Lower plate & Lower nozzle bore diameter, (mm) | 80 |
| Lower plate thickness + Lower nozzle length (mm) | 160 |
| SEN whole length (mm) | 714 |
| SEN upper part bore diameter, (mm) | 80 |
| SEN upper part length (mm) | 40 |
| SEN tapered part length (mm) | 40 |
| SEN lower part bore diameter, (mm) | 75 |
| SEN lower part length (mm) | 634 |
| Port width × port height (mm × mm) | 60 × 80 |
| Port angle (down) (deg.) | 15 |
| Port thickness (mm) | 23.5 |
| Slab geometry: T (thickness) × W (width) (m) | 0.3 × 1.9 |
| Operating Condition | Values |
|---|---|
| Slab size (m) | 1.9 |
| Slide-gate orientation (deg.) | 90 (orthogonal to mold width direction) |
| Slide-gate opening | 0.4 |
| Tundish depth (mm) | 1030 |
| Casting speed (m/min) | 0.60 |
| Argon gas flow rate (SLPM) | 3.8 (from UTN wall) 2.2 (from upper plate) |
| Submergence depth (m) | 0.21 |
| Absolute average roughness of nozzle wall (mm) | 1 (nonclogged condition) |
| Hot argon gas temperature (K) | 1823 |
| Hot argon gas pressure (kPa) | 70.7 (=) |
| Material Property | Values |
| Liquid steel density ( | 7000 |
| Liquid steel viscosity (Pas) | 0.006 |
| Argon gas density ( | 1.6228 |
| Argon gas viscosity (Pas) | 2.125 |
| Mixture density ( | 6580 |
| Results | |||
|---|---|---|---|
| Plant data | 0.40 | 1030 | 0.0057 |
| 3-D model | 0.40 (input) | 995 (output) | 0.0057 (input) |
| 1-D model | 0.3992 (output) | 1030 (input) | 0.0057 (input) |
| No. | Slab Size (m) | (m/min) | (SLPM) | Tundish Depth (m) | Slide-Gate Opening, (%) 1-D Model | Slide-Gate Opening, (%) Plant Data | Clogging Condition |
| 1 | 1.9 | 0.60 | 6 | 1.03 | 40.0 | 40 | Nonclogged |
| 2 | 1.9 | 0.60 | 6 | 1.03 | 40.0 | 40 | Nonclogged |
| 3 | 2.1 | 0.66 | 4.3 | 1.08 | 44.4 | 43 | Nonclogged |
| 4 | 2.1 | 0.66 | 4 | 1.10 | 44.2 | 46 | Nonclogged |
| 5 | 2.1 | 0.66 | 8.2 | 1.02 | 46.1 | 45 | Nonclogged |
| 6 | 2.1 | 0.70 | 4.2 | 1.02 | 46.8 | 37 | Nonclogged |
| 7 | 1.7 | 0.80 | 7 | 1.02 | 45.1 | 45 | Clogged |
| 8 | 1.7 | 0.80 | 7 | 0.98 | 45.2 | 39 | Clogged |
| 9 | 1.7 | 0.74 | 6.5 | 1.02 | 42.8 | 49 | Clogged |
| 10 | 2.1 | 0.70 | 8.6 | 1.02 | 48.2 | 61 | Severely Clogged |
| 11 | 2.1 | 0.70 | 10.2 | 1.02 | 48.7 | 66 | Severely Clogged |
| 12 | 2.1 | 0.70 | 8.4 | 0.93 | 48.9 | 63 | Severely Clogged |
| Cases | Liquid Steel | (Friction Factor) | (Slide-Gate Opening) | |
|---|---|---|---|---|
| Original (Case 1) | 75 | 0.0057 | 0.0424 | 0.400 |
| Parametric case A | 66 | 0.0057 | 0.0443 | 0.407 |
| Parametric case B | 58 | 0.0057 | 0.0463 | 0.428 |
| Parametric case C | 51 | 0.0057 | 0.0485 | 0.456 |
| Cases | All (mm) | Liquid Steel Throughput Q | All (Friction Factor) | (Slide-Gate Opening) |
| Original (Case 1) | 75 | 0.0057 | 0.0424 | 0.400 |
| Parametric case D | 66 | 0.0057 | 0.0443 | 0.5118 |
| Parametric case E | 58 | 0.0057 | 0.0463 | 0.6334 |
| Parametric case F | 52.6 | 0.0057 | 0.0480 | 1.000 |
| Cases | Submergence Depth (mm) | Liquid Steel | (Slide-Gate Opening) |
|---|---|---|---|
| Parametric case G | 100 | 0.0057 | 0.3936 |
| Original (Case 1) | 210 | 0.0057 | 0.4000 |
| Parametric case H | 350 | 0.0057 | 0.4072 |
| Parametric case I | 500 | 0.0057 | 0.4171 |
| Cases | Tundish Level (mm) | Liquid Steel | (Slide-Gate Opening) |
|---|---|---|---|
| Parametric case J | 400 | 0.0057 | 0.4568 |
| Parametric case K | 600 | 0.0057 | 0.4345 |
| Parametric case L | 800 | 0.0057 | 0.4165 |
| Original (Case 1) | 1030 | 0.0057 | 0.4 |
| Parametric case M | 1300 | 0.0057 | 0.3820 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Olia, H.; Thomas, B.G. Modeling Air Aspiration in Steel Continuous Casting Slide-Gate Nozzles. Metals 2021, 11, 116. https://doi.org/10.3390/met11010116
Yang H, Olia H, Thomas BG. Modeling Air Aspiration in Steel Continuous Casting Slide-Gate Nozzles. Metals. 2021; 11(1):116. https://doi.org/10.3390/met11010116
Chicago/Turabian StyleYang, Hyunjin, Hamed Olia, and Brian G. Thomas. 2021. "Modeling Air Aspiration in Steel Continuous Casting Slide-Gate Nozzles" Metals 11, no. 1: 116. https://doi.org/10.3390/met11010116
APA StyleYang, H., Olia, H., & Thomas, B. G. (2021). Modeling Air Aspiration in Steel Continuous Casting Slide-Gate Nozzles. Metals, 11(1), 116. https://doi.org/10.3390/met11010116






