A Systematic Review of Structural Reliability Methods for Deformation and Fatigue Analysis of Offshore Jacket Structures

Abstract

This paper presents the state of the art in Structural Reliability Analysis (SRA) methods with a view of identifying key applications of each method and its proposed variations, qualifying characteristics, advantages, and limitations. Due to the increasing complexity and scale of modern offshore jacket structures, it becomes increasingly necessary to propose an accurate and efficient approach for the assessment of uncertainties in their material properties, geometric dimensions, and operating environments. SRA, as a form of uncertainty analysis, has been demonstrated to be a useful tool in the design of structures because it can directly quantify how uncertainty about input parameters can affect structural performance. Herein, attention was focused specifically on the probabilistic fracture mechanics approach because this accounts accurately for fatigue reliability mostly encountered as being dominant in the design of such structures. The well-established analytical/approximate methods such as the First- and Second-Order Reliability Methods (FORM/SORM) are widely used as they offer a good balance between accuracy and efficiency for realistic problems. They are, however, inaccurate in cases of highly non-linear systems. As a result, they have been modified using methods such as conjugate search direction approach, saddle point approximation, subset simulation, evidence theory, etc. in order to improve accuracy. Initially, direct simulations methods such as the Monte Carlo Simulation Method (MCS) with its various variance reduction techniques such as the Importance Sampling (IS), Latin Hypercube Sampling (LHS), etc. are ideal for structures having non-linear limit states but perform poorly for problems that calculate very low probabilities of failure. Overall, each method has its own merits and limitation, with FORM/SORM being the most commonly used, but recently, simulation methods have increasingly been used due to continuous advances in computation powers. Other relevant methods include the Response Surface Methods (RSM) and the Surrogate Models/Meta-models (SM/MM), which are advanced approximation methods and are ideal for structures with implicit limit state functions and high-reliability indices. Combinations of advanced approximation methods and reliability analysis methods are also found in literature as they can be suitable for complex, highly non-linear problems.

1. Introduction

Modern offshore jacket structures such as those supporting wind turbines are often exposed to severe environmental conditions. Besides environmental impacts, failures occurring will result in significant financial losses. This moves the point of focus toward structural reliability assessment of such structures [1]. Most of the existing offshore wind turbines (OWTs) use monopile foundations and are installed in water depths less than 50 m. However, for larger turbines in deeper waters, monopiles become very large and increasingly uneconomical due to the difficulty of fabricating and installing such systems, as well as the consideration of modal requirements. Space frame structures, such as jackets derived from the petroleum industry, offer a lighter and yet stiff alternative to monopiles. Jackets can be cheaper in deep-water circumstances and, hence, they can contribute to the offshore wind industry’s quest for the reduction of Levelized Cost of Energy (LCoE). However, an effective design of these structures is resource-intensive, especially when designing to withstand the wide set of dynamic loading mechanisms. Thus, research is still required to improve the design and analysis of modern jacket-type support structures, with due consideration of the requirement for manufacturing optimization if ever these structures are to be mass produced [2,3,4].

Structural reliability (SR) can be defined as ‘the ability that a structure complies with given requirements under specific conditions during its intended design life’ [4,5,6,7]. Suitable SR levels will, therefore, avoid intolerable damage to a structure over a specified period of time [8,9]. Use of probabilistic methods in structural design is increasing, and many standards have made allowance for reliability analysis (RA) either in the calibration of partial safety factors or in design and analysis [10]. ISO 2394 gives information on the principles of reliability methods. Safety margins and factors in design are determined considering T-D (Time-dependent) deterioration mechanisms [11] (see Figure 1). RA allows for methods that analyze the service life variation of Failure Probability for specified modes of failure, treating uncertainties systematically. The cause of structural failure is the exceedance of limit state. When $g\left(\mathit{x}\right)<0$ (Limit State Function) they are defined as a failure domain, when $g\left(\mathit{x}\right)>0$ a safe domain, and a failure surface when $g\left(\mathit{x}\right)=0$. Structural reliability analysis (SRA) revolves around modeling uncertainties emanating from poor knowledge of design quantities, such as likelihood of events, variability, lack of knowledge, degree of belief, inaccuracy, etc. [6]. These terms are considered basic variables that consist of quantities of material properties and structural dimensions, yield stress, and other limitations in ultimate response, operational conditions and degradation, loading and environmental factors, etc. Uncertainties for SRA can be mainly grouped into two categories: aleatory and epistemic [12]. Aleatory uncertainties are the unavoidable natural randomness associated with an uncertain quantity [6]. Epistemic uncertainties result from inadequate knowledge or information about a quantity. Since epistemic uncertainties stem from inadequate knowledge, they can be minimized by gathering data for a longer period, taking more measurements, or carrying out further tests, among others. The present methodologies available for characterization of uncertainties can be classified into three groups, namely: the non-probabilistic approach, the precise probability approach, and the imprecise probability approach. Further information on these can be found in [13].

Reliability methods have four levels (levels I to IV) of classification, according to the way that uncertainty is considered in the analysis [5]. Level I methods are deterministic reliability methods, which only apply one characteristic value to define each uncertain variable. Popular design standard formats, allowable stress, and load resistance belong to this category. They can be applied in combination with more advanced, higher-order methods in the case of calibration of partial safety factors, which can lead to their optimization [7]. Level II applies two values for the description of each random variable (e.g., the mean and the variance) and a supplementary measure of the correlation between the variables (e.g., covariance). Reliability can be interpreted geometrically as a relative distance from the mean values of loads and their effects. In Level III, the joint probability distribution of the sum of the uncertain variables is introduced, directly computing the POF (Probability of Failure) for a performance function (PF). This category consists of the approximate analytical methods, including the First- and Second-Order Reliability Methods, advanced mathematical techniques such as numerical integration (NI), and simulation methods, such as the Monte Carlo Simulation (MCS) and the Directional Sampling methods. Level IV reliability methods introduce elements of target cost to the engineering principles, so as to derive a technically feasible and, as such, an economically optimized solution. These methods are the most advanced and can set a target reliability level, which is acceptable such that Level III methods can be applied.

This paper aimed to present a state-of-the-art review of Level II and III reliability methods, identifying key applications of each method, qualifying characteristics, advantages and limitations. To the best of the authors’ knowledge, the work performed herein is the first study to review research works conducted on the reliability/probabilistic assessment/evaluation of structures focusing specifically on applicability to design of modern offshore jacket structures against deformation and fatigue. The findings of this research can provide invaluable insights to researchers about the method used for such analyses. In order to identify relevant sources, a systematic review approach was followed, focusing the search mainly on works published from 2005 to 2020, using predefined words and combinations of words, which included “first-order reliability method” or “FORM” or “second-order reliability method” or “SORM” or “Monte Carlo” or “probability of failure (POF)” or “reliability index (RI)” or “safety” or “probabilistic safety” or “safety level” or “reliability safety” or “stochastic” or “probabilistic” or “structural reliability” or “reliability” and “analysis” or “assessment” or “evaluation”, etc. on Scopus, science direct, web of science, ASME (American Society of Mechanical Engineers) digital collection, ASCE (American Society of Civil Engineers) library, ICE (Institution of Civil Engineers)virtual library, one petro, etc. Figure 2 illustrates a classification of the various SRA methods that are presented in a structured form.

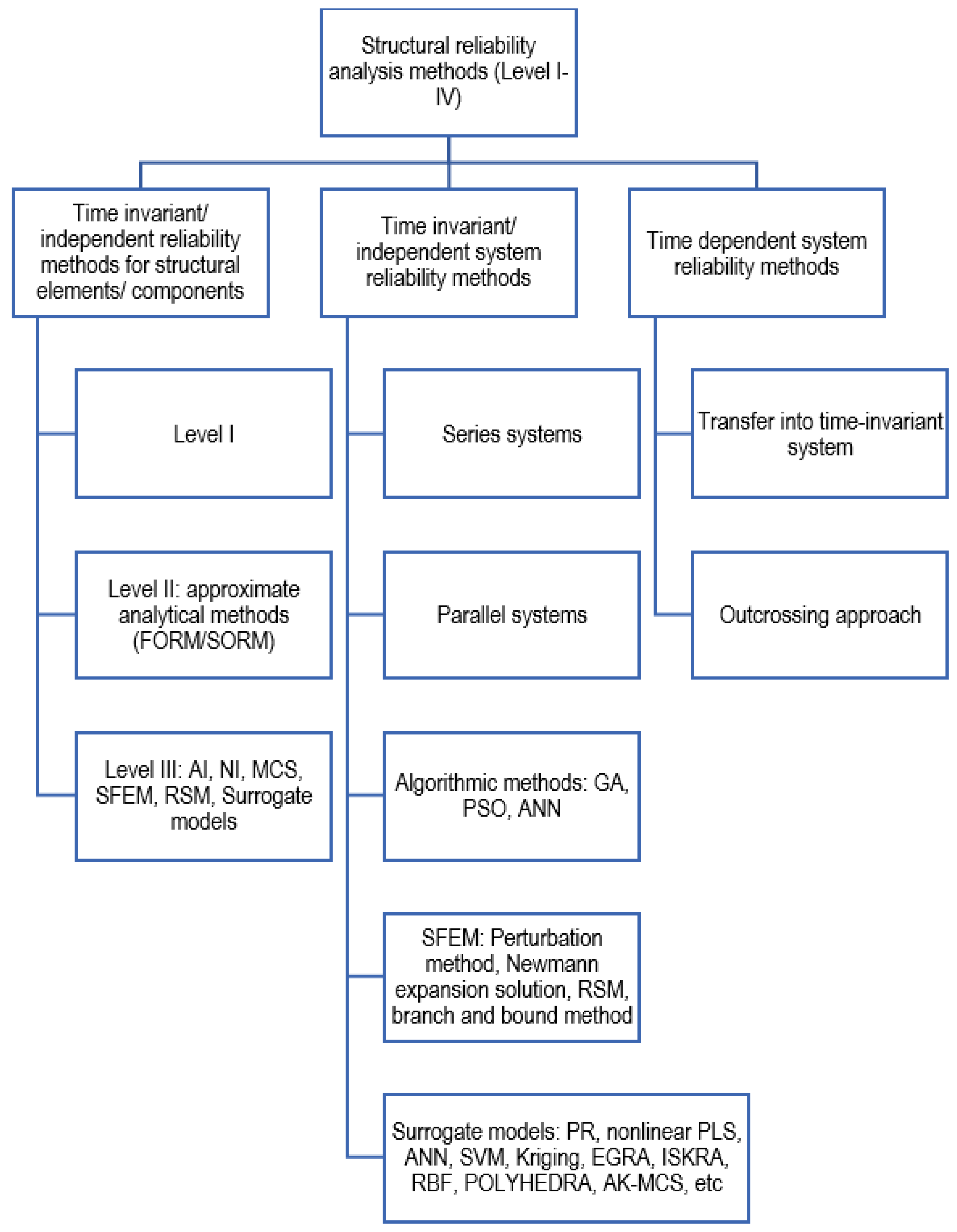
2. Level III Analytical Structural Reliability Analysis Methods

The probability of failure (POF) of a structural element with regards to a single mode of failure can be formally expressed as [16]:

$$P_f={{\displaystyle \int }}_{g\left(\mathit{x}\right)\le 0}{f}_{\mathit{X}}\left(\mathit{x}\right)d\mathit{x}.$$

(1)

The complexity in directly calculating the failure probability $P_f$ from the integral expressed in Equation (1) resulted in the establishment of approximate reliability methods. Such methods involve approximating the failure surface to some simple forms, e.g., hyperplane or quadratic surfaces at certain locations, referred to as design points. This procedure is known as forward SRA. The method used for this computation algorithm is a level II technique, whereby the multidimensional integral expressed in Equation (1) is estimated after the operations: (1) The basic uncertain variables are transferred onto a set of independent Gaussian random variables represented by the $U$ vector. The transformation operation is denoted by $T$ such that $U=T\left(\mathit{X}\right).$ (2) The $\mathrm{LSF}$ in the U space $Z=g\left(\mathit{u}\right)$ is approximated to a linear or second-order (quadratic) function at the limit state surface, which forms a hyperplane or a quadratic failure surface. Methods based on linear approximation are referred to as the “First-Order Reliability Methods (FORM)” and those based on quadratic approximation are known as the “Second-Order Reliability Methods (SORM)” [4,5].

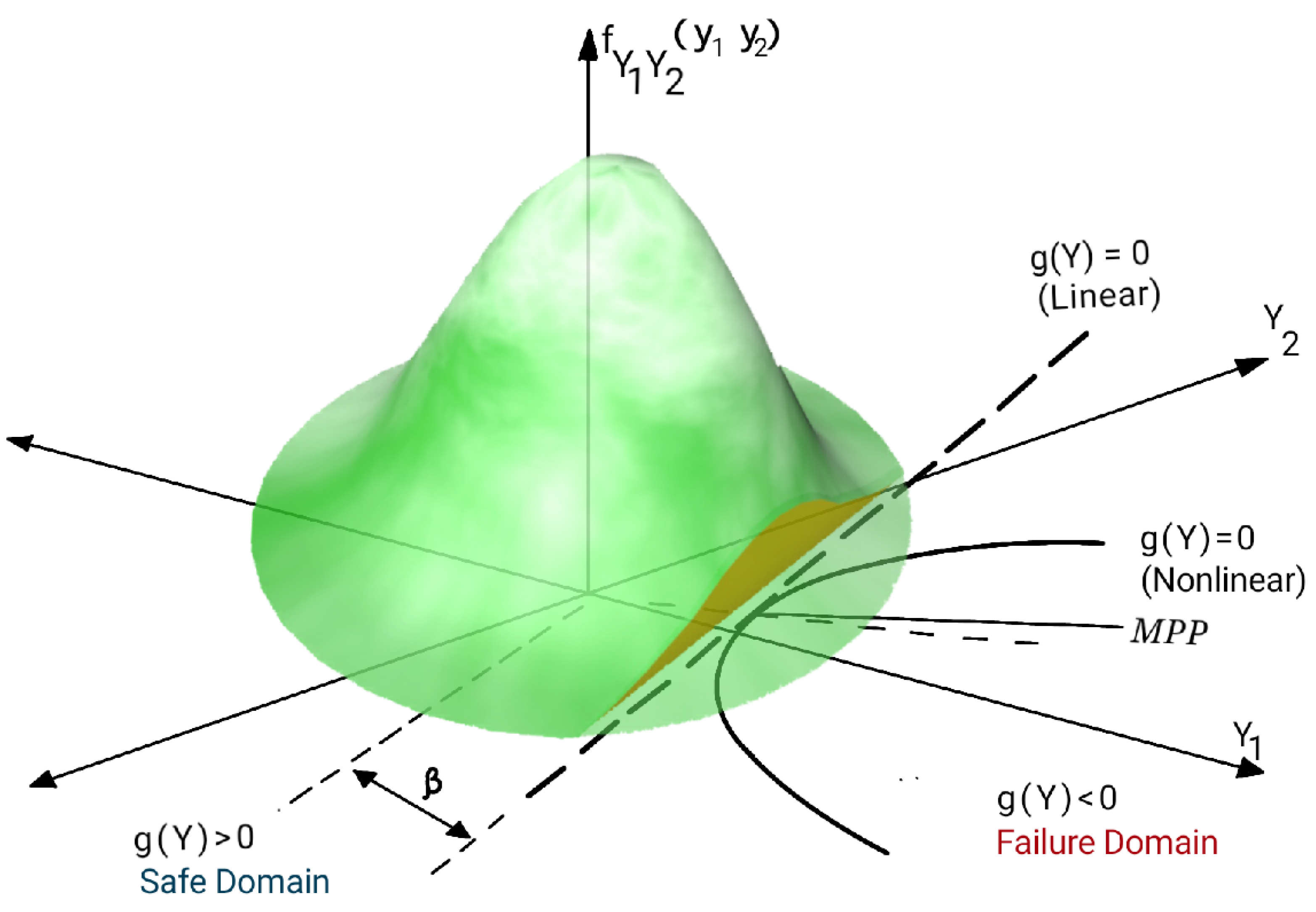
2.1. First-Order Reliability Method (FORM)

Theoretical background about FORM can be found in [5,17]. In the FORM, the random variables are represented by means and variances and assume normal distributions. The reliability levels are measured based on the RI. Iterative correlation procedures are used to predict the POF of a structural system or structure. In general, this involves an idealization of the failure domain and it is usually assumed to be a basic representation of the joint probability distribution of a variable. This method of RA is computationally efficient and produces results with desired degree of accuracy (see Figure 3).

The Mean Value FOSM (MVFOSM) simplifies the process of calculating the POF of an LSF. Following this method, the LSF is estimated by the first-order Taylor series expansion at the mean value point. In the Hasofer and Lind (HL) method, the RI is expressed as the minimum geometrical distance of Most Probable failure Point (MPP) on the limit state surface from the origin of a u-dimensional space. The HL RI method changes the expansion point from the point of mean value to the MPP, thereby optimizing the approach. For instance, once the PF is ascertained, the HL algorithm is employed in calculating the RI, $\beta$. This recursive algorithm is summarized below [2,3,16,19].

(1)

Define the PF for the corresponding LS, e.g., ultimate limit state (ULS), serviceability limit state (SLS), fatigue limits state (FLS), etc.

(2)

Let the mean value point be the initial design point, i.e., ${\mathit{x}}_{i,k}={\mu }_{{\mathit{x}}_i}$ $i=1,2,\dots ,n$, and evaluate the gradients $\nabla g\left({\mathit{X}}_k\right)$ of the LSF at this design point, where ${\mathit{x}}_{i,k}$ represents the $i\mathrm{th}$ element in the vector ${\mathit{X}}_k$ of the $k\mathrm{th}$ iteration and ${\mu }_{{\mathit{x}}_i}$ is the mean value of the $i\mathrm{th}$ element.

(3)

Compute the initial RI, $\beta$ adopting the mean-value approach, i.e., $\beta =\frac{{\mu }_{\tilde{g}}}{{\sigma }_{\tilde{g}}}$ and its direction cosine $\alpha$.

$$\beta =\frac{{\mu }_{\tilde{g}}}{{\sigma }_{\tilde{g}}}=\frac{g\left({\mathit{\mu }}_{\mathit{X}}\right)}{{\left[{{\displaystyle \sum }}_{i=1}^n{\left(\frac{\partial g\left({\mathit{\mu }}_{\mathit{X}}\right)}{\partial {\mathit{x}}_i}\right)}^2·{\sigma }_{\mathit{x}i}^2\right]}^{\frac{1}{2}}}$$

(2)

$${\alpha }_i=-\frac{\left(\frac{\partial g\left({\mathit{X}}^{*}\right)}{\partial {\mathit{x}}_i}\right)·{\sigma }_{{\mathit{x}}_i}}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(\frac{\partial g\left({\mathit{X}}^{*}\right)}{\partial {\mathit{x}}_i}{\sigma }_{{\mathit{x}}_i}\right)}^2}}$$

(3)

(4)

Calculate a new design point ${\mathit{X}}_k$ and $U_k$ function value, as well as gradients at this new design point.

$${\mathit{x}}_{i,k}={\mathit{\mu }}_{{\mathit{x}}_i}+\beta {\sigma }_{{\mathit{x}}_i}{\alpha }_i$$

(4)

$${\mathit{u}}_{i,k}=\frac{{\mathit{x}}_{i,k}-{\mathit{\mu }}_{{\mathit{x}}_i}}{{\sigma }_{{\mathit{x}}_i}}$$

(5)

(5)

Compute the RI $\beta$ and direction cosine ${\alpha }_i$ using Equations (4) and (5) respectively.

$$\beta =\frac{g\left(U^{*}\right)-{{\displaystyle \sum }}_{i=1}^n\frac{\partial g\left(U\right)}{\partial {\mathit{x}}_i}{\sigma }_{{\mathit{x}}_i}{\mathit{u}}_i^{*}}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(\frac{\partial g\left(U^{*}\right)}{\partial {\mathit{x}}_i}{\sigma }_{{\mathit{x}}_i}\right)}^2}}$$

(6)

$${\alpha }_i=-\frac{\left(\frac{\partial g\left({\mathit{X}}^{*}\right)}{\partial {\mathit{x}}_i}\right)·{\sigma }_{{\mathit{x}}_i}}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(\frac{\partial g\left({\mathit{X}}^{*}\right)}{\partial {\mathit{x}}_i}{\sigma }_{{\mathit{x}}_i}\right)}^2}}$$

(7)

Iterate steps (4) to (5) until the values of the RI $\beta$ converge. The failure probability $P_f$ can then be calculated from the following:

$$P_f=\Phi \left(-\beta \right)=1-\Phi \left(\beta \right)$$

(8)

where $\Phi (·)$ is the standard normal cumulative distribution function (CDF) given as

$$\Phi \left(\beta \right)={{\displaystyle \int }}_{-\infty }^{\beta }\frac{1}{\sqrt{2\pi }}{e}^{-(\frac{1}{2})z^2}dz.$$

(9)

The Hasofer Lind–Rackwitz Fiessler (HL–RF) method is an improvement to the HL method such that its accuracy is close to level III method. This method is ideal for cases of non-Gaussian variables, and it further enables information on the distribution of the random variables to be incorporated (i.e., apart from the mean and standard deviation included in the HL algorithm, information on distributions such as Weibull, Lognormal, Normal, etc. of the random variables are also incorporated in the HL–RF (Hasofer Lind-Rackwitz Fiessler) algorithm). This method involves transformation to the normalized space, and an example is the application of the Rosenblatt transformation, a transformation method for dependent non-normal design variables [5]. An alternative matrix procedure for the HL–RF algorithm is presented in [16]. For the case of correlated random variables, the HL–RF algorithm is modified by introducing a correlation matrix $\left[\rho \right]$. The correlation matrix $\left[\rho \right]$ is the matrix of correlation coefficients for the uncertain variables involved in the LSF. Further information on this can be found in [4,5,20].

To enhance the precision of the original HL–RF method, specific modifications were suggested in several sources. Keshtegar and Chakraborty [21] presented a conjugate search direction approach that overcomes the unstable solutions resulting from periodic nature and chaos for RA problems that involve highly non-linear PFs. In the study, two recursive FORM schemes were examined based on the conjugate descent direction applying hybrid self-adaptive conjugate (HSAC) and the self-adaptive conjugate (SAC) search directions for the estimation of RI. Keshtegar and Meng [22] developed a relaxed HL–RF (RHL–RF) based on a relaxed factor, which is calculated dynamically by the second-order interpolation between zero and one. They proposed a hybrid relaxed HL–RF (HRHL–RF) method whereby the HL–RF and RHL–RF are implemented adaptively by using an angle criterion to enhance the efficiency and robustness of the FORM formula. In [23], an efficient and robust iterative algorithm, referred to as finite-based Armijo search direction (FAL) method, was proposed for FORM-based SRA. To achieve the stabilization of the FORM algorithm, a finite step size was developed applying the Armijo rule and sufficient descent condition. The FAL is adjusted adaptively based on the information acquired from the recursive algorithm at each iteration and Armijo rule.

According to [24], the HL–RF algorithm of the FORM has a drawback of the phenomena of convergence failure, for example, chaos, periodic oscillation, and bifurcation for some non-linear problems. The essential reasons for numerical instabilities due to chaotic dynamics that include chaos and periodic oscillation common to recursive FORM solutions were revealed. According to Keshtegar [25], the STM with chaos feedback control is inefficient for both concave and convex reliability issues. The author proposed the STM with chaotic conjugate search direction to enhance both the efficiency and robustness of the FORM algorithm, by developing a chaos control factor based on a logistic map and following a recursive procedure involving the RI and the logistic map to adaptively define a transformation matrix. See Figure 4 for an illustration. Pedroso [26] presented a solution to reliability problems using a parallel evolutionary algorithm with accuracy and repeatability of results. The stochastic nature of evolutionary algorithms prevents it from generating identical results. Consideration was given to an optimization problem resulting from the FORM with an implicit LSF that can include a call to Finite Element Analysis (FEA). A detailed explanation was given on a strategy to handle failure from the transformation of random variables or from the finite element call during the evolution process.

Shi et al. [27] investigated the efficiency of different SRA approaches with implicit LSF. Response data sets determined via non-linear FEA are then applied in RA. They proposed an efficient response variability method and RA method. The approach is a combination of the Maximum Entropy Fitting Method (MEM) used to model the responses stochastically and the FORM for RA.

2.2. Second-Order Reliability Method (SORM)

Theoretical background on SORM can be found in [5,28]. RI estimates predicted through FORM produce adequate results when the LSF is nearly linear close to the design point and the LSS (Limit State Surface) has only one minimal distance point. For other conditions, the POF predicted by FORM, using the RI $\beta$, may produce inaccurate and unreliable results [5]. To overcome this drawback, second-order Taylor series expansions (or other polynomials) may be introduced [28]. Where a second-order (parabolic) LSS is attached to the non-linear LSF at the design point, it is then regarded as a SORM. According to this approach, the LSF is represented in terms of two independent random functions, whereby one is linear while the other is quadratic in the u-dimensional space.

According to [29], in the SORM, the LSF in arbitrarily distributed random variables is approximated by a quadratic polynomial of standard normal variables where the fitted quadratic polynomial is then applied in calculating the POF of the LS. Due to the unavailability of a closed-form solution for the failure probability of a general quadratic polynomial surface, a new SORM for RA using saddle point approximation (SPA) was developed. In their study, a new SORM was presented where the failure probability was derived directly from the fitted quadratic polynomial surface because parabolic approximation consideration was removed and the accompanying errors were eliminated [29]. In the new SORM approach, first, a Nataf transformation to a standard normal u-space is carried out. Then the design point is located and a quadratic fit at the design point is carried out, after which the cumulant generating function (CGF) of the fitted quadratic polynomial surface is analytically derived. Finally, the Probability Density Function (PDF), Cumulative Density Function (CDF), and failure probability of the LS are established by applying SPA.

3. Level III (Direct) Reliability Methods

The POF of a structural element in relation to a single failure mode is derived from the probability integration expression in Equation (1). Calculating this integration expects that the LSS, $g\left(\mathit{x}\right)=0$, and the joint PDF of X, $f_x\left(\mathit{x}\right)$, are known. The methods that calculate the POF directly from this integration are known as Level III reliability methods, which are perceived to be most accurate. The most common relevant level III methods are: (1) Monte Carlo Methods (MC), (2) NI, (3) Analytical Integration (AI), (4) Surrogate Models (SMs), and (5) Stochastic Finite Element Method (SFEM) [1,8,9]. Theoretical background on AI, NI, and MCS can be found in [30].

Computation of the exact failure probability from Equation (1) by using analytical and NIs involves approximations in the solution process and may become inefficient for certain problems. This drawback can be overcome by applying the MCS technique, which avoids the extra layer of approximation; however, it becomes inefficient when the LS needs a continuous calculation procedure such as FEA [5,30], in which case it will be impractical. The concept behind MCS is that the number of samples falling into the failure domain $\left(N_f\right)$ is determined by sampling the basic random variables/vector X, each possessing different probability distributions.

An effective sampling method is the Latin Hypercube sampling (LHS). LHS is a method whereby multiple variables can be represented such that overlapping data sets are avoided. First, the application divides each stochastic variable distribution in $n$, non-overlapping intervals with equal probability. This involves associating the analysis point derived from each data set by randomly selecting one value of each variable from each interval. In comparison with the crude Monte Carlo (MC) sampling, this method yields small variance in the response because of the homogeneous allocation of intervals on the PDF [5].

Besides the LHS, other available variance reduction techniques include (1) Adaptive Sampling, which updates sampling density dynamically as the simulation proceeds [5], and (2) Conditional Expectation techniques, which consist of Axis-orthogonal Simulation techniques for convex failure sets, and Directional Simulation for convex safe sets. The IS (Importance Sampling) method is a derivation from the MCS whereby to achieve greater efficiency the simulation is biased; the sampling is basically carried out in the tail of the distribution to ensure the occurrence of adequate simulation failures. An alternative variance reduction technique is the subset sampling, where the failure event is expressed as a sequence of partial failure events (subsets). In the design-point simulation method, the MC sampling is applied around the design point. Initially, having approximated the MPP in the u-dimensional space, MCS is used here instead of performing simulations in the wider range of each distribution. In [31], it was reported that MCS is a powerful tool, straightforward in implementation and capable of solving a wide range of SRA problems. In the same study, neural networks were combined with MCS to address the issues of low POF for highly reliable structures at low computational cost, and the validity of the methodology was demonstrated.

Zhang et al. [32] considered SR when statistical parameters of distribution functions could not be ascertained accurately as a result of epistemic uncertainties. Interval bounds were used to model uncertainties in estimates constructed from confidence intervals. They developed an interval MC method that combines the simulation process with the interval analysis. Naess et al. [33] proposed a new MC-based method for approximating system reliabilities, which aims to reduce the computational burden involved in the brute force MCS methods for complicated systems. It harnesses the regularity of tail probabilities to establish an approximation procedure for the calculation of far tail POFs based on the POFs estimated from MCS at more moderate levels. Gaspar et al. [34] claimed the reliability of complex structural systems could be predicted accurately by MCS. They proposed an MCS method for evaluating system reliabilities, which aims to reduce the computational cost associated with highly reliable structural systems. This method applied non-linear FEA combined with response surface (RS) modeling.

Jahani et al. [35] presented SRA such that stochastic variables are modeled as fuzzy random variables, and Interval MCS (IMC) combined with Interval Finite Element Method (IFEM) was applied in approximating the POF. IMC-IFEM and Genetic Algorithm (GA) were compared to ascertain the most efficient. It was concluded that the IMC-IFEM provided higher efficiency compared to the GA method. Dai et al. [36] developed an IS method based on support vector density estimation and adaptive Markov chain simulation. According to the methodology, samples that can adaptively populate the importance region by the adaptive metropolis algorithm were generated and IS density by support vector density was constructed. In [37] directional simulation was merged with IS. This involves defining a sampling function on the unit hyper-sphere, which samples random directions aiming toward the MPP. Random directions are generated from the sampling function (made adaptive by a closed-form rule to renew the sampling parameters) using spherical coordinates. Zhang [38] developed a new interval IS method by applying the IS technique to an imprecise probability. This methodology has the advantage that an expensive interval analysis is not necessary. Recently, [3] reported the use of direct simulations applying the LHS to predict POF of a complex frame-type structure in the presence of stochastic loads based on studies previously conducted in [39].

According to [40], Subset Simulation (SS) is an adaptive simulation method, which solves SRA problems having numerous random variables efficiently. In the study, a novel approach for Markov Chain MC (MCMC) sampling was introduced in the standard normal space. This developed two algorithm variants: a basic variant that is simpler than existing formulations with equal efficiency and accuracy and a superior variant with adaptive scaling. The accuracy of the SS method was reportedly improved. In [41], an approach to SRA of deteriorating systems that accounts for stochastic dependence among element deterioration was presented. Bayesian updating of the system deterioration model was applied. The updated system reliability is then derived via coupling a probabilistic structural model with the updated deterioration model. SS was reported as a robust and efficient sampling-based scheme ideal for such analyses as solving the underlying high-dimensional SR problems.

4. Advanced Approximation Modeling Methods

RS method modeling is applied in deriving equation(s) to express one or more independent variables in terms of a dependent variable. The fundamental idea is to replace the true LSF by an approximation whose function values can be computed more easily [42]. RSM (Response Surface Model) and SM (Surrogate Modelling) methods are classifications of approximation methods usually applied in modeling complex engineering systems. RSM derives an analytical expression of the system (defined as polynomial equations) while the latter enters the system data sets normally in a matrix closed form for post-processing [43,44]. The expression derived from either category of methods can further be incorporated with RA methods, such as FORM/SORM and MCS, and applied in multidisciplinary optimization problems [1,45].

4.1. Response Surface Method

RSMs revolve around creating a polynomial closed-form approximation, $\widehat{g}\left(\mathit{x}\right)$, for the exact LSF, $g\left(\mathit{x}\right)$, which is usually recognized through an algorithmic procedure, via (1) a few select deterministic analyses and (2) regression analysis of these results. Quadratic functions are commonly employed in practice, as:

$$g\left(\mathit{x}\right)\approx \widehat{g}\left(\mathit{x}\right)=a_0+{\displaystyle \sum }_{i=1}^N{a}_i{\mathit{x}}_i+{\displaystyle \sum }_{i=1}^N{a}_{ii}{\mathit{x}}_i{}^2+{\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1,j\ne i}^N{a}_{ij}{\mathit{x}}_i{\mathit{x}}_j=V^T\left(\mathit{x}\right)a$$

(10)

where the coefficients $a^T=\left\{a_0,a_i,a_{ii},a_{ij}\right\}$ are to be determined and the vector $V\left(\mathit{x}\right)$ is described as $V^T\left(\mathit{x}\right)=\left\{1,{\mathit{x}}_i,{\mathit{x}}_i{}^2,{\mathit{x}}_i{\mathit{x}}_j\right\}$. To develop the RS, a finite number of evaluations of the LSF, for instance, by applying finite element runs, is needed. Then the RA can be carried out analytically by means of the expression given by Equation (10). This approach is especially desirable when simulation methods are used to determine reliability. The unknown coefficients, $a^T=\left\{a_0, a_i,a_{ii},a_{ij}\right\}$, are determined via the least-square method. Having identified a set of fitting points, {${\mathit{x}}^k,k=1,\dots ,NF$}, where NF denotes the number of fitting points, referred to as the experimental design, the exact values $y^k=g\left({\mathit{x}}^k\right)$ are calculated and the error is calculated as:

$$error\left(a\right)={{\displaystyle \sum }}_{k=1}^{NF}{\left(y^k-V^T\left({\mathit{x}}^k\right)·a\right)}^2.$$

(11)

The error expression is minimized with respect to the vector $a$ to calculate the unknown coefficients. After determining a response surface failure function from Equation (10), a standard reliability technique is used to compute the POF [8,9].

According to [7], the response of a structure subjected to certain loading conditions can be evaluated through FEA modeling. The work used a methodology, based on a generalized SRSM (Stochastic Response Surface Method) for the SRA of an offshore jacket, selected as a reference application. According to the methodology, FEA simulation results were incorporated with numerical reliability techniques through multivariate (quadratic) polynomial regression (MPR), so as to predict the reliability levels of components. This approach is particularly useful as it enables enhanced analysis of elements under a stochastic perspective, accounting for design uncertainties efficiently [46]. In [2,3,47,48,49], the efficiency of the SRSM for advanced RA of Offshore Wind Turbine (OWT) jacket support structures was demonstrated. According to the authors, a parametric FEA model was developed, and then stochastic FEA simulations were performed. The results obtained from the FEA were post-processed through MPR in order to obtain the PFs expressed in terms of the stochastic variables, and the RI was then computed through FORM. In the presence of Structural Health Monitoring/Condition Monitoring (SHM/CM) data, the structure may be reassessed and updated. The updated safety index gives vital information for decision making for the inspection and maintenance of OWT support structures. According to [50], the SRSM is a technique employed for RA of complex structural systems with time-consuming, implicit, or computational costly LSFs. The collection of sample points, the approximation of RS, and the estimation of the POF are the main aspects of the SRSM. Sample points were selected close to the MPP and the actual LS surface (LSS). They used the weighted regression technique to fit the RS, which enables the fitting points to be weighted based on their distance from the failure surface. They analytically derived the cumulant generating function (CGF) of the RS. The POF of the structural system was computed by utilizing the Saddle point Approximation (SPA) method.

RSM is a popular method for RA, especially when the LSF is meant to be highly non-linear or closed-form mechanical models to define complex structural systems that are not available [6]. According to [51], the SRSM is used for RA of complex systems with low POF, for which approximate methods are inaccurate and MCS is too computationally intensive. The SRSM approximates by fitting the polynomial to a number of sampling points from the LSF with a multidimensional quadratic polynomial. To address the problem related to ill-conditioned systems and an approximated LS (which is very imprecise outside the domain of the stochastic parameters) an algorithm using orthogonal polynomials was proposed.

According to [52], RA of a jacket-type OWT support structure under extreme ocean environment loads was performed. The use of the RSM methodology was demonstrated to express the LSF and RI was calculated using the FORM. Rücker and Faber [53] presented the RA of an OWT support structure building upon structural, loading, LS, and uncertainty models comprising design, production, and erection data by applying the SFEM. An algorithm that accounts for complexity in the individual models dictates an efficient solution scheme for reliability. This consists of an adaptive RS and an IS-MC algorithm. The RS algorithm is based on predetermined DoE (Design of Experiments), which facilitates the adjustment of design parameters for an optimized prediction variance in the domain of the design points.

4.2. Surrogate Models (SMs)

Theoretical background on SMs can be found in [54,55,56]. According to [55], SMs, or meta-models (MM) or RSM [55,56], are used for time-consuming implicit LSFs in the context of SRA. To reduce the computational burden of the direct MCS approach, the SMs can be applied to estimate implicitly the LSFs involving FEA. Artificial neural network (ANN), Kriging, adaptive Kriging, support vector regression (SVR), etc. are applied to estimate the failure probability based on the prediction of the probabilistic model with uncertainties [21].

According to [2], the SRA of a complex OWT support structure subjected to pitting-corrosion fatigue was assessed based on the damage tolerance modeling approach. A non-intrusive formulation incorporating ANN-SM and FORM was proposed to perform the SRA of the crack propagation regime following a sequence of steps. Figure 5 depicts a flowchart of a non-intrusive formulation for probabilistic fracture mechanics in the presence of pitting-corrosion fatigue employing the stochastic parametric FEA.

4.2.1. Kriging Incorporated with FORM

Kriging or Gaussian process regression is a stochastic process where distribution is defined over a basis function that can take any form, for example, a squared exponent function. The methodology of earlier instances of Gaussian Process used for curve fitting is as follows: After obtaining a predictive distribution, the regression is then applied over a basis function that projects the input onto the feature space, using a Bayesian approach to take a prior distribution and updating it to form a posterior distribution. The output of the Gaussian Process is defined as the mean and covariance matrix. The covariance matrix defines the smoothness and can be represented by the kernel function. Given a set of independent variables, $\mathit{x}$, Gaussian process can be fully defined with a mean, $m\left(\mathit{x}\right)$, and a covariance, $k\left(\mathit{x}, \mathit{x}{}^{\prime }\right)$ [57].

$$\mathcal{F}\left(\mathit{x}\right)~GP\left(m\left(\mathit{x}\right),k\left(\mathit{x}, \mathit{x}{}^{\prime }\right)\right)$$

(12)

Gaspar et al. [55] proposed an adaptive kriging SM that applies a moderate number of input basic random variables with active refinement, to overcome component RA problems associated with non-linear computationally intensive implicit LSFs. The presented model applies an adaptive, kriging-based, trust-region approach to search for the design point in the standard normal space and calculates an initial POF based on the FORM and sensitivity factors for the input stochastic variables. In the second stage, the initial estimate is then verified or enhanced using MCS with IS based on Kriging SM defined recursively around the MPP by employing an active refinement algorithm. In addition, they developed a convergence criterion, which detects the stabilization of the POF approximation during the active refinement process, per Figure 6.

4.2.2. Kriging Incorporated with IS/SS

In [58], an efficient reliability method combining adaptive IS and KIM (Kriging Interpolation Method) based on active learning mechanism was presented. It was claimed that the Kriging MM, adaptive IS, and active learning mechanism superiorities are inherited and only enable evaluating the interested samples in actual PF. In [59], a modification to an algorithm for the efficient estimation of small probabilities, combining FORM and an adaptive Kriging-based IS strategy (AK-IS), was proposed. It was reported that the modification overcomes an important limitation of the original AK-IS, providing the algorithm with the flexibility to deal with multiple failure regions characterized by complex, non-linear LS. In [60], the time-consuming task inherent in the SS and SM method when the PF needs to be numerically evaluated was addressed by an active learning method combining KIM and SS (AK-SS). It was asserted that the efficiency of the new method relies upon the advantages of SS in evaluating small POFs and the KIM with active learning for approximating the true PF.

4.2.3. Efficient Global Reliability Analysis (EGRA)

Bichon et al. [61] developed an efficient RA method known as the Efficient Global RA (EGRA) that characterizes the LS across the domain of random variables accurately. The technique begins by building a KIM from a small number of samples and then selecting adaptively where to generate subsequent samples to enhance the accuracy of the model near the LS. The KIM produced is then sampled by applying multimodal adaptive IS to compute the reliability level of interest. Highly non-linear complex LS can be modeled by locating multiple points on or around the LS, resulting in a more accurate probability integration. Few numbers of true function evaluations are required to generate a quality SM by concentrating the samples in the region where accuracy is essential.

4.2.4. Sequential Kriging Reliability Analysis (SKRA)

According to [54], the sequential Kriging reliability analysis (SKRA) method was proposed for non-linear implicit PFs, which were computationally unaffordable and included EGRA and AK-MCS. An adaptive sampling regions’ strategy was developed to avoid selecting samples in the areas where the probability density is so low, thereby having an insignificant impact on the results. The size of the sampling space was adapted based on the POF approximated by the last recursion.

4.2.5. Support Vector Approach

Support vector machines (SVM) can be applied for regression, and when doing so are called Support Vector Regression (SVR). SVMs work via linear domain division where the division is made to be as large as possible. This can also be extended to higher-order domains and be used for regression through the use of kernels. In this method, a support vector is drawn such that the error is minimized by selecting a hyperplane that maximizes the margin. For linear SVR, an approximation can be derived from [57]:

$$y={\displaystyle \sum }_{i=1}^N\left({\alpha }_i-{\alpha }_i^{*}\right){\mathit{x}}_i,\mathit{x}+b$$

(13)

where ${\alpha }_i$ and ${\alpha }_i^{*}$ are Lagrange multipliers, there are $N$ training variables, and $b$ is a real number constant. For non-linear SVR, a kernel is applied to ${\mathit{x}}_i,\mathit{x}$. For a Gaussian radial basis function kernel this becomes:

$$K\left({\mathit{x}}_i,{\mathit{x}}_j\right)=e^{\left(-\frac{{\mathit{x}}_i-{\mathit{x}}_j^2}{2{\sigma }^2}\right)}$$

(14)

where $\sigma$ is a free parameter.

Support vector machines can be applied in either regression or classification form and have been used in a wide range of applications where it was proven that it provides predictions with high fidelity and that hybrid method can enhance predictions. In other applications, SVM gives a good performance, but also relatively quick training times compared to other methods tested due to its simplicity.

According to [62], metamodeling has been widely adopted for RA to enhance computational efficiency. They developed an efficient reliability method that harnesses Adaptive Support Vector Machine (ASVM) and the MCS. This applied a pool-based ASVM for the construction of MM with the minimum number of training samples, whereby a learning function was proposed to sequentially select informative training samples. Then the MCS was used to calculate the POF based on the SVM classifier obtained. Dai et al. [63] presented a multiwavelet linear programming SVR method for RA that mitigates the difficulties inherent in the standard quadratic programming SVR, such as being computationally expensive and possessing the inability to guarantee sufficient model sparsity. The method involves developing a novel multiwavelet kernel by the construction of an autocorrelation function of multiwavelets and uses this kernel in context of linear programming SVR for predicting the LS.

4.2.6. Artificial Neural Network Approach

ANNs are established to be universal function approximators and have found applications in Structural Reliability Assessment (SRA) by several researchers [4,64]. The neural structure of the brain has been employed in creating mathematical models defining ANNs. ANNs establish a functional relationship between two spaces of data during a learning process and replicate that connection during a recall process. According to [31], ANNs can approximate highly non-linear functions accurately over the entire domain with very high fidelity. Several studies [2,42,65] have also been carried out, proving the precision and efficiency of the response surface method based on ANN in comparison with the conventional response surface methods for reliability assessment.

Multilayer Perceptron Neural Networks use more than one layer of neurons: an input layer, one or more hidden layers, and an output layer. The neurons have activation functions to relate the input they receive to the output they send to the next layer. Furthermore, there are weights between different neurons and biases that are trained iteratively, conventionally using reinforcement learning via back propagation where the weights are adjusted between each neuron depending on how accurate the prediction is to the desired result. The model can be applied to an approximation problem by applying a suitable output layer function and minimizing a cost function [57].

To address the extreme number of FEA required to achieve accuracy, a directional approach was developed, which was reported to significantly improve efficiency. This utilizes deterministic point sets to preserve the underlying joint probability distribution of the random vector describing the structure and adopts neural networks to focus the simulation efforts in the most crucial regions [66]. In [67], two adaptive stochastic search algorithms are used to locate and trace an implicitly defined function to construct an SM for RA. An ANN-SM was applied in the implementation, and it was claimed that the method could, in principle, be applied with any form of SM. In both algorithms proposed, the SM evolved continuously with sample selection and was used in the choice of new samples such that convergence was achieved rapidly to an accurate representation of the limit surface.

4.2.7. Radial Basis Function Approach

A typical Radial Basis Function (RBF) model is a form of a feed-forward neural network composed of single neurons using RBF transfer functions. The result of this approach is that a radial basis function fits a surface through the measured sample points. The values between the sample points are calculated from functions based on the radial distance from the original point. The equation for a multi-quadratic basis function is expressed as [57]

$$\phi \left(r\right)=\sqrt{1+{\left(\epsilon r\right)}^2}$$

(15)

where $\epsilon$ is the shape parameter and $r$ is the radius. The output is from the entire model, whose basis function is a function of the Euclidian norm, which is effectively the radius,

$$s\left(\mathit{x}\right)={\displaystyle \sum }_{i=1}^n{\lambda }_i\phi \left(\mathit{x}-{\mathit{x}}_i\right)$$

(16)

where $s\left(\mathit{x}\right)$ is the output of the model and ${\lambda }_i$ is the weight of the $i\text{-}\mathrm{th}$ node.

RBF nodes can be employed in a variety of models; however, they are usually applied in a single-layer model with a single node for each sample point in the training set.

Bucher and Most [42] compared approximate response functions in terms of their capacities to reduce computational costs in SRA. The RS approaches are based on polynomial functions, radial basis functions (RBFs), and ANN. In the polynomial approach, the higher-order polynomial shows severe oscillations, requiring too many support points, and this drawback could be addressed via the application of smoothing techniques, e.g., the moving least-squares method (MLS). In the ANN method, the output is linked with the input parameters via simple, flexible functions including linear, step, or sigmoid functions that are combined by adjustable weights. The RBF approach also allows for flexible adjustment of the interpolation scheme. The availability of interpolating functions that can be augmented incrementally by allowing extra support points implies that it permits approximation sequences to be provided, ensuring quick convergence of its reliability estimates to the true value.

Zhang et al. [68] proposed an efficient RSM to evaluate structural reliability using evidence theory in order to overcome the associated high computational cost. They developed a DoE technique whose key issue is the search of the important control points at intersections of the LS and uncertainty domain. These points have a significant contribution to the accuracy of the subsequent RS. Based on these, a highly precise RBF to the actual LSS was introduced.

5. Probabilistic Fatigue and Fracture Mechanics Approaches

Since limit state design is a common trend in modern design, details of this will be presented in this section [7]. The general design requirement is to provide structures with sufficient safety margins taking into account all types of uncertainties having effects on its integrity (i.e., load and capacity variability, modeling idealizations, etc.). Limit state design can be defined simply as that the load/demand of a structural system should under no circumstances exceed its resistance/capacity. For offshore and marine structures, various limit states are prescribed in design standards that should be assessed within a comprehensive design. According to the DNV (Det Norske Veritas) [69], the four main types of limit states that should be considered are: (1) serviceability limit state (SLS): deformation and vibration limit states; (2) ultimate limit state (ULS): buckling and stress limit states; (3) fatigue limit state (FLS); and (4) accidental limit state (ALS).

Significant cyclic loads induced by wind and wave imposed on OWT support structures make their design to be generally dominated by FLS. The assessment of the FLS is performed using two types of methods, i.e., the S-N (Stress-Number of Cycles) curve method and fracture mechanics (FM) method. The S-N curve approach is based on experimental fatigue-test data. This approach is commonly used in practice and well described in standards for fatigue design of offshore structures [34,69]. Based on the S-N curve approach, the number of loading cycles to failure, N, can be determined from [3]:

$$logN=A-mlog\Delta S$$

(17)

where $A$ and $m$ represents the intercept and the slope of the S-N curve on the log-log plot, respectively, and $\Delta S$ is the stress range. Design standards, such as the DNVGL-ST-0126 (Det Norske Veritas Germanischer Lloyd Standard), prescribe values for the intercept $A$ and slope $m$ in Equation (17). The Equation (17) can also be referred to as the Basquin’s formulation. The PF of FRA, according to the S-N curve method, is given as [2]:

$$g_{f,SN}=logN-logN\left(t\right)$$

(18)

where subscripts $f$ and $SN$ represent the FLS and S-N curve method, respectively, $N$ is the number of loading cycles to failure, as given by Equation (17), and $N\left(t\right)$ is the expected number of loading cycles during the given design life.

FM method is applied at the design stage of offshore structures, as this provides a platform for predicting the fatigue life, and during the operational stage, to allow the decision-making process strategies for inspection scheduling and repair. Common among large and complex structures, such as offshore tubular structures, crack-like imperfections, notches, or other forms of discontinuities exist. The basic concept of the FM approach revolves around the characterization of the stress field in terms of a single parameter, $\Delta K$, which is known as the stress intensity factor (SIF) near the crack [5,30]. This parameter is a function of both the stress $S$ and crack size $a$.

The FM approach is based on the models created to predict the crack growth in a material when variable loads are applied. The crack growth is a process not fully understood at the atomic level. The engineering analysis of this is studied using relationships between SIF and crack-growth rates. The Paris law can be expressed as

$$\frac{da}{dN}=C{\left(\Delta K\right)}^m$$

(19)

where $a$ is the crack length, $N$ is the number of cycles, $\Delta K$ is the SIF range, and $C$ and $m$ are material constants. State-of-the-art numerical and experimental research on bilinear crack-growth law phenomena can be found in [70,71,72,73,74,75,76,77,78,79]. The safety margin for fatigue reliability analysis based on LEFM (Linear Elastic Fracture Mechanics) is given by:

$$g_{f, FM}={{\displaystyle \int }}_{a_o}^{a_c}\frac{1}{Y{\left(a\right)}^m{\left(\sqrt{\pi a}\right)}^m}da-C\Delta S^m\left(N\left(t\right)-N_o\right)$$

(20)

where subscript f and FM represent the fatigue limit state and FM method, respectively; $a_o$ is the initial crack depth (or the crack depth at time $t_0$); $a_{\mathrm{c}}$ denotes the critical crack depth; $Y\left(a\right)$ is the compliance function, which is related to crack depth $a$; $m$ and $C$ are Paris’ law constants; $N\left(t\right)$ is the total number of stress cycles in the time period $\left[t_0, t\right]$; and $N_o$ is the initial number of stress cycles. The findings of the state-of-the-art-review studied herein will be presented later in Section 7.

6. Other Methods and Applications

6.1. Stochastic Finite Element Method (SFEM)

Component reliability methods are based on a failure function $g\left(\vartheta \right)$ in the space of basic random variables, which are collated in the vector $\theta$ (here $\theta$ is used for random field instead of X to prevent confusion between spatial variation and random field). It is easy to implement if $g\left(\vartheta \right)$ is explicitly defined or known. In practical cases, the failure function is usually unavailable explicitly in the closed form, and the response is derived via FEA. Several computational techniques may be employed for the RA with implicit failure functions. The major techniques include Perturbation Techniques, Neumann expansion solution, RS approach, and branch and bound techniques [8,9]. A state-of-the-art review on SFEM is presented in [80].

The perturbation techniques are desirable owing to their efficiency in computation times and accuracy. Theoretical background on perturbation method can be found in [8,9]. Li et al. [81] proposed a new class of hybrid perturbation-Galerkin methods to establish the response function (surface) to overcome the major challenge in the RA of the complex structure of being unable to find the response function from which the LS can be determined. Single-variable and double-variable approximations are the main methods incorporating a combination of the perturbation technique and Bubnov–Gerlekin projection, where several orders of summation terms of polynomial expansions are adopted as the Galerkin trial functions or basis vectors.

Feng et al. [82] presented a robust stochastic-free vibration analysis for engineering structures involving hybrid, yet spatially variant, uncertain system parameters. Both the stochastic and non-stochastic representations of the spatial dependencies of the uncertainties are simultaneously incorporated within the unified analysis as distinguished from the conventional hybrid uncertain eigenvalue problem. It was asserted that the applicability and effectiveness of the proposed computational framework were demonstrated by the numerical investigations on various engineering structures.

In [83], a general FE (Finite Element)-based formulation was proposed for the assessment of the mean and mean-square response of stochastic structural systems with material properties defined by random fields governed by a flexibility-based formulation without involving approximations. Integral expressions of closed form for the mean and mean-square value of the displacement response of structures that are stochastic and statically indeterminate was introduced. Two new quantities, variability response function (VRF) and the mean response function (MRF) for the mean-square response and the uncertain material properties, were modeled using the stochastic field spectral density function, which can be referred to as integral expressions. Toward achieving an efficient and accurate numerical evaluation of the VRF and MRF, a FEM-based fast MCS procedure (FEM-FMCS) was introduced.

6.2. Reliability Analysis of Systems

System RA could be conducted directly or as a follow-up of a set of a single element or mode analysis. The first option is through NI or MC methods. It may be viable, in many cases, to begin with an analysis of individual components and process the outcomes afterwards to compute the POF for the system, and it may be evident that the methods of the series and parallel systems are capable of providing solutions to the combined system problems. For complicated structural systems, applying the FORM/SORM and MC techniques directly could either be too computationally expensive or the LSF could be unavailable explicitly in the closed form. For realistic structures, then, the response is obtained through a numerical technique such as FEA, whereby the derivatives are unavailable and each evaluation of the implicit LSF is time demanding. A wide range of computational procedures can be used for the RA with implicit failure functions in the form of the Stochastic Finite Element Method (SFEM) [8,9]. Detailed explanation on Parallel System can be found in [8,9,30].

In the series system, failure of the weakest link results in failure of the entire system. Series systems are modeled commonly by assuming multiple failure modes of a component or multiple failure paths of a structure. A detailed explanation of this can be found in [8,9]. Gong and Zhou [84] evaluated the system reliability of series systems using a proposed improved equivalent component approach. The FORM context was considered for an analytical expression derived to estimate the unit normal vector related to the equivalent component. Hence, the computational efficiency for establishing the correlation coefficients between the equivalent component approach and the system is enhanced. At each combining step, the two components with the utmost correlation coefficient are combined in an adaptive combining process. The efficiency and accuracy of the enhanced equivalent component approach were demonstrated for a series system with unequally and equally correlated components.

Zhang et al. [85] described a framework for developing reliability-based system resistance factors suitable for use with a Direct Design Method (DDM), which is a system-based, design-by-advanced analysis approach. A design-by-inelastic analysis method that relies on existing resistance factors originally developed from member reliability considerations was implemented for minimum system reliability requirements [68].

6.3. Time-Variant Reliability of Systems

Theoretical background on the transfer into T-V (Time-variant) system method and on the outcrossing approach can be found in [8,9,30]. In many cases, reliability aspects are T-V, for instance, some kind of degrading mechanism on the resistance side or fluctuating loads may be the reason. In [11], T-D RA of aging structures was presented, wherein uncertainties such as structural deterioration and non-stationarities in structural load process were taken into account. It was claimed that the improved approximate method, which requires only low-dimensional integration, reduces significantly the cost of assessing T-V reliability over a service life extending to 50 years. In [86], a T-V reliability method was formulated as a large-scale series system consisting of T-V response functions obtained by discretizing T-V continuous response functions within the forecast time period. This is used instead of analyzing outcrossing rates, which have a limitation of being inaccurate for low boundary reliability with dependent outcrossing rates. In [87], an efficient cross-entropy-based adaptive IS method was proposed to facilitate the wide application of stochastic process-based T-V reliability methods in complex problems. The LHS with proper correlation control is used to extend cross-entropy-based IS to T-V RA.

7. Critical Discussion

Various challenges, as well as their respective solutions, with respect to SRA methods were identified and presented in Section 2, Section 3, Section 4, Section 5 and Section 6 in this study. This section collates and discusses key aspects from the studies that stand out as particularly important.

Table 1. Capabilities and limitations of the most common level III approximation structural reliability methods.

Method		Capabilities	Limitations
First Order Reliability Method (FORM)	Mean Value First Order Second Moment Reliability Method	Simplest and least expensive reliability method A simplistic technique used in calculating reliability indices, using a minimum representation of basic variables	The applicability range of this method is diminished as a result of the following reasons: Non-linearity or large variations may not be handled by this method efficiently because linearization of the LSF about the mean values may result in inaccurate results. The MVFOSM algorithm is dependent on different (mathematically equivalent) formulations of the same problem; for both non-linear and linear LSF expressions.
	Hasofer and Lind Method	FORM approximation gives adequate outcome when the function is nearly linear close to the MPP, and the LSS has only one minimal distance point.	For cases where the LSS is characterized by irregular/large curvatures (high non-linearity), the POF estimated by FORM, using the RI $\beta$, may yield inaccurate and unreliable results. MVFOSM method is a straightforward procedure, while the HL method needs several iterations to converge, especially for non-linear problems
	Hasofer and Lind-Rackwitz Fiessler Method	Widely used approximate analytical method since it provides a good balance between efficiency and accuracy in realistic engineering RA.	It may yield unstable results, such as severe oscillations and chaotic solutions for highly non-linear problems (gives non-convergence problems). Cannot be used for implicit LS and also limited to only one dominant failure mechanism
Second-Order Reliability Method		Ideal for cases where the LSS has large or irregular curvatures (high non-linearity), the POF estimated by FORM, using the RI $\beta$, can produce inaccurate and unreliable results. By introducing second-order Taylor series expansions (or other polynomials), this drawback may be overcome.	It is basically a more time-consuming and complex process For highly non-linear PF with wide input data sets the estimated FORM/SORM RI results may not be sufficiently precise as a result of non-normal to normal transformations and multiple MPPs as well as the application of only first/second-order terms to calculate the original PFs. As a result of the parabolic approximation, there is an additional error in such SORMs besides the quadratic approximation error.

,

Table 2. Capabilities and limitations of the most common level III direct structural reliability methods.

Method			Capabilities	Limitations
Analytical Integration			Ideal for simple failure surface	Only possible for some special cases of limited practical interest Due to rapidly increasing computational demands as the number of dimension increases (the so-called ‘curse of dimensionality’) it has not found great favor in reliability computations.
Numerical Integration			Standard routines are found in most computer systems	Not always feasible, owing to the growth-off errors and excessive computational times
Crude Monte Carlo Simulation Technique (MCS)			Most versatile, clear, and well understood exact method available Requires no partial derivative of LSF; therefore, the method can be used for implicit LSF.	Computationally unaffordable/exorbitant for real engineering problems (for very small POFs) Simplest MC approach for reliability problems but not the most efficient It becomes inefficient when the LS needs a continuous calculation procedure such as FEA, in which case it will be impractical.
Variance Reduction Techniques	MCS with Importance Sampling Technique		Reduce computational time compared to the crude MCS Has been demonstrated to be very robust and effective for a range of possible LSF shapes. Increases the accuracy for the same number of runs	IS distribution $h_v(·)$ may not be chosen well, such as being too flat or being skewed Extremely concave LSFs may result in inefficient sampling A maximum likelihood unique point ${\mathit{x}}^{*}$ may not be identifiable: If $f_{\mathit{x}}(·)$ has a ‘flat’ contour region If the PF $G(·)=0$ coincides with a contour of $f_{\mathit{x}}(·)$ in a region of interest, or If the PF $G(·)=0$ is non-smooth (e.g., Ripple-like) and has a series of candidate locations for ${\mathit{x}}^{*}$ There can be more than one point of local maximum likelihood such as when $f_{\mathit{x}}(·)$ is not uni-modal The application of IS is sometimes referred to as an art that must be applied with caution.
	Adaptive Sampling		Involves a prior analysis to locate the design point for problems of high dimensionality in particular; a search algorithm with the constraint that the point must lie along the LS would fix the desirable location of $h_v(·)$. It is also possible to modify $h_v(·)$, depending on the information being obtained during the search process. Can be applied for multiple failure mechanisms and small probabilities of failure.	Application of the directional sampling and adaptive sampling is limited to a moderate number of random variables
	Conditional Expectation Techniques	Directional Simulation	Has the advantage of simulation in polar coordinate standard normal (y) space. Is recommended for convex safe sets Is applicable specifically to LSS which are nearly spherical (in standard normal space y) The amount of sampling required usually is reduced considerably compared to IS in Cartesian coordinates The special case of hyperspherical LS surface in standard normal space, only one directional sample is required (to fix the radius) and would give the exact result immediately.	The technique is not very efficient for one or a few planar LS.
		Axis Orthogonal Simulation Technique	Is recommended for convex failure sets	They typically require a large number of response function evaluations, which makes them impractical if the response function is expensive to evaluate.
	Design Point Simulation		Makes use of the FORM design point which makes it less cumbersome in the search for the POF
	Subset Simulation		Efficiently deals with small failure probabilities Converts the simulation of a rare event into sequence simulation of more frequent events.	Additional complexity as it involves the use of Markov Chain MCS Method. Inefficient for expensive PF.

,

Table 3. Capabilities and limitations of the most common advanced approximation structural reliability methods.

Method			Capabilities	Limitations
Parallel System			A parallel system fails when all the links (potential failure modes) fail. The most consistent function of the parallel system is for modelling the sequential failure of components in a single failure path leading to structural failure	Redundant members are introduced which introduces a computationally intensive procedure
Series System			Ideal for pipelines	Failure of one component leads to failure of the system
Stochastic Finite Element Method	Perturbation Method		The perturbation techniques are desirable owing to their efficiency in terms of computation times and accuracy	Too mathematically intensive
	Neumann Expansion Solution		Can be referred to as a computational scheme to lessen the amount of calculation time and to increase the efficiency of standard techniques as FORM/SORM and MC Is adopted to prevent repeated inversion of the random system-stiffness-matrix while undergoing the MC simulation approach. The matrix $k_o$ has to be decomposed only once for all samples in conjunction with the MCS. Due to this single matrix decomposition, computing time can be significantly reduced.	Determining the covariance matrix among all elements of the fluctuation part of the stiffness matrix involves prohibitively high computational effort.
	Response Surface Method		It is desirable when the simulation is used to determine reliability results Ideal for implicit LSFs It is not restrained by the number of random variables It is simple to perform with high accuracy	May sometimes be inefficient for highly non-linear failure function Restricted to small dimensions of uncertainty space Inefficient for large complex structures If the initial point of choice in the RSM is unreasonable, and the objective function is highly non-linear, then the rate of convergence of the RSM is slow. Therefore, the RSM for SR estimation in a wide range of applications has been limited.
	Branch and Bound Method		Are useful for the elastic-plastic analysis of frame structures where effects of plasticity like the formation of plastic hinges give sharp changes in the stiffness behavior	Its application is limited
Surrogate Models/Response Surface Model/Meta-Models	Polynomial Regression Models		The most widely used due to their simple formulations and implementation	Higher-order polynomials tend to show severe oscillations They sometimes face non-convergence issues for cases with an increasing number of support points centered at the mean value of the basic random variables
	Approaches Based on:	Radial Basis Function	SM has the advantage of been more affordable compare with other exact methods Has the merit of defining failure conditions of structural systems such that RA can be conducted with high fidelity. Have been validated to be the best interpolation methods compared to others by using examples of different kinds of scattered data.	Computationally efficient but at the expense of accuracy
		Local Interpolation Model (Polyhedra)	These are highly flexible to local approximations and should converge in the long run to the exact LSF. It is possible to construct approximation whose reliability estimates converge fast to the true value, as a result of their availability which can be augmented incrementally by providing additional support points.	It is an approximate method
		Artificial Neural Network	Possess the capability of describing failure conditions of structural systems such that RA can be carried out with high fidelity. They are flexible in nature and have the ability to capture complex non-linear relationships between input and output through appropriate learning. Have practical advantages over classical RSM due to their superior mapping capabilities and the flexibility in the functional form	Overfitting could occur, whereby the number of hidden nodes is too large for the number of training samples Have the main challenge of suitably choosing the learning parameters that help restrain under or overfitting, as both are equally disastrous.
		Support vector Machine	In comparison to ANNs, SVM employs the theory of minimizing the structure risk to avoid the problems of excessive study, calamity data, local minimum value etc.	Its implementation involves high computational efforts, and sufficient model sparsity cannot be guaranteed.
		Moving Least Squares	The optimization problem of the overdetermined system of equations can be solved by using the least-squares approach. As a result of the approximate character of the classical MLS method, the exact representation of support point values cannot be achieved, which is a positive aspect.	If the input data is noisy, it is owing to the fact that due to the approximative character of the classical MLS method, the support point values cannot be represented exactly. The application of this in the framework of RA this property result in significant errors in the calculation of the POF
		Kriging Models	Have more general approximation capability, i.e., predicts highly accurate POF values compared to the polynomial regression models Have important features that have been explored in the context of SRA such as the interpolation capability, the flexibility to estimate arbitrary functions with high precision as well as being capable of providing a measure of local uncertainty for the model predictions. Provides prediction uncertainty measure which has been used in the development of effective adaptive SMs for SRA with active refinement algorithms for the DoE.	Significantly more complex compared to polynomial regression models

and

Table 4. Capabilities and limitations of the other common structural reliability methods.

Method			Capabilities	Limitations
Stochastic Expansion	Non-Intrusive	Stochastic Response Surface Method	It is an extension of the conventional RSM, the PF of structures are replaced with polynomials while the traditional one employs polynomial sequences, and the SRSM uses Polynomial Chaos. Describes uncertainties in a non-explicit way, assuming the analysis code to be a “black box” such that access to the analysis code will not be required. The mean square error is minimized by selecting the collocation points and from high probability regions, therefore, resulting in fewer function evaluations for enhanced precision The method is applicable to the analysis of SR with any distribution type Higher accuracy could be attained from the higher-order RS function	It is widely used in chemical Engineering. Its application in Structural Engineering is still burgeoning.
	Intrusive	Spectral Stochastic FEM	Gives more reliable results	Complicated and demands access to simulation procedure Linear and non-linear SFEM is not yet practical if the original random field is discretized into a high dimensional random vector
Time variant reliability Methods			In a lot of cases, reliability aspects are T-V. For instance, some kind of degrading mechanism on the resistance side or fluctuating loads may be the reason. Fatigue and corrosion phenomenon are T-V	Practical application of T-V reliability methodology appears rather limited, partially because only very few computer codes are available

summarize the most popular SR methods and their capabilities and limitations [1,5,6,16,17,19,22,28,29,30,55,64,80].

The developments over the last 40 years, with an emphasis on recent development in the FORM and SORM, were reviewed in great detail by Breitung [17] and show that the FORM and SORM are relevant and indispensable in the area of RA as applied to structural engineering. This is in agreement with previous studies carried out by Rackwitz [28]. The well-practiced quantitative approaches to reliability-based risk analysis of analytical nature, such as the concept of LS and FORM/SORM or MCS methods, are still common practice [1]. The conventional SR methods, such as FORM/SORM and MCS, still remain the de facto methods and serve as the basis for enhanced methods that overcome their inherent limitations. Recent research [80] shows that the FORM is the most efficient SRA method ahead of the SORM. The concepts underlining the intricate FORM/SORM algorithms, including the application of numerical optimization methods that form the basis of advancements already discussed in Section 2, are examined in depth and elucidated below [17].

Having defined the LSF $g\left(u_1,\dots ,u_n\right)$ in the u-dimensional Euclidean space, Equation (7), the FORM aims to approximate the failure domain $F=\left\{\mathit{u};g\left(\mathit{u}\right)<0\right\}$ by a halfspace by replacing the LSF by a linear tangent hyper-plane at the point ${\mathit{u}}^{*}$. The LSS $G=\left\{\mathit{u};g\left(\mathit{u}\right)=0\right\}$ has the nearest geometric distance to the origin, which means that the PDF is maximal there since it is proportional to $-{\left|\mathit{u}\right|}^2$. The HL algorithm revolves around finding a point ${\mathit{u}}^{*}$ for an LSF $g\left(\mathit{u}\right)$ at the normal standard space such that

$$\left|{\mathit{u}}^{*}\right|=\underset{g\left(\mathit{u}\right)=0}{\min }\left|\mathit{u}\right|=\underset{g\left(\mathit{u}\right)\le 0}{\min }\left|\mathit{u}\right|,$$

(21)

i.e., with the shortest distance to the origin. Basically, this involves linearizing the LSF at an initial point, calculating the design point for the linearized LSF, and then proceeding recursively, always again linearizing until convergence is achieved.

Line-search and trust-region methods are common deterministic minimization approaches for differentiable functions [88]. In terms of saving computational costs, the former is usually employed. In the line-search approach, to find the minimum of a function $f\left(\mathit{x}\right),$ a sequence ${\mathit{x}}_k$ of points, of which convergence toward a minimum is sought, can be calculated iteratively via:

$${\mathit{x}}_{k+1}={\mathit{x}}_k-{\alpha }_k{\mathit{H}}_k^{-1}\nabla f\left({\mathit{x}}_k\right)$$

(22)

where ${\mathit{x}}_k$ is the iteration point at present, ${\mathit{H}}_k$ a symmetric and positive definite matrix, $\nabla f\left({\mathit{x}}_k\right)$ the gradient, and ${\alpha }_k$ the step length.

The search direction ${\mathit{H}}_k^{-1}\nabla f\left({\mathit{x}}_k\right)$ is assumed as a direction such that the target function decreases and ${\alpha }_k$ in such a way that the decrease based on a certain criterion is sufficient. Only a step length is chosen for a somehow sufficient decrease as no exact line search is often made for ${\alpha }_k$—an inexact line search [88]. The inexact line search is carried out either by finding the minimum value after polynomial approximation is made to the function on the line or by calculating the function value for a decreasing sequence of step lengths until attaining a sufficient decrease.

${\mathit{H}}_k$ is selected based on the information and storage space available. Newton methods, where ${\mathit{H}}_k={\nabla }^{2}f\left({\mathit{x}}_k\right),$ or quasi-Newton methods, where ${\mathit{H}}_k$ is an approximation of the Hessian, are applied if the information on second derivatives can be collected. However, if this information is unavailable, steepest descent approaches, which use the n-dimensional unity matrix ${\mathit{H}}_k={\mathit{I}}_n,$ or conjugate gradient approaches are applied. In the full Newton approaches, knowledge about Hessian of the target function is required, which implies that these are usually computationally costly for problems having high dimension.

It seems the steepest descent method, $-\nabla f\left({\mathit{x}}_k\right)$, should be the optimal search direction choice. However, this approach does not possess optimal convergence characteristics [88]. This has linear convergence speed and its application is usually discouraged according to literature.

A superior approach that makes use of only gradient information is the conjugate gradient method [88]. Quasi-Newton methods involving reconstructing the Hessian from the change in the gradients are more efficient. Calculation of second derivatives is avoided here but storing the approximate $n\times n-\mathrm{matrix}$ Hessian is required.

This sequence of steps is applied in modified form for finding constrained extrema. The extrema of $f\left(\mathit{x}\right)$ under $g\left(\mathit{x}\right)$ are found under some regularity conditions under the stationary Lagrangian function ($L\left(\mathit{x},\lambda \right)=f\left(\mathit{x}\right)+\lambda g\left(\mathit{x}\right)$) points with:

$$\begin{array}{c}{\nabla }_{\mathit{x}}L\left(\mathit{x},\lambda \right)=0\\ g\left(\mathit{x}\right)=0\end{array}$$

(23)

in such a way that determining these points involves altering the minimization algorithms.

In the SQP (sequential quadratic programming) method, the original problem is replaced in each iteration step by a quadratic function in which its minimum under the linearized constraint must be calculated, i.e.,

$$\min {\mathit{x}}^T{\mathit{A}}_k\mathit{x}+{\mathit{b}}_k^T\mathit{x}+c \mathrm{under} g\left({\mathit{x}}_k\right)+\nabla g{\left({\mathit{x}}_k\right)}^T\left(\mathit{x}-{\mathit{x}}_k\right)=0,$$

(24)

provided the original constraint condition $g\left(\mathit{x}\right)=0$ is not violated by much and this method predicts a direction whereby the target function $f\left(\mathit{x}\right)$ is decreasing accurately. In order to achieve this, a merit function $M\left(\mathit{x}, C\right)$ in the direction given by $\mathit{p}$ is minimized via adjusting the step length. Depending on a parameter $C$, the merit function is that in which its constrained minimum approximately coincides at least with the unconstrained minimum of the target function for parameter $C$ of sufficiently large magnitude.

Alternatively, the augmented Lagrangian method, which involves replacing the constrained optimization problem by a sequence of unconstrained optimization problems, can be utilized. The Lagrangian $L \left(\mathit{x}, \lambda \right)$ function is replaced by the minimized augmented Lagrangian $L\left(\mathit{x}, \lambda ,\mu \right)=f\left(\mathit{x}\right)+\lambda g\left(\mathit{x}\right)+\mu g{\left(\mathit{x}\right)}^2$ and then by adjusting the parameters $\lambda$ and $\mu$. The unconstrained minima of $L \left(\mathit{x}, \lambda , \mu \right),$ given a large enough $\mu$, are also the minima of the constrained problem [88]. In order to determine the minimum of the augmented Lagrangian, any approach for the unconstrained optimization can be applied.

In order to overcome the deficiencies of non-convergence encountered in running the original HL–RF algorithm, several modifications were developed. These are critically discussed below [17].

In exceptional cases, the HL–RF algorithm behaves like the Newton–Raphson method with a unique feature of possessing quadratic convergence speed, assuming the algorithm starts on the connecting line of the origin with the beta point, such that the LSF gradient at a point $\mathit{u}$ on this line is parallel always to the position vector $\mathit{u}$. For example, in a hyperparabolic LSF problem, having defined $h\left(v\right)=g\left(v\nabla g\left(\mathit{u}\right)\right),$ then the iterative HL–RF algorithm can be expressed as:

$$v_{n+1}=v_n-\frac{h\left(v_n\right)}{h^{\prime }\left(v_n\right)}.$$

(25)

This is the 1D Newton–Raphson method used to find the zero of the function $h\left(v\right)$ characterized by quadratic convergence speed.

Since steepest descent procedure uses only local descent direction information and due to its inability to establish more efficient search directions as quasi-Newton methods via varying the search direction, problems of considerable starting point-beta point distance may run a long time through valleys. In the case of steepest descent close to the MPP, the problem is that the Lagrangian in the tangential space there is approximately equal to its second-order Taylor series expansion $L\left({\mathit{u}}^{*},{\lambda }^{*}\right)+{\left(\mathit{u}-{\mathit{u}}^{*}\right)}^T{\nabla }_{\mathit{u}}^{2}L\left({\mathit{u}}^{*},{\lambda }^{*}\right)\left(\mathit{u}-{\mathit{u}}^{*}\right)/2$ at the design point ${\mathit{u}}^{*}$ (wherein ${\lambda }^{*}$ is the Lagrange multiplier), where the gradient is vanishing. Thus, these methods have slow convergence and zigzagging characteristics.

Conversely, these methods need only one evaluation of the LSF gradient at each step and appear to be quite robust. Most studies performed in the last years proposing improvements have failed to address the inherent challenges, such as convergence speed in the original iteration scheme, because these approaches only apply not such a significant step-length adjustment.

Most optimization schemes revolve around arriving at super-linear convergence rate, such that

$$d_{n+1}\approx \gamma d_n^{\alpha } \mathrm{with} 1<\alpha \le 2 \mathrm{and} \gamma >0,$$

(26)

so as to avoid the slow linear convergence found in the steepest descent approach. In order to achieve fast convergence and avoid zigzag circumstances, a better option might be to restrict in the vicinity of beta point methods that aim at reconstructing the Hessian of the Lagrangian. It was asserted in [2] that in SQP methods the approximating matrix for the Hessian is unreliable and tends to become indefinite. This is because beta point Hessian can be indefinite there, as it is not necessarily positively definite. In regular circumstances, assuming that the Hessian is definitely positive, semi-definite only in the tangential space at the MPP is valid.

Reduced Hessian methods, which aim at reconstructing only the Hessian projected onto the tangential space, seem to be more reliable [88]. Given that the constrained minimum is regular, this projected matrix is positively definite. According to [17], it is difficult to recommend which approach to use, as these variations are problem-specific. Methods such as reduced Hessian, quasi-Newton, or conjugate gradients may have better convergence characteristics close to the beta point but are less robust compared to the HL–RF algorithm for problems with LSF that is not sufficiently smooth. Here, all approaches discussed are variants of or associated with the SQP method. Alternative methods are the augmented Lagrangian approaches but they seem to be inefficient for the beta point search.

Due to the volume of research, developments in the area of SRA are tending toward the use of RS and SM/MM. The PF of most realistic engineering structures today are highly non-linear and implicit (i.e., cannot be solved without the use of FEA) and, thus, analytical methods are incapable of solving them efficiently. Also, the MCS cannot efficiently provide accurate solution of LS with very low failure probabilities. Despite the fact that numerical techniques, such as IS, LHS, and SS, have been developed to reduce computational costs, this drawback, among others, still exists. There have been several alternative methods that involve a combination of two or more reliability methods to overcome these drawbacks. The RSM provides an efficient vehicle to combine the high-fidelity FEA modeling with conventional SRA methods. SM SRA methods are ideal for cases requiring implicit PF to be evaluated point-wise using FEM. The PCE (Polynomial Chaos Expansion) has been used as a regression technique to model accurately the global behavior of computational models, while the KIM with high fidelity models local variations, owing to its interpolation capabilities. Global methods, such as the Active Learning Reliability Method combining Kriging and MCS (AK-MCS) and the EGRA [56], have been found to be very efficient, as they give accurate results for implicit, time-consuming, unaffordable PFs, as demonstrated in [14]. For the treatment of problems, such as complex geotechnical designs and those involving high-frequency vibrations and of elastic stability, SFEM has been found to be ideal as it accounts for spatially varying stochastic structural heterogeneity [80,83]. Numerous studies were carried out on reliability analysis in other related areas such as in geotechnical engineering, fluid mechanics, rock engineering, etc. The scope of the present study is limited to only reliability assessment with respect to metal offshore jacket structures associated with structural engineering.

Applications of the T-D SRA for the design of modern metal structures such as those deployed offshore (i.e., in environments characterized by highly stochastic loads and resistance properties, thus necessitating the need for SRA to account for such uncertainties systematically) include [2,3,44,47,48,49,89,90,91,92,93,94]. In [95], the fatigue reliability of fixed offshore platforms was investigated by analyzing different failure scenarios. The analysis was divided into a finite number of sub-scenarios in order to evaluate the occurrence probability of a special scenario. The Palmgren–Miner’s rule and S-N curve were employed to estimate the accumulated fatigue damages in the LSF. Extensive research has been carried out in the area of probabilistic fracture mechanics approach to FRA, some of which include: According to [96], to accurately evaluate the effect of an inspection and repair strategy of structures subjected to degradation resulting from crack growth, application of FM models are required to describe crack propagation. The reliability methods applied to account for inherent uncertainties with respect to selecting an optimal tool for making the proper decision, which enables a balance between design criteria, inspection, and repair plans, include SN and FM formulations. These include a crack-growth formulation based on bilinear crack-growth law, assuming both crack-growth law segments to be correlated and non-correlated in the POF calculation. The FORM and SORM, as well as MCS, were used to illustrate the effect of inspection in the updated reliabilities. It was reported that crack initiation time, initial crack size, and the crack aspect ratio play significant roles in the calibration of FM methods.

Dong et al. [91] investigated the fatigue reliability of welded multi-planar tubular joints of the support structure of a fixed-jacket, offshore wind turbine in a water depth of 70 m. The long-term statistical distribution of hot-spot stress ranges was fitted using a two-parameter Weibull function by combining time-domain simulation for the inherent environmental conditions (wind/sea states) in operational condition. The SN-Miner–Palmgren approach-based fatigue design criteria were satisfied by normalizing the load histories and, thus, the estimated safety levels refer to fatigue design of tubular joints that meet design criteria. The FM analysis of crack growth was applied for the reliability analysis. The hot-spot stress range was increased, assumed to be due to changes of the nominal stress and stress concentration factors produced by thickness thinning (wastage) effects of selected components with a general uniform corrosion model in order to account for the corrosion-induced crack-growth rate. Also investigated were factors such as the effects of geometry function and corrosion-induced material degradation on the reliability evaluation. The influence of inspection and repair with and without considering corrosion were investigated based on the quality of inspection in terms of probability of crack detection curves. FM models were applied to describe crack propagation models, which were calibrated based on SN-data since the initiation of cracks and their initial stages at growth are subject to uncertainties that are hard to quantify. The FORM was applied in the calculation of the RI at the welded joint, representing the failure-critical hot-spot location where the most cumulative fatigue damage occurs.

According to [97], the FM approach is more complicated than the SN-curve design, which increases the risk of gross errors. In [4,90], it was assumed that the errors due to the complexity of the FM approach may be reduced as a result of using the ANSYS SMART Fracture^© FEA facility. Hence, in their study, owing to the high fidelity of the FEA model, it was assumed that this accounted for model uncertainties that may exist due to errors if analytical calculations were to be used. The non-intrusive formulation used therein enables an enhanced analysis, leading to more accurate results as it utilizes the 3D simulation method, as established in [2,4].

In [4,90], SN-curve and FM approaches to fatigue reliability assessment were compared. A non-intrusive stochastic framework that includes 3D parametric FEA model of OWT jacket support structures was developed, taking account of soil–structure interactions. According to the results revealed from the study, the structural reliability prediction produced following the SN-curve method gave conservative results compared to those produced using the FM approach at the start of the service life of the structure, but toward the end of the design life, the results may be overly optimistic. Hence, the authors inferred from the foregoing that it is ideal for applying the S-N curve approach during the design stage, while the FM approach should be used as the structure approaches failure. Furthermore, other fatigue reliability assessment exercises performed included estimating the maximum inspection time for the support structure determined via updating the developed reliability framework with structural health monitoring/condition monitoring (SHM/CM) data. Hence, the updated reliability assessment provides valuable information for making decisions concerning the inspection, maintenance, and repair (IMR) of OWT jacket support structures.

A subcategory under this, which is an area open to further investigations due to the sparse amount of research, is the damage tolerance approach for probabilistic pitting-corrosion fatigue life prediction performed by [2], wherein comprehensive mechanistic-based probabilistic models for pitting-corrosion fatigue life prediction by including all stages were presented, and the FORM was implemented with the proposed models. In [2], a generic RA framework that combines parametric FEA modeling, RSM, and RA specifically for complex OWT jacket-type support structures in the presence of highly stochastic variables and taking into consideration, specifically, T-D phenomena such as fatigue as well as degradation mechanisms such as corrosion was developed. Two ANNs were trained to relate various stochastic variables for predicting the PF. The two ANNs were employed in order to have an intermediate predictor for a stochastic variable, which is more advantageous because of the added interpretability of results. An advantage of the proposed methodology is that the first ANN architecture enabled a significant reduction in the computational cost, which would have been required to simulate global behavior of the support structure, thus allowing other global parameters to be incorporated [4].

Despite the high volume of research in this area, it has proven troublesome to establish a model that adequately describes the growth of short cracks, particularly for corrosive environments. Different uncertainties were reported in the two-stage crack-growth law with the (lower) near-threshold segment having the largest variability. The larger variability may be because the knuckle region is very close to the short-crack regime and, thus, the inherent uncertainty of the $\Delta K$ threshold, whereby the material experiences no crack growth below this. It is not clear how the material behaves around this region. Coupled with the difficulty of carrying out measurements of such fatigue, growth rates in tests entails that further research is required on this. It was suggested in [2,4] that one way to overcome this drawback is by introducing effective initial flaw size (EIFS) concepts, which are alternative solutions to the K-T (Kitagawa-Takahashi) diagram.

Several studies have been performed on applying GA in SRA and on sensitivity analysis and design optimization, referred to as the stochastic/structural reliability sensitivity analysis (SSA) and RBDO (Reliability-based Design Optimization), respectively. The scope of this study was limited to only SRA methods, due to the myriads of research performed in these areas (i.e., GA, SSA, and RBDO). It should be noted that this review did not cover all the papers published on this subject, but attempted to present the main techniques, with the intent of producing an important document, which serves as a guide to designers/researchers on this subject.

8. Conclusions

This work presents the state of the art in methods used for structural reliability analysis (SRA) based on a systematic review focusing mainly on literature from 2005 to 2020. The paper focused on presentations of methods and their variations, aiming to qualify their advantages and limitations with applicability to design of metal offshore jacket structures. Improvements to the fundamental analytical methods facing issues with highly non-linear performance function (PF) structures were modified with conjugate search direction approach, Saddle Point Approximation (SPA), the introduction of the merit function, subset simulation (SS), and evidence theory, among others. To reduce the computational burden of MCS, the approximation methods can be applied to estimate implicitly or explicitly the limit state functions (LSFs) involving Finite Element Analysis (FEA). Combinations of advanced approximation methods and RA methods are also found in literature, as they can be suitable for complex, highly non-linear problems.

• The FORM was improved by the development of the conjugate search direction, finite-based Armijo search direction method, Hybrid Relaxed HL–RF, stability transformation method (STM) with chaos feedback control, STM with chaos feedback control, and STM with chaotic conjugate search direction, among others. The combination of Maximum Entropy Fitting Method and the FORM was applied to problems of implicit LSFs. The SORM is an improvement on the FORM, to provide solutions to highly non-linear LSFs. A new SORM for RA was developed using the SAP in order to overcome some of the issues inherent in the traditional SORM.
• The MCS method was improved by the development of interval MC method, which combines simulation process with interval analysis, new MC-based methods involving the use of brute force MCS methods for complicated structural systems, IMC-IFEM, merging IS with directional simulation, etc. Improvements in variance reduction techniques were achieved, such as the development of interval importance sampling (IS) method, which applies the IS technique and imprecise probability, and the LHS-based quasi-random polar sampling technique.
• The advanced approximation modeling methods include the well-established Response Surface Models/Method (RSM) and the Surrogate Models (SM) as well as the Stochastic RSM (SRSM). The SRSM is a model for the RA of complex systems with low Probability of Failure (POF) for which approximate methods are inaccurate and for which Monte Carlo Simulation (MCS) is too computationally intensive. The efficiency of the RSMs developed for implicit LSFs studied herein include the Collocation Based SRSM, novel SRSM combining FEA, MPR, and FORM/SORM, incorporating the SRSM with Saddle point approximation (SPA), among others. Examples of SM include the Kriging, Adaptive Kriging, EGRA, Support vector machines, ANN, RBF, etc. These can be combined with conventional reliability methods for problems of implicit LSFs. Kriging and Adaptive Kriging interpolation models were combined with the FORM, Line sampling, IS, SS, MCS, etc.
• This study focused specifically on the probabilistic fatigue and fracture mechanics approaches because the fatigue limit state in most cases is the design-driving criterion for structural components of offshore jacket structures. Consequently, the SRA of structures considering pitting-corrosion fatigue phenomenon was identified as particularly of note and is recommended as an area open to further investigation.