On the Evaluation of Energy Dissipation at the Beginning of Fatigue
Abstract
:1. Introduction
2. The Relationship between Energy Dissipation and Temperature
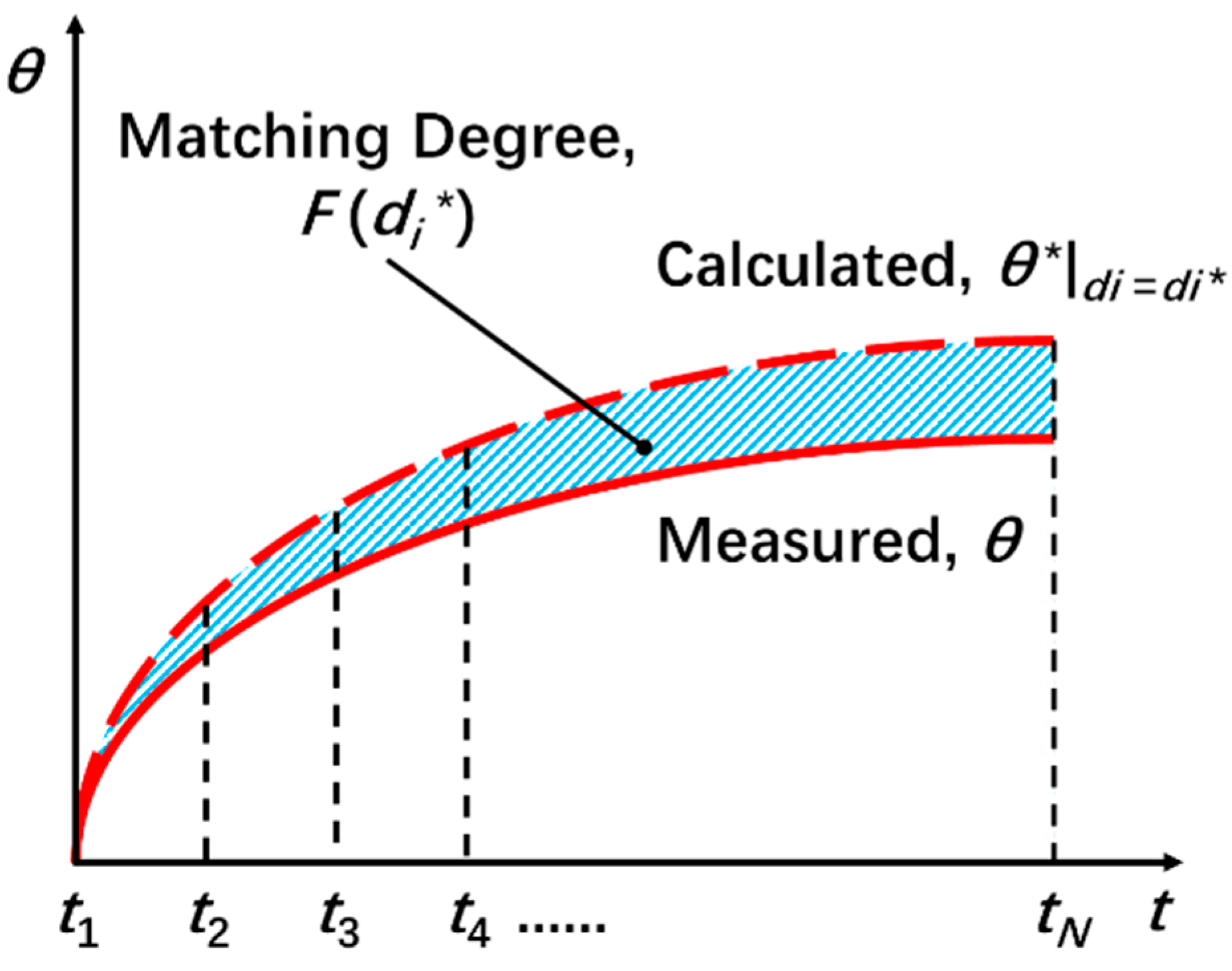
3. The Optimization Method Considering Thermal Boundary Conditions
4. Numerical Simulation of Temperature Evolution during Fatigue
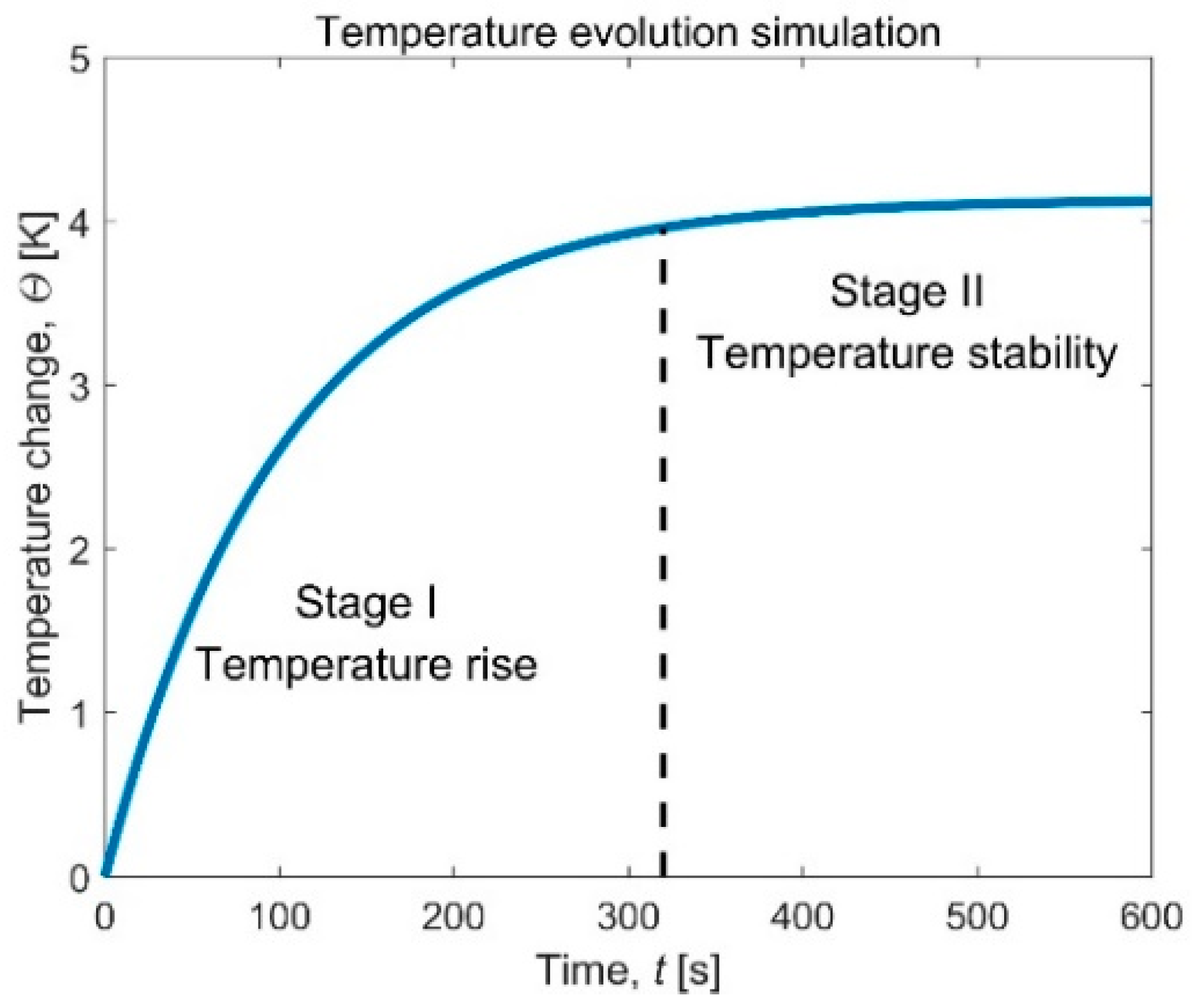
4.1. Temperature Evolution with Constant Energy Dissipation
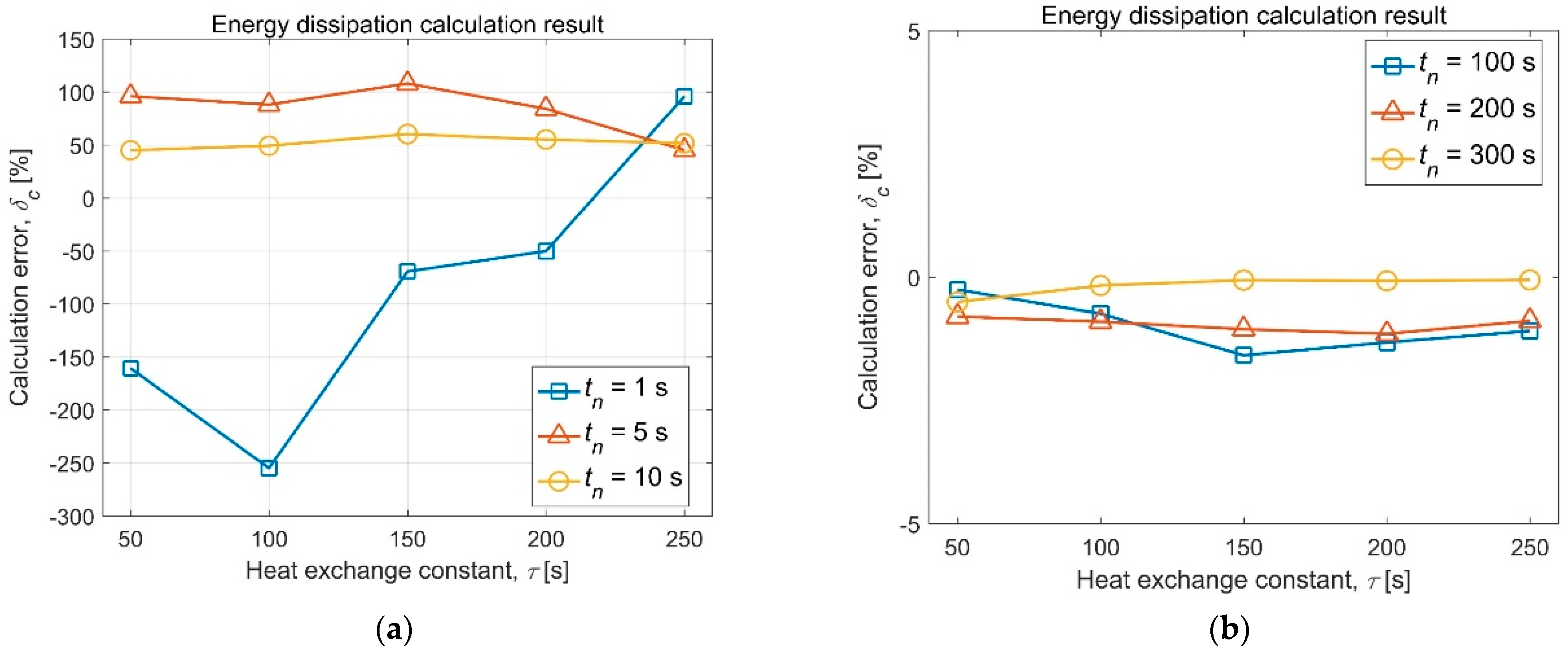
4.2. Influence of Thermal Boundary Conditions
5. Validation of the Optimization Method Based on Numerical Simulation
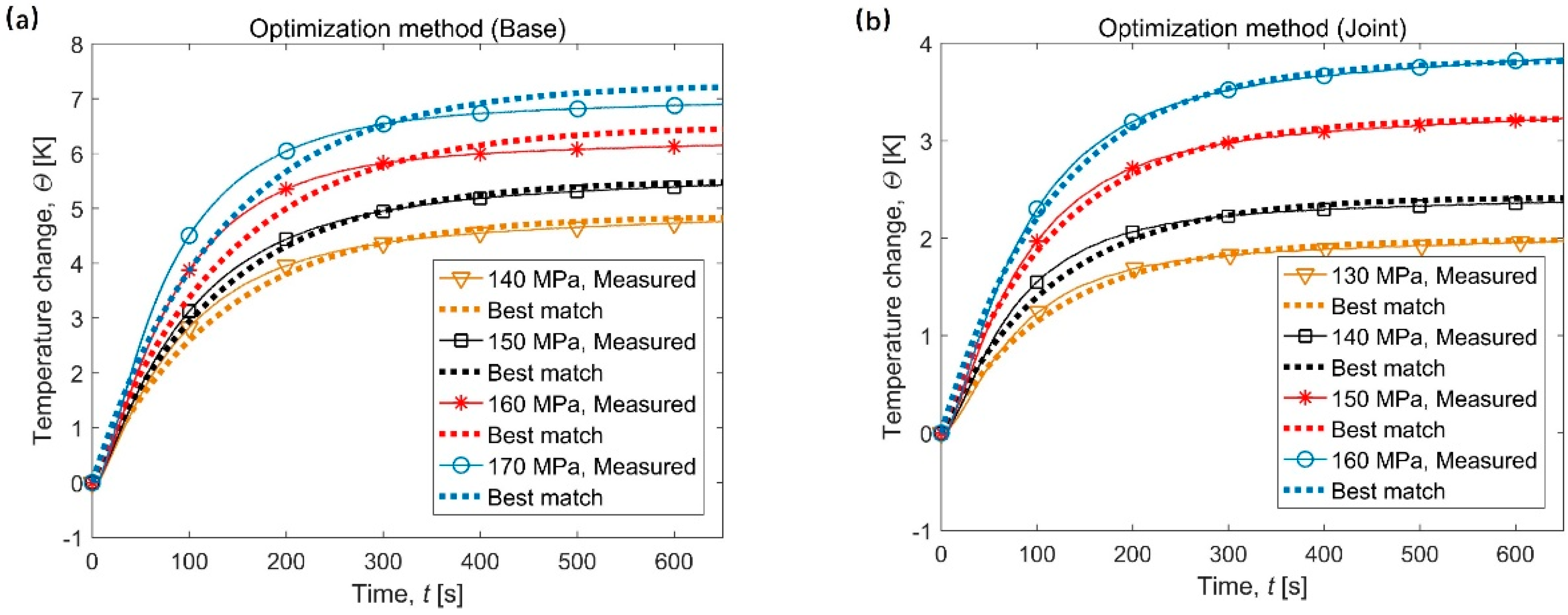
5.1. Result of the Optimization Method
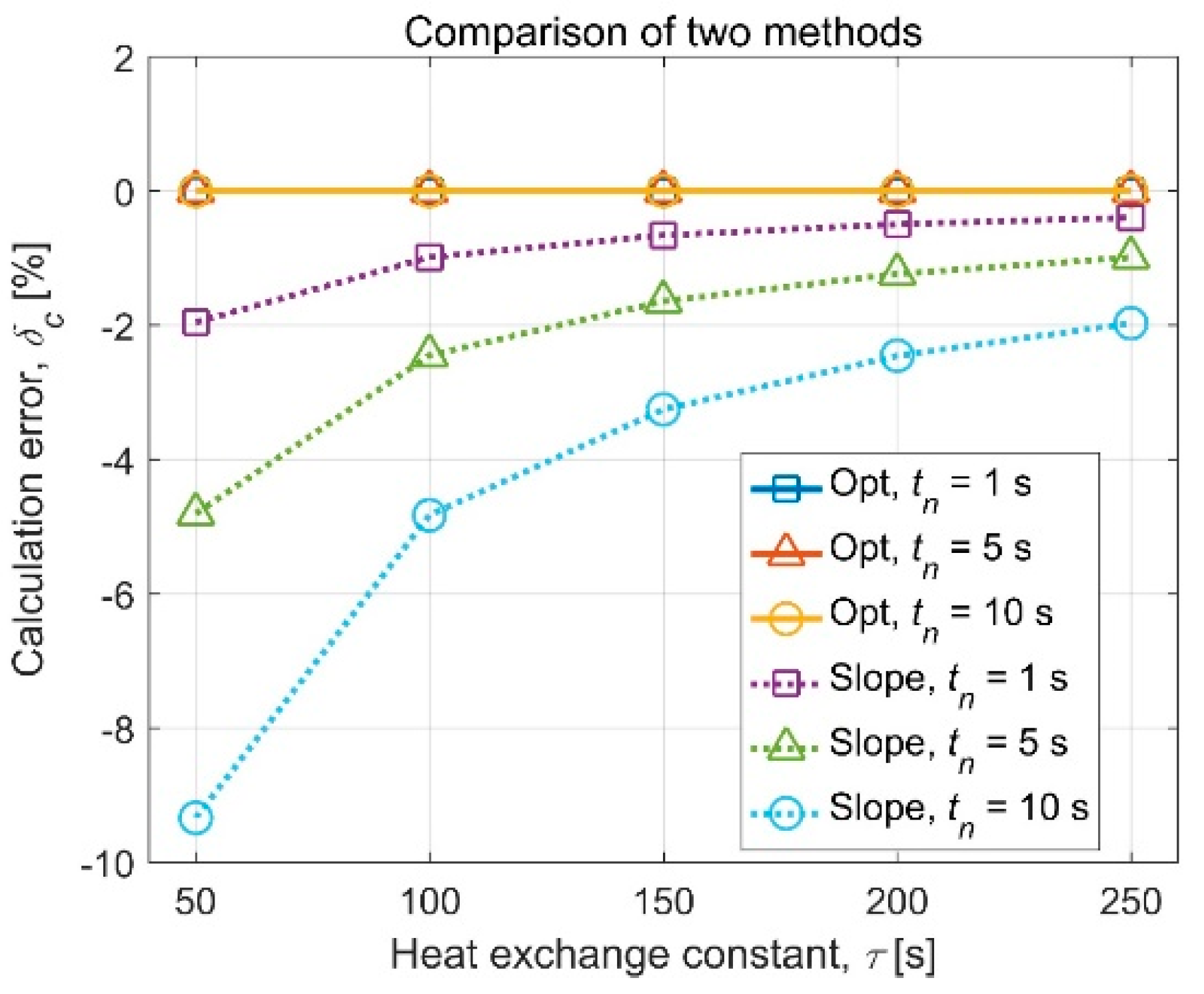
5.2. Comparison with the Slope Method
6. Application: Fatigue Life Analysis
6.1. Experimental Materials and Procedures
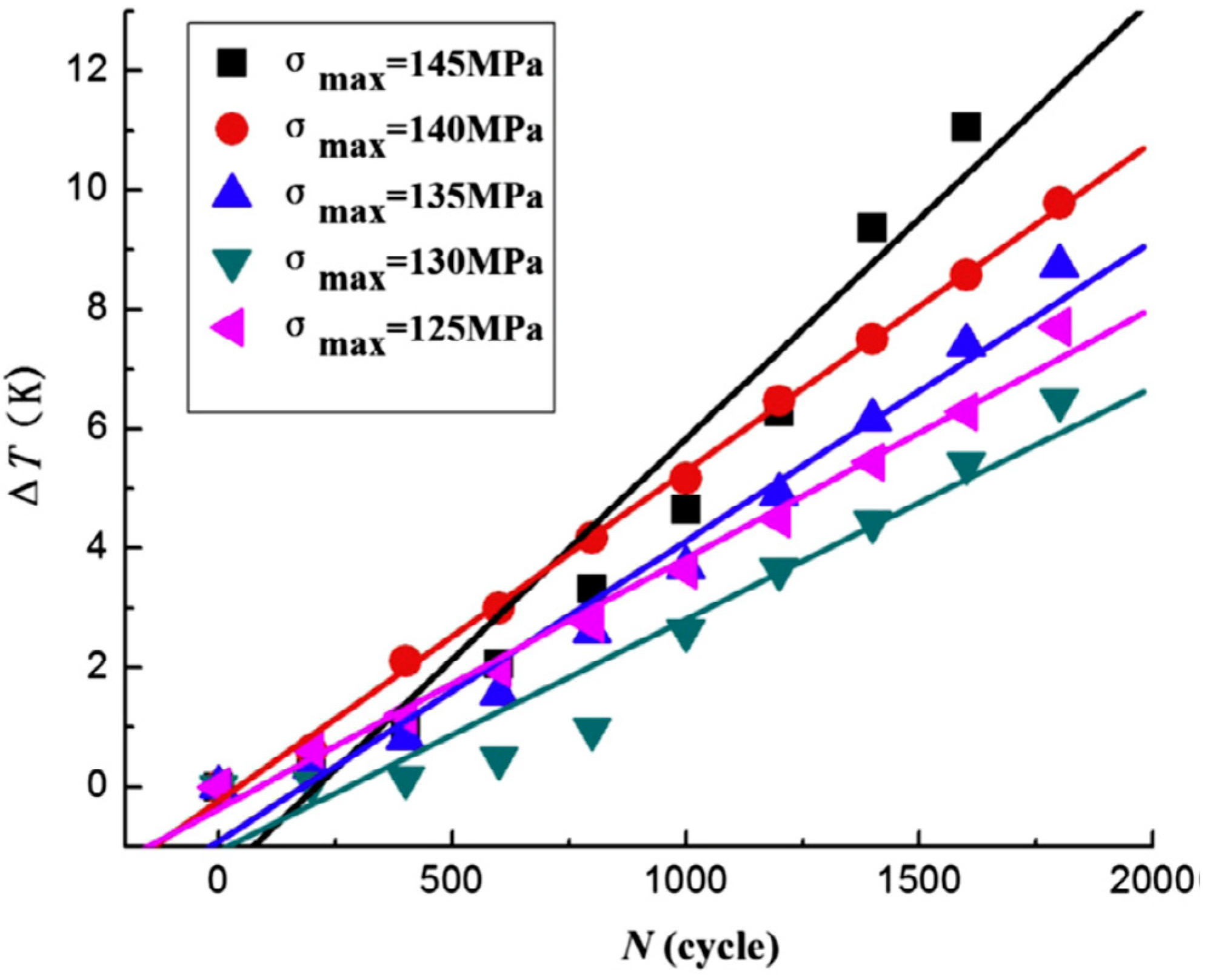
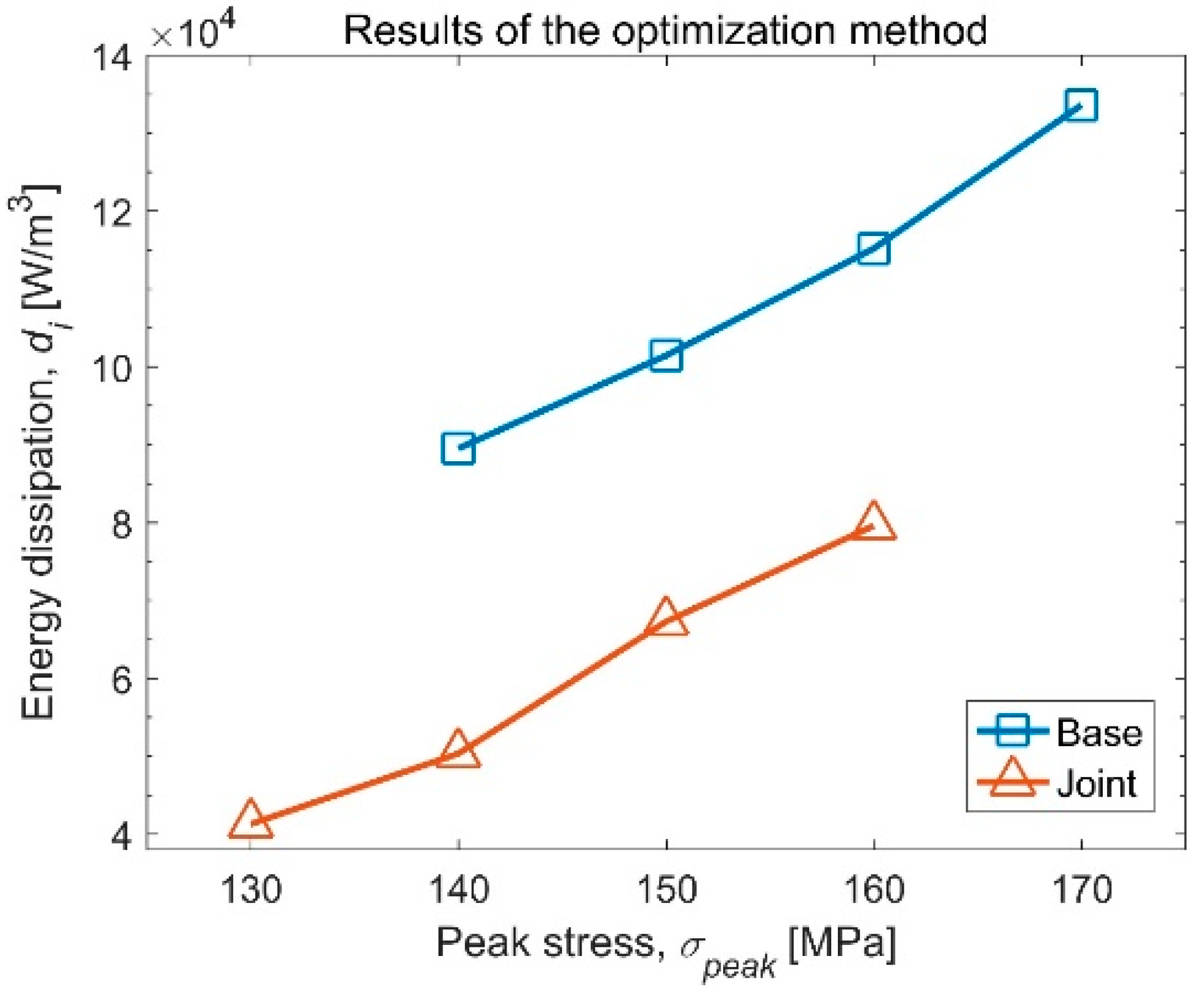
6.2. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khonsari, M.M.; Amiri, M. Introduction to Thermodynamics of Mechanical Fatigue; CRC Press: New York, NY, USA, 2013. [Google Scholar]
- Connesson, N.; Maquin, F.; Pierron, F. Dissipated Energy Measurements as a Marker of Microstructural Evolution: 316L and DP600. Acta Mater. 2011, 59, 4100–4115. [Google Scholar] [CrossRef]
- Zhang, H.X.; Wu, G.H.; Yan, Z.F.; Guo, S.F.; Chen, P.D.; Wang, W.X. An Experimental Analysis of Fatigue Behavior of AZ31B Magnesium Alloy Welded Joint Based on Infrared Thermography. Mater. Des. 2014, 55, 785–791. [Google Scholar] [CrossRef]
- Crupi, V. An Unifying Approach to Assess the Structural Strength. Int. J. Fatigue 2008, 30, 1150–1159. [Google Scholar] [CrossRef]
- Luong, M.P. Fatigue Limit Evaluation of Metals Using an Infrared Thermographic Technique. Mech. Mater. 1998, 28, 155–163. [Google Scholar] [CrossRef]
- La Rosa, G.; Risitano, A. Thermographic Methodology for Rapid Determination of the Fatigue Limit of Materials and Mechanical Components. Int. J. Fatigue 2000, 22, 65–73. [Google Scholar] [CrossRef]
- Fargione, G.; Geraci, A.; La Rosa, G.; Risitano, A. Rapid Determination of the Fatigue Curve by the Thermographic Method. Int. J. Fatigue 2002, 24, 11–19. [Google Scholar] [CrossRef]
- Bouache, T.; Pron, H.; Caron, D. Identification of the Heat Losses at the Jaws of a Tensile Testing Machine. Exp. Mech. 2016, 56, 287–295. [Google Scholar] [CrossRef]
- Facchinetti, M.; Florin, P.; Doudard, C.; Calloch, S. Identification of Self-Heating Phenomena under Cyclic Loadings Using Full-Field Thermal and Kinematic Measurements: Application to High-Cycle Fatigue of Seam Weld Joints. Exp. Mech. 2015, 55, 681–698. [Google Scholar] [CrossRef]
- Chrysochoos, A.; Louche, H. An Infrared Image Processing to Analyse the Calorific Effects Accompanying Strain Localisation. Int. J. Eng. Sci. 2000, 38, 1759–1788. [Google Scholar] [CrossRef]
- Guo, S.; Zhou, Y.; Zhang, H.; Yan, Z.; Wang, W.; Sun, K.; Li, Y. Thermographic Analysis of the Fatigue Heating Process for AZ31B Magnesium Alloy. Mater. Des. 2015, 65, 1172–1180. [Google Scholar] [CrossRef]
- Guo, Q.; Guo, X.; Fan, J.; Syed, R.; Wu, C. An Energy Method for Rapid Evaluation of High-Cycle Fatigue Parameters Based on Intrinsic Dissipation. Int. J. Fatigue 2015, 80, 136–144. [Google Scholar] [CrossRef]
- Guo, Q.; Guo, X. Research on High-Cycle Fatigue Behavior of FV520B Stainless Steel Based on Intrinsic Dissipation. Mater. Des. 2016, 90, 248–255. [Google Scholar] [CrossRef]
- Boulanger, T.; Chrysochoos, A.; Mabru, C.; Galtier, A. Calorimetric Analysis of Dissipative and Thermoelastic Effects Associated with the Fatigue Behavior of Steels. Int. J. Fatigue 2004, 26, 221–229. [Google Scholar] [CrossRef]
- Meneghetti, G. Analysis of the Fatigue Strength of a Stainless Steel Based on the Energy Dissipation. Int. J. Fatigue 2007, 29, 81–94. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. Rapid Determination of Fatigue Failure Based on Temperature Evolution: Fully Reversed Bending Load. Int. J. Fatigue 2010, 32, 382–389. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. Life Prediction of Metals Undergoing Fatigue Load Based on Temperature Evolution. Mater. Sci. Eng. A 2010, 527, 1555–1559. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, X.S.; Wu, S.H.; Ma, Z.Q.; Fang, H.Y. Rapid Determination of Fatigue Life Based on Temperature Evolution. Int. J. Fatigue 2013, 54, 1–6. [Google Scholar] [CrossRef]
- Liu, X.Q.; Zhang, H.X.; Yan, Z.F.; Wang, W.X.; Zhou, Y.G.; Zhang, Q.M. Fatigue Life Prediction of AZ31B Magnesium Alloy and its Welding Joint through Infrared Thermography. Theor. Appl. Fract. Mech. 2013, 67–68, 46–52. [Google Scholar]
- Amiri, M.; Khonsari, M.M. Nondestructive Estimation of Remaining Fatigue Life: Thermography Technique. J. Fail. Anal. Prev. 2012, 12, 683–688. [Google Scholar] [CrossRef]
- Liakat, M.; Naderi, M.; Khonsari, M.M.; Kabir, O.M. Nondestructive Testing and Prediction of Remaining Fatigue Life of Metals. J. Nondestruct. Eval. 2014, 33, 309–316. [Google Scholar] [CrossRef]
- Liakat, M.; Khonsari, M.M. An Experimental Approach to Estimate Damage and Remaining Life of Metals under Uniaxial Fatigue Loading. Mater. Des. 2014, 57, 289–297. [Google Scholar] [CrossRef]
- Williams, P.; Liakat, M.; Khonsari, M.M.; Kabir, O.M. A Thermographic Method for Remaining Fatigue Life Prediction of Welded Joints. Mater. Des. 2013, 51, 916–923. [Google Scholar] [CrossRef] [Green Version]
- Haghshenas, A.; Khonsari, M.M. Non-Destructive Testing and Fatigue Life Prediction at Different Environmental Temperatures. Infrared Phys. Technol. 2019, 96, 291–297. [Google Scholar] [CrossRef]
- Mehdizadeh, M.; Khonsari, M.M. On the Application of Fracture Fatigue Entropy to Variable Frequency and Loading Amplitude. Theor. Appl. Fract. Mech. 2018, 98, 30–37. [Google Scholar] [CrossRef]
- Mehdizadeh, M.; Khonsari, M.M. On the Role of Internal Friction in Low-And High-Cycle Fatigue. Int. J. Fatigue 2018, 114, 159–166. [Google Scholar] [CrossRef]
- Mareau, C.; Favier, V.; Weber, B.; Galtier, A. Influence of the Free Surface and the Mean Stress on the Heat Dissipation in Steels under cyclic loading. Int. J. Fatigue 2009, 31, 1407–1412. [Google Scholar] [CrossRef]
- Wang, X.G.; Feng, E.S.; Jiang, C. A Microplasticity Evaluation Method in Very High Cycle Fatigue. Int. J. Fatigue 2017, 94, 6–15. [Google Scholar] [CrossRef] [Green Version]
- Delpueyo, D.; Balandraud, X.; Grédiac, M.; Stanciu, S.; Cimpoesu, N. A Specific Device for Enhanced Measurement of Mechanical Dissipation in Specimens Subjected to Long-Term Tensile Tests in Fatigue. Strain 2018, 54, e12252. [Google Scholar] [CrossRef]
- De Finis, R.; Palumbo, D.; Da Silva, M.M.; Galietti, U. Is the Temperature Plateau of a Self-Heating Test a Robust Parameter to Investigate the Fatigue Limit of Steels with Thermography? Fatigue Fract. Eng. Mater. Struct. 2018, 41, 917–934. [Google Scholar] [CrossRef]
- Fan, J.; Guo, X.; Wu, C. A New Application of the Infrared Thermography for Fatigue Evaluation and Damage Assessment. Int. J. Fatigue 2012, 44, 1–7. [Google Scholar] [CrossRef]
- Fan, J.; Zhao, Y.; Guo, X. A Unifying Energy Approach for High Cycle Fatigue Behavior Evaluation. Mech. Mater. 2018, 120, 15–25. [Google Scholar] [CrossRef]
- Guo, Q.; Zaïri, F.; Guo, X. An Intrinsic Dissipation Model for High-Cycle Fatigue Life Prediction. Int. J. Mech. Sci. 2018, 140, 163–171. [Google Scholar] [CrossRef]
- Fan, J.L.; Guo, X.L.; Wu, C.W.; Zhao, Y.G. Research on Fatigue Behavior Evaluation and Fatigue Fracture Mechanisms of Cruciform Welded Joints. Mater. Sci. Eng. A 2011, 528, 8417–8427. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]







| Yield Strength, σs [MPa] | Density, ρ [kg/m3] | Heat Capacity, C [J/(kg·K)] | Thermal Conductivity, λ [W/(m·K)] |
|---|---|---|---|
| 327 | 2690 | 900 | 119 |
| Materials | Si | Fe | Cu | Mu | Mg | Cr | Zn | Ti | Al |
|---|---|---|---|---|---|---|---|---|---|
| A7N01 | 0.35 | 0.40 | 0.20 | 0.15 | 1.20 | 0.20 | 4.60 | - | Bal. |
| ER5356 | 0.057 | 0.12 | 0.011 | <0.13 | 4.9 | 0.065 | 0.13 | 0.11 | Bal. |
| σpeak (MPa) | di (W/m3) | Nexp | Φi (J/m3) | Φ (J/m3) | Npre | δp (%) |
|---|---|---|---|---|---|---|
| 140 | 8.95 × 104 | 582,528 | 4.07 × 108 | 4.12 × 108 | 589,791 | 1.25 |
| 150 | 1.01 × 105 | 499,585 | 3.96 × 108 | 520,401 | 4.17 | |
| 160 | 1.15 × 105 | 501,696 | 4.51 × 108 | 458,319 | −8.65 | |
| 170 | 1.34 × 105 | 378,432 | 3.95 × 108 | 395,158 | 4.42 |
| σpeak (MPa) | di (W/m3) | Nexp | Φi (J/m3) | Φ (J/m3) | Npre | δp (%) |
|---|---|---|---|---|---|---|
| 130 | 4.13 × 104 | 1,358,528 | 4.38 × 108 | 2.79 × 108 | 866,184 | −36.24 |
| 140 | 5.03 × 104 | 626,177 | 2.46 × 108 | - | 710,410 | 13.45 |
| 150 | 6.73 × 104 | 457,023 | 2.40 × 108 | - | 531,458 | 16.29 |
| 160 | 7.96 × 104 | 310,080 | 1.93 × 108 | - | 449,247 | 44.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, L.; Guo, S.; Liu, X. On the Evaluation of Energy Dissipation at the Beginning of Fatigue. Metals 2021, 11, 1512. https://doi.org/10.3390/met11101512
Lan L, Guo S, Liu X. On the Evaluation of Energy Dissipation at the Beginning of Fatigue. Metals. 2021; 11(10):1512. https://doi.org/10.3390/met11101512
Chicago/Turabian StyleLan, Ling, Shaofei Guo, and Xuesong Liu. 2021. "On the Evaluation of Energy Dissipation at the Beginning of Fatigue" Metals 11, no. 10: 1512. https://doi.org/10.3390/met11101512
APA StyleLan, L., Guo, S., & Liu, X. (2021). On the Evaluation of Energy Dissipation at the Beginning of Fatigue. Metals, 11(10), 1512. https://doi.org/10.3390/met11101512






