Computational Determination of Macroscopic Mechanical and Thermal Material Properties for Different Morphological Variants of Cast Iron
Abstract
:1. Introduction
2. Creating Simulation Domains for Cast Iron with Lamellar Graphite
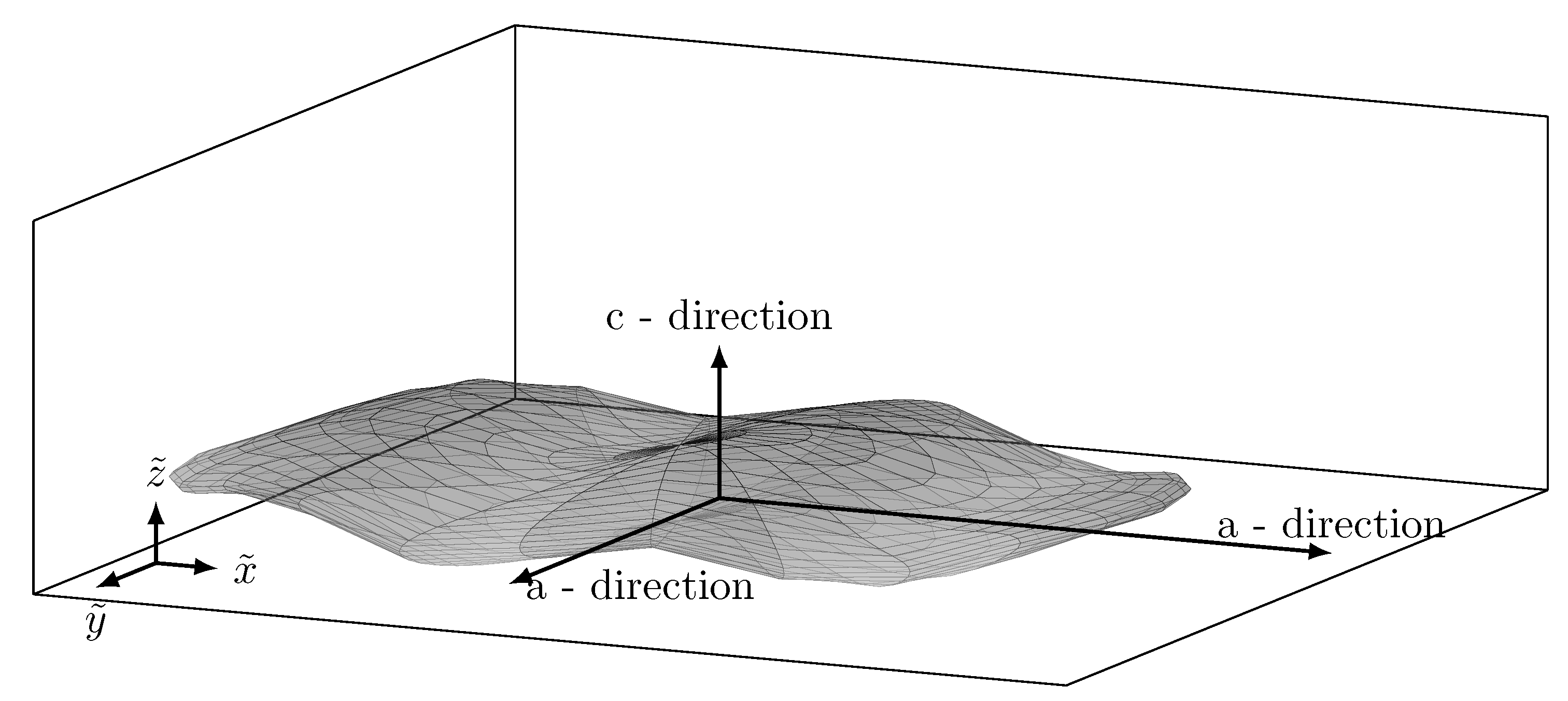
2.1. Modelling the Morphology of Cast Iron with Lamellar Graphite
2.2. The Volume Elements
3. Model Formulation
3.1. Mechanical and Thermal Model for Pearlite
3.2. Mechanical and Thermal Model for the Graphite Lamellae
4. Mechanical Simulations
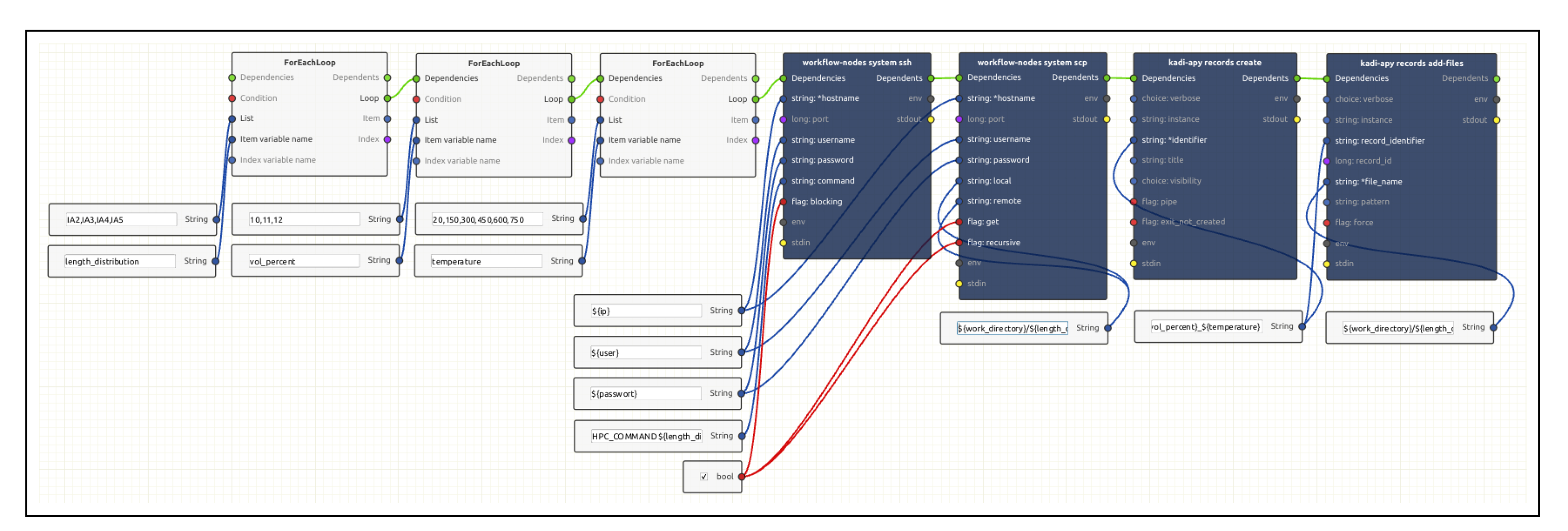
4.1. Key Points of the Numerics and the Simulation Setup
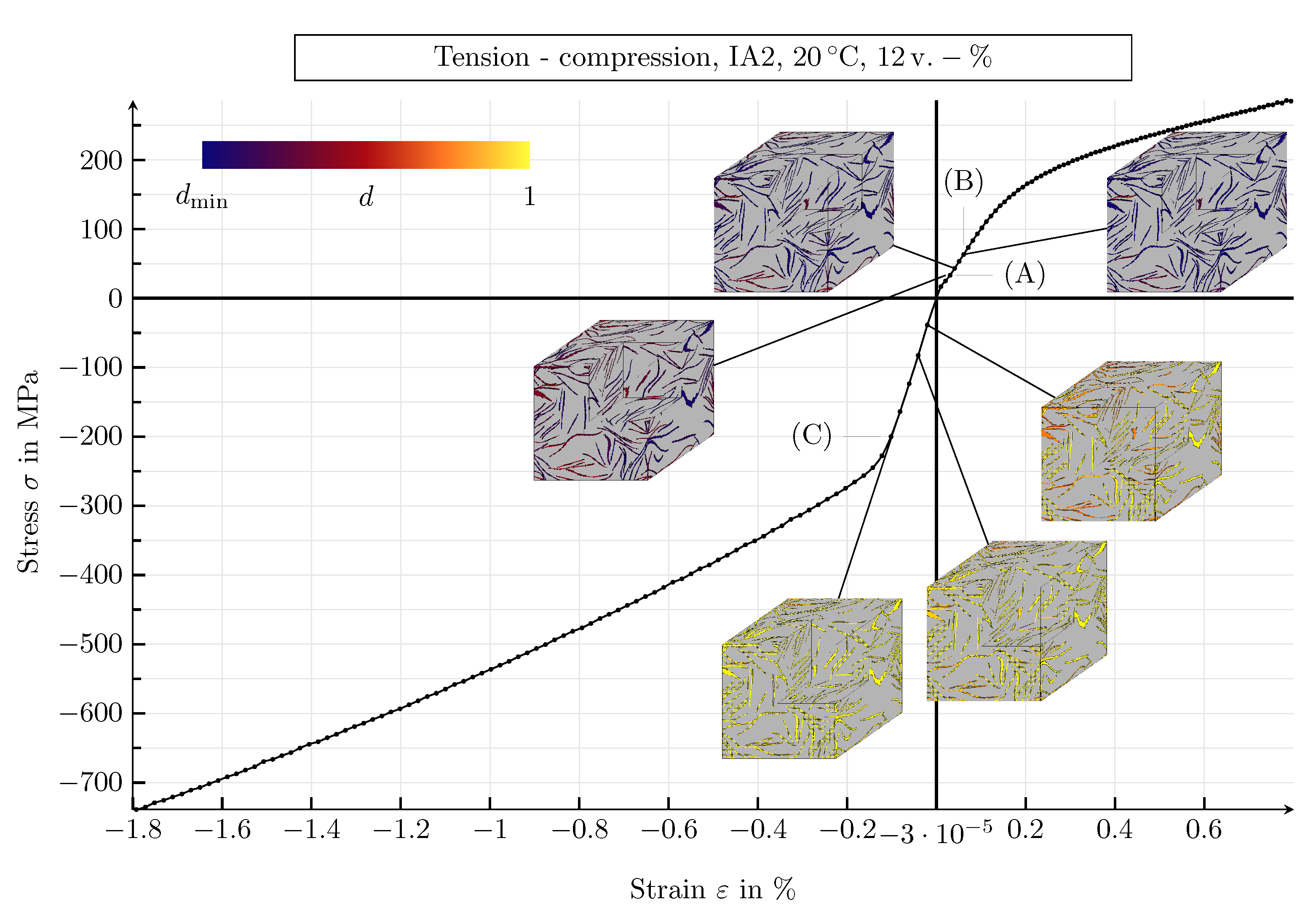
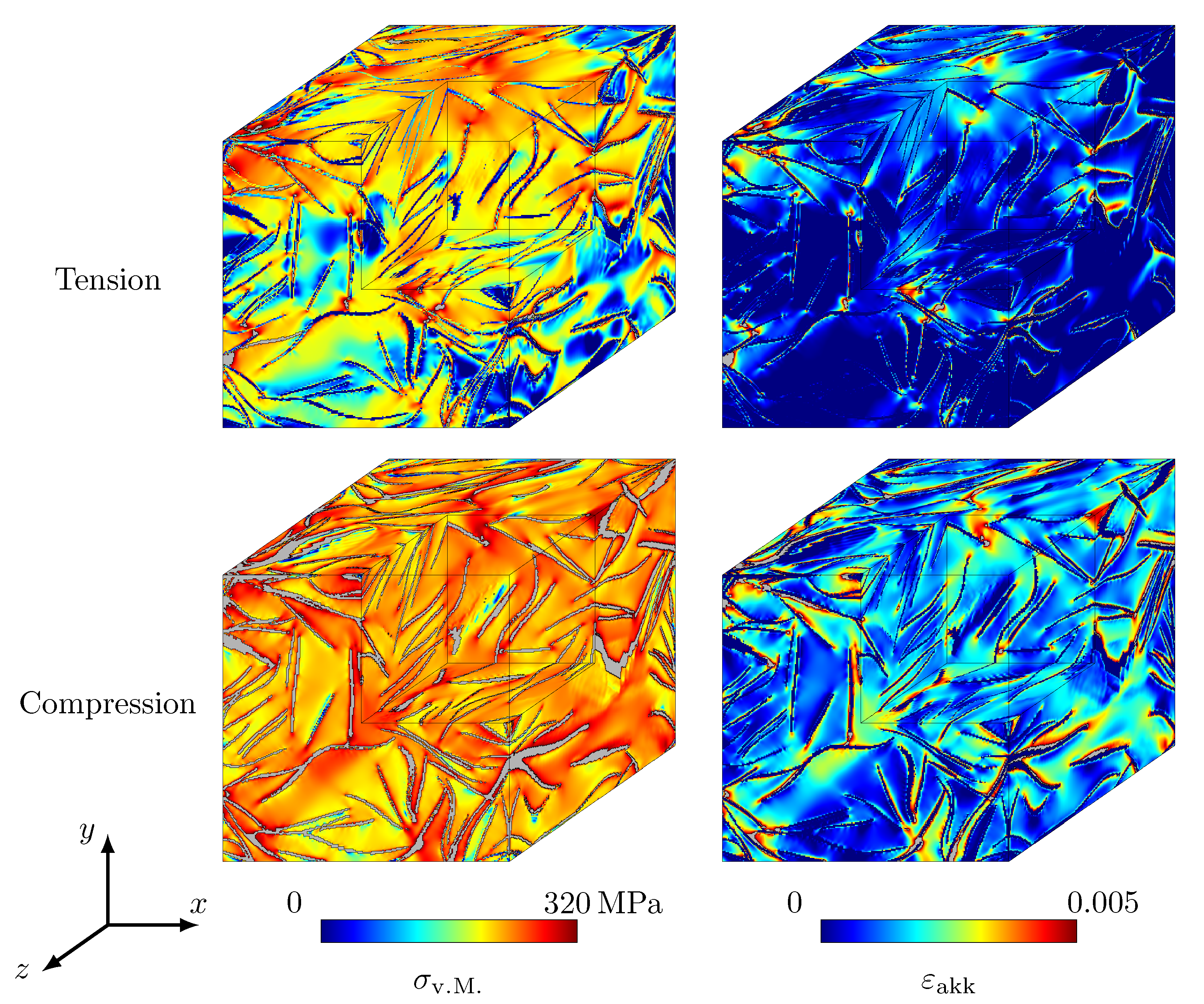
4.2. Analysis of the Mechanical Model
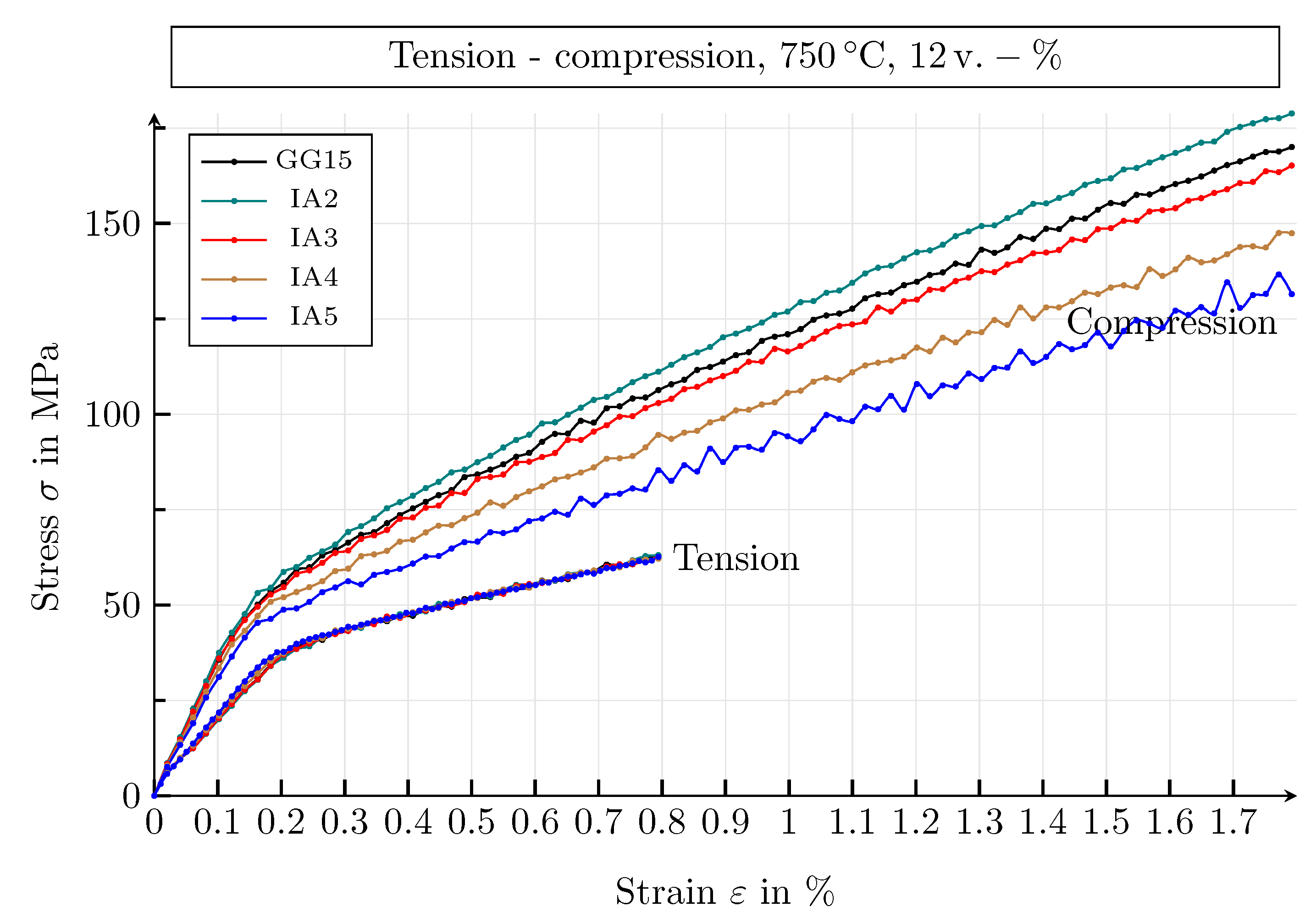
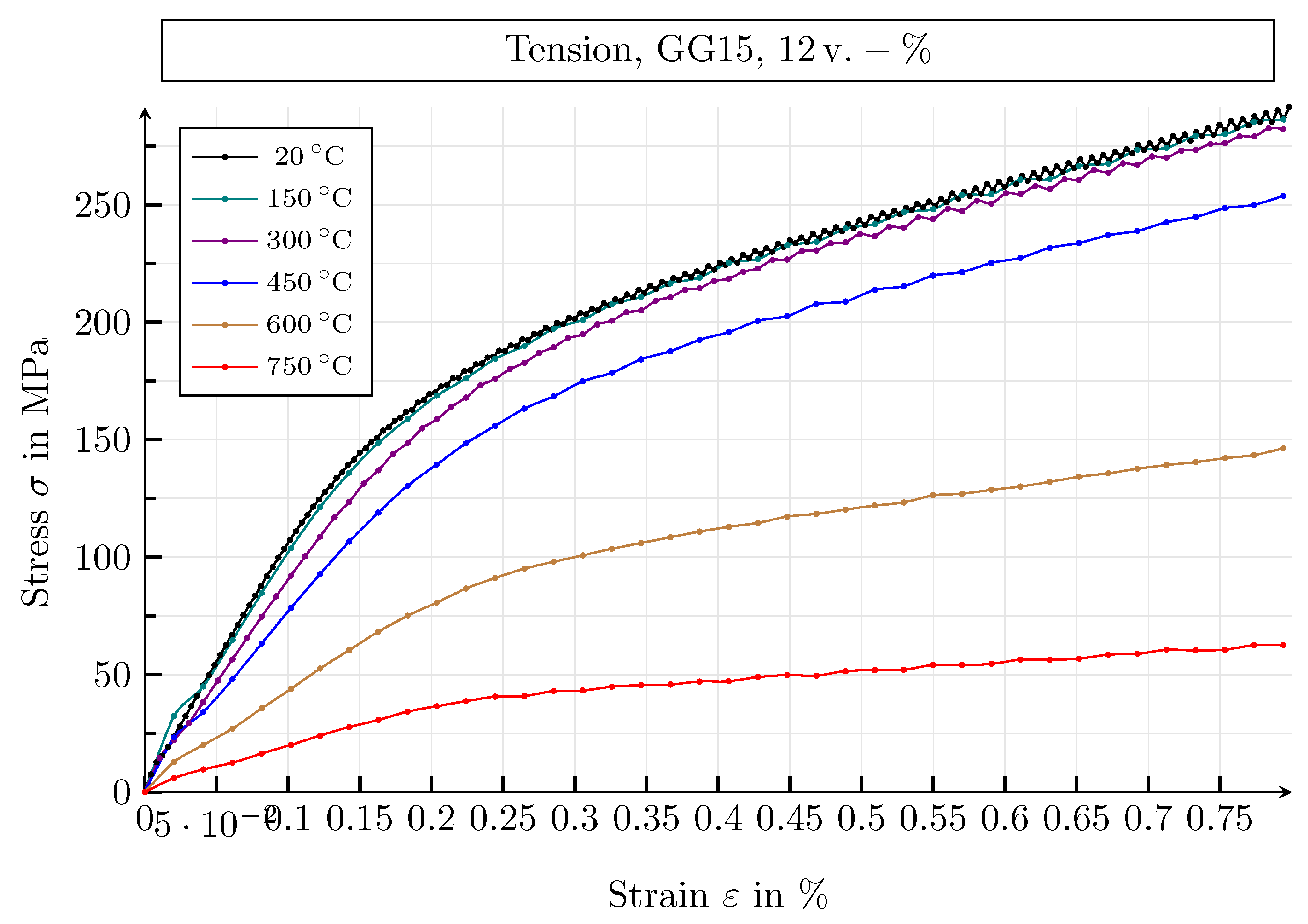
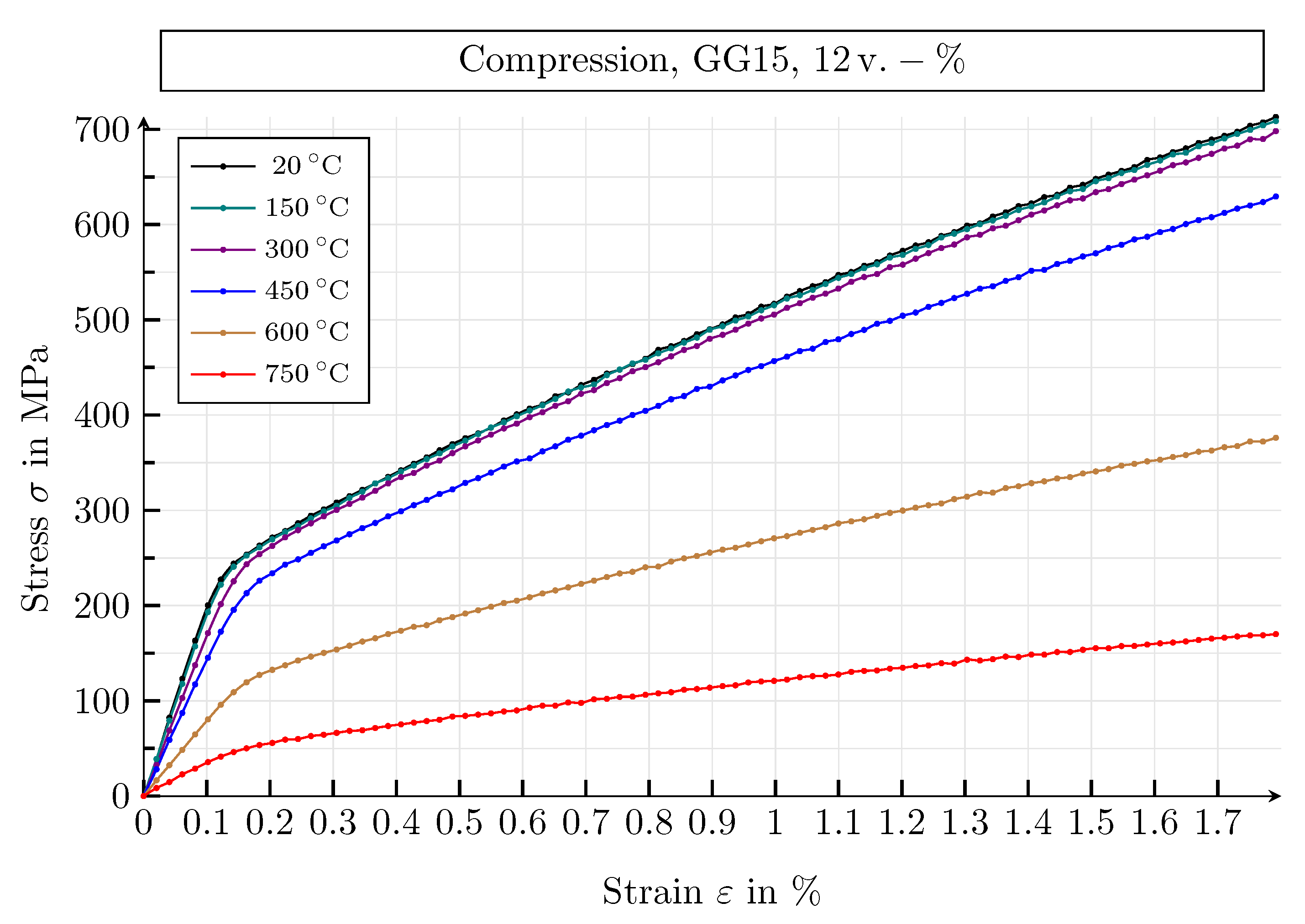
4.3. Mechanical Simulation Study
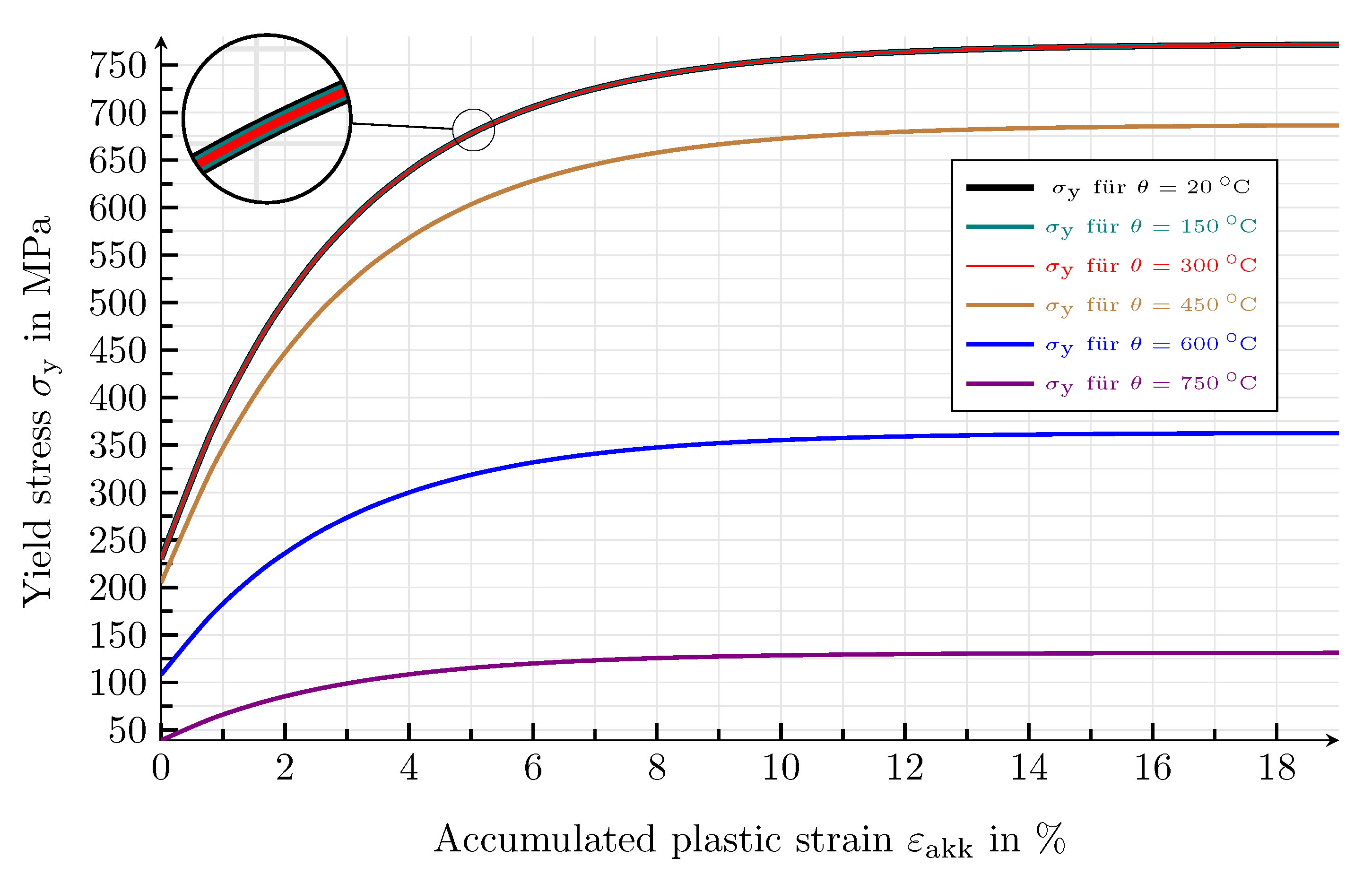
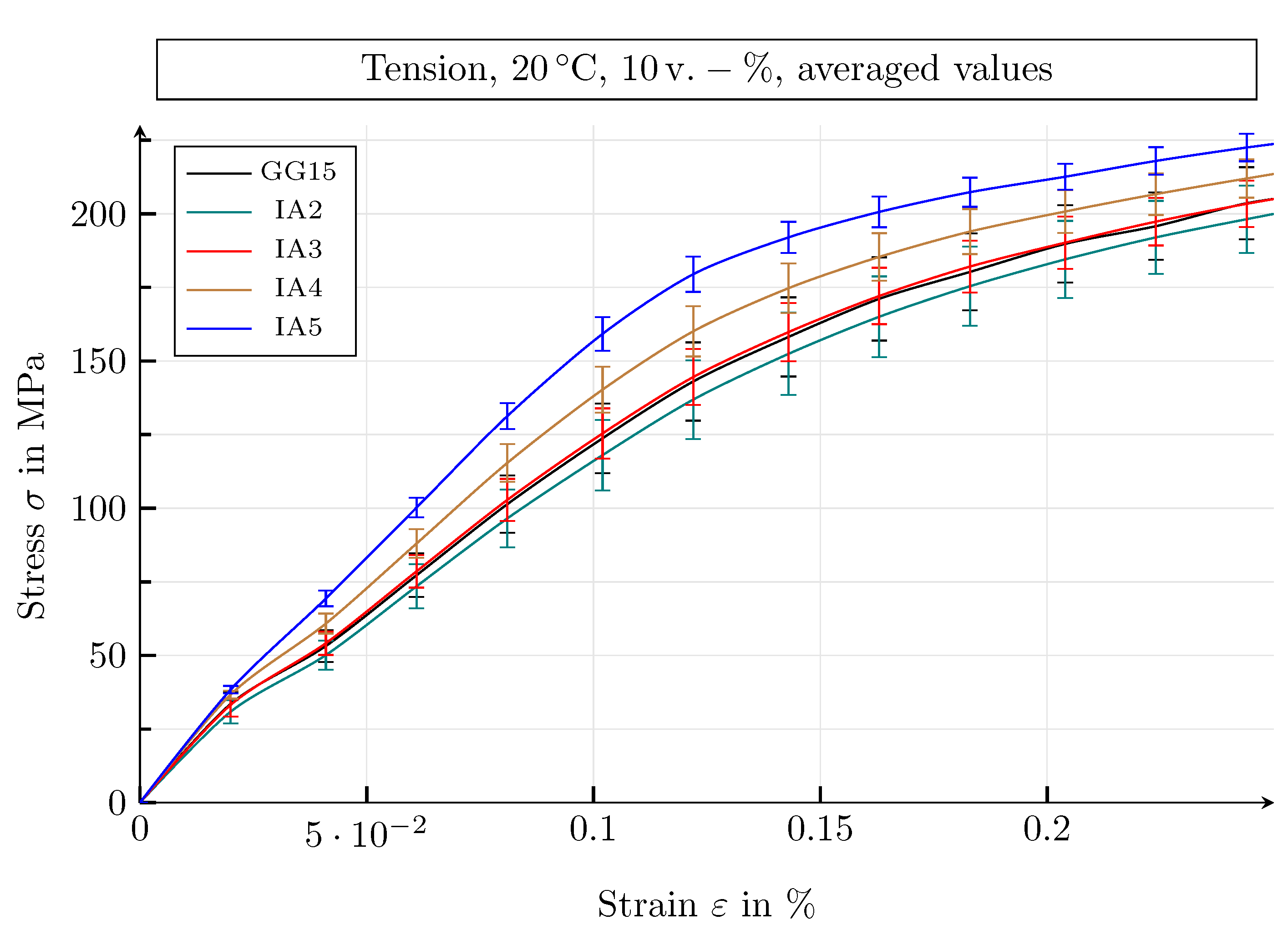
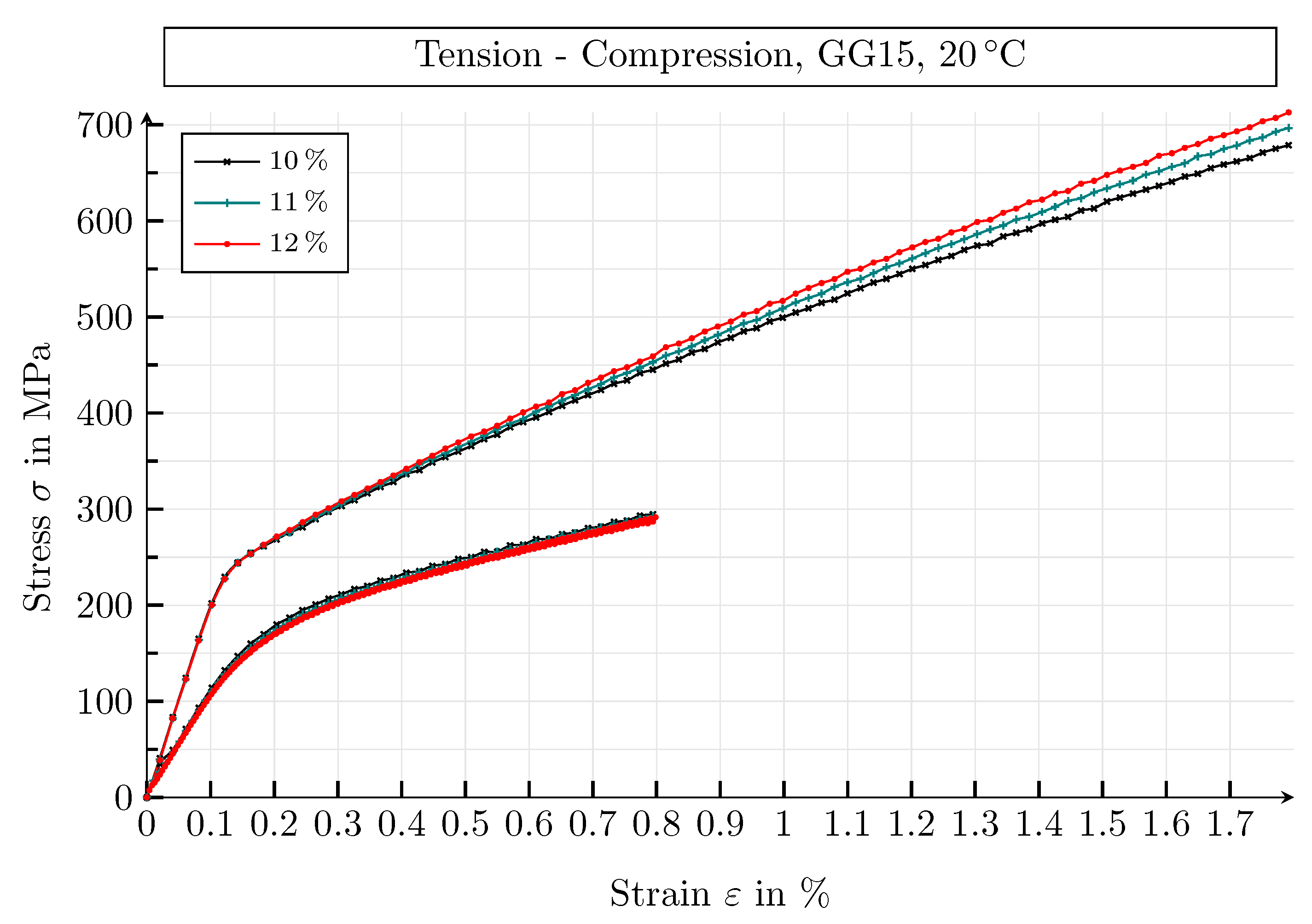
4.3.1. Results of the Mechanical Simulation Study
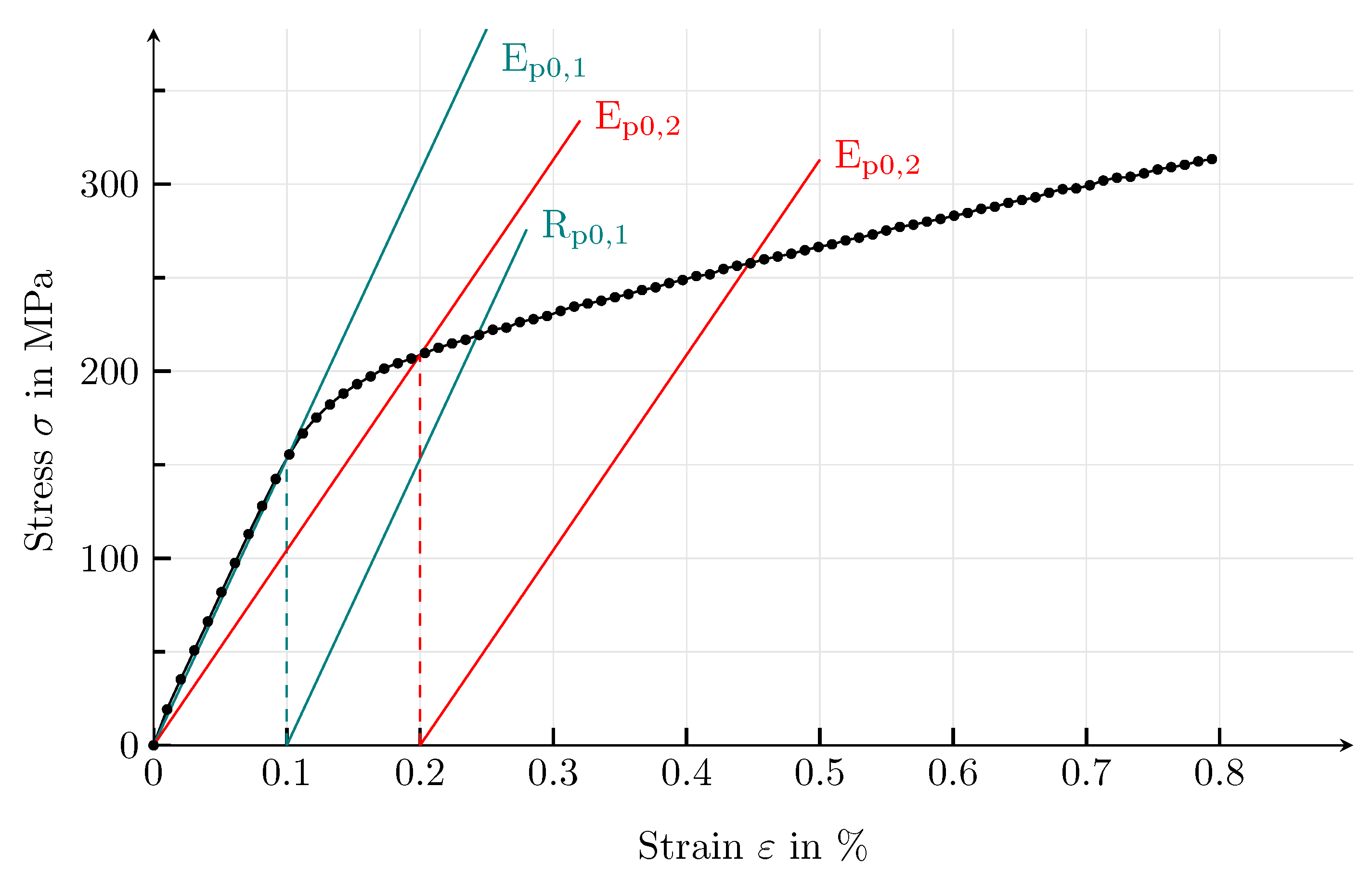
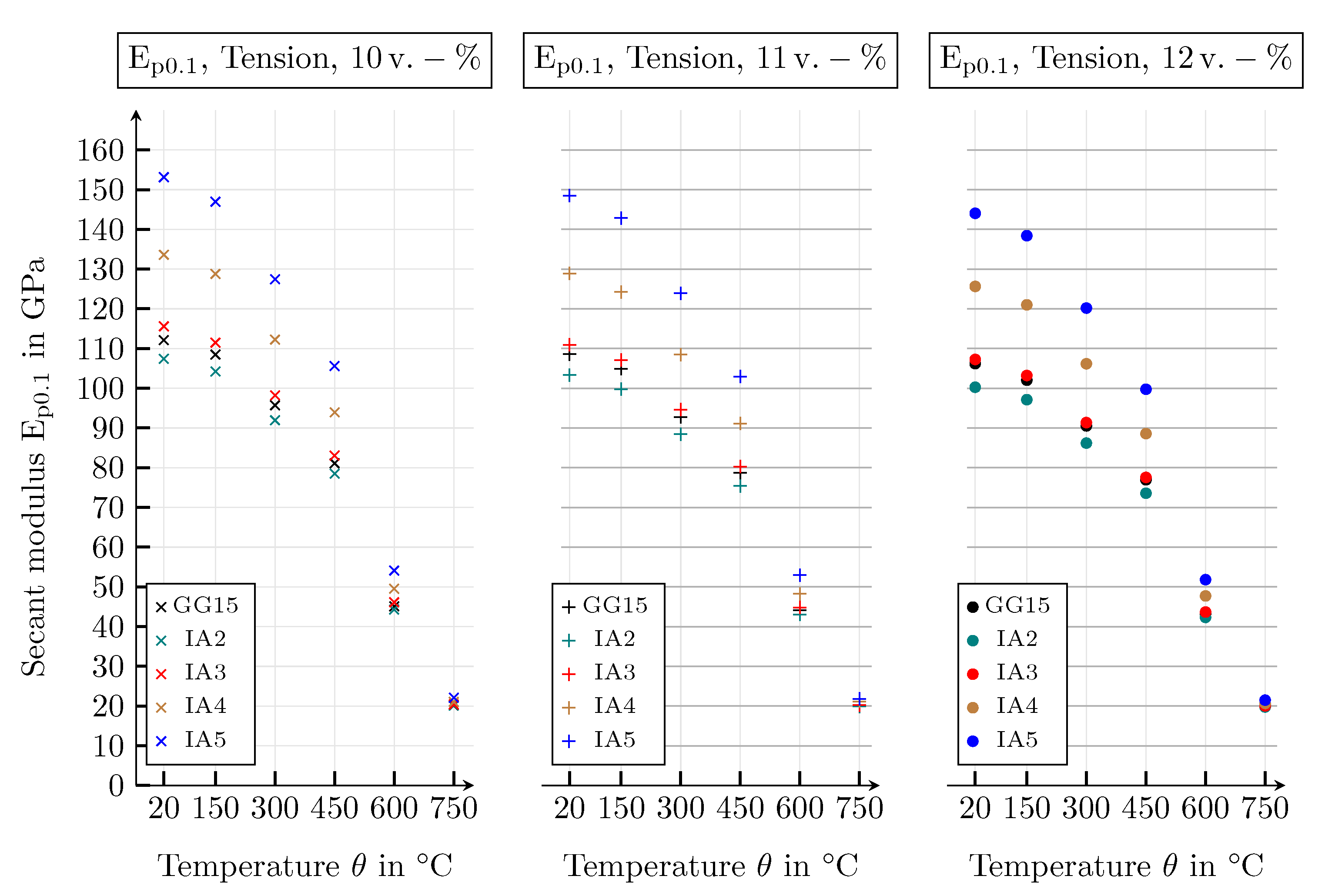
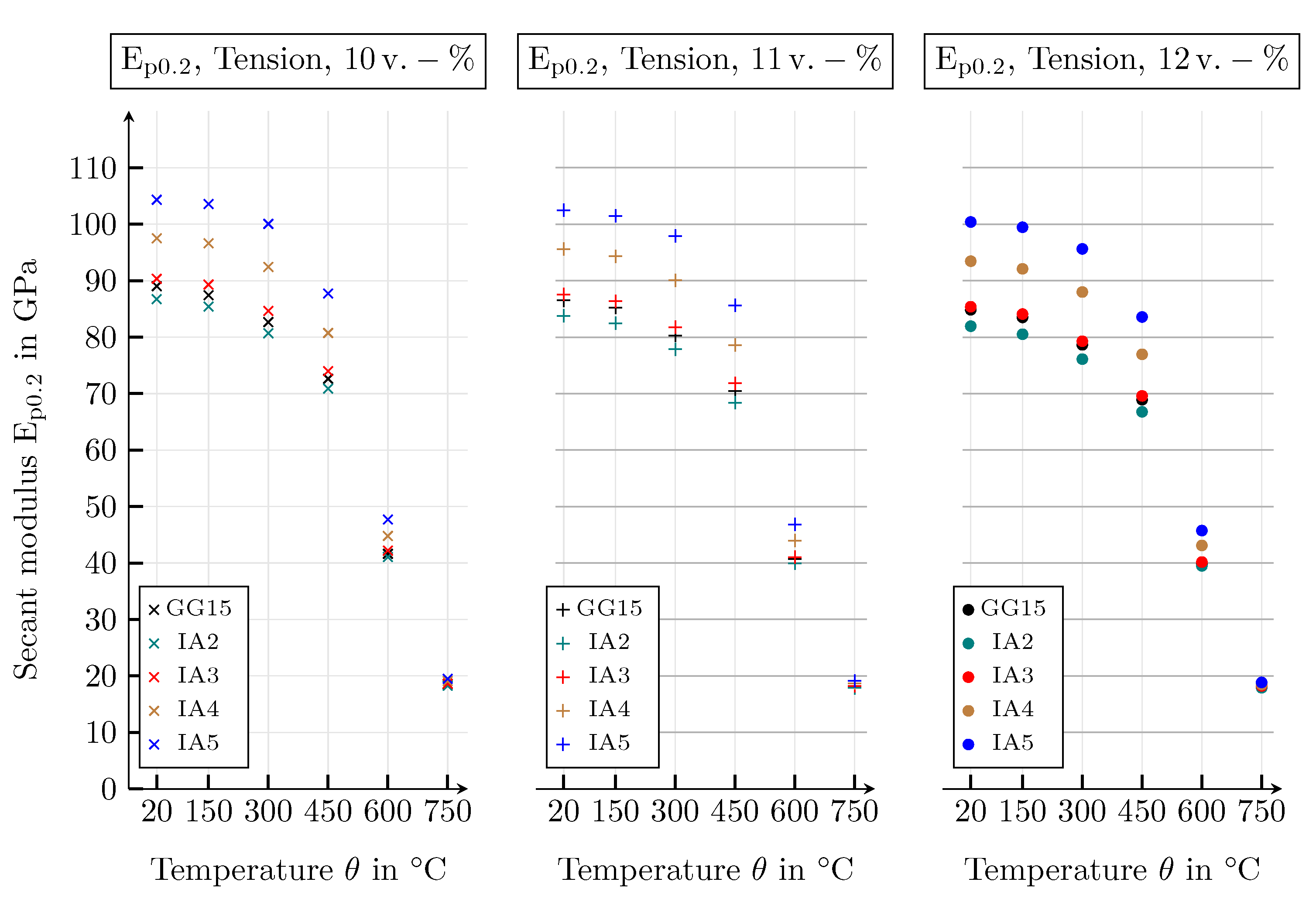
4.3.2. Mechanical Parameters
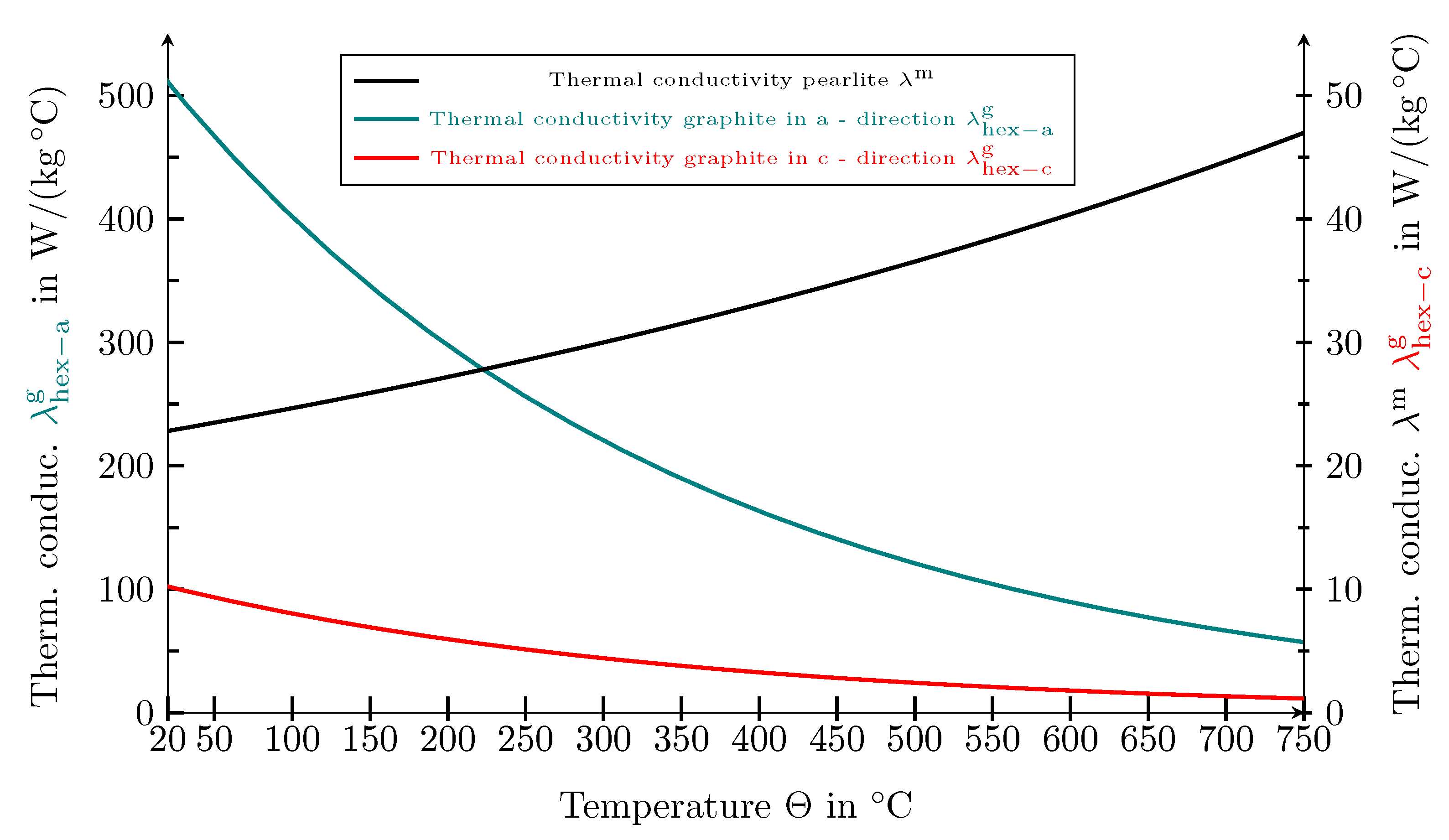
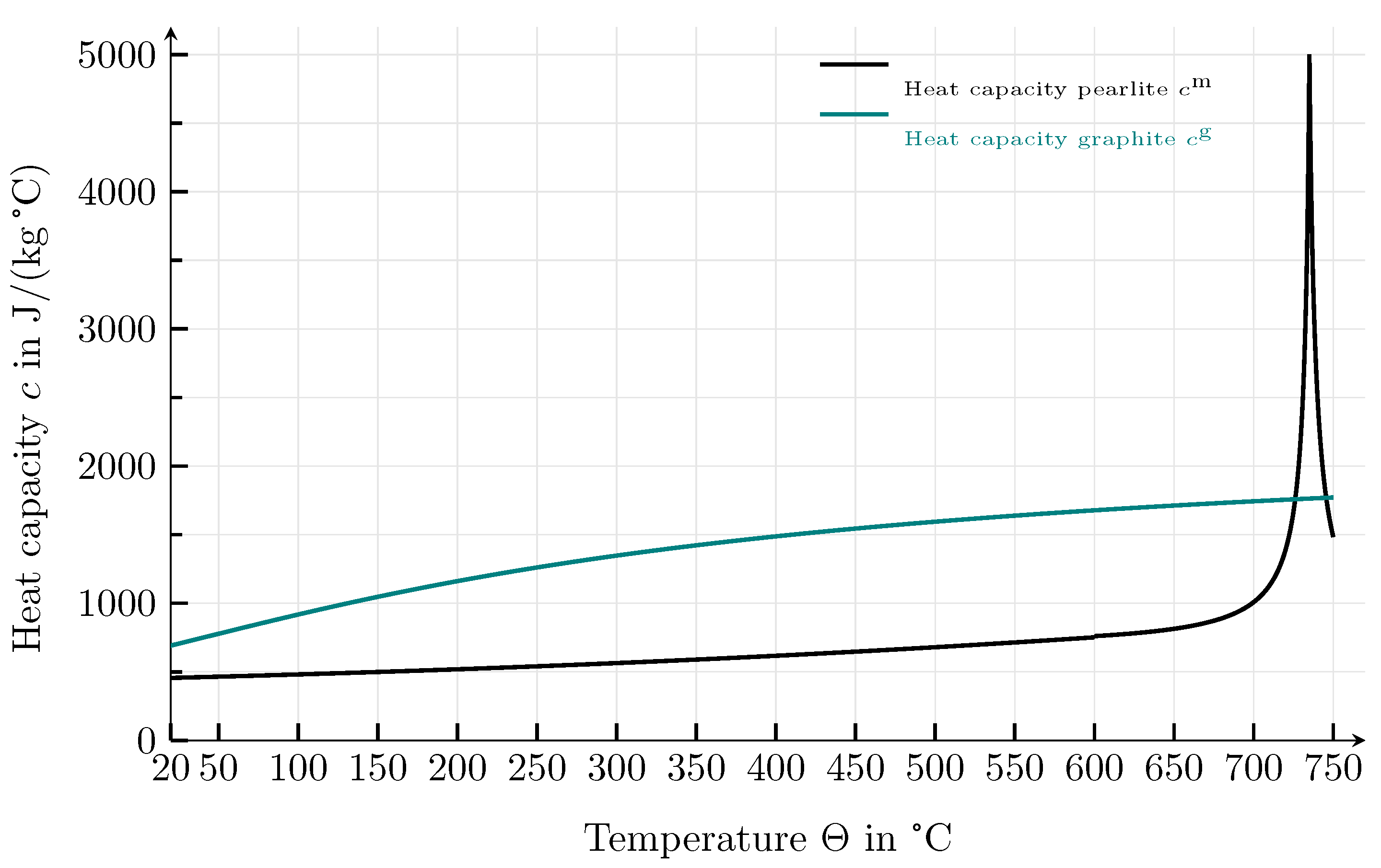
5. Thermal Simulations
6. Correlation of Thermal and Mechnical Properties
7. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bonora, N.; Ruggiero, A. Micromechanical modeling of ductile cast iron incorporating damage. Part I: Ferritic ductile cast iron. Int. J. Solids Struct. 2005, 42, 1401–1424. [Google Scholar] [CrossRef]
- Herfurth, K. Gusseisen—Kleine Werkstoffkunde eines viel genutzten Eisenwerkstoffs. Konstr. Und Gießen 2007, 32, 2. [Google Scholar]
- Velichko, A.; Wiegmann, A.; Mücklich, F. Estimation of the effective conductivities of complex cast iron microstructures using FIB-tomographic analysis. Acta Mater. 2009, 57, 5023–5035. [Google Scholar] [CrossRef]
- Pina, J.C.; Shafqat, S.; Kouznetsova, V.G.; Hoefnagels, J.P.M.; Geers, M.G.D. Microstructural study of the mechanical response of compacted graphite iron: An experimental and numerical approach. Mater. Sci. Eng. A 2016, 658, 439–449. [Google Scholar] [CrossRef]
- Rundman, K.B.; Iacoviello, F. Cast irons. In Encyclopedia of Materials: Science and Technology, 2nd ed.; Elsevier: Oxford, UK, 2001; pp. 1003–1010. [Google Scholar]
- Collini, L.; Nicoletto, G.; Konečná, R. Microstructure and mechanical properties of pearlitic gray cast iron. Mater. Sci. Eng. A 2008, 488, 529–539. [Google Scholar] [CrossRef]
- Bartels, C.; Gerhards, R.; Hanselka, H.; Herfurth, K.; Kaufmann, H.; Kleinkröger, W.; Lampic, M.; Löblich, H.; Menk, W.; Pusch, G.; et al. Gusseisen mit Kugelgraphit. 2007. Available online: https://www.kug.bdguss.de/fileadmin/content/Publikationen-Normen-Richtlinien/buecher/Gusseisen_mit_Kugelgraphit_klein.pdf (accessed on 16 February 2021).
- Deike, R.; Engels, A.; Hauptvogel, F.; Henke, P.; Röhrig, K.; Siefer, W.; Werning, H.; Wolters, D. Gusseisen mit Lamellengraphit. 2000. Available online: https://www.kug.bdguss.de/fileadmin/content/Publikationen-Normen-Richtlinien/Gusseisen_mit_Lamellengraphit_klein.pdf (accessed on 16 February 2021).
- Lampic, M.; Walz, M. Gusseisen mit Vermiculargrafit. 2014. Available online: https://www.kug.bdguss.de/fileadmin/content/themen/Gusseisen_mit_Vermiculargrafit_Teil_3/G-03-14-S60-71-PDF.pdf (accessed on 16 February 2021).
- Bertolino, G.; Perez-Ipina, J.E. Geometrical effects on lamellar grey cast iron fracture toughness. J. Mater. Process. Technol. 2006, 179, 202–206. [Google Scholar] [CrossRef]
- Norman, V.; Calmunger, M. On the micro-and macroscopic elastoplastic deformation behaviour of cast iron when subjected to cyclic loading. Int. J. Plast. 2019, 115, 200–215. [Google Scholar] [CrossRef]
- Haenny, L.; Zambelli, G. Strain mechanisms in grey cast iron. Eng. Fract. Mech. 1983, 18, 377–387. [Google Scholar] [CrossRef]
- Wiese, J.W.; Dantzig, J.A. Modeling stress development during the solidification of gray iron castings. Metall. Trans. A 1990, 21, 489–497. [Google Scholar] [CrossRef]
- Metzger, M.; Seifert, T. Computational assessment of the microstructure-dependent plasticity of lamellar gray cast iron—Part I: Methods and microstructure-based models. Int. J. Solids Struct. 2015, 66, 184–193. [Google Scholar] [CrossRef]
- Lampic, M.; Walz, M. Gusseisen mit Vermiculargrafit. Teil 1: Definition, Geschichte, Herstellung, GJV als grüner Werkstoff. 2014. Available online: https://www.kug.bdguss.de/fileadmin/content/themen/Gusseisen_mit_Vermiculargraphit_Tl._1/G-01-14-S214-227-PDF.pdf (accessed on 16 February 2021).
- Pina, J.C.; Kouznetsova, V.G.; Geers, M.G.D. Thermo-mechanical analyses of heterogeneous materials with a strongly anisotropic phase: The case of cast iron. Int. J. Solids Struct. 2015, 63, 153–166. [Google Scholar] [CrossRef]
- DIN EN ISO 945-1:2010-09. Mikrostruktur von Gusseisen—Teil 1: Graphitklassifizierung durch visuelle Auswertung. 2010.
- Velichko, A.; Holzapfel, C.; Mücklich, F. 3D characterization of graphite morphologies in cast iron. Adv. Eng. Mater. 2007, 9, 39–45. [Google Scholar] [CrossRef]
- Limodin, N.; Salvo, L.; Boller, E.; Suéry, M.; Felberbaum, M.; Gailliègue, S.; Madi, K. In situ and real-time 3-D microtomography investigation of dendritic solidification in an Al–10 wt.% Cu alloy. Acta Mater. 2009, 57, 2300–2310. [Google Scholar] [CrossRef] [Green Version]
- Chawla, N.; Ganesh, V.V.; Wunsch, B. Three-dimensional (3D) microstructure visualization and finite element modeling of the mechanical behavior of SiC particle reinforced aluminum composites. Scr. Mater. 2004, 51, 161–165. [Google Scholar] [CrossRef]
- Holmgren, D.; Källbom, R.; Svensson, I.L. Influences of the graphite growth direction on the thermal conductivity of cast iron. Metall. Mater. Trans. A 2007, 38, 268–275. [Google Scholar] [CrossRef]
- Shebatinov, M.P. A study of the fine structure of graphite inclusions in gray cast irons by means of the scanning electron microscope. Met. Sci. Heat Treat. 1974, 16, 288–293. [Google Scholar] [CrossRef]
- Noguchi, T.; Shimizu, K. Accurate evaluation of the mechanical properties of grey cast iron. Cast Met. 1993, 6, 146–152. [Google Scholar] [CrossRef]
- Schmid, S.; Schneider, D.; Herrmann, C.; Selzer, M.; Nestler, B. A Multiscale approach for thermo-mechanical simulations of loading courses in cast iron brake discs. Int. J. Multiscale Comput. Eng. 2016, 14, 25–43. [Google Scholar] [CrossRef]
- Schmid, S. Mesoskopischer Ansatz zur Festigkeitsberechnung von Bremsscheiben. Ph.D. Thesis, Karlsruher Institut für Technologie (KIT), Karlsruhe, Germany, 2016. [Google Scholar] [CrossRef]
- Langford, G. Deformation of pearlite. Metall. Trans. A 1977, 8, 861–875. [Google Scholar] [CrossRef]
- Peng, X.; Fan, J.; Zeng, J. Microstructure-based description for the mechanical behavior of single pearlitic colony. Int. J. Solids Struct. 2002, 39, 435–448. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Cooke, G. An introduction to the mechanical properties of structural steel at elevated temperatures. Fire Saf. J. 1988, 13, 45–54. [Google Scholar] [CrossRef]
- Allain, S.; Bouaziz, O. Microstructure based modeling for the mechanical behavior of ferrite-pearlite steels suitable to capture isotropic and kinematic hardening. Mater. Sci. Eng. A 2008, 496, 329–336. [Google Scholar] [CrossRef]
- Eurocode. Design of Steel Structures: Part 1.2, General Rules-Structural fire Design; European Committee for Standardization. DD ENV.: Brussels, Belgium, 1993; Volume 1. [Google Scholar]
- Committee on Fire Protection. Structural Fire Protection; Technical Report; American Society of Civil Engineers: Reston, VA, USA, 1992.
- Kodur, V.; Dwaikat, M.; Fike, R. High-temperature properties of steel for fire resistance modeling of structures. J. Mater. Civ. Eng. 2010, 22, 423–434. [Google Scholar] [CrossRef]
- Helsing, J.; Grimvall, G. Thermal conductivity of cast iron: Models and analysis of experiments. J. Appl. Phys. 1991, 70, 1198–1206. [Google Scholar] [CrossRef]
- Umino, S. On the specific heat of carbon steels. Sei. Repts. Tôhôku Imp. Univ. Ser 1926, 1, 331. [Google Scholar]
- Chung, D.D.L. Review graphite. J. Mater. Sci. 2002, 37, 1475–1489. [Google Scholar] [CrossRef]
- Kelly, B.T. Physics of Graphite; Applied Science Publishers Ltd.: London, UK, 1981. [Google Scholar]
- Holmgren, D. Review of thermal conductivity of cast iron. Int. J. Cast Met. Res. 2005, 18, 331–345. [Google Scholar] [CrossRef]
- Blakslee, O.L.; Proctor, D.G.; Seldin, E.J.; Spence, G.B.; Weng, T. Elastic constants of compression-annealed pyrolytic graphite. J. Appl. Phys. 1970, 41, 3373–3382. [Google Scholar] [CrossRef]
- Bosak, A.; Krisch, M.; Mohr, M.; Maultzsch, J.; Thomsen, C. Elasticity of single-crystalline graphite: Inelastic x-ray scattering study. Phys. Rev. B 2007, 75, 153408. [Google Scholar] [CrossRef] [Green Version]
- Pascal, T.A.; Karasawa, N.; Goddard, W.A., III. Quantum mechanics based force field for carbon (QMFF-Cx) validated to reproduce the mechanical and thermodynamics properties of graphite. J. Chem. Phys. 2010, 133, 134114. [Google Scholar] [CrossRef] [Green Version]
- Hill, R. On constitutive macro-variables for heterogeneous solids at finite strain. Proc. R. Soc. Lond. A Math. Phys. Sci. 1972, 326, 131–147. [Google Scholar]
- August, A.; Ettrich, J.; Rölle, M.; Schmid, S.; Berghoff, M.; Selzer, M.; Nestler, B. Prediction of heat conduction in open-cell foams via the diffuse interface representation of the phase-field method. Int. J. Heat Mass Transf. 2015, 84, 800–808. [Google Scholar] [CrossRef]
- Hötzer, J.; Reiter, A.; Hierl, H.; Steinmetz, P.; Selzer, M.; Nestler, B. The parallel multi-physics phase-field framework Pace3D. J. Comput. Sci. 2018, 26, 1–12. [Google Scholar] [CrossRef]
- Brandt, N.; Griem, L.; Herrmann, C.; Schoof, E.; Tosato, G.; Zhao, Y.; Zschumme, P.; Selzer, M. Kadi4Mat: A research data infrastructure for materials science. Data Sci. J. 2021, 20, 8. [Google Scholar] [CrossRef]
- Wilkinson, M.D.; Dumontier, M.; Aalbersberg, I.J.; Appleton, G.; Axton, M.; Baak, A.; Blomberg, N.; Boiten, J.W.; da Silva Santos, L.B.; Bourne, P.E.; et al. The FAIR guiding principles for scientific data management and stewardship. Sci. Data 2016, 3, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Fang, L.Y.; Metzloff, K.; Voigt, R.; Loper, C. Der Elastizitätsmodul von graphitischen Gusseisen. Konstr. Und Gießen 1998, 23, 8–13. [Google Scholar]
- ASTME. Standard Test Method for Young’s Modulus, Tangent Modulus, and Chord Modulus; Standard, ASTM International: West Conshohocken, PA, USA, 2004. [Google Scholar]
- DIN EN ISO 6892-1:2016. Metallische Werkstoffe-Zugversuch—Teil 1: Prüfverfahren bei Raumtemperatur. 2016. [Google Scholar]
- Fischer, U.; Gomeringer, R.; Heinzler, M.; Kilgus, R.; Näher, F.; Österle, S.; Pätzold, H.; Stephan, A. Tabellenbuch Metall: Mit Formelsammlung; Verlag Europa-Lehrmittel: Haan, Germany, 2011. [Google Scholar]
- Hecht, R.L.; Dinwiddie, R.B.; Wang, H. The effect of graphite flake morphology on the thermal diffusivity of gray cast irons used for automotive brake discs. J. Mater. Sci. 1999, 34, 4775–4781. [Google Scholar] [CrossRef]
- DIN 1691:1964-08. Gußeisen mit Lamellengraphit (Grauguß). 1964. [Google Scholar]









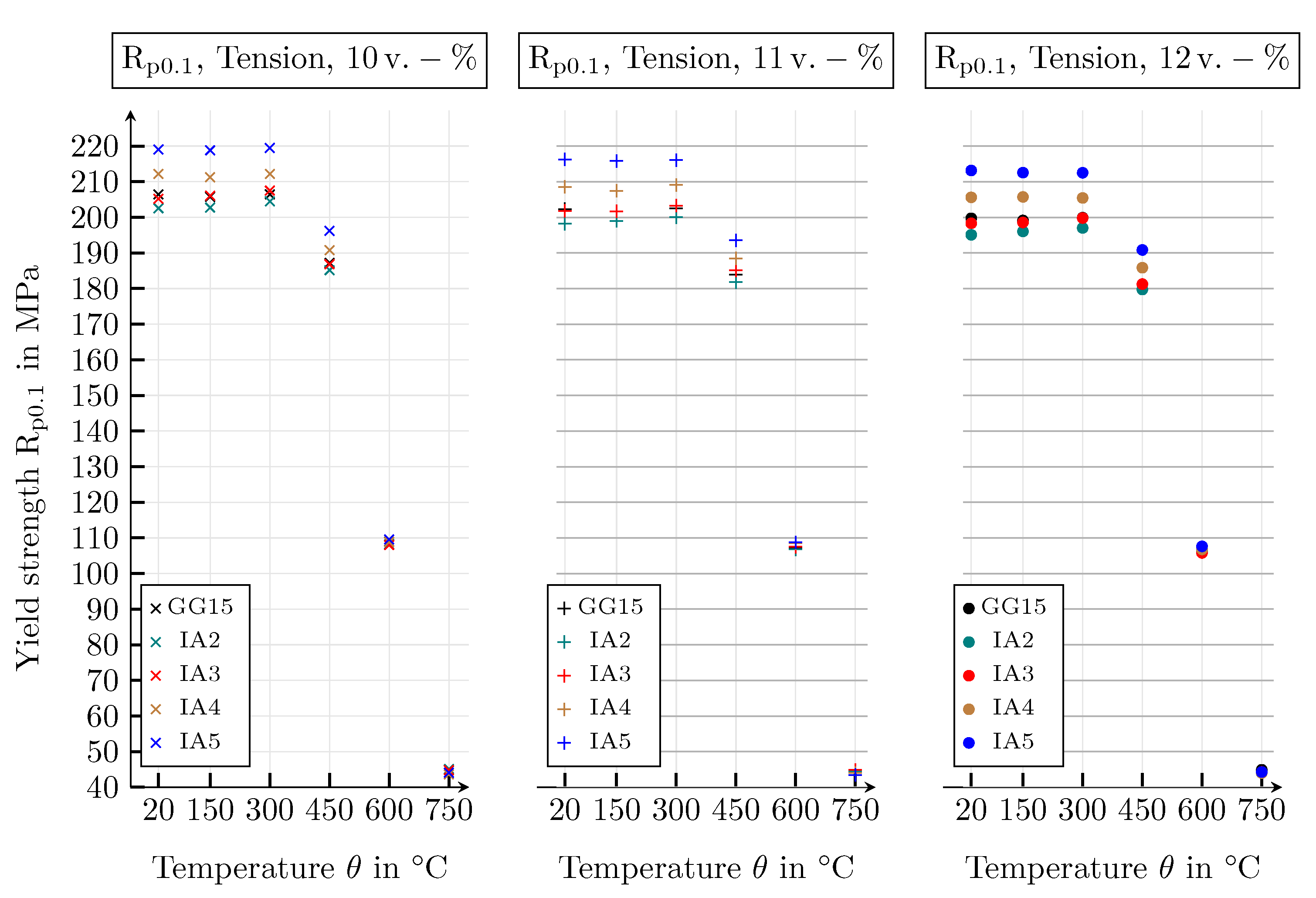




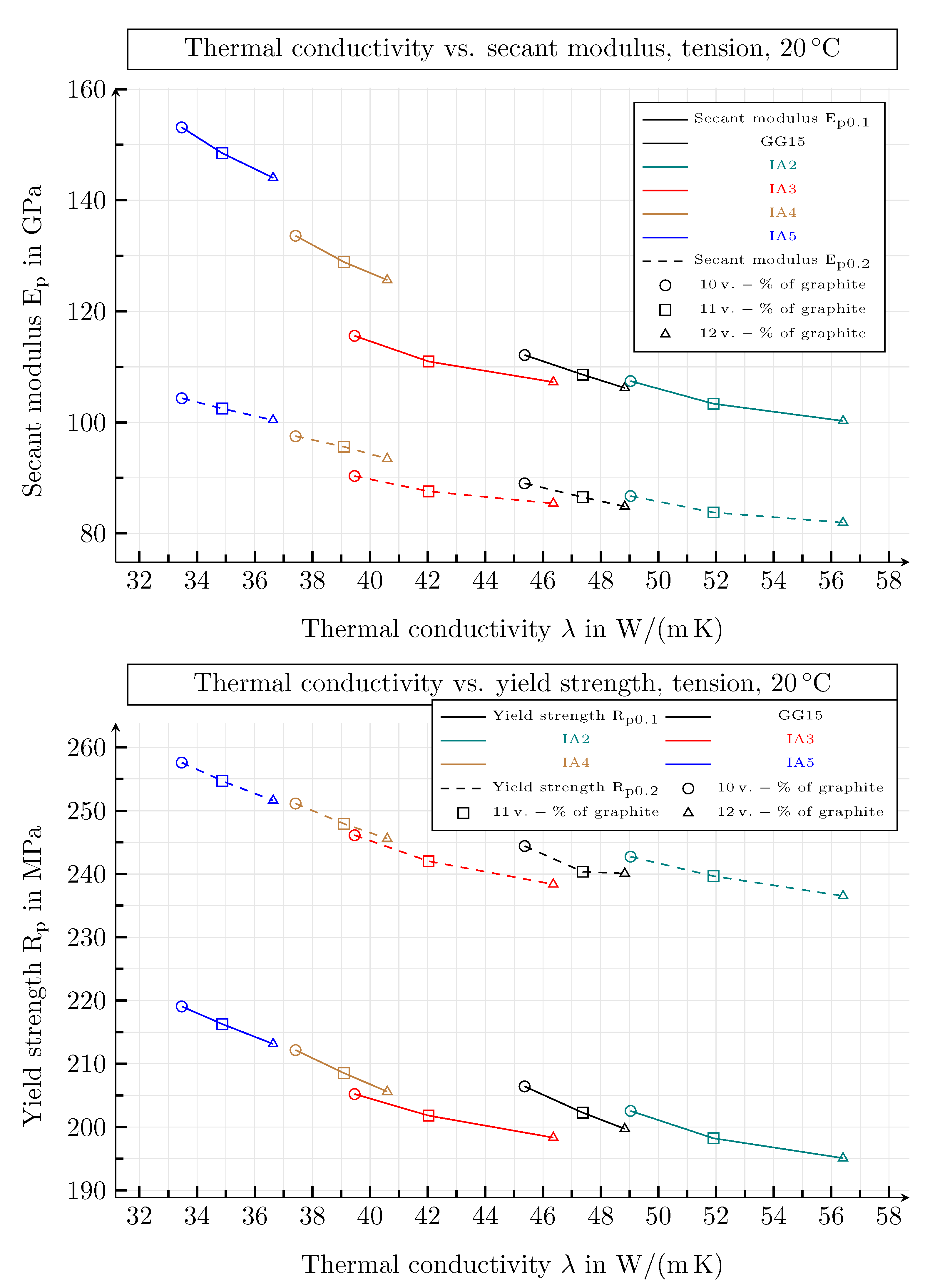
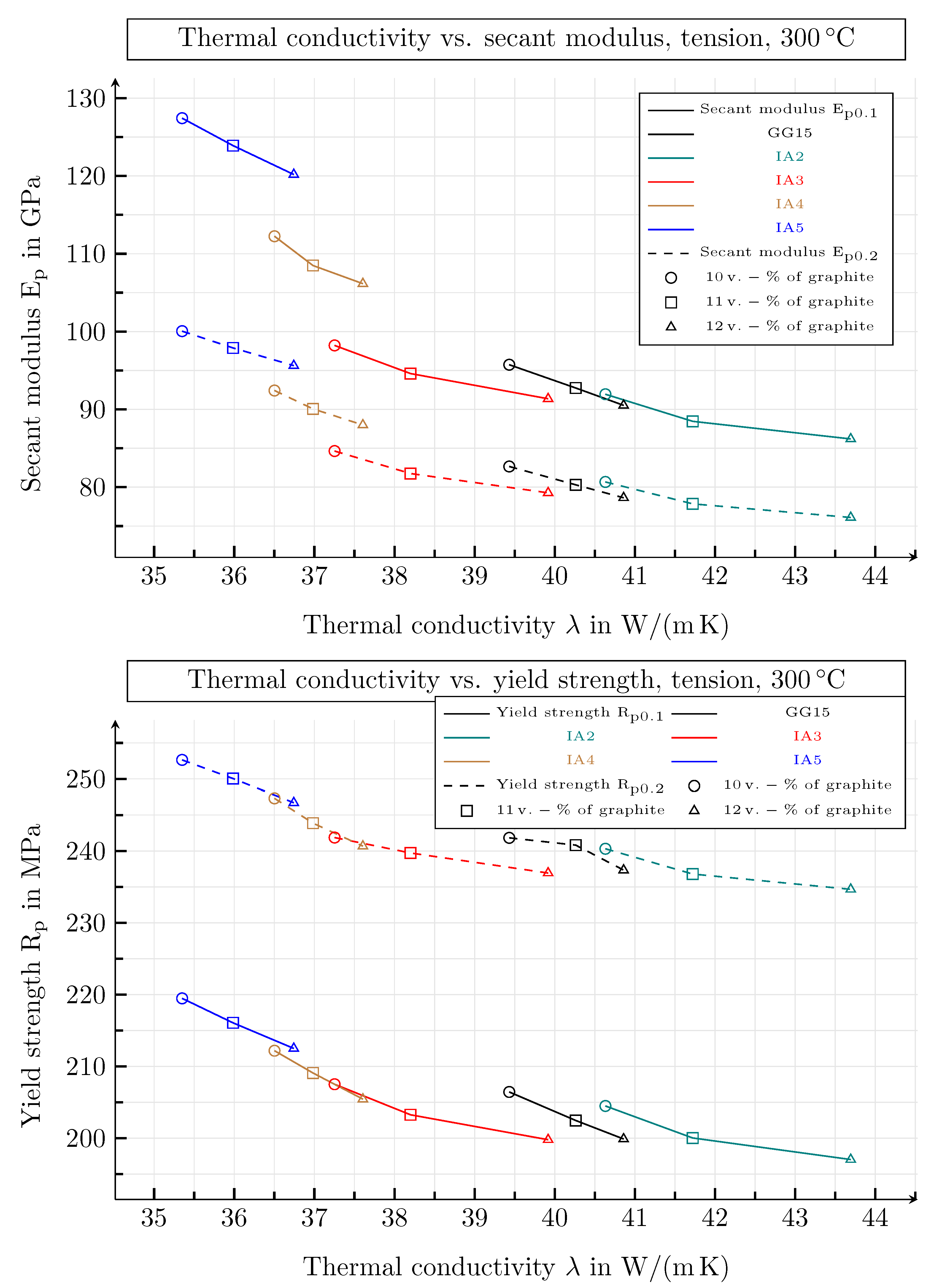
| Guide Number | Value | Unit |
|---|---|---|
| IA2 | to | |
| IA3 | to | |
| IA4 | to | |
| IA5 | to |
| 20 | 1.0 | 210.0 | 1.0 | 230.0 | 772.0 | 19.0 |
| 150 | 0.95 | 199.5 | 1.0 | 230.0 | 772.0 | 19.0 |
| 300 | 0.8 | 168.0 | 1.0 | 230.0 | 772.0 | 19.0 |
| 450 | 0.65 | 136.5 | 0.89 | 204.7 | 687.1 | 19.0 |
| 600 | 0.31 | 65.1 | 0.47 | 108.1 | 362.8 | 19.0 |
| 750 | 0.11 | 23.1 | 0.17 | 39.1 | 131.2 | 19.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herrmann, C.; Schmid, S.; Schneider, D.; Selzer, M.; Nestler, B. Computational Determination of Macroscopic Mechanical and Thermal Material Properties for Different Morphological Variants of Cast Iron. Metals 2021, 11, 1588. https://doi.org/10.3390/met11101588
Herrmann C, Schmid S, Schneider D, Selzer M, Nestler B. Computational Determination of Macroscopic Mechanical and Thermal Material Properties for Different Morphological Variants of Cast Iron. Metals. 2021; 11(10):1588. https://doi.org/10.3390/met11101588
Chicago/Turabian StyleHerrmann, Christoph, Stefan Schmid, Daniel Schneider, Michael Selzer, and Britta Nestler. 2021. "Computational Determination of Macroscopic Mechanical and Thermal Material Properties for Different Morphological Variants of Cast Iron" Metals 11, no. 10: 1588. https://doi.org/10.3390/met11101588
APA StyleHerrmann, C., Schmid, S., Schneider, D., Selzer, M., & Nestler, B. (2021). Computational Determination of Macroscopic Mechanical and Thermal Material Properties for Different Morphological Variants of Cast Iron. Metals, 11(10), 1588. https://doi.org/10.3390/met11101588





