The Effect of Nickel on the Viscosity of Iron-Based Multicomponent Melts
Abstract
:1. Introduction
2. Materials and Methods
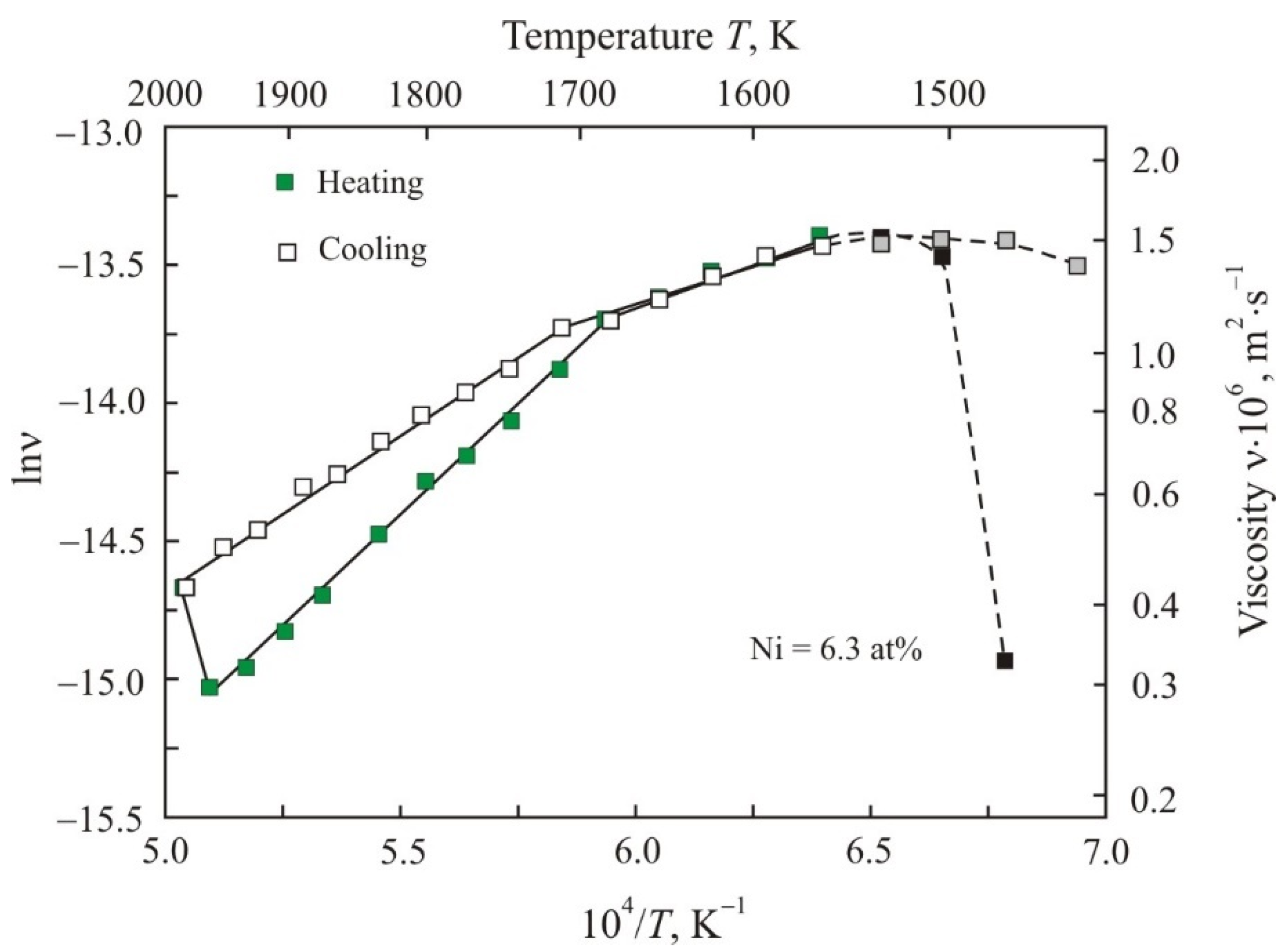
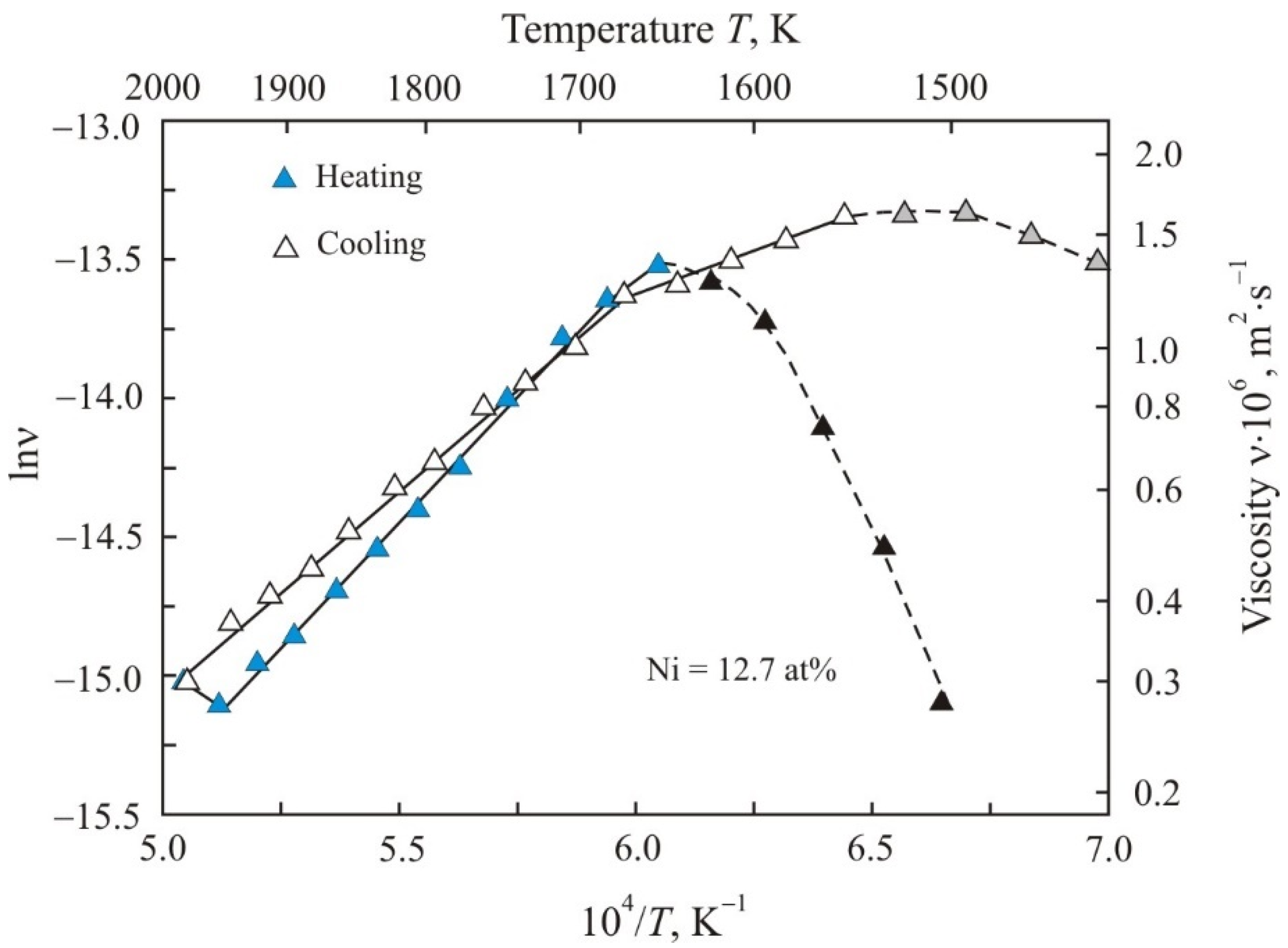
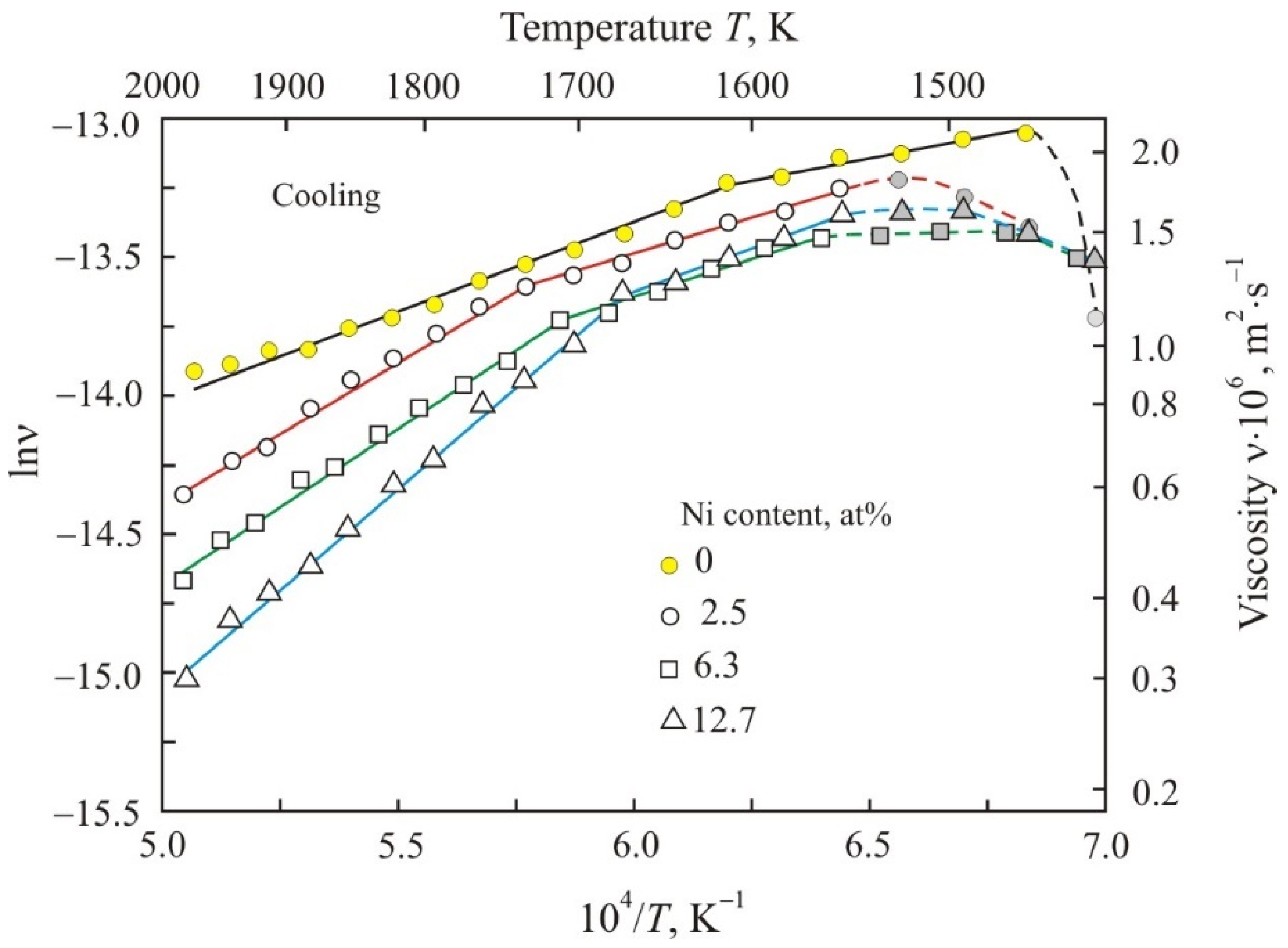
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mehrer, H. Fundamentals, Methods, Materials, Diffusion-Controlled Processes. In Diffusion in Solids; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007; pp. 127–132. [Google Scholar]
- Frenkel, J. Kinetic Theory of Liquids; Nauka: Leningrad, Russia, 1975; pp. 224–228. [Google Scholar]
- Tanaka, H. General view of a liquid-liquid phase transition. Phys. Rev. E 2000, 62, 6968–6976. [Google Scholar] [CrossRef]
- Vasin, M.G.; Lad’yanov, V.I. Structural transitions and nonmonotonic relaxation processes in liquid metals. Phys. Rev. E 2003, 68, 051202. [Google Scholar] [CrossRef] [Green Version]
- Zu, F.-Q. Temperature-induced liquid-liquid transition in metallic melts: A brief review on the new physical phenomenon. Metals 2015, 5, 395–417. [Google Scholar] [CrossRef]
- Dong, B.; Zhou, S.; Qin, J.; Li, Y.; Chen, H.; Wang, Y. The hidden disintegration of cluster heterogeneity in Fe-based glass-forming. Prog. Nat. Sci. Mater. 2018, 28, 696–703. [Google Scholar] [CrossRef]
- Dong, B.S.; Zhou, S.X.; Wang, Y.G.; Li, Y.; Qin, J.Y.; Li, G.Z. Revealing a structure transition in typical Fe-based glass-forming alloy. J. Non-Cryst. Solids 2018, 498, 305–308. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, C.; Zheng, H.; Tian, Z.; Hu, L. The role of liquid-liquid transition in glass formation of CuZr alloys. Phys. Chem. Chem. Phys. 2018, 19, 15962–15972. [Google Scholar] [CrossRef]
- He, Y.; Li, J.; Wang, J.; Kou, H.; Beagunon, E. Liquid-liquid structure transition and nucleation in undercooled Co-B eutectic alloys. Appl. Phys. A 2017, 123, 391. [Google Scholar] [CrossRef]
- Tsepelev, V.S.; Starodubtsev, Y.N.; Kochetkova, Y.A. Anomalous temperature dependence of kinematic viscosity in a multicomponent metal melts. Key Eng. Mater. 2021, 902, 3–8. [Google Scholar]
- Tsepelev, V.S.; Starodubtsev, Y.N.; Konashkov, V.V.; Kochetkova, Y.A. Kinematic viscosity and electrical resistivity of a multicomponent melt due to liquid-liquid structure transition. Key Eng. Mater. 2021, 904, 11–116. [Google Scholar]
- Yoshizawa, Y.; Oguma, S.; Yamauchi, K. New Fe-based soft magnetic alloys composed of ultrafine grain structure. J. Appl. Phys. 1988, 64, 6044–6046. [Google Scholar] [CrossRef]
- Tsepelev, V.S.; Starodubtsev, Y.N. Nanocrystalline soft magnetic iron-based materials from liquid state to ready product. Nanomatarials 2021, 11, 108. [Google Scholar] [CrossRef] [PubMed]
- Yoshizawa, Y.; Fujii, S.; Ping, D.H.; Ohnuma, M.; Hono, K. Magnetic properties of nanocrystalline FeMCuNbSiB alloys (M: Co, Ni). Scr. Mater. 2003, 48, 863–868. [Google Scholar] [CrossRef]
- Kataev, V.A.; Starodubtsev, Y.N.; Mikhalitsyna, E.A.; Belozerov, V.Y.; Tsyngalov, R.V. Magnetic properties and induced anisotropy of nanocrystalline Fe72.5−xNixCu1.1Nb1.9Mo1.5Si14.3B8.7 alloys. Phys. Met. Metallogr. 2017, 118, 558–563. [Google Scholar] [CrossRef]
- Lukshina, V.A.; Dmitrieva, N.V.; Volkova, E.G.; Shishkin, D.A. Magnetic properties of the Fe63.5Ni10Cu1Nb3Si13.5B9 alloy nanocrystallized in the presence of tensile stresses. Phys. Met. Metallogr. 2019, 120, 320–324. [Google Scholar] [CrossRef]
- Ruban, A.V.; Skriver, H.L.; Nørskov, J.K. Surface segregation energy in transition-metal alloys. Phys. Rev. B 1999, 59, 15990–16000. [Google Scholar] [CrossRef] [Green Version]
- Ruban, A.V. On segregation in multicomponent alloys: Surface segregation in austenite and FeCrCoNiMn alloys. Comp. Mater. Sci. 2021, 187, 110080. [Google Scholar] [CrossRef]
- Tsepelev, V.S.; Starodubtsev, Y.N.; Wu, K.M. Influence of Ni on crystallization and magnetic properties of Fe72.5−xNixCu1.1Nb2Mo1.5Si14B9 alloys. J. Cryst. Growth 2019, 528, 125256. [Google Scholar] [CrossRef]
- Tsepelev, V.; Konashkov, V.; Starodubtsev, Y.; Belozerov, Y.; Gaipishevarov, D. Optimum regime of heat treatment of soft magnetic amorphous materials. IEEE Trans. Magn. 2012, 48, 1327–1330. [Google Scholar] [CrossRef]
- Glasstone, S.; Laidler, K.; Eyring, H. The Kinetics of Chemical Reactions, Viscosity, Diffusion and Electrochemical Phenomena. In The Theory of Rate Processes; McGraw Hill: New York, NY, USA; London, UK, 1941; pp. 477–551. [Google Scholar]
- Starodubtsev, Y.N.; Tsepelev, V.S.; Tsepeleva, N.P. Kinematic viscosity of multicomponent FeCuNbSiB-based melts. Nanomaterials 2021, 11, 1042. [Google Scholar] [CrossRef]
- Starodubtsev, Y.N.; Tsepelev, V.S. Analisys of the kinematic viscosity and self-diffusion of liquid metals at the melting temperature. High Temp. 2021, 59, 306–311. [Google Scholar]
- Starodubtsev, Y.N.; Tsepelev, V.S. Analisys of surface tension and viscosity of liquid metals. Metall. Mater. Trans. B 2021, 52, 1886–1890. [Google Scholar] [CrossRef]
- Koca, H.D.; Doganay, S.; Turgut, A.; Tavman, I.H.; Saidur, R.; Mahbubul, I.M. Effect of particles size on viscosity of nanofluids: A review. Renew. Sust. Energy Rev. 2018, 82, 1664–1674. [Google Scholar] [CrossRef] [Green Version]
- Thi, H.N.; Drevet, B.; Debierre, J.M.; Camel, D.; Dabo, Y.; Billia, B. Preparation of the initial solid-liquid interface and melt in directional solidification. J. Cryst. Growth 2003, 253, 539–548. [Google Scholar]
- Mas, F.; Tassin, C.; Roch, F.; Yescas, M.; Todeschini, P.; Bréchet, Y. Growth morphologies and primary solidification modes in a dissimilar weld between a low-alloy steel and an austenitic stainless steel. Metals 2018, 8, 284. [Google Scholar] [CrossRef] [Green Version]
- Filippov, G.G.; Gorbunov, A.I. Novel approach to selection of practical scale of electronegativity of atoms. Ross. Chim. Zh. 1995, 39, 39–43. [Google Scholar]
- Greim, J.; Schwetz, K.A. Boron carbide, boron nitride, and metal borides. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag: Weinheim, Germany, 2012; Volume 6, pp. 219–236. [Google Scholar]
- Kiessling, R.; Lange, N. Non-Metallic Inclusions in Steel; Metallurgiya: Moscow, Russia, 1978; pp. 23–34. [Google Scholar]
- Tsepelev, V.S.; Starodubtsev, Y.N.; Tsepeleva, N.P. Thermophysical properties of pipe steel in liquid state. Metals 2021, 11, 1099. [Google Scholar] [CrossRef]
- Smirnov, B.M. The properties of fractal clusters. Phys. Rep. 1990, 188, 1–78. [Google Scholar] [CrossRef]
- Yang, M.H.; Li, J.H.; Liu, B.X. Fractal analysis on the cluster network in metallic liquid and glass. J. Alloys Comp. 2018, 757, 228–232. [Google Scholar] [CrossRef]
- Goldschmidt, H.J. Interstitial Alloys; Butterworths: London, UK, 1967; pp. 88–101. [Google Scholar]


| Ni Content (at. %) | Activation Energy Ea (kJ·mol−1) | |||
|---|---|---|---|---|
| Heating | Cooling | |||
| T > 1700 K | T < 1700 K | T > 1700 K | T < 1700 K | |
| 0 | – | – | 55 | 24 |
| 2.5 | 141 | 42 | 88 | 43 |
| 6.3 | 134 | 54 | 95 | 44 |
| 12.7 | 151 | – | 120 | 50 |
Publisher’ Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsepelev, V.S.; Starodubtsev, Y.N.; Konashkov, V.V. The Effect of Nickel on the Viscosity of Iron-Based Multicomponent Melts. Metals 2021, 11, 1724. https://doi.org/10.3390/met11111724
Tsepelev VS, Starodubtsev YN, Konashkov VV. The Effect of Nickel on the Viscosity of Iron-Based Multicomponent Melts. Metals. 2021; 11(11):1724. https://doi.org/10.3390/met11111724
Chicago/Turabian StyleTsepelev, Vladimir S., Yuri N. Starodubtsev, and Viktor V. Konashkov. 2021. "The Effect of Nickel on the Viscosity of Iron-Based Multicomponent Melts" Metals 11, no. 11: 1724. https://doi.org/10.3390/met11111724






