XFEM Simulation of Tensile and Fracture Behavior of Ultrafine-Grained Al 6061 Alloy
Abstract
1. Introduction
2. Experimental Procedure
2.1. Processing
2.2. Testing
3. Simulation Procedure
3.1. XFEM Methodology
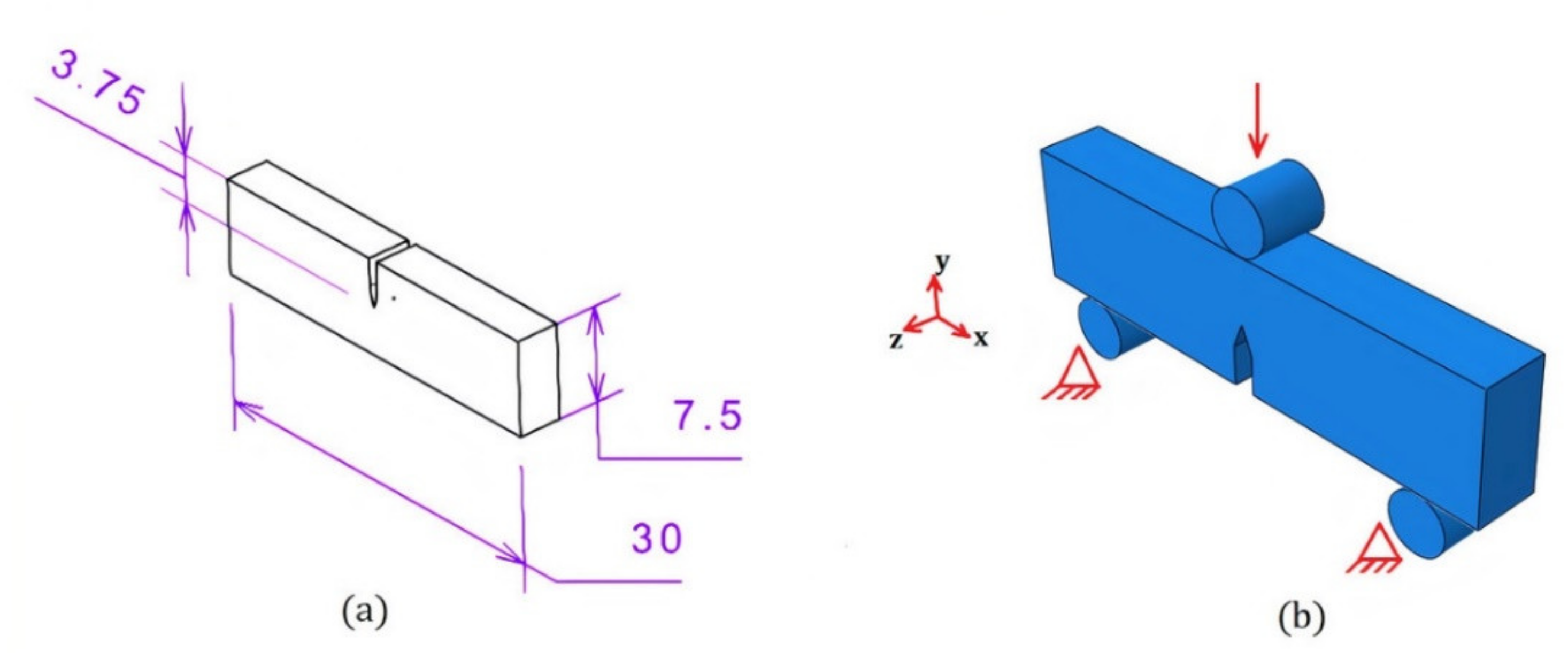
3.2. Tensile Simulation
Flow Curve
3.3. Three-Point Bend Test Simulation
3.4. Compact Tension Simulation
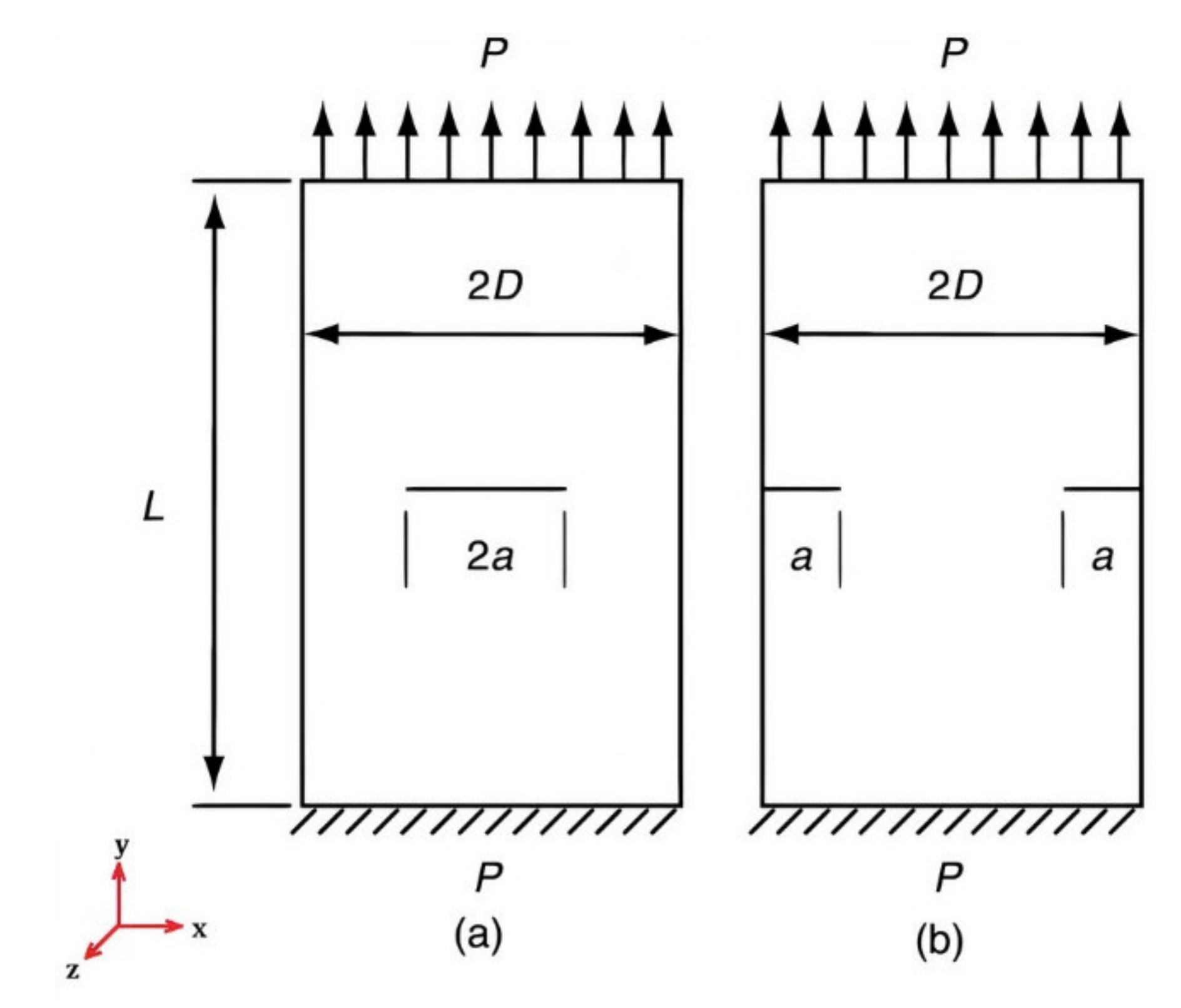
3.5. Center Crack and Double Edge Cracked Specimen
4. Results and Discussion
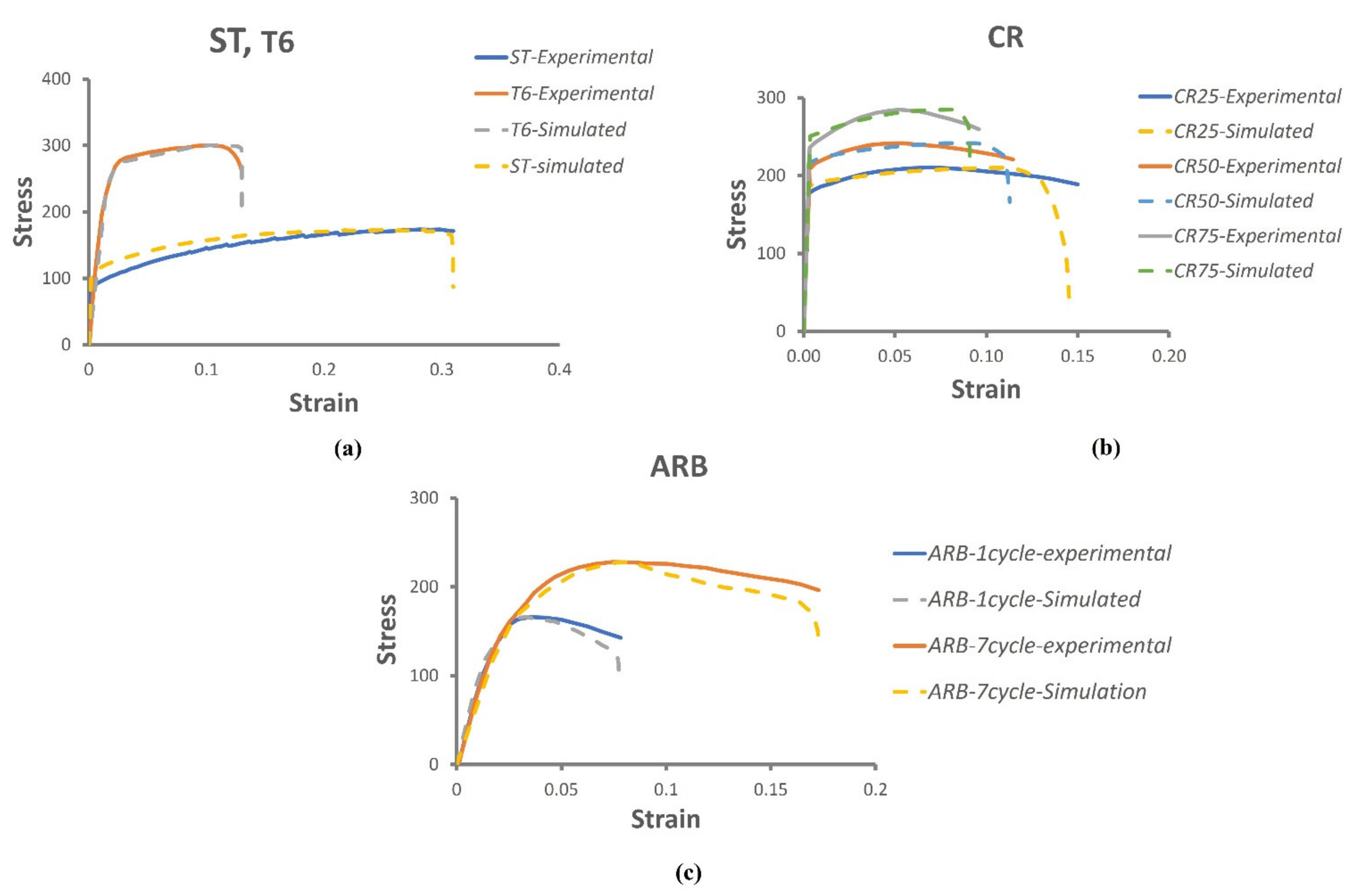
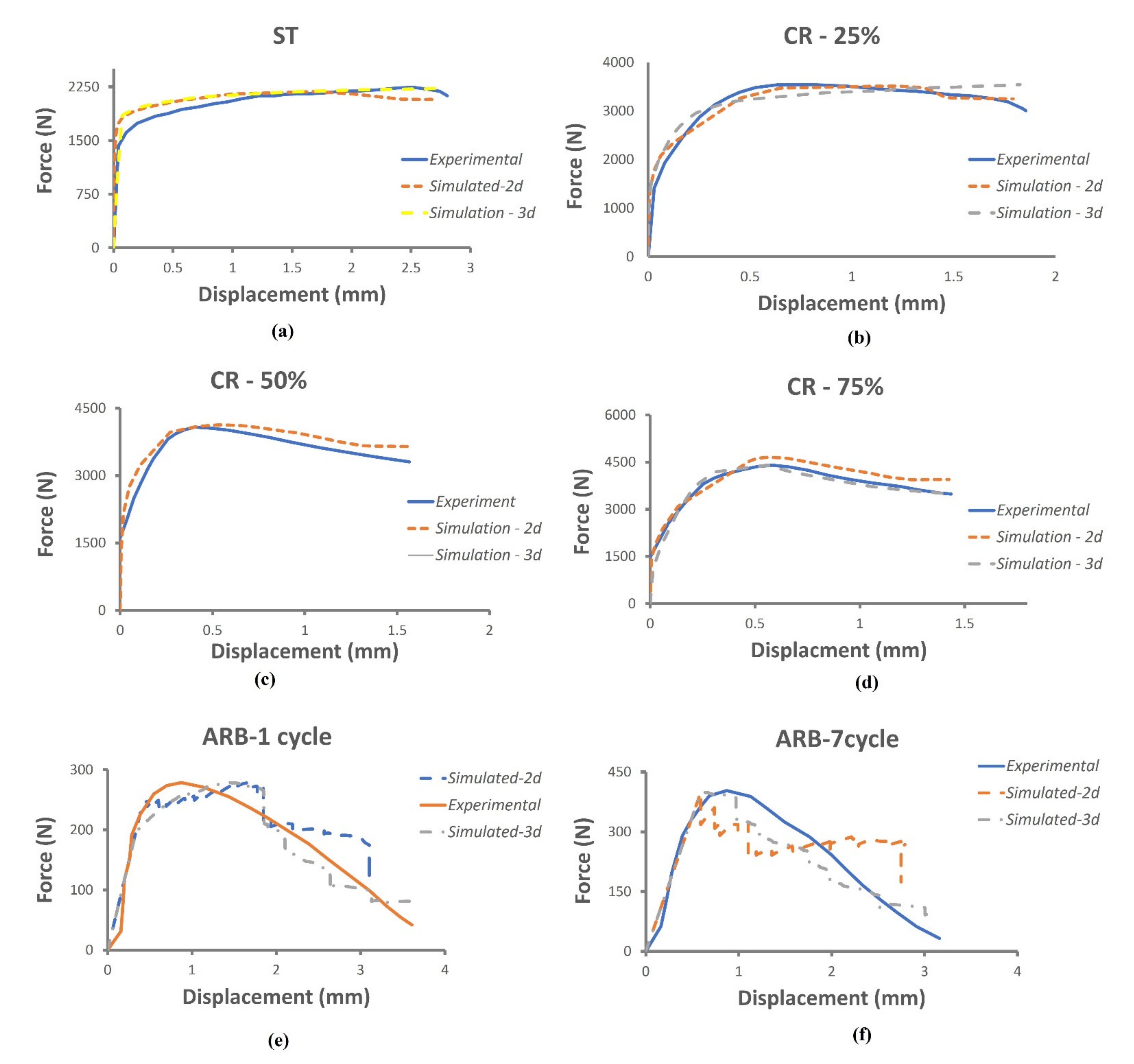
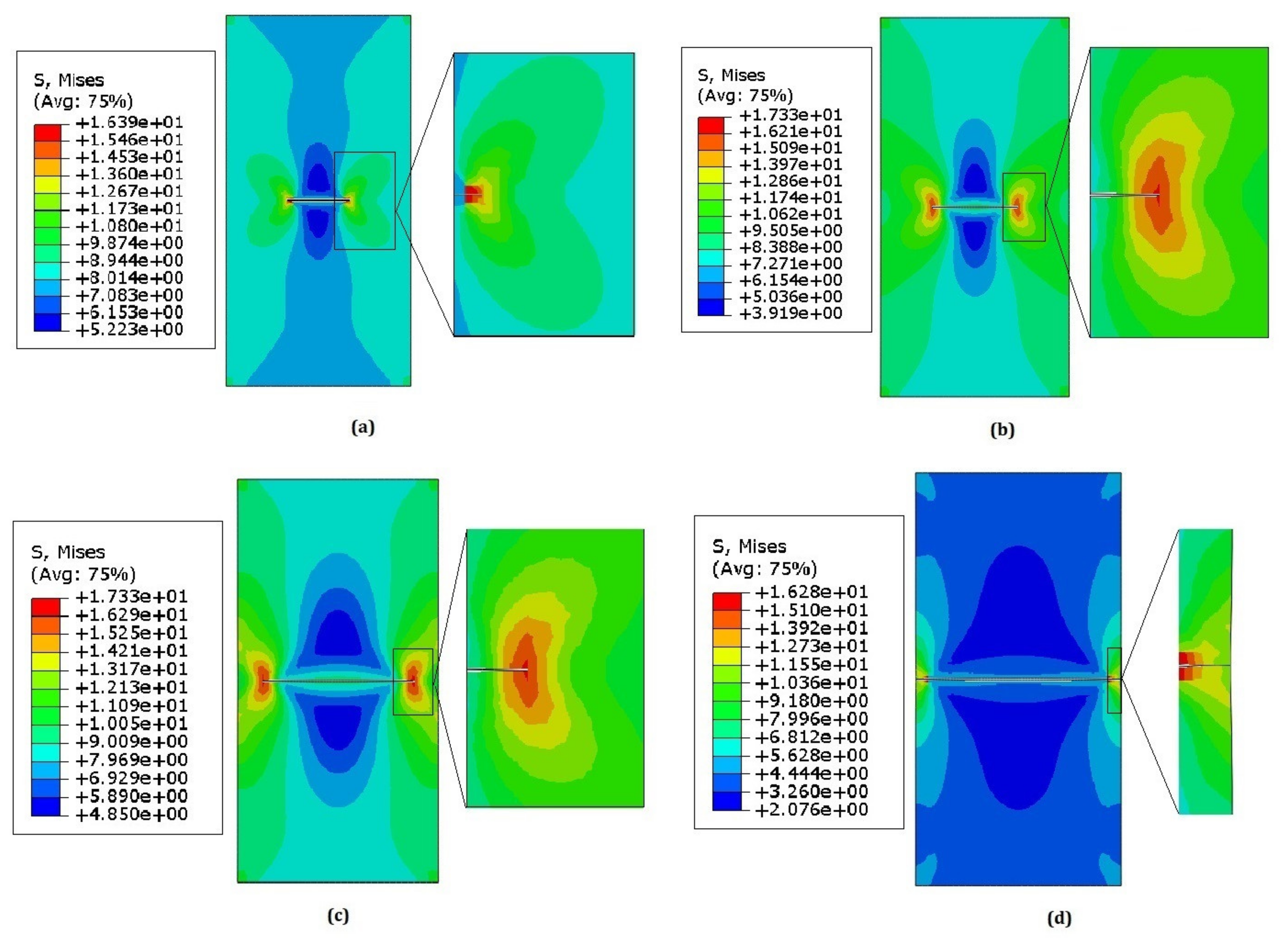
4.1. Tensile Test Simulation
Flow Curve
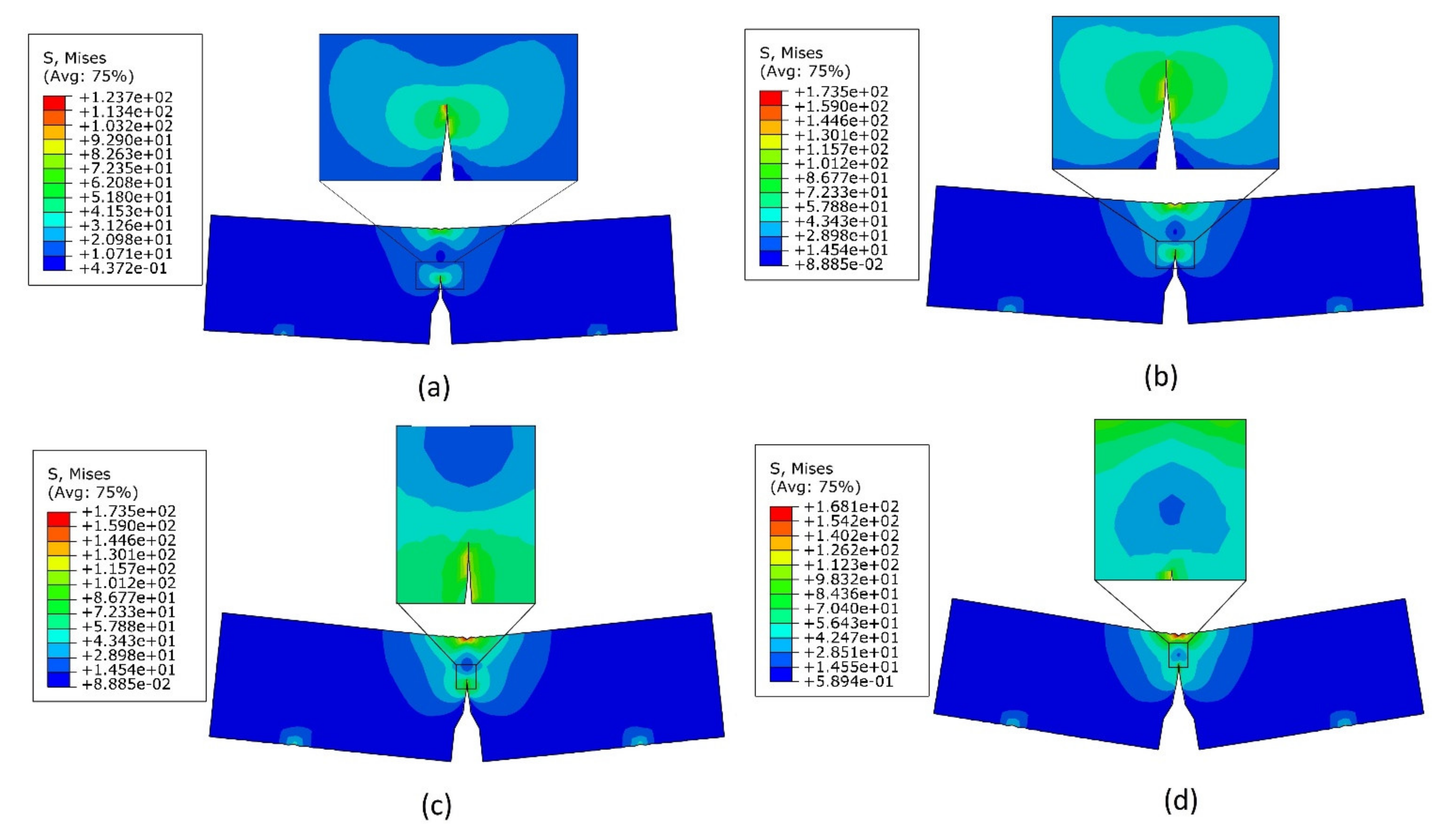
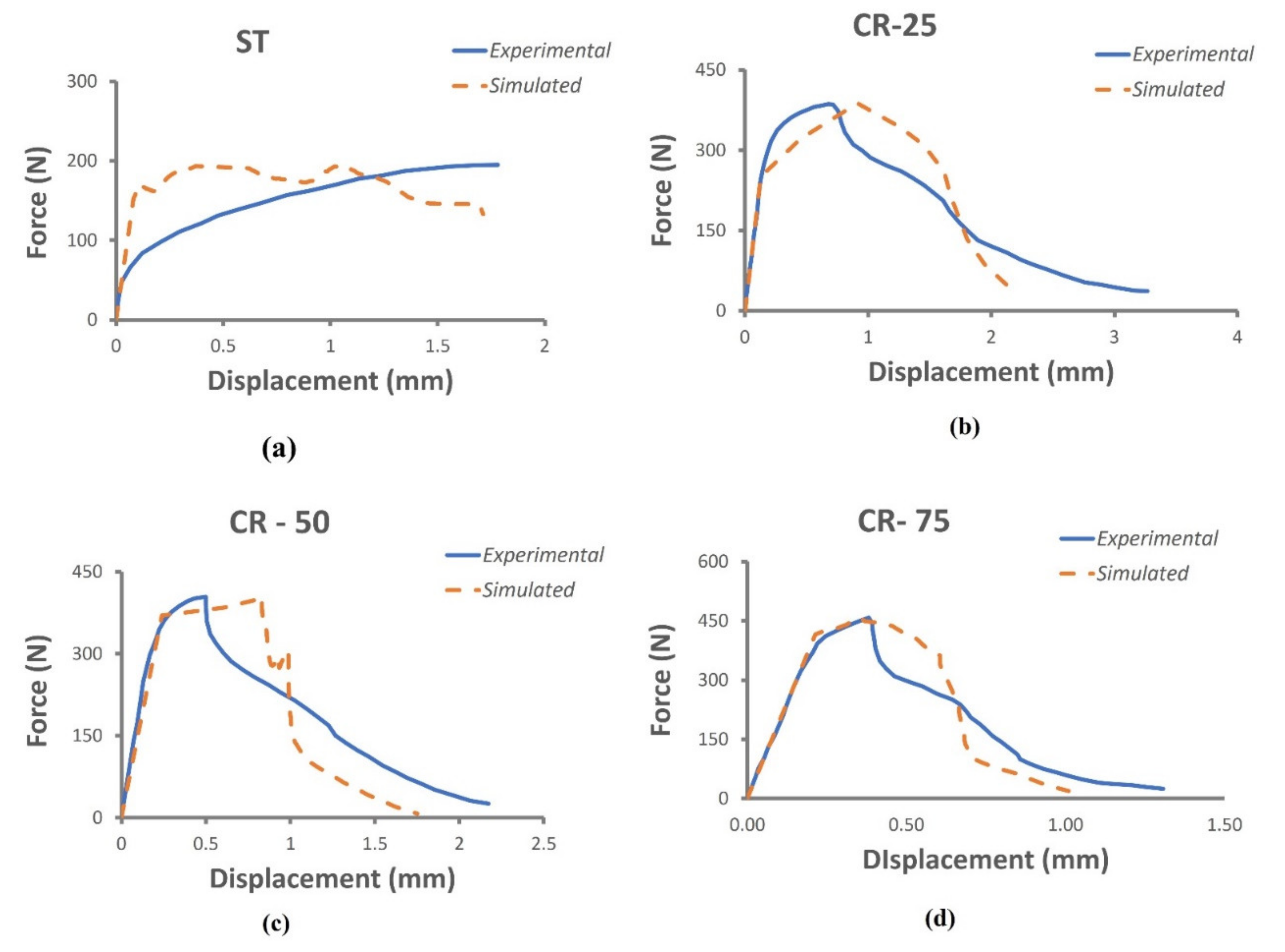
4.2. Three-Point Bend Test
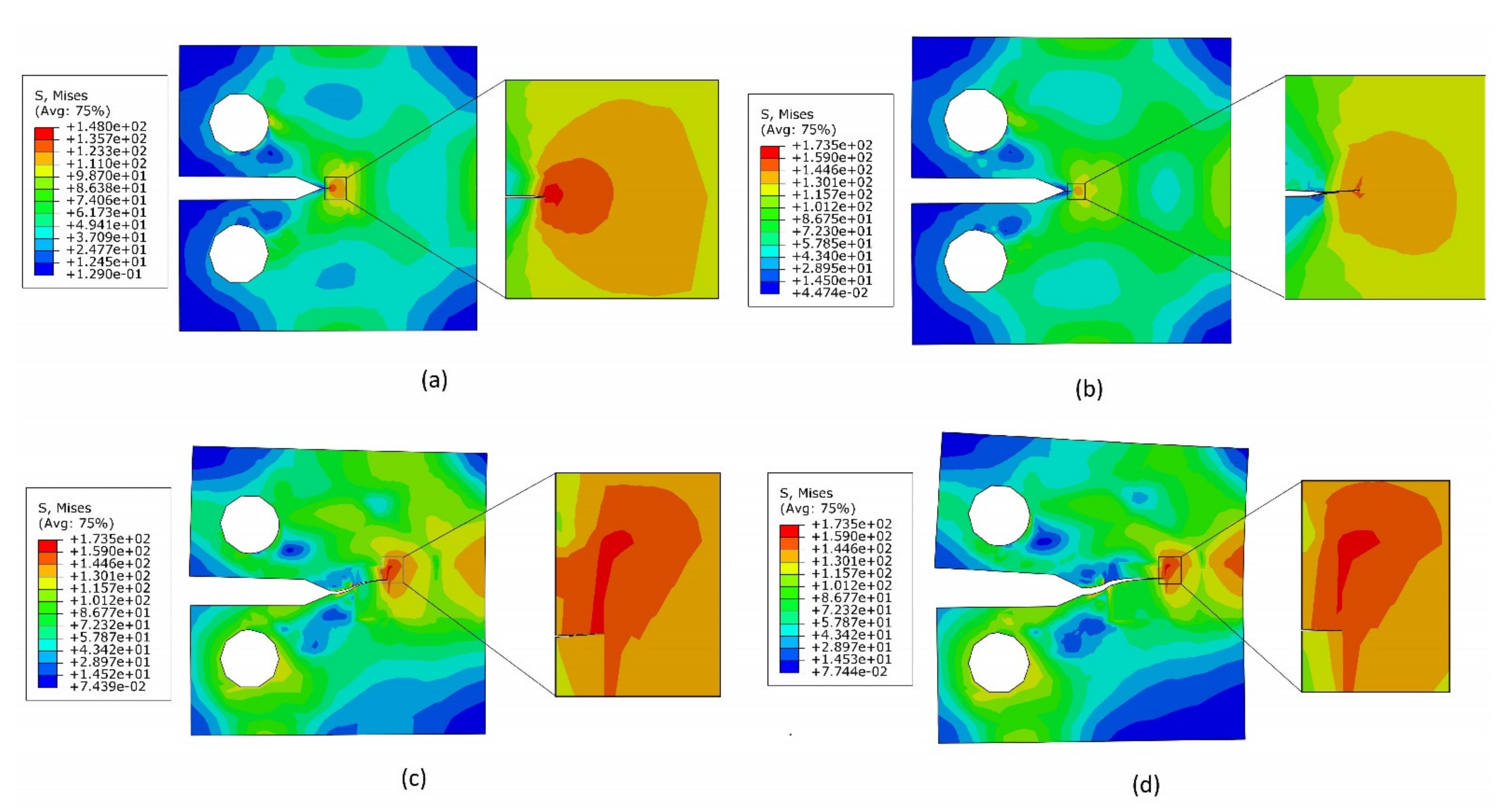
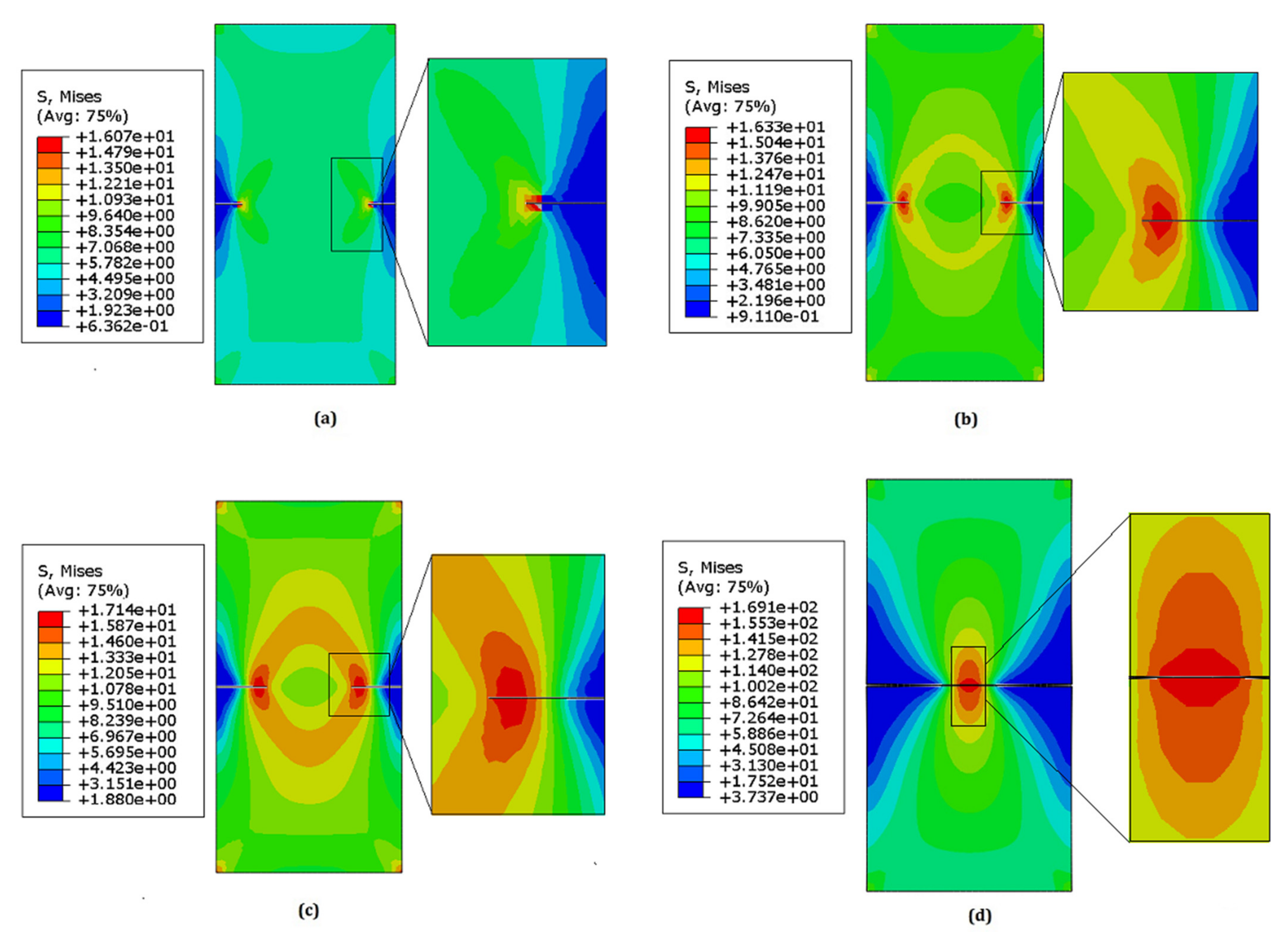
4.3. Compact Tension Test
4.4. Center Crack and Double Edge Crack under Mode-I Loading
5. Conclusions
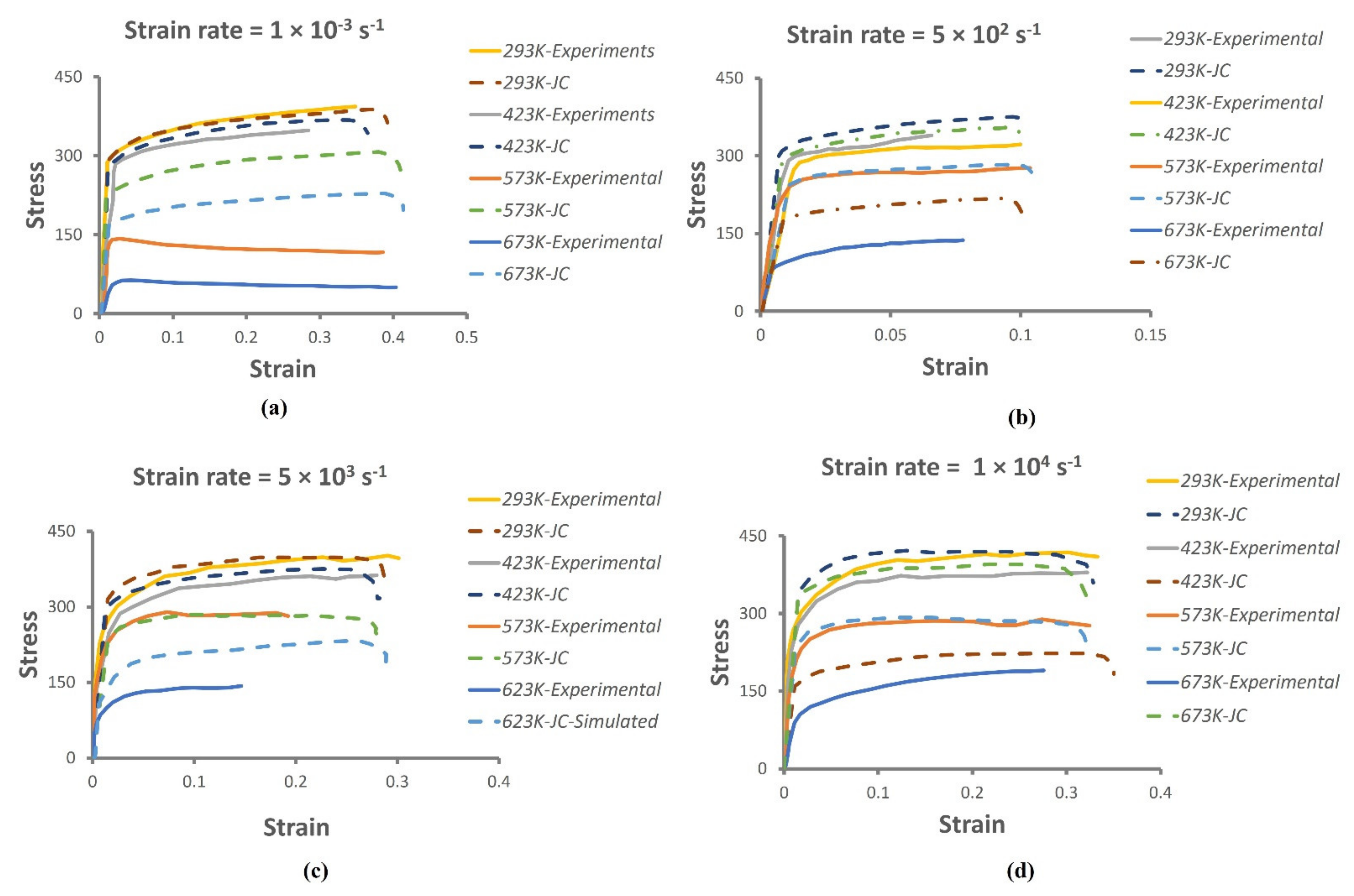
- Prediction of tensile behavior at different strain rates and temperatures was made using the JC material model. The properties at lower temperatures were comparable to the experimental properties, but at a higher temperature, 623K, the JC model failed to predict the tensile behavior.
- Fracture toughness was calculated in different testing conditions such as the three-point bend test, compact tension specimen, center-cracked specimen, and double edge cracked specimen. UFG alloys have higher fracture toughness compared to their bulk counterparts due to their finer grain size and higher dislocation density. In CR samples, as thickness reduction increases, the stress intensity factor increases from 17.45 MPa. M1/2 in ST samples to 27.53 MPa. M1/2 in CR25, 31.64 MPa. M1/2 in CR50 and finally 34.01 MPa. M1/2 in CR75 samples, but J integral in CR samples decreases as thickness reduction decreases. This decrease is due to a decrease in ductility with an increase in thickness reduction. In ARB samples, the strength as well as ductility increases, which leads to increase in both stress intensity factor and J integral.
- The fracture toughness obtained from XFEM simulation was in tandem with the experimental results. In the case of CT specimen, the 3D simulation produced slightly better results on fracture toughness compared to the 2D model, but the time required for the 3D simulation is approximately 2–2.5 times higher compared to the 2D simulation. The fracture toughness in center cracked, and double edge cracked specimen is lower compared to the fracture toughness in CT and three-point bend test specimen.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| UFG | Ultra fine grained |
| XFEM | Extended finite element method |
| SPD | Severe plastic deformation |
| ARB | Accumulative roll bonding |
| CR | Cryorolling |
| CR25 | Cryorolling with 25% thickness reduction |
| CR50 | Cryorolling with 50% thickness reduction |
| CR75 | Cryorolling with 75% thickness reduction |
| JC | Johnson Cook material model |
| PU | Partition of unity |
References
- Robson, J.D.; Engler, O.; Sigli, C.; Deschamps, A.; Poole, W.J. Advances in Microstructural Understanding of Wrought Aluminum Alloys. Metall. Mater. Trans. A 2020, 51, 4377–4389. [Google Scholar] [CrossRef]
- Engler, O.; Hirsch, J. Recrystallization textures and plastic anisotropy in Al-Mg-Si sheet alloys. Mater. Sci. Forum 1996, 217—222, 479–486. [Google Scholar] [CrossRef]
- Aryshenskii, E.V.; Guk, S.V.; Galiev, E.E.; Drits, A.M.; Kavalla, R. Possibility of application of a 1565ch alloy in the automotive industry. Russ. Metall. 2018, 2018, 995–1001. [Google Scholar] [CrossRef]
- Hellier, A.K.; Chaphalkar, P.P.; Prusty, B.G. Fracture toughness measurement for aluminium 6061-T6 using notched round bars. In Proceedings of the 9th Australasian Congress on Applied Mechanics 2017 (ACAM 9), Sydney, Australia, 27–29 November 2017. [Google Scholar]
- Gairola, S.; Joshi, A.; Gangil, B.; Rawat, P.; Verma, R. Correlation of Tensile Properties and Fracture Toughness with Microstructural Features for Al–Li 8090 Alloy Processed by Cryorolling and Post-rolled Annealing. Trans. Indian Inst. Met. 2019, 72, 1743–1755. [Google Scholar] [CrossRef]
- Kapil, R.; Joshi, A.; Jayaganthan, R.; Gairola, S.; Verma, R. Improvement of fracture toughness of ultra fine grained Al-Li 8090 alloy processed through multi axial forging. Mater. Res. Express 2019, 6, 085064. [Google Scholar] [CrossRef]
- Verma, R.; Jayaganthan, R.; Nath, S.K.; Srinivasan, A. Effect of multiaxial forging followed by hot rolling on non-basal planes and its influence on tensile and fracture toughness behaviour of Mg–4Zn–4Gd alloy. Mater. Sci. Eng. A 2020, 774, 138890. [Google Scholar] [CrossRef]
- Roy, S.; Singh, D.S.; Suwas, S.; Kumar, S.; Chattopadhyay, K. Microstructure and texture evolution during accumulative roll bonding of aluminium alloy AA5086. Mater. Sci. Eng. A 2011, 528, 8469–8478. [Google Scholar] [CrossRef]
- Singh, G.; Verma, R.; Narayanan, K.I.; Arora, U.K.; Jayaganthan, R. Effect of swaging feed rate and annealing phenomena on tensile, fracture toughness and microstructural evolution of Zr-4 alloy. Mater. Sci. Eng. A 2021, 831, 142219. [Google Scholar] [CrossRef]
- Balakrishnan, V.; Roshan, P.; Goel, S.; Jayaganthan, R.; Singh, I.V. Experimental and XFEM Simulation of Tensile and Fracture Behavior of Al 6061 Alloy Processed by Severe Plastic Deformation. Metallogr. Microstruct. Anal. 2017, 6, 55–72. [Google Scholar] [CrossRef]
- Toth, L.S.; Gu, C. Ultrafine-grain metals by severe plastic deformation. Mater. Charact. 2014, 92, 1–14. [Google Scholar] [CrossRef]
- Singh, S.P.; Bhattacharya, S.; Sehgal, D.K. Evaluation of high temperature mechanical strength of Cr-Mo grade steel through small punch test technique. Eng. Fail. Anal. 2014, 39, 207–220. [Google Scholar] [CrossRef]
- Zhong, S.; Oyadiji, S.O. Crack detection in simply supported beams without baseline modal parameters by stationary wavelet transform. Mech. Syst. Signal Process. 2007, 21, 1853–1884. [Google Scholar] [CrossRef]
- Patil, D.P.; Maiti, S.K. Detection of multiple cracks using frequency measurements. Eng. Fract. Mech. 2003, 70, 1553–1572. [Google Scholar] [CrossRef]
- Vadiraj, A.; Kamaraj, M. Characterization of fretting fatigue damage of PVD TiN coated biomedical titanium alloys. Surf. Coat. Technol. 2006, 200, 4538–4542. [Google Scholar] [CrossRef]
- Vadiraj, A.; Kamaraj, M. Damage characterization of unmodified and surface modified medical grade titanium alloys under fretting fatigue condition. Mater. Sci. Eng. A 2006, 416, 253–260. [Google Scholar] [CrossRef]
- Samant, S.S.; Pandey, V.B.; Singh, I.V.; Singh, R.N. Effect of double austenitization treatment on fatigue crack growth and high cycle fatigue behavior of modified 9Cr–1Mo steel. Mater. Sci. Eng. A 2020, 788, 139495. [Google Scholar] [CrossRef]
- Samant, S.S.; Singh, I.V.; Singh, R.N. Effect of Tempering and Rolling on Fatigue Crack Growth Behavior of Modified 9Cr-1Mo Steel. J. Mater. Eng. Perform. 2018, 27, 5898–5912. [Google Scholar] [CrossRef]
- Goel, S.; Nikhil, K.; Devsari, F.; Jayaganthan, Y.; Singh, I.V.; Srivastava, D.; Dey, G.K.; Saibaba, N. Evaluating Fracture Toughness of Rolled Zircaloy-2 at Different Temperatures Using XFEM. J. Mater. Eng. Perform. 2016, 25, 4046–4058. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Sharma, K.; Bui, T.Q.; Zhang, C.; Bhargava, R.R. Analysis of a subinterface crack in piezoelectric bimaterials with the extended finite element method. Eng. Fract. Mech. 2013, 104, 114–139. [Google Scholar] [CrossRef]
- Liu, P.; Yu, T.; Bui, T.Q.; Zhang, C.; Xu, Y.; Lim, C.W. Transient thermal shock fracture analysis of functionally graded piezoelectric materials by the extended finite element method. Int. J. Solids Struct. 2014, 51, 2167–2182. [Google Scholar] [CrossRef]
- Nguyen-Vinh, H.; Abu Bakar, I.A.; Abdulrazzak Msekh, M.; Song, J.-H. Extended finite element method for dynamic fracture of piezo-electric materials. Eng. Fract. Mech. 2012, 92, 19–31. [Google Scholar] [CrossRef]
- Jafarlou, D.M.; Zalnezhad, E.; Hassan, M.A.; Ezazi, M.A. Severe plastic deformation of tubular AA 6061 via equal channel angular pressing. Mater. Des. 2016, 90, 1124–1135. [Google Scholar] [CrossRef]
- Tan, E.; Kibar, A.A.; Gür, C.H. Mechanical and microstructural characterization of 6061 aluminum alloy strips severely deformed by Dissimilar Channel Angular Pressing. Mater. Charact. 2011, 62, 391–397. [Google Scholar] [CrossRef]
- Moreno-Valle, E.C.; Sabirov, I.; Perez-Prado, M.T.; Murashkin, M.Y.; Bobruk, E.V.; Valiev, R.Z. Effect of the grain refinement via severe plastic deformation on strength properties and deformation behavior of an Al6061 alloy at room and cryogenic temperatures. Mater. Lett. 2011, 65, 2917–2919. [Google Scholar] [CrossRef]
- Rao, P.N.; Jayaganthan, R. Effects of warm rolling and ageing after cryogenic rolling on mechanical properties and microstructure of Al 6061 alloy. Mater. Des. 2012, 39, 226–233. [Google Scholar] [CrossRef]
- Rahmatabadi, D.; Hashemi, R.; Mohammadi, B.; Shojaee, T. Experimental evaluation of the plane stress fracture toughness for ultra-fine grained aluminum specimens prepared by accumulative roll bonding process. Mater. Sci. Eng. A 2017, 708, 301–310. [Google Scholar] [CrossRef]
- Fan, X.; Suo, T.; Sun, Q.; Wang, T. Dynamic mechanical behavior of 6061 al alloy at elevated temperatures and different strain rates. Acta Mech. Solida Sin. 2013, 26, 111–120. [Google Scholar] [CrossRef]
- Qian, Y.; Zhao, J. Fracture toughness calculation method amendment of the dissimilar steel welded joint based on 3D XFEM. Metals 2019, 9, 509. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, I.V.; Mishra, B.K. Numerical investigation of stable crack growth in ductile materials using XFEM. Procedia Eng. 2013, 64, 652–660. [Google Scholar] [CrossRef]
- Das, P.; Singh, I.V.; Jayaganthan, R. Crack growth simulation of bulk and ultrafine grained 7075 Al alloy by XFEM. Int. J. Mater. Prod. Technol. 2012, 44, 252–276. [Google Scholar] [CrossRef]
- Abaqus/CAE 6. 14 User’s Manual; Dassault Systémes Inc.: Johnston, RI, USA, 2014; Volume IV, pp. 1–6. [Google Scholar]
- Džugan, J.; Španiel, M.; Prantl, A.; Konopík, P.; Růžička, J.; Kuželka, J. Identification of ductile damage parameters for pressure vessel steel. Nucl. Eng. Des. 2018, 328, 372–380. [Google Scholar] [CrossRef]
- Murugesan, M.; Jung, D.W. Johnson cook material and failure model parameters estimation of AISI-1045 medium carbon steel for metal forming applications. Materials 2019, 12, 609. [Google Scholar] [CrossRef] [PubMed]
- ASTM. E8 ASTM E8/E8M Standard Test Methods for Tension Testing of Metallic Materials 1; ASTM: West Conshohocken, PA, USA, 2010; pp. 1–27. [Google Scholar] [CrossRef]
- Sobolev, A.V.; Radchenko, M.V. Use of Johnson–Cook plasticity model for numerical simulations of the SNF shipping cask drop tests. Nucl. Energy Technol. 2016, 2, 272–276. [Google Scholar] [CrossRef]
- Rao, P.N.; Singh, D.; Jayaganthan, R. Effect of annealing on microstructure and mechanical properties of Al 6061 alloy processed by cryorolling. Mater. Sci. Technol. 2013, 29, 76–82. [Google Scholar] [CrossRef]
- Rao, P.N.; Kaurwar, A.; Singh, D.; Jayaganthan, R. Enhancement in Strength and Ductility of Al-Mg-Si Alloy by Cryorolling followed by Warm Rolling. Procedia Eng. 2014, 75, 123–128. [Google Scholar] [CrossRef][Green Version]
- Panigrahi, S.K.; Devanand, D.; Jayaganthan, R. A comparative study on mechanical properties of ultrafine-grained Al 6061 and Al 6063 alloys processed by cryorolling. Trans. Indian Inst. Met. 2008, 61, 159–163. [Google Scholar] [CrossRef]
- Satish, D.R.; Feyissa, F.; Kumar, D.R. Cryorolling and warm forming of AA6061 aluminum alloy sheets. Mater. Manuf. Process. 2017, 32, 1345–1352. [Google Scholar] [CrossRef]
- Pathak, M.K.; Joshi, A.; Mer, K.K.S.; Jayaganthan, R. Mechanical Properties and Microstructural Evolution of Bulk UFG Al 2014 Alloy Processed Through Cryorolling and Warm Rolling. Acta Metall. Sin. 2019, 32, 845–856. [Google Scholar] [CrossRef]
- Joshi, A.; Yogesha, K.K.; Jayaganthan, R. Influence of cryorolling and followed by annealing on high cycle fatigue behavior of ultrafine grained Al 2014 alloy. Mater. Charact. 2017, 127, 253–271. [Google Scholar] [CrossRef]
- Farahmand, B. Fracture Mechanics of Metals, Composites, Welds, and Bolted Joints; Springer: Boston, MA, USA, 2001. [Google Scholar]
- Joshi, A.; Yogesha, K.K.; Kumar, N.; Jayaganthan, R. Influence of Annealing on Microstructural Evolution, Precipitation Sequence, and Fracture Toughness of Cryorolled Al–Cu–Si Alloy. Metallogr. Microstruct. Anal. 2016, 5, 540–556. [Google Scholar] [CrossRef]
- Tong-Yi, Z.; Lee, S. Stress intensity factors of interfacial cracks. Eng. Fract. Mech. 1993, 44, 539–544. [Google Scholar] [CrossRef]
- Chen, X.; Chen, Z.; Zhao, Y. Analysis of sheet fracture failure based on XFEM. Open Mech. Eng. J. 2015, 9, 887–891. [Google Scholar] [CrossRef]




| Element Size (mm) | Number of Elements | UTS (MPa) |
|---|---|---|
| 0.5 | 8580 | 174.15 |
| 0.6 | 4692 | 174.15 |
| 0.8 | 2176 | 174.16 |
| 1.0 | 1404 | 174.23 |
| 1.2 | 690 | 174.29 |
| 1.5 | 360 | 174.38 |
| Processing Condition | UTS | % Elongation | ||||
|---|---|---|---|---|---|---|
| Experimental | Simulated | Absolute Error (%) | Experimental | Simulated | Absolute Error (%) | |
| ST | 173 [28] | 174 | 0.6 | 30.9 | 31.2 | 1 |
| T6 | 300 [28] | 298 | 0.7 | 13.0 | 12.8 | 1.5 |
| CR25 | 211 [10] | 211 | 0 | 15 | 14.7 | 2 |
| CR50 | 242 [10] | 242 | 0 | 11.5 | 11.2 | 2.6 |
| CR75 | 285 [10] | 286 | 0.4 | 8.62 | 8.4 | 2.6 |
| ARB-1 cycle | 153 [29] | 154 | 0.7 | 3.5 | 3.5 | 0 |
| ARB-7 cycle | 231 [29] | 230 | 0.4 | 7.8 | 7.4 | 5.1 |
| Condition | Temperature | UTS (MPa) | % Strain at the Fracture | ||||
|---|---|---|---|---|---|---|---|
| Experimental [30] | Simulated | Absolute Error (%) | Experimental [30] | Simulated | Absolute Error (%) | ||
| 1 × 10−3 s−1 | 293K | 394 | 388 | 1.5 | 34.8 | 39.2 | 12.6 |
| 423K | 348 | 368 | 5.7 | 28.4 | 36.5 | 28.5 | |
| 573K | 143 | 307 | 114.7 | 37.7 | 40.9 | 8.5 | |
| 673K | 63 | 229 | 263.5 | 40.4 | 41.3 | 2.2 | |
| 5 × 102 s−1 | 293K | 339 | 375 | 10.6 | 6.6 | 10.2 | 54.5 |
| 423K | 332 | 355 | 6.9 | 10 | 10.1 | 1 | |
| 573K | 277 | 283 | 2.2 | 10.4 | 10.5 | 1 | |
| 673K | 137 | 218 | 59.1 | 7.8 | 10 | 28.2 | |
| 5 × 103 s−1 | 293K | 401 | 398 | 0.7 | 30.1 | 28.7 | 4.7 |
| 423K | 363 | 375 | 3.3 | 28 | 28.2 | 0.7 | |
| 573K | 290 | 285 | 1.7 | 18.3 | 28.2 | 54.1 | |
| 673K | 143 | 233 | 62.9 | 14.6 | 29 | 98.6 | |
| 1 × 104 s−1 | 293K | 418 | 421 | 0.7 | 33.3 | 32.8 | 1.5 |
| 423K | 379 | 395 | 4.2 | 32.2 | 32.1 | 0.3 | |
| 573K | 289 | 292 | 1 | 32.4 | 32.1 | 0.9 | |
| 673K | 190 | 233 | 22.6 | 27.6 | 35.1 | 27.2 | |
| Element Size (mm) | Number of Elements | Stress Intensity Factor (MPa m1/2) |
|---|---|---|
| 0.5 | 7680 | 12.93 |
| 0.7 | 2365 | 12.93 |
| 0.9 | 1088 | 12.80 |
| 1.0 | 960 | 12.78 |
| 1.2 | 519 | 12.6 |
| Processing Condition | Stress Intensity Factor (MPa m1/2) | J Integral (KJ/m2) | ||||
|---|---|---|---|---|---|---|
| Experimental [10] | Simulated | Absolute Error (%) | Experimental [10] | Simulated | Absolute Error (%) | |
| ST | 13.6 | 12.9 | 5.1 | 12 | 12.9 | 7.5 |
| CR25 | 29.5 | 29 | 1.7 | 27.4 | 25.5 | 6.9 |
| CR50 | 29.9 | 28.5 | 4.7 | 18.5 | 16.3 | 11.9 |
| CR75 | 33.7 | 32.5 | 3.6 | 11.4 | 11.2 | 1.8 |
| Stress Intensity Factor (MPa m1/2) | ||||
|---|---|---|---|---|
| Element Size | CT | Center Cracked | Double Edge Cracked | |
| 2d | 3d | |||
| 0.5 | 18.21 | 17.83 | 15.32 | 15.10 |
| 0.7 | 18.21 | 17.83 | 15.32 | 15.10 |
| 0.9 | 18.22 | 17.7 | 15.33 | 15.11 |
| 1.0 | 18.35 | 17.67 | 15.4 | 15.18 |
| 1.2 | 18.4 | 17.5 | 15.42 | 15.2 |
| Processing Condition | Fracture Toughness Parameters | Experimental | CT | Center Cracked | Double Edge Cracked | |||
|---|---|---|---|---|---|---|---|---|
| 2d | 3d | |||||||
| Abs. Error (%) | Abs. Error (%) | |||||||
| ST | Stress intensity factor (MPa m1/2) | 17.5 [10] | 18.2 | 4 | 17.8 | 1.7 | 15.3 | 15.1 |
| J integral (KJ/m2) | 13.2 | 14.1 | 6.8 | 13.5 | 2.3 | 10.9 | 11.4 | |
| CR25 | Stress intensity factor (MPa m1/2) | 27.5 [10] | 28.5 | 3.6 | 28 | 1.8 | 26.1 | 25.8 |
| J integral (KJ/m2) | 25.3 | 25.1 | 0.8 | 25.2 | 0.4 | 21.5 | 21 | |
| CR50 | Stress intensity factor (MPa m1/2) | 31.6 [10] | 30.8 | 2.5 | 31.8 | 0.6 | 29.5 | 29 |
| J integral (KJ/m2) | 21 | 20.1 | 4.3 | 20.8 | 1 | 18.3 | 18.9 | |
| CR75 | Stress intensity factor (MPa m1/2) | 34 [10] | 34.78 | 2.3 | 33.9 | 0.3 | 31.9 | 31.5 |
| J integral (KJ/m2) | 15.2 | 14.4 | 5.3 | 14.8 | 2.6 | 12.2 | 11.8 | |
| ARB- 1 cycle | Stress intensity factor (MPa m1/2) | 16.1 [38] | 15.7 | 2.5 | 16.3 | 1.2 | 15.1 | 15.4 |
| J integral (KJ/m2) | 11.5 | 10.8 | 6.1 | 11.9 | 3.5 | 9.8 | 10.2 | |
| ARB- 7 cycle | Stress intensity factor (MPa m1/2) | 25.4 [38] | 24.8 | 2.4 | 25.2 | 0.8 | 22.7 | 22.1 |
| J integral (KJ/m2) | 24 | 23.2 | 3.3 | 23.4 | 2.5 | 20.9 | 21.4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gairola, S.; Jayaganthan, R. XFEM Simulation of Tensile and Fracture Behavior of Ultrafine-Grained Al 6061 Alloy. Metals 2021, 11, 1761. https://doi.org/10.3390/met11111761
Gairola S, Jayaganthan R. XFEM Simulation of Tensile and Fracture Behavior of Ultrafine-Grained Al 6061 Alloy. Metals. 2021; 11(11):1761. https://doi.org/10.3390/met11111761
Chicago/Turabian StyleGairola, Saurabh, and Rengaswamy Jayaganthan. 2021. "XFEM Simulation of Tensile and Fracture Behavior of Ultrafine-Grained Al 6061 Alloy" Metals 11, no. 11: 1761. https://doi.org/10.3390/met11111761
APA StyleGairola, S., & Jayaganthan, R. (2021). XFEM Simulation of Tensile and Fracture Behavior of Ultrafine-Grained Al 6061 Alloy. Metals, 11(11), 1761. https://doi.org/10.3390/met11111761






