Evolution of Face-Centered Cubic Ti Alloys Transformation by X-ray Diffraction Profile Analysis in Mechanical Alloying
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis of Ti Alloys
2.2. X-ray Diffraction Pattern Analysis
2.2.1. Microstructural Characterization
2.2.2. Determination of Dislocation Density from XRD
2.2.3. Determination of Dislocation Density in Ti13Ta6Sn
3. Results and Discussion
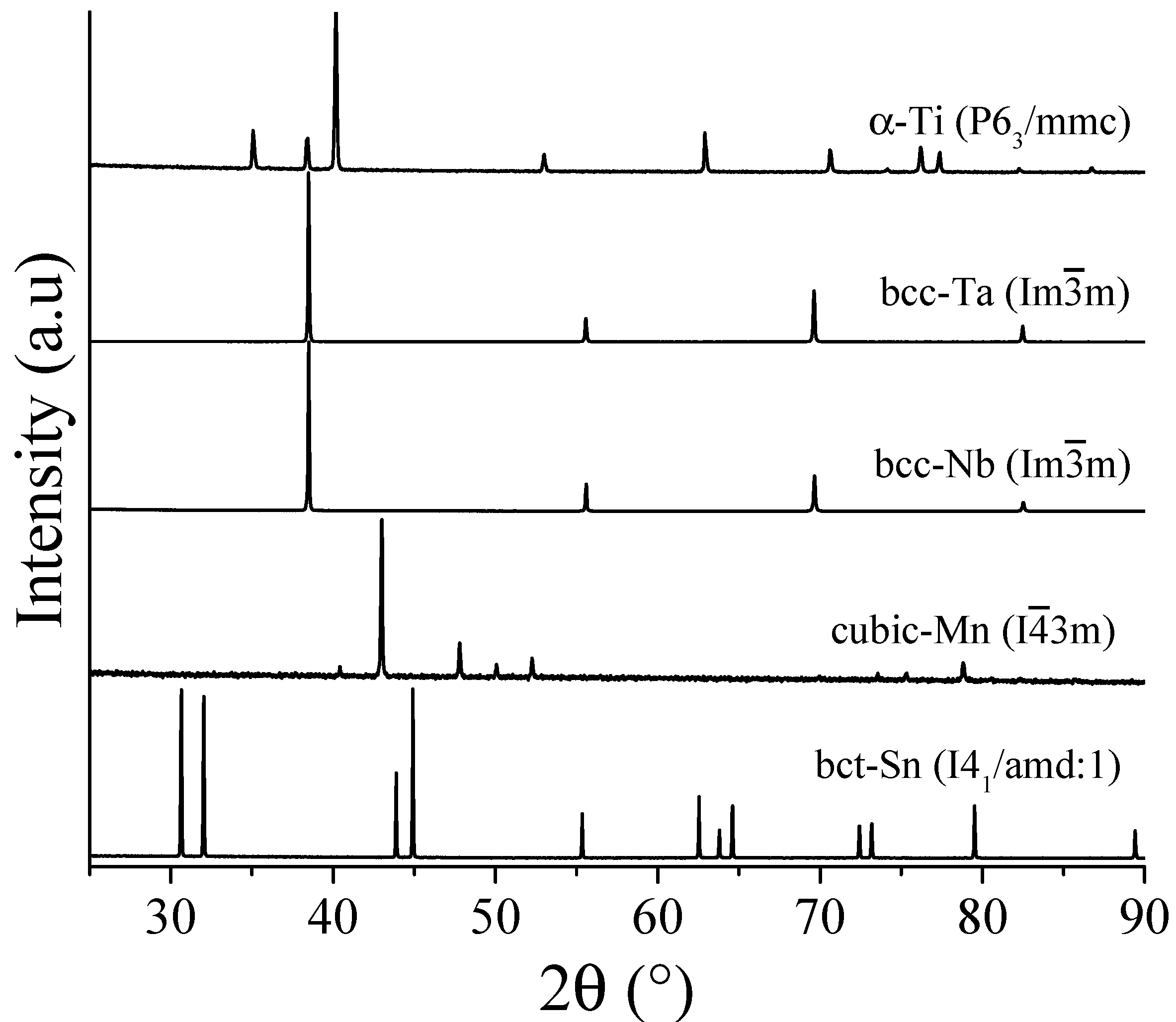
3.1. Pure Powders Characterization
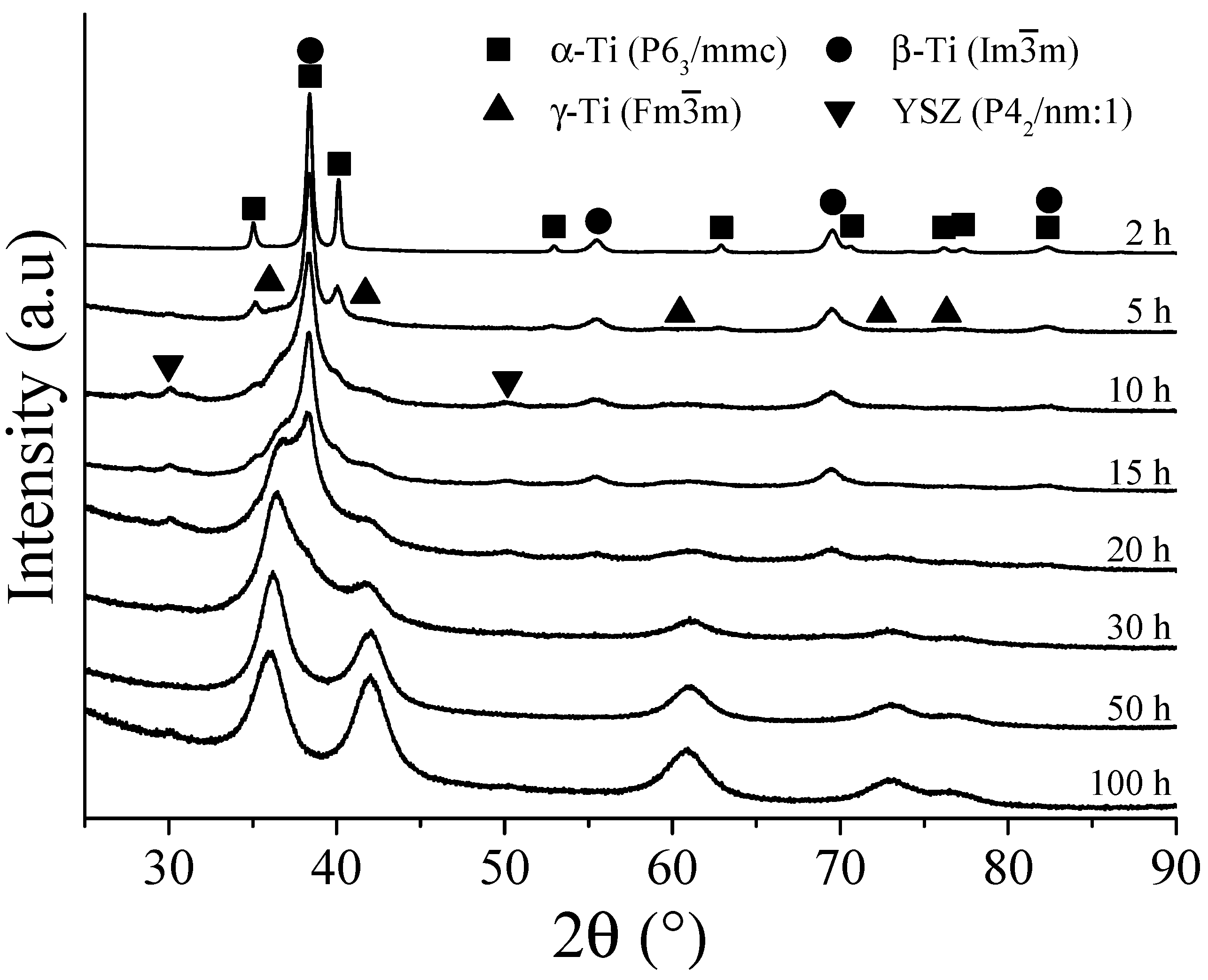
3.2. Ti-13Ta Alloy
3.3. Ti-13Ta-6Sn Alloy
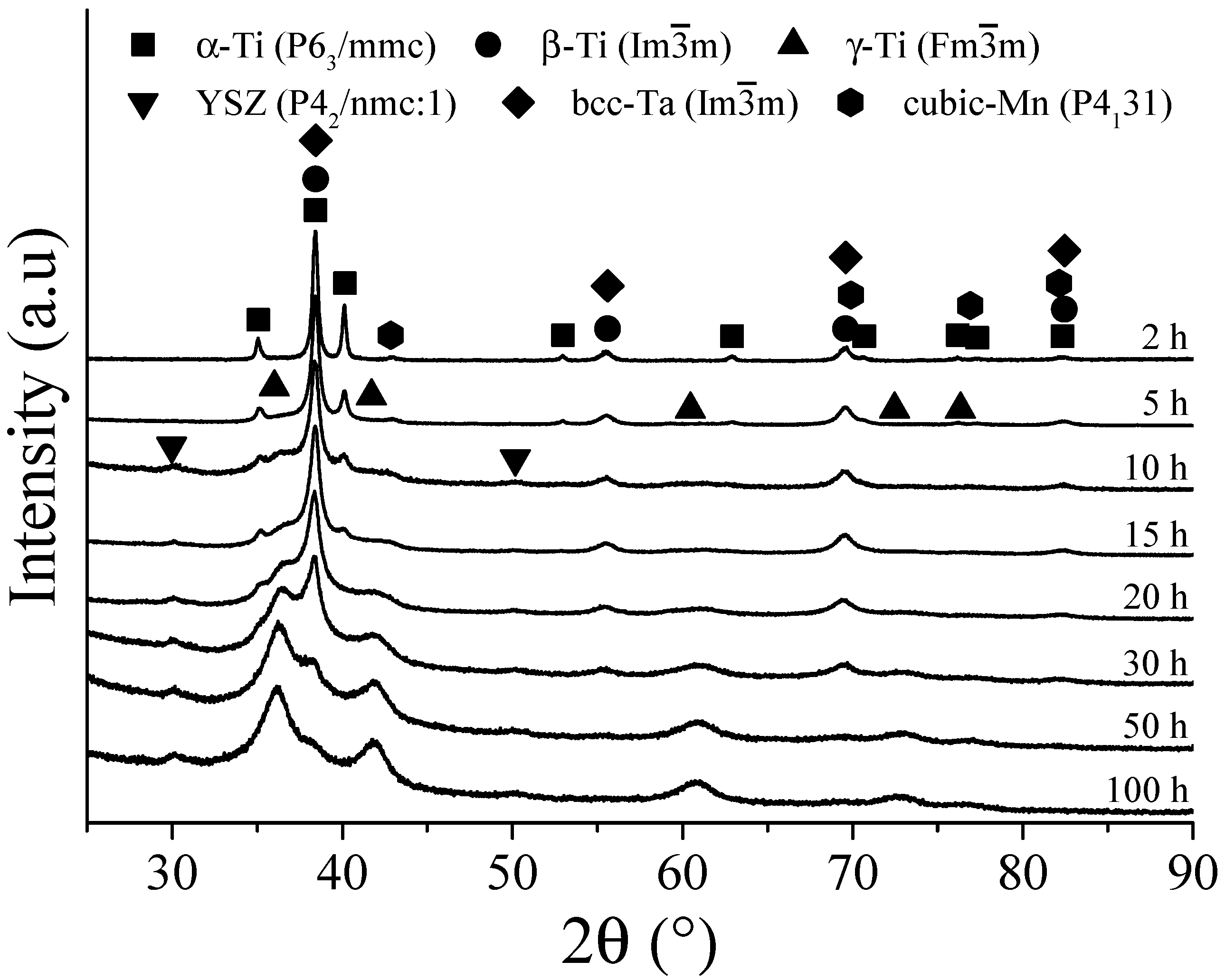
3.4. Ti-13Ta-6Mn Alloy
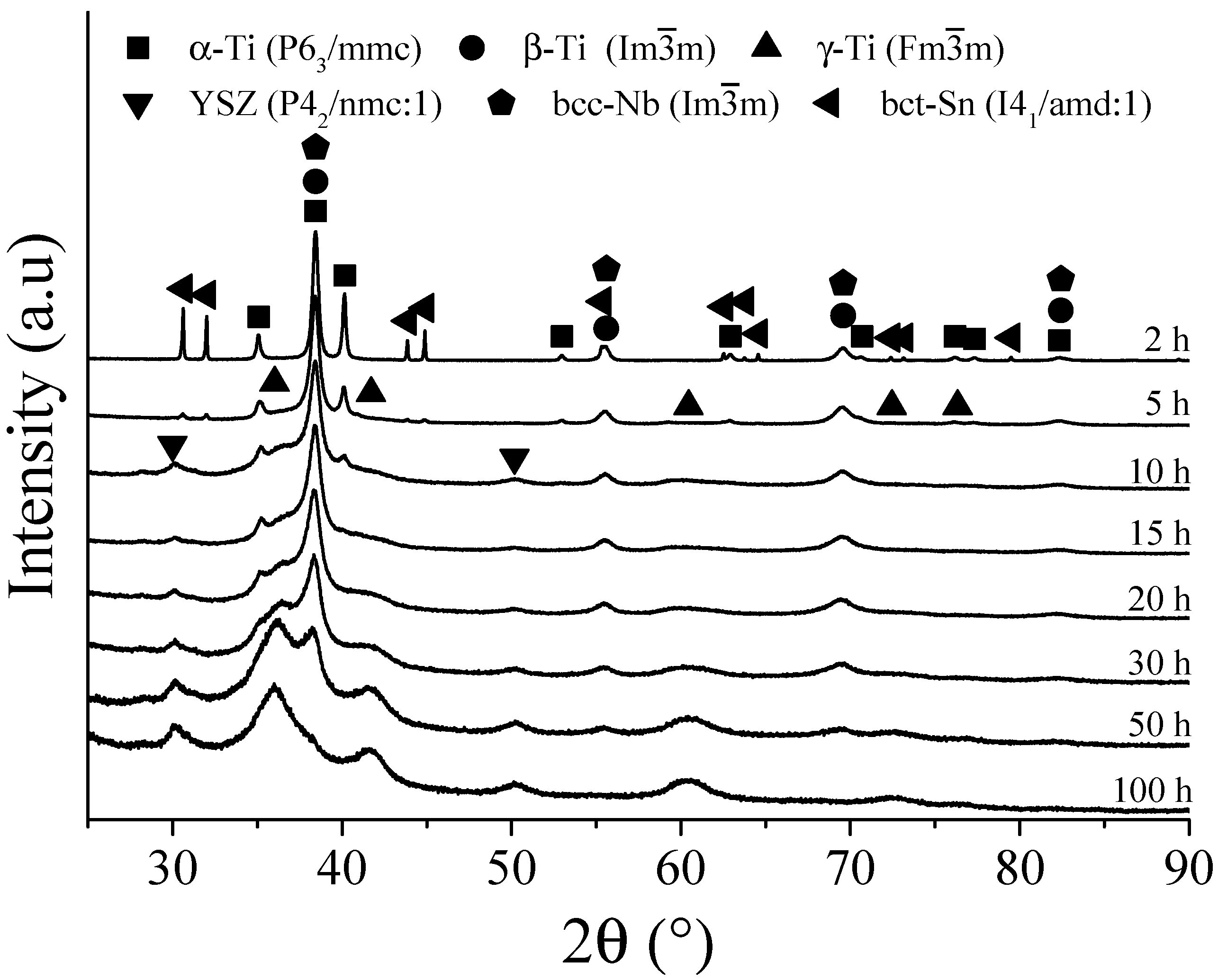
3.5. Ti-30Nb-6Sn Alloy
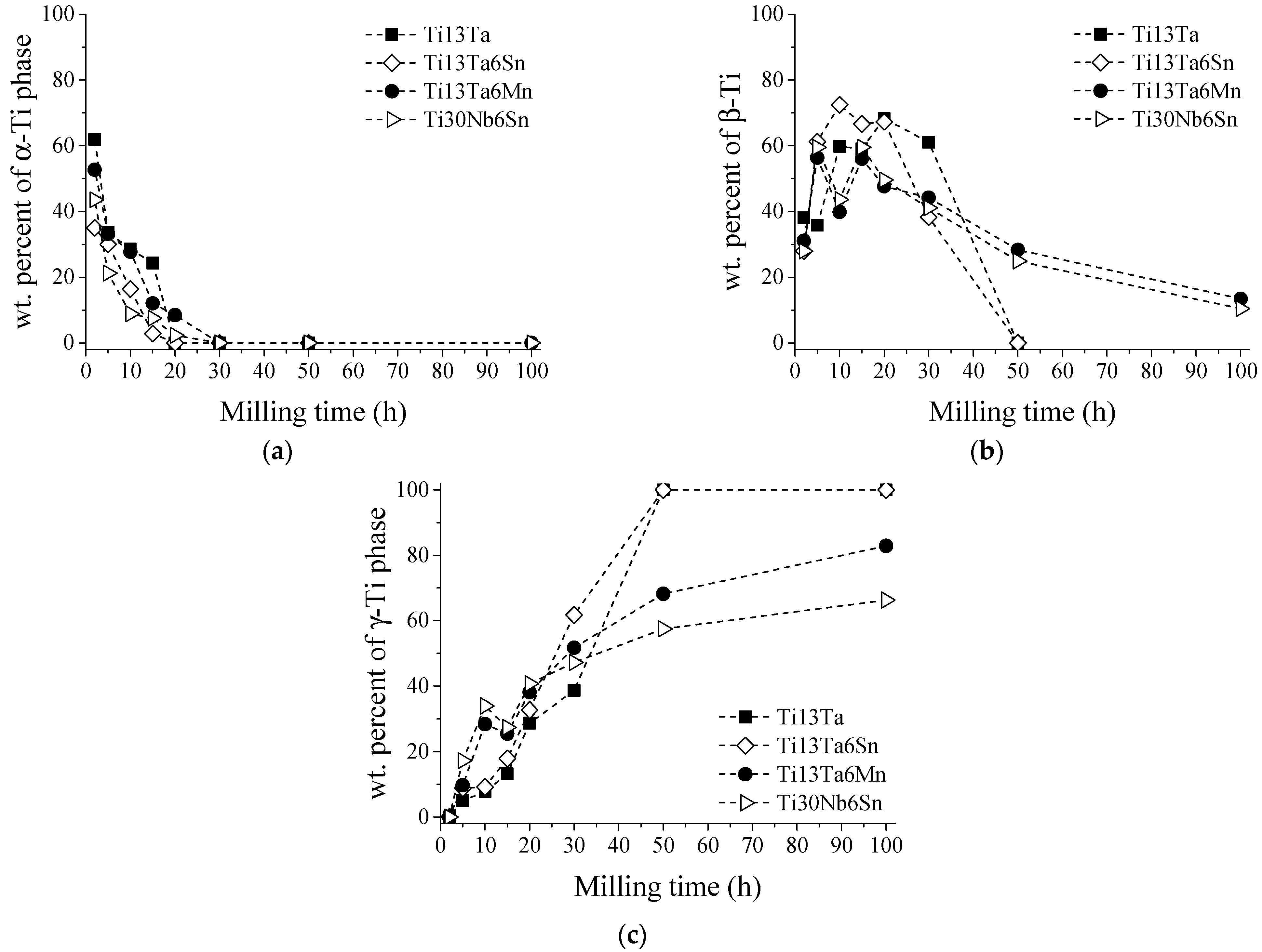
3.6. Microstructural Evolution of the Ti-Based Phases
3.7. Analysis of Dislocation Density Obtained by TEM and XRD for Ti13Ta6Sn Alloy
4. Conclusions
- In the first hours of MA (2–5 h), the diffusion of solute elements and solid solution formation was performed. At the same time, the transformation conditions from hcp to bcc or fcc were identified. During the transformation from hcp to bcc crystal structure, low microstrain values, dislocation density, and crystalline size were observed, in a range of 1.8 × 10−3 m−2 to 6.47 × 10−3 m−2, 5.4 × 1014 m−2 to 1.77 × 1016 m−2, and 14 nm to 34 nm, respectively. In addition, high microstrain and crystalline size values were identified, around 2.5 × 10−2 to 3.23 × 10−2 and 119 nm to 327 nm, respectively, during the transformation from hcp to fcc crystal structure.
- In the period from 5 h to 15 h of MA, the α-Ti phase content decreased, and the microstrain and crystallite size values increased. The content of the β-Ti phase, microstrain, crystallite size, and dislocation density remained relatively constant, indicating its stability in this interval of time. However, the microstrain and crystalline size decreased as the dislocation intensity increased. These facts were associated with the γ-Ti phase stabilizing in long milling times.
- From 15 to 30 h, the total absence of the α-Ti phase was identified for Ti-13Ta and Ti-13Ta-6Sn alloys. Except for Ti-13Ta-6Mn and Ti-30Nb-6Sn alloys, this result indicates that adding Mn and Nb stabilizes the α-Ti phase for long milling times. The content of the β-Ti phase starts decreasing without changes in its crystallite size (except to the Ti-13Ta) but increasing its microstrain, indicating the instability of the bcc-Ti crystal structure. Nevertheless, the content of the γ-Ti phase increased at all milling times while the microstrain, crystallite size, and dislocation density decreased, which indicates the stable conditions of the γ-Ti. From 30 h onwards, high microstrain values of the β-Ti phase were registered. In the next hour of milling, 100% of the γ-Ti phase (50 h) for the Ti-13Ta and Ti-13Ta-6Sn alloys were observed. This condition could be due to the transformation from β-Ti to γ-Ti, for which a big microstrain is required. On the other hand, in the Ti-13Ta-6Mn and Ti-30Nb-6Sn alloys, the microstrain of β-Ti increased after 50 h. However, at 100 h, a high content of γ-Ti with low quantities of β-Ti phases was quantified, indicating that these alloys keep the β-Ti phase stable over long milling times.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cardarelli, F.; Cardarelli, F. Less Common Nonferrous Metals. In Materials Handbook; Springer: Cham, Switzerland, 2018; pp. 317–695. [Google Scholar] [CrossRef]
- Froes, F.H. Titanium: Physical Metallurgy, Processing, and Applications; ASM International: Almere, The Netherlands, 2015; ISBN 9781627080804. [Google Scholar]
- Boyer, R.; Welsch, G.; Collings, E.W. Materials Properties Handbook—Titanium Alloys: 17.7 High-Temperature Strength; ASM International: Almere, The Netherlands, 1994; ISBN 978-0-87170-481-8. [Google Scholar]
- Bhattacharjee, A.; Saha, B.; Williams, J.C. Titanium Alloys: Part 1—Physical Metallurgy and Processing; Springer: Singapore, 2017; pp. 91–115. [Google Scholar]
- Eylon, D.; Fujishiro, S.; Postans, P.J.; Froes, F.H. High-Temperature Titanium Alloys—A Review. JOM J. Miner. Met. Mater. Soc. 1984, 36, 55–62. [Google Scholar] [CrossRef]
- Mouritz, A.P. Titanium alloys for Aerospace Structures and Engines. Introd. Aerosp. Mater. 2012, 202–223. [Google Scholar]
- Peters, M.; Kumpfert, J.; Ward, C.H.; Leyens, C. Titanium alloys for aerospace applications. Adv. Eng. Mater. 2003, 5, 419–427. [Google Scholar] [CrossRef]
- Gurrappa, I. Characterization of titanium alloy Ti-6Al-4V for chemical, marine and industrial applications. Mater. Charact. 2003, 51, 131–139. [Google Scholar] [CrossRef]
- Balazic, M.; Kopac, J.; Jackson, M.J.; Ahmed, W. Review: Titanium and titanium alloy applications in medicine. Int. J. Nano Biomater. 2007, 1, 3–34. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, L.; Tian, M. Application of Biomedical-Grade Titanium Alloys in Trabecular Bone and Artificial Joints; Woodhead Publishing Limited: Southston, UK, 2013; ISBN 9780857090171. [Google Scholar]
- Koizumi, H.; Takeuchi, Y.; Imai, H.; Kawai, T.; Yoneyama, T. Application of titanium and titanium alloys to fixed dental prostheses. J. Prosthodont. Res. 2019, 63, 266–270. [Google Scholar] [CrossRef]
- Lyasotskaya, V.S.; Knyazeva, S.I. Metastable phases in titanium alloys and conditions of their formation. Met. Sci. Heat Treat. 2008, 50, 373–377. [Google Scholar] [CrossRef]
- Gao, J.; Rainforth, W.M. The Effect of Heating Rate on Discontinuous Grain Boundary Alpha Formation in a Metastable Beta Titanium Alloy. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2020, 51, 3766–3771. [Google Scholar] [CrossRef]
- Skvortsova, S.V.; Ilyin, A.A. Mechanisms of phase and structural transformations and texture formation in titanium alloy sheet semiproducts. Russ. Metall. 2007, 2007, 355–363. [Google Scholar] [CrossRef]
- Xing, L.L.; Zhao, C.C.; Chen, H.; Shen, Z.J.; Liu, W. Microstructure of a Ti–50 Wt% Ta alloy produced via laser powder bed fusion. Acta Metall. Sin. 2020, 33, 981–990. [Google Scholar] [CrossRef]
- Prasanthi, T.N.; Sudha, C.; Ravikirana; Saroja, S. Formation and reversion of metastable fcc phase in a Ti-5Ta-2Nb explosive clad. Mater. Charact. 2016, 116, 24–32. [Google Scholar] [CrossRef]
- Chatterjee, P.; Sen Gupta, S.S. An X-Ray diffraction study of strain localization and anisotropic dislocation contrast in nanocrystalline titanium. Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop. 2001, 81, 49–60. [Google Scholar] [CrossRef]
- Chicardi, E.; García-Garrido, C.; Sayagués, M.J.; Torres, Y.; Amigó, V.; Aguilar, C. Development of a novel fcc structure for an amorphous-nanocrystalline Ti-33Nb-4Mn (at.%) ternary alloy. Mater. Charact. 2018, 135, 46–56. [Google Scholar] [CrossRef]
- Guo, W.; Martelli, S.; Padella, F.; Magini, M.; Burgio, N.; Paradiso, E.; Franzoni, U.F.C.C. Metastable Phase Induced in the Ti-Al System by Mechanical Alloying of Pure Elemental Powders. Mater. Sci. Forum 1992, 88–90, 139–146. [Google Scholar] [CrossRef]
- Shechtman, D.; Van Heerden, D.; Jose, D. Fcc titanium in Ti-Al multilayers. Mater. Lett. 1994, 20, 329–334. [Google Scholar] [CrossRef]
- Manna, I.; Chattopadhyay, P.P.; Nandi, P.; Banhart, F.; Fecht, H.J. Formation of face-centered-cubic titanium by mechanical attrition. J. Appl. Phys. 2003, 93, 1520–1524. [Google Scholar] [CrossRef]
- Zhang, D.L.; Ying, D.Y. Formation of fcc titanium during heating high energy ball milled Al-Ti powders. Mater. Lett. 2002, 52, 329–333. [Google Scholar] [CrossRef]
- Sun, F. Synthesis and characterization of mechanical-alloyed Ti– x Mg alloys. J. Alloy. Compd. 2002, 340, 220–225. [Google Scholar] [CrossRef]
- Asano, K.; Enoki, H.; Akiba, E. Synthesis of HCP, FCC and BCC structure alloys in the Mg-Ti binary system by means of ball milling. J. Alloys Compd. 2009, 480, 558–563. [Google Scholar] [CrossRef]
- Wu, H.C.; Kumar, A.; Wang, J.; Bi, X.F.; Tomé, C.N.; Zhang, Z.; Mao, S.X. Rolling-Induced Face Centered Cubic Titanium in Hexagonal Close Packed Titanium at Room Temperature. Sci. Rep. 2016, 6, 24370. [Google Scholar] [CrossRef]
- Bolokang, A.S.; Phasha, M.J.; Motaung, D.E.; Cummings, F.R.; Muller, T.F.G.; Arendse, C.J. Microstructure and phase transformation on milled and unmilled Ti induced by water quenching. Mater. Lett. 2014, 132, 157–161. [Google Scholar] [CrossRef]
- Aguilar, C.; Pio, E.; Medina, A.; Martínez, C.; Sancy, M.; Guzman, D. Evolution of synthesis of FCC nanocrystalline solid solution and amorphous phase in the Ti-Ta based alloy by high milling energy. J. Alloys Compd. 2021, 854, 155980. [Google Scholar] [CrossRef]
- Chatterjee, P.; Gupta, S.S. An X-Ray diffraction study of nanocrystalline titanium prepared by high-energy vibrational ball milling. Appl. Surf. Sci. 2001, 182, 372–376. [Google Scholar] [CrossRef]
- Bera, S.; Manna, I. Hexagonal close packed to face centered cubic polymorphic transformation in nanocrystalline titanium-zirconium system by mechanical alloying. J. Alloys Compd. 2006, 417, 104–108. [Google Scholar] [CrossRef]
- Dercz, G.; Matuła, I.; Zubko, M.; Liberska, A. Structure characterization of biomedical Ti-Mo-Sn alloy prepared by mechanical alloying method. In Acta Physica Polonica A; Polish Academy of Sciences: Warsaw, Poland, 2016; Volume 130, pp. 1029–1032. [Google Scholar]
- Tamura, I. Deformation-induced martensitic transformation and transformation-induced plasticity in steels. Met. Sci. 1982, 16, 245–253. [Google Scholar] [CrossRef]
- Pereloma, E.; Timokhina, I. Deformation-induced phase transformations. Metals 2018, 8, 886. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Ni, S.; Liao, X.; Song, M.; Zhu, Y. Structural evolutions of metallic materials processed by severe plastic deformation. Mater. Sci. Eng. R Rep. 2018, 133, 1–59. [Google Scholar] [CrossRef]
- Dehghan-Manshadi, A.; Dippenaar, R.J. Strain-induced phase transformation during thermo-mechanical processing of titanium alloys. Mater. Sci. Eng. A 2012, 552, 451–456. [Google Scholar] [CrossRef] [Green Version]
- Dahmen, U. Phase Transformations, Crystallographic Aspects. Encycl. Phys. Sci. Technol. 2003, 821–853. [Google Scholar] [CrossRef] [Green Version]
- Cayron, C. Shifting the Shear Paradigm in the Crystallographic Models of Displacive Transformations in Metals and Alloys. Crystals 2018, 8, 181. [Google Scholar] [CrossRef] [Green Version]
- Wayman, C.M. Shear transformations and microstructure. Metallography 1975, 8, 105–130. [Google Scholar] [CrossRef]
- Baek, E.R.; Suprobo, G. Massive Phase Transformation as a New Prospective on Microstructural Design in a Titanium Alloy—A Review. Mater. Sci. Forum 2020, 1000, 428–435. [Google Scholar] [CrossRef]
- McQuillan, M.K. Phase Transformations in Titanium and Its Alloys. Metall. Rev. 2013, 8, 41–104. [Google Scholar] [CrossRef]
- Burgers, W.G. On the process of transition of the cubic-body-centered modification into the hexagonal-close-packed modification of zirconium. Physica 1934, 1, 561–586. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Z.; Wang, B.; Hassan Mohsan, A.U. Stress-Induced orientation relationship variation for phase transformation of α-Ti to β-Ti during high speed machining Ti-6Al-4V. Mater. Sci. Eng. A 2017, 690, 32–36. [Google Scholar] [CrossRef]
- Zhu, W.; Kou, W.; Tan, C.; Zhang, B.; Chen, W.; Sun, Q.; Xiao, L.; Sun, J. Face centered cubic substructure and improved tensile property in a novel β titanium alloy Ti–5Al–4Zr–10Mo–3Cr. Mater. Sci. Eng. A 2020, 771, 138611. [Google Scholar] [CrossRef]
- Hong, D.H.; Lee, T.W.; Lim, S.H.; Kim, W.Y.; Hwang, S.K. Stress-induced hexagonal close-packed to face-centered cubic phase transformation in commercial-purity titanium under cryogenic plane-strain compression. Scr. Mater. 2013, 69, 405–408. [Google Scholar] [CrossRef]
- Aguilar, C.; Pio, E.; Medina, A.; Parra, C.; Mangalaraja, R.; Martin, P.; Alfonso, I.; Tello, K. Effect of Sn on synthesis of nanocrystalline Ti-Based alloy with fcc structure. Trans. Nonferrous Met. Soc. China 2020, 30, 2119–2131. [Google Scholar] [CrossRef]
- Chicardi, E.; Aguilar, C.; Sayagués, M.J.; García-Garrido, C. Influence of the Mn content on the TiNbxMn Alloys with a novel fcc structure. J. Alloys Compd. 2018, 746, 601–610. [Google Scholar] [CrossRef]
- Lutterotti, L.; Matthies, S.; Wenk, H.-R. MAUD: A friendly Java program for Material Analysis Using Diffraction. IUCr Newsl. CPD 1999, 21, 15. [Google Scholar]
- Lutterotti, L.; Scardi, P. Simultaneous structure and size–strain refinement by the Rietveld method. J. Appl. Crystallogr. 1990, 23, 246–252. [Google Scholar] [CrossRef]
- Scardi, P.; Lutterotti, L.; Maistrelli, P. Experimental determination of the instrumental broadening in the Bragg–Brentano geometry. Powder Diffr. 1994, 9, 180–186. [Google Scholar] [CrossRef]
- Delhez, R.; de Keijser, T.H.; Langford, J.I.; Louër, D.; Mittemeijer, E.J.; Sonneveld, E.J. Crystal imperfection broadening and peak shape in the Rietveld method. In The Rietveld Method; Young, R.A., Ed.; Oxford University: Oxford, UK, 1993. [Google Scholar]
- de Keijser, T.H.; Langford, J.I.; Mittemeijer, E.J.; Vogels, A.B.P. Use of the Voigt function in a single-line method for the analysis of X-Ray diffraction line broadening. J. Appl. Crystallogr. 1982, 15, 308–314. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Sheng, H.W.; Lu, K. Microstructure evolution and thermal properties in nanocrystalline Fe during mechanical attrition. Acta Mater. 2001, 49, 365–375. [Google Scholar] [CrossRef]
- Susila, P.; Sturm, D.; Heilmaier, M.; Murty, B.S.; Subramanya Sarma, V. Microstructural studies on nanocrystalline oxide dispersion strengthened austenitic (Fe-18Cr-8Ni-2W-0.25Y2O3) alloy synthesized by high energy ball milling and vacuum hot pressing. J. Mater. Sci. 2010, 45, 4858–4865. [Google Scholar] [CrossRef]
- Rajabi, A.; Ghazali, M.J. Quantitative analyses of TiC nanopowders via mechanical alloying method. Ceram. Int. 2017, 43, 14233–14243. [Google Scholar] [CrossRef]
- Dini, G.; Ueji, R.; Najafizadeh, A.; Monir-Vaghefi, S.M. Flow stress analysis of TWIP steel via the XRD measurement of dislocation density. Mater. Sci. Eng. A 2010, 527, 2759–2763. [Google Scholar] [CrossRef]
- Laala-Bouali, H.; Bentayeb, F.Z.; Louidi, S.; Guo, X.; Tria, S.; Suñol, J.J.; Escoda, L. X-ray line profile analysis of the ball-milled Fe–30Co Alloy. Adv. Powder Technol. 2013, 24, 168–174. [Google Scholar] [CrossRef]
- Khitouni, M.; Mhadhbi, M.; Escoda, L.; Suñol, J.J.; Dammak, M. Characterization of mechanically alloyed nanocrystalline Fe(Al): Crystallite size and dislocation density. J. Nanomater. 2010, 2010, 712407. [Google Scholar]
- Zribi, Z.; Ktari, H.H.; Herbst, F.; Optasanu, V.; Njah, N. EBSD, XRD and SRS characterization of a casting Al-7wt%Si alloy processed by equal channel angular extrusion: Dislocation density evaluation. Mater. Charact. 2019, 153, 190–198. [Google Scholar] [CrossRef]
- Saastamoinen, A.; Kaijalainen, A.; Porter, D.; Suikkanen, P.; Yang, J.R.; Tsai, Y.T. The effect of finish rolling temperature and tempering on the microstructure, mechanical properties and dislocation density of direct-quenched steel. Mater. Charact. 2018, 139, 1–10. [Google Scholar] [CrossRef]
- Williamson, G.K.; Smallman, R.E., III. Dislocation densities in some annealed and cold-worked metals from measurements on the X-Ray Debye-Scherrer spectrum. Philos. Mag. 1956, 1, 34–46. [Google Scholar] [CrossRef]
- Smallman, R.E.; Westmacott, K.H. Stacking Faults in Face-Centred Cubic Metals and Alloys. Philos. Mag. 1957, 2, 669–683. [Google Scholar] [CrossRef]
- Griffiths, M.; Winegar, J.E.; Mecke, J.F.; Holt, R.A. Determination of Dislocation Densities in Hexagonal Close-Packed Metals using X-ray diffraction and Transmission Electron Microscopy. Adv. X-ray Anal. 1991, 35, 593–599. [Google Scholar] [CrossRef]
- Yoo, M.H.; Agnew, S.R.; Morris, J.R.; Ho, K.M. Non-basal slip systems in HCP metals and alloys: Source mechanisms. Mater. Sci. Eng. A 2001, 319–321, 87–92. [Google Scholar] [CrossRef]
- Britton, T.B.; Dunne, F.P.E.; Wilkinson, A.J. On the mechanistic basis of deformation at the microscale in hexagonal close-packed metals. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140881. [Google Scholar] [CrossRef] [Green Version]
- Rai, R.; Triloki, T.; Singh, B.K. X-ray diffraction line profile analysis of KBr thin films. Appl. Phys. A Mater. Sci. Process. 2016, 122, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Cayron, C. Continuous atomic displacements and lattice distortions during martensitic transformations in fcc-bcc-hcp Systems. Acta Mater. 2015, 111, 417–441. [Google Scholar] [CrossRef] [Green Version]
- Kurdjumow, G.; Sachs, G.; Kurdjumow, G.; Sachs, G. Über den mechanismus der Stahlhärtung. Z. Phys. 1930, 64, 325–343. [Google Scholar] [CrossRef]
- Nishiyama, Z. Martensiti Transformatio; Academic Press: Cambridge, MA, USA, 1972; p. 480. [Google Scholar]
- Kruml, T.; Paidar, V.; Martin, J.L. Dislocation density in Ni3(Al,Hf). Intermetallics 2000, 8, 729–736. [Google Scholar] [CrossRef]
- Lewis, D.; Northwood, D.O. X-ray diffraction measurement of microstrains. Strain 1968, 4, 19–23. [Google Scholar] [CrossRef]
- Leineweber, A. Understanding anisotropic microstrain broadening in Rietveld refinement. Z. Krist. 2011, 226, 905–923. [Google Scholar] [CrossRef]
- Will, G. Powder Diffraction—The Rietveld Method and the Two Stage Method to Determine and Refine Crystal Structures from Powder Diffraction Data; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 9783540279860. [Google Scholar]
- Shafi, P.M.; Bose, A.C. Impact of crystalline defects and size on X-ray line broadening: A phenomenological approach for tetragonal SnO2 nanocrystals. AIP Adv. 2015, 5, 057137. [Google Scholar] [CrossRef]
- Rajender, G.; Giri, P.K. Strain induced phase formation, microstructural evolution and bandgap narrowing in strained TiO2 nanocrystals grown by ball milling. J. Alloys Compd. 2016, 676, 591–600. [Google Scholar] [CrossRef]
- Krivoglaz, M.A. X-ray and Neutron Diffraction in Nonideal Crystals; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]
- Noyan, I.C.; Cohen, J.B. Residual Stress: Measurement by Diffraction and Interpretation; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Fogagnolo, J.B.; Velasco, F.; Robert, M.H.; Torralba, J.M. Effect of mechanical alloying on the morphology, microstructure and properties of aluminium matrix composite powders. Mater. Sci. Eng. A 2003, 342, 131–143. [Google Scholar] [CrossRef]
- Chatterjee, P.P.; Pabi, S.K.; Manna, I. An allotropic transformation induced by mechanical alloying. J. Appl. Phys. 1999, 86, 5912. [Google Scholar] [CrossRef]
- Ma, E.; Atzmon, M. Phase transformations induced by mechanical alloying in binary systems. Mater. Chem. Phys. 1995, 39, 249–267. [Google Scholar] [CrossRef]
- Bakker, H.; Zhou, G.F.; Yang, H. Mechanically driven disorder and phase transformations in alloys. Prog. Mater. Sci. 1995, 39, 159–241. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.C.; Aindow, M. Morphology and interfacial structure of gamma precipitates in the beta phase of a Ti-Al-Nb-Zr alloy. J. Mater. Sci. 2006, 41, 611–619. [Google Scholar] [CrossRef]
- Machio, C.; Nyabadza, D.; Sibanda, V.; Chikwanda, H.K. Characterization of mechanically alloyed f.c.c. Ti–Mg-based powders. Powder Technol. 2011, 207, 387–395. [Google Scholar] [CrossRef]
- Aguilar, C.; Guerra, C.; Lascano, S.; Guzman, D.; Rojas, P.A.; Thirumurugan, M.; Bejar, L.; Medina, A. Synthesis and characterization of Ti-Ta-Nb-Mn foams. Mater. Sci. Eng. C 2016, 58, 420–431. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, C.; Castro, F.; Martínez, V.; Guzmán, D.; de las Cuevas, F.; Lozada, L.; Vielma, N. Structural study of nanocrystalline solid solution of Cu-Mo obtained by mechanical alloying. Mater. Sci. Eng. A 2012, 548, 189–194. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Zavalij, P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-0-387-09578-3. [Google Scholar]
- Suryanarayana, C.; Norton, M.G.; Suryanarayana, C.; Norton, M.G. X-rays and Diffraction. In X-ray Diffraction; Springer: Berlin/Heidelberg, Germany, 1998; pp. 3–19. [Google Scholar]
- Waseda, Y.; Matsubara, E.; Shinoda, K.; Waseda, Y.; Matsubara, E.; Shinoda, K. Fundamental Properties of X-rays. In X-ray Diffraction Crystallography; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–20. [Google Scholar]
- Toby, B.H. R factors in Rietveld Analysis: How good is good enough? Powder Diffr. 2006, 21, 67–70. [Google Scholar] [CrossRef] [Green Version]
- Mccusker, L.B.; Von Dreele, R.B.; Cox, D.E.; Louer, D.; Scardi, P. Rietveld refinement guidelines. Int. Union Crystallogr. J. Appl. Crystallogr. J. Appl. Cryst 1999, 32, 36–50. [Google Scholar] [CrossRef] [Green Version]
- Young, R.A. The Rietveld Method; International Union of Crystallograph: Paris, Frnace; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Yang, J.X.; Zhao, H.L.; Gong, H.R.; Song, M.; Ren, Q.Q. Proposed mechanism of HCP → FCC phase transition in titianium through first principles calculation and experiments. Sci. Rep. 2018, 8, 1992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benjamin, J.S.; Volin, T.E. The mechanism of mechanical alloying. Metall. Trans. 1974, 5, 1929–1934. [Google Scholar] [CrossRef]
- Suryanarayna, C. Mechanical Alloying and Milling; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Koch, C.C. Materials Synthesis by Mechanical Alloying. Annu. Rev. Mater. Sci. 1989, 19, 121–143. [Google Scholar] [CrossRef]
- Zeng, Z.; Jonsson, S.; Roven, H.J. The effects of deformation conditions on microstructure and texture of commercially pure Ti. Acta Mater. 2009, 57, 5822–5833. [Google Scholar] [CrossRef]
- Koike, J.; Shimoyama, Y.; Ohnuma, I.; Okamura, T.; Kainuma, R.; Ishida, K.; Maruyama, K. Stress-induced phase transformation during superplastic deformation in two-phase Ti-Al-Fe alloy. Acta Mater. 2000, 48, 2059–2069. [Google Scholar] [CrossRef]
- Chen, C.L.; Lu, W.; Sun, D.; He, L.L.; Ye, H.Q. Deformation-induced A2 → γ phase transformation in TiAl alloys. Mater. Charact. 2010, 61, 1029–1034. [Google Scholar] [CrossRef]
- Al-Aqeeli, N.; Suryanarayana, C.; Hussein, M.A. Formation of an amorphous phase and its crystallization in the immiscible Nb-Zr system by mechanical alloying. J. Appl. Phys. 2013, 114, 153512. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Beyerlein, I.J.; LeSar, R. Slip band formation and mobile dislocation density generation in high rate deformation of single fcc crystals. Philos. Mag. 2008, 88, 1321–1343. [Google Scholar] [CrossRef]
- Follansbee, P.S. High Strain Rate Deformation in FCC Metals and Alloys; Los Alamos National Lab.: Los Alamos, NM, USA, 1985. [Google Scholar]
- Dobromyslov, A.V.; Dolgikh, G.V.; Dutkevich, Y.; Trenogina, T.L. Phase and structural transformations in Ti-Ta alloys. Phys. Met. Metallogr. 2009, 107, 502–510. [Google Scholar] [CrossRef]
- Maurice, D.; Courtney, T.H. Modeling of mechanical alloying: Part I. Deformation, coalescence, bdand fragmentation mechanisms. Metall. Mater. Trans. A 1994, 25, 147–158. [Google Scholar] [CrossRef]
- Sharma, S.; Suryanarayana, C. Mechanical crystallization of Fe-based amorphous alloys. J. Appl. Phys. 2007, 102, 083544. [Google Scholar] [CrossRef] [Green Version]
- Xiong, S.; Qi, W.; Huang, B.; Wang, M.; Li, Z.; Liang, S. Size–Temperature Phase Diagram of Titanium Nanosolids. J. Phys. Chem. C 2012, 116, 237–241. [Google Scholar] [CrossRef]
- Koch, C.C. Synthesis of nanostructured materials by mechanical milling: Problems and opportunities. Nanostruct. Mater. 1997, 9, 13–22. [Google Scholar] [CrossRef]
- Patil, U.; Hong, S.J.; Suryanarayana, C. An unusual phase transformation during mechanical alloying of an Fe-based bulk metallic glass composition. J. Alloys Compd. 2005, 389, 121–126. [Google Scholar] [CrossRef]
- Chang, L.; Zhou, C.-Y.; Pan, X.-M.; He, X.-H. Size-dependent deformation mechanism transition in titanium nanowires under high strain rate tension. Mater. Des. 2017, 134, 320–330. [Google Scholar] [CrossRef]
- Ma, Z.C.; Tang, X.Z.; Mao, Y.; Guo, Y.F. The plastic deformation mechanisms of hcp single crystals with different orientations: Molecular dynamics simulations. Materials 2021, 14, 733. [Google Scholar] [CrossRef]
- Bailey, J.E.; Hirsch, P.B. The dislocation distribution, flow stress, and stored energy in cold-worked polycrystalline silver. Philos. Mag. 2006, 5, 485–497. [Google Scholar] [CrossRef]




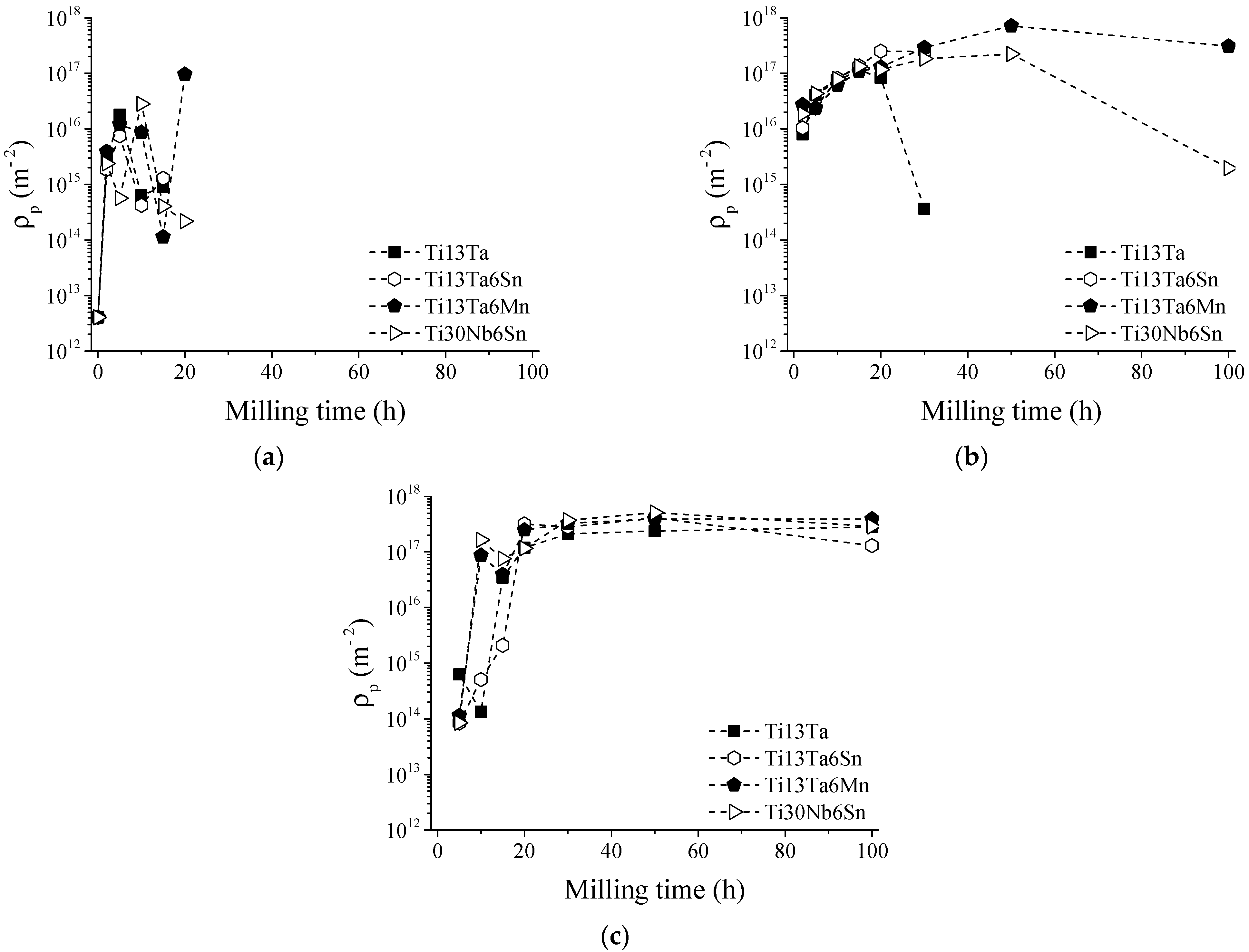
| Solute Elements (at. %) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Elements | Ta | Sn | Nb | Mn | ||||
| Alloys | 0 h | 2 h | 0 h | 2 h | 0 h | 2 h | 0 h | 2 h |
| Ti13Ta | 13 | |||||||
| Ti13Ta6Sn | 13 | 11 | 6 | 2 | ||||
| Ti13Ta6Mn | 13 | 4 | 0 | 6 | 4 | |||
| Ti30Nb6Sn | 6 | 3 | 30 | 13 | ||||
| Milling Time (h) | Analysis | α-Ti | β-Ti | γ-Ti |
|---|---|---|---|---|
| ×1015 (m2) | ×1015 (m2) | ×1015 (m2) | ||
| 5 | DRX | 1.64800 | 2.20624 | 220.405 |
| TEM | 1.60994 | 3.71431 | 10.5484 | |
| 15 | DRX | 62.8685 | 0.182689 | 173.746 |
| TEM | 2.63892 | 6.59731 | 9.83077 | |
| 50 | DRX | * | * | 8.34252 |
| TEM | * | * | 13.8044 | |
| 100 | DRX | * | * | 41.1297 |
| TEM | * | * | 6.7415 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pio, E.; Medina, A.; Martínez, C.; Cerda, F.M.C.; Aguilar, C. Evolution of Face-Centered Cubic Ti Alloys Transformation by X-ray Diffraction Profile Analysis in Mechanical Alloying. Metals 2021, 11, 1841. https://doi.org/10.3390/met11111841
Pio E, Medina A, Martínez C, Cerda FMC, Aguilar C. Evolution of Face-Centered Cubic Ti Alloys Transformation by X-ray Diffraction Profile Analysis in Mechanical Alloying. Metals. 2021; 11(11):1841. https://doi.org/10.3390/met11111841
Chicago/Turabian StylePio, Edgar, Ariosto Medina, Carola Martínez, Felipe Manuel Castro Cerda, and Claudio Aguilar. 2021. "Evolution of Face-Centered Cubic Ti Alloys Transformation by X-ray Diffraction Profile Analysis in Mechanical Alloying" Metals 11, no. 11: 1841. https://doi.org/10.3390/met11111841
APA StylePio, E., Medina, A., Martínez, C., Cerda, F. M. C., & Aguilar, C. (2021). Evolution of Face-Centered Cubic Ti Alloys Transformation by X-ray Diffraction Profile Analysis in Mechanical Alloying. Metals, 11(11), 1841. https://doi.org/10.3390/met11111841







