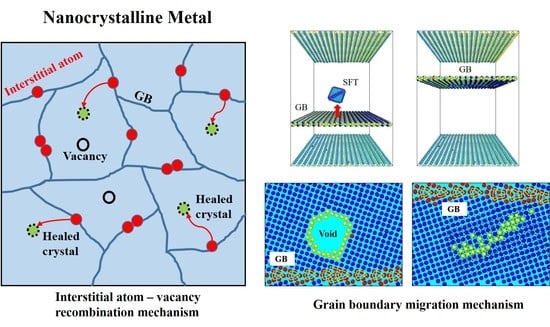
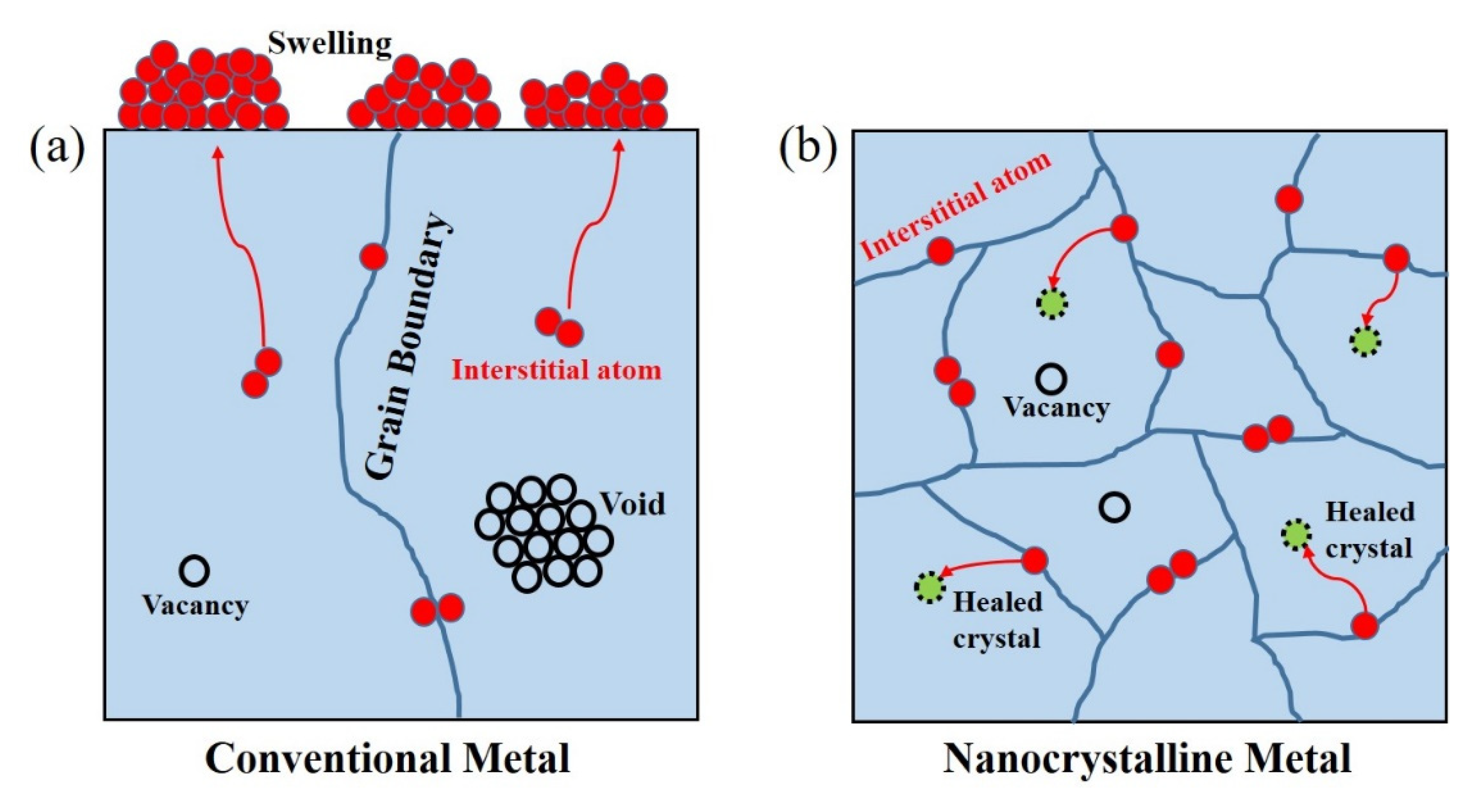
Understanding the Radiation Resistance Mechanisms of Nanocrystalline Metals from Atomistic Simulation
Abstract
:1. Introduction
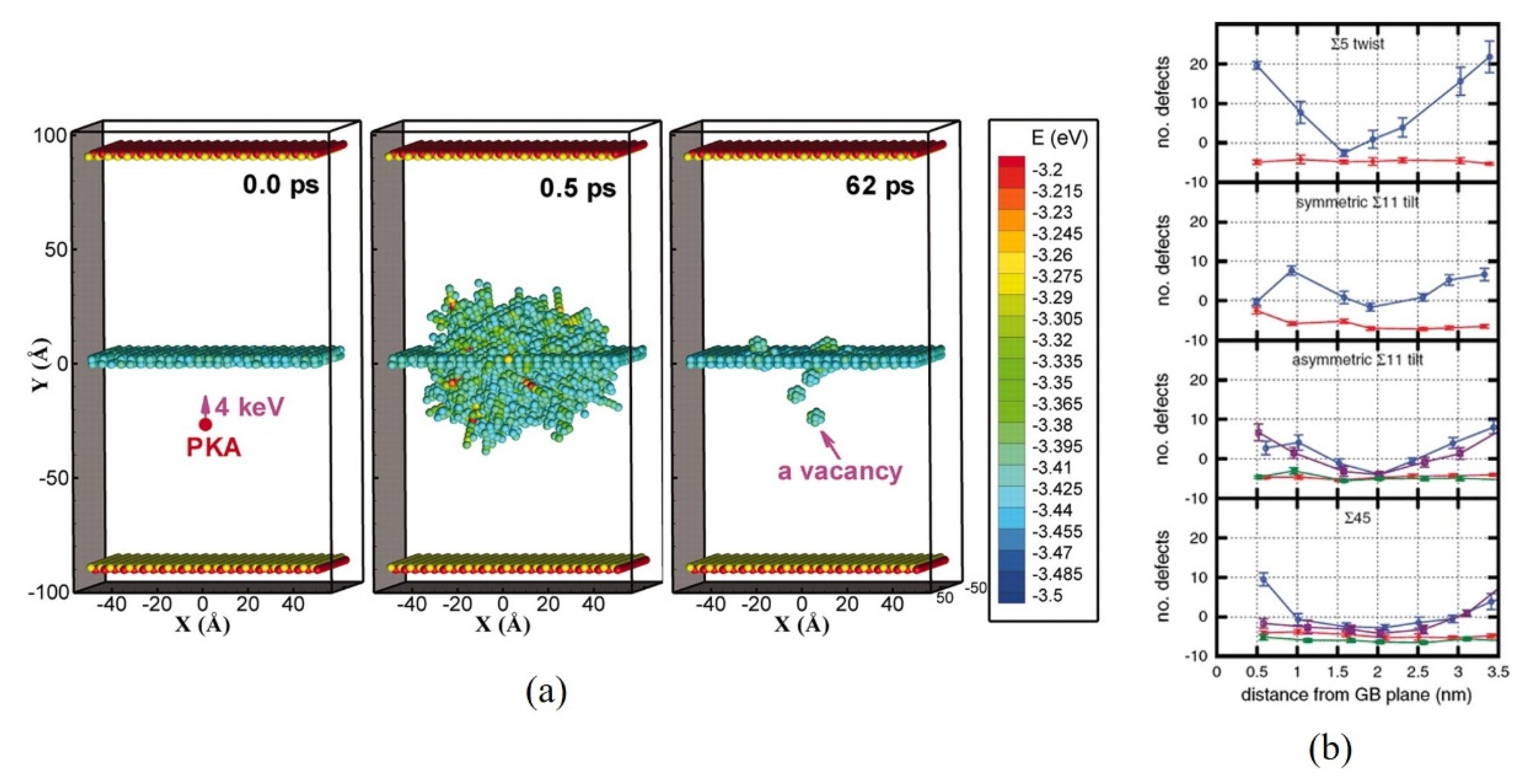
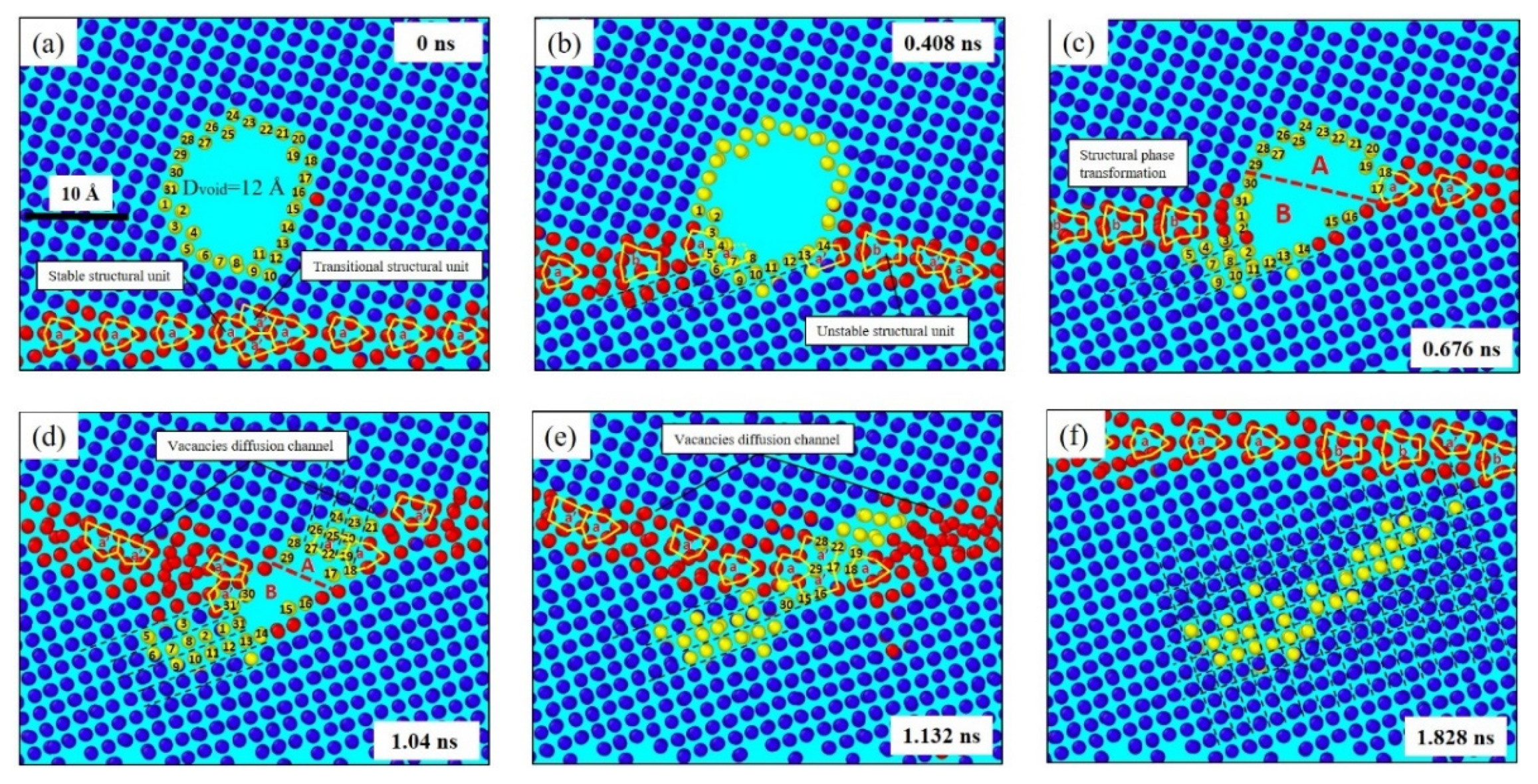
2. Influence of GBs on Collision Cascade
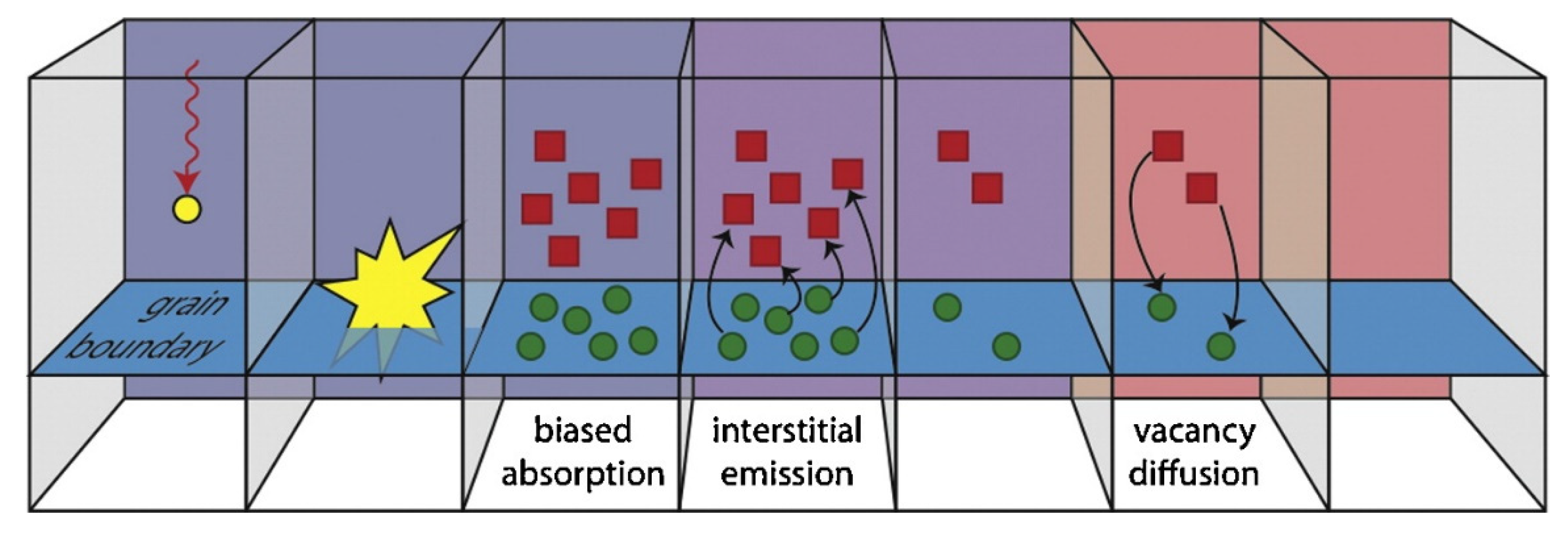
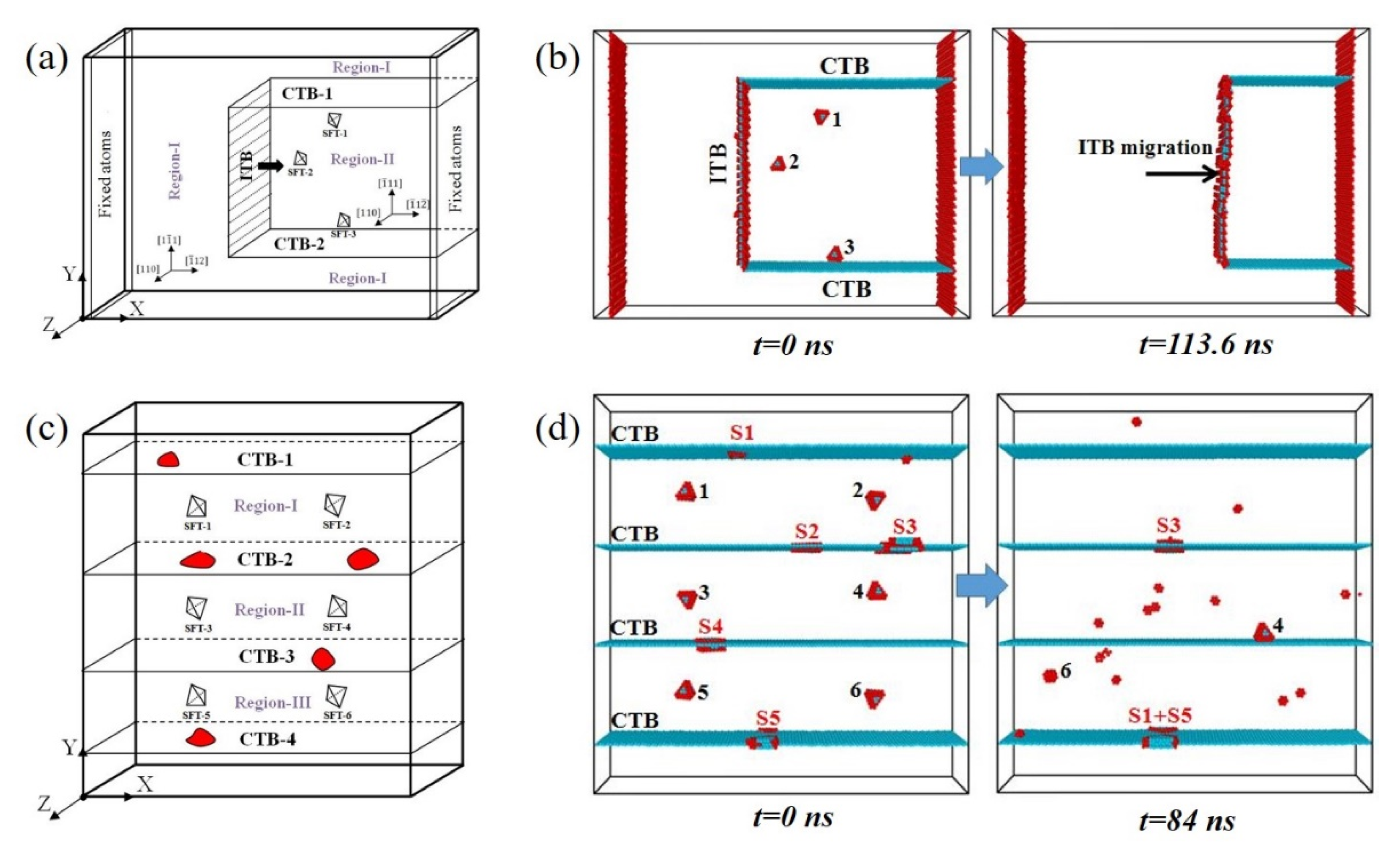
3. Dynamic Interaction between GBs and Structural Defects
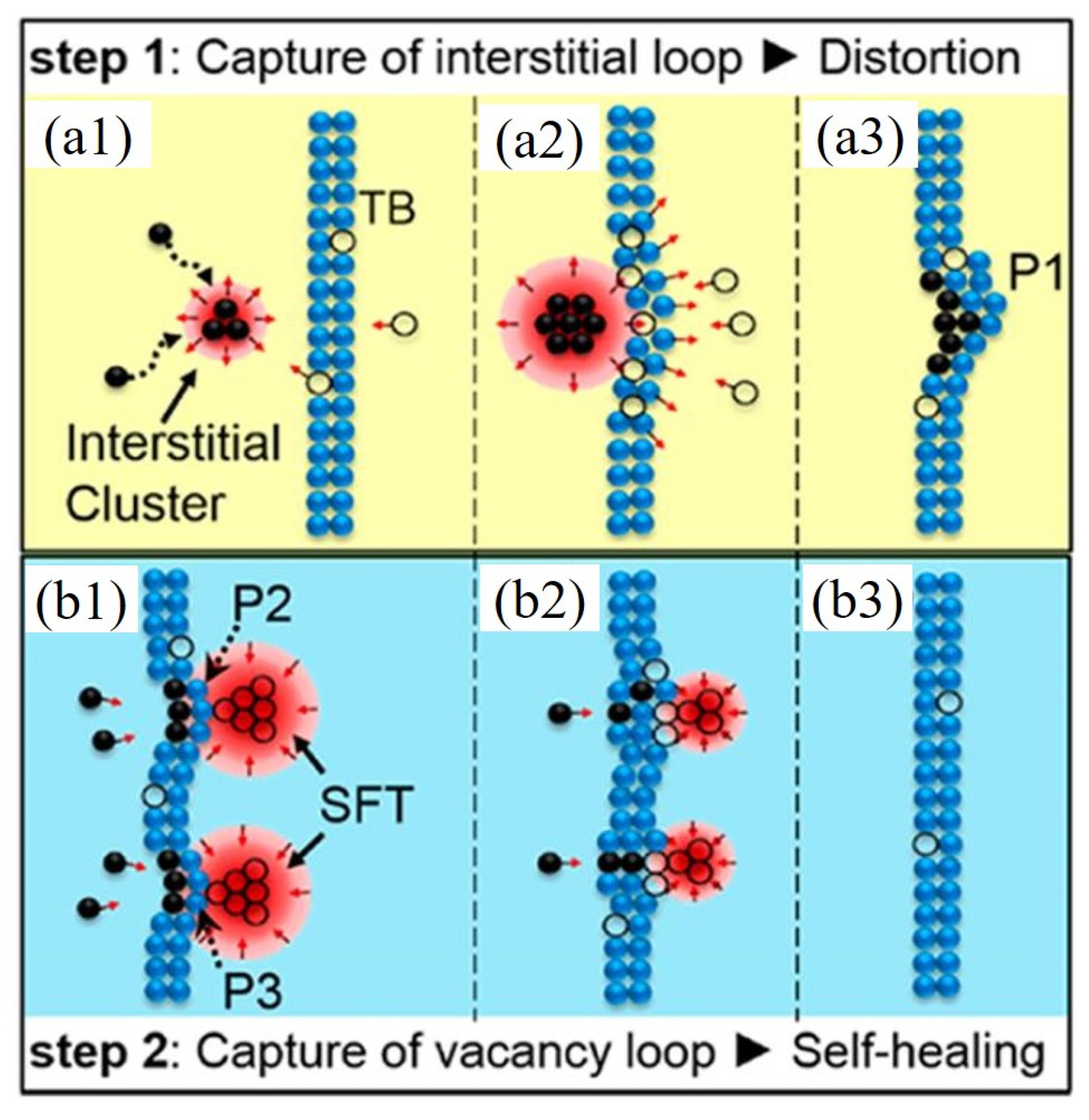
4. Self-Healing Mechanism of Nanotwinned Metals under Radiation
5. Summary and Outlook
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Hattar, K.; Chen, Y.; Shao, L.; Li, J.; Sun, C.; Yu, K.; Li, N.; Taheri, M.L.; Wang, H.; et al. Radiation damage in nanostructured materials. Prog. Mater. Sci. 2018, 96, 217–321. [Google Scholar] [CrossRef]
- Grimes, R.W.; Konings, R.J.M.; Edwards, L. Greater tolerance for nuclear materials. Nat. Mater. 2008, 7, 683–685. [Google Scholar] [CrossRef] [PubMed]
- Ackland, G. Controlling Radiation Damage. Science 2010, 327, 1587–1588. [Google Scholar] [CrossRef]
- Bai, X.M.; Voter, A.F.; Hoagland, R.G.; Nastasi, M.; Uberuaga, B.P. Efficient annealing of radiation damage near grain boundaries via interstitial emission. Science 2010, 327, 1631–1634. [Google Scholar] [CrossRef] [PubMed]
- Kuksenko, V.; Pareige, C.; Pareige, P. Intra granular precipitation and grain boundary segregation under neutron irradiation in a low purity Fe-Cr based alloy. J. Nucl. Mater. 2012, 425, 125–129. [Google Scholar] [CrossRef]
- Yu, K.Y.; Bufford, D.; Sun, C.; Liu, Y.; Wang, H.; Kirk, M.A.; Li, M.; Zhang, X. Removal of stacking-fault tetrahedra by twin boundaries in nanotwinned metals. Nat. Commun. 2013, 4, 1377. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, C.; Tieu, K.; Su, L.; Zhao, X.; Pei, L. Stacking fault tetrahedron induced plasticity in copper single crystal. Mater. Sci. Eng. A 2017, 680, 27–38. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Lu, C.; Pei, L.; Zhao, X.; Zhang, J.; Tieu, K. Evaluation of Mechanical Properties of Σ5(210)/[001] Tilt Grain Boundary with Self-Interstitial Atoms by Molecular Dynamics Simulation. J. Nanomater. 2017, 2017, 11. [Google Scholar] [CrossRef] [Green Version]
- Bacon, D.J.; Gao, F.; Osetsky, Y.N. The primary damage state in fcc, bcc and hcp metals as seen in molecular dynamics simulations. J. Nucl. Mater. 2000, 276, 1–12. [Google Scholar] [CrossRef]
- Wirth, B.D. How does radiation damage materials? Science 2007, 318, 923–924. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, M. A review of microstructure evolution in zirconium alloys during irradiation. J. Nucl. Mater. 1988, 159, 190–218. [Google Scholar] [CrossRef]
- Ukai, S.; Fujiwara, M. Perspective of ODS alloys application in nuclear environments. J. Nucl. Mater. 2002, 307–311, 749–757. [Google Scholar] [CrossRef]
- El-Genk, M.S.; Tournier, J.-M. A review of refractory metal alloys and mechanically alloyed-oxide dispersion strengthened steels for space nuclear power systems. J. Nucl. Mater. 2005, 340, 93–112. [Google Scholar] [CrossRef]
- Alinger, M.J.; Odette, G.R.; Hoelzer, D.T. On the role of alloy composition and processing parameters in nanocluster formation and dispersion strengthening in nanostuctured ferritic alloys. Acta Mater. 2009, 57, 392–406. [Google Scholar] [CrossRef]
- Hsiung, L.L.; Fluss, M.J.; Tumey, S.J.; Choi, B.W.; Serruys, Y.; Willaime, F.; Kimura, A. Formation mechanism and the role of nanoparticles in Fe-Cr ODS steels developed for radiation tolerance. Phys. Rev. B 2010, 82, 184103. [Google Scholar] [CrossRef]
- Kirk, M.; Yi, X.; Jenkins, M. Characterization of irradiation defect structures and densities by transmission electron microscopy. J. Mater. Res. 2015, 30, 1195–1201. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, E.G.; Misra, A.; Demkowicz, M.J. Interface-enabled defect reduction in He ion irradiated metallic multi-layers. JOM 2010, 62, 75–78. [Google Scholar] [CrossRef]
- Demkowicz, M.J.; Misra, A.; Caro, A. The role of interface structure in controlling high helium concentrations. Curr. Opin. Solid State Mater. Sci. 2012, 16, 101–108. [Google Scholar] [CrossRef] [Green Version]
- Heinisch, H.L.; Gao, F.; Kurtz, R.J. The effects of interfaces on radiation damage production in layered metal composites. J. Nucl. Mater. 2004, 329–333, 924–928. [Google Scholar] [CrossRef]
- Wang, J.; Kang, K.; Zhang, R.F.; Zheng, S.J.; Beyerlein, I.J.; Mara, N.A. Structure and Property of Interfaces in ARB Cu/Nb Laminated Composites. JOM 2012, 64, 1208–1217. [Google Scholar] [CrossRef]
- Farrell, K.; Maziasz, P.J.; Lee, E.H.; Mansur, L.K. Modification of radiation damage microstructure by helium. Radiat. Eff. 1983, 78, 277–295. [Google Scholar] [CrossRef]
- Zinkle, S.J.; Farrell, K. Void swelling and defect cluster formation in reactor-irradiated copper. J. Nucl. Mater. 1989, 168, 262–267. [Google Scholar] [CrossRef]
- Thorsen, P.A.; Bilde-Sørensen, J.B.; Singh, B.N. Bubble formation at grain boundaries in helium implanted copper. Scr. Mater. 2004, 51, 557–560. [Google Scholar] [CrossRef]
- Matsukawa, Y.; Zinkle, S.J. One-Dimensional Fast Migration of Vacancy Clusters in Metals. Science 2007, 318, 959–962. [Google Scholar] [CrossRef] [PubMed]
- Beyerlein, I.J.; Caro, A.; Demkowicz, M.J.; Mara, N.A.; Misra, A.; Uberuaga, B.P. Radiation damage tolerant nanomaterials. Mater. Today 2013, 16, 443–449. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Li, J. AtomEye: An efficient atomistic configuration viewer. Model. Simul. Mater. Sci. Eng. 2003, 11, 173–177. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Stukowski, A. Structure identification methods for atomistic simulations of crystalline materials. Model. Simul. Mater. Sci. Eng. 2012, 20, 045021. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K. Dislocation detection algorithm for atomistic simulations. Model. Simul. Mater. Sci. Eng. 2010, 18, 025016. [Google Scholar] [CrossRef]
- Samaras, M.; Derlet, P.M.; van Swygenhoven, H.; Victoria, M. Computer Simulation of Displacement Cascades in Nanocrystalline Ni. Phys. Rev. Lett. 2002, 88, 125505. [Google Scholar] [CrossRef] [Green Version]
- Samaras, M.; Derlet, P.M.; van Swygenhoven, H.; Victoria, M. Radiation damage near grain boundaries. Philos. Mag. 2003, 83, 3599–3607. [Google Scholar] [CrossRef]
- Samaras, M.; Derlet, P.M.; van Swygenhoven, H.; Victoria, M. Stacking fault tetrahedra formation in the neighbourhood of grain boundaries. Nucl. Instrum. Methods Phys. Res. Sect. B 2003, 202, 51–55. [Google Scholar] [CrossRef]
- Samaras, M.; Derlet, P.M.; Swygenhoven, H.V.; Victoria, M. Atomic scale modelling of the primary damage state of irra-diated fcc and bcc nanocrystalline metals. J. Nucl. Mater. 2006, 351, 47–55. [Google Scholar] [CrossRef]
- Demkowicz, M.J.; Anderoglu, O.; Zhang, X.; Misra, A. The influence of ∑3 twin boundaries on the formation of radia-tion-induced defect clusters in nanotwinned Cu. J. Mater. Res. 2011, 26, 1666–1675. [Google Scholar] [CrossRef]
- Bai, X.-M.; Vernon, L.J.; Hoagland, R.G.; Voter, A.F.; Nastasi, M.; Uberuaga, B.P. Role of atomic structure on grain bound-ary-defect interactions in Cu. Phys. Rev. B 2012, 85, 214103. [Google Scholar] [CrossRef]
- Bai, X.-M.; Uberuaga, B.P. Multi-timescale investigation of radiation damage near TiO2 rutile grain boundaries. Philos. Mag. 2012, 92, 1469–1498. [Google Scholar] [CrossRef]
- Pérez, F.J.P.; Smith, R. Modelling radiation effects at grain boundaries in bcc iron. Nucl. Instrum. Methods Phys. Res. Sect. B 1999, 153, 136–141. [Google Scholar] [CrossRef]
- Pérez-Pérez, F.J.; Smith, R. Structural changes at grain boundaries in bcc iron induced by atomic collisions. Nucl. Instrum. Methods Phys. Res. Sect. B 2000, 164–165, 487–494. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Pérez, F.J.; Smith, R. Preferential damage at symmetrical tilt grain boundaries in bcc iron. Nucl. Instrum. Methods Phys. Res. Sect. B 2001, 180, 322–328. [Google Scholar] [CrossRef]
- Van Brutzel, L.; Vincent-Aublant, E. Grain boundary influence on displacement cascades in UO2: A molecular dynamics study. J. Nucl. Mater. 2008, 377, 522–527. [Google Scholar] [CrossRef]
- van Brutzel, L.; Vincent-Aublant, E.; Delaye, J.M. Large molecular dynamics simulations of collision cascades in sin-gle-crystal, bi-crystal, and poly-crystal UO2. Nucl. Instrum. Methods Phys. Res. Sect. B 2009, 267, 3013–3016. [Google Scholar] [CrossRef]
- Moriani, A.; Cleri, F. Point-defect recombination efficiency at grain boundaries in irradiated SiC. Phys. Rev. B 2006, 73, 214113. [Google Scholar] [CrossRef]
- Gao, F.; Chen, D.; Hu, W.; Weber, W.J. Energy dissipation and defect generation in nanocrystalline silicon carbide. Phys. Rev. B 2010, 81, 184101. [Google Scholar] [CrossRef]
- Swaminathan, N.; Kamenski, P.J.; Morgan, D.; Szlufarska, I. Effects of grain size and grain boundaries on defect produc-tion in nanocrystalline 3C–SiC. Acta Mater. 2010, 58, 2843–2853. [Google Scholar] [CrossRef]
- Swaminathan, N.; Wojdyr, M.; Morgan, D.D.; Szlufarska, I. Radiation interaction with tilt grain boundaries in β-SiC. J. Appl. Phys. 2012, 111, 054918. [Google Scholar] [CrossRef]
- Sugio, K.; Shimomura, Y.; Rubia, T.D.d. Computer Simulation of Displacement Damage Cascade Formation near Sigma 5 Twist Boundary in Silver. J. Phys. Soc. Jpn. 1998, 67, 882–889. [Google Scholar] [CrossRef]
- Bai, X.M.; Uberuaga, B.P. The Influence of Grain Boundaries on Radiation-Induced Point Defect Production in Materials: A Review of Atomistic Studies. JOM 2013, 65, 360–373. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Solanki, K.N.; Gao, F.; Sun, X.; Khaleel, M.A.; Horstemeyer, M.F. Probing grain boundary sink strength at the nanoscale: Energetics and length scales of vacancy and interstitial absorption by grain boundaries in α-Fe. Phys. Rev. B 2012, 85, 064108. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Liu, W.; Xu, Y.; Liu, C.S.; Pan, B.C.; Liang, Y.; Fang, Q.F.; Chen, J.L.; Luo, G.N.; Lu, G.H.; et al. Radiation resistance of nano-crystalline iron: Coupling of the fundamental segregation process and the annihilation of interstitials and vacancies near the grain boundaries. Acta Mater. 2016, 109, 115–127. [Google Scholar] [CrossRef]
- Martinez, E.; Uberuaga, B.P. Mobility and coalescence of stacking fault tetrahedra in Cu. Sci. Rep. 2015, 5, 9084. [Google Scholar] [CrossRef] [Green Version]
- Rose, M.; Balogh, A.G.; Hahn, H. Instability of irradiation induced defects in nanostructured materials. Nucl. Instrum. Methods Phys. Res. Sect. B 1997, 127–128, 119–122. [Google Scholar] [CrossRef]
- Chimi, Y.; Iwase, A.; Ishikawa, N.; Kobiyama, M.; Inami, T.; Okuda, S. Accumulation and recovery of defects in ion-irradiated nanocrystalline gold. J. Nucl. Mater. 2001, 297, 355–357. [Google Scholar] [CrossRef]
- Shen, T.D.; Feng, S.; Tang, M.; Valdez, J.A.; Wang, Y.; Sickafus, K.E. Enhanced radiation tolerance in nanocrystalline MgGa2O4. Appl. Phys. Lett. 2007, 90, 263115. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Demkowicz, M.J.; Misra, A.; Uberuaga, B.P. Defect-interface interactions. Prog. Mater. Sci. 2015, 74, 125–210. [Google Scholar] [CrossRef] [Green Version]
- Borovikov, V.; Tang, X.Z.; Perez, D.; Bai, X.M.; Uberuaga, B.P.; Voter, A.F. Coupled motion of grain boundaries in bcc tungsten as a possible radiation-damage healing mechanism under fusion reactor conditions. Nucl. Fusion 2013, 53, 063001. [Google Scholar] [CrossRef]
- Martínez, E.; Uberuaga, B.P.; Beyerlein, I.J. Interaction of small mobile stacking fault tetrahedra with free surfaces, dislo-cations, and interfaces in Cu and Cu-Nb. Phys. Rev. B 2016, 93, 054105. [Google Scholar] [CrossRef] [Green Version]
- Mansur, L.K. Theory and experimental background on dimensional changes in irradiated alloys. J. Nucl. Mater. 1994, 216, 97–123. [Google Scholar] [CrossRef]
- Abe, H.; Sekimura, N.; Tadokoro, T.J.M.T. Stability and mobility of interstitial-type defect clusters generated from displacement cascades in copper and gold by in-situ transmission electron microscopy. Mater. Trans. 2005, 46, 433–439. [Google Scholar] [CrossRef] [Green Version]
- Merkle, K.L.; Thompson, L.J.; Phillipp, F. In-Situ HREM Studies of Grain Boundary Migration. Interface Sci. 2004, 12, 277–292. [Google Scholar] [CrossRef]
- Molodov, K.D.; Molodov, D.A. Grain boundary mediated plasticity: On the evaluation of grain boundary migration—Shear coupling. Acta Mater. 2018, 153, 336–353. [Google Scholar] [CrossRef]
- Rupert, T.J.; Gianola, D.S.; Gan, Y.; Hemker, K.J. Experimental observations of stress-driven grain boundary migration. Science 2009, 326, 1686–1690. [Google Scholar] [CrossRef] [Green Version]
- Farkas, D.; Frøseth, A.; van Swygenhoven, H. Grain boundary migration during room temperature deformation of nanocrystalline Ni. Scr. Mater. 2006, 55, 695–698. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, C.; Shibuta, Y. Shear response of grain boundaries with metastable structures by molecular dynamics sim-ulations. Model. Simul. Mater. Sci. Eng. 2018, 26, 035008. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, C.; Michal, G.; Tieu, K.; Zhao, X.; Deng, G. Influence of temperature and local structure on the shear-coupled grain boundary migration. Phys. Status Solidi B 2017, 254, 1600477. [Google Scholar] [CrossRef]
- Jin, M.; Cao, P.; Yip, S.; Short, M.P. Radiation damage reduction by grain-boundary biased defect migration in nanocrystalline Cu. Acta Mater. 2018, 155, 410–417. [Google Scholar] [CrossRef]
- Molodov, D.A.; Gorkaya, T.; Gottstein, G. Mechanically driven migration of <100> tilt grain boundaries in Al-Bicrystals. In Materials Science Forum; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2007; pp. 927–932. [Google Scholar]
- Mompiou, F.; Caillard, D.; Legros, M. Grain boundary shear-migration coupling—I. In situ TEM straining experiments in Al polycrystals. Acta Mater. 2009, 57, 2198–2209. [Google Scholar] [CrossRef]
- Yu, K.Y.; Bufford, D.; Khatkhatay, F.; Wang, H.; Kirk, M.A.; Zhang, X. In situ studies of irradiation-induced twin boundary migration in nanotwinned Ag. Scr. Mater. 2013, 69, 385–388. [Google Scholar] [CrossRef]
- Cahn, J.W.; Mishin, Y.; Suzuki, A. Coupling grain boundary motion to shear deformation. Acta Mater. 2006, 54, 4953–4975. [Google Scholar] [CrossRef]
- Zhang, H.; Du, D.; Srolovitz, D.J. Effects of boundary inclination and boundary type on shear-driven grain boundary migration. Philos. Mag. 2008, 88, 243–256. [Google Scholar] [CrossRef]
- Zhang, H.; Srolovitz, D.J.; Douglas, J.F.; Warren, J.A. Atomic motion during the migration of general [0 0 1] tilt grain boundaries in Ni. Acta Mater. 2007, 55, 4527–4533. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, C.; Tieu, K.; Shibuta, Y. Dynamic interaction between grain boundary and stacking fault tetrahedron. Scr. Mater. 2018, 144, 78–83. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Shibuta, Y.; Lu, C.; Huang, X. Interaction between nano-voids and migrating grain boundary by molecular dynamics simulation. Acta Mater. 2019, 173, 206–224. [Google Scholar] [CrossRef]
- Lu, L.; Shen, Y.; Chen, X.; Qian, L.; Lu, K. Ultrahigh Strength and High Electrical Conductivity in Copper. Science 2004, 304, 422–426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, L.; Chen, X.; Huang, X.; Lu, K. Revealing the maximum strength in nanotwinned copper. Science 2009, 323, 607–610. [Google Scholar] [CrossRef]
- Zhang, X.; Misra, A.; Wang, H.; Nastasi, M.; Embury, J.D.; Mitchell, T.E.; Hoagland, R.G.; Hirth, J.P. Na-noscale-twirming-induced strengthening in austenitic stainless steel thin films. Appl. Phys. Lett. 2004, 84, 1096–1098. [Google Scholar] [CrossRef]
- Han, W.Z.; Demkowicz, M.J.; Fu, E.G.; Wang, Y.Q.; Misra, A. Effect of grain boundary character on sink efficiency. Acta Mater. 2012, 60, 6341–6351. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Yu, K.Y.; Wang, H.; Kirk, M.A.; Li, M.; Zhang, X. In situ studies on radiation tolerance of nanotwinned Cu. Acta Mater. 2016, 111, 148–156. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Yu, K.Y.; Liu, Y.; Shao, S.; Wang, H.; Kirk, M.A.; Wang, J.; Zhang, X. Damage-tolerant nanotwinned metals with nanovoids under radiation environments. Nat. Commun. 2015, 6, 7036. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Yu, K.Y.; Chen, Y.; Song, M.; Wang, H.; Kirk, M.A.; Li, M.; Zhang, X. In Situ Study of Defect Migration Kinetics and Self-Healing of Twin Boundaries in Heavy Ion Irradiated Nanotwinned Metals. Nano Lett. 2015, 15, 2922–2927. [Google Scholar] [CrossRef] [PubMed]
- Jiao, S.; Kulkarni, Y. Radiation tolerance of nanotwinned metals—An atomistic perspective. Comput. Mater. Sci. 2018, 142, 290–296. [Google Scholar] [CrossRef]
- Wu, L.; Yu, W.; Hu, S.; Shen, S. Radiation response of nanotwinned Cu under multiple-collision cascades. J. Nucl. Mater. 2018, 505, 183–192. [Google Scholar] [CrossRef]
- Pei, L.; Lu, C.; Zhao, X.; Zhang, L.; Cheng, K.; Michal, G.; Tieu, K. Brittle versus ductile behaviour of nanotwinned copper: A molecular dynamics study. Acta Mater. 2015, 89, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Lu, C.; Tieu, A.K.; Pei, L.; Zhang, L.; Cheng, K.; Huang, M. Strengthening mechanisms and dislocation processes in <111> textured nanotwinned copper. Mater. Sci. Eng. A 2016, 676, 474–486. [Google Scholar] [CrossRef]
- Zhao, X.; Lu, C.; Tieu, A.K.; Pei, L.Q.; Zhang, L.; Su, L.H.; Zhan, L.H. Deformation mechanisms in nanotwinned copper by molecular dynamics simulation. Mater. Sci. Eng. A 2017, 687, 343–351. [Google Scholar] [CrossRef]
- Jin, Z.H.; Gumbsch, P.; Albe, K.; Ma, E.; Lu, K.; Gleiter, H.; Hahn, H. Interactions between non-screw lattice dislocations and coherent twin boundaries in face-centered cubic metals. Acta Mater. 2008, 56, 1126–1135. [Google Scholar] [CrossRef]
- Wang, Y.M.; Sansoz, F.; LaGrange, T.; Ott, R.T.; Marian, J.; Barbee, T.W.; Hamza, A.V. Defective twin boundaries in nanotwinned metals. Nat. Mater. 2013, 12, 697–702. [Google Scholar] [CrossRef] [PubMed]
- Greer, J.R. Nanotwinned metals: It’s all about imperfections. Nat. Mater. 2013, 12, 689–690. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Xu, D.; Tu, K.N.; Cai, Y.; Wang, N.; Dixit, P.; Pang, J.H.L.; Miao, J.M. Structure and migration of (112) step on (111) twin boundaries in nanocrystalline copper. J. Appl. Phys. 2008, 104, 113717. [Google Scholar] [CrossRef]
- Zhang, L.; Shibuta, Y.; Lu, C.; Huang, X. Atomistic Simulation of the Interaction Between Point Defects and Twin Boundary. Phys. Status Solidi B 2018, 255, 1800228. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L. Understanding the Radiation Resistance Mechanisms of Nanocrystalline Metals from Atomistic Simulation. Metals 2021, 11, 1875. https://doi.org/10.3390/met11111875
Zhang L. Understanding the Radiation Resistance Mechanisms of Nanocrystalline Metals from Atomistic Simulation. Metals. 2021; 11(11):1875. https://doi.org/10.3390/met11111875
Chicago/Turabian StyleZhang, Liang. 2021. "Understanding the Radiation Resistance Mechanisms of Nanocrystalline Metals from Atomistic Simulation" Metals 11, no. 11: 1875. https://doi.org/10.3390/met11111875