Practical Approbation of Thermodynamic Criteria for the Consolidation of Bimetallic and Functionally Gradient Materials
Abstract
:1. Introduction
2. Theoretical Foundations of the Research Method
3. Materials and Methods
4. Results and Discussion
4.1. Experimental Results
4.2. Calculation of the Consolidation Criteria
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miyamoto, Y. Functionally Graded Materials Design; Processing and Applications Springer Science: New York, NY, USA, 1999. [Google Scholar]
- Liyanage, T.; Kilbourne, J.; Gerlich, A.P.; North, T.H. Joint Formation in Dissimilar Al Alloy/Steel and Mg Alloy/Steel Friction Stir Spot Welds. Sci. Technol. Weld. Join 2009, 14, 500–508. [Google Scholar] [CrossRef]
- Saleh, B.; Jiang, J.; Fathi, R.; Al-hababi, T.; Xu, Q.; Wang, L.; Song, D.; Ma, A. 30 Years of functionally graded materials: An overview of manufacturing methods. Appl. Future Chall. Compos. Part B Eng. 2020, 201, 108376. [Google Scholar] [CrossRef]
- Yang, J.; Chen, J.; Zhao, W.; Zhang, P.; Yu, Z.; Li, Y.; Zeng, Z.; Zhou, N. Diode Laser Welding/Brazing of Aluminum Alloy to Steel Using a Nickel Coating. Appl. Sci. 2018, 8, 922. [Google Scholar] [CrossRef] [Green Version]
- Olson, D.L.; Siewert, T.A.; Liu, S.; Edwards, G.R. ASM Handbook: Volume 6. Welding, Brazing, and Soldering, 10th ed.; ASM International: Novelty, OH, USA, 1993. [Google Scholar]
- Trykov, Y.P.; Shmorgun, V.G.; Pronichev, D.V. Methods for Studying the Structure and Properties of the Transition Zones of Explosion-Welded Metal; Politekhnik: Volgograd, Russia, 2002. [Google Scholar]
- Mehrpouya, M.; Gisario, A.; Barletta, M.; Natali, S.; Veniali, F. Dissimilar Laser Welding of NiTi Wires. Lasers Manuf. Mater. Process 2019, 6, 99–112. [Google Scholar] [CrossRef]
- Tanaka, Y.; Kajihara, M. Kinetics of Isothermal Reactive Diffusion between Solid Fe and Liquid Al. J. Mater. Sci. 2010, 45, 5676–5684. [Google Scholar] [CrossRef]
- Shishkovsky, I.V.; Nazarov, A.P.; Kotoban, D.V.; Kakovkina, N.G. Comparison of Additive Technologies For Gradient Aerospace Part Fabrication From Nickel Based Superalloys. In Superalloys; Aliofkhazraei, M., Ed.; IntechOpen: London, UK, 2015; pp. 221–245. [Google Scholar]
- Shishkovsky, I.; Missemer, F.; Smurov, I. Direct metal deposition of functional graded structures in Ti-Al system. Phys. Procedia 2012, 39, 382–391. [Google Scholar] [CrossRef] [Green Version]
- Shishkovsky, I.; Missemer, F.; Kakovkina, N.; Smurov, I. Intermetallics synthesis in the Fe–Al system via layer-by layer 3D laser cladding. Crystals 2013, 3, 517–529. [Google Scholar] [CrossRef] [Green Version]
- Balzani, C.; Wagner, W.; Wilckens, D.; Degenhardt, R.; Busing, S.; Reimerdes, H.-G. Adhesive Joints in Composite Laminates—A Combined Numerical/Experimental Estimate of Critical Energy Release Rates. Int. J. Adhes. Adhes. 2012, 32, 23–38. [Google Scholar] [CrossRef] [Green Version]
- Oyane, M.; Sato, T.; Okimoto, K.; Shima, S. Criteria for ductile fracture and their applications. J. Mech. Work. Technol. 1980, 4, 65–81. [Google Scholar] [CrossRef]
- Clift, S.E.; Hartley, P.; Sturgess, C.E.N.; Rowe, G.W. Fracture prediction in plastic deformation processes. Int. J. Mech. Sci. 1990, 32, 1–17. [Google Scholar] [CrossRef]
- Ko, Y.; Lee, J.; Huh, H.; Kim, H.; Park, S. Prediction of fracture in hub-hole expanding process using a new ductile fracture criterion. J. Mater. Process. Technol. 2007, 187–188, 358–362. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H.; Lim, S.; Pack, K. New ductile fracture criterion for prediction of fracture forming limit diagrams of sheet metals. Int. J. Solids Struct. 2012, 49, 3605–3615. [Google Scholar] [CrossRef] [Green Version]
- Liebowitz, H. Fracture-An Advanced Treatise, Vol. II, Mathematical Fundamentals; Pergamon Press: Oxford, UK, 1968. [Google Scholar]
- Kinloch, A.; Wang, Y.; Williams, J.; Yayla, P. The mixed-mode delamination of fibre composite materials. Compos. Sci. Technol. 1993, 47, 225–237. [Google Scholar] [CrossRef]
- Reeder, J.R. An Evaluation of Mixed-Mode Delamination Failure Criteria; Technical Memorandum TM-1992-104210; NASA, Langley Research Center: Hampton, VA, USA, 1992. [Google Scholar]
- Balzani, C.; Wagner, W. An interface element for the simulation of delamination in unidirectional fiber-reinforced composite laminates. Eng. Fract. Mech. 2008, 75, 2597–2615. [Google Scholar] [CrossRef]
- Rose, J.H.; Ferrante, J.; Smith, J.R. Universal Binding Energy Curves for Metals and Bimetallic Interfaces. Phys. Rev. Lett. 1981, 47, 675–678. [Google Scholar] [CrossRef]
- Khaimovich, A.I.; Abulhanov, S.R. Equations of state of plastically deformed polycrystalline medium considering plastic deformation thermal effect. ARPN J. Eng. Appl. Sci. 2014, 9, 2867–2875. [Google Scholar]
- Landau, L.D.; Lifshits, Е.М. Statistical Physics. Part 1. In Theoretical Physics; Fizmatlit: Moscow, Russia, 2005. [Google Scholar]
- Moracheskij, A.G.; Sladkov, I.B. Thermodynamic Calculations in Metallurgy; Metallurgiya: Moscow, Russia, 1985. [Google Scholar]
- Leitner, J.; Voňka, P.; Sedmidubský, D.; Svoboda, P. Application of Neumann–Kopp rule for the estimation of heat capacity of mixed oxides. Thermochim. Acta 2010, 497, 7–13. [Google Scholar] [CrossRef]
- Voight, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Wied. Ann. 1889, 38, 573–587. [Google Scholar] [CrossRef] [Green Version]
- Karch, C. Micromechanical Analysis of Thermal Expansion Coefficients Modeling and Numerical. Simul. Mater. Sci. 2014, 4, 104–118. [Google Scholar]
- Kerner, E.H. The Elastic and Thermo-elastic Properties of Composite Media. Proc. Phys. Soc. B 1956, 69, 808. [Google Scholar] [CrossRef]
- Wakashima, K.; Tsukamoto, H. A Unified Micromechanical Approach toward Thermomechanical Tailoring of Metal Matrix Composites. ISIJ Int. 1992, 32, 883–892. [Google Scholar] [CrossRef] [Green Version]
- Nigmatulin, R.I. Fundamentals of Mechanics of Heterogeneous Media; Nauka: Moscow, Russia, 1978. [Google Scholar]
- Lupis, К. Chemical Thermodynamics of Materials; Metallurgia: Moscow, Russia, 1983. [Google Scholar]
- Truesdell, C.; Toupin, R. The Classical Field Theories. In Principles of Classical Mechanics and Field Theory. Encyclopedia of Physics; Flügge, S., Ed.; Springer: Berlin, Germany, 1960; Volume 3. [Google Scholar] [CrossRef]
- Khaimovich, A.; Erisov, Y.; Smelov, V.; Agapovichev, A.; Petrov, I.; Razhivin, V.; Bobrovskij, I.; Kokareva, V.; Kuzin, A. Interface Quality Indices of Al–10Si–Mg Aluminum Alloy and Cr18–Ni10–Ti Stainless-Steel Bimetal Fabricated via Selective Laser Melting. Metals 2021, 11, 172. [Google Scholar] [CrossRef]
- Rivling, V.G.; Raynor, G.V. Critical evaluation of constitution of chromium-iron-nickel system. Int. Met. Rev. 1980, 1, 21–38. [Google Scholar]
- Bannykh, О.А.; Budberg, P.B.; Alisova, S.P. State Diagrams of Binary and Multicomponent Systems Based on Iron; Bannykh, О.А., Dritsa, М.Е., Eds.; Metallurgy: Moscow, Russia, 1986. [Google Scholar]
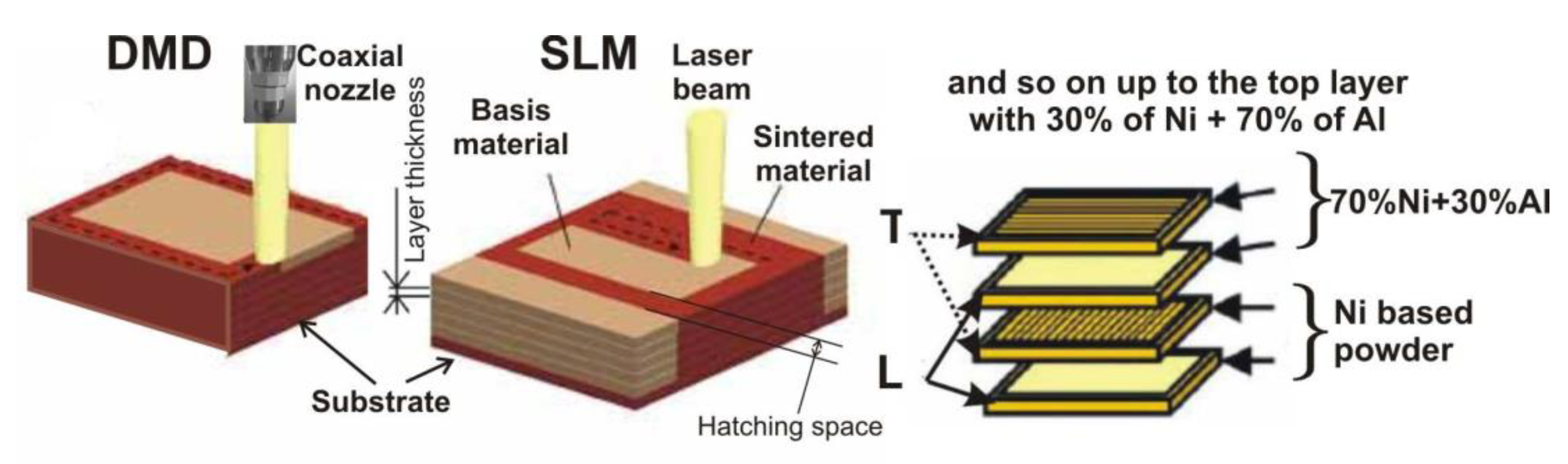



| Mass Fraction of Elements. % | ||||
|---|---|---|---|---|
| Al | Si | C | O | Mg |
| 81.83 | 10.73 | 3.35 | 2.41 | 1.30 |
| Mass Fraction of Elements. % | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| С | Mn | Р | S | Si | Cr | Ni | Mo | Ti | Fe |
| <0.07 | <2.0 | <0.045 | <0.03 | <1.0 | 16.0–18.0 | 10.0–14.0 | 2.0–3.0 | <0.5 | Other |
| Mode No. | Laser Power P, W | Scanning Speed V, mm/s | Scan Step, mm | Layer Thickness h, mm | Energy Density E, J/mm3 |
|---|---|---|---|---|---|
| 1 | 350 | 450 | 0.19 | 0.05 | 82 |
| 2 | 350 | 350 | 0.19 | 0.05 | 105 |
| 3 | 350 | 250 | 0.19 | 0.05 | 147 |
| 4 | 350 | 150 | 0.19 | 0.05 | 246 |
| 5 | 350 | 50 | 0.19 | 0.05 | 737 |
| Step, μm | Content of Elements, wt% | ||||
|---|---|---|---|---|---|
| Fe | Cr | Ni | Al | Si | |
| SLM scanning mode 1 | |||||
| 20 | 57.09 | 14.11 | 8.27 | 18.34 | 2.18 |
| 0 | 37.39 | 9.54 | 5.33 | 43.5 | 4.25 |
| −20 | 11.43 | 2.1 | 0 | 80.76 | 5.71 |
| SLM scanning mode 2 | |||||
| 20 | 60.08 | 15.16 | 8.66 | 14.19 | 1.91 |
| 0 | 37.53 | 9.23 | 5.5 | 43.85 | 3.89 |
| −20 | 4.86 | 0 | 0 | 87.61 | 7.53 |
| SLM scanning mode 3 | |||||
| 20 | 61.87 | 15.25 | 8.45 | 12.78 | 1.65 |
| 0 | 28.72 | 6.7 | 3.25 | 55.58 | 5.75 |
| −20 | 5.84 | 1.51 | 0.72 | 84.83 | 7.1 |
| SLM scanning mode 4 | |||||
| 20 | 55.58 | 13.93 | 8.54 | 19.73 | 2.23 |
| 0 | 47.39 | 11.34 | 5.73 | 31.33 | 4.21 |
| −20 | 37.09 | 9.72 | 5.15 | 43.74 | 4.31 |
| SLM scanning mode 5 | |||||
| 20 | 69.38 | 16.75 | 10.12 | 2.86 | 0.89 |
| 0 | 67.35 | 15.79 | 10.21 | 5.91 | 0.74 |
| −20 | 62.77 | 14.91 | 10.1 | 10.56 | 1.67 |
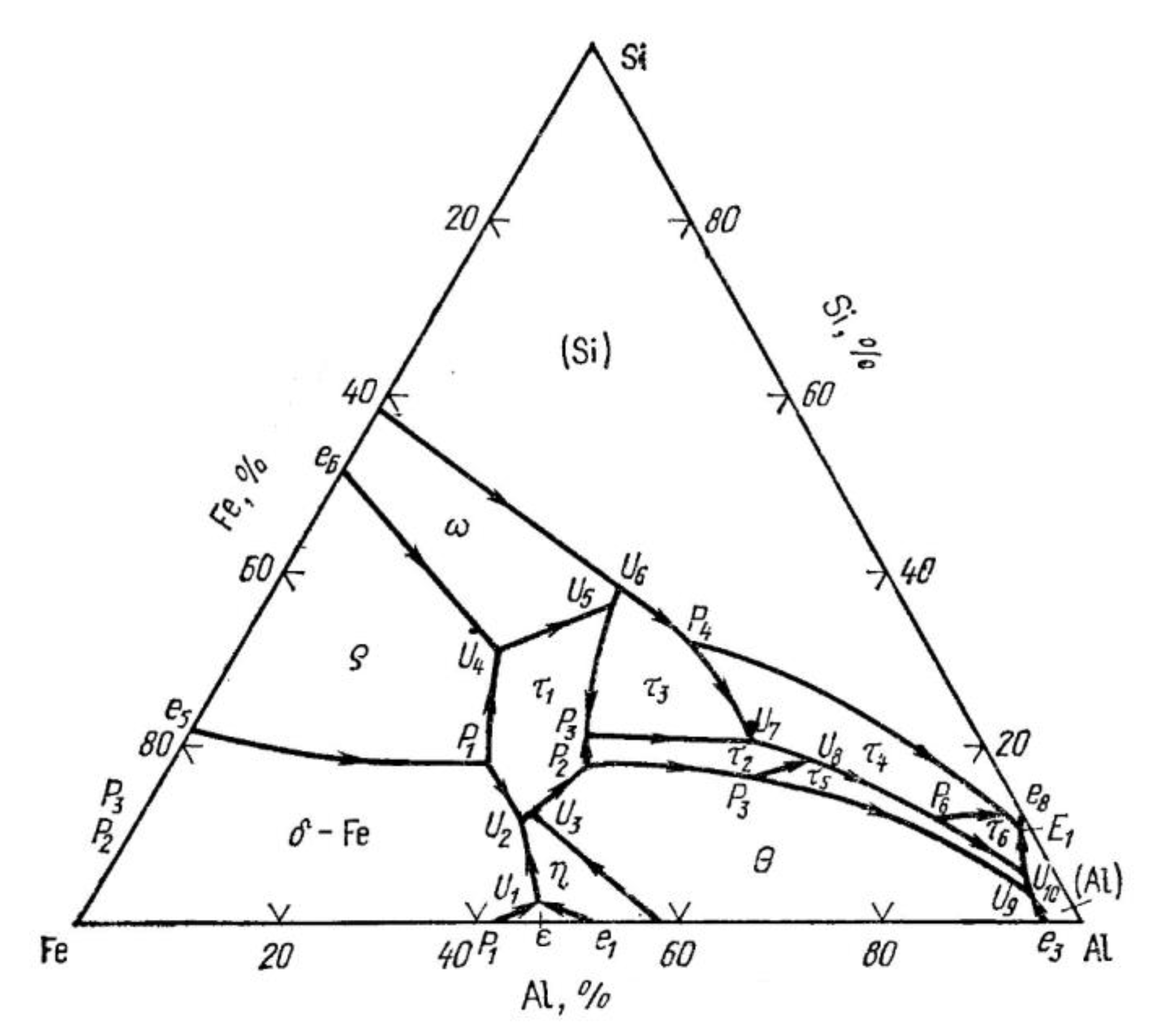
| Place of Phase Separation | Phase Designation and Its Formula | Melting Temperature Range, °C | Invariant Reaction (See Figure 3) |
|---|---|---|---|
| From the side of 316L | 935–940 | ||
| From the side of AlSi10Mg | 615–620 | ||
| <577 |
| Element | Sum of Element Content in All Phases, wt% | Content of Elements for Each SLM Scanning Mode, wt% | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Fe | 57.09 | 60.08 | 61.87 | 55.58 | 69.38 | |
| Al | 18.34 | 14.19 | 12.78 | 19.73 | 2.86 | |
| Si | 2.18 | 1.91 | 1.65 | 2.23 | 0.89 | |
| Cr | 14.11 | 15.16 | 15.25 | 13.93 | 16.75 | |
| Ni | 8.27 | 8.66 | 8.45 | 8.54 | 10.12 | |
| Element | Sum of Element Content in All Phases, wt% | Content of Elements for Each SLM Scanning Mode, wt% | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Fe | 57.09 | 60.08 | 61.87 | 55.58 | 69.38 | |
| Al | 18.34 | 14.19 | 12.78 | 19.73 | 2.86 | |
| Si | 2.18 | 1.91 | 1.65 | 2.23 | 0.89 | |
| Cr | 14.11 | 15.16 | 15.25 | 13.93 | 16.75 | |
| Ni | 8.27 | 8.66 | 8.45 | 8.54 | 10.12 | |
| Location | Phase Content, wt% | |||||
|---|---|---|---|---|---|---|
| γ, α + γ | Sum | |||||
| SLM scanning mode 1 | ||||||
| From 316L side | 11.85 | - | - | 67.57 | 15.19 | 94.61 |
| From AlSi10Mg side | - | 18.72 | 14.77 | - | 63.00 | 96.49 |
| SLM scanning mode 2 | ||||||
| From 316L side | 10.38 | - | - | 70.75 | 11.40 | 92.53 |
| From AlSi10Mg side | - | 6.07 | 8.75 | - | 82.00 | 96.82 |
| SLM scanning mode 3 | ||||||
| From 316L side | 8.97 | - | - | 80.87 | 10.02 | 99.86 |
| From AlSi10Mg side | - | 5.87 | 9.37 | 1.25 | 72.00 | 91.49 |
| SLM scanning mode 4 | ||||||
| From 316L side | 11.73 | - | - | 69.77 | 18.00 | 99.5 |
| From AlSi10Mg side | - | 17.75 | 10.06 | 38.91 | 26.62 | 93.34 |
| SLM scanning mode 5 | ||||||
| From 316L side | 4.84 | - | - | 89.87 | 1.57 | 96.28 |
| From AlSi10Mg side | - | 10.44 | - | 82.52 | 5.76 | 98.72 |
| Location | |||||
|---|---|---|---|---|---|
| SLM scanning mode 1 | |||||
| From 316L side | 73.213 | 76.344 | 0.959 | 0.993 | 0.604 |
| From AlSi10Mg side | 32.928 | 35.947 | 0.916 | ||
| SLM scanning mode 2 | |||||
| From 316L side | 85.662 | 88.974 | 0.963 | 0.973 | 0.548 |
| From AlSi10Mg side | 26.942 | 29.462 | 0.914 | ||
| SLM scanning mode 3 | |||||
| From 316L side | 96.090 | 99.520 | 0.966 | 0.969 | 0.518 |
| From AlSi10Mg side | 27.657 | 30.223 | 0.915 | ||
| SLM scanning mode 4 | |||||
| From 316L side | 67.969 | 71.001 | 0.957 | 1.088 | 0.724 |
| From AlSi10Mg side | 55.259 | 59.076 | 0.935 | ||
| SLM scanning mode 5 | |||||
| From 316L side | 190.227 | 194.936 | 0.976 | 1.018 | 0.701 |
| From AlSi10Mg side | 135.418 | 140.433 | 0.964 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khaimovich, A.; Erisov, Y.; Agapovichev, A.; Shishkovsky, I.; Smelov, V.; Razzhivin, V. Practical Approbation of Thermodynamic Criteria for the Consolidation of Bimetallic and Functionally Gradient Materials. Metals 2021, 11, 1960. https://doi.org/10.3390/met11121960
Khaimovich A, Erisov Y, Agapovichev A, Shishkovsky I, Smelov V, Razzhivin V. Practical Approbation of Thermodynamic Criteria for the Consolidation of Bimetallic and Functionally Gradient Materials. Metals. 2021; 11(12):1960. https://doi.org/10.3390/met11121960
Chicago/Turabian StyleKhaimovich, Alexander, Yaroslav Erisov, Anton Agapovichev, Igor Shishkovsky, Vitaliy Smelov, and Vasilii Razzhivin. 2021. "Practical Approbation of Thermodynamic Criteria for the Consolidation of Bimetallic and Functionally Gradient Materials" Metals 11, no. 12: 1960. https://doi.org/10.3390/met11121960
APA StyleKhaimovich, A., Erisov, Y., Agapovichev, A., Shishkovsky, I., Smelov, V., & Razzhivin, V. (2021). Practical Approbation of Thermodynamic Criteria for the Consolidation of Bimetallic and Functionally Gradient Materials. Metals, 11(12), 1960. https://doi.org/10.3390/met11121960









