First-Principles Calculations of Thermal and Electrical Transport Properties of bcc and fcc Dilute Fe–X (X = Al, Co, Cr, Mn, Mo, Nb, Ni, Ti, V, and W) Binary Alloys
Abstract
:1. Introduction
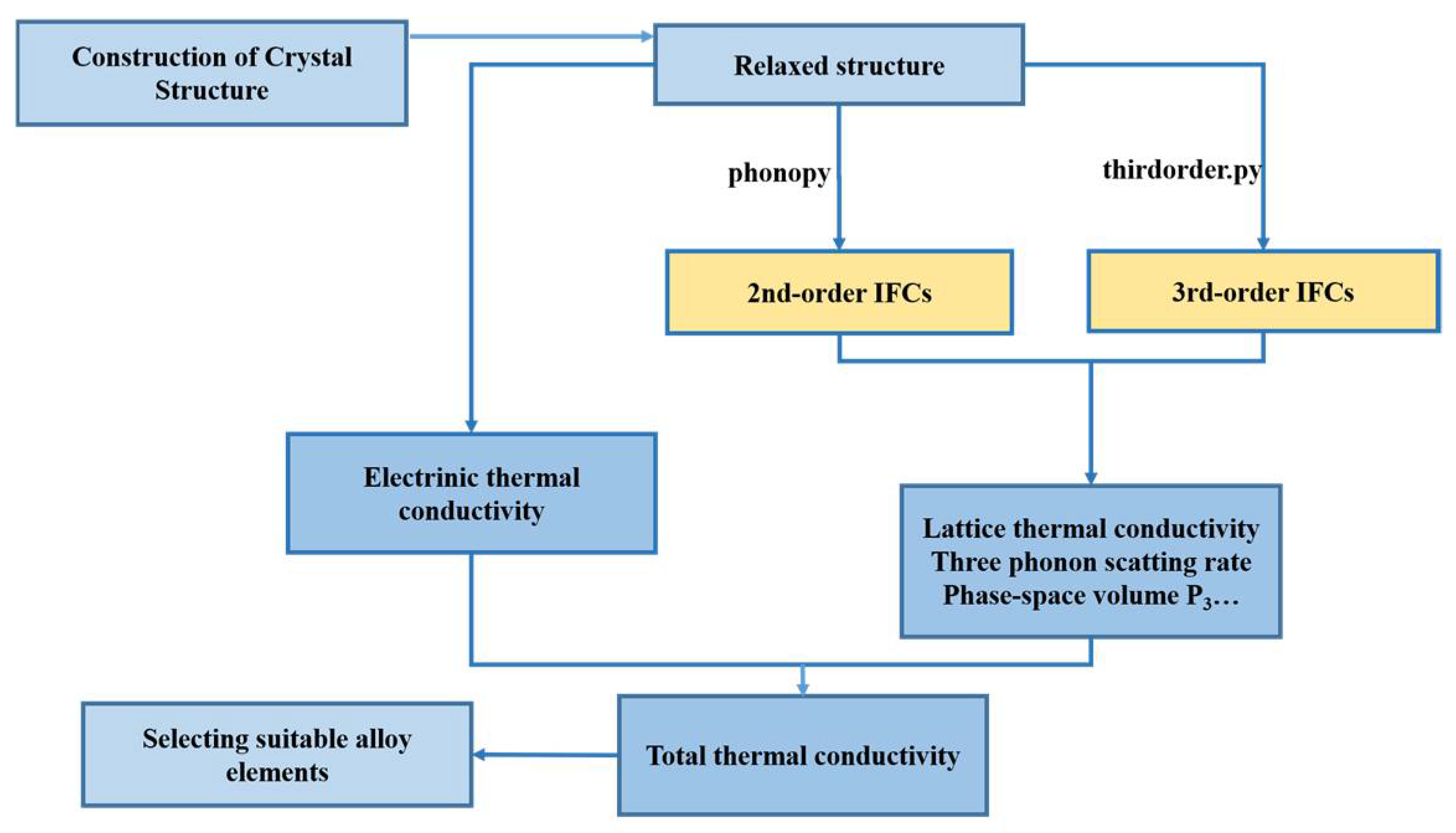
2. Computational Methodology
3. Results and Discussion
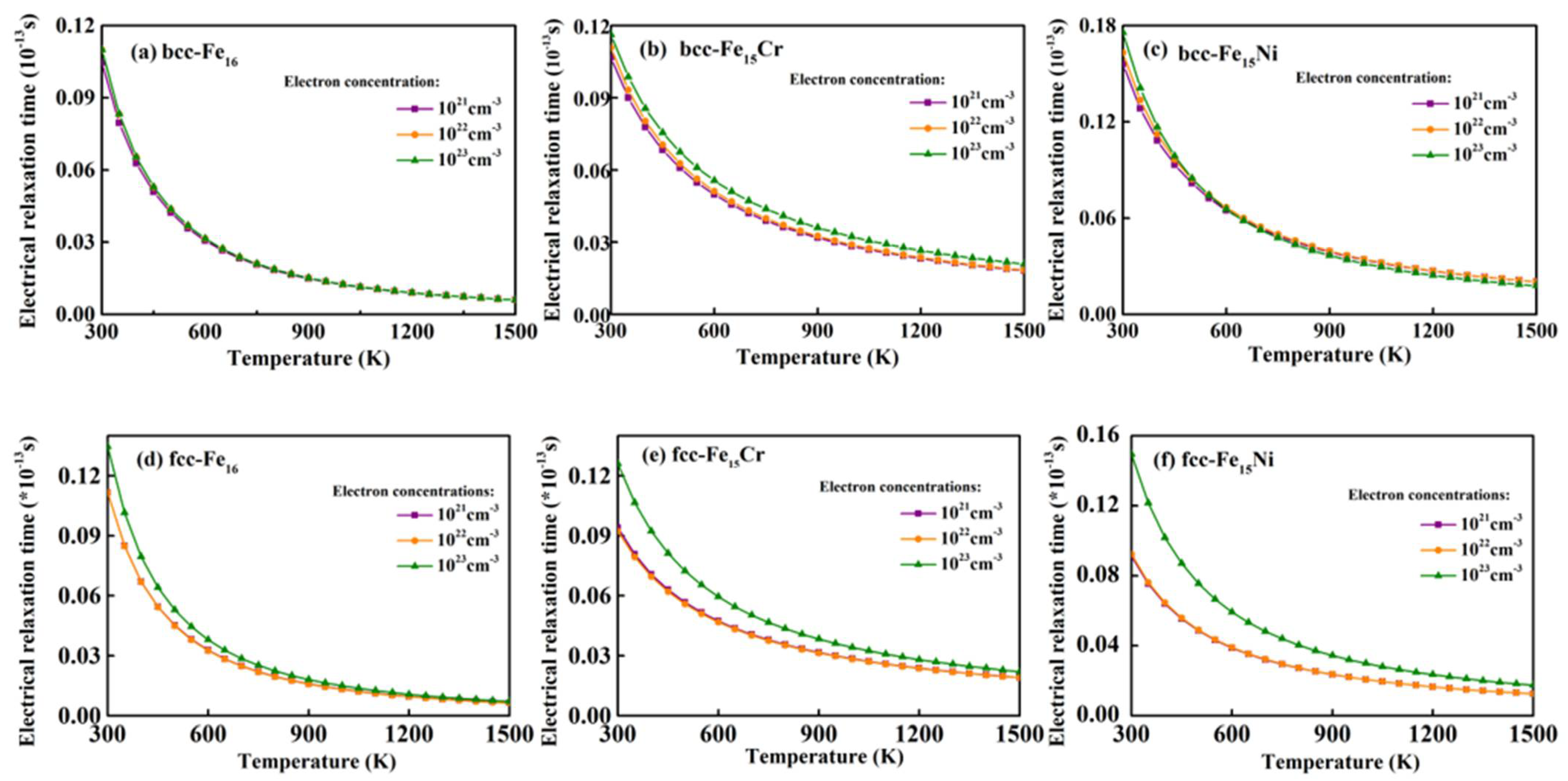
3.1. Electron Relaxation Time
3.2. Electrical Thermal Conductivity
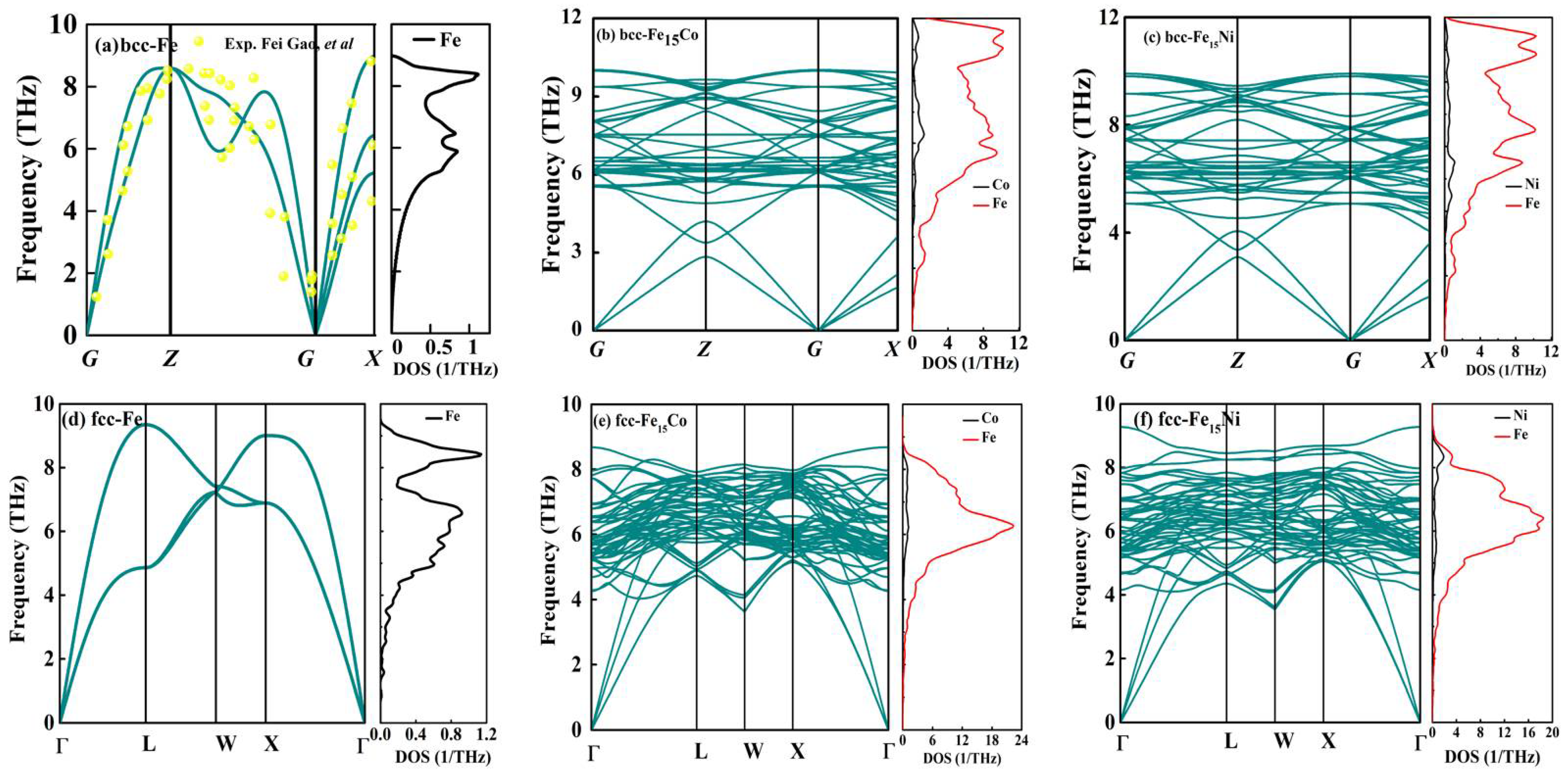
3.3. Phonon Spectral Analysis
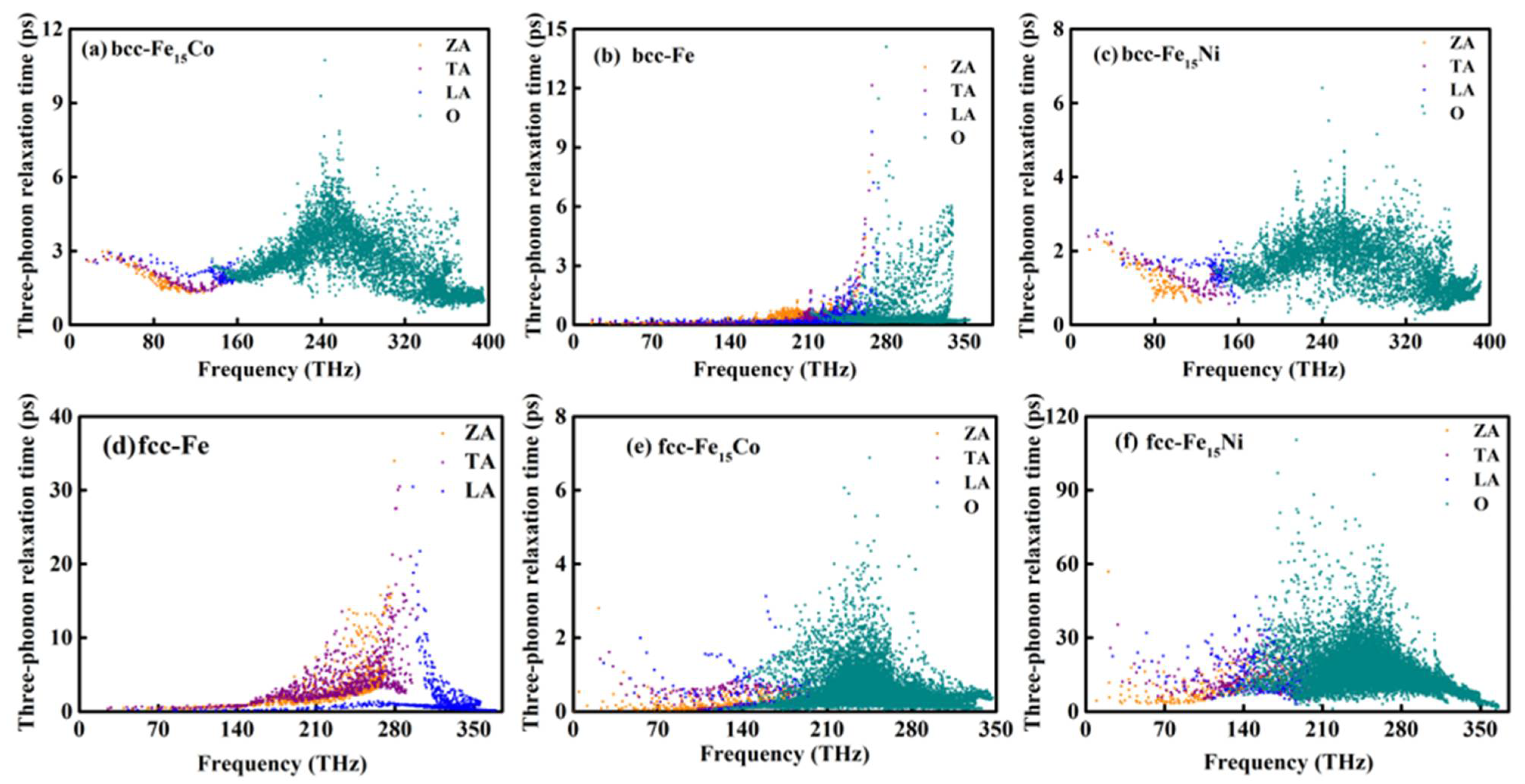
3.4. Phonon-Relaxation Time
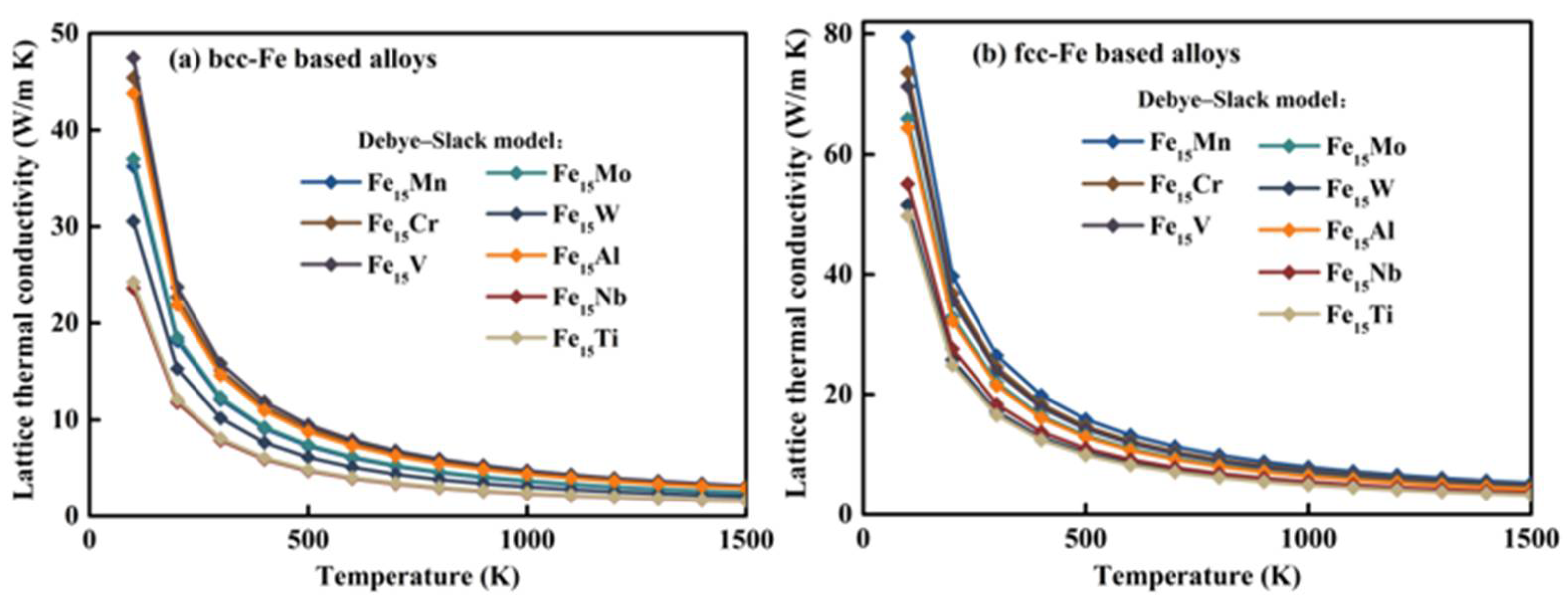
3.5. Lattice Thermal Conductivity
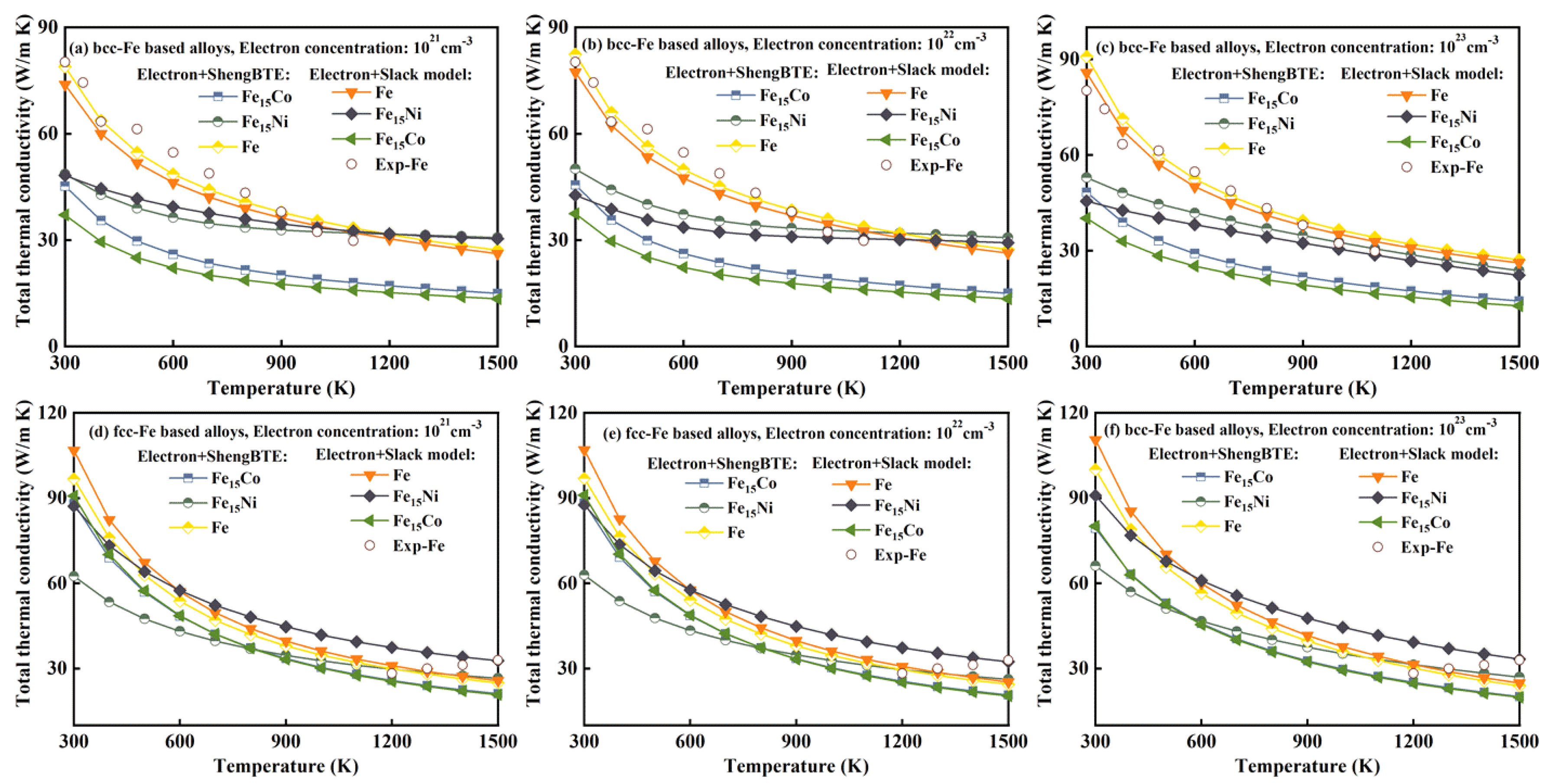
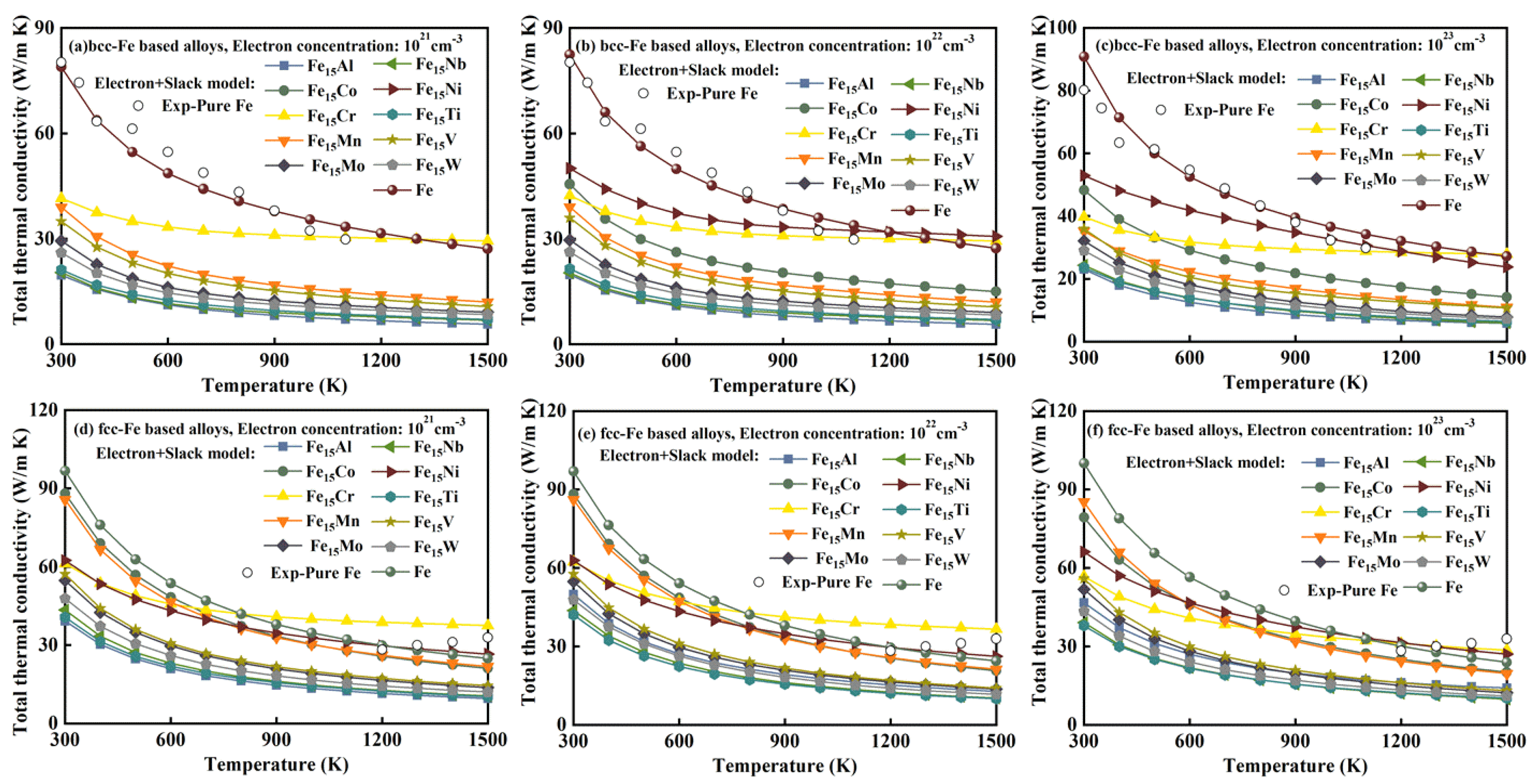
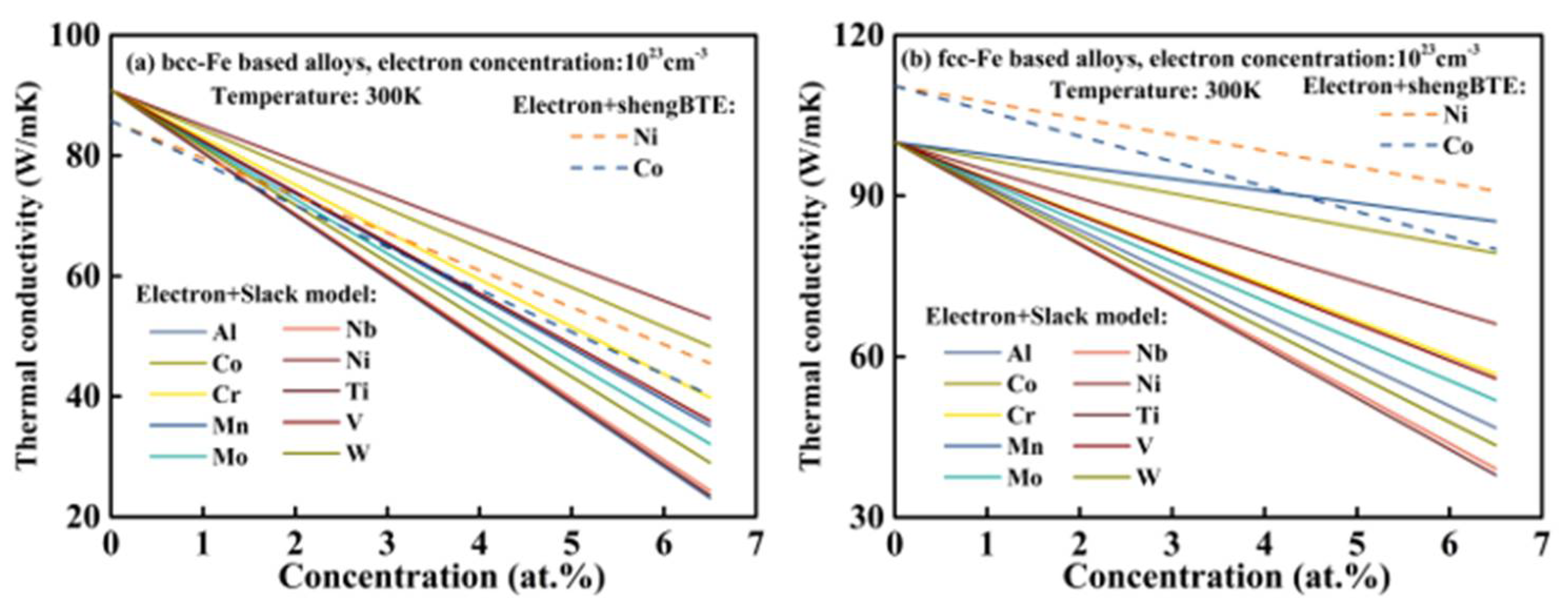
3.6. Total Thermal Conductivity
4. Outlook
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sperle, J.-O.; Olsson, K. High strength and ultra high strength steels for weight reduction in structural and safety-related applications. In Proceedings of the 29th International Symposium on Automotive Technology and Automation, Florence, Italy, 3–6 June 1996; Volume 1, pp. 115–125. [Google Scholar]
- Veerababu, R.; Satya Prasad, K.; Phani, S.K.; Balamuralikrishnan, R.; Karthikeyan, S. Austenite stability and M2C carbide decomposition in experimental secondary hardening ultra-high strength steels during high temperature austenitizing treatments. Mater. Charact. 2018, 144, 191–204. [Google Scholar] [CrossRef]
- Jones, W.B.; Swearengen, J.C. Mechanical stability of ultrahigh strength steels. Mater. Sci. Eng. 1979, 41, 225–235. [Google Scholar] [CrossRef]
- Ban, H.Y.; Shi, G.; Shi, Y.J.; Wang, Y.Q. Research Progress on the Mechanical Property of High Strength Structural Steels. Adv. Mater. Res. 2011, 250, 640–648. [Google Scholar] [CrossRef]
- Thomas, R.L.S.; Li, D.; Gangloff, R.P.; Scully, J.R. Trap-governed hydrogen diffusivity and uptake capacity in ultrahigh-strength AERMET 100 steel. Metall. Mater. Trans. A 2002, 33, 1991–2004. [Google Scholar] [CrossRef]
- Bäcklund, N.G. An experimental investigation of the electrical and thermal conductivity of iron and some dilute iron alloys at temperatures above 100°K. J. Phys. Chem. Solids 1961, 20, 1–16. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of Strain Rate Upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Xi, J.; Long, M.; Tang, L.; Wang, D.; Shuai, Z. First-principles prediction of charge mobility in carbon and organic nanomaterials. Nanoscale 2012, 4, 4348–4369. [Google Scholar] [CrossRef]
- Meyers, M.A.; Xu, Y.B.; Xue, Q.; Pérez-Prado, M.T.; McNelley, T.R. Microstructural evolution in adiabatic shear localization in stainless steel. Acta Mater. 2003, 51, 1307–1325. [Google Scholar] [CrossRef]
- Lee, S.; Cho, K.; Lee, C.; Choo, W. Microstructural study of adiabatic shear band formed by ballistic impact in an HY-100 steel. Metall. Trans. A 1993, 24, 2217–2224. [Google Scholar] [CrossRef]
- Rogers, H. Adiabatic Plastic Deformation. Annu. Rev. Mater. Sci. 2003, 9, 283–311. [Google Scholar] [CrossRef]
- Walley, S.M. Shear Localization: A Historical Overview. Metall. Mater. Trans. A 2007, 38, 2629–2654. [Google Scholar] [CrossRef]
- Yan, N.; Li, Z.; Xu, Y.; Meyers, M.A. Shear localization in metallic materials at high strain rates. Prog. Mater. Sci. 2020, 119, 100755. [Google Scholar] [CrossRef]
- Baik, S.-I.; Gupta, R.K.; Kumar, K.S.; Seidman, D.N. Temperature increases and thermoplastic microstructural evolution in adiabatic shear bands in a high-strength and high-toughness 10 wt.% Ni steel. Acta Mater. 2021, 205, 116568. [Google Scholar] [CrossRef]
- Zheng, X.; Cahill, D.; Krasnochtchekov, P.; Averback, R.; Zhao, J. High-throughput thermal conductivity measurements of nickel solid solutions and the applicability of the Wiedemann–Franz law. Acta Mater. 2007, 55, 5177–5185. [Google Scholar] [CrossRef]
- Yu, W.; Zhou, Y.; Chong, X.; Wei, Y.; Hu, C.; Zhang, A.; Feng, J. Investigation on elastic properties and electronic structure of dilute Ir-based alloys by first-principles calculations. J. Alloys Compd. 2021, 850, 156548. [Google Scholar] [CrossRef]
- Chong, X.; Hu, M.; Wu, P.; Shan, Q.; Jiang, Y.; Li, Z.; Feng, J. Tailoring the anisotropic mechanical properties of hexagonal M7X3 (M = Fe, Cr, W, Mo; X = C, B) by multialloying. Acta Mater. 2019, 169, 193–208. [Google Scholar] [CrossRef]
- Das, A.; Kumar, A.; Banerji, P. First principles study of electronic structure and thermoelectric transport in tin selenide and phase separated tin selenide-copper selenide alloy. J. Phys. Condens. Matter 2020, 32, 265501. [Google Scholar] [CrossRef]
- Tong, Z.; Bao, H. Decompose the electron and phonon thermal transport of intermetallic compounds NiAl and Ni3Al by first-principles calculations. Int. J. Heat Mass Transf. 2018, 117, 972–977. [Google Scholar] [CrossRef]
- Ding, Y.; Xiao, B.; Tang, G.; Hong, J. Transport Properties and High Thermopower of SnSe2: A Full Ab-Initio Investigation. J. Phys. Chem. C 2016, 121, 225–236. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Chong, X.; Paz Soldan Palma, J.; Wang, Y.; Shang, S.-L.; Drymiotis, F.; Ravi, V.; Star, K.; Fleurial, J.-P.; Liu, Z.-K. Thermodynamic properties of the Yb-Sb system predicted from first-principles calculations. Acta Mater. 2021, 217, 117169. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.; Tang, G.; Geng, W. VASPKIT: A User-friendly Interface Facilitating High-throughput Computing and Analysis Using VASP Code. Comput. Phys. Commun. 2019, 267, 108033. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Carrete, J.; Katcho, N.A.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Shea, J.J. Smithells Metal Reference Book, 8th ed.; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2005. [Google Scholar]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, S.; Mahanti, S.D. Energy and temperature dependence of relaxation time and Wiedemann-Franz law on PbTe. Phys. Rev. B 2010, 81, 165203. [Google Scholar] [CrossRef]
- Choi, G.; Kim, H.S.; Lee, K.; Park, S.H.; Cha, J.; Chung, I.; Lee, W.B. Study on thermal conductivity and electrical resistivity of Al-Cu alloys obtained by Boltzmann transport equation and first-principles simulation: Semi-empirical approach. J. Alloys Compd. 2017, 727, 1237–1242. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, J.F.; Liu, Y.; Feng, S.; Jin, C.; Hou, M.; Yoshino, T. Electrical Resistivity of Fe-C Alloy at High Pressure: Effects of Carbon as a Light Element on the Thermal Conductivity of the Earth’s Core. J. Geophys. Res. Solid Earth 2018, 123, 3564–3577. [Google Scholar] [CrossRef]
- Rossiter, P.L. Order-disorder and the electrical resistivity of FeCo. J. Phys. F Met. Phys. 1981, 11, 615–621. [Google Scholar] [CrossRef]
- Ingersoll, L.R. Some Physical Properties of Nickel-Iron Alloys. Phys. Rev. 1920, 16, 126–132. [Google Scholar] [CrossRef]
- Mermin, N.D. Lindhard Dielectric Function in the Relaxation-Time Approximation. Phys. Rev. B 1970, 1, 2362–2363. [Google Scholar] [CrossRef]
- D’Humieres, D.; Ginzburg, I.; Krafczyk, M.; Lallemand, P.; Luo, L.S. Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef]
- Chester, G.V.; Thellung, A. The Law of Wiedemann and Franz. Proc. Phys. Soc. 1961, 77, 1005–1013. [Google Scholar] [CrossRef]
- Kim, H.-S.; Gibbs, Z.M.; Tang, Y.; Wang, H.; Snyder, G.J. Characterization of Lorenz number with Seebeck coefficient measurement. APL Mater. 2015, 3, 041506. [Google Scholar] [CrossRef] [Green Version]
- Marzo, A.; Trigo-Gonzalez, M.; Alonso-Montesinos, J.; Martínez-Durbán, M.; López, G.; Ferrada, P.; Fuentealba, E.; Cortés, M.; Batlles, F.J. Daily global solar radiation estimation in desert areas using daily extreme temperatures and extraterrestrial radiation. Renew. Energy 2017, 113, 303–311. [Google Scholar] [CrossRef]
- Slack, G.A. The Thermal Conductivity of Nonmetallic Crystals. J. Phys. C Solid State Phys. 1979, 34, 1–71. [Google Scholar]
- Wu, Y.Y.; Zhu, X.L.; Yang, H.Y.; Wang, Z.G.; Li, Y.H.; Wang, B.T. First principles calculations on the thermoelectric properties of bulk Au2S with ultra-low lattice thermal conductivity. Chin. Phys. B 2020, 29, 087202. [Google Scholar] [CrossRef]
- Wen, S.; Ma, J.; Kundu, A.; Li, W. Large lattice thermal conductivity, interplay between phonon-phonon, phonon-electron, and phonon-isotope scatterings, and electrical transport in molybdenum from first principles. Phys. Rev. B 2020, 102, 064303. [Google Scholar] [CrossRef]
- Fulkerson, W.; Moore, J.P.; McElroy, D.L. Comparison of the Thermal Conductivity, Electrical Resistivity, and Seebeck Coefficient of a High-Purity Iron and an Armco Iron to 1000 °C. J. Appl. Phys. 1966, 37, 2639–2653. [Google Scholar] [CrossRef]
- Powell, R. Further Measurements of Thermal and Electrical Conductivity of Iron at High Temperatures. Proc. Phys. Soc. 2002, 51, 407. [Google Scholar] [CrossRef]
- Ghosh, G.; Olson, G. The isotropic shear modulus of multicomponent Fe-base solid solutions. Acta Mater. 2002, 50, 2655–2675. [Google Scholar] [CrossRef]
- Adams, J.; Agosta, D.; Leisure, R.; Ledbetter, H. Elastic constants of monocrystal iron from 3 to 500 K. J. Appl. Phys. 2007, 100, 113530. [Google Scholar] [CrossRef]
- Peet, M.J.; Hasan, H.S.; Bhadeshia, H.K.D.H. Prediction of thermal conductivity of steel. Int. J. Heat Mass Transf. 2011, 54, 2602–2608. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.-K. Computational thermodynamics and its applications. Acta Mater. 2020, 200, 745–792. [Google Scholar] [CrossRef]
- Liu, Z.-K. First-Principles Calculations and CALPHAD Modeling of Thermodynamics. J. Phase Equilibria Diffus. 2009, 30, 517–534. [Google Scholar] [CrossRef]
- Ho, C.Y.; Ackerman, M.W.; Wu, K.Y.; Havill, T.N.; Bogaard, R.H.; Matula, R.A.; Oh, S.G.; James, H.M. Electrical Resistivity of Ten Selected Binary Alloy Systems. J. Phys. Chem. Ref. Data 1983, 12, 183–322. [Google Scholar] [CrossRef] [Green Version]

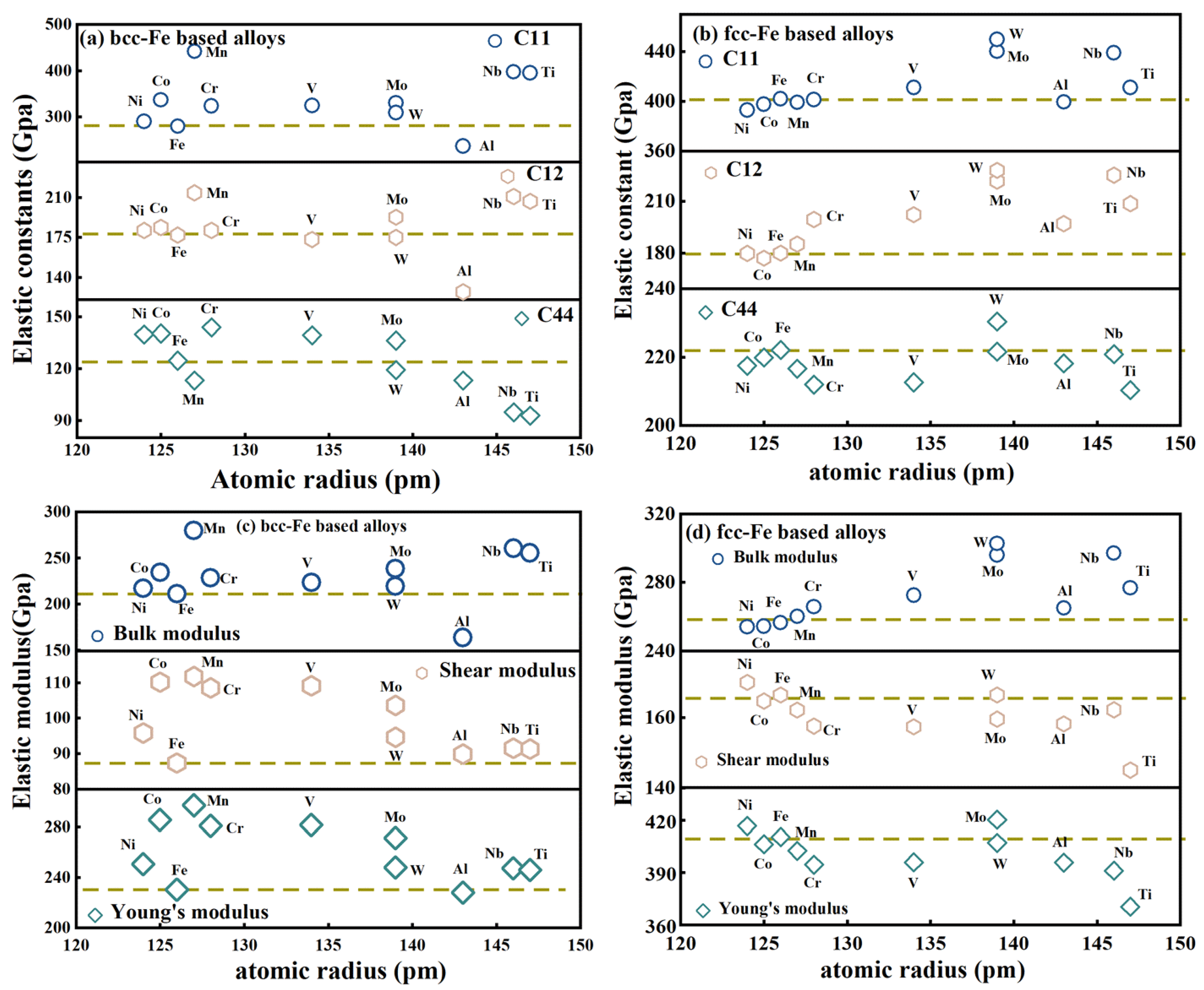

| Structure | C11 (GPa) | C12 (Gpa) | C44 (GPa) | B/G (GPa) | E (GPa) | ν |
|---|---|---|---|---|---|---|
| bcc-Fe15Ni | 290.0 | 180.9 | 139.8 | 2.27 | 250.6 | 0.308 |
| bcc-Fe15Co | 336.9 | 183.6 | 140.4 | 2.13 | 285.7 | 0.297 |
| bcc-Fe | 279.8 | 177.0 | 124.6 | 2.42 | 230.4 | 0.318 |
| bcc-Fe a | 233.1 | 135.4 | 117.8 | 2.1 | 208 | |
| bcc-Fe15Mn | 441.5 | 213.8 | 113.1 | 2.51 | 297.1 | 0.324 |
| bcc-Fe15Cr | 323.5 | 181.1 | 143.9 | 2.11 | 281.1 | 0.295 |
| bcc-Fe15V | 324.7 | 173.0 | 139.3 | 2.05 | 281.6 | 0.290 |
| bcc-Fe15Mo | 330.2 | 192.6 | 136.3 | 2.30 | 271.4 | 0.310 |
| bcc-Fe15W | 309.1 | 174.9 | 119.2 | 2.32 | 248.1 | 0.312 |
| bcc-Fe15Al | 237.1 | 127.1 | 113.1 | 1.82 | 227.9 | 0.268 |
| bcc-Fe15Nb | 397.7 | 210.6 | 94.6 | 2.85 | 247.4 | 0.343 |
| bcc-Fe15Ti | 395.0 | 206.6 | 92.7 | 2.80 | 246.0 | 0.340 |
| fcc-Fe15Ni | 392.9 | 179.8 | 217.5 | 1.49 | 416.9 | 0.226 |
| fcc-Fe15Co | 397.6 | 177.1 | 219.8 | 1.54 | 406.3 | 0.234 |
| fcc-Fe | 401.9 | 179.9 | 222.1 | 1.54 | 410.4 | 0.233 |
| fcc-Fe15Mn | 399.0 | 185.2 | 216.6 | 1.60 | 402.6 | 0.242 |
| fcc-Fe15Cr | 401.2 | 199.5 | 211.9 | 1.69 | 394.7 | 0.252 |
| fcc-Fe15V | 411.0 | 202.2 | 212.6 | 1.73 | 395.9 | 0.258 |
| fcc-Fe15Mo | 440.1 | 221.5 | 221.5 | 1.78 | 420.4 | 0.263 |
| fcc-Fe15W | 449.8 | 227.7 | 230.3 | 1.90 | 407.1 | 0.276 |
| fcc-Fe15Al | 399.3 | 197.0 | 218.1 | 1.68 | 395.8 | 0.251 |
| fcc-Fe15Nb | 438.8 | 225.0 | 220.8 | 1.83 | 391.1 | 0.269 |
| fcc-Fe15Ti | 411.0 | 208.6 | 210.2 | 1.91 | 370.4 | 0.277 |
| Debye Temperature (K) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fe15Ni | Fe15Co | Fe | Fe15Mn | Fe15Cr | Fe15V | Fe15Mo | Fe15W | Fe15Al | Fe15Nb | Fe15Ti | |
| bcc | 498 | 533 | 477 | 540 | 532 | 534 | 510 | 466 | 490 | 483 | 494 |
| fcc | 657 | 647 | 651 | 644 | 637 | 639 | 643 | 603 | 649 | 638 | 617 |
| Ni a | Co a | Mn a | Cr a | V a | Mo a | W a | Al a | Nb a | Ti a | Ni b | Co b | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bcc | 10.84 | 6.80 | 8.17 | 8.91 | 9.40 | 10.64 | 6.06 | 10.76 | 8.78 | 9.89 | 6.44 | 7.29 |
| fcc | 8.53 | 3.31 | 6.91 | 2.36 | 7.71 | 9.74 | 5.42 | 9.93 | 7.05 | 9.05 | 3.14 | 4.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Chong, X.; Ding, Y.; Zhou, Y.; Gan, M.; Xu, L.; Wei, S.; Feng, J. First-Principles Calculations of Thermal and Electrical Transport Properties of bcc and fcc Dilute Fe–X (X = Al, Co, Cr, Mn, Mo, Nb, Ni, Ti, V, and W) Binary Alloys. Metals 2021, 11, 1988. https://doi.org/10.3390/met11121988
Lin Y, Chong X, Ding Y, Zhou Y, Gan M, Xu L, Wei S, Feng J. First-Principles Calculations of Thermal and Electrical Transport Properties of bcc and fcc Dilute Fe–X (X = Al, Co, Cr, Mn, Mo, Nb, Ni, Ti, V, and W) Binary Alloys. Metals. 2021; 11(12):1988. https://doi.org/10.3390/met11121988
Chicago/Turabian StyleLin, Yang, Xiaoyu Chong, Yingchun Ding, Yunxuan Zhou, Mengdi Gan, Liujie Xu, Shizhong Wei, and Jing Feng. 2021. "First-Principles Calculations of Thermal and Electrical Transport Properties of bcc and fcc Dilute Fe–X (X = Al, Co, Cr, Mn, Mo, Nb, Ni, Ti, V, and W) Binary Alloys" Metals 11, no. 12: 1988. https://doi.org/10.3390/met11121988
APA StyleLin, Y., Chong, X., Ding, Y., Zhou, Y., Gan, M., Xu, L., Wei, S., & Feng, J. (2021). First-Principles Calculations of Thermal and Electrical Transport Properties of bcc and fcc Dilute Fe–X (X = Al, Co, Cr, Mn, Mo, Nb, Ni, Ti, V, and W) Binary Alloys. Metals, 11(12), 1988. https://doi.org/10.3390/met11121988






