Numerical Investigation of Segregation Evolution during the Vacuum Arc Remelting Process of Ni-Based Superalloy Ingots
Abstract
:1. Introduction
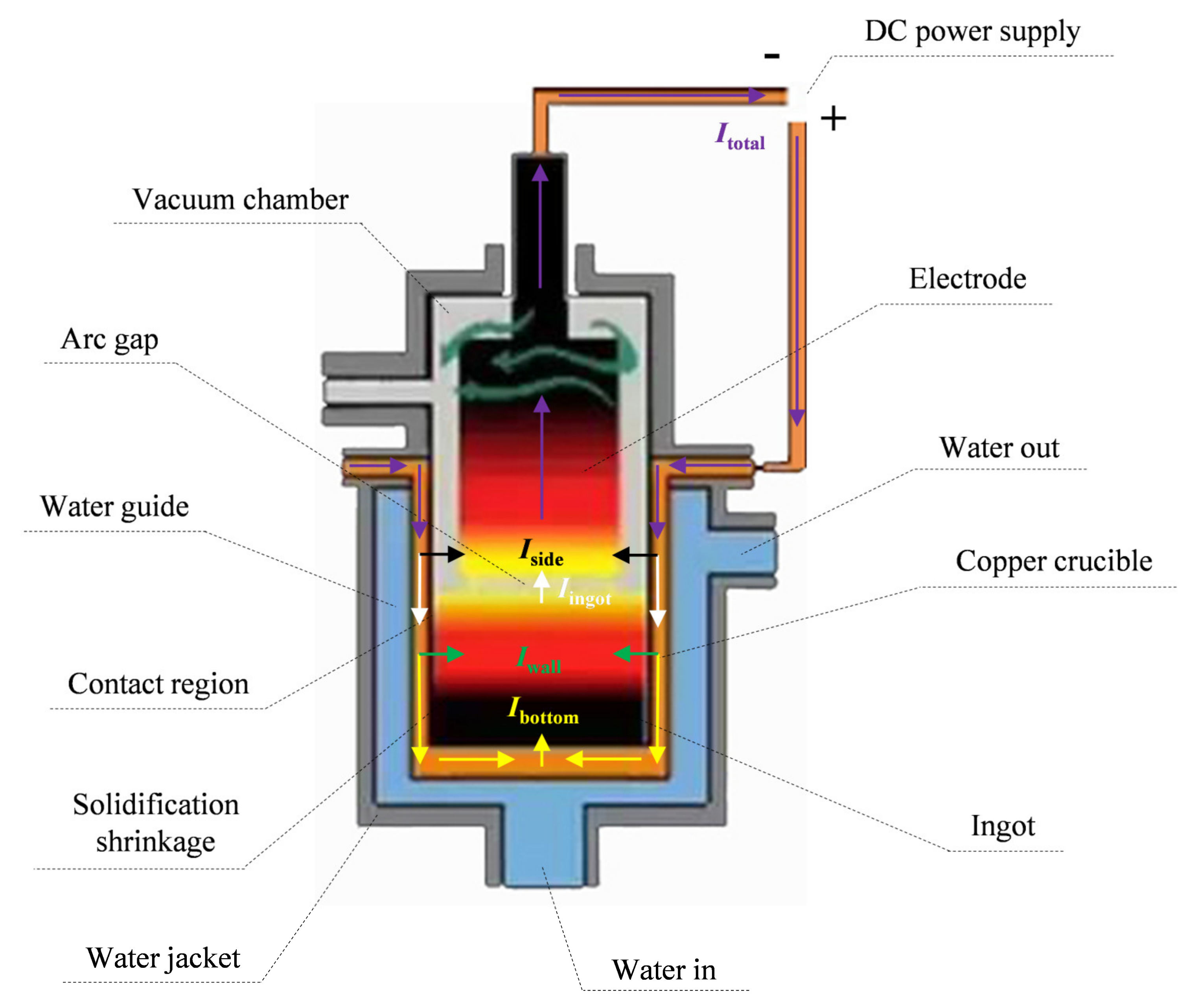
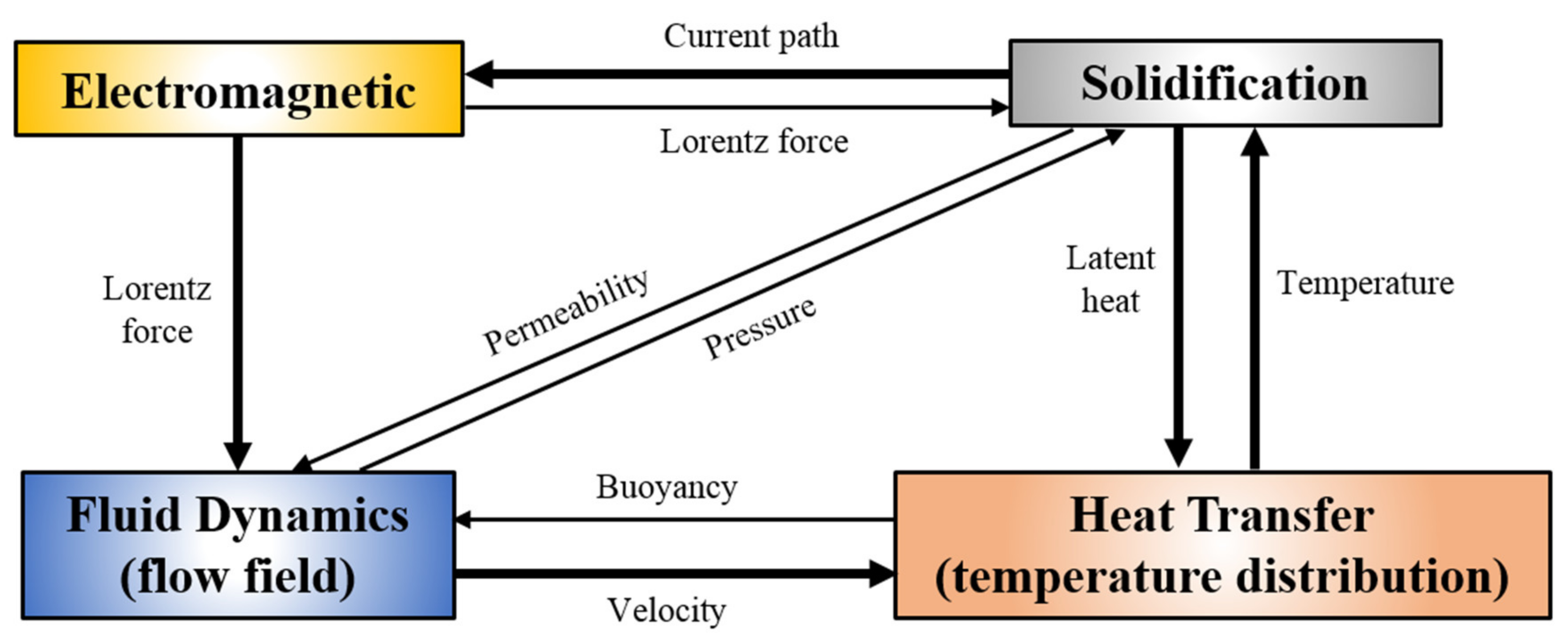
2. Model Description
- (1)
- The incompressible flow is assumed, ignoring the chemical reaction and Marangoni effect in the molten pool,
- (2)
- The metal density varies with temperature only in the buoyancy term of momentum equation, while the changing thermal conductivity with temperature calculated by thermodynamic software JMatPro (Version 7.0, Sente Software Ltd., Guildford, Surrey, UK) is adopted in this study. All other thermophysical properties are considered to be constant during the solidification process,
- (3)
- The current and heat flux provided by the arc to the top of the molten pool follow a Gaussian distribution [3],
- (4)
- In the melting stage of the consumable electrode, the thermal radiation on the surface of the molten pool is ignored and will be considered after the melting is completed.
2.1. Electric Potential Method
2.2. Coupling of Fluid Flow, Temperature, and Solute Distribution
- (1)
- Continuity equation:
- (2)
- Considering the viscous force, the thermosolutal buoyancy, and the Lorentz force in the mushy zone, the momentum conservation equation can be written as follows:where, ρ is the density; u, v and w are the components of fluid velocity in x, y and z directions, respectively; Fx, Fy and Fz are the Lorentz forces in each direction; K is the permeability of the mushy zone, which is described by the Kozeny Carman equation, as shown in Equation (11). Sg is the thermosolutal buoyancy, which indicates the effect of density change caused by temperature and solute concentration on the fluid flow, as shown in Equation (12).where, δ is the secondary dendrite arm spacing; βT and βC are the thermal and solutal expansion coefficients, respectively; T is temperature; C is solute concentration. The subscript l represents the liquid phase, ref is the reference value; the superscript i represents each component. The liquid fraction fl can be obtained from the following equation:where Tsol and Tliq are the solidus and liquidus temperatures in the alloy solidification system, respectively.
- (3)
- Considering the effects of solute convection and heat conduction during solidification, the energy conservation equation is expressed as follows:where, λ is the thermal conductivity; cp is the specific heat capacity; L is the latent heat; fs is the solid fraction.
- (4)
- Ignoring the solute diffusion in the solid phase, the solute conservation equation during solidification can be described as:where D is the solute diffusion coefficient in the liquid phase.
- (5)
- In order to close the governing equations of flow, heat transfer, and mass transfer and realize the coupling solution, the relationship between liquid fraction and solute concentration should also be given. The phase diagram method is used to update the solid fraction equation for the solidification process of multi-component alloy. The liquidus temperature in the alloy solidification system can be obtained by the following equation:where Tm is the melting temperature of pure solvent. and the average liquidus slope is as follows:
3. Simulation Conditions
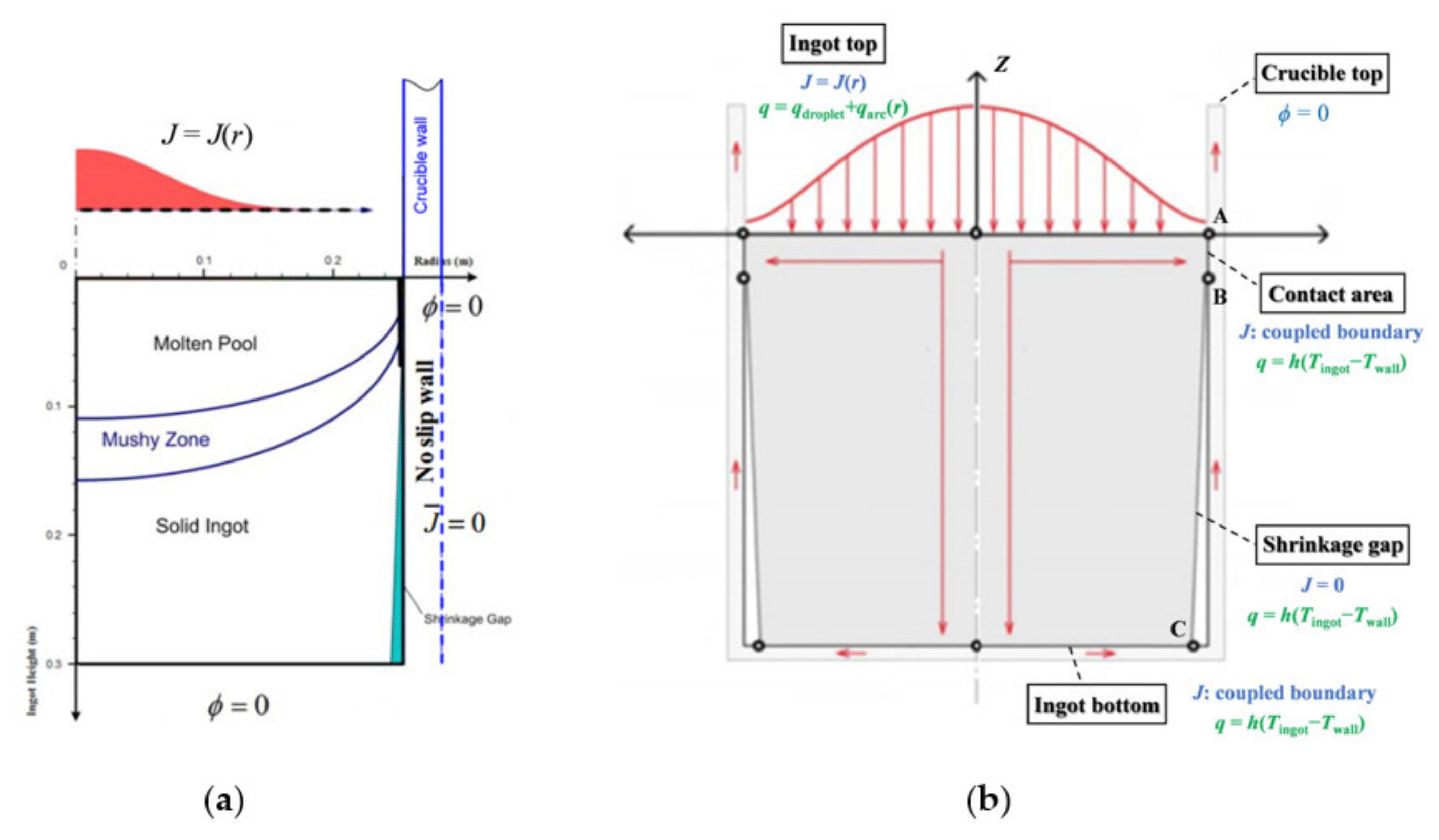
3.1. Boundary Conditions
- (1)
- Electromagnetic boundary condition
- (2)
- Dynamic boundary condition
- (3)
- Thermal boundary condition
3.2. Physical and Process Parameters
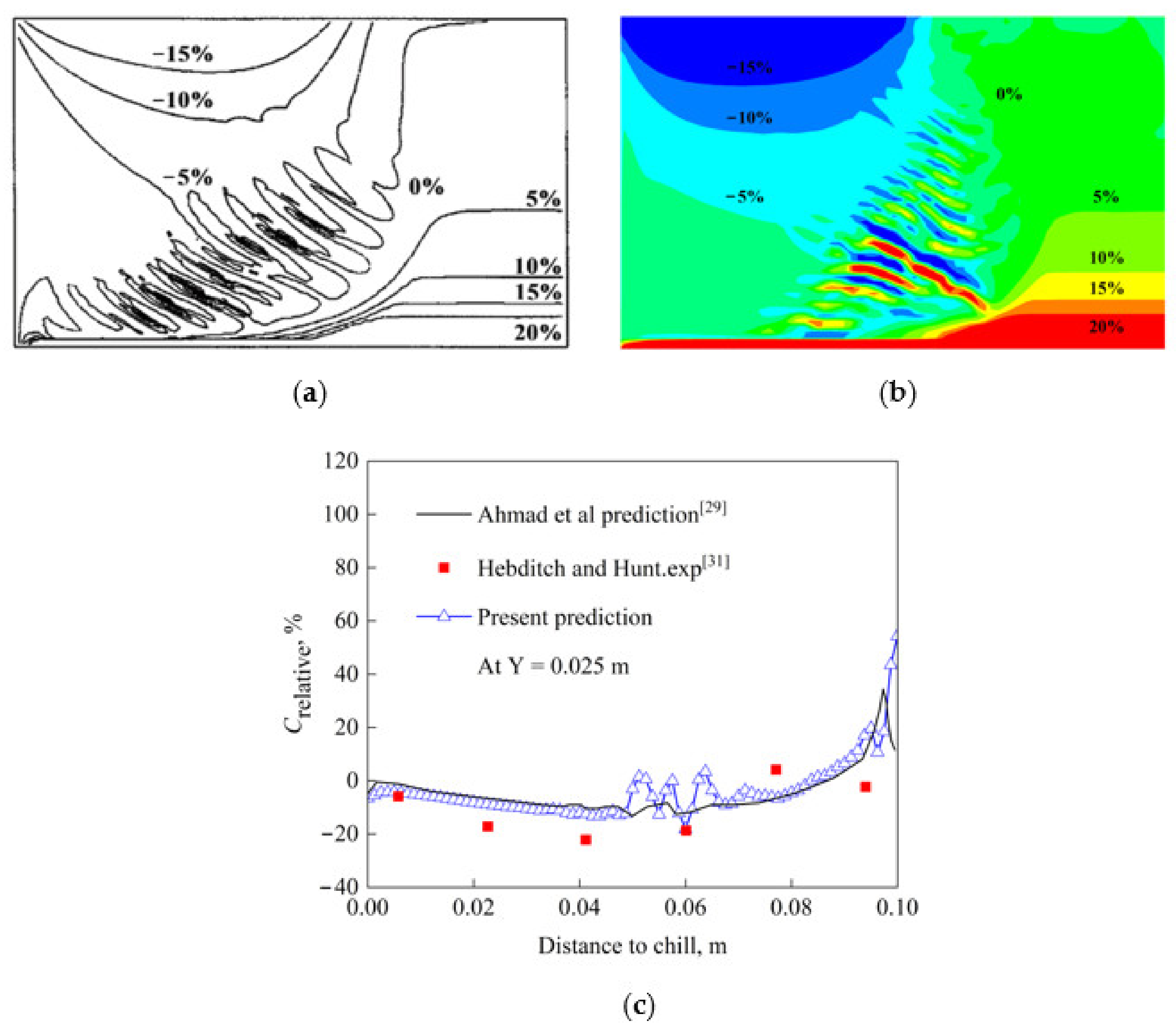
3.3. Model Validation
4. Results and Discussion
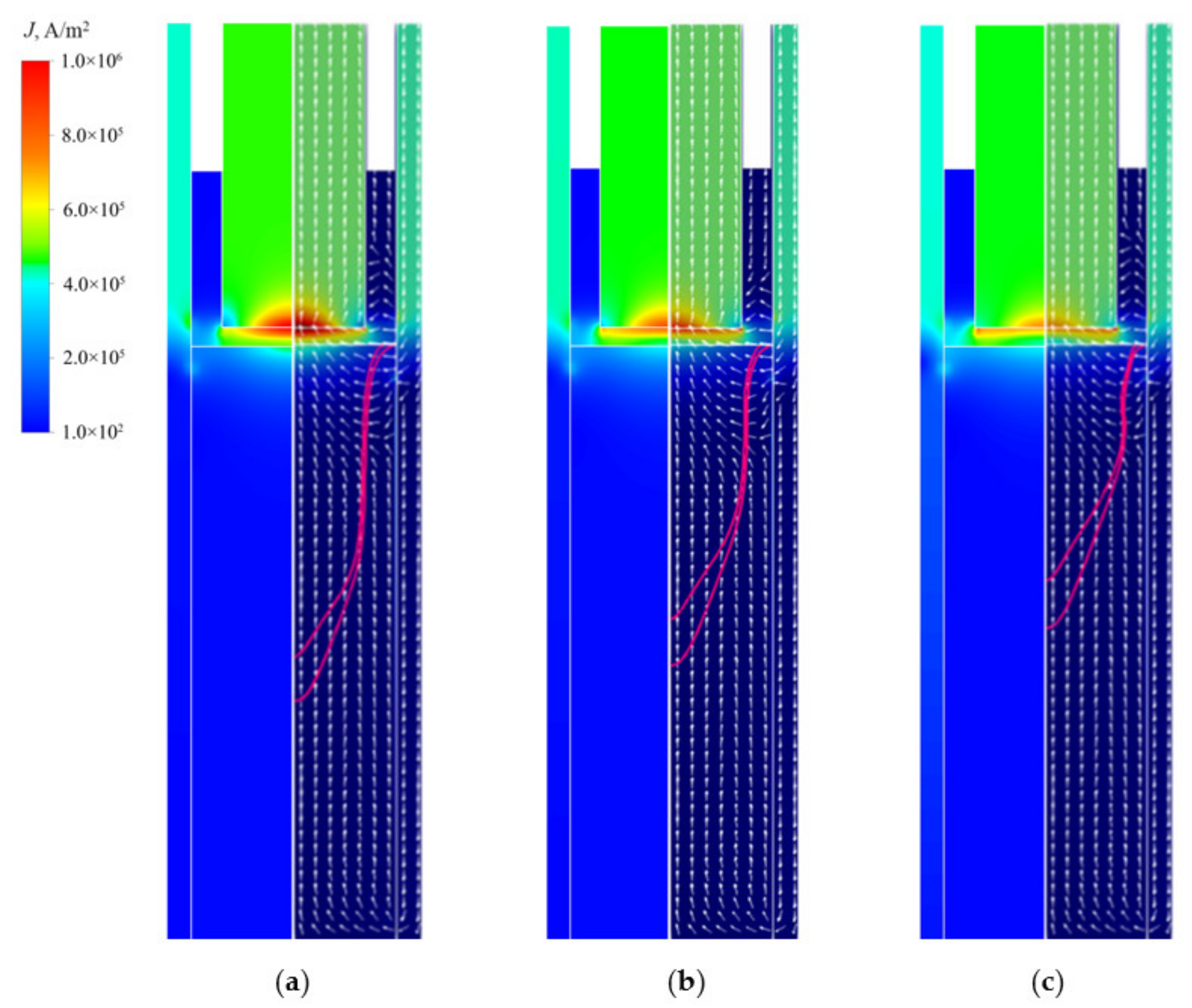
4.1. Electromagnetic Fields
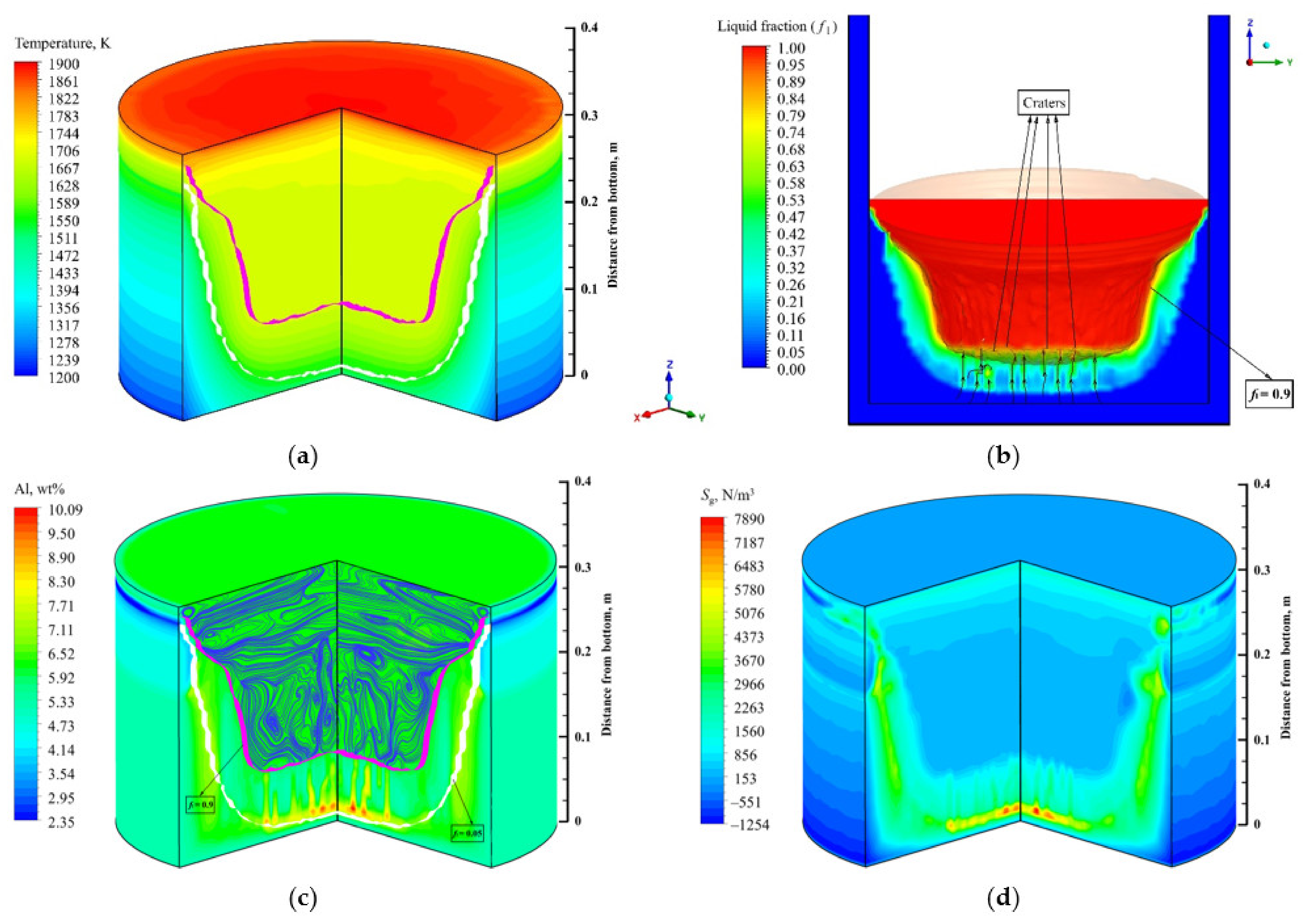
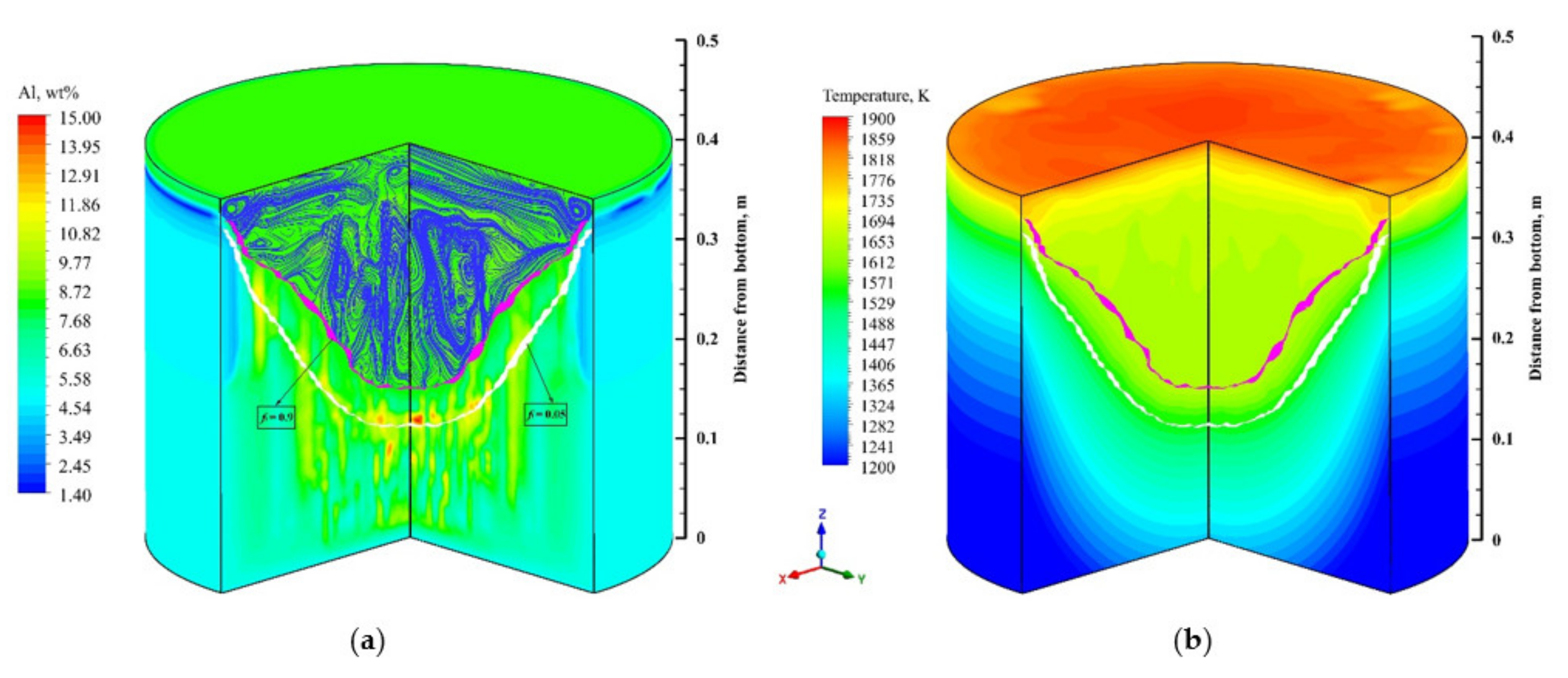
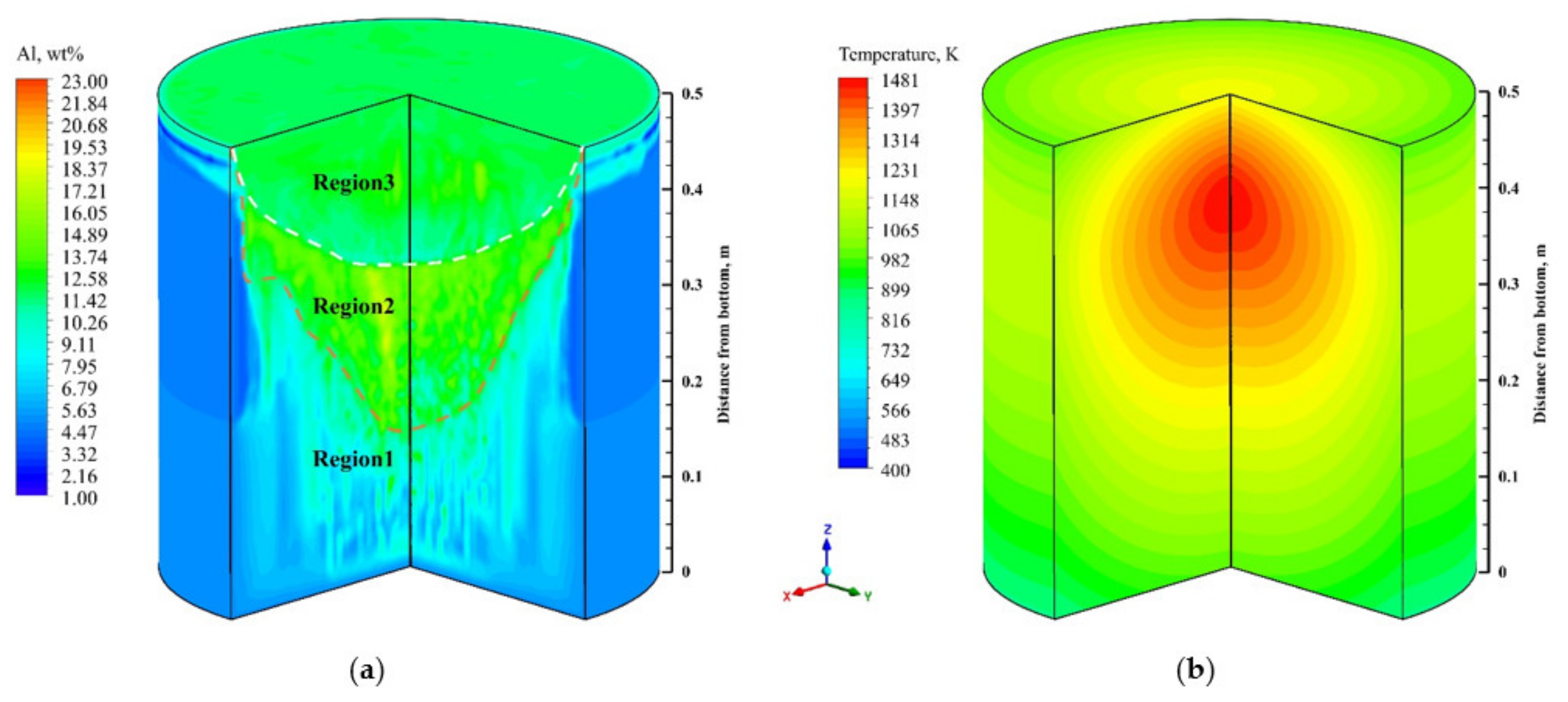
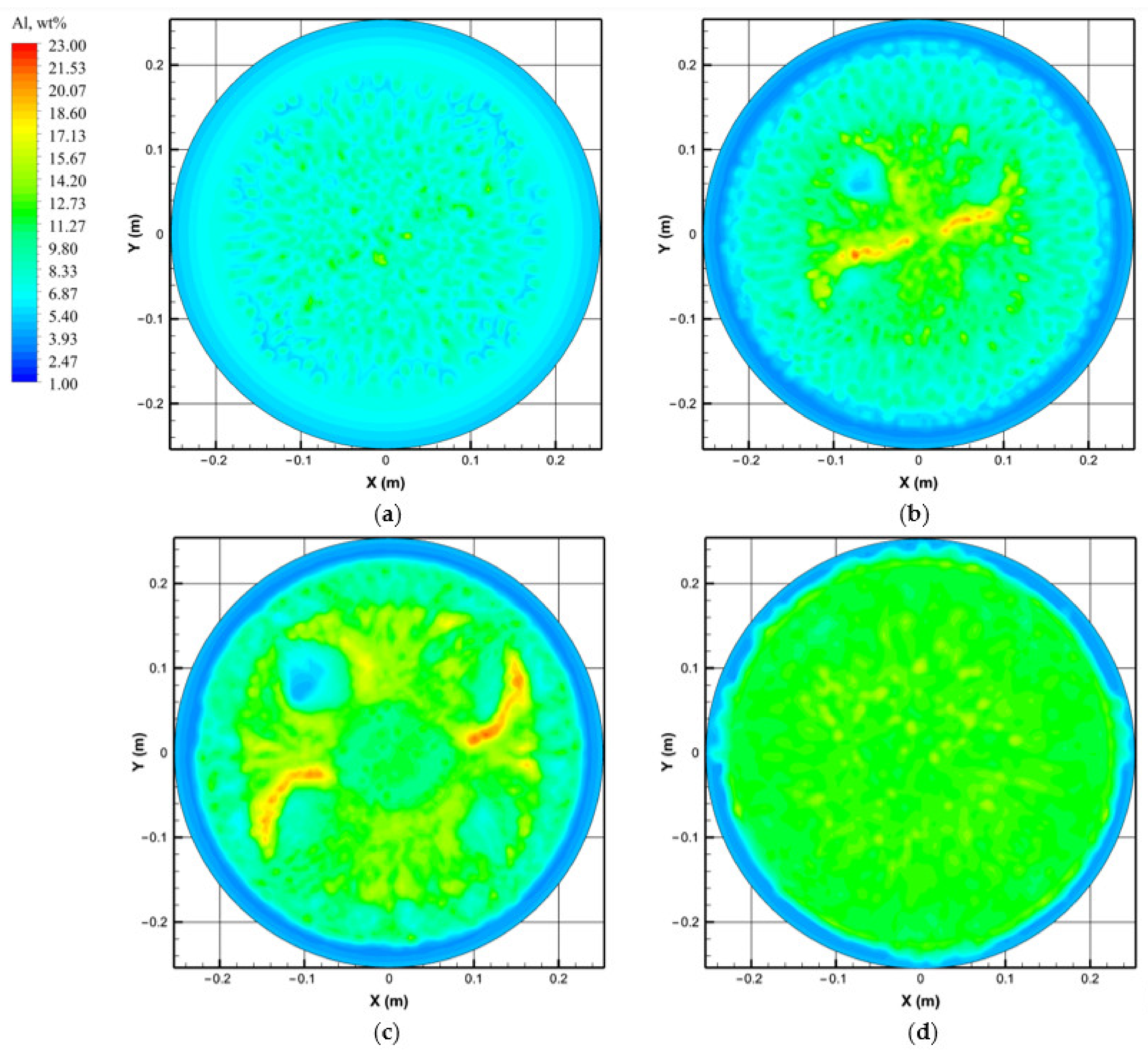
4.2. Flow field, Temperature, and Solute Distribution
5. Conclusions
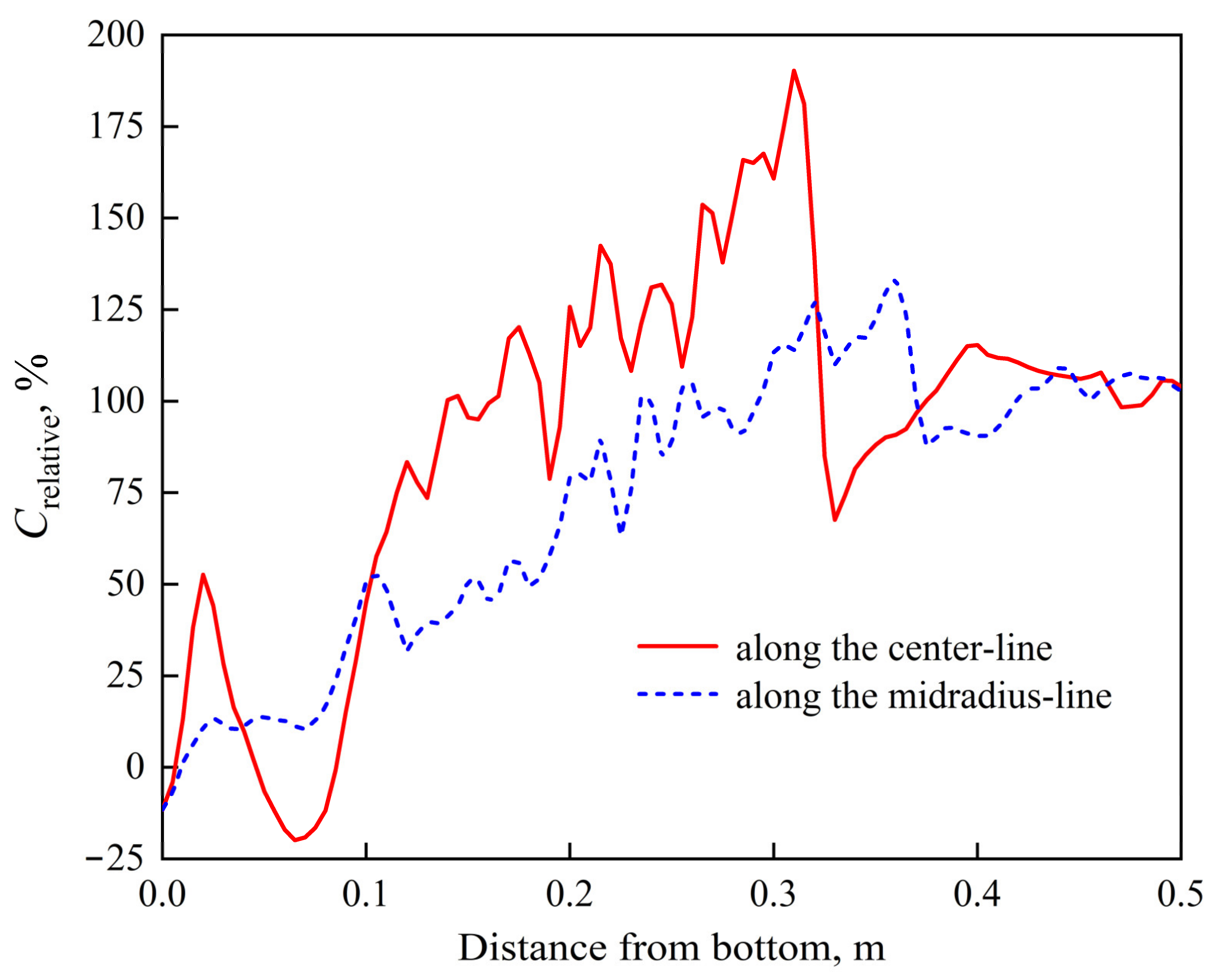
- The Lorentz force mainly affects the flow pattern at the top of the molten pool, which has less influence on the flow field inside the ingot. The complex flow of multiple vortices in the molten pool is dominated by the thermosolutal buoyancy. The position where thermosolutal buoyancy is larger corresponds to the position where the solute enrichment channel is formed in the mushy zone.
- Freckles, that is, channel-type solute enrichment, mainly concentrated in the lower part of the ingot. With the growth of the ingot, some adjacent channels in the central part of the ingot merged, resulting in the solute enrichment channel gradually developing into the solute enrichment region, and channel segregation evolving into macrosegregation. The solutes in the middle and upper parts of the ingot are mainly concentrated in the macrosegregation area in the center, while negative segregation appears at the side of the ingot.
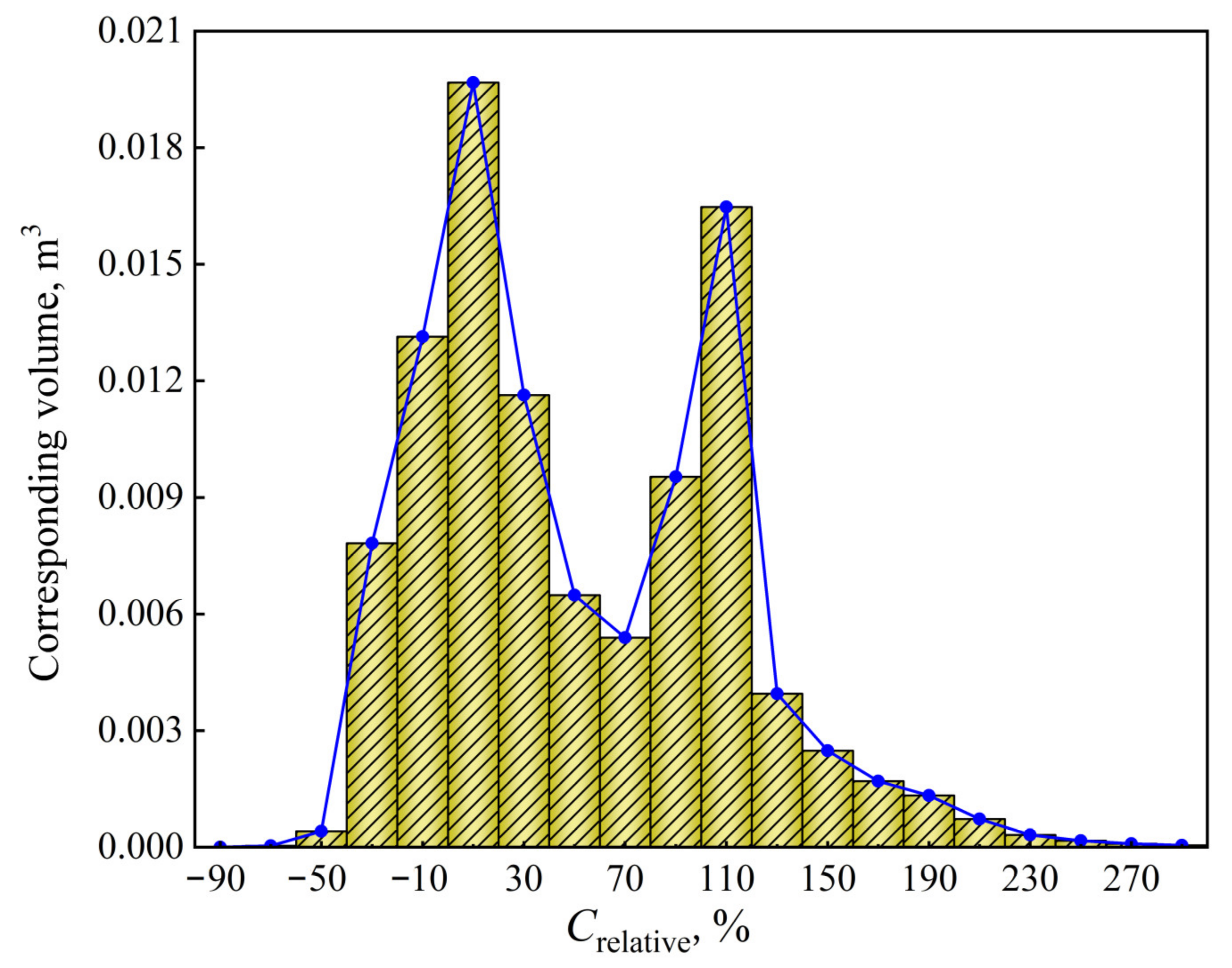
- The maximum and minimum relative segregation ratio inside the ingot can reach 290% and –90%, respectively, and about 79% of the total volume presents positive segregation. In the range of negative segregation, the volume of the corresponding range will decrease as the negative segregation becomes more serious. In the range of positive segregation, the volume of the corresponding range has two maximum values, which are located in the range of 0~20% and 100%~120%, respectively, rather than the monotonous variation trend as in the negative segregation region.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, B.; Pei, Y.L.; Gong, S.K.; Li, S.S. Orientation Dependence of High Cycle Fatigue Behavior of a <111> Oriented Single-Crystal Nickel-Based Superalloy. Metals 2021, 11, 1248. [Google Scholar] [CrossRef]
- Descotes, V.; Quatravaux, T.; Bellot, J.-P.; Witzke, S.; Jardy, A. Titanium Nitride (TiN) Germination and Growth During Vacuum Arc Remelting of a Maraging Steel. Metals 2020, 10, 541. [Google Scholar] [CrossRef] [Green Version]
- Karimi-Sibaki, E.; Kharicha, A.; Wu, M.H.; Ludwig, A.; Bohacek, J. A Parametric Study of the Vacuum Arc Remelting (VAR) Process: Effects of Arc Radius, Side-Arcing, and Gas Cooling. Metall. Mater. Trans. B 2019, 51, 222–235. [Google Scholar] [CrossRef] [Green Version]
- Spitans, S.; Franz, H.; Scholz, H.; Reiter, G.; Baake, E. Numerical Simulation of the Ingot Growth During the Vacuum Arc Remelting Process. Magnetohydrodynamics 2017, 53, 557–569. [Google Scholar] [CrossRef]
- Shevchenko, D.M.; Ward, R.M. Liquid Metal Pool Behavior During the Vacuum Arc Remelting of INCONEL 718. Metall. Mater. Trans. B 2008, 40, 263–270. [Google Scholar] [CrossRef]
- Zhu, B.; Xue, X.Y.; Kou, H.C.; Xiao, C.; Li, J.S. Macroscale Modeling of Multi-Physics Fields During Vacuum Arc Remelting of Ti-6Al-4V. Mater. Sci. Forum 2014, 789, 603–607. [Google Scholar] [CrossRef]
- Zhao, X.H.; Li, J.S.; Chang, H.; Yang, Z.J.; Kou, H.C.; Hu, R.; Zhou, L. Numerical Simulation of Electromagnetic Field in Vacuum Arc Remelting Process. Chin. J. Nonferrous Met. 2010, 20, 538–543. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, B.J.; Huang, S.; Zhang, W.Y.; Tian, Q.; Chen, S.F. Recent Development of Nickel-Based Disc Alloys and Corresponding Cast-wrought Processing Techniques. Acta Metall. Sin. 2019, 55, 1095–1114. (In Chinese) [Google Scholar] [CrossRef]
- Madison, J.; Spowart, J.; Rowenhorst, D.; Aagesen, L.K.; Thornton, K.; Pollock, T.M. Modeling Fluid Flow in Three-Dimensional Single Crystal Dendritic Structures. Acta Mater. 2010, 58, 2864–2875. [Google Scholar] [CrossRef]
- Yang, Z.J.; Kou, H.C.; Li, J.S.; Hu, R.; Chang, H.; Zhou, L. Macrosegregation Behavior of Ti-10V-2Fe-3Al Alloy During Vacuum Consumable Arc Remelting Process. J. Mater. Eng. Perform. 2010, 20, 65–70. [Google Scholar] [CrossRef]
- Fan, K.; Wu, L.C.; Li, J.J.; Wang, J.C. Numerical Simulation of Macrosegregation Caused by Buoyancy Driven Flow During VAR Process for Titanium Alloys. Rare Met. Mater. Eng. 2020, 49, 871–877. (In Chinese) [Google Scholar]
- Shang, J.J.; He, Y.S.; Yang, C.; Wu, M.; Luo, W.Z.; Wang, K.X. Freckles Pattern and Microstructure Feature of Nb-Ti Alloy Produced by Vacuum Arc Remelting. In MATEC Web of Conferences; EDP Sciences: Nantes, France, 2020; Volume 321, p. 12. [Google Scholar] [CrossRef]
- Wang, X.H.; Ward, R.M.; Jacobs, M.H.; Barratt, M.D. Effect of Variation in Process Parameters on the Formation of Freckle in INCONEL 718 by Vacuum Arc Remelting. Metall. Mater. Trans. A 2008, 39, 2981–2989. [Google Scholar] [CrossRef]
- Zagrebelnyy, D.; Krane, M.J.M. Segregation Development in Multiple Melt Vacuum Arc Remelting. Metall. Mater. Trans. B 2008, 40, 281–288. [Google Scholar] [CrossRef]
- Pericleous, K.; Djambazov, G.; Ward, M.; Yuan, L.; Lee, P.D. A Multiscale 3D Model of the Vacuum Arc Remelting Process. Metall. Mater. Trans. A 2013, 44, 5365–5376. [Google Scholar] [CrossRef]
- Leder, M.O.; Kondrashov, E.N. Columnar-to-Equiaxed Transition During the Solidification of a Ti–10V–2Fe–3Al Alloy. Russ. Metall. 2017, 2016, 1125–1128. [Google Scholar] [CrossRef]
- Nastac, L. A Multiscale Transient Modeling Approach for Predicting the Solidification Structure in VAR-Processed Alloy 718 Ingots. Metall. Mater. Trans. B 2012, 45, 44–50. [Google Scholar] [CrossRef]
- Kermanpur, A.; Evans, D.G.; Siddall, R.J.; Lee, P.D.; Mclean, M. Effect of Process Parameters on Grain Structure Formation During VAR of INCONEL alloy 718. J. Mater. Sci. 2004, 39, 7175–7182. [Google Scholar] [CrossRef]
- Kou, H.C.; Zhang, Y.J.; Yang, Z.J.; Li, P.F.; Li, J.S.; Zhou, L. Liquid Metal Flow Behavior During Vacuum Consumable Arc Remelting Process for Titanium. Int. J. Eng. Technol. 2014, 12, 50–56. [Google Scholar]
- Wang, C.J.; Liu, Z.Q.; Li, B.K. Combined Effects of EMBr and SEMS on Melt Flow and Solidification in a Thin Slab Continuous Caster. Metals 2021, 11, 948. [Google Scholar] [CrossRef]
- Kaygısız, Y.; Maraşlı, N. Directional Solidification of Al–Cu–Si–Mg Quaternary Eutectic Alloy. J. Alloy. Compd. 2017, 721, 764–771. [Google Scholar] [CrossRef]
- Ren, N.; Li, J.; Panwisawas, C.; Xia, M.X.; Dong, H.B.; Li, J.G. Thermal-Solutal-Fluid Flow of Channel Segregation During Directional Solidification of Single-Crystal Nickel-Based Superalloys. Acta Mater. 2021, 206, 116620. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Niu, R.; Wu, Y.D.; Li, B.K.; Gan, Y.; Wu, M.H. Physical and Numerical Simulation of Mixed Columnar-Equiaxed Solidification During Cold Strip Feeding in Continuous Casting. Int. J. Heat Mass Transf. 2021, 173, 121237. [Google Scholar] [CrossRef]
- Wu, M.H.; Ludwig, A.; Kharicha, A. Volume-Averaged Modeling of Multiphase Flow Phenomena During Alloy Solidification. Metals 2019, 9, 229. [Google Scholar] [CrossRef] [Green Version]
- Quatravaux, T.; Ryberon, S.; Hans, S.; Jardy, A.; Lusson, B.; Richy, P.E.; Ablitzer, D. Transient VAR ingot growth modelling: Application to specialty steels. J. Mater. Sci. 2004, 39, 7183–7191. [Google Scholar] [CrossRef]
- ANSYS FLUENT 14. 5-Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2012.
- Xu, X.; Zhang, W.; Lee, P.D. Tree-Ring Formation During Vacuum Arc Remelting of INCONEL 718: Part II. Mathematical Modeling. Metall. Mater. Trans. A 2002, 33, 1805–1815. [Google Scholar] [CrossRef]
- Tin, S.; Pollock, T.M. Predicting Freckle Formation in Single Crystal Ni-Base Superalloys. J. Mater. Sci. 2009, 39, 7199–7205. [Google Scholar] [CrossRef]
- Sung, P.K.; Poirier, D.R. Liquid-Solid Partition Ratios in Nickel-Base Alloys. Metall. Mater. Trans. A 1999, 30, 2173–2181. [Google Scholar] [CrossRef]
- Wu, Y.D.; Liu, Z.Q.; Wang, F.; Li, B.K.; Gan, Y. Experimental Investigation of Trajectories, Velocities and Size Distributions of Bubbles in a Continuous-Casting Mold. Powder Technol. 2021, 387, 325–335. [Google Scholar] [CrossRef]
- Ahmad, N.; Combeau, H.; Desbiolles, J.-L.; Jalanti, T.; Lesoult, G.; Rappaz, J.; Rappaz, M.; Stomp, C. Numerical Simulation of Macrosegregation: A Comparison Between Finite Volume Method and Finite Element Method Predictions and a Confrontation with Experiments. Metall. Mater. Trans. A 1998, 29, 617–630. [Google Scholar] [CrossRef]
- Li, W.S.; Shen, H.F.; Liu, B.C. A Response to Numerical Benchmark for Solidification of Binary Alloys: Macro-Segregation with Thermo-Solutal Convection. China Foundry 2012, 9, 171–177. [Google Scholar] [CrossRef]
- Hebditch, D.J.; Hunt, J.D. Observations of Ingot Macrosegregation on Model Systems. Metall. Trans. 1974, 5, 1557–1564. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, H.G.; Ren, N.; Li, B.K. Effect of Current on Solute Transport in Electroslag Remelting Dual Alloy Ingot. Appl. Therm. Eng. 2016, 101, 564–567. [Google Scholar] [CrossRef]




| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Ingot radius, Ri/mm | 254 |
Ingot growth rate, V0/m·s−1 | 4.22 × 10−5 |
| Electrode radius, R0/mm | 215 | Proportion of Iingot, ηI | 0.6 |
| Arc focus, Ra/mm | 178 | Power efficiency, ηp | 0.65 |
| Current, Itotal/A | 5600 | Heat transfer coefficient, h(T)/W·m−2·K−1 |
20 (300 K), 40 (1000 K), 100 (1400 K), 300 (1580 K), 1000 (1620 K), 2000 (1700 K) |
| Volts, U/V | 23 | Wall thickness of crucible, δ0/mm | 30 |
| Melt rate, qm/kg·s−1 | 0.063 | Temperature of crucible wall, Twall/K | 400 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Density, ρ/kg·m−3 | 7365 | Equilibrium partition coefficient, kTa | 0.48 |
| Specific heat, cp/J·k−1·K−1 | 660 | Solutal expansion coefficient, /(wt%)−1 | 2.26 × 10−2 |
| Thermal conductivity, λ/W·m−1·K−1 | 18(600 K), 20(800 K), 23(1000 K), 26(1200 K), 29(1400 K), 33(1600 K), 41(1800 K), 45(2000 K) | Solutal expansion coefficient, /(wt%)−1 | −3.82 × 10−3 |
| Dynamic viscosity, μ/kg·m−1·s−1 | 4.9 × 10−3 | Reference temperature, Tref/K | 1685 |
| Solutal diffusivity, D/m2·s−1 | 5 × 10−9 | Eutectic mass fraction, /% | 37.5 |
| Latent heat, L/J·kg−1 | 2.9 × 105 | Eutectic mass fraction, /% | 76.1 |
| Thermal expansion coefficient, βT/K−1 | 1.2 × 10−4 | Eutectic temperature, Te/K | 1560 |
| Slope of liquidus, mAl/K·(wt%)−1 | −5.17 | Melting temperature, Tm/K | 1754 |
| Slope of liquidus, mTa/K·(wt%)−1 | −2.55 | Electrical conductivity, σ/Ω−1·m−1 | 7.3 × 105 |
| Equilibrium partition coefficient, kAl | 0.54 | Magnetic permeability, μ/H·m−1 | 1.26 × 10−6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, J.; Li, B.; Liu, Z.; Qi, F.; Zhang, B.; Zhang, J. Numerical Investigation of Segregation Evolution during the Vacuum Arc Remelting Process of Ni-Based Superalloy Ingots. Metals 2021, 11, 2046. https://doi.org/10.3390/met11122046
Cui J, Li B, Liu Z, Qi F, Zhang B, Zhang J. Numerical Investigation of Segregation Evolution during the Vacuum Arc Remelting Process of Ni-Based Superalloy Ingots. Metals. 2021; 11(12):2046. https://doi.org/10.3390/met11122046
Chicago/Turabian StyleCui, Jiajun, Baokuan Li, Zhongqiu Liu, Fengsheng Qi, Beijiang Zhang, and Ji Zhang. 2021. "Numerical Investigation of Segregation Evolution during the Vacuum Arc Remelting Process of Ni-Based Superalloy Ingots" Metals 11, no. 12: 2046. https://doi.org/10.3390/met11122046
APA StyleCui, J., Li, B., Liu, Z., Qi, F., Zhang, B., & Zhang, J. (2021). Numerical Investigation of Segregation Evolution during the Vacuum Arc Remelting Process of Ni-Based Superalloy Ingots. Metals, 11(12), 2046. https://doi.org/10.3390/met11122046





