Future Trends on Displacive Stress and Strain Induced Transformations in Steels

Abstract

Displacive stress and strain induced transformations are those transformations that occur when the formation of martensite or bainitic ferrite is promoted by the application of stress or strain. These transformations have been shown to be one of the mechanisms by which the mechanical properties of a microstructure can be improved, as they lead to a better ductility and strength by the transformation induced plasticity effect. This review aims to summarize the fundamental knowledge about them, both in fully austenitic or in multiphase structures, pointing out the issues that—according to the authors’ opinion—need further research. Knowing the mechanisms that govern the stress and strain induced transformation could enable to optimize the thermomechanical treatments and improve the final microstructure properties.

1. Introduction

Displacive stress induced transformations (SIT) and strain/deformation induced transformations (DIT) include the transformations from austenite (γ), which has a face-centered cubic (fcc) structure, to either martensite or bainitic ferrite, promoted by the application of elastic stress or plastic strain, respectively [1,2,3,4]. This type of transformations can happen from the austenite in microstructures in which the austenite is the only phase [5,6,7,8,9,10,11], which are called fully austenitic microstructures, from now on. They can also occur from the retained austenite in microstructures which consist of different phases [1,4,12,13,14,15,16,17,18,19], which are named multiphase microstructures, from now on. Some examples of multiphase microstructures are microstructures consisting of allotriomorphic ferrite, martensite, bainitic ferrite, and retained austenite [20], bainitic microstructures with retained austenite [21] or microstructures obtained by a quenching and partitioning (Q&P) treatment with retained austenite [22]. The SIT/DIT can happen while a microstructure is subjected to a mechanical test or in a thermomechanical treatment by which a certain final microstructure is aimed.

With respect to the first scenario (SIT/DIT in mechanical tests), the former research on displacive SIT and DIT has mainly focused on the martensite transformation induced plasticity (TRIP) effect at room temperature, which can happen in austenitic or in multiphase microstructures. The TRIP effect refers to the effect by which a SIT/DIT may lead to improved mechanical properties, as these transformations are associated to an increase of volume, i.e., an increase of elongation and an increase of the dislocation density. However, the optimization of the mechanical properties by TRIP effect is not straightforward. The effect of the stress or strain induced martensite on the mechanical properties can vary depending on several factors, such as the thermal or mechanical austenite stability [23,24] and the product phase [25]. In addition, the complexity of the initial microstructure can also have other effects on these transformations, such as the effect of the matrix in multiphase steels [26,27,28]. Oppositely to the wide knowledge about martensite TRIP effect, the bainite TRIP effect has not been so studied. Although this transformation has been detected in multiphase steels deformed above room temperature [2,3,4,19,29], its effect on the mechanical properties and its differences with respect to the martensite TRIP effect have not been assessed yet.

Concerning the second case (SIT/DIT happening in thermomechanical treatments), there are many scenarios that have not received much attention, especially the ones involving the formation of bainite. For instance, although the bainite SIT/DIT has been studied under constant stress [30,31,32,33,34], the formation of bainite while straining fully austenitized steels [35,36] has not been deeply assessed.

In this review, the knowledge about displacive SIT/DIT is summarized, emphasizing some controversial issues or questions that have not been answered yet and that need further research at this point. This review is focused on the phase transformations, regardless of in which process they take place. Therefore, transformations which happen in thermomechanical treatments and in mechanical tests are discussed in many cases concurrently if the authors consider that it helps to better understand the concepts. We believe that a better knowledge of the SIT/DIT mechanisms and their characteristics could help to improve the final mechanical properties of a microstructure. This improvement could imply the correct selection of the steel chemical compositions and the thermal/thermomechanical processes parameters, with the aim of either getting microstructures composed of phases that are obtained by SIT/DIT during a thermomechanical treatment or to optimize the TRIP effect that a given austenitic or multiphase microstructure presents.

2. Metastable Phases Formed by Stress and Strain Induced Transformations

As mentioned, the product of SIT and DIT include martensite and bainitic ferrite. The structure of the bainitic ferrite (α_B) is always either body-centered cubic (bcc) or body centered tetragonal (bct) and it has morphology of plate or lath. Depending on the chemical composition of the steel, a bainitic microstructure can contain cementite, martensite, and/or retained austenite, apart from α_B. Figure 1a,b show two micrographs showing the granular bainite and plate-like bainite microstructures that were formed in a medium carbon high silicon steel by a DIT at 520 °C and 400 °C, respectively [35].

However, the structure of martensite is not always the same. In many cases, two different types of martensite are detected: α′-martensite and ε-martensite. The former one is the most common type of martensite, with a bcc or bct structure and whose nucleation is associated with dislocation pile-ups on the active slip plane of γ [39]. On the other hand, ε-martensite, which has a hexagonal close-packed (hcp) structure, is less common. ε-martensite has been mainly studied in high manganese steels or in austenitic steels (>12 wt. %) [39,40,41,42,43,44,45,46], although it has also been observed in a low fraction in low-alloy steels [47]. Its nucleation occurs from randomly spaced overlapping γ stacking faults formed at grain boundaries [39] and, in many occasions, it is an intermediate phase during the α′-martensite, i.e., the martensitic transformation follows the sequence γ→ ε →α′ [48]. Whereas Figure 1c is an example of a direct γ →α′ transformation observed while straining a 304 stainless steel at −32 °C, Figure 1d is an example of a γ→ ε →α′ transformation in a 304L steel deformed at −196 °C, as in the micrograph one can see a α′ embryo on a band of ε. In multiphase structures, the transformation process is usually γ →α′, where the transformation γ→ ε is only sporadically reported [47].

The appearance of the metastable phases named in this section as a product of SIT/DIT mainly depends on the chemical composition of the steel and on the deformation temperature. Hence, whereas the formation of stress or strain induced α′ is very common in many different microstructures [23,25,35,49,50,51,52,53,54,55,56], ε is mainly found in austenitic steels [23,25,39,48,52], although it has been sporadically detected in multiphase steels [47]. The formation of α_B has not been reported, to the authors’ knowledge, at room temperature, although it has been found in fully austenitized steels [35] and in multiphase steels [1,3,57] deformed at high temperatures.

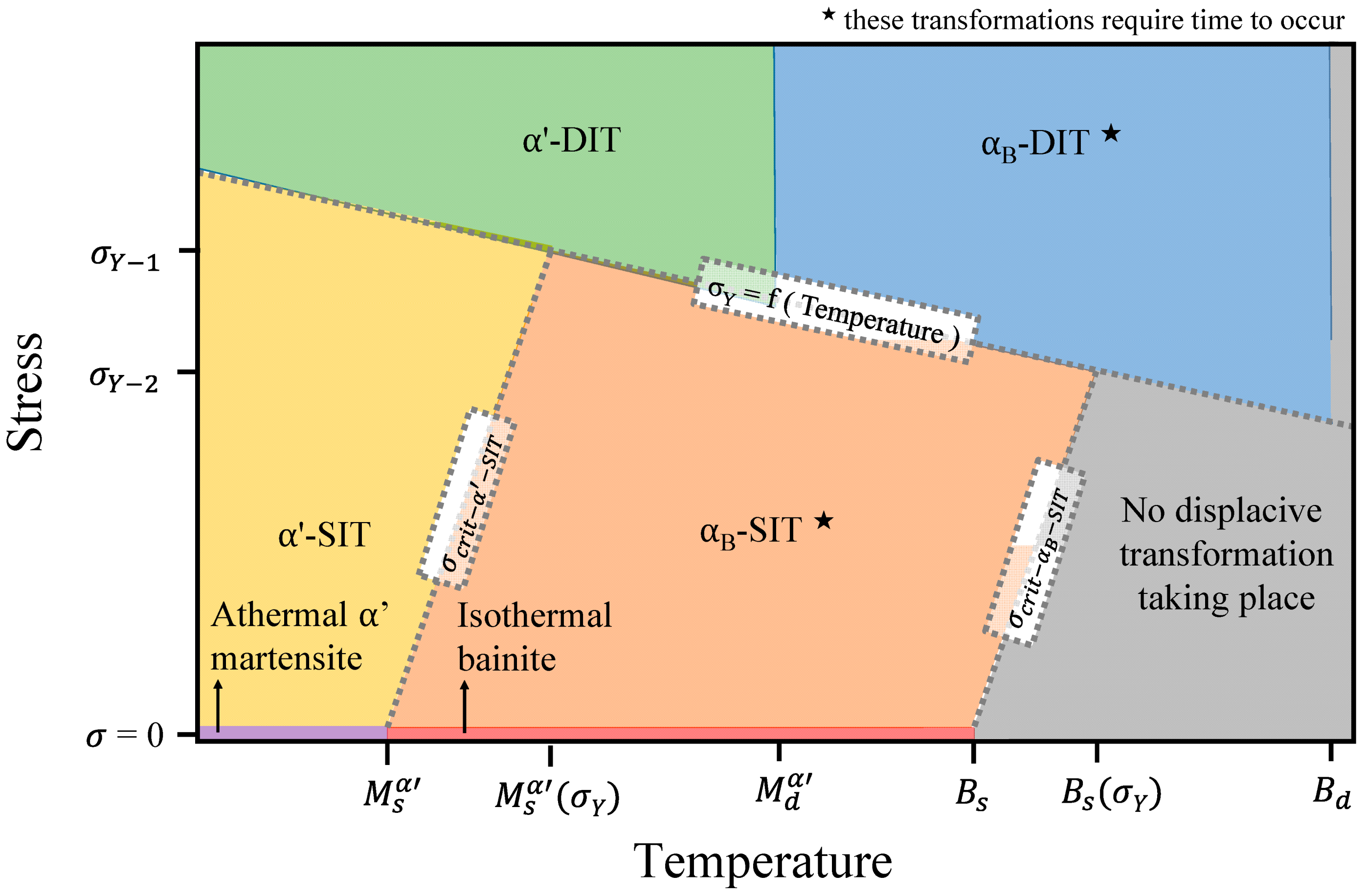
3. Conditions of Stress/Strain Induced Transformations

3.1. Stacking Fault Energy

The deformation mechanisms of γ mainly depend on the structure stacking fault energy (SFE) [58], which is a function of the chemical composition and temperature [59,60,61]. These mechanisms can be of different types: (a) the displacive SIT/DIT are promoted if SFE <18 mJ m⁻², (b) twinning occurs if SFE is in the range 18–45 mJ m⁻² and (c) dislocation glide happens if SFE >45 mJ m⁻² [62]. In addition, for SIT/DIT to happen, it is not only the SFE that must be below 18 mJ m⁻², but also the transformation must be thermodynamically feasible. An austenitic structure is said to be highly stable if it is required that a very high stress/strain is applied so that the transformation is induced. Although the γ stability mainly depends on the SFE, the driving force for the transformation also has an effect [63].

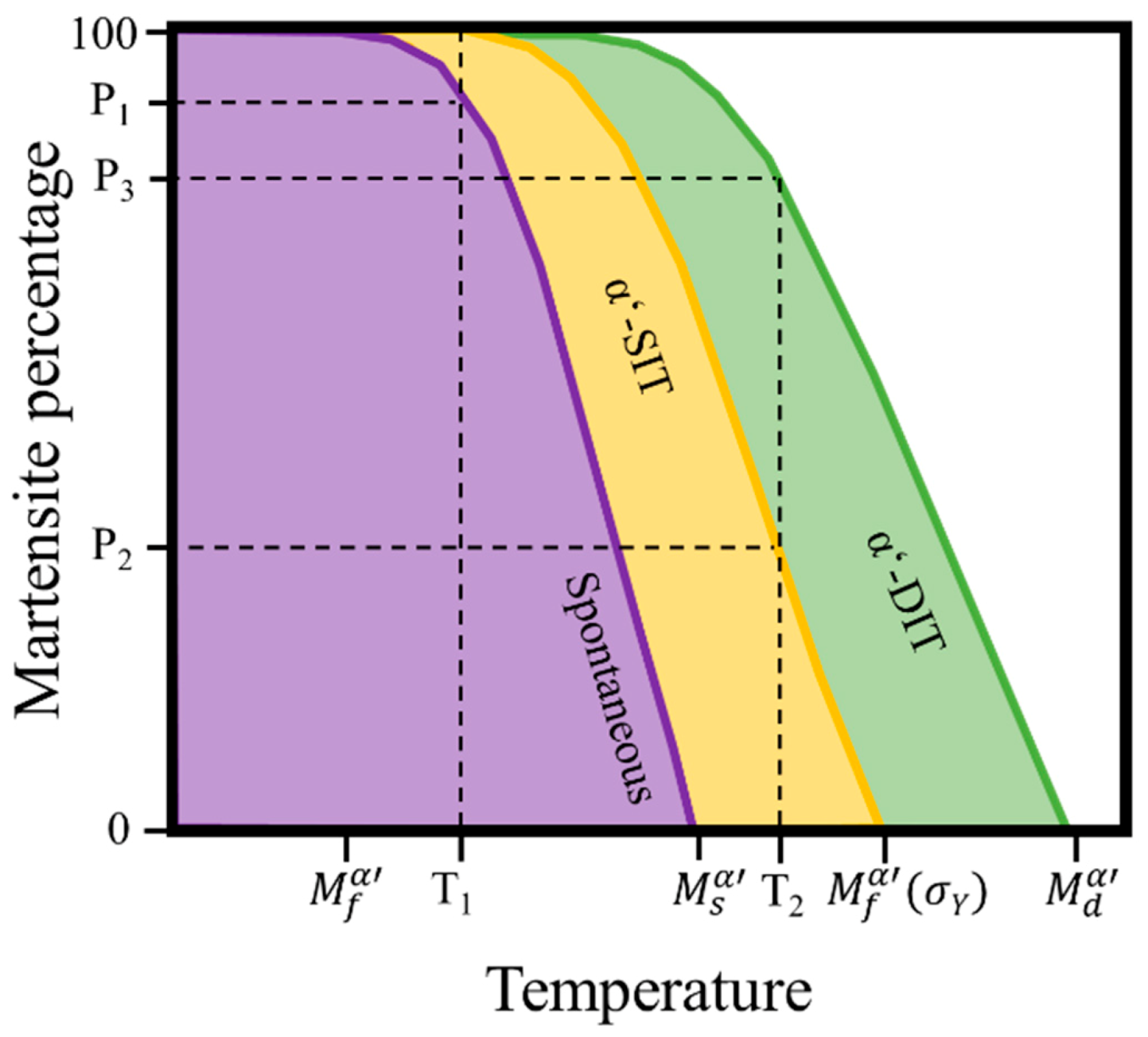
3.2. Critical Temperatures and Thermodynamics

In order to show the temperature and stress ranges in which different displacive SIT and DIT happen, Figure 2 is used. The schematic representation shown in that figure has been adapted from the diagram that Olson and Cohen made in [64] after the results of Bolling and Richman in Fe-Ni-C alloys [65,66,67,68], adding the different options for bainite transformations to it. It is worth noting that, for the sake of clarity, the diagram in Figure 2 does not include the formation of ε martensite. A similar diagram including the formation of ε and α′ can be found in [25]. All the transformations present in the diagram can be classified into three different groups: non-deformation-related or spontaneous transformations, SIT and DIT. While spontaneous transformations are those that happen when no stress or strain is involved, SIT an DIT can be distinguished according to the work by Fahr [24]. A transformation is considered as SIT if no plastic deformation is applied while/before the transformation happens, i.e., the applied stress is below the bulk parent austenite yield strength (${\sigma }_Y$). Therefore, the fcc structure is only elastically strained and no dislocations are introduced. In the same fashion, DIT involve austenite dislocation slipping during/before the transformation. Thus, as can be seen in Figure 2, the SIT upper limit is the line ${\sigma }_Y$ = f (Temperature), above which DIT occur. Note that this classification does not enable to describe the mechanisms triggering the phase transformation, as opposite to Chaterjee and Bhadeshia’s [69]. However, it is useful as it states whether the introduction of dislocations and its effect on the transformation are implicit or not.

3.2.1. Spontaneous Martensite and Bainite Transformations

To start with, spontaneous martensite and bainite transformations are those that happen when neither stress nor strain is involved. The former ones occur below $M_s^{{\alpha }^{\prime }}$ or $M_s^{\epsilon }$ —the α′ and ε martensite start temperatures—and they are athermal. For simplicity, from now on, it is referred to the highest of the $M_s^{{\alpha }^{\prime }}$ and $M_s^{\epsilon }$ temperatures as $M_s$, since a martensite transformation starts as soon as the temperature goes below $M_s$. If $M_s^{{\alpha }^{\prime }}$>$M_s^{\epsilon }$, ε martensite is never formed and the transformation is of the type γ→ α′, where the α′ martensite volume fraction increases as the temperature is decreased down to $M_f^{\alpha }$, the martensite finish temperature [70]. If $M_S^{{\alpha }^{\prime }}$<$M_S^{\epsilon }$, the transformation is of the type γ→ ε →α′. Thus, once the temperature goes below $M_S^{\epsilon }$, the transformation γ→ ε starts, increasing the ε fraction as the temperature decreases until $M_S^{{\alpha }^{\prime }}$ is reached, moment in which the transformation ε →α′ begins [41]. Among other factors, the $M_s^{{\alpha }^{\prime }}$ and $M_s^{\epsilon }$ temperatures are mainly functions of the chemical composition, the prior austenite grain size (PAGS) [45,46,71] and the cooling rate [44,72]. One can express the thermodynamic condition for a α′ transformation as stated in Equation (1). The $M_S^{{\alpha }^{\prime }}$ temperature is the maximum temperature at which that balance is met.

$$\Delta G^{\gamma \to \alpha }\le \Delta G_N^{{\alpha }^{\prime }}$$

(1)

In Equation (1), $\Delta G^{\gamma \to \alpha }$ is the total driving force of the system and $\Delta G_N^{{\alpha }^{\prime }}$ is the critical driving force needed to stimulate martensite by an athermal, diffusionless nucleation and growth mechanism [73]. Note that, for a spontaneous transformation, $\Delta G^{\gamma \to \alpha }=\Delta G_{ch}^{\gamma \to \alpha }$, where $\Delta G_{ch}^{\gamma \to \alpha }$ is the chemical driving force. The critical driving force $\Delta G_N^{{\alpha }^{\prime }}$ can be calculated by the expression derived by Ghosh and Olson as a function of the chemical composition [73].

Although there is scarce information on the thermodynamics of ε martensite, it would be intuitive to think that the transformation would happen ruled by a balance similar to that of Equation (1). However, this approach has been shown only to work in some cases if Thermo-Calc is used to calculate the corresponding driving force $\Delta G^{\gamma \to \epsilon }$ [74,75], most likely because of the lack of databases that make the thermodynamic calculations inaccurate [76]. There are some other studies that propose other methodologies to calculate $\Delta G^{\gamma \to \epsilon }$ [77,78], suggesting to include the effect of the PAGS on the thermodynamic balance [45], suggesting a value for the critical driving force for the transformation γ→ ε [45,75] or deriving empirical formulae for the calculation of $M_S^{\epsilon }$ [74,76,79]. However, there is still no agreement in which is the most accurate or which has a wider range of applicability in terms of chemical composition. Further research on this topic is required.

Regarding bainite transformations, they are thermally activated, which means that they require some time in order to start. In the absence of stress or strain, they are thermodynamically possible in the range $M_s$-$B_s$, where $B_s$ is the bainite start temperature. The $B_s$ also depends on the chemical composition of the steel and on the PAGS [80]. Thermodynamically, bainite transformations occur as long as the conditions in Equations (2) and (3) are met.

$$\Delta G^{\gamma \to {\gamma }^{\prime }+\alpha }\le \Delta G_N$$

(2)

$$\Delta G^{\gamma \to \alpha }\le -\Delta G_{SB}$$

(3)

where $\Delta G^{\gamma \to {\gamma }^{\prime }+\alpha }$ is the nucleation driving force under paraequibrium conditions, $G_{SB}$ is the stored energy of bainite (usually assumed to be 400 J mol⁻¹ [31]) and $\Delta G_N$ is the critical driving force for the nucleation (in J mol⁻¹), which can be calculated by the expression derived by Bhadeshia as a function of the temperature [81,82].

3.2.2. Stress-Induced Martensite and Bainite Transformations

Displacive SIT cannot happen at any temperature or stress level, but they must meet some criteria to be thermodynamically possible. For a given applied stress $\sigma$, the critical temperatures above which the α′, ε and α_B SIT cannot take place are named $M_s^{{\alpha }^{\prime }}\left(\sigma \right)$, $M_s^{\epsilon }\left(\sigma \right)$ and $B_s\left(\sigma \right)$, respectively. If one considers the maximum stress for a SIT, ${\sigma }_Y$, one can define the critical temperatures for any α′, ε and α_B SIT: $M_s^{{\alpha }^{\prime }}\left({\sigma }_Y\right)$, $M_s^{\epsilon }\left({\sigma }_Y\right)$, and $B_s\left({\sigma }_Y\right)$ [35,64]. For a given temperature, the critical stress that must be applied so that a α′, ε or a α_B SIT starts is called ${\sigma }_{crit-{\alpha }^{\prime }-SIT}$, ${\sigma }_{crit-\epsilon -SIT}$ and ${\sigma }_{crit-{\alpha }_B-SIT}$, respectively. For the sake of clarity, in this review, the terms $M_s\left({\sigma }_Y\right)$ and $M_s\left(\sigma \right)$ are used to refer to the highest temperature at which a martensite SIT can happen under a stress ${\sigma }_Y$ or $\sigma$, respectively. Similarly, the critical stress for which a SIT of any type starts at a given temperature is referred to as ${\sigma }_{crit-SIT}$.

Once these terms are defined, one can go on to define the corresponding thermodynamic balances. First, only the conditions for α′and α_B are assessed. Regarding the second phase, so far, it has been assumed that the stress does not affect the α_B nucleation [31,83]. Therefore, to calculate ${\sigma }_{crit-{\alpha }^{\prime }-SIT}$ and ${\sigma }_{crit-{\alpha }_B-SIT}$ as a function of the temperature, as shown in Figure 2, one can use the balances in Equations (1)–(3). In this case, $\Delta G^{\gamma \to \alpha }$ is no longer equal to $\Delta G_{ch}^{\gamma \to \alpha }$, but equal to $\Delta G_{ch}^{\gamma \to \alpha }+\Delta G_{mech}$, where $\Delta G_{mech}$ is defined in Equation (4) [84]. Also, note that the critical temperatures $M_s^{{\alpha }^{\prime }}\left({\sigma }_Y\right)$ and $B_s\left({\sigma }_Y\right)$ coincide with the temperatures at which the ${\sigma }_{crit-{\alpha }^{\prime }-SIT}$ and ${\sigma }_{crit-{\alpha }_B-SIT}$ lines meet the austenite ${\sigma }_Y$ line in Figure 2 [64].

$$\Delta G_{mech}=- \sigma :\epsilon$$

(4)

$\sigma$ and $\epsilon$ are the stress tensor and the tensor describing the strains induced by the formation of a ferrite subunit, respectively. If the coordinate system is taken so that its Y axis is normal to the subunit habit plane and the x-axis is along the shear direction, then the tensor $\epsilon$ can be calculated as shown in Equation (5), where $s$ and $\zeta$ are the shear and dilatational strains associated with the α or α_B transformation, which usually lie in the ranges 0.20–0.45 [85,86,87,88,89] and 0.03–0.04, respectively [85,86,87,89].

$$\epsilon =\left(\begin{array}{ccc}0& \frac{1}{2}s& 0\\ \frac{1}{2}s& \zeta & 0\\ 0& 0& 0\end{array}\right)$$

(5)

Patel and Cohen derived the expression in Equation (4) assuming different deformation modes. Hence, in the case of uniaxial deformation, $\Delta G_{mech}$ can be calculated as shown in Equation (6), where the second term is preceded by a plus sign in the case the deformation mode is compression and a minus sign in the case the deformation mode is tension [84]. Although the angle $\theta$ was originally defined as the angle between the compression/tension direction and the normal to any potential habit plane, it is usually considered as the angle for which the transformation is promoted the most (i.e., $\Delta G_{mech}$ is maximum in absolute value): $\theta =\arctan \left(\frac{s}{\zeta }\right)/2$ [84]. In the case of hydrostatic pressure, $\Delta G_{mech}$ can be calculated as shown in Equation (7). Hence, in the case of uniaxial deformation, the stress application always promotes the α′ and the α_B transformations, where the transformation is promoted in a higher extent if the deformation mode is tension. However, if an hydrostatic deformation is applied, the transformation is not promoted, but impeded [84]. Note that an expression for other deformation modes that have been studied, such as torsion, were not derived by Patel and Cohen, although it would be possible to derive their expressions from Equation (4).

$$\Delta G_{mech}=-\frac{1}{2}s\sigma \sin 2\theta \pm \frac{1}{2}\zeta \sigma \left(1+\cos 2\theta \right)$$

(6)

$$\Delta G_{mech}=\frac{1}{2}\zeta \sigma$$

(7)

Although these definitions of $\Delta G_{mech}$ by Patel and Cohen [84] are the most commonly used to explain the effect of stress on the driving force for the transformation and to calculate $M_s^{{\alpha }^{\prime }}\left({\sigma }_Y\right)$ and $B_s\left({\sigma }_Y\right)$, there are more recent models or studies that also consider other parameters, such as the PAGS [90,91], the chemical composition [92] or the austenite texture [93].

The authors would like to emphasize that, as can be seen in Figure 2, the SIT lower limits are not considered $M_s^{{\alpha }^{\prime }}$ and $B_s$, even though below those temperatures the α′ and α_B transformations are thermodynamically possible in the absence of stress or strain. This has been considered because the application of stress in those temperature ranges further stimulates the corresponding reaction and the transformation stops once the stress is removed. For instance, in the case of α′, if a steel is cooled down to a temperature T₁ in the range $M_f^{{\alpha }^{\prime }}$-$M_s^{{\alpha }^{\prime }}$, see Figure 3, a certain volume fraction P₁ < 100% transforms to α′. However, if a stress below ${\sigma }_Y$ is applied to the structure, the driving force for the transformation increases (in absolute value) and so does the volume fraction of α′, reaching even 100% in some cases. It has been previously reported that austenitic structures subjected to stress are able to transform to α′ in a higher extent than the same structures in a stress-free state [49]. After that, if the load was removed, the volume fraction of austenite would not further go up. In the case of bainite, let us take austenite to the α_B temperature range and hold the temperature for a long enough time so that the transformation is finished. Subsequently, an external stress is applied to the structure, which increases the driving force for the transformation and, thus, shifts the T₀ curve, line that shows the carbon content in austenite above which bainitic transformation becomes thermodynamically impossible [94]. This promotes that the transformation goes further and the volume fraction of α_B further increases. If the stress is removed before the new T₀ carbon content is achieved, the transformation stops. Note that, although this behavior is ‘theoretically’ expected, so far, this type of experiment has not been carried out.

Concerning the formation of ε martensite, the calculation of $M_s^{ϵ}\left(\sigma \right)$ was assessed by Andersson et al. [96], who thermodynamically considered the applied stress by adding the effect of the mechanical driving force to the chemical driving force for the transformation $\Delta G^{\gamma \to \epsilon }$, similarly than for α′. Although they proved that their methodology worked for their cases of study in Fe-Mn-Si alloys, the γ→ ε transformation is not fully understood from a thermodynamic point of view, as there is no way of calculating the $M_s^{ϵ}$ temperature that works for any steel. The solution firstly involves the full understanding of the thermodynamics governing the γ→ ε transformation before trying to understand the transformation under stress.

3.2.3. Strain Induced Martensite and Bainite Transformations

Regarding α′, ε, and α_B DIT, they happen below the critical temperatures $M_d^{{\alpha }^{\prime }}$, $M_d^{\epsilon }$ and $B_d$, respectively, provided that the applied stress is higher than a critical stress ${\sigma }_{crit-{\alpha }^{\prime }-DIT}$, ${\sigma }_{crit-\epsilon -DIT}$, or ${\sigma }_{crit-{\alpha }_B-DIT}$, respectively, always higher than the austenite ${\sigma }_Y$, as previously mentioned and shown in Figure 2 [23,25]. Similarly to martensite SIT, from now on, when it is aimed to talk about a critical temperature for martensite DIT and it is not necessary to specify whether the product phase is α′ or ε, the general term $M_d$ is used. Also, the critical stress for a DIT at a given temperature is named ${\sigma }_{crit-DIT}$. Although the ε DIT has been reported in many studies [39,40,41], it has not been formulated how the application of stress and plastic strain affects the thermodynamic state of the system. Regarding α′ and α_B, the dislocations introduced during the deformation affect the growth of both of them, altering the nucleation and growth energy balance in Equation (1) and the growth balance in Equation (3). For a plate/lath to grow, there is an additional driving force needed to overcome the dislocation density introduced by plastic deformation, ${\Delta G}_{disl}$. The new energy balances read now as shown in Equations (8) and (9) [70,97,98].

$$\Delta G^{\gamma \to \alpha }\le \Delta G_N^{{\alpha }^{\prime }}-{\Delta G}_{disl}$$

(8)

$$\Delta G^{\gamma \to \alpha }\le -\Delta G_{SB}-{\Delta G}_{disl}$$

(9)

The value of ${\Delta G}_{disl}$ depends on the initial and final (after deformation) dislocation densities (${\rho }_0$ and $\rho$, respectively), on the austenite Poisson ratio $\nu$, on the austenite Burgers vector $b_T$, on the austenite shear modulus, ${\mu }_T,$ and on the temperature T, as shown in [70,97,98], see Equation (10).

$${\Delta G}_{disl}=\frac{{\mu }_T{b}_T\left({\rho }^{1/2}-{\rho }_0^{1/2}\right)}{8 \pi \left(1-\nu \right)}$$

(10)

Regarding the nucleation of α_B, although it is known that is promoted by the presence of a larger amount of defects or slip bands [99] generated during plastic deformation [31], it has not been reported how the nucleation condition found in Equation (2) is modified because of the increase of nucleation sites. Further information on the calculation of the $M_d^{{\alpha }^{\prime }}$ and $B_d$ critical temperatures or energies can be found in [35].

Again, it is considered that α′ and α_B DIT can happen below the $M_s^{{\alpha }^{\prime }}\left({\sigma }_Y\right)$ and $B_s\left({\sigma }_Y\right)$ temperatures, respectively, as seen in Figure 2 because, even though the α′ and α_B transformations are thermodynamically possible below those temperatures if plastic deformation is not applied, the application of plastic strain enables to further stimulate both transformations. Coming back to Figure 3 and assuming that austenite is cooled down to a temperature T₂ in the range $M_s^{{\alpha }^{\prime }}$-$M_s^{{\alpha }^{\prime }}\left({\sigma }_Y\right)$, if neither stress nor strain are applied, the structure remains fully austenitic. However, if stress is increased up to σ_Y, the α′ transformation is induced by stress until a fraction P₂ is reached. If the stress is further increased, α′ is be strain-induced and the fraction could increase up to P₃. Note that, in this case, P₃ < 100%. Also, in the case of α_B, it is possible that the modification of the thermodynamics due to the application of strain also modifies the kinetics, although only while the stress is applied. For instance, it has been previously reported that a α_B DIT taking place while deforming a fully austenitized medium carbon steel at 520 °C and 400 °C got interrupted after the load was removed. Bainitic transformation did not start again until several tens of seconds later [35].

4. Resultant Microstructures of Stress and Strain Induced Transformations and Their Strain Hardening Capacity

In this section, the characteristics of α′/ε/α_B SIT and DIT are described. These transformations can be obtained by different routes that are detailed next. The most common scenarios are shown in Figure 4. Note that the deformation temperatures could be reached in Figure 4b,c by heating, instead of cooling, depending on the chemical composition of the steel and on whether an initial fully austenitic or multiphase microstructure is aimed. In those cases, the microstructure may need a previous austenitization or a previous heat-treatment, respectively. The characteristics of the SIT/DIT taking place during the mentioned treatments would only be expected to vary significantly depending on the initial structure and not on how the initial structure was obtained.

4.1. Stress or Strain Induced Martensite Transformations

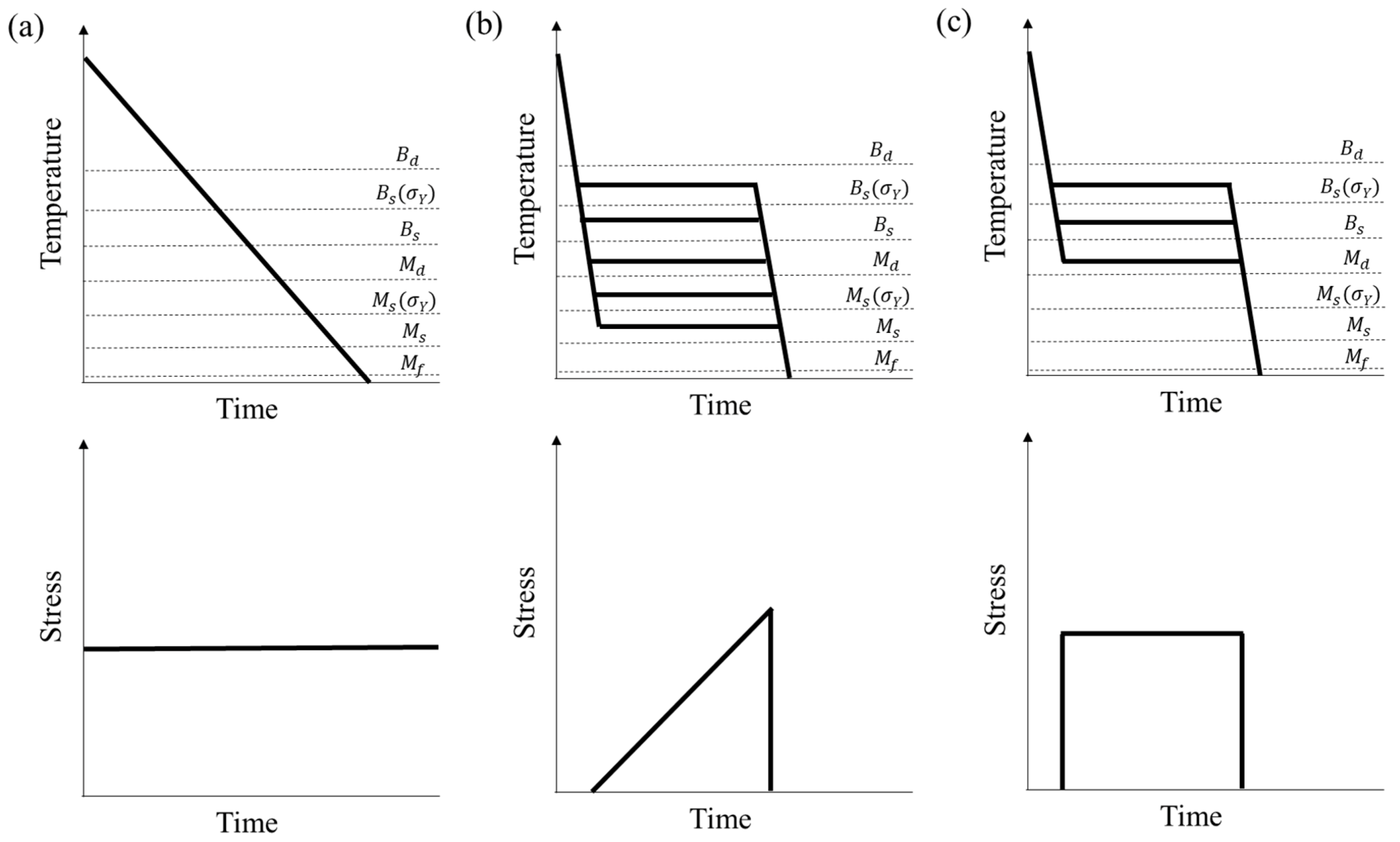
4.1.1. Continuous Cooling Treatments under Constant Stress

One of the most studied treatments during which martensite is induced is the continuous cooling treatment under constant stress $\sigma$, see Figure 4a. Usually, the initial structure is fully austenitic, either because the steel of study is austenitic or because it has been previously austenitized (high temperature deformation). In this case, if the cooling rate was high enough to avoid ferritic/pearlitic/bainitic transformations, a martensite transformation would happen [49,92,100]. The transformation would be athermal, it would start at a temperature $M_s\left(\sigma \right)$ [49,92,100], where $M_s\left(\sigma \right)$ would be higher than $M_s$ if the deformation mode was uniaxial tension, uniaxial compression or torsion [49,92,100,101,102,103]. In addition, in cases in which the $M_f^{{\alpha }^{\prime }}$ temperature was above room temperature, the α′ volume fraction would increase under stress, because of the additional mechanical driving force and (if the applied stress was above the austenite ${\sigma }_Y$) the increase in nucleation sites [49]. In cases in which no plastic deformation was introduced, the addition of the mechanical driving force would not only affect the start of the α′ transformation, but also the selection of specific crystallographic variants [84,104,105,106], especially during the first stages of the transformation [106]. The selected variants would have the highest total driving force in absolute value, as $\Delta G_{mech}$ is a function of the position of the habit plane [84,104,105]. Variant selection in α′ has also been reported in transformations on continuous cooling under stresses higher than the ${\sigma }_Y$ by Liu et al. and it has been associated to the application of stress rather than to the introduction of dislocations [49]. This assumption would follow the same line of thought of Tamura, who suggested that the strain-induced transformations can be understood only in terms of the applied stress [50,107] or of Chatterjee and Bhadeshia, who reached the same conclusion later [69]. Regarding the martensite scale, Liu et al. reported that, the α′ microstructure obtained by applying 70 MPa to an austenitized medium carbon steel during continuous cooling was more refined than the stress-free α′ microstructure obtained by a continuous cooling. They attributed this refinement to the small applied plastic deformation (<5%), which led to the recrystallization of some prior austenite grains at high temperature and to a dislocation density increase in the non-recrystallized grains. The scale of the α′ strain-induced laths/plates has not been reported in any other study, to the authors’ knowledge.

No work in which multiphase structures with retained austenite were cooled under stress have been found by the authors. Although it would be expected that the transformation of the retained austenite would also be promoted at higher temperatures than the ones at which the stress-free martensite transformation would happen, it is important to consider that the retained austenite may also be subjected to hydrostatic stresses that would lead to the stabilization of the retained austenite.

4.1.2. Deformation at a Constant Temperature

Martensite can also be induced when a steel is held at a fixed temperature T—always below $M_d$—while an increasing stress is applied, see Figure 4b. When martensite is induced during straining in austenite structures, it is possible that the transformation process is γ→ ε, γ→ ε →α′, or γ →α′ [25], depending on the applied strain and the deformation temperature [25], where the formation of ε is always preceded by the formation of stacking faults [39]. In addition, the application of stress can also lead to the coalescence of α′ or ε, as previously reported [108,109,110,111].

Regarding variant selection, stress/strain induced α′ [23,50,51,52,112], and ε [23,48,52] present this phenomenon. Even when the transformation happens from a fully austenitic structure, there is no agreement about the reasons of the variant selection phenomenon. While some authors claim that variant selection in transformations from a fully austenitic structure may be explained by the mechanical driving force criterion [48,50,51,52], other authors suggest that some transformation sequences lead to local stress fields which make the analysis more complex [23]. The rules governing variant selection in TRIP transformations in multiphase structures—i.e., formation of stress or strain induced phases from retained austenite—have not been deeply studied. Yamashita et al. studied this phenomenon in a microstructure consisting of ferrite, bainitic ferrite, and retained austenite which was subjected to tensile tests. The retained austenite transformed to α′, always governed by variant selection, although the explanation for this variant selection was not always based on the mechanical driving force, but depended on the location of the retained austenite (at the ferrite grain boundaries or inside the ferrite matrix) [112]. The effect of other types of matrices on the selection of variants of α′ formed by TRIP effect in multiphase microstructures is still unclear.

The mechanical response that is observed when a fully austenitic structure is subjected to tension has been assessed in many austenitic steels. To better understand how a stress–strain curve changes under the influence of the appearance of martensite and why those changes occur, one can use Figure 5, where there are three stress–strain and their corresponding strain hardening rate-strain curves which correspond to three different steels which are fully austenitic before testing. The austenite ${\sigma }_Y$ of those three steels are the same at the testing temperature. Note that the steel B seems to yield at a lower stress, although this is only an effect of a stress-induced transformation, as is explained subsequently. Because of the different thermodynamics of the steels, steel A does not undergo any SIT/DIT while being deformed, steel B does undergo a SIT and steel C undergoes a DIT. Using the strain hardening rate-strain curve enables to notice much subtler abnormalities. As can be observed, if the transformation is SIT/DIT (steel B/C), the stress–strain curve takes a sigmoidal curve. After reaching ${\sigma }_{crit-SIT}$ and ${\sigma }_{crit-DIT}$, a SIT/DIT starts and the stress–strain behavior is no longer as would expected. From this point onwards, the martensite fraction increases as the stress to which the austenite is subjected is higher [107,113,114], mainly as a function of the strain and not of the temperature [115], until it reaches a limit, see Figure 3. There are several effects that compete when a SIT/DIT takes place during loading and they can be studied by looking at the strain hardening rate–strain curves in Figure 5b. The first of them is called dynamic softening and it is a product of the transformation working as a competing deformation mechanism. It is associated with the fact that the SIT/DIT transformation strain contributes to the total strain, while the stress increases more slowly [116,117] and it usually predominates at low strain values [10]. In some cases, this phenomenon has also been associated to the formation of ε in the early stages [118], as this phase has been proved to be almost ideally plastic [119]. Dynamic softening is characterized by a rapid decrease of the strain hardening rate, as happens for steels B and C in Figure 5b at low strain values. For higher strains, one can observe that the second effect, called static hardening, is predominant. Static hardening is characterized by a strong increase of the strain hardening rate due to the presence of martensite which acts as a reinforcing phase [116,117]. It has been previously reported that, during the static hardening effect, the martensite volume fraction can increase up to a given amount, called percolation threshold [120], and that, up to this point, the austenite stress level is similar to the macroscopic stress [63]. Once the martensite volume fraction is higher than the percolation threshold, the martensite forms a percolating cluster which extends through the whole structure [120]. In this stage, the strain hardening rate further increases until it reaches its maximum value and the austenite stress level deviates from the macroscopic stress level, suggesting that the material is acting as a composite [10,63]. Finally, once the volume fraction of martensite is close to the unity, the material behavior starts to resemble the martensite behavior and, hence, the strain hardening rate starts to decrease [63]. This final hardening has also been attributed to the activation of strain hardening mechanisms which involve a high dislocation density or a complex state of stress, among others [10]. Note that, although all the mentioned effects are predominant at different stages, it could be possible that some of them were not noticeable during the deformation process. These concepts can be extrapolated to the mechanical behavior of a multiphase structure if one understands that the initial microstructure has already a composite-like behavior [26], as would happen for an austenite structure in which α′ has formed by TRIP effect in a high fraction, i.e., after the percolation threshold has been overcome. However, in this case, the retained austenite may be more stable against deformation depending on several factors: (a) its chemical stability, which depends on its chemical composition [121]; (b) in the case that the matrix phase has formed by a displacive transformation, the stability of the retained austenite increases because of the hydrostatic stresses that the matrix exerts on this retained austenite, as reported in Section 3.2.2. [28]; and (c) if the matrix phase is α_B, the amount of dislocations introduced during the transformation in the retained austenite mechanically stabilize it [122].

Therefore, if one wants to control the mechanical properties of a microstructure which contains retained austenite or that is fully austenitic and that is expected to undergo TRIP effect, one must control several factors. First, as mentioned, the austenite stability is one of the most important factors controlling the mechanical properties of these structures. If the austenite stability is low, a SIT or DIT starts at very low strain values and the material yield strength and elongation are lower, although their ultimate tensile strength is high [23,24,123]. If the austenite is too stable, the TRIP effect may never occur, hence, its benefits cannot be exploited [123]. If the austenite stability is high enough, the ultimate tensile strength of the material is not so high, although its elongation is higher [24]. In addition, it has been reported that, in an austenitic steel with rather stable austenite, the formation of martensite—specially α′, rather than ε—during straining leads to higher uniform elongations [25] because of the suppression or delay of the necking phenomenon [124]. Previous studies have shown that the uniform elongation can be maximized if it is made sure that the induced transformation continues until the latter stage of deformation or the onset of necking [107,115,125] and that the transformation rate is slow, as the dislocations have time to be accommodated and the local stresses can be suppressed [23,115]. The combination of high strength and high ductility can be obtained at temperatures close to $M_d$ at which the DIT starts for high strains, before the necking effect takes place, enabling its suppression [24]. A similar effect has been reported in multiphase microstructures [126,127,128].

Second, the strain rate can also affect the mechanical behavior, depending on whether the specimen is deformed under isothermal or under adiabatic conditions, on the product phase and on the deformation temperature. Generally, under isothermal conditions, an increase of the strain rate leads to an increase of the final fraction of stress or strain induced martensite [6,129]. However, if the strain rate is too high, there is a transition from isothermal to adiabatic material behavior, which makes the SFE increase [9,120,129,130] and the driving force for the transformation decrease (in absolute value) [131]. Therefore, using higher strain rates would decrease the volume fraction of stress/strain induced martensite as the strain rate is higher [9,131,132,133,134]. In multiphase microstructures, the effect of the strain rate follows similar trends [135,136,137].

4.2. Stress or Strain Induced Bainite Transformations

The stress or strain induced bainite transformations have not been as studied as the martensite ones. For instance, the authors have not found any work where the effect of a constant stress on the bainite transformation in continuous cooled structures is assessed. However, the effect of a constant uniaxial stress on the α_B transformation has been assessed in isothermal treatments, as in Figure 4c. It has been found out that the application of an elastic uniaxial stress accelerates the α_B transformation [30,31,32,33,34], provided that the stress is not very low (few MPa) [33], attributed to the increase of driving force (in absolute value). The kinetics of the transformation were also shown to be accelerated when plastic uniaxial deformation was applied during the isothermal holding [31,99,138,139,140] as a result of the increase in nucleation sites (defects) [31]. Regarding the α_B volume fraction, although it would be expected to increase if the transformation happened under elastic stress due to the addition of the mechanical driving force, Shipway and Bhadeshia did not report changes for $\sigma$ < ${\sigma }_Y$ in a Fe-0.45C2.08Si-2.69Mn (wt %) steel [32]. If higher stresses are applied, the effect on the volume fraction of α_B is not clear, though. Although previous results have shown that the introduction of dislocations prior to the transformation mechanically stabilizes the austenite against either α_B or α′ transformation [97,98,141], theoretically, the addition of the mechanical driving force would shift the T₀ curve towards higher carbon content values. This would imply that the transformation would not stop until the austenite reached a higher carbon content, which may lead to a higher fraction of α_B. Although this fact was not discussed by Freiwillig et al., they showed that, when deformation was applied during an isothermal holding, the final volume fraction of α_B decreased with respect to the one obtained by the standard treatment if the steel carbon content was above 0.86 wt %, while it increased with respect to the one obtained by the standard treatment for a steel with carbon content of 0.43 wt % [138]. The application of stress has also been shown to lead to transformation plasticity strains, i.e., anisotropic portion of the transformation strains: the changes in length due to the α_B transformation are not the same along all axes [32,33,34,142,143]. This transformation plasticity is due to variant selection effects driven by the same mechanisms that drive the α′ transformations during continuous cooling under constant stresses, i.e., variants which are preferentially promoted by the applied stress (those whose habit plane lies at about 45° with respect to the deformation direction) tend to form first and their fraction tends to be the highest [30,33,34,104,143,144,145]. Variant selection affects the microstructure, which becomes much more organized after transformation under stress, i.e., in each PAG, there are fewer sheaves which are bigger than the ones obtained by stress-free transformation. The reduction of sheaves affects the number of blocks of austenite that are present in the microstructure, i.e., microstructures show less blocky γ if they have been transformed under the effect of stress [145]. To the best knowledge of the authors, the effect of the stress on the thickness of the α_B has not been assessed, although it would be expected that microstructures are refined because of the increase of driving force [146,147,148], ${\sigma }_Y$ (in the case ${\sigma }_Y$ is overcome) [146,147,148], and transformation kinetics [149]. It has been reported, though, that applying stress while a specimen is isothermally treated promoted the coalescence of α_B plates [150]. Nevertheless, further research is needed.

Finding studies about α_B SIT/DIT happening while straining a fully austenitic structure is not very common, only reported in [35,36] to the authors’ knowledge. In multiphase structures, the α_B SIT/DIT at temperatures higher than room temperature have been reported in few studies [2,3,4,19,29], although their effect on the mechanical properties or the differences with respect to the SIT/DIT taking place in fully austenitic structures has not been discussed. Further research would be needed in order to know if the conclusions made with the α′ and ε transformations could be extrapolated to α_B transformations, although some differences are expected, such as: (a) while the martensite transformation can be spontaneous, the bainitic transformation is thermally activated, which may inhibit the SIT/DIT in some extent; (b) while martensite transformation does not lead to any carbon partition, carbon is partitioned from α_B after a plate/lath is fully grown, which is expected to increase the SFE [151,152] and the driving force for the transformation [149], inhibiting the SIT/DIT in a higher extent as the transformation progresses [153]; (c) bainitic ferrite may not be as hard as martensite because of their different carbon contents, hence, the α_B TRIP effect may not lead to such a pronounced strengthening as the α′ TRIP.

5. Issues That Require Further Research

In this work, the knowledge about displacive stress and strain/deformation induced transformations—SIT and DIT—is reviewed, stating the different thermodynamic conditions, thermomechanical treatments and deformation conditions that are required for them to happen, either from a fully austenitic microstructure or from a multiphase one. Several issues that need further research, most of them associated to the formation of bainite, have been identified:

-

there is no agreement about the thermodynamic conditions that govern the formation of ε, neither athermally nor induced by stress or strain

-

it has been assumed that the nucleation of bainite is not affected by elastic stress, although it has not been experimentally proven

-

although it is known that the application of plastic deformation promotes the nucleation of α_B, this fact has not been modeled thermodynamically yet

-

the scale of the α′ and α_B stress/strain-induced laths/plates formed during continuous cooling or during isothermal treatments, respectively, has not been previously reported

-

the effect of a constant stress on continuous cooling bainitic microstructures has not been assessed in the literature so far

-

the effect on the volume fraction of strain induced α_B formed during isothermal treatments under constant stresses needs to be clarified

-

the effect of the matrix on the selection of variants of metastable phases formed by TRIP effect in multiphase microstructures is still unclear

-

the α_B SIT/DIT during tensile/compression deformation from a fully austenitic microstructure has not been studied in the literature and, therefore, it would be necessary to study these transformations, as there are several reasons that suggest that their mechanisms could be different to the ones governing the formation of martensite in the same conditions.