1. Introduction
The long service life and wear of technical infrastructure elements make it necessary to implement advanced computational methods that allow for the assessment of their operational safety, especially in the presence of damage such as voids and cracks. Starting from the twentieth century, fracture mechanics provided various types of solutions allowing for predicting the structural integrity of elements containing defects. The models described in the literature can be divided into several groups. In classical fracture mechanics, the material continuum is adopted, taking into consideration the phenomena occurring around the crack tip. Although this type of approach has been used for a long time, its significant limitation is the difficulty of transferring the results obtained from the laboratory experiments to the full scale structural elements. This is due to the fact that the results of laboratory tests relate to strictly defined conditions (geometry of the tested element, state of stress, etc.), therefore they cannot be generalized, and thus useful in engineering practice.
Micromechanical models, which describe the process of defect development on the basis of changes in the material microstructure, primarily nucleation, growth, and coalescence of microvoids [
1,
2,
3], are less limited in that sense. These types of models are not so sensitive to loading conditions, which makes them more universal, and thus more likely to be used in engineering [
4,
5].
Another approach involves application of phenomenological models, for instance, cohesive models, widely described in the literature. Their idea is to separate the process zone, in which the damage development is expected, and to assign a stress-displacement relation, with the simultaneous formulation of the failure criterion. It should be noted, however, that the traction–separation laws (TSL) in cohesive models are phenomenological in nature and do not take into account changes in the microstructure of the material. Thus, modeling the failure using cohesive models involves the use of an elastic or elastic–plastic material with a cohesive zone embedded in the analyzed structural element.
The application of the cohesive model does not require the presence of an initial crack, although the direction of the crack development is determined by the location of the cohesive surface in the model.
Currently, with the development of numerical methods and the increase in the available computing power, cohesive models have become a very useful and convenient tool for an engineer to solve problems of structural integrity. Cohesive models are currently used for a wide range of materials (metals, polymers, ceramics, composites, etc.).
2. Cohesive Models in Engineering
The cohesive zone concept was formulated in 1960s. Dugdale [
6] introduced plastic zone in the vicinity of the crack tip (
Figure 1).
As the stress in the plastic zone was limited to the value of (yield stress), the problem of stress state singularity in the crack tip vanishes. No strain hardening was considered, which results in the assumption of elastic–perfectly plastic material. The Dugdale model is restricted to plane stress conditions.
Barenblatt [
7] developed the above idea, replacing the plastic zone with a cohesive one (
Figure 2).
The distribution of cohesive stresses is a function of distance from the crack tip and does not depend on the applied load. The cohesive zone is thus a process zone in which both plastic deformation as well as voids and microcracks development take place, leading to crack propagation.
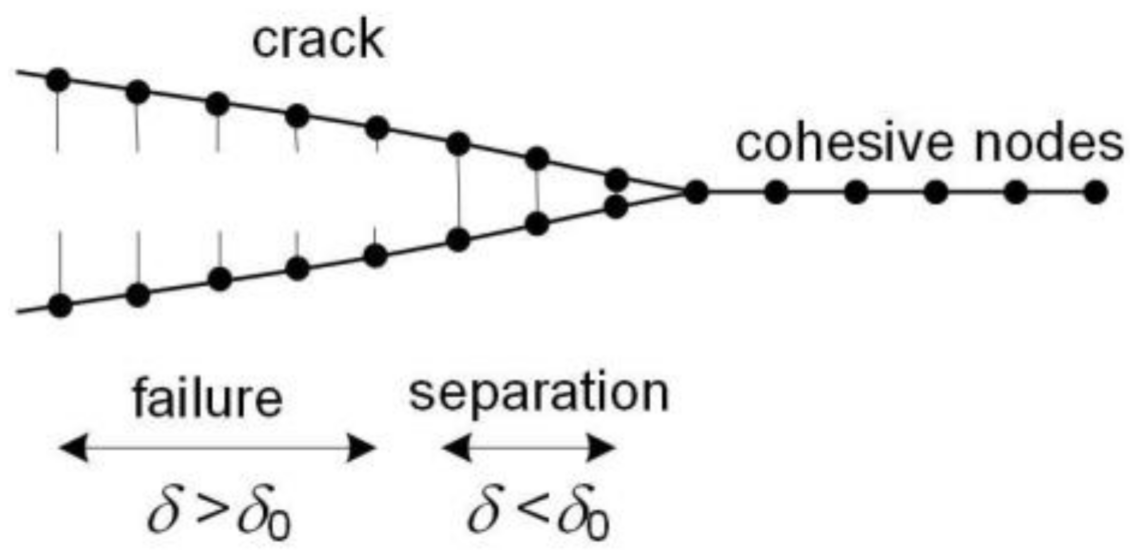
Currently used cohesive models combine the values of stresses
(traction) and displacements
(separation), as well as the energy needed to create a new surface. The relation between stresses and displacements is the so-called traction separation law (TSL). The cohesive surfaces are placed in the plane of the expected crack propagation, as shown in
Figure 3. When the critical displacement
is reached (according to the TSL), traction drops to 0, and local separation occurs, increasing the crack length.
Other important parameters of the TSL are the maximum traction
(cohesive strength) and the corresponding separation (
). Regardless of the critical values of stresses and displacements, TSL dependence curves can take various forms, depending on the type of material (brittle or ductile) and separation mechanism. The integration of the TSL function allows the value of the dissipated energy to be determined for a specific increase in the crack length. The separation energy thus corresponds to the critical Griffith energy release rate. Traction–separation laws most often cited in the literature are presented in
Figure 4.
As mentioned above, the basic factor influencing the nature of the TSL curve is the ductility of the material. In brittle materials, the cohesive strength is achieved with displacement
(
Figure 4a,b), therefore the failure process is initiated properly without local deformations in the cohesive area (rigid–plastic material). On the contrary, in the cohesive models dedicated to ductile materials, the maximum stress value is achieved with a non-zero displacement
value.
One of the first cohesive models as understood today was the Hillerborg model (
Figure 4a), used for brittle materials [
8]. Hillerborg et al., analyzing the process of crack development in concrete, proposed a linear, constantly decreasing, TSL condition with infinite initial material stiffness:
Bažant [
9], developing the concept of Hillerborg et al., applied the bilinear traction–separation relation to analyze the crack development in concrete. The adopted shape of the TSL curve required the introduction of additional model parameters (
and
—
Figure 4b), defining the break point of the curve. Tractions are calculated from Equation (2):
Similar to the Hillerborg model, the initial stiffness is infinite. It should be emphasized, however, that the use of an initially rigid cohesive model in the FEM framework may lead to numerical problems [
13].
Needleman [
10] proposed a cubic TSL function for ductile materials (mainly metals,
Figure 4c). Contrary to the Hillerborg and Bažant models mentioned above, the initial material response (traction ranging from 0 to
) is elastic. After reaching the maximum value, the stress drops steadily down to 0, when material separation occurs. In its general form, the Needleman solution takes into account the law of separation in 3 directions (1 normal and 2 tangential separation directions). By analyzing only the normal direction, the constitutive equation is simplified to the following form:
The work of separation is determined as the area under the TSL curve for
, according to the given relation:
The influence of tangential loading directions was captured in the constitutive model using the coefficient, which is another material parameter in the model.
Tvergaard [
14] generalized the above dependence, introducing the failure parameter, defined by the formula:
In the above relation, the indexes N and T denote separation in the normal and tangential directions, respectively. Taking the above into account, the TSL function for the normal direction is defined by the equation:
In a subsequent paper [
11], Needleman suggested the exponential function of TSL, based on atomistic simulations of the decohesion process carried out by Rose et al. [
15]. According to [
11], if shear separation is not taken into account, normal traction is described by the function:
where
and
.
The concept of using the exponential TSL equation was developed by Xu and Needleman [
16]. The proposed phenomenological model made it possible to simulate the total loss of the load capacity of the interface in the tangential direction. Xu and Needleman’s solution was developed and improved in [
17,
18].
In [
12], Tvergaard and Hutchinson used the trilinear TSL function (
Figure 4e) to model crack propagation under small-scale yielding conditions. The proposed shape of the TSL function required the introduction of additional material parameters
and
, according to Equation (8):
The formulation postulated by Tvergaard and Hutchinson introduces initial compliance
, which has no physical meaning, but only numerical significance, and thus should be adopted as small as possible [
19]. Assuming
and
one can obtain the TSL proposed by Lin et al. [
20].
Tvergaard and Hutchinson, in [
12], also analyzed the effect of the values of
and
on the results of the crack growth resistance. As demonstrated, the change of parameters in the analyzed range had little effect on the obtained results.
3. Recent Advances in Cohesive Zone Modeling
As mentioned before, due to their universality and relative simplicity of application, cohesive models are now increasingly used, and thus subjected to continuous development. Currently, the main topics of research and modification of cohesive models concern mixed mode loading, unloading and reverse loading, rate dependency, effect of triaxial stress state, fatigue, etc.
Due to its practical significance, the problem of analysis of the cohesive zone under a mixed mode loading has received considerable attention in recent years. Cohesive models taking into account mixed mode loading can be divided into potential and non-potential based function. In the models of the first group, the cohesive traction function is obtained by differentiating the potential function with respect to displacements. Their significant advantage is the small number of parameters and the associated ease of practical application. Non potential models incorporate an additional damage parameter to consider the cohesive zone degradation. This formulation requires, however, the introduction of additional variables, such as the failure activation criterion, the damage evolution law, and the failure criterion [
21,
22].
The disadvantage of potential-based models is the possibility of non-physical negative tractions, especially in the case where the value of the shear separation exceeds the normal separation. Such a phenomenon occurs, inter alia, in the classic Xu and Needleman model (
Section 2 of the present work). In recent years, several solutions have been proposed in the literature to reduce or overcome this limitation. McGarry et al. [
23,
24] modified the Xu and Needleman condition by introducing an additional parameter m, which regulates the influence of the tangent component in the mixed mode loading conditions. However, it should be emphasized that this type of solution does not completely eliminate the problem of negative traction and dissipation, but only reduces it.
Nowadays, cohesive zone models (CZMs) are extensively used to model macroscopic crack extension. However, for small, submicron crack lengths, typical CZMs may give incorrect results [
25]. Therefore, Zeng and Li [
26] developed a multi-scale cohesive model in which the bulk material is considered to be quasi-continuum medium. The TSL function was formulated in the accordance with coarse grained depletion potential formulation, related to the Derjaguin [
27] approximation of nonlocal colloidal interactions. This approach made it possible to develop a macro-scale atomistic cohesive model with reasonable computational effort. The numerical simulations of dynamic cracking showed the usefulness of the model in simulations of material discontinuities, such as grain boundaries, inclusions, slip lines, and others.
Currently, the Park-Paulino-Roesler (PPR) potential-based model [
28] is widely cited in the literature. An independent definition of the separation energy for pure loading modes allows for the analysis of high mode-mixity phenomena. The PPR formulation incorporates the physical fracture parameters, such as fracture energy, cohesive strength, and shape of the cohesive interactions. Due to its versatility and easy incorporation of additional features, it can be used in modeling of various material failure behavior. The introduction of dimensionless shape parameters
and
enables simple control of the softening scheme. A three-dimensional generalization of the PPR model was proposed in [
29].
Confalonieri and Perego [
30] established a cohesive model in the framework of non-potential approach. The proposed concept takes into account the energy distribution between pure loading modes (normal and shear separations), as well as the bilinear TSL function. The advantage of the model is the limitation of the number of model parameters, i.e., the TSL relationships for pure loading modes, critical energy values for each of them, and two phenomenological parameters taking into account the interaction of mixed loading modes. The adopted approach and the free energy density decomposition also results in a clear criterion for the failure activation function. Moreover, the model gives rational results for any proportion of loading modes, without necessity to determine equivalent traction and displacement values (compare [
31]). Likewise, there is no need to define the evolution of the fracture energy with changing ratios of the loading modes. The proposed model was extensively validated in [
30] in the field of mixed mode crack development of composite materials, obtaining a good agreement with the experimental results.
Giraldo-Londoño et al. [
32] analyzed two approaches to modeling mixed mode separation, taking into account the effect of strain rate. The first method involves the use of existing cohesive models in which the applied parameter values are rate dependent. Although this approach is not computationally demanding, it does not allow for a complete description of the physical phenomena occurring during dynamic fracture. Therefore, the authors proposed a viscoelastic model to analyze the behavior of the material in the front of crack. The model assumed the presence of two springs, the stiffness of which depends on the crack opening rate. The first spring acted in the normal direction, the second one in the direction tangent to the fracture plane. The method of the failure modeling was based on the PPR model.
The effect of the strain rate in the cohesive model was also taken into account in [
33]. The multi-scale model proposed by the authors describes the macroscopic behavior of the cohesive zone in relation to phenomena occurring at the molecular level. Thus, the effect of strain rate in the model results from the kinetics of the evolution of microdamages as a thermally activated process. The use of the proposed model for the simulation of rate-dependent fracture of silicon/epoxy interface allowed to obtain reasonable results with a small number of parameters needed.
Since in most cases the constitutive relations in cohesive models combine traction and separation, they do not take into account the stress state triaxiality. An attempt to incorporate the effect of the stress state in cohesive models was undertaken in [
34,
35,
36]. However, numerical simulations of crack development under plane strain conditions [
37] showed that taking into account the stress triaxiality in the cohesive model does not significantly affect the predicted fracture toughness curve. This is due to the fact that the cohesive energy is only a small part of the energy released during the crack development. The energy dissipated in the process of plastic deformation plays therefore the greatest role.
A separate, currently very intensively developed problem related to cohesive modeling is the consideration of cyclic loadings and fatigue. In addition to the problems discussed above, two key issues should be solved: Loading/unloading path and accumulation of damage [
38].
The unloading model is included in the traction–separation law. There are two different approaches. In the first one, regardless of the applied load, after unloading, the material returns to its initial state, in which both traction and separation are equal to 0 (
Figure 5a). This type of approach describes brittle failure, in which microcracks are able to fully close after complete unloading.
Modeling of ductile fracture, in turn, requires taking into account permanent separations (
Figure 5b), i.e., the unloading path is parallel to the initial load curve in TSL. Thus, after complete unloading (
), a permanent, non-zero separation value remains.
Consideration of the unloading is not sufficient to fully describe the fatigue process in the cohesive zone, because without taking into account the additional damage parameter, the cohesive model would only track the given loading/unloading path, which is not physical [
38].
To overcome this problem, 2 solutions have been proposed. In the first one, the paths of loading and unloading are defined independently, modifying the TSL law so that the traction value decreases with an increase in the number of cycles [
39]. The second method involves the introduction of an additional damage parameter, which gradually increases with the rising number of cycles, taking into account the decrease in traction [
40].
Regardless of the solution used, modeling of fatigue in the cohesive zone is time-consuming and computationally demanding, as it requires the analysis of subsequent loading cycles.
4. Problem of Parameters Identification
In practical applications, the problem of parameter identification is of particular importance. As a rule, the TSL dependence is characterized by the value of the critical separation at failure and maximum traction , which is sometimes replaced by the value of the unit separation energy .
Although the cohesive parameters are often treated as material constants, in fact their values depend on many factors, such as element thickness [
41], stress triaxiality [
42,
43], strain rate [
44,
45], and others.
In general, a complete analysis of the failure process requires the determination of the cohesive parameters separately for each of the 3 main loading modes and, depending on the model used, the determination of additional factors to incorporate the mixed mode loading conditions.
Taking into account the phenomenological nature of the cohesive models, the parameters can be determined by direct methods, i.e., by means of experimental tests, optionally combined with numerical analysis. The second group of methods, more widespread, is the classic method of fitting the results obtained experimentally and numerically. The two approaches can be combined by using the direct method to roughly estimate parameter values, which are then modified to achieve the best convergence of experimental and numerical results.
General recommendations regarding the methods of determining cohesive parameters are discussed in [
38]. The method of direct determination of the maximum traction
depends on the crack development mechanism (namely flat and slant fracture). The flat fracture requires a tensile test on a round specimen with a ring notch, with continuous recording of force F and the reduction of the cross-section diameter at the notch bottom (
). The next stage involves a numerical simulation of the test, using an elastic–plastic material model. The both experimental and numerical
curves should coincide up to the failure initiation, which takes place at the point of sudden drop of the
curve. In such a determined point of the diagram, the highest local stress value determined in the numerical model should be read, indicating maximum cohesive traction
(
Figure 6).
Determination of the cohesive strength in the slant fracture mechanism involves a procedure similar to that described above, although for this purpose, flat samples are used, for which a homogeneous stress distribution can be assumed. The value of the maximum traction is obtained by dividing the force value at the moment of failure initiation (defined above) by the current cross-sectional area of the neck.
In the direct method of determining the separation energy for flat fracture, it is assumed that the energy is equal to the critical value of the J integral at the crack initiation. The critical value is determined by marking on the R curve a vertical line, whose position corresponds to the critical width of the stretch zone. The ordinate of the point of intersection of the vertical line with the R curve corresponds to the value of the separation energy. The procedure is described in detail in [
38].
For slant fracture, no direct method of determining the cohesive energy has been developed so far, therefore, in this case, the indirect method of fitting curves obtained numerically and experimentally should be used.
As mentioned above, the indirect method of determining the cohesive parameters (fitting curve method) requires the comparison of numerical and experimental results. Standard specimens used in fracture mechanics are employed, but special care should be taken to ensure that the stress state and constraints in both specimens (used to determine the parameters and ultimately analyzed) are similar, to provide a similar failure mechanism.
The adjustment of the numerical and experimental results most often concerns the force—displacement relation or the R curve. As the first approximation of the cohesive parameters, one can adopt the values obtained by the direct method, described above.
Nielsen and Hutchinson [
46] used the results of a tensile test of a steel plate to determine the TSL function and the value of the separation energy in the cohesive model. For the problem of crack development under plane stress conditions, the cohesive energy was identified as the value of energy dissipated after the onset of necking, taking into account neck formation, shear localization, and slant fracture (
Figure 7). As the cohesive law describes the process of failure, the basis for determining the cohesive energy was the normalized stress—normalized displacement curve, in the softening range (
Figure 7). The value of the separation energy per unit area is therefore equal to the value of the area under the diagram in
Figure 7. As indicated in the figure, the separation energy is dissipated in two stages. The first one covers the range from the neck formation to the shear localization (energy
), and the latter further to failure (energy
). In total, the value of released energy is
, although, as shown in the figure, it is definitely dominated by the energy released in the first stage.
As mentioned above, the cohesive parameters can be identified by the mixed method, in which the parameter values are initially determined experimentally, and then calibrated by fitting numerical and experimental results. An example of the use of this type of procedure can be found in [
47]. The determination of maximum traction included a tensile test of the notched specimens and its numerical simulation using the elastic–plastic material. The value of the cohesive strength was assumed to be equal to the maximum local stress read on the sample axis in the FEM model. In order to determine the separation energy, the value of the J integral was identified experimentally using a standard CT specimen. The value determined in the experiment was then subjected to numerical calibration. Finally, the obtained values of the cohesive parameters were used to predict the R curve for the standard SE(B) specimen.
In the already mentioned work [
12], Tvergaard and Hutchinson used the Gurson model [
3] to determine the shape of the TSL curve and its parameters in the uniaxial stress state. It was assumed that the failure develops in a narrow zone, in which microvoid growth and coalescence occurs. The width of the zone was equal to the mean distance between voids. The normalized stress–elongation curve, obtained from the Gurson model, was the requested TSL function. Additionally, the effect of the initial void volume fraction in the Gurson model on the shape and maximum value of traction in the TSL curve was analyzed.
Similarly, the concept of using the Gurson model to determine cohesive parameters in a ductile material was used by Siegmund and Brocks in [
34]. The unit cell simulation using the Gurson model allowed for the identification of cohesive parameters (maximum traction and separation energy), depending on the stress state triaxiality factor (T). As the value of T increased, an increase in cohesive strength and a decrease in the separation energy were observed, which confirms the results obtained in [
48,
49]. The numerical analysis, discussed in the paper, involved procedure of cohesive parameters modification depending on the local value of T.
The simultaneous application of the cohesive model and the analysis of the phenomenological mechanism of the void development allowed separation of the energy dissipation rate into two components: The work of separation and the plastic dissipation rate. In the analyzed case, depending on the type and size of the specimen as well as on the crack length, the share of the separation work in the total dissipated energy did not exceed 12%.
A different approach is presented in [
50], where the cohesive parameters of epoxy and TR (transparent thermoplastic) resin interface were analyzed. The authors made an attempt to define the cohesive law and its parameters in the case of mixed-mode loading. Using the displacement values measured in the experiment and the results of the numerical simulation, the cohesive parameters were inversely determined by the field projection method. Nonlinear deformations and damage near the crack tip were the basis for determining the cohesive parameters (tractions and separations) on the crack surface behind the crack tip.
Currently, cohesive models are also used to model the failure initiation on a microscopic scale, including the process of separation of the material matrix and the second phase particles. In this case, the determination of cohesive parameters is more complex and requires a microstructural analysis, most often combined with numerical methods. For example, Giovanola et al. [
51] analyzed the critical separation stress of the matrix and carbide particles in steel using a combination of experimental studies and FEM analyses. In order to obtain different values of stress triaxiality, various tensile and compression-torsion experiments were carried out. The same experiment was conducted several times, and then interrupted at various stages. After the specimen unloading metallographic examination was performed to indicate areas of the initiation of matrix–particle separation. Using the macro scale numerical model of the specimen, the values of stresses and strains in these zones were determined. Basing on these values, local decohesion stresses were determined at the interface of phases using the Kwon and Asaro [
52] dislocation model, based on the earlier work of Brown and Stobbs [
53].
5. Application
As mentioned in the introduction, cohesive models are nowadays a convenient and effective tool for analysis of various engineering problems. For this reason, a huge amount of works on them can be found in the literature, and it is not possible to provide a comprehensive review. In this chapter, therefore, an analysis of several subjectively selected examples of the application of cohesive models in various engineering issues is presented.
Chandra et al. [
54] used the cohesive approach to analyze the initiation of fiber-titanium matrix debonding in a metal composite. The experiment included a push out test, as presented in
Figure 8.
A multi-stage FEM analysis was carried out, taking into account technological processes related to the composite production, including the influence of thermal residual stress (TRS).
Two cohesive models were employed: Exponential [
16] and bilinear [
55]. The comparative analysis of the results showed that, contrary to the view widespread in literature, the choice of the TSL curve shape had a significant effect on the coincidence of the predicted and experimental force-displacement curves, i.e., only the bilinear model ensures high quality of the obtained simulation results. Moreover, the adoption of the same separation energy in both models (bilinear and exponential) resulted in completely different simulation results, which contradicts the common assumption that the separation process is primarily controlled by energy. The authors also suggest that the selection of the TSL curve shape should be preceded by an analysis of microstructural phenomena occurring in the process zone.
Furthermore, the discussed article addresses the problem of effect of cohesive parameters on the overall model response. Since the shear cohesion parameters played the most important role in the analyzed case, the analysis of the influence of the maximum tangential stress , corresponding displacement and the separation energy on the simulation results was performed. The change in the characteristic length resulted in significant changes in the calculated force-displacement curve, confirming the earlier remark on the influence of the TSL curve shape on the overall model response. The analysis of maximum traction and separation energy values confirmed the common belief on their influence on the global simulation results. In the authors’ opinion, apart from the commonly accepted cohesive parameters ( and ) the value of should be incorporated in order to obtain the full description of the bilinear TSL function.
An interesting example of the application of the cohesive model to the analysis of crack development in full-scale structural elements is presented in [
56]. The research concerned quasi-static and dynamic four-point bending tests of pipes with pre-existing cracks of various types (
Figure 9).
The stress–strain curve for the analyzed material was determined from the standard quasi-static uniaxial tensile test of flat samples. A piecewise-polynomial traction–separation law was adopted. Cohesive parameters (maximum traction , separation energy and initial stiffness ) were determined on the basis of matching numerical results to the C(T) (compact tension) specimen tensile test data. The cohesive parameters determined in the above way were directly transferred to the numerical model of the pipe under bending. FEM simulations carried out for different crack geometries and strain rates allowed for obtaining a good agreement of the numerical and experimental results.
Another example of the use of cohesive models to solve a practical engineering issue is discussed in [
57]. The problem of a wooden beam subjected to four-point bending, reinforced with CFRP (Carbon Fiber Reinforced Polymer) composite tapes, was analyzed. The adhesive layer between the wooden element and the composite tape was modeled using the exponential TSL model. Although the authors do not provide the values of the applied cohesive parameters and the method of their determination, the adopted approach allowed for obtaining relatively good compliance of the predicted force-deflection curves of the beam with the results of the experiment.
In the paper [
58], the Park-Paulino-Roesler [
28] cohesive model was used to analyze the failure of polycrystalline ice beams subjected to four-point bending. In order to take into account the intercrystalline cracking, randomly distributed grains with cohesive surfaces were modeled. The simulations made it possible to determine the relationship between the grain size and the macroscopic flexural strength of ice.
A study on the practical application of the cohesive model and methods of determining its parameters under mixed-mode loading was presented by Wu et al. [
59]. The authors performed a numerical analysis of a double-cantilever beam, shown schematically in
Figure 10. The individual elements of the beam were made of different materials, connected along the contact surface using the cohesive model and loaded in different ways at the ends, which resulted in the formation of a complex stress state in the cohesive area.
The most important achievement in the discussed work was the independent analysis of the TSL in the normal and tangential direction. The next step involved determination of the cohesive parameters on the basis of experimental measurements of the J integral and crack tip displacements (CTD). Finally, the derivatives of both components of the J integral (normal and tangent) with respect to the corresponding CTDs made it possible to determine the cohesive parameters for both directions. The main advantage of the approach presented above is its versatility and the possibility of applying to any proportion of normal and tangential loading.
Cohesive models can be used to simulate the crack initiation process on a microscopic scale. Needleman [
10] used the cubic TSL function (
Section 2) to analyze the separation of the metal matrix from the cylindrical Fe
3C particle. The values of the cohesive parameters were adopted on the basis of the observations of Argon et al. [
60], Goods and Brown [
61] and Fisher and Gurland [
62], as
,
,
. Using the cohesive model implemented into the FEM code, the effect of stress state triaxiality on the critical void nucleation strain
was investigated. Application of a cohesive model made it possible to formulate the deformation criterion of microvoids initiation by the matrix–cylindrical particle separation, in which the value of nucleation strain decreases with the increase of the stress state triaxiality ratio. Additionally, the influence of characteristic length
(related to the critical separation—
Section 2) was taken into account. Depending on the ratio
(where
is the particle radius), different particle separation mechanisms were found. Low
values promoted “brittle” failure of the interface, while for higher values, a ductile mechanism was observed.
The above-mentioned examples do not fully reflect the extremely wide range of application of cohesive models, but only indicate the directions of research carried out in recent years. Many other interesting examples can be found in numerous works, for example [
63].