Molecular Insight into the Deformation of Single Crystal Copper Loaded by High-Speed Shock Wave
Abstract
:1. Introduction
2. Simulation Methodology
3. Results and Discussion
3.1. Particle Velocities of Copper Loaded by Shock Waves
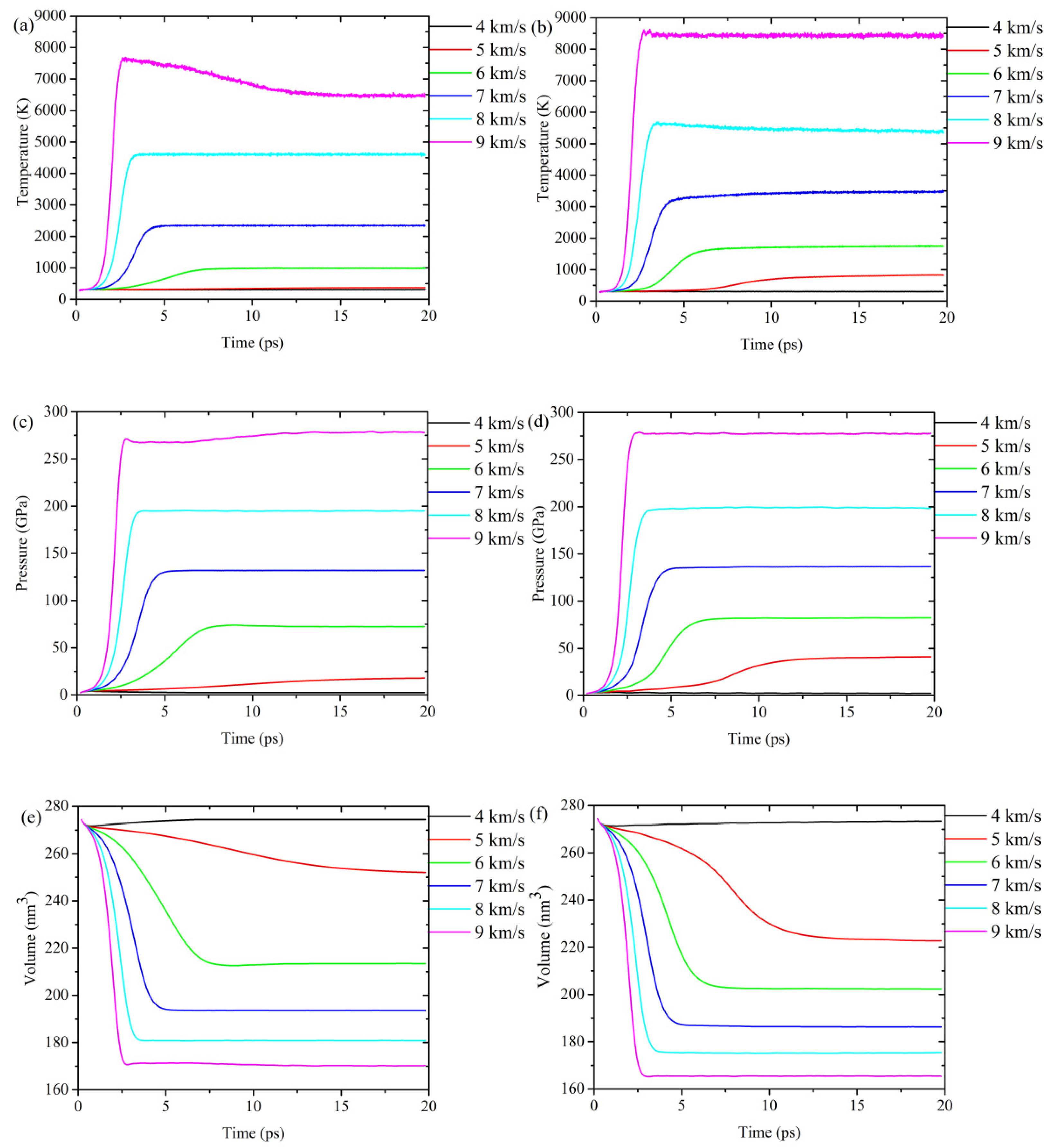
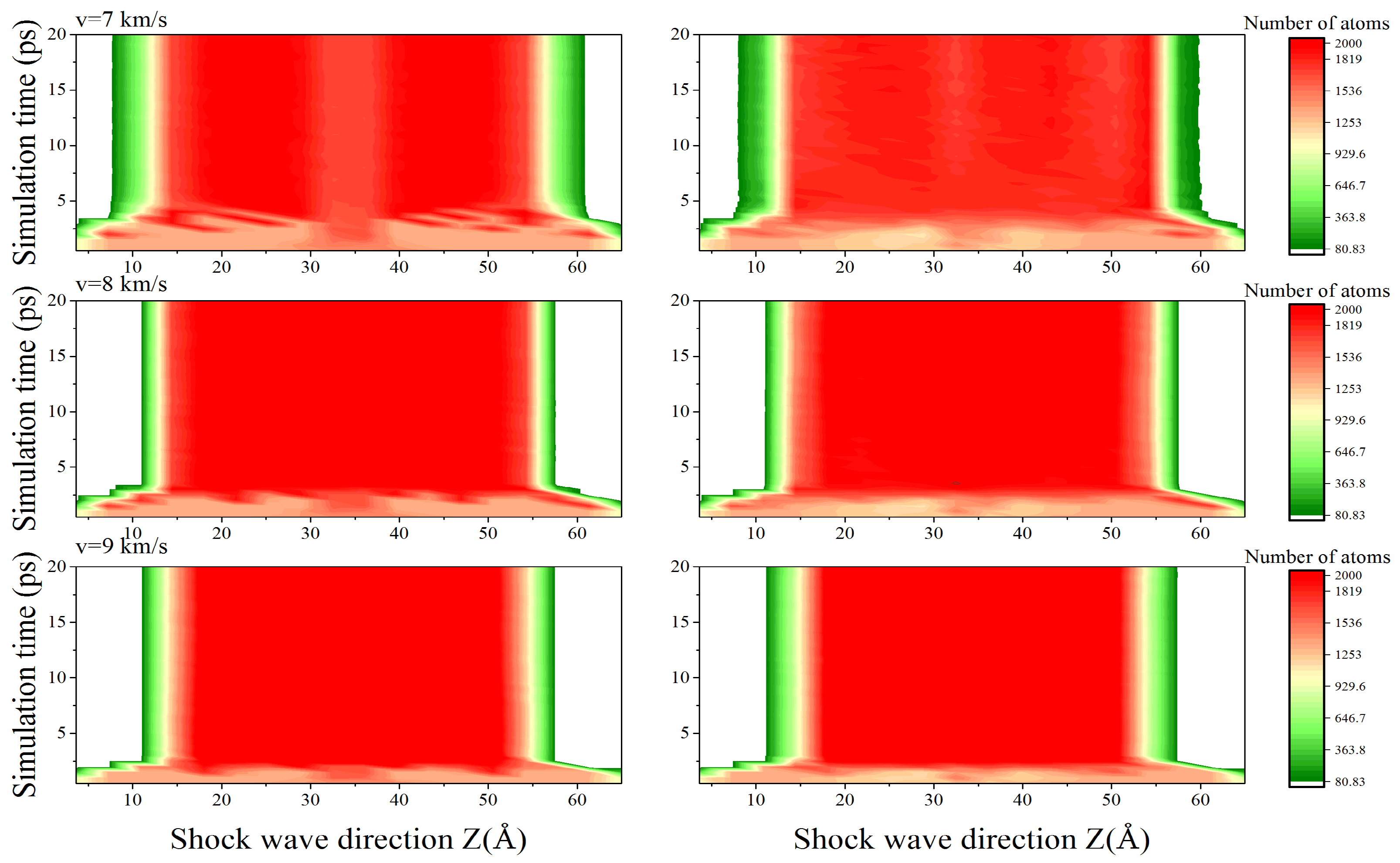
3.2. Time Evolution of Thermodynamic Parameters
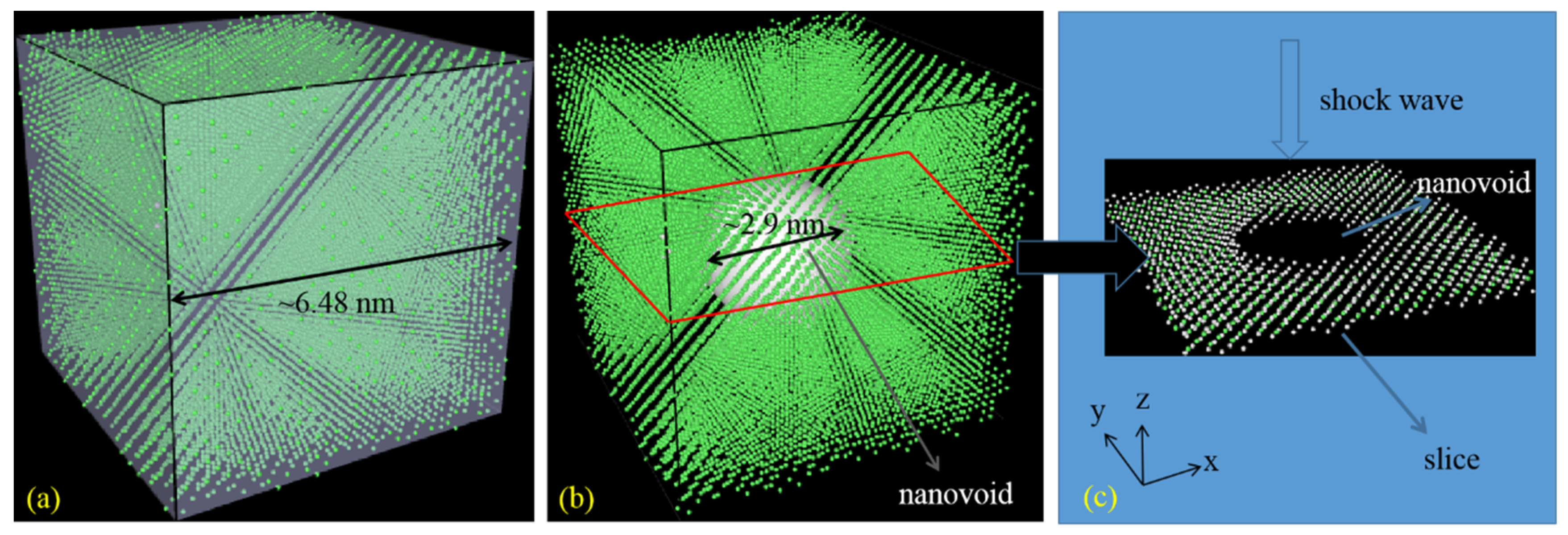
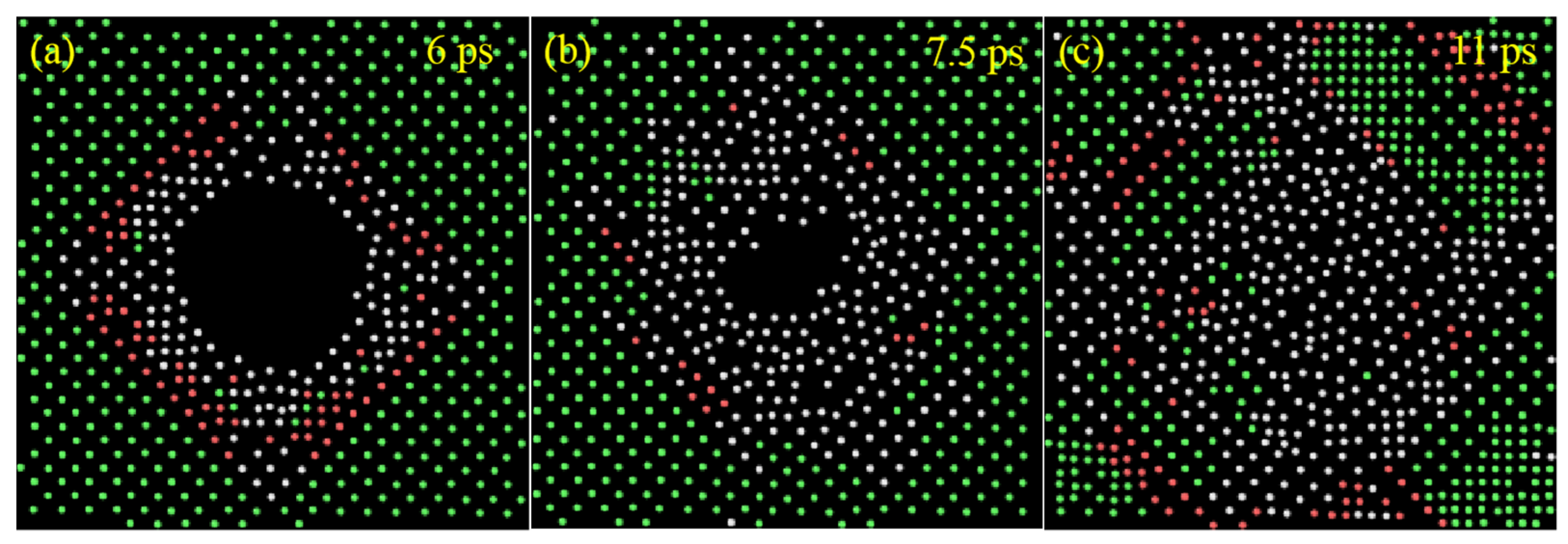
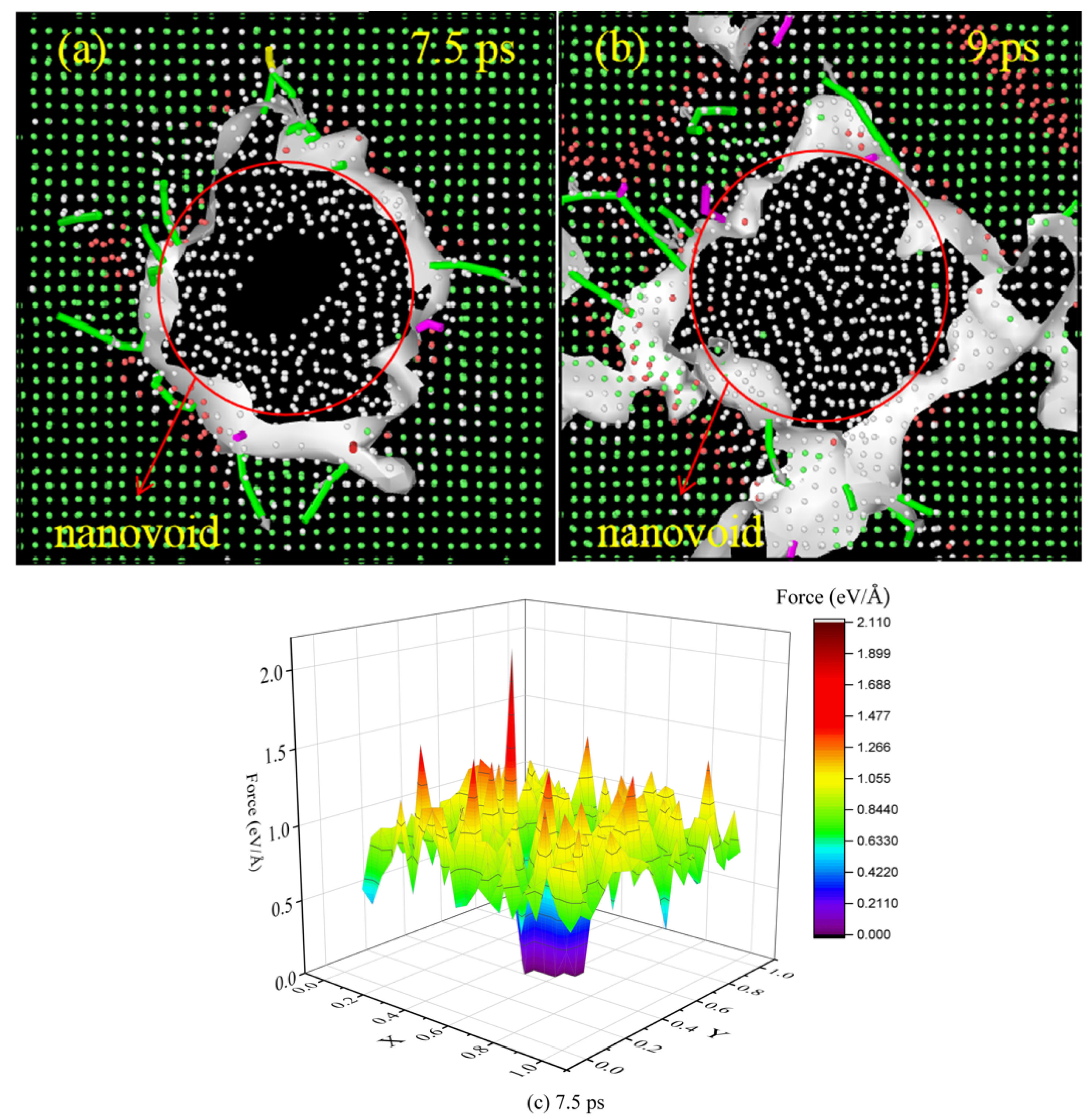
3.3. Phase Transition and Dislocation Pathway
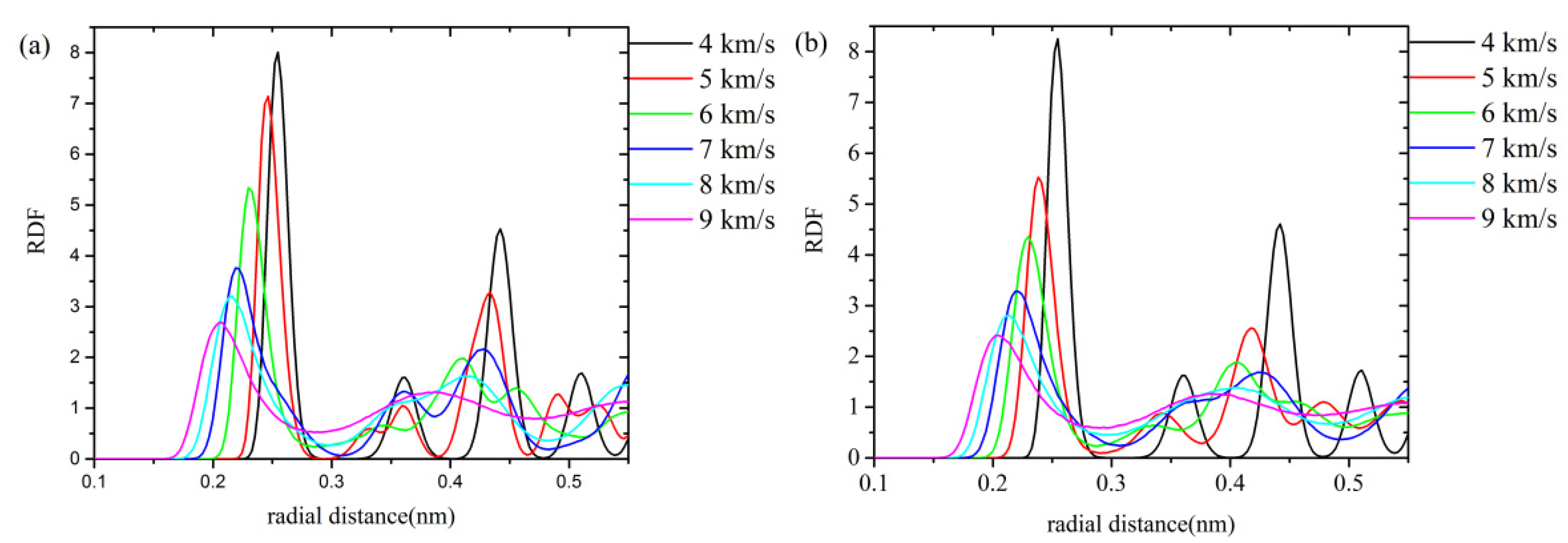
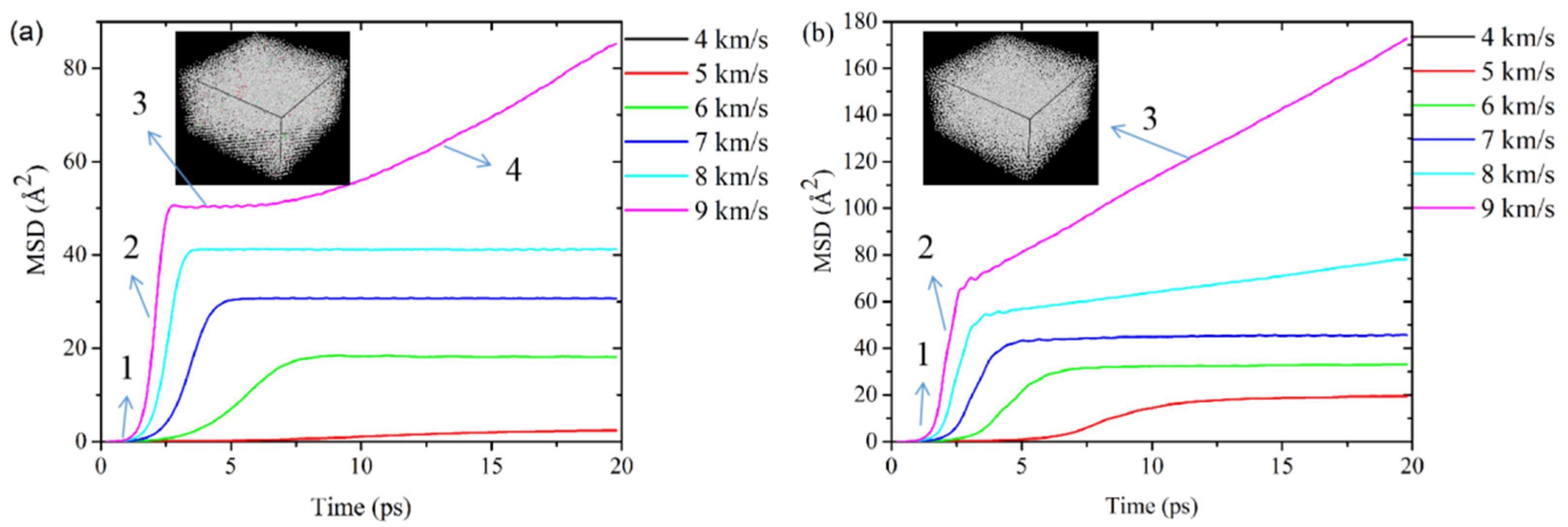
3.4. RDF and MSD
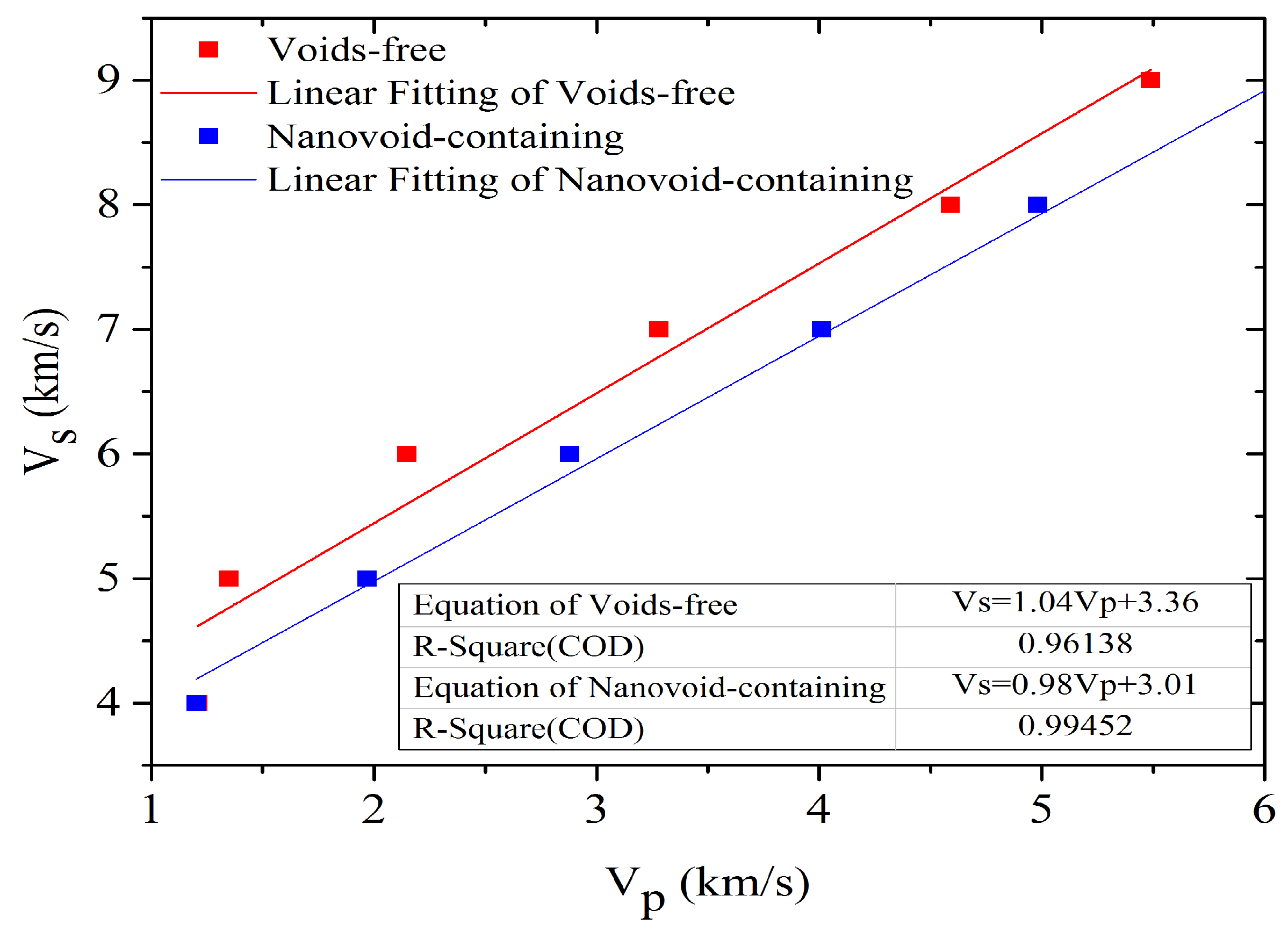
3.5. Time Evolution of System Stress
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, M.; Luo, Y.; Hu, X.; Han, Z.; Liu, X.; Cui, J. Co-regulation of the copper vacancy concentration and point defects leading to the enhanced thermoelectric performance of Cu 3 In 5 Te 9-based chalcogenides. RSC Adv. 2019, 9, 31747–31752. [Google Scholar] [CrossRef] [Green Version]
- Noell, P.J.; Sabisch, J.E.C.; Medlin, D.L.; Boyce, B.L. Nanoscale conditions for ductile void nucleation in copper: Vacancy condensation and the growth-limited microstructural state. Acta Mater. 2020, 184, 211–224. [Google Scholar] [CrossRef]
- Xue, L.; Ren, Y.; Hu, Z.; Hu, Y.; Li, Z. First principles study the influence of copper-vacancy on electronic, mechanical and thermal properties of CuGaTe2. Results Phys. 2019, 15, 102765. [Google Scholar] [CrossRef]
- Zhou, S.J.; Preston, D.L.; Lomdahl, P.S.; Beazley, D.M. Large-scale molecular dynamics simulations of dislocation intersection in copper. Science 1998, 279, 1525–1527. [Google Scholar] [CrossRef]
- Ahn, D.C.; Sofronis, P.; Kumar, M.; Belak, J.; Minich, R. Void growth by dislocation-loop emission. J. Appl. Phys. 2007, 101, 063514. [Google Scholar] [CrossRef]
- Jian, W.R.; Zhang, M.; Xu, S.; Beyerlein, I.J. Atomistic simulations of dynamics of an edge dislocation and its interaction with a void in copper: A comparative study. Model. Simul. Mater. Sci. Eng. 2020, 28, 045004. [Google Scholar] [CrossRef]
- Wei, D.A.; Zaiser, M.; Feng, Z.; Kang, G.; Fan, H.; Zhang, X. Effects of twin boundary orientation on plasticity of bicrystalline copper micropillars: A discrete dislocation dynamics simulation study. Acta Mater. 2019, 176, 289–296. [Google Scholar] [CrossRef]
- Xiong, J.; Wei, D.; Lu, S.; Kan, Q.; Kang, G.; Zhang, X. A three-dimensional discrete dislocation dynamics simulation on micropillar compression of single crystal copper with dislocation density gradient. Acta Metall. Sin. 2019, 55, 1477–1486. [Google Scholar] [CrossRef]
- Huang, S.H.; Chen, T.; Chen, Q.; Zhao, Z.D.; Xia, X.S. Verification of dislocation density and dynamic recrystallization in deformed pure copper. Strength Mater. 2020, 52, 1–8. [Google Scholar] [CrossRef]
- Koju, R.K.; Mishin, Y. Direct atomistic modeling of solute drag by moving grain boundaries. Acta Mater. 2020, 198, 111–120. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Ye, H.; Zheng, Y. Twin boundaries merely as intrinsically kinematic barriers for screw dislocation motion in fcc metals. Sci. Rep. 2016, 6, 22893. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, K. Stabilizing nanostructures in metals using grain and twin boundary architectures. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Han, L.B.; An, Q.; Fu, R.S.; Zheng, L.; Luo, S.N. Local and bulk melting of Cu at grain boundaries. Phys. B 2010, 405, 748–753. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Wang, S. Correlation of materials property and performance with internal structures evolvement revealed by laboratory X-ray tomography. Materials 2018, 11, 1795. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Ding, Z.; Zhao, Y.; Zhao, R. Strength and its prediction models based on fracture mechanics of thin layers copper cladding steel wires under different amount of deformation. J. Mater. Sci. 2016, 27, 12499–12505. [Google Scholar] [CrossRef]
- Kondo, T.; Bi, X.C.; Hirakata, H.; Minoshima, K. Mechanics of fatigue crack initiation in submicron-thick freestanding copper films. Int. J. Fatigue 2016, 82, 12–28. [Google Scholar] [CrossRef]
- Li, P.; Li, Z. Theoretical Insights into the Thermodynamics and Kinetics of Graphene Growth on Copper Surfaces. J. Phys. Chem. C 2020, 124, 16233–16247. [Google Scholar] [CrossRef]
- Song, H.B.; Wang, X.; Patton, J.R.; Stansbury, J.W.; Bowman, C.N. Kinetics and mechanics of photo-polymerized triazole-containing thermosetting composites via the copper (I)-catalyzed azide-alkyne cycloaddition. Dent. Mater. 2017, 33, 621–629. [Google Scholar] [CrossRef]
- Malinskiy, T.V.; Mikolutskiy, S.I.; Rogalin, V.E.; Khomich, Y.V.; Yamshchikov, V.A.; Kaplunov, I.A.; Ivanova, A.I. Plastic Deformation of Copper under the Action of High-Power Nanosecond UV Laser Pulse. Tech. Phys. Lett. 2020, 46, 831–834. [Google Scholar] [CrossRef]
- Kim, H.S.; Estrin, Y.; Bush, M.B. Plastic deformation behaviour of fine-grained materials. Acta Mater. 2000, 48, 493–504. [Google Scholar] [CrossRef]
- Mousavi, S.E.; Sonboli, A.; Naghshehkesh, N.; Meratian, M.; Aslehi, A.; Sanayei, M. Different behavior of alpha and beta phases in a Low Stacking Fault Energy copper alloy under severe plastic deformation. Mater. Sci. Eng. A 2020, 788, 139550. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Sun, M.Y.; Xu, B.; Hu, X.; Liu, S.; Xie, B.J.; Li, D.Z. Evolution of the interfacial microstructure during the plastic deformation bonding of copper. Mater. Sci. Eng. A 2019, 746, 1–10. [Google Scholar] [CrossRef]
- Bai, X.M.; Li, M. Nucleation and melting from nanovoids. Nano Lett. 2006, 6, 2284–2289. [Google Scholar] [CrossRef]
- He, A.M.; Duan, S.; Shao, J.L.; Wang, P.; Qin, C.S. Shock melting of single crystal copper with a nanovoid: Molecular dynamics simulations. J. Appl. Phys. 2012, 112, 074116. [Google Scholar] [CrossRef]
- Seppälä, E.T.; Belak, J.; Rudd, R.E. Onset of void coalescence during dynamic fracture of ductile metals. Phys. Rev. Lett. 2004, 93, 245503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haug, C.; Ruebeling, F.; Kashiwar, A.; Gumbsch, P.; Kübel, C.; Greiner, C. Early deformation mechanisms in the shear affected region underneath a copper sliding contact. Nat. Commun. 2020, 11, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Kardani, A.; Montazeri, A. Metal-matrix nanocomposites under compressive loading: Towards an understanding of how twinning formation can enhance their plastic deformation. Sci. Rep. 2020, 10, 1–15. [Google Scholar] [CrossRef]
- Davila, L.P.; Erhart, P.; Bringa, E.M.; Meyers, M.A.; Lubarda, V.A.; Schneider, M.S.; Becker, R.; Kumar, M. Atomistic modeling of shock-induced void collapse in copper. Appl. Phys. Lett. 2005, 86, 161902. [Google Scholar] [CrossRef] [Green Version]
- Lubarda, V.A.; Schneider, M.S.; Kalantar, D.H.; Remington, B.A.; Meyers, M.A. Void growth by dislocation emission. Acta Mater. 2004, 52, 1397–1408. [Google Scholar] [CrossRef]
- Marian, J.; Knap, J.; Ortiz, M. Nanovoid cavitation by dislocation emission in aluminum. Phys. Rev. Lett. 2004, 93, 165503. [Google Scholar] [CrossRef] [Green Version]
- Gungor, M.R.; Maroudas, D. Atomistic mechanisms of strain relaxation due to ductile void growth in ultrathin films of face-centered-cubic metals. J. Appl. Phys. 2005, 97, 113527. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, W.J.; Li, L.B.; Liang, H.H.; Jing, F.Q. Molecular dynamics simulation of void growth in single crystal copper under uniaxial impacting. Acta Phys. Sin. 2005, 54, 2791–2798. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, L.C.; Xiang, S.K.; Jing, F.Q.; Chen, D.Q. Simulation of ab initio molecular dynamics of shock wave on copper. Chin. Phys. Lett. 2003, 20, 2091. [Google Scholar] [CrossRef]
- Bringa, E.M.; Cazamias, J.U.; Erhart, P.; Stölken, J.; Tanushev, N.; Wirth, B.D.; Rudd, R.E.; Caturla, M.J. Atomistic shock Hugoniot simulation of single-crystal copper. J. Appl. Phys. 2004, 96, 3793–3799. [Google Scholar] [CrossRef] [Green Version]
- Lin, E.; Shi, H.; Niu, L. Effects of orientation and vacancy defects on the shock Hugoniot behavior and spallation of single-crystal copper. Model. Simul. Mater. Sci. Eng. 2014, 22, 035012. [Google Scholar] [CrossRef]
- Neogi, A.; Mitra, N. On shock response of nano-void closed/open cell copper material: Non-equilibrium molecular dynamic simulations. J. Appl. Phys. 2014, 115, 013504. [Google Scholar] [CrossRef] [Green Version]
- Xiong, Q.; Kitamura, T.; Li, Z. Cylindrical voids induced deformation response of single crystal coppers during low-speed shock compressions: A molecular dynamics study. Mech. Mater. 2019, 138, 103167. [Google Scholar] [CrossRef]
- Xiong, Q.; Tian, X.; Lu, T. Atomistic modeling of electron relaxation effect on femtosecond laser-induced thermoelastic response of gold films. J. Appl. Phys. 2012, 112, 024313. [Google Scholar] [CrossRef]
- Xiong, Q.; Li, Z.; Tian, X. Ultrafast thermomechanical responses of a copper film under femtosecond laser trains: A molecular dynamics study. Proc. R. Soc. A 2015, 471, 20150614. [Google Scholar] [CrossRef]
- Xiong, Q.; Li, Z.; Kitamura, T. Effect of crystal orientation on femtosecond laser-induced thermomechanical responses and spallation behaviors of copper films. Sci. Rep. 2017, 7, 9218. [Google Scholar] [CrossRef] [Green Version]
- Neogi, A.; Mitra, N. A metastable phase of shocked bulk single crystal copper: An atomistic simulation study. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, B.; Bringa, E.M.; Meyers, M.A. Shock compression of monocrystalline copper: Atomistic simulations. Metall. Mater. Trans. A 2007, 38, 2681–2688. [Google Scholar] [CrossRef]
- Patil, S.P.; Ambarish, K.; Bernd, M. Shockwave response of graphene aerogels: An all-atom simulation study. Comput. Mater. Sci. 2021, 189, 110252. [Google Scholar] [CrossRef]
- Patil, S.P.; Parag, S.; Bernd, M. Molecular dynamics investigation of the shock response of silica aerogels. Materialia 2019, 6, 100315. [Google Scholar] [CrossRef]
- Kadau, K.; Germann, T.C.; Lomdahl, P.S.; Holian, B.L. Microscopic view of structural phase transitions induced by shock waves. Science 2002, 296, 1681–1684. [Google Scholar] [CrossRef] [Green Version]
- Reed, E.J.; Fried, L.E.; Joannopoulos, J.D. A method for tractable dynamical studies of single and double shock compression. Phys. Rev. Lett. 2003, 90, 235503. [Google Scholar] [CrossRef] [Green Version]
- Reed, E.J.; Fried, L.E.; Henshaw, W.D.; Tarver, C.M. Analysis of simulation technique for steady shock waves in materials with analytical equations of state. Phys. Rev. E 2006, 74, 056706. [Google Scholar] [CrossRef]
- Reed, E.J.; Manaa, M.R.; Fried, L.E.; Glaesemann, K.R.; Joannopoulos, J.D. A transient semimetallic layer in detonating nitromethane. Nat. Phys. 2008, 4, 72–76. [Google Scholar] [CrossRef]
- Mundy, C.J.; Curioni, A.; Goldman, N.; Kuo, W.; Reed, E.J.; Fried, L.E.; Ianuzzi, M. Ultrafast transformation of graphite to diamond: An ab initio study of graphite under shock compression. J. Chem. Phys. 2008, 128, 184701. [Google Scholar] [CrossRef] [Green Version]
- Ju, Y.; Zhang, Q.; Gong, Z.; Ji, G.F.; Zhou, L. Molecular dynamics simulation of shock melting of aluminum single crystal. J. Appl. Phys. 2013, 114, 093507. [Google Scholar] [CrossRef]
- Mei, J.; Davenport, J.W.; Fernando, G.W. Analytic embedded-atom potentials for fcc metals: Application to liquid and solid copper. Phys. Rev. B 1991, 43, 4653. [Google Scholar] [CrossRef]
- Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A. Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63, 224106. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Parks, M.L.; Lehoucq, R.B.; Plimpton, S.J.; Silling, S.A. Implementing peridynamics within a molecular dynamics code. Comput. Phys. Commun. 2008, 179, 777–783. [Google Scholar] [CrossRef] [Green Version]
- Thompson, A.P.; Plimpton, S.J.; Mattson, W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 2009, 131, 154107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the open visualization tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Faken, D.; Jónsson, H. Systematic analysis of local atomic structure combined with 3D computer graphics. Comput. Mater. Sci. 1994, 2, 279–286. [Google Scholar] [CrossRef]
- Wang, L.; Bian, X.F.; Li, H. Molecular dynamics simulation of metal Cu during melting and crystallizing process. Chin. J. Chem. Phys. 2000, 13, 544–550. [Google Scholar] [CrossRef]
- An, Q.; Luo, S.N.; Han, L.B.; Zheng, L.Q.; Tschauner, O. Melting of Cu under hydrostatic and shock wave loading to high pressures. J. Phys. 2008, 20, 095220. [Google Scholar] [CrossRef]
- Patil, S.P.; Murkute, R.; Shirafkan, N.; Markert, B. Deformation of stacked metallic sheets by shock wave loading. Metals 2018, 8, 679. [Google Scholar] [CrossRef] [Green Version]

| Velocity (km/s) | 6 | 7 | 8 | 9 |
|---|---|---|---|---|
| Voids-free system (ps) | 8.08 | 5.27 | 3.54 | 2.8 |
| Nanovoid-containing system (ps) | 7.5 | 5.17 | 3.21 | 2.5 |
| Shock Wave Velocities (km/s) | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|
| diffusion coefficient (m2/s) | 3.2 × 10−10 | 6.4 × 10−9 | 1.9 × 10−8 | 4.0 × 10−8 | 6.5 × 10−8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Fang, B.; Meng, J.; Cao, J.; Zhao, Y.; Lü, T. Molecular Insight into the Deformation of Single Crystal Copper Loaded by High-Speed Shock Wave. Metals 2021, 11, 446. https://doi.org/10.3390/met11030446
Zhang C, Fang B, Meng J, Cao J, Zhao Y, Lü T. Molecular Insight into the Deformation of Single Crystal Copper Loaded by High-Speed Shock Wave. Metals. 2021; 11(3):446. https://doi.org/10.3390/met11030446
Chicago/Turabian StyleZhang, Changjiang, Bin Fang, Jiuling Meng, Jingrui Cao, Yupeng Zhao, and Tao Lü. 2021. "Molecular Insight into the Deformation of Single Crystal Copper Loaded by High-Speed Shock Wave" Metals 11, no. 3: 446. https://doi.org/10.3390/met11030446
APA StyleZhang, C., Fang, B., Meng, J., Cao, J., Zhao, Y., & Lü, T. (2021). Molecular Insight into the Deformation of Single Crystal Copper Loaded by High-Speed Shock Wave. Metals, 11(3), 446. https://doi.org/10.3390/met11030446





