Study on a New Forming Method—Thread Rolling by Crystal Plasticity Finite Element Simulation
Abstract
1. Introduction
2. Theoretical Model
2.1. Kinematics Model
2.2. Constitutive Model
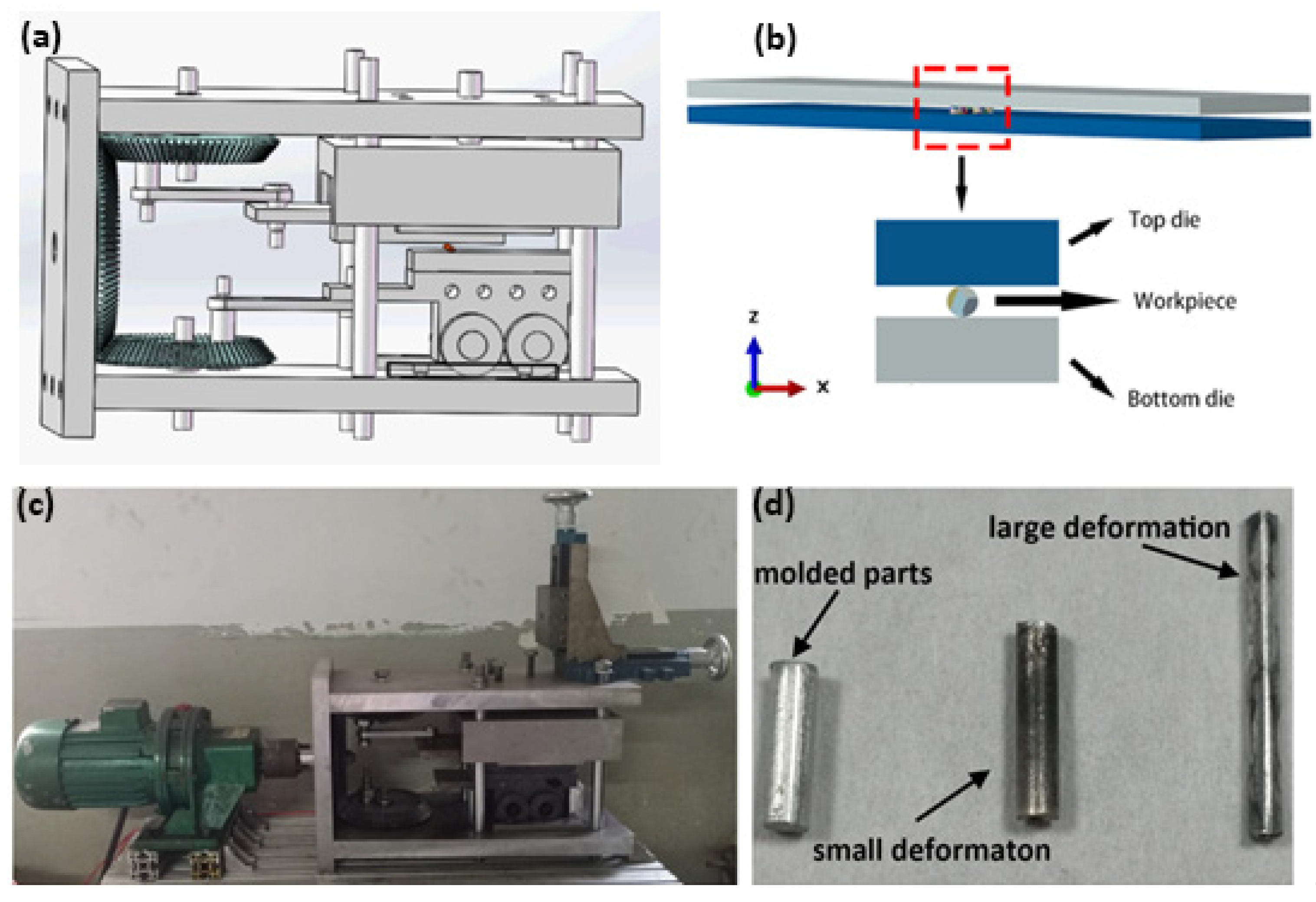
3. Finite Element Model
4. Simulation Results and Discussion
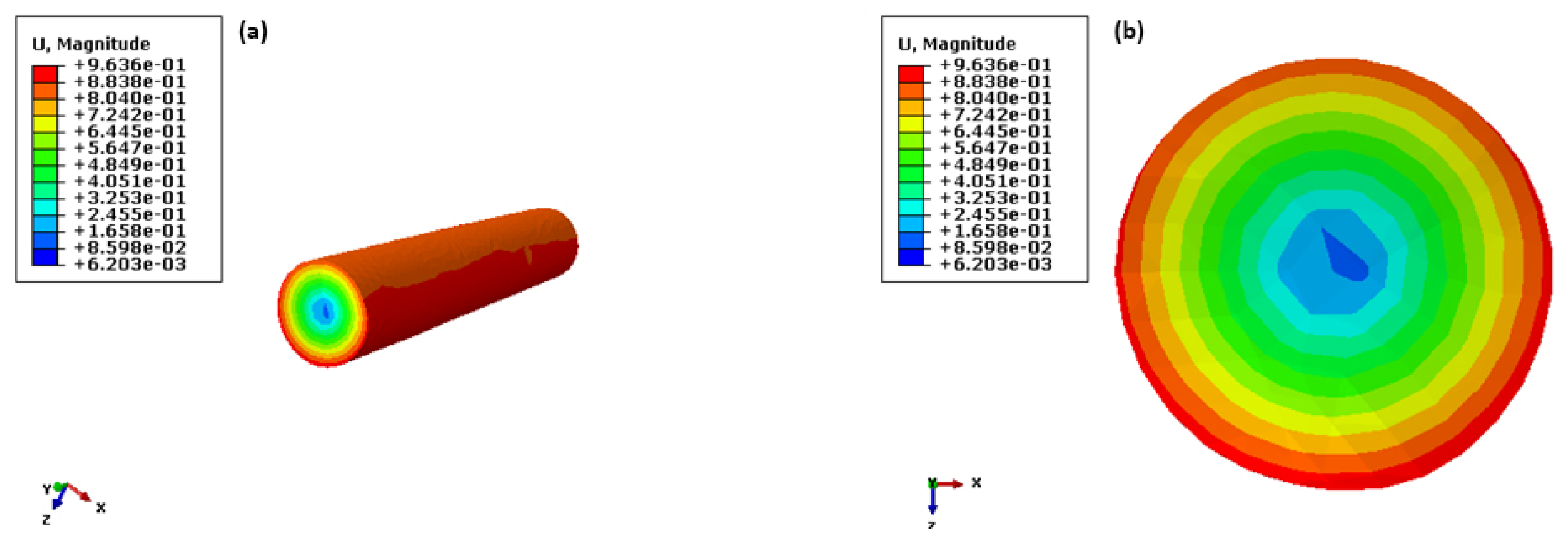
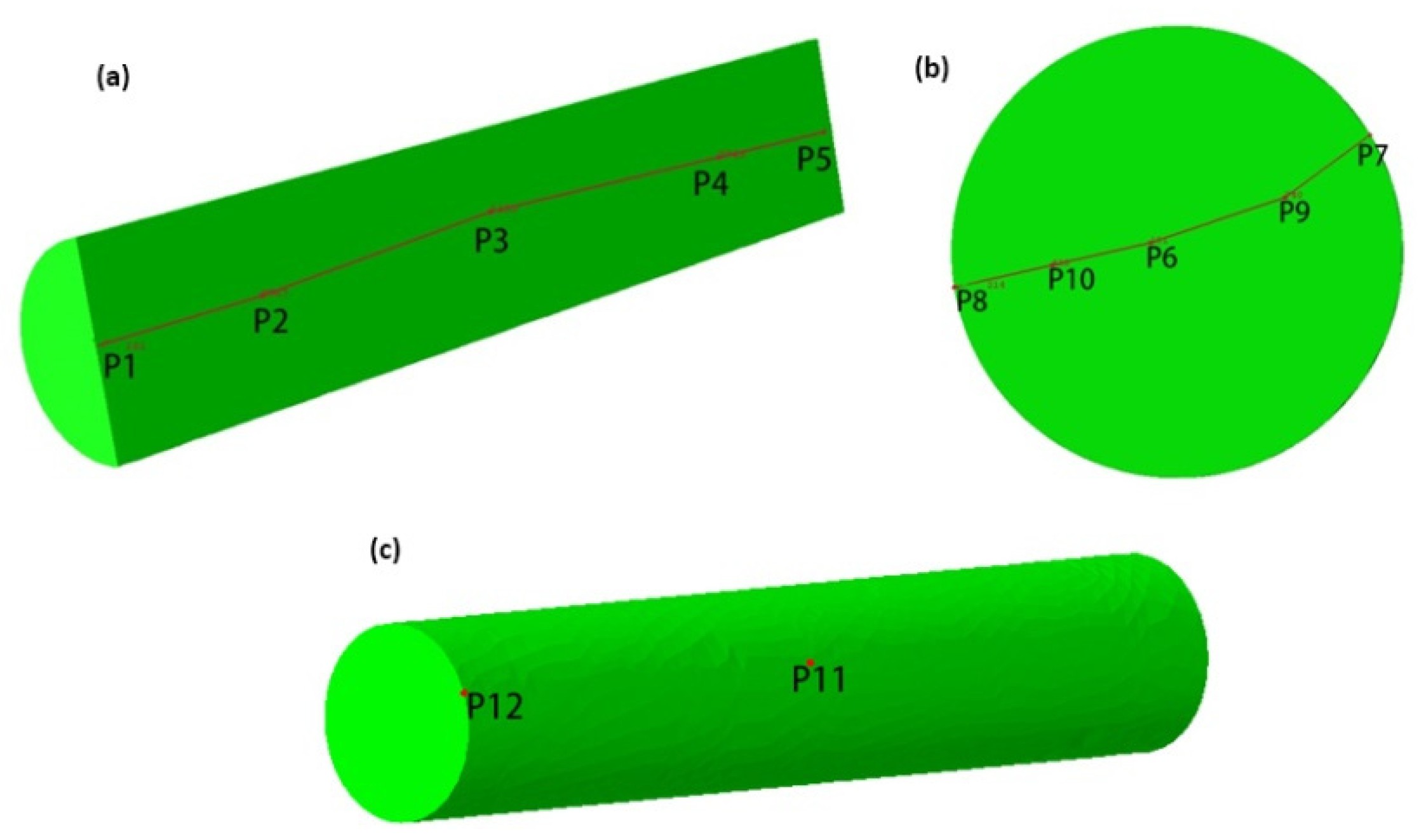
4.1. Metal Fluidity Analysis
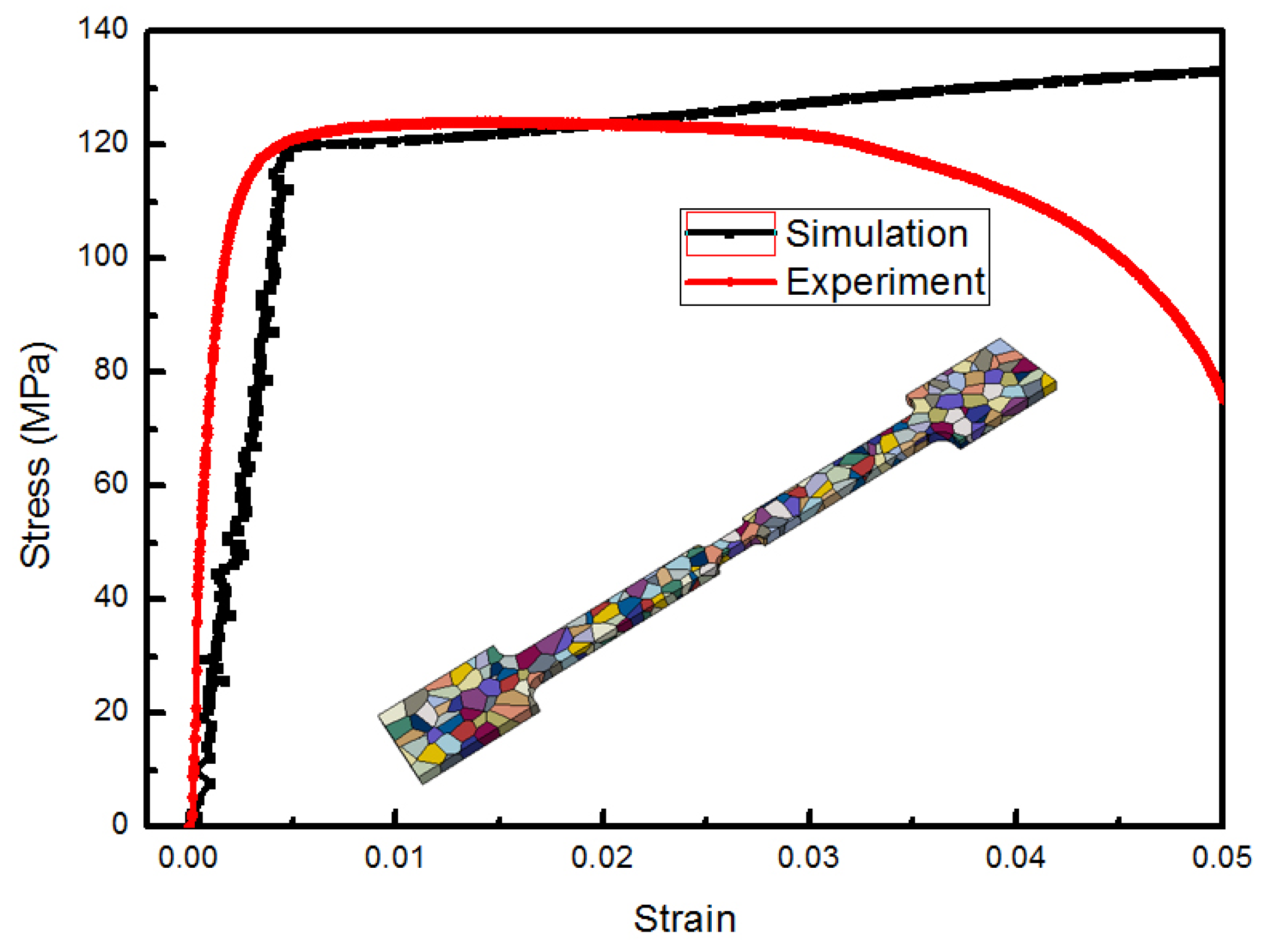
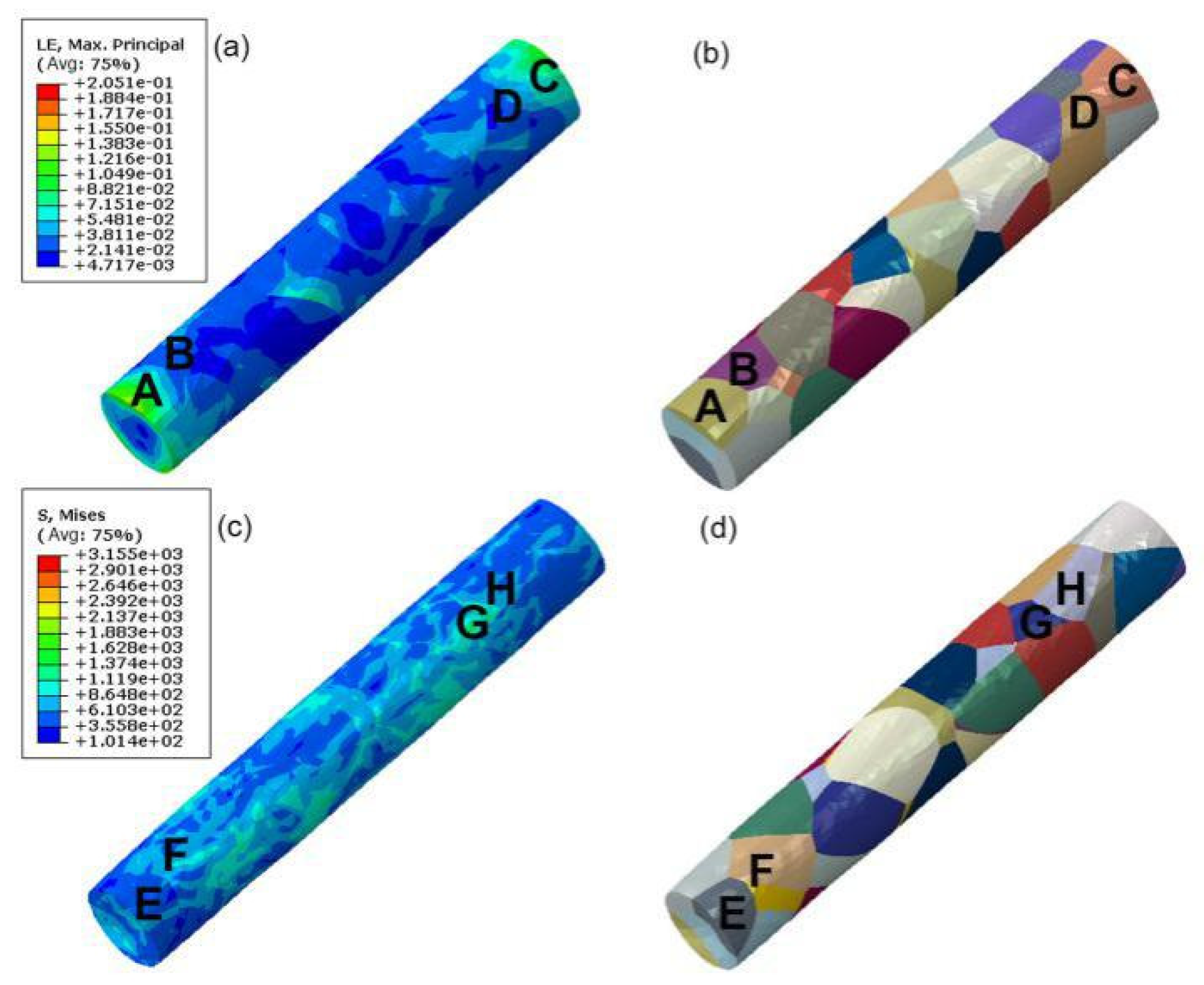
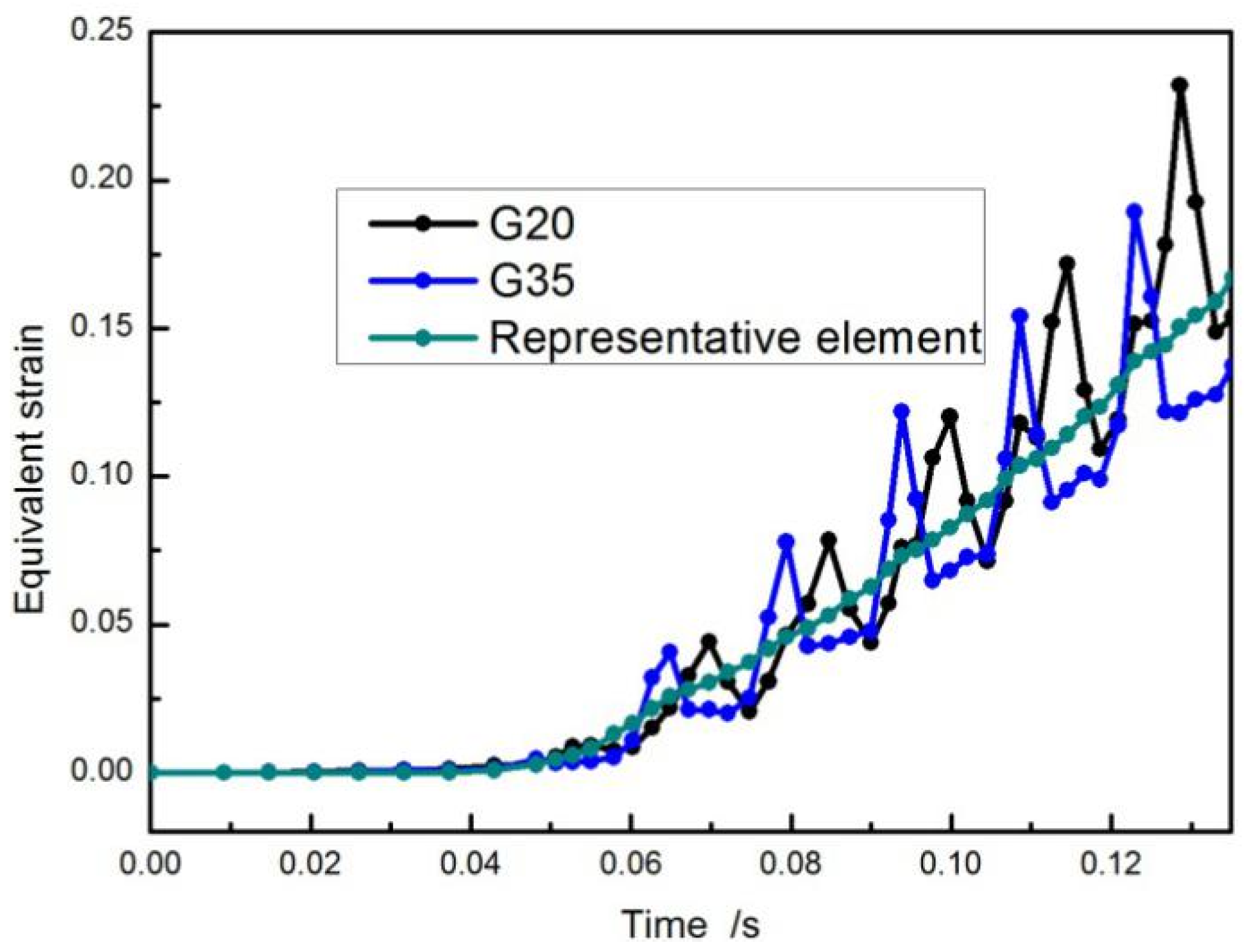
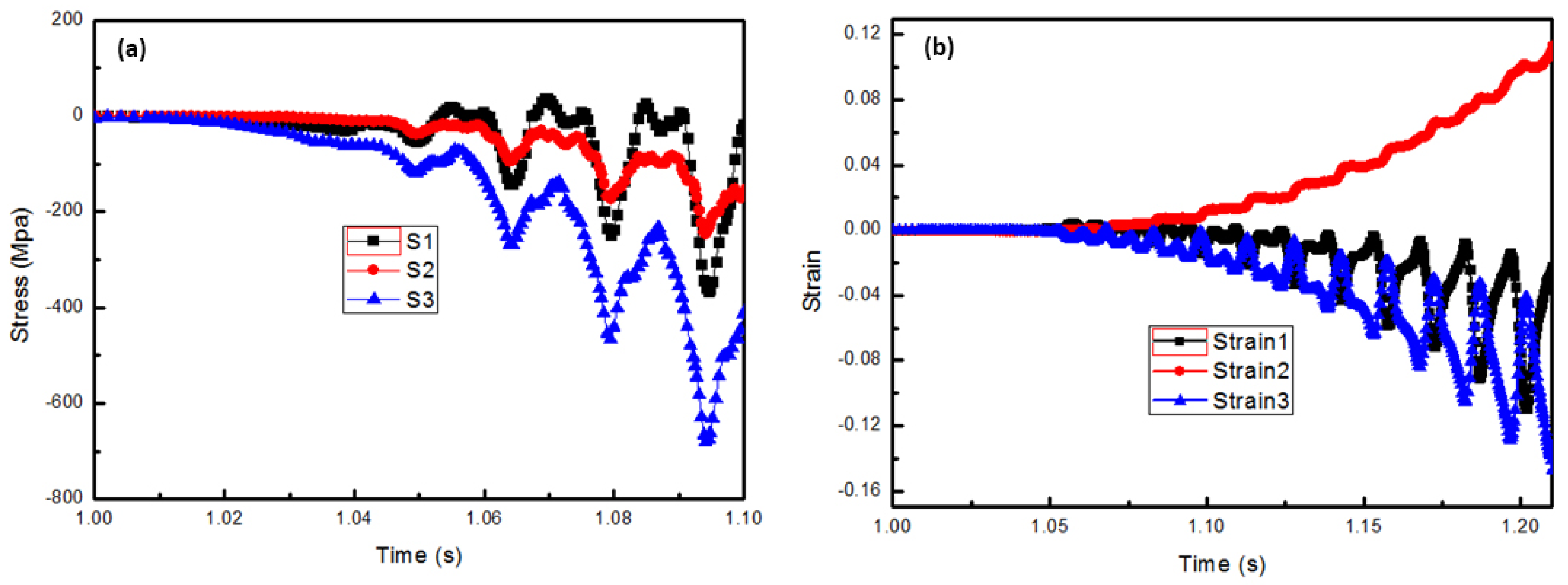
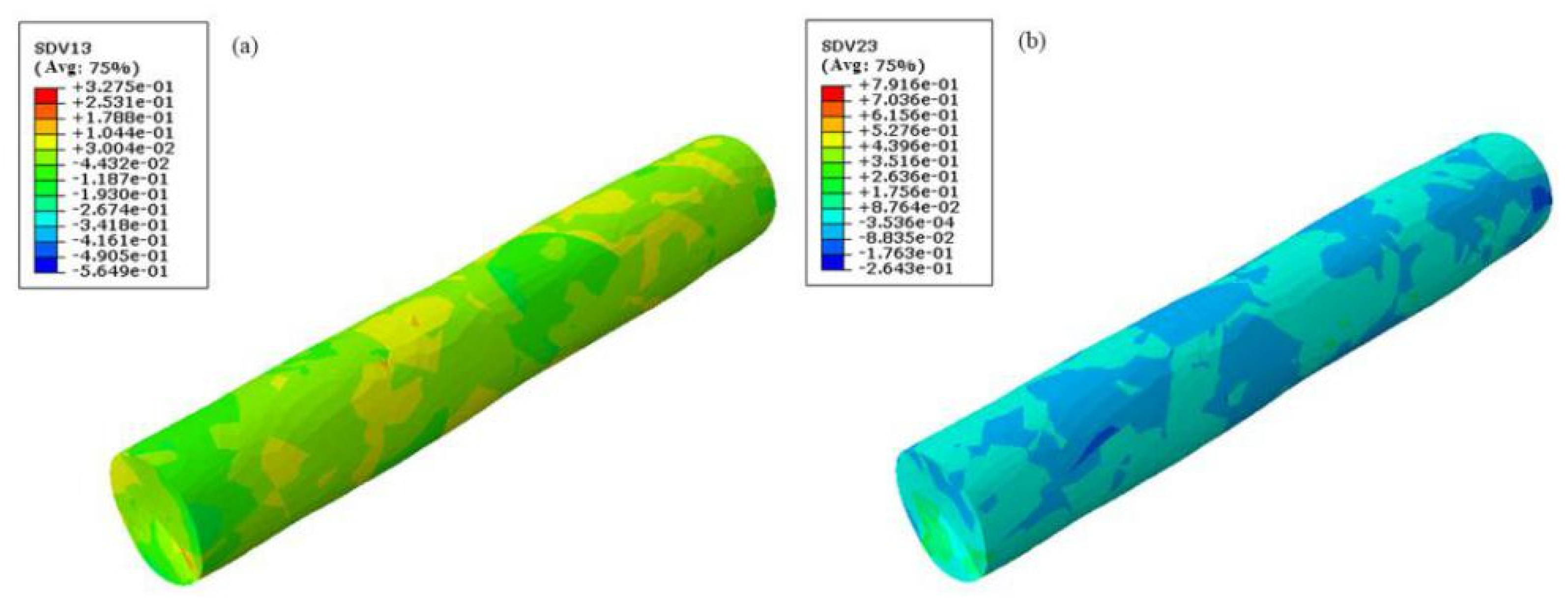
4.2. Stress–Strain Analysis
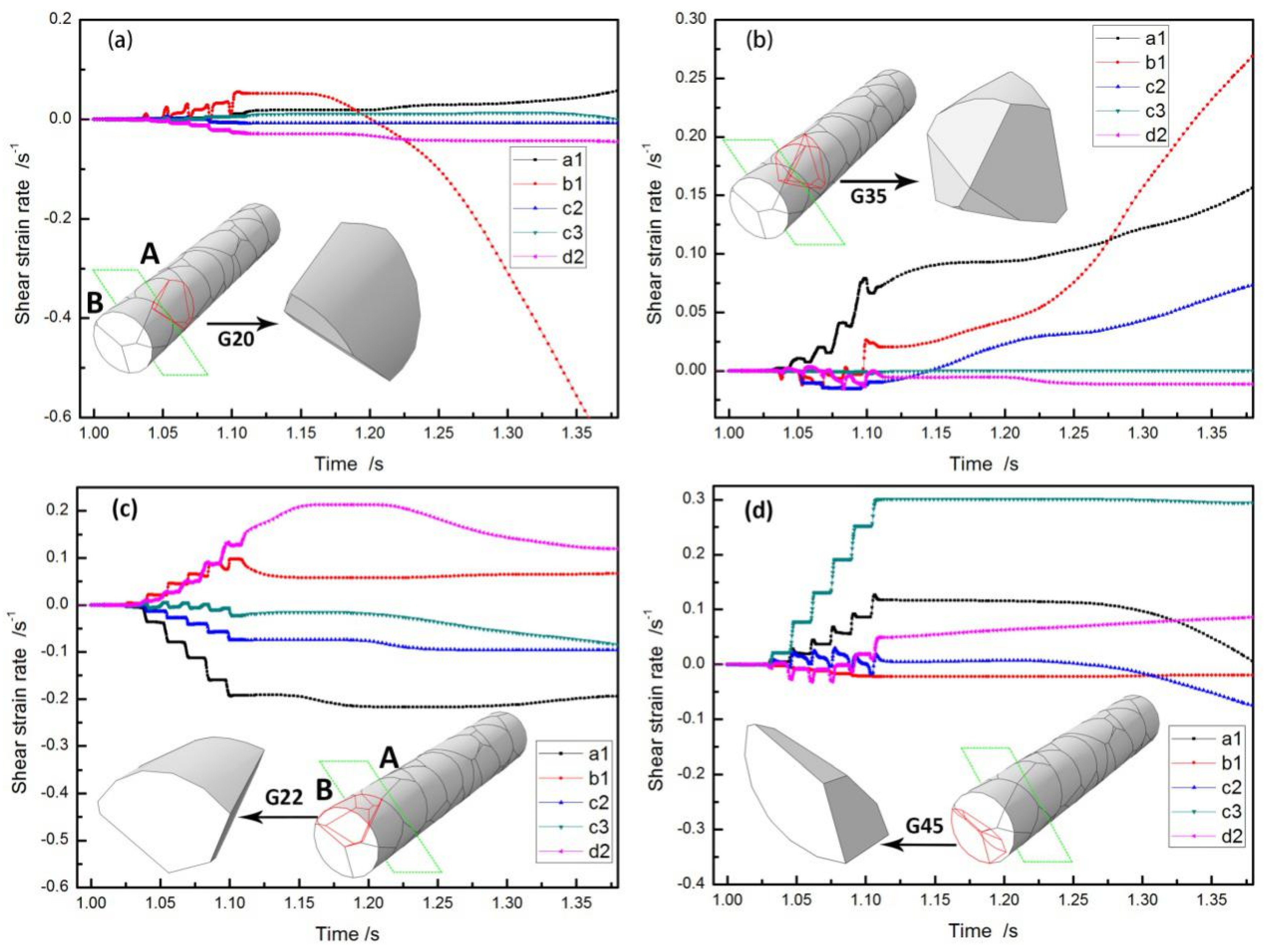
4.3. Evolution of the Slip Systems
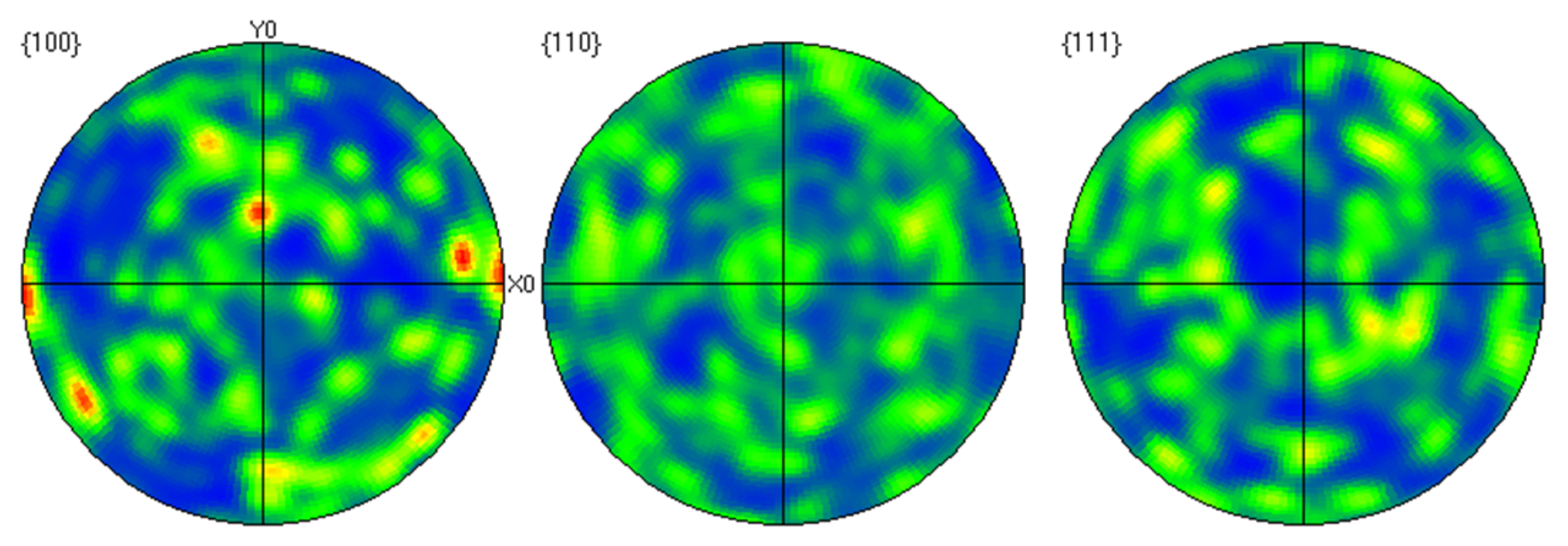
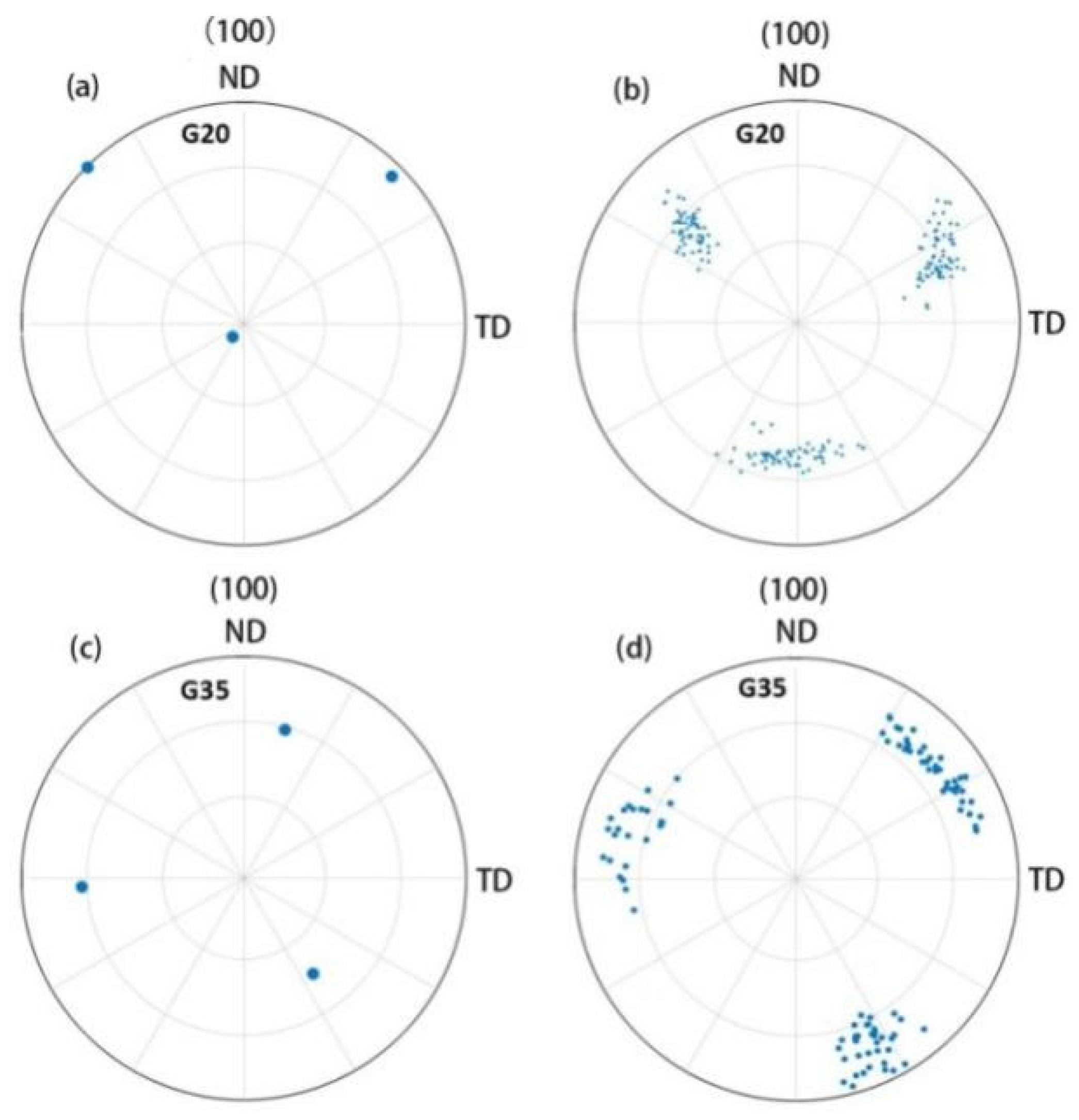
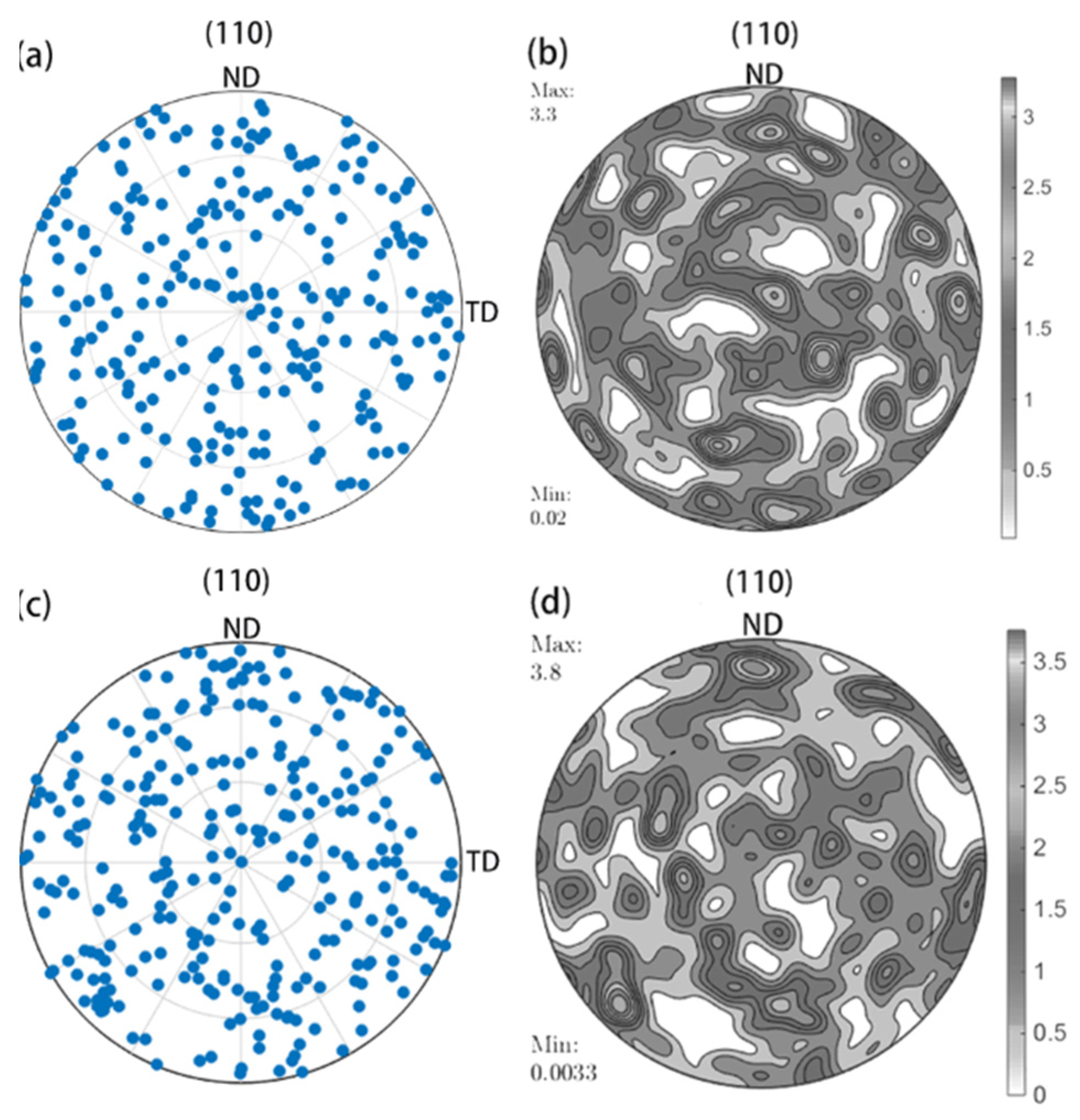
4.4. Pole Figures Analysis
5. Conclusions
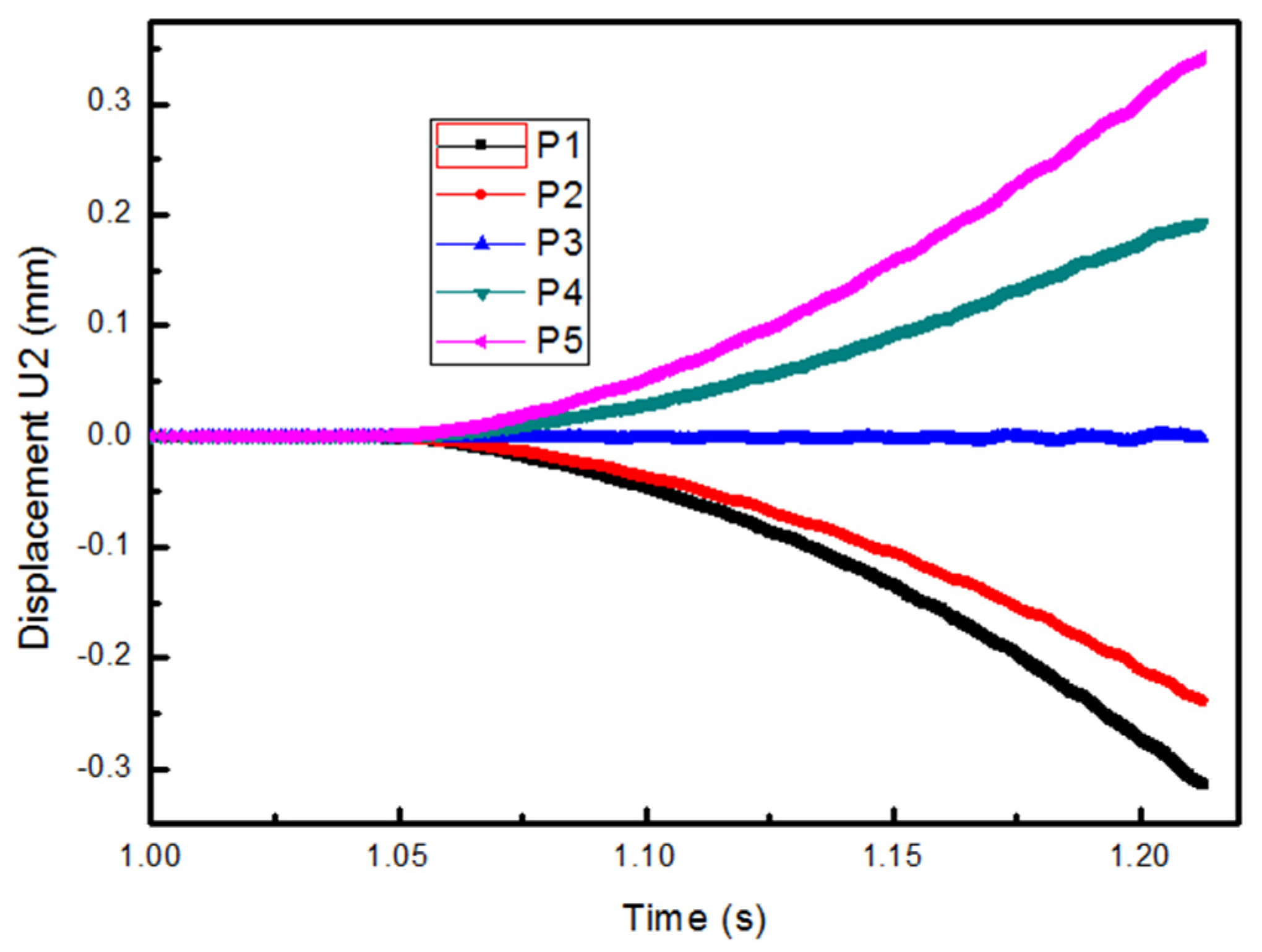
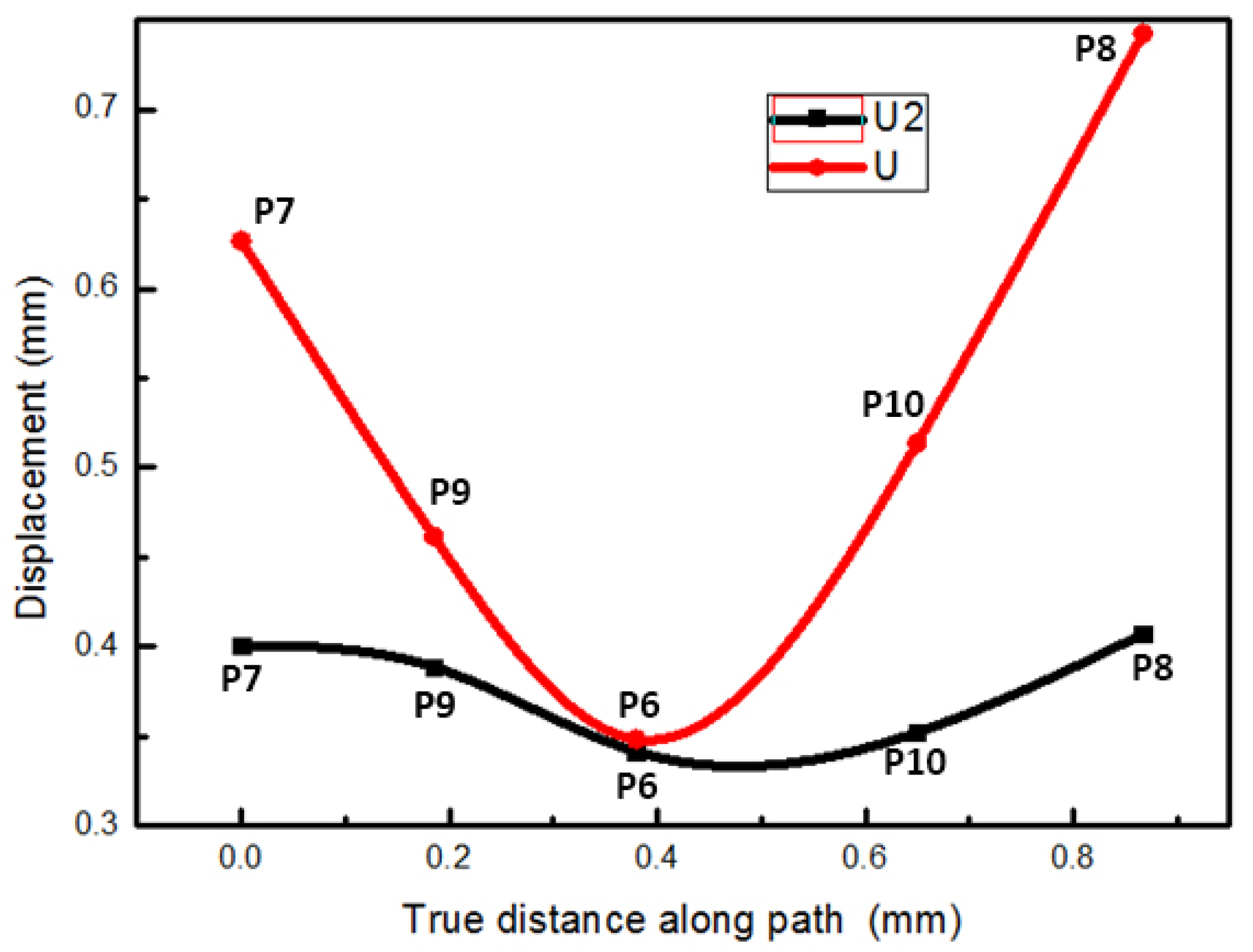
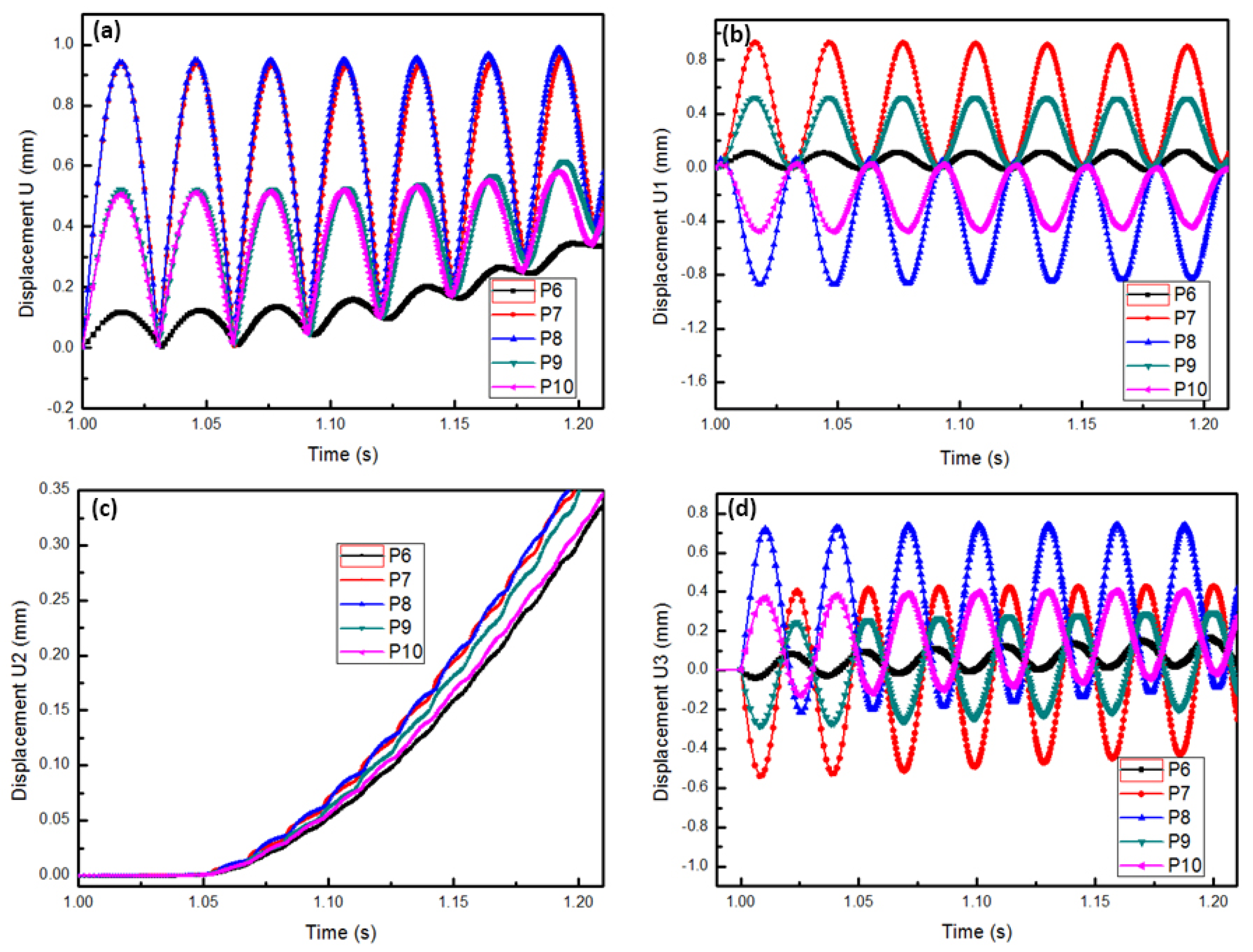
- The displacement field of the thread rolling was studied. It shows a trend of symmetrical extension on both sides during the forming process. The axial extension of the outer characteristic point is about 0.05 mm more than the axial extension at the center. This explains the reason for the concave core at the workpiece end.
- The volume average method was used in the polycrystalline model to obtain the mechanical response of the representative element after homogenization. It can better reflect the force state of the entire material than a single grain.
- The evolution of each slip system was determined by the initial grain orientations and grain locations. The grains at the end of the workpiece require less resistance due to coordinated deformation among the grains. The grain orientation after deformation appears near to the initial orientation.
- The pole figure obtained by the experiment is basically consistent with the pole figure by the simulation. The grains are elongated in the axial direction and compressed in the radial direction without obvious texture, indicating thread rolling deformation is more uniform than ordinary rolling due to the periodic rotation effect.
Author Contributions
Funding
Conflicts of Interest
Nomenclatures
| total deformation gradient | |
| elastic deformation gradient | |
| Plastic deformation gradient | |
| second Piola–Kirchhoff stress | |
| anisotropic elasticity matrix | |
| Lagrangian elastic strain tensor | |
| Cauchy stress tensor | |
| rate of change of | |
| inverse matrix of | |
| shear strain rate | |
| slip direction vector | |
| normal direction vector | |
| unit normal direction vector | |
| unit slip direction vector | |
| mass density of reference state | |
| mass density of current state | |
| Schmid tensor | |
| resolved shear stress | |
| critical resolved shear stress | |
| reference shear strain rate | |
| strain rate sensitive coefficient | |
| critical shear rate | |
| initial hardening modulus | |
| total number of slip systems | |
| self-hardening modulus | |
| latent hardening modulus. | |
| cumulative shear strain rates | |
| initial critical shear stress | |
| saturation value of | |
| latent hardening parameter. |
References
- Chen, Y.; Kraft, O.; Walter, M. Size effects in thin coarse-grained gold microwires under tensile and torsional loading. Acta Mater. 2015, 87, 78–85. [Google Scholar] [CrossRef]
- Xu, Z.T.; Peng, L.F.; Fu, M.W.; Lai, X.M. Size effect affected formability of sheet metals in micro/meso scale plastic deformation: Experiment and modeling. Int. J. Plast. 2014, 68, 34–54. [Google Scholar] [CrossRef]
- Liu, W.; Chen, B.K.; Pang, Y. Numerical investigation of evolution of earing, anisotropic yield and plastic potentials in cold rolled FCC aluminium alloy based on the crystallographic texture measurements. Eur. J. Mech. A-Solids 2019, 75, 41–55. [Google Scholar] [CrossRef]
- Bishoyi, B.; Debta, M.K.; Yadav, S.K.; Sabat, R.K.; Sahoo, S.K. Simulation of texture evolution during uniaxial deformation of commercially pure Titanium. IOP Conf. Ser. Mater. Sci. Eng. 2018, 338, 012038. [Google Scholar] [CrossRef]
- Huang, S.Y.; Zhang, S.R.; Li, D.Y.; Peng, Y.H. Simulation of texture evolution during plastic deformation of FCC, BCC and HCP structured crystals with crystal plasticity based finite element method. Trans. Nonferr. Met. Soc. China 2011, 21, 1817–1825. [Google Scholar] [CrossRef]
- Fan, W.W.; Ren, Z.K.; Hou, J.; Wang, T. Finite element simulation of mesoscale inhomogeneous deformation in 304 stainless steel foil tensile. Mater. Res. Express 2019, 6, 096540. [Google Scholar] [CrossRef]
- Lu, J.W.; Sun, W.; Becker, A. Material characterization and finite element modelling of cyclic plasticity behavior for 304 stainless steel using a crystal plasticity model. Int. J. Mech. Sci. 2015, 105, 315–329. [Google Scholar] [CrossRef]
- Si, L.Y. Simulation of the Texture Evolution During Cold Deformation of FCC Metal with Crystal Plasticity FEM. Ph.D. Thesis, Northeastern University, Shenyang, China, 2009. [Google Scholar]
- Kalidindi, S.R.; Schoenfeld, S.E. On the prediction of yield surfaces by the crystal plasticity models for fcc polycrystals. Mater. Sci. Eng. A 2000, 293, 120–129. [Google Scholar] [CrossRef]
- Ma, X.G.; Zhao, J.W.; Du, W.; Zhang, X.; Jiang, L.Z.; Jiang, Z.Y. An analysis of ridging of ferritic stainless steel 430. Mater. Sci. Eng. A 2017, 685, 358–366. [Google Scholar] [CrossRef]
- Zhang, P.; Karimpour, M.; Balint, D.; Lin, J.G.; Farrugia, D. A controlled Poisson Voronoi tessellation for grain and cohesive boundary generation applied to crystal plasticity analysis. Comput. Mater. Sci. 2012, 64, 84–89. [Google Scholar] [CrossRef]
- Rawat, S.; Chandra, S.; Chavan, V.M.; Sharma, S.; Warrier, M.; Chaturvedi, S.; Patel, R.J. Integrated experimental and computational studies of deformation of single crystal copper at high strain rates. J. Appl. Phys. 2014, 116, 213507. [Google Scholar] [CrossRef]
- Ren, Z.K.; Fan, W.W.; Hou, J.; Wang, T. A Numerical Study of Slip System Evolution in Ultra-Thin Stainless Steel Foil. Materials 2019, 12, 1819. [Google Scholar] [CrossRef]
- Rehrl, C.; Volker, B.; Kleber, S.; Antretter, T.; Pippan, R. Crystal orientation changes: A comparison between a crystal plasticity finite element study and experimental results. Acta Mater. 2012, 60, 2379–2386. [Google Scholar] [CrossRef]
- Huang, Y.G. A User-Material Subroutine Incroporating Single Crystal Plasticity in the Abaqus Finite Element Program; Harvard University: Cambridge, MA, USA, 1991. [Google Scholar]
- Sun, C.Y.; Guo, X.R.; Guo, N.; Yang, J.; Huang, J. Investigation of plastic deformation behavior on coupling twinning of polycrystal twip steel. Acta Metall. Sin. 2015, 51, 1507–1515. [Google Scholar]
- Tang, B.; Xie, S.; Liu, Y.; Han, F.B.; Kou, H.C.; Li, J.S. Crystal Plasticity Finite Element Simulations for Single Phase Titanium Alloys: Effect of Polycrystalline Aggregate Features on the Mechanical Response. Rare Metal Mat. Eng. 2015, 44, 267–271. [Google Scholar]
- Alharbi, H.F.; Kalidindi, S.R. Crystal plasticity finite element simulations using a database of discrete Fourier transforms. Int. J. Plast. 2015, 66, 71–84. [Google Scholar] [CrossRef]
- Chen, S.D.; Liu, X.H.; Liu, L.Z.; Song, M. Crystal plasticity finite element simulation of slip and deformation in ultrathin copper strip rolling. Acta Metall. Sin. 2016, 52, 120–128. [Google Scholar]
- Pi, H.C.; Han, J.T.; Zhang, C.G.; Tieu, A.K.; Jiang, Z.Y. Simulation of the rolling texture of pure Al using crystal plasticity finite element method. J. Univ. Sci. Technol. Beijing 2007, 29, 920–924. [Google Scholar]
- Pi, H.C.; Han, J.T.; Zhang, C.G.; Tieu, A.K.; Jiang, Z.Y. Modeling uniaxial tensile deformation of polycrystalline Al using CPFEM. J. Univ. Sci. Technol. Beijing 2008, 15, 43–47. [Google Scholar] [CrossRef]
- Hama, T.; Takuda, H. Crystal-plasticity finite-element analysis of inelastic behavior during unloading in a magnesium alloy sheet. Int. J. Plast. 2011, 27, 1072–1092. [Google Scholar] [CrossRef]
- Hama, T.; Takuda, H. Crystal plasticity finite-element simulation of work-hardening behavior in a magnesium alloy sheet under biaxial tension. Comput. Mater. Sci. 2012, 51, 156–164. [Google Scholar] [CrossRef]
- Alankar, A.; Mastorakos, I.N.; Field, D.P. A dislocation-density-based 3D crystal plasticity model for pure aluminum. Acta Mater. 2009, 57, 5936–5946. [Google Scholar] [CrossRef]
- Ha, S.; Jang, J.H.; Kim, K.T. Finite element implementation of dislocation-density-based crystal plasticity model and its application to pure aluminum crystalline materials. Int. J. Mech. Sci. 2017, 120, 249–262. [Google Scholar] [CrossRef]
- Li, Z.; Yang, F. Grain rotations during uniaxial deformation of gradient nano-grained metals using crystal plasticity finite element simulations. Extreme Mech. Lett. 2017, 16, 41–48. [Google Scholar] [CrossRef]
- Ritz, H.; Dawson, P.R. Sensitivity to grain discretization of the simulated crystal stress distributions in FCC polycrystals. Modell. Simul. Mater. Sci. Eng. 2009, 17, 015001. [Google Scholar] [CrossRef]
- Nakamachi, E.; Tam, N.N.; Morimoto, H. Multi-scale finite element analyses of sheet metals by using SEM-EBSD measured crystallographic RVE models. Int. J. Plast. 2007, 23, 450–489. [Google Scholar] [CrossRef]
- Kami’nski, M.; Sokołowski, D. Dual probabilistic homogenization of the rubber-based composite with random 373 carbon black particle reinforcement. Comp. Struct. 2016, 140, 783–797. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic strain in metals. J. Inst. Met. 1938, 62, 307–324. [Google Scholar]
- Hill, R.; Rice, J.R. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. An analysis of nonuniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Asaro, R.J.; Needleman, A. Texture development and strain hardening in rate dependent polycrystals. Acta Metall. 1985, 33, 923–953. [Google Scholar] [CrossRef]
- Quey, R.; Dawson, P.R.; Barbe, F. Large-scale 3D random polycrystals for the finite element method:Generation, meshing and remeshing. Comput. Meth. Appl. Mech. Eng. 2011, 200, 1729–1745. [Google Scholar] [CrossRef]



| 60 | 21 | 61 | 0.001 | 10 | 1.2 |
| Plane | Direction | Slip System |
|---|---|---|
| (111) | [01] | a1 |
| [10] | a2 | |
| [10] | a3 | |
| (11) | [101] | b1 |
| [110] | b2 | |
| [01] | b3 | |
| (11) | [011] | c1 |
| [110] | c2 | |
| [10] | c3 | |
| (11) | [011] | d1 |
| [101] | d2 | |
| [10] | d3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Hu, Z.; Guo, L. Study on a New Forming Method—Thread Rolling by Crystal Plasticity Finite Element Simulation. Metals 2021, 11, 503. https://doi.org/10.3390/met11030503
Zhang Y, Hu Z, Guo L. Study on a New Forming Method—Thread Rolling by Crystal Plasticity Finite Element Simulation. Metals. 2021; 11(3):503. https://doi.org/10.3390/met11030503
Chicago/Turabian StyleZhang, Yuheng, Zhiqing Hu, and Liming Guo. 2021. "Study on a New Forming Method—Thread Rolling by Crystal Plasticity Finite Element Simulation" Metals 11, no. 3: 503. https://doi.org/10.3390/met11030503
APA StyleZhang, Y., Hu, Z., & Guo, L. (2021). Study on a New Forming Method—Thread Rolling by Crystal Plasticity Finite Element Simulation. Metals, 11(3), 503. https://doi.org/10.3390/met11030503





