Influence of HPT and Accumulative High-Pressure Torsion on the Structure and Hv of a Zirconium Alloy
Abstract
:1. Introduction
2. Materials and Methods
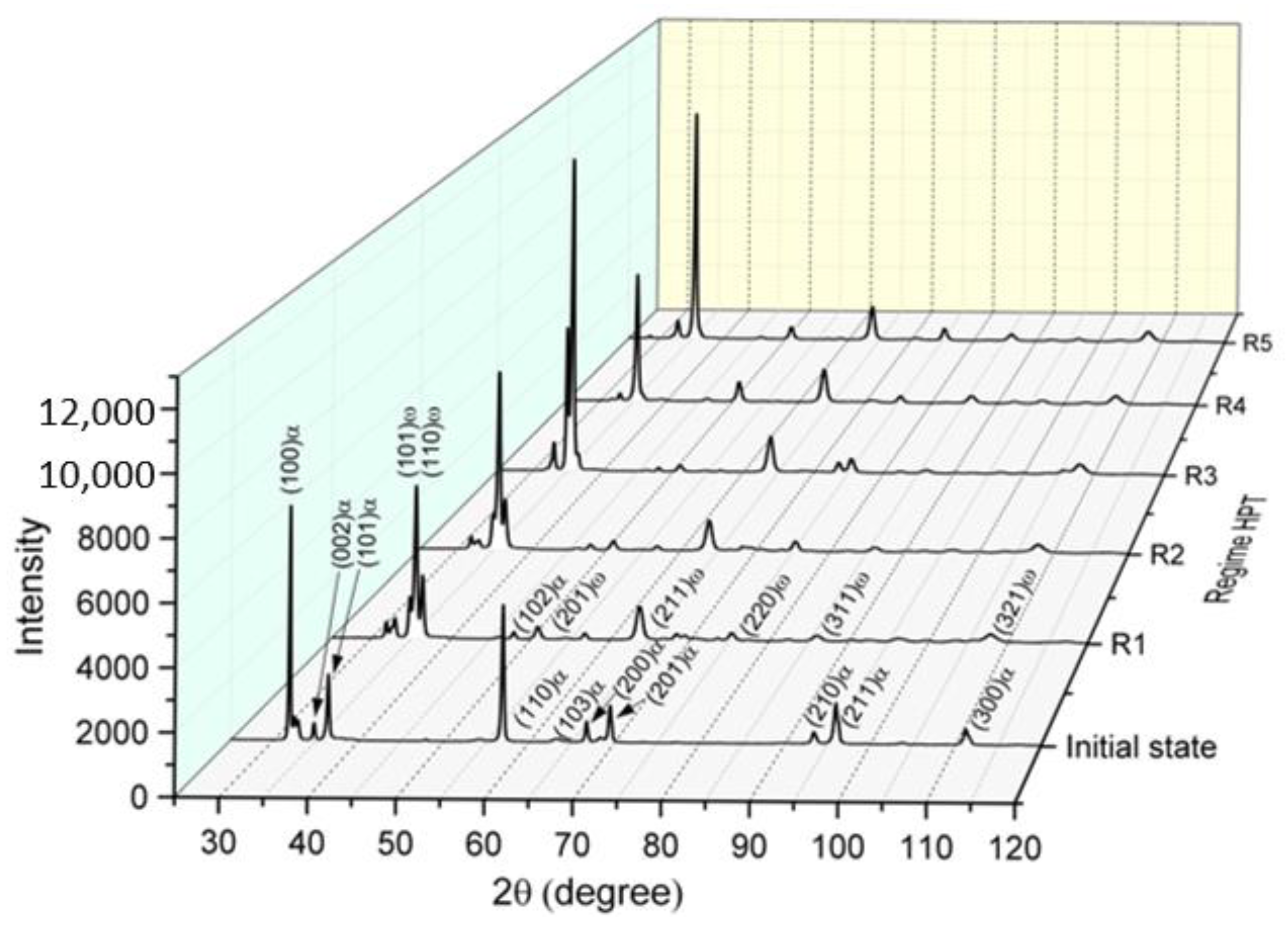
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Williams, D.F. On the mechanisms of biocompatibility. Biomaterials 2008, 29, 2941–2953. [Google Scholar] [CrossRef] [PubMed]
- Brunette, D.M.; Tengvall, P.; Textor, M.; Thomsen, P. Titanium in Medicine. In Material Science, Surface Science, Engineering, Biological Responses and Medical Applications; Springer: Berlin, Germany, 2001; pp. 145–162. [Google Scholar]
- Valiev, R.; Zhilyaev, A.; Langdon, T. Bulk Nanostructured Materials: Fundamentals and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; 456p. [Google Scholar]
- Zhou, W.; Yu, J.; Lin, J.; Dean, T. Manufacturing a curved profile with fine grains and high strength by differential velocity sideways extrusion. Int. J. Mach. Tools Manuf. 2019, 140, 77–88. [Google Scholar] [CrossRef]
- Zhilyaev, A.P.; Langdon, T.G. Using high-pressure torsion for metal processing: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 893–979. [Google Scholar] [CrossRef]
- Banerjee, S.; Mukhopadhyay, P. Phase Transformations: Examples from Titanium and Zirconium Alloys, 1st ed.; Pergamon Materials Series; Elsevier: Amsterdam, The Netherlands, 2007; Volume 12, 803p. [Google Scholar]
- Steinemann, S.G. Corrosion of surgical implants—In vivo and in vitro tests. In Evaluation of Biomaterials; Winter, G.D., Leray, J.L., De Groot, K., Eds.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1980; pp. 1–34. [Google Scholar]
- Zhao, Y.; Zhang, J.; Pantea, C.; Qian, J.; Daemen, L.L.; Rigg, P.A.; Hixson, R.S.; Gray, G.T., III; Yang, Y.; Wang, L.; et al. Thermal equations of state of the α, β, and ω phases of zirconium. Phys. Rev. B 2005, 71, 184119. [Google Scholar] [CrossRef]
- Zhilyaev, A.; Galvez, F.; Sharafutdinov, A.; Perez-Prado, M.T. Influence of the high pressure torsion die geometry on the allotropic phase transformations in pure Zr. Mater. Sci. Eng. A 2010, 527, 3918–3928. [Google Scholar] [CrossRef]
- Edalati, K.; Horita, Z.; Yagi, S.; Matsubara, E. Allotropic phase transformation of pure zirconium by high-pressure torsion. Mater. Sci. Eng. A 2009, 523, 277–281. [Google Scholar] [CrossRef]
- Straumal, B.; Gornakova, A.; Mazilkin, A.; Fabrichnaya, O.; Kriegel, M.; Baretzky, B.; Jiang, J.-Z.; Dobatkin, S. Phase transformations in the severely plastically deformed Zr–Nb alloys. Mater. Lett. 2012, 81, 225–228. [Google Scholar] [CrossRef]
- Straumal, B.B.; Gornakova, A.S.; Fabrichnaya, O.B.; Kriegel, M.J.; Mazilkin, A.A.; Baretzky, B.; Gusak, A.; Dobatkin, S.V. Effective Temperature of High Pressure Torsion in Zr-Nb Alloys. High Temp. Mater. Process. 2012, 31, 339–350. [Google Scholar] [CrossRef]
- Rogachev, S.O.; Nikulin, S.A.; Rozhnov, A.B.; Gorshenkov, M.V. Microstructure, Phase Composition, and Thermal Stability of Two Zirconium Alloys Subjected to High-Pressure Torsion at Different Temperatures. Adv. Eng. Mater. 2018, 20, 1800151. [Google Scholar] [CrossRef]
- Nikulin, S.; Dobatkin, S.; Rogachev, S. Nanocrystalline zirconium alloys obtained by severe plastic deformation. J. Phys. Conf. Ser. 2013, 416, 012005. [Google Scholar] [CrossRef] [Green Version]
- Feng, B.; Levitas, V.I.; Kamrani, M. Coupled strain-induced alpha to omega phase transformation and plastic flow in zirconium under high pressure torsion in a rotational diamond anvil cell. Mater. Sci. Eng. A 2018, 731, 623–633. [Google Scholar] [CrossRef] [Green Version]
- Edalati, K.; Horita, Z.; Langdon, T. The significance of sliding in processing by high-pressure torsion. Scr. Mater. 2009, 60, 9–12. [Google Scholar] [CrossRef]
- Kovács, Z.; Schafler, E.; Szommer, P.; Révész, Á. Localization of plastic deformation along shear bands in Vitreloy bulk metallic glass during high pressure torsion. J. Alloys Comp. 2014, 593, 207–212. [Google Scholar] [CrossRef]
- Hohenwarter, A.; Bachmaier, A.; Gludovatz, B.; Scheriau, S.; Pippan, R. Technical parameters affecting grain refinement by high pressure torsion. Int. J. Mater. Res. 2009, 100, 1653–1661. [Google Scholar] [CrossRef]
- Gunderov, D.; Churakova, A.; Boltynjuk, E.; Ubyivovk, E.; Astanin, V.; Asfandiyarov, R.; Valiev, R.; Xioang, W.; Wang, J. Observation of shear bands in the Vitreloy metallic glass subjected to HPT processing. J. Alloys Compd. 2019, 800, 58–63. [Google Scholar] [CrossRef]
- Gunderov, D.; Churakova, A.; Astanin, V.; Asfandiyarov, R.; Hahn, H.; Valiev, R. Accumulative HPT of Zr-based bulk metallic glasses. Mater. Lett. 2020, 261, 127000. [Google Scholar] [CrossRef]
- Gunderov, D.; Astanin, V.; Churakova, A.; Sitdikov, V.; Ubyivovk, E.; Islamov, A.; Wang, J.T. Influence of High-Pressure Torsion and Accumulative High-Pressure Torsion on Microstructure and Properties of Zr-Based Bulk Metallic Glass Vit105. Metals 2020, 10, 1433. [Google Scholar] [CrossRef]
- Gunderov, D.V.; Khasanova, D.A.; Astanin, V.V.; Churakova, A.A.; Ramazanov, I.A.; Prokoshkin, S.D.; Sheremetyev, V.A. Accumulative high-pressure torsion of steel 316 and β-Ti alloy. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1008, 012013. [Google Scholar] [CrossRef]
- Grabovetskaya, G.; Stepanova, E.; Dubrovskaya, A. Effect of hydrogen on the creep of the ultrafine-grained zirconium Zr–1Nb alloy at 673 K. Int. J. Hydrogen Energy 2017, 42, 22633–22640. [Google Scholar] [CrossRef]
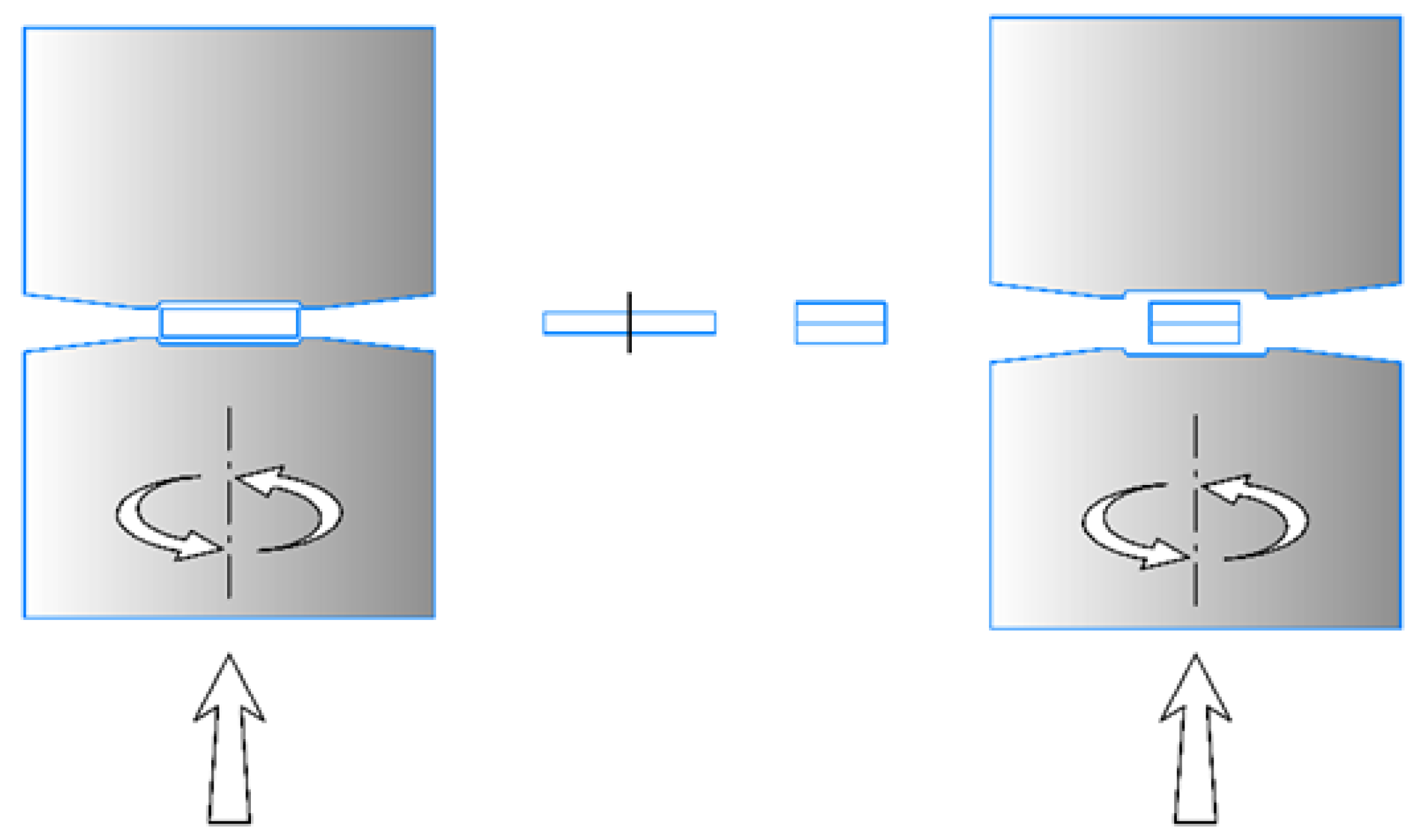
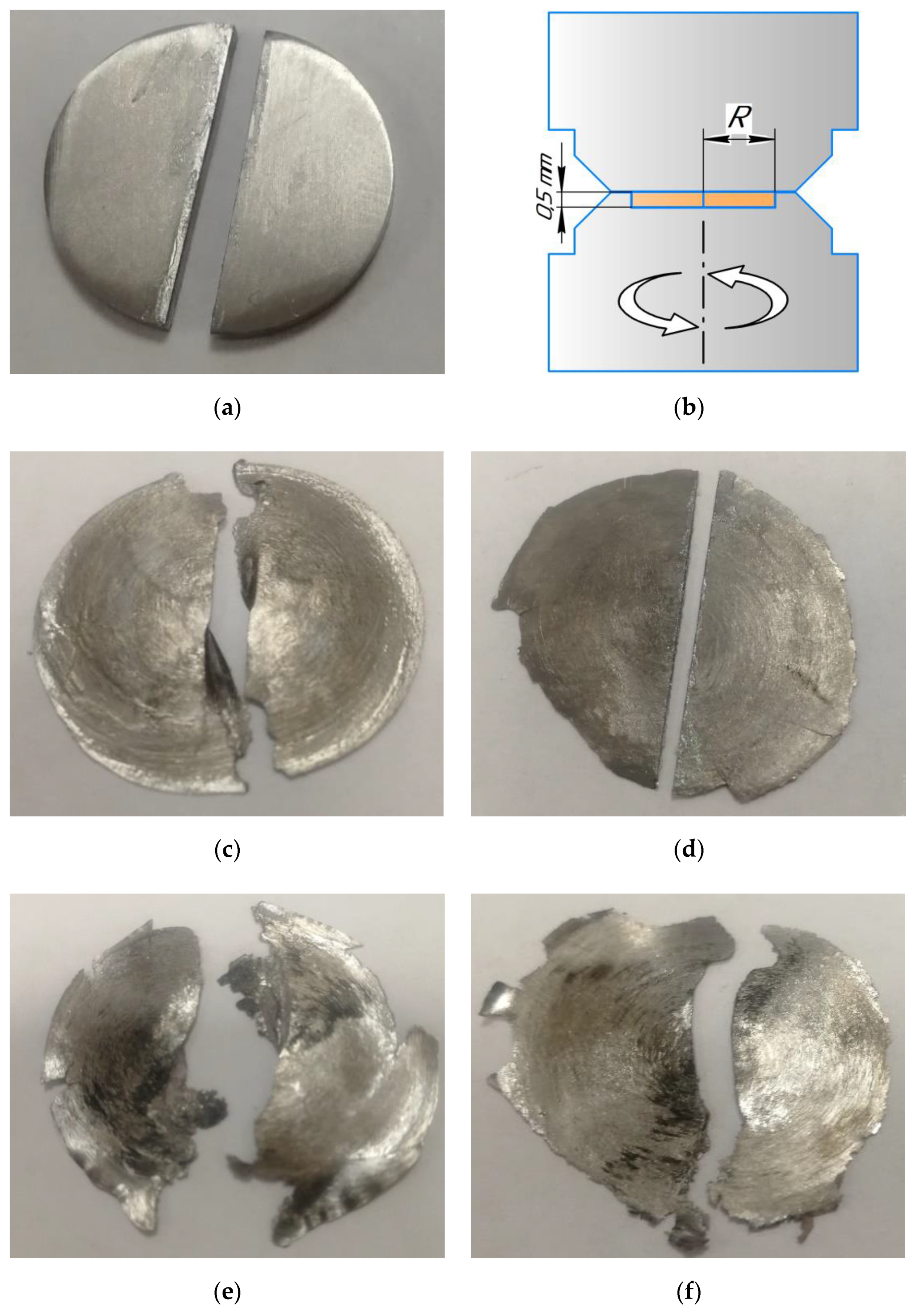
| Zr | Nb | O | Hf | Fe | Ca | C | Ni | Cr | Si |
|---|---|---|---|---|---|---|---|---|---|
| Base | 1.1 | 0.1 | 0.05 | 0.05 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 |
| Conditions/Designations | Method | Applied Pressure, GPa | Number of Revolutions |
|---|---|---|---|
| R1 | HPT | 2 | 10 |
| R2 | ACC HPT | 2 | nΣ = 10 |
| R3 | HPT | 6 | 1 |
| R4 | HPT | 6 | 10 |
| R5 | ACC HPT | 6 | nΣ = 10 |
| Treatment | X-ray Analysis | Microhardness, HV | |||
|---|---|---|---|---|---|
| α-Phase, % | ω-Phase, % | Center | 0.5R | Edge | |
| Initial state | 100 | - | 149 ± 5 | ||
| R1 (2 GPa, n = 10) | 20 | 80 | 283 ± 35 | 366 ± 17 | 343 ± 13 |
| R2 ACC (2 GPa, n = 10) | 18 | 82 | 347 ± 14 | 362 ± 24 | 346 ± 22 |
| R3 (6 GPa, n = 1) | 7 | 93 | 300 ± 7 | 375 ± 13 | 372 ± 21 |
| R4 (6 GPa, n = 10) | 4 | 96 | 371 ± 15 | 372 ± 6 | 368 ± 15 |
| R5 ACC (6 GPa, n = 10) | 3 | 97 | 410 ± 17 | 385 ± 19 | 396 ± 24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunderov, D.; Stotskiy, A.; Lebedev, Y.; Mukaeva, V. Influence of HPT and Accumulative High-Pressure Torsion on the Structure and Hv of a Zirconium Alloy. Metals 2021, 11, 573. https://doi.org/10.3390/met11040573
Gunderov D, Stotskiy A, Lebedev Y, Mukaeva V. Influence of HPT and Accumulative High-Pressure Torsion on the Structure and Hv of a Zirconium Alloy. Metals. 2021; 11(4):573. https://doi.org/10.3390/met11040573
Chicago/Turabian StyleGunderov, Dmitry, Andrey Stotskiy, Yuri Lebedev, and Veta Mukaeva. 2021. "Influence of HPT and Accumulative High-Pressure Torsion on the Structure and Hv of a Zirconium Alloy" Metals 11, no. 4: 573. https://doi.org/10.3390/met11040573
APA StyleGunderov, D., Stotskiy, A., Lebedev, Y., & Mukaeva, V. (2021). Influence of HPT and Accumulative High-Pressure Torsion on the Structure and Hv of a Zirconium Alloy. Metals, 11(4), 573. https://doi.org/10.3390/met11040573






