Effects of Zn and Mg Segregations on the Grain Boundary Sliding and Cohesion in Al: Ab Initio Modeling
Abstract
1. Introduction
2. Methods of Calculations
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lejček, P. Grain Boundary Segregation in Metals; Springer Series in Materials Science; Springer: New York, NY, USA, 2010. [Google Scholar]
- Gayle, F.W.; Goodway, M. Precipitation hardening in the first aerospace aluminum alloy: The wright flyer crankcase. Science 1994, 266, 1015–1017. [Google Scholar] [CrossRef]
- Andersen, S.J.; Marioara, C.D.; Friis, J.; Wenner, S.; Holmestad, R. Precipitates in aluminium alloys. Adv. Phys. X 2018, 3, 1479984. [Google Scholar] [CrossRef]
- Valiev, R.Z. Nanostructuring of metals by severe plastic deformation for advanced properties. Nat. Mater. 2004, 3, 511. [Google Scholar] [CrossRef] [PubMed]
- Sauvage, X.; Wilde, G.; Divinski, S.V.; Horita, Z.; Valiev, R.Z. Grain boundaries in ultrafine grained materials processed by severe plastic deformation and related phenomena. Mater. Sci. Eng. A 2012, 540, 1–12. [Google Scholar] [CrossRef]
- Edalati, K.; Horita, Z.; Valiev, R.Z. Transition from poor ductility to room-temperature superplasticity in a nanostructured aluminum alloy. Sci. Rep. 2018, 8, 6740. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Starink, M. Precipitates and intermetallic phases in precipitation hardening Al-Cu-Mg-(Li) based alloys. Int. Mater. Rev. 2005, 50, 193–215. [Google Scholar] [CrossRef]
- Nicolas, M.; Deschamps, A. Characterisation and modelling of precipitate evolution in an Al-Zn-Mg alloy during non-isothermal heat treatments. Acta Mater. 2003, 51, 6077–6094. [Google Scholar] [CrossRef]
- Yi, G.; Cullen, D.A.; Littrell, K.C.; Golumbfskie, W.; Sundberg, E.; Free, M.L. Characterization of Al-Mg alloy aged at low temperatures. Metall. Mater. Trans. A 2017, 48, 2040–2050. [Google Scholar] [CrossRef]
- Valiev, R.Z. Nanomaterial Advantage. Nature 2002, 419, 887. [Google Scholar] [CrossRef]
- Sauvage, X.; Enikeev, N.; Valiev, R.; Nasedkina, Y.; Murashkin, M. Atomic-scale analysis of the segregation and precipitation mechanisms in a severely deformed Al–Mg alloy. Acta Mater. 2014, 72, 125–136. [Google Scholar] [CrossRef]
- Li, H.Q.; Ebrahimi, F. An investigation of thermal stability and microhardness of electrodeposited nanocrystalline nickel-21% iron alloys. Acta Mater. 2003, 51, 3905–3913. [Google Scholar] [CrossRef]
- Chinh, N.Q.; Valiev, R.Z.; Sauvage, X.; Varga, G.; Havancsak, K.; Kawasaki, M.; Straumal, B.B.; Langdon, T.G. Grain Boundary Phenomena in an Ultrafine-Grained Al–Zn Alloy with Improved Mechanical Behavior for Micro-Devices. Adv. Eng. Mater. 2014, 16, 1000–1009. [Google Scholar] [CrossRef]
- Bobruk, E.V.; Sauvage, X.; Enikeev, N.A.; Straumal, B.B.; Valiev, R.Z. Mechanical behavior of ultrafine-grained Al-5Zn, Al-10Zn, Al-30Zn alloys. Rev. Adv. Mater. Sci. 2015, 43, 45–51. [Google Scholar]
- Lozovoi, A.Y.; Paxton, A.T.; Finnis, M.W. Structural and chemical embrittlement of grain boundaries by impurities: A general theory and first-principles calculations for copper. Phys. Rev. B 2006, 74, 155416. [Google Scholar] [CrossRef]
- Karkina, L.E.; Karkin, I.N.; Kuznetsov, A.R.; Razumov, I.K.; Korzhavyi, P.A.; Gornostyrev, Y.N. Solute–grain boundary interaction and segregation formation in Al: First principles calculations and molecular dynamics modeling. Comput. Mater. Sci. 2016, 112, 18–26. [Google Scholar] [CrossRef]
- Petrik, M.V.; Kuznetsov, A.R.; Enikeev, N.; Gornostyrev, Y.N.; Valiev, R.Z. Peculiarities of Interactions of Alloying Elements with Grain Boundaries and the Formation of Segregations in Al–Mg and Al–Zn Alloys. Phys. Met. Metallogr. 2018, 119, 607–612. [Google Scholar] [CrossRef]
- Wu, R.; Freeman, A.J.; Olson, G.B. First principles determination of the effects of phosphorus and boron on iron grain boundary cohesion. Science 1994, 265, 376–380. [Google Scholar] [CrossRef] [PubMed]
- Geng, W.T.; Freeman, A.J.; Wu, R.; Olson, G.B. Effect of Mo and Pd on the grain-boundary cohesion of Fe. Phys. Rev. B 2000, 62, 6208–6215. [Google Scholar] [CrossRef]
- Schweinfest, R.; Paxton, A.T.; Finnis, M.W. Bismuth embrittlement of copper is an atomic size effect. Nature 2004, 432, 1008–1011. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, M.; Shiga, M.; Kaburaki, H. Grain-boundary decohesion by impurity segregation in a nickel-sulfur system. Science 2005, 307, 393–397. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, X.; Wang, J.; Zhang, H.J. First-principles investigation of Mg segregation at Σ = 11(113) grain boundaries in Al. J. Phys. Condens. Matter 2005, 17, 4301–4308. [Google Scholar] [CrossRef]
- Zhang, L.; Shu, X.; Jin, S.; Zhang, Y.; Lu, G.H. First-principles study of He effects in a bcc Fe grain boundary: Site preference, segregation and theoretical tensile strength. J. Phys. Condens. Matter 2010, 22, 375401. [Google Scholar] [CrossRef]
- Christensen, M.; Angeliu, T.M.; Ballard, J.D.; Vollmer, J.; Najafabadi, R.; Wimmer, E. Effect of impurity and alloying elements on Zr grain boundary strength from first-principles computations. J. Nucl. Mater. 2010, 404, 121–127. [Google Scholar] [CrossRef]
- Yuasa, M.; Mabuchi, M.J. Effects of segregated Cu on an Fe grain boundary by first-principles tensile tests. Phys. Condens. Matter 2010, 22, 505705. [Google Scholar] [CrossRef]
- Wachowicz, E.; Kiejna, A. Effect of impurities on grain boundary cohesion in bcc iron. Comput. Mater. Sci. 2008, 43, 736–743. [Google Scholar] [CrossRef]
- Karkina, L.; Karkin, I.; Kuznetsov, A.; Gornostyrev, Y. Alloying Element Segregation and Grain Boundary Reconstruction, Atomistic Modeling. Metals 2019, 9, 1319. [Google Scholar] [CrossRef]
- Zhang, S.; Kontsevoi, O.Y.; Freeman, A.J.; Olson, G.B. First principles investigation of zinc-induced embrittlement in an aluminum grain boundary. Acta Mater. 2011, 59, 6155–6167. [Google Scholar] [CrossRef]
- Zhao, D.; Løvvik, O.M.; Marthinsen, K.; Li, Y. Segregation of Mg, Cu and their effects on the strength of Al Σ5 (210) [001] symmetrical tilt grain boundary. Acta Mater. 2018, 145, 235–246. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys. Condens. Matter 1994, 6, 8245–8258. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Cao, F.; Jiang, Y.; Hu, T.; Yin, D. Correlation of grain boundary extra free volume with vacancy and solute segregation at grain boundaries: A case study for Al. Philos. Mag. 2018, 98, 464–483. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Macdowell, D.L. Asymmetric tilt grain boundary structure and energy in copper and aluminium. Philos. Mag. 2007, 87, 3871. [Google Scholar] [CrossRef]
- Xiao, Z.; Hu, J.; Liu, Y.; Dong, F.; Huang, Y. Segregation of Sc and its effects on the strength of Al Σ5 (210) [100] symmetrical tilt grain boundary. Mater. Sci. Eng. A 2019, 756, 389–395. [Google Scholar] [CrossRef]
- Karkina, L.E.; Karkin, I.N.; Kuznetsov, A.R.; Gornostyrev, Y.N. Grain boundary shear-migration coupling in Al bicrystalls. Atomistic modeling. Phys. Solid State 2018, 60, 1916–1923. [Google Scholar] [CrossRef]
- Bollmann, W. Crystal Defects and Crystalline Interfaces; Springer: Berlin, Germany, 1970. [Google Scholar]
- Gorbatov, O.I.; Stroev, A.Y.; Gornostyrev, Y.N.; Korzhavyi, P.A. Effective cluster interactions and pre-precipitate morphology in binary Al-based alloys. Acta Mater. 2019, 179, 70–84. [Google Scholar] [CrossRef]
- Razumovskiy, V.I.; Ruban, A.V.; Razumovskii, I.M.; Lozovoi, A.Y.; Butrim, V.N.; Vekilov, Y.K. The effect of alloying elements on grain boundary and bulk cohesion in aluminum alloys: An ab initio study. Scr. Mater. 2011, 65, 926–929. [Google Scholar] [CrossRef]
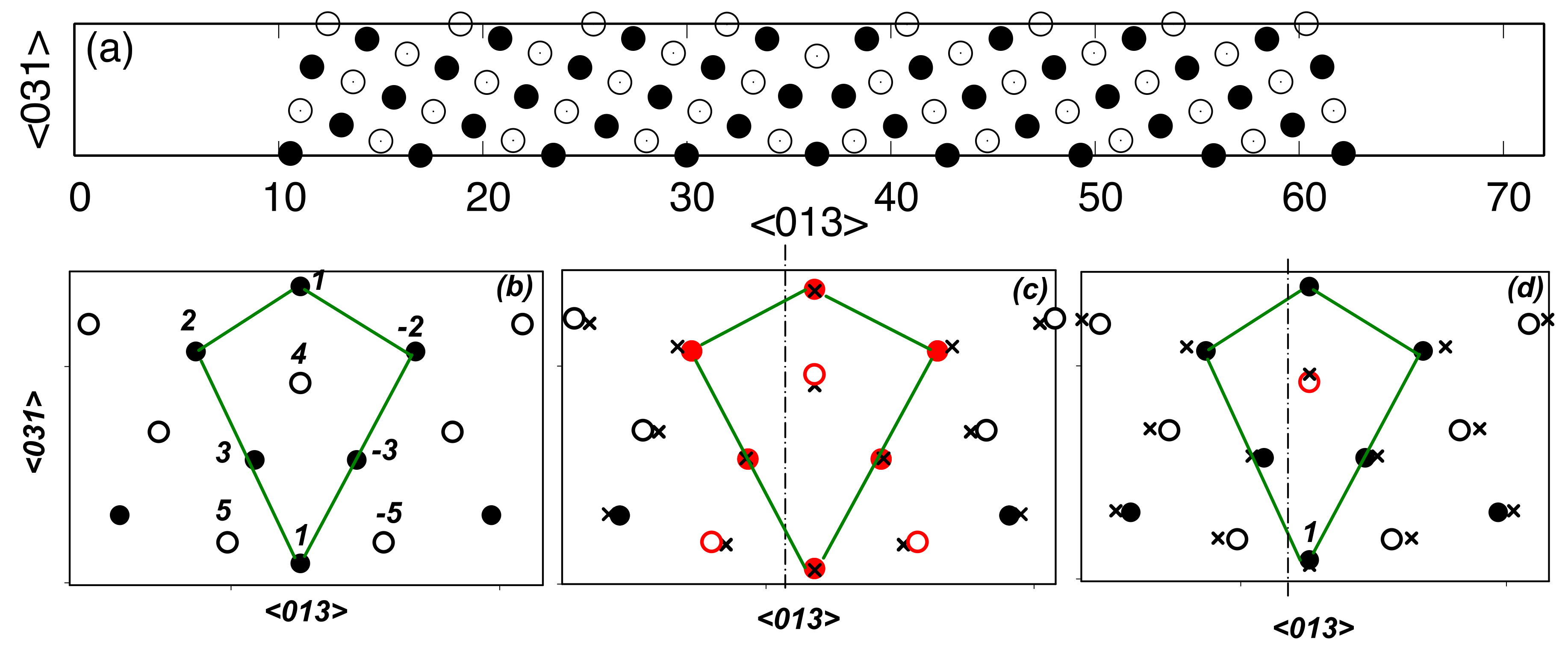
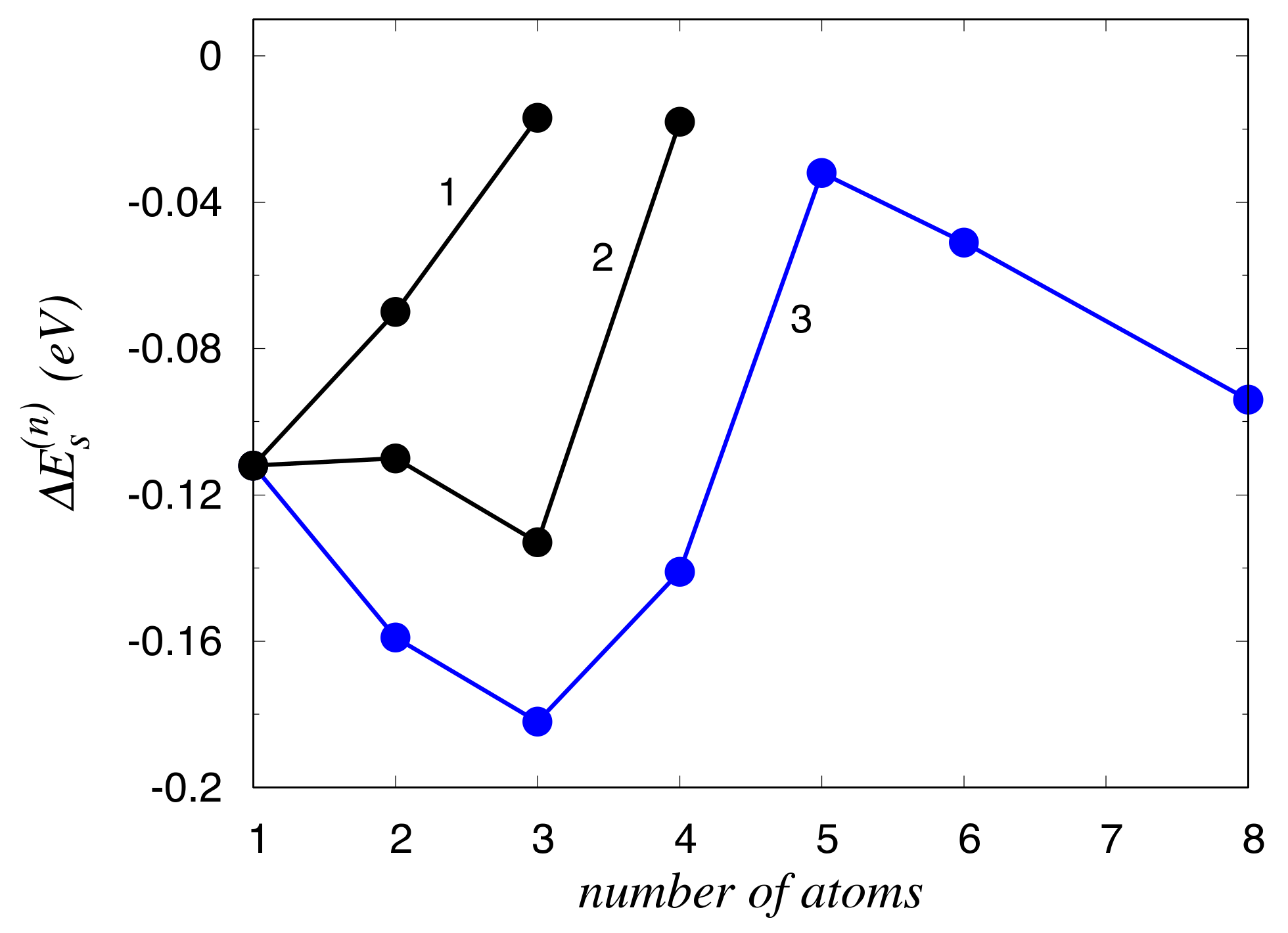
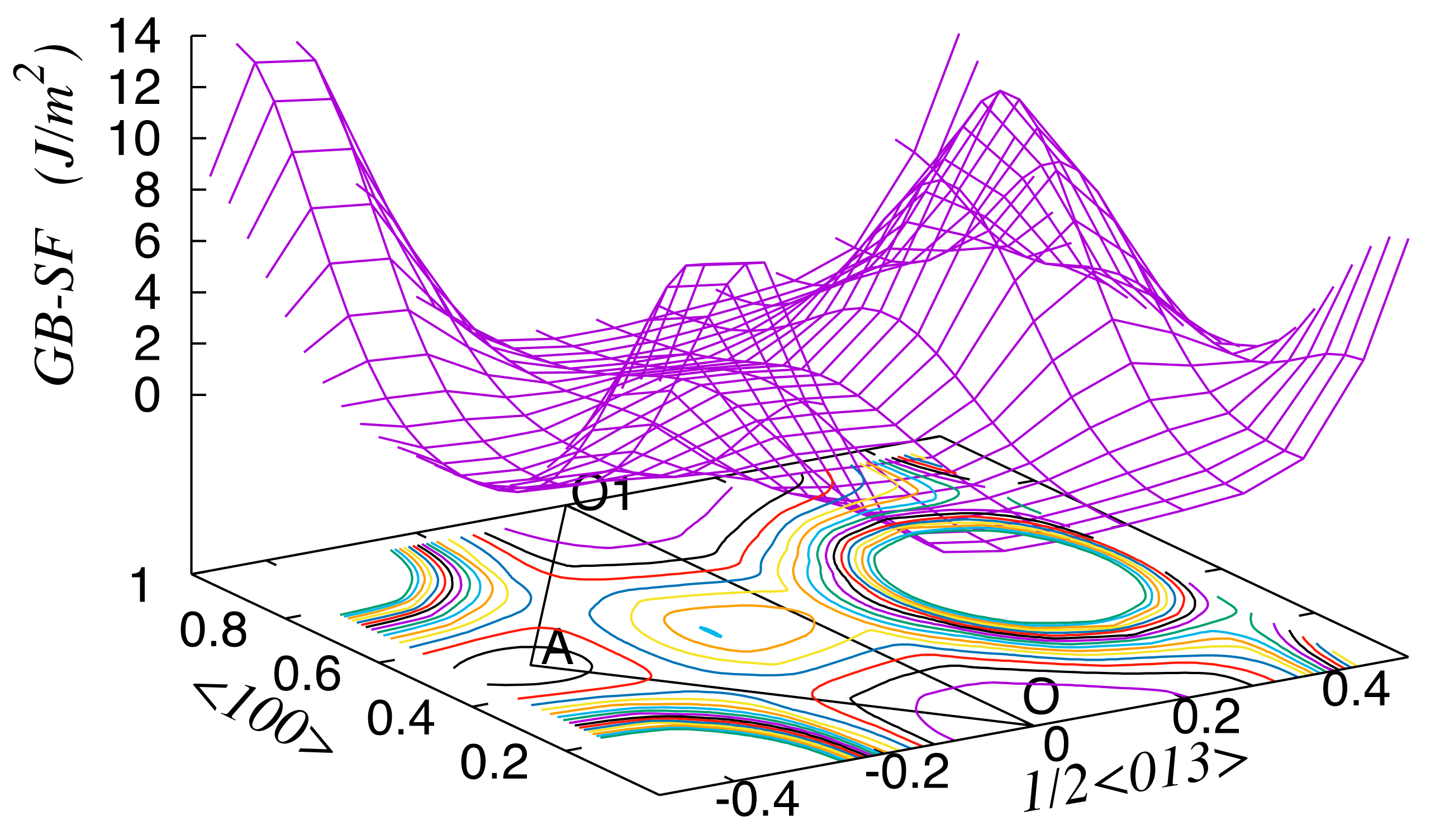
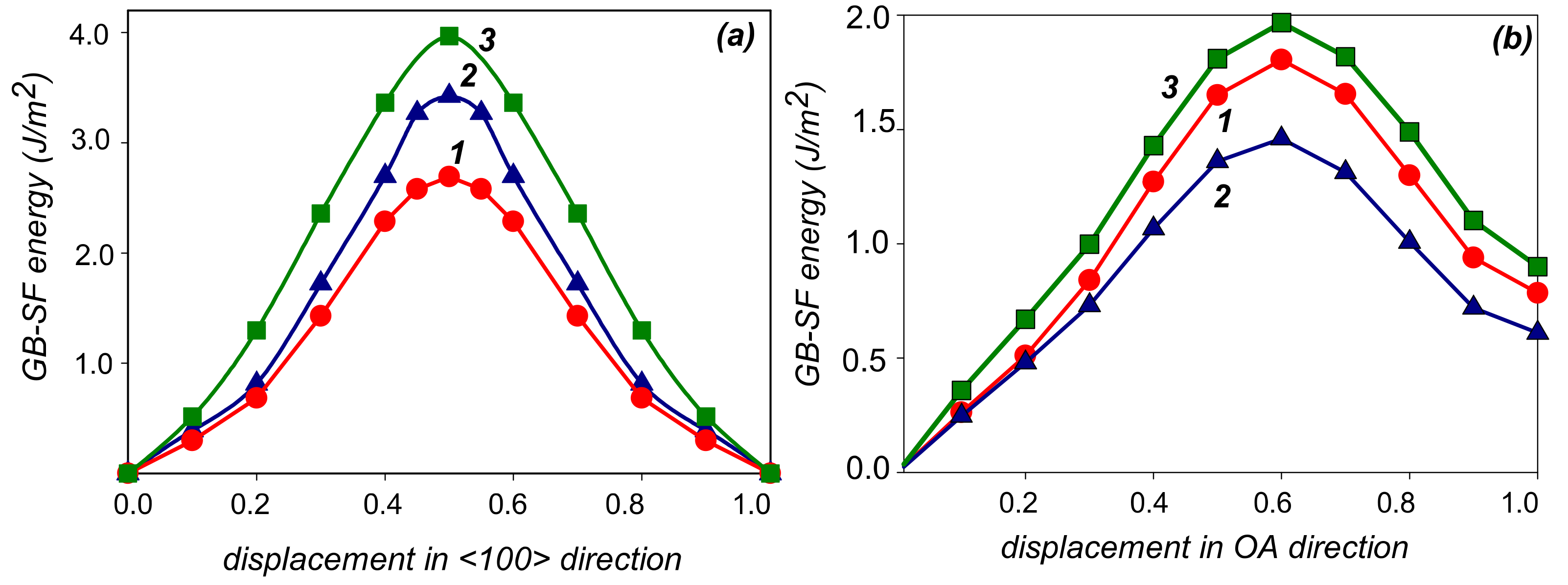
| Site | δu | ΔEs (Zn) | ΔEs (Mg) |
|---|---|---|---|
| 1 | −0.9 | −0.109 | 0.132 |
| 2 (−2) | 2.5 | −0.031 | 0.005 |
| 3 (−3) | −1.6 | −0.112 | 0.040 |
| 4 | 9.8 | 0.028 | −0.408 |
| 5 (−5) | 1.5 | −0.032 | 0.002 |
| Zn Atoms | Mg Atoms | ||
|---|---|---|---|
| Occupied Sites | Occupied Sites | ||
| (1)−(3); (1)−(−3)(3)−(1); (−3)−(1) | −0.16 | (4)−(3); (4)−(−3) | 0.21 |
| (3)−(−3) | −0.11 | (4)−(1) | 0.21 |
| (3)−(5) | −0.07 | (4)−(5); (4)−(−5) | 0.05 |
| (1)−(5) | −0.05 | (4)−(2); (4)−(−2) | 0.04 |
| (−3)−(2); (3)−(−2) | −0.04 | - | - |
| (1)−(2); (1)−(−2) | −0.03 | - | - |
| (3)−(2); (−3)−(−2) | −0.02 | - | - |
| (3)−(4); (−3)−(4) | 0.01 | - | - |
| O–O1 <100> | O–A | |||
|---|---|---|---|---|
| Unrelaxed | Relaxed | Unrelaxed | Relaxed | |
| Al | 2.58 | 0.37 | 1.80 | 0.53 |
| Al-Zn | 3.42 | 0.49 | 1.46 | 0.43 |
| Al-Mg | 3.96 | 0.72 | 1.97 | 0.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznetsov, A.; Karkina, L.; Gornostyrev, Y.; Korzhavyi, P. Effects of Zn and Mg Segregations on the Grain Boundary Sliding and Cohesion in Al: Ab Initio Modeling. Metals 2021, 11, 631. https://doi.org/10.3390/met11040631
Kuznetsov A, Karkina L, Gornostyrev Y, Korzhavyi P. Effects of Zn and Mg Segregations on the Grain Boundary Sliding and Cohesion in Al: Ab Initio Modeling. Metals. 2021; 11(4):631. https://doi.org/10.3390/met11040631
Chicago/Turabian StyleKuznetsov, Andrey, Lidia Karkina, Yuri Gornostyrev, and Pavel Korzhavyi. 2021. "Effects of Zn and Mg Segregations on the Grain Boundary Sliding and Cohesion in Al: Ab Initio Modeling" Metals 11, no. 4: 631. https://doi.org/10.3390/met11040631
APA StyleKuznetsov, A., Karkina, L., Gornostyrev, Y., & Korzhavyi, P. (2021). Effects of Zn and Mg Segregations on the Grain Boundary Sliding and Cohesion in Al: Ab Initio Modeling. Metals, 11(4), 631. https://doi.org/10.3390/met11040631








