Vibration Damping and Acoustic Behavior of PU-Filled Non-Stochastic Aluminum Cellular Solids
Abstract
:1. Introduction
2. Materials and Methods
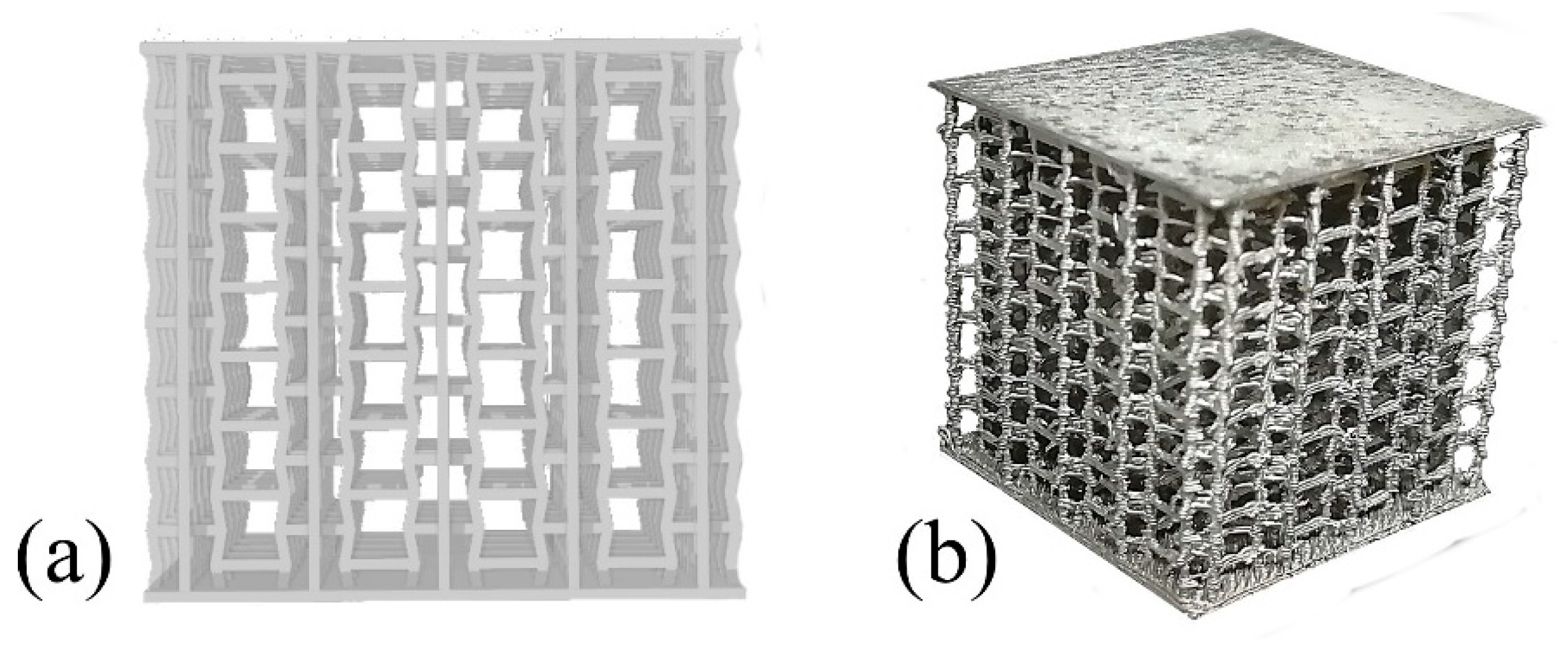
2.1. Cellular Lattice Design and Manufacturing
2.2. Polyurethane Filling
2.3. Vibration Testing
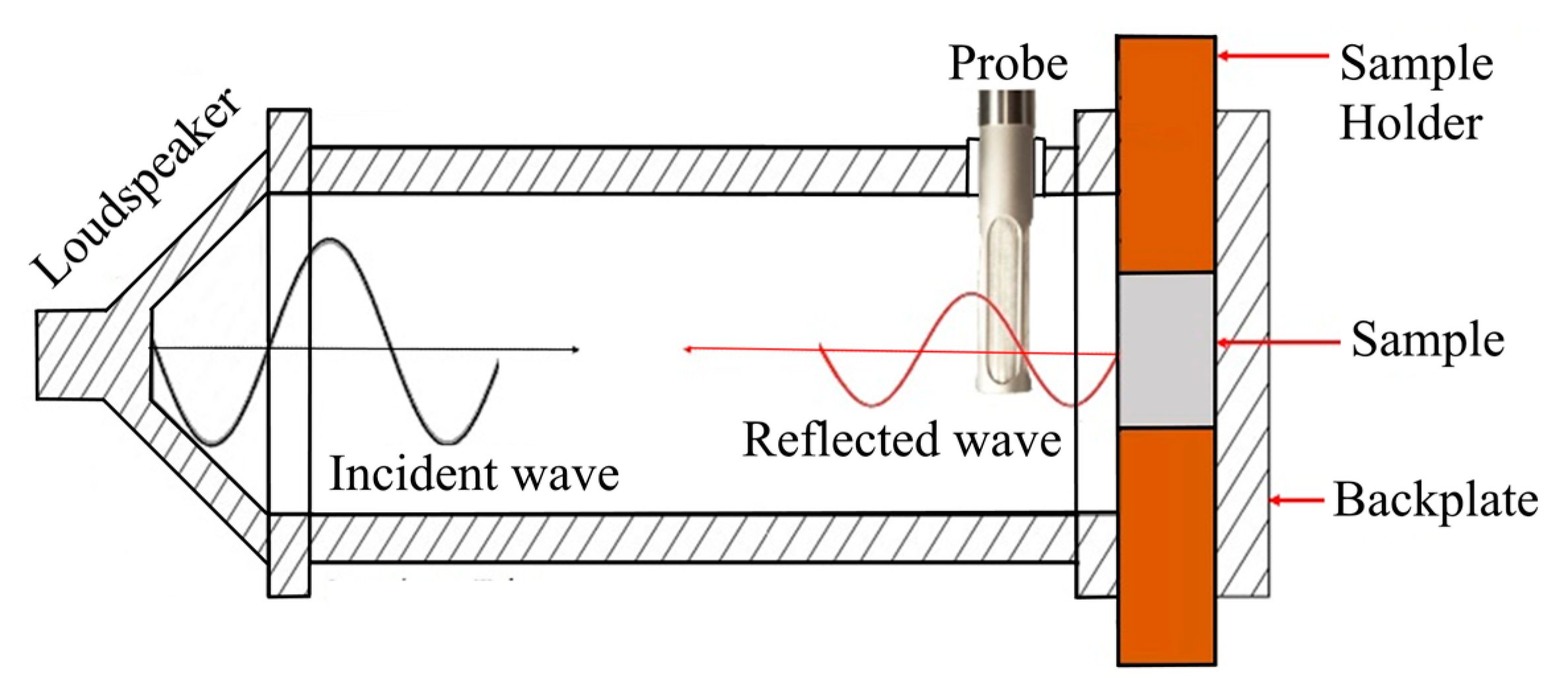
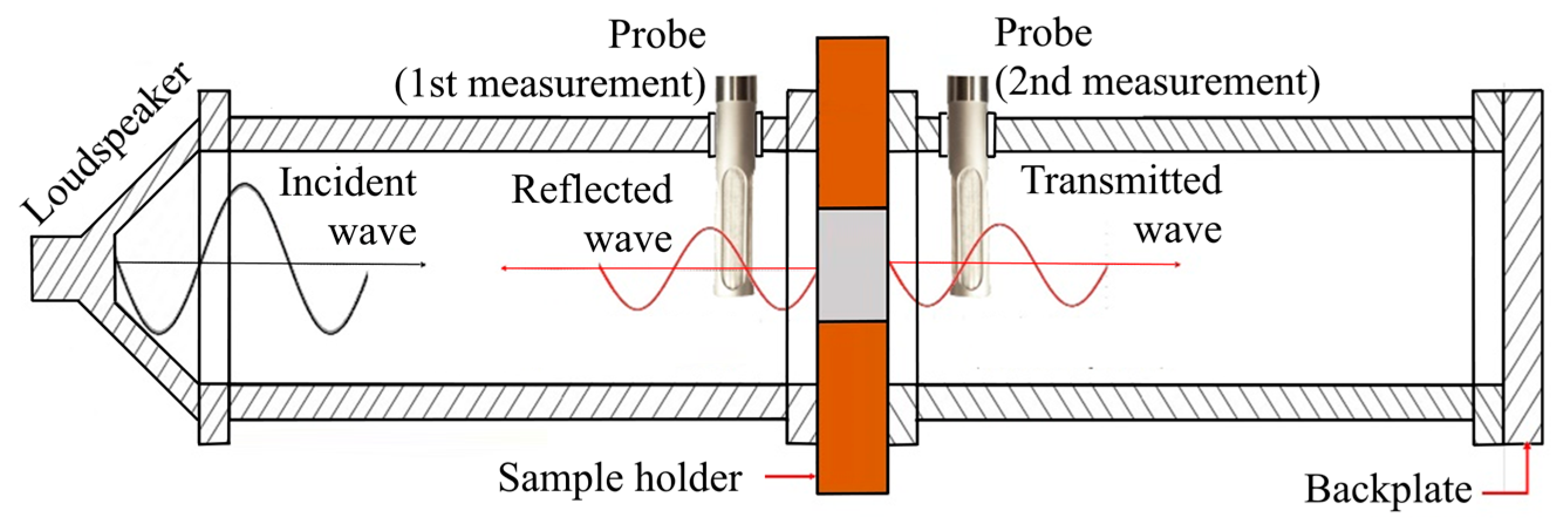
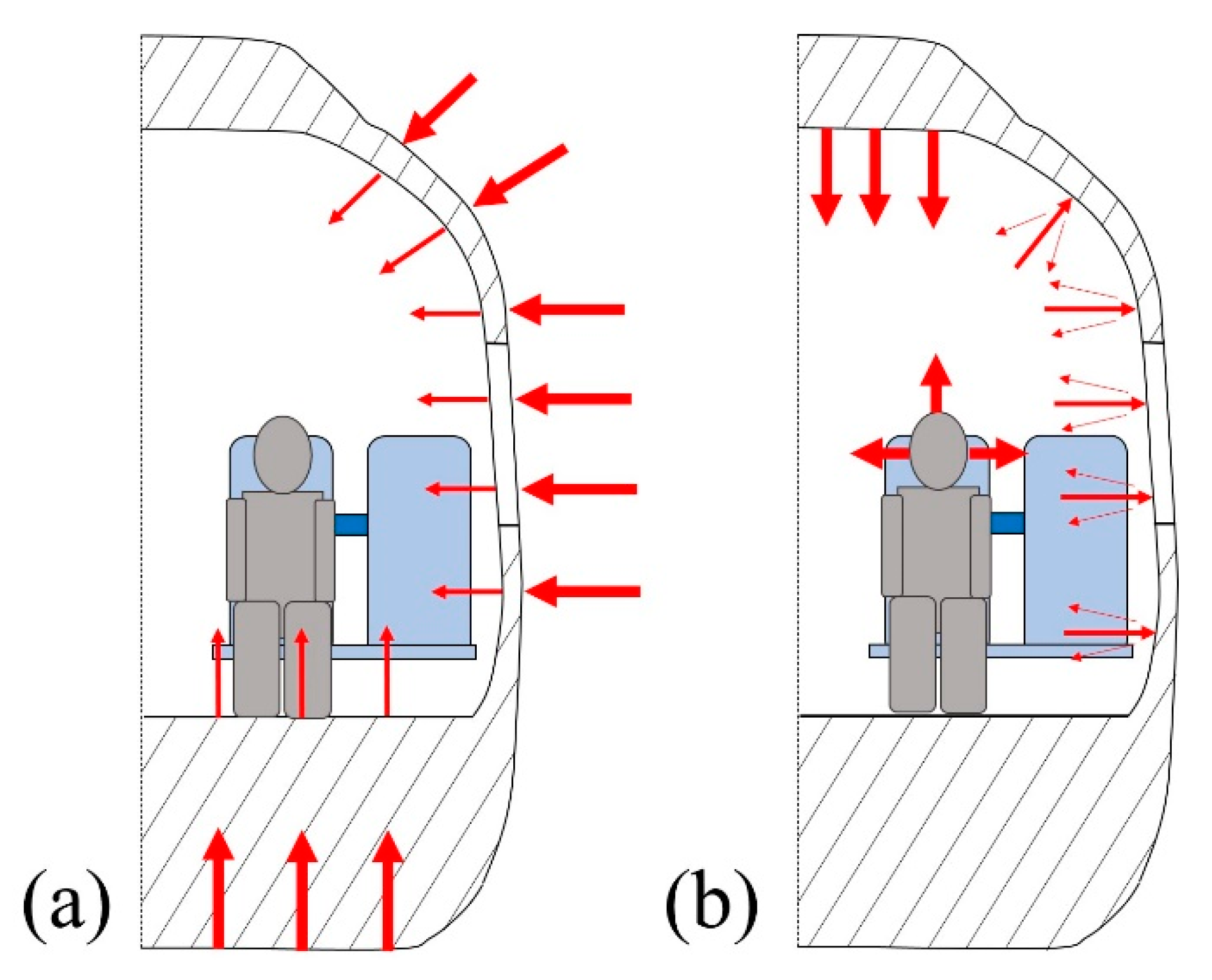
2.4. Acoustic Testing of the Samples
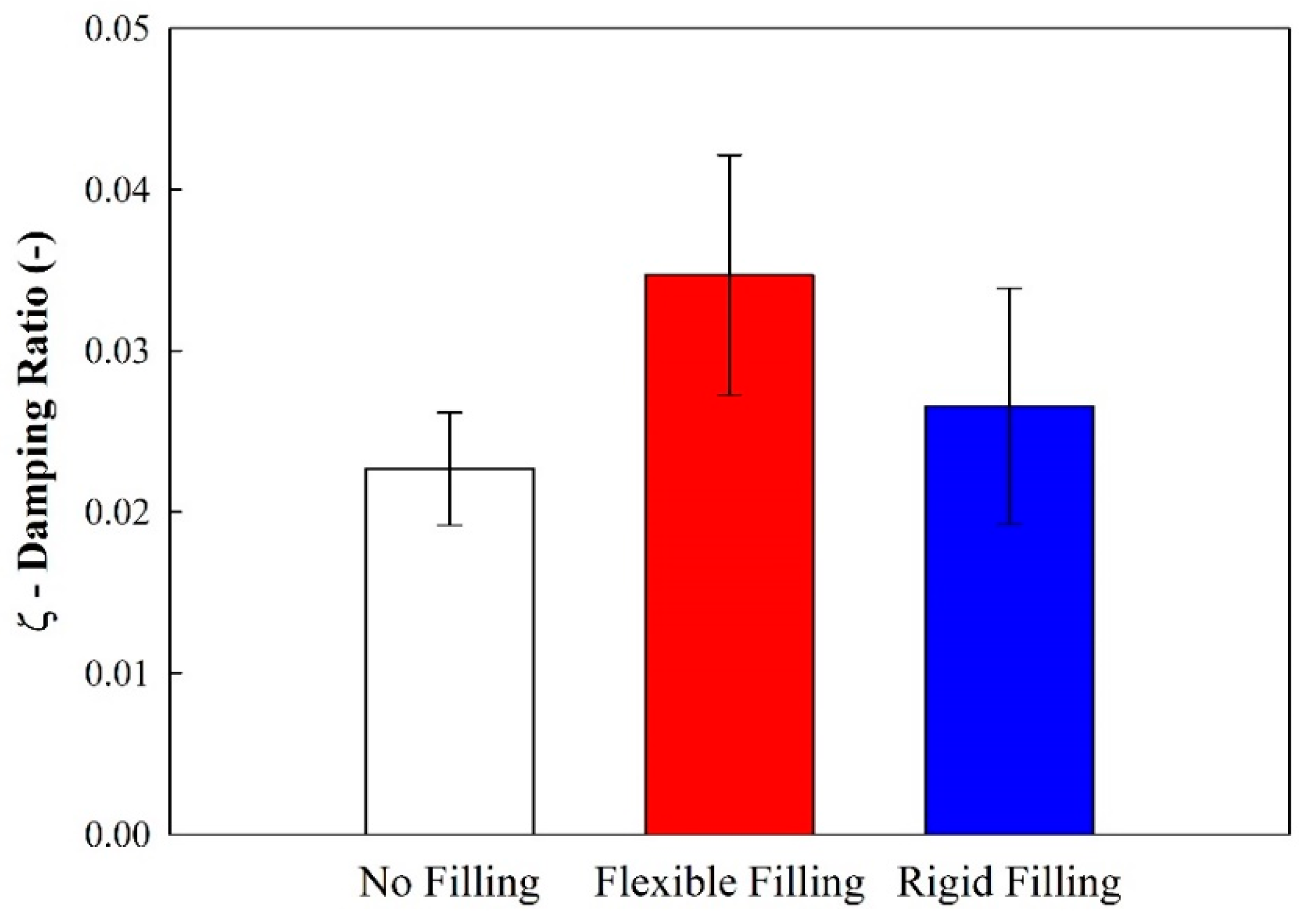
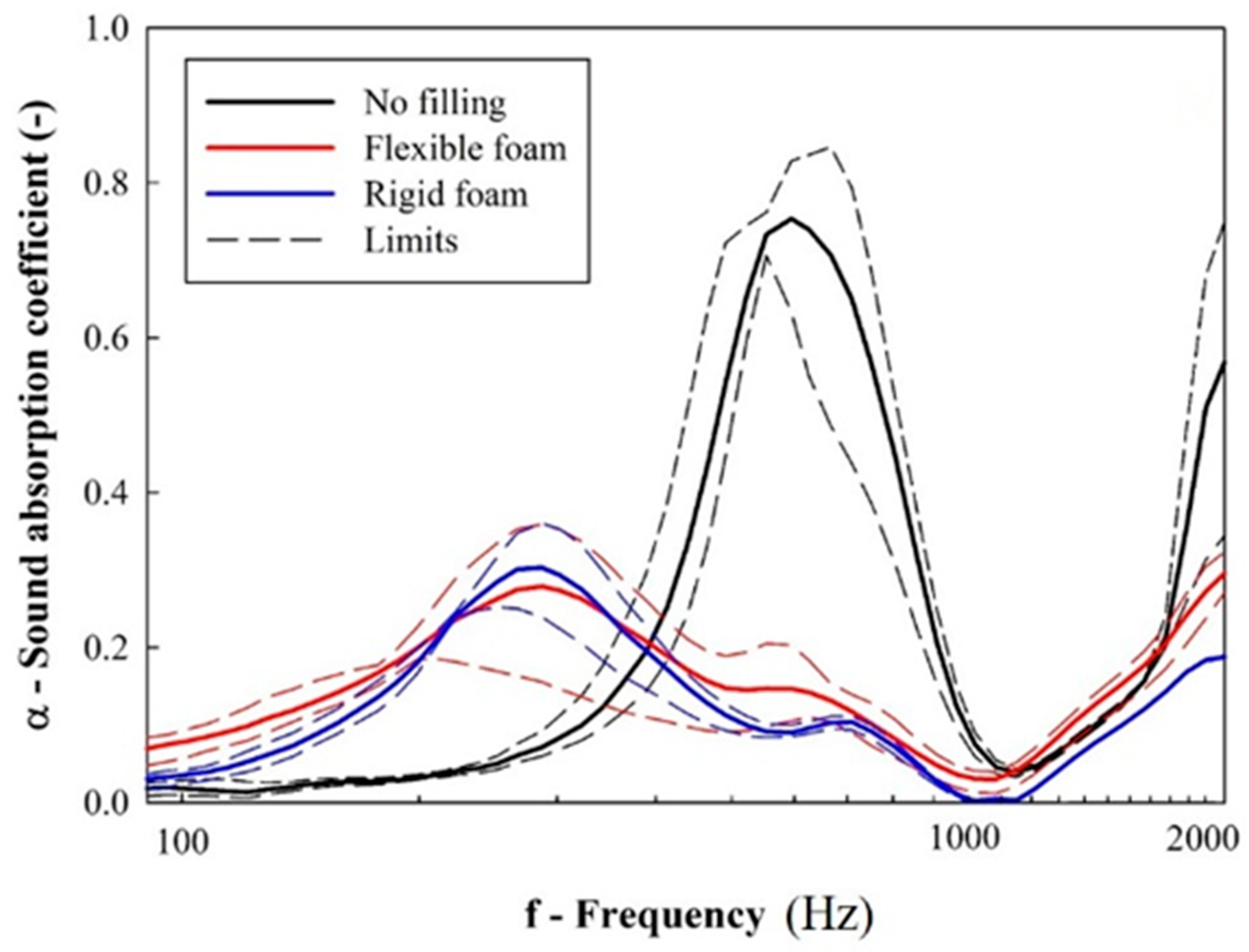
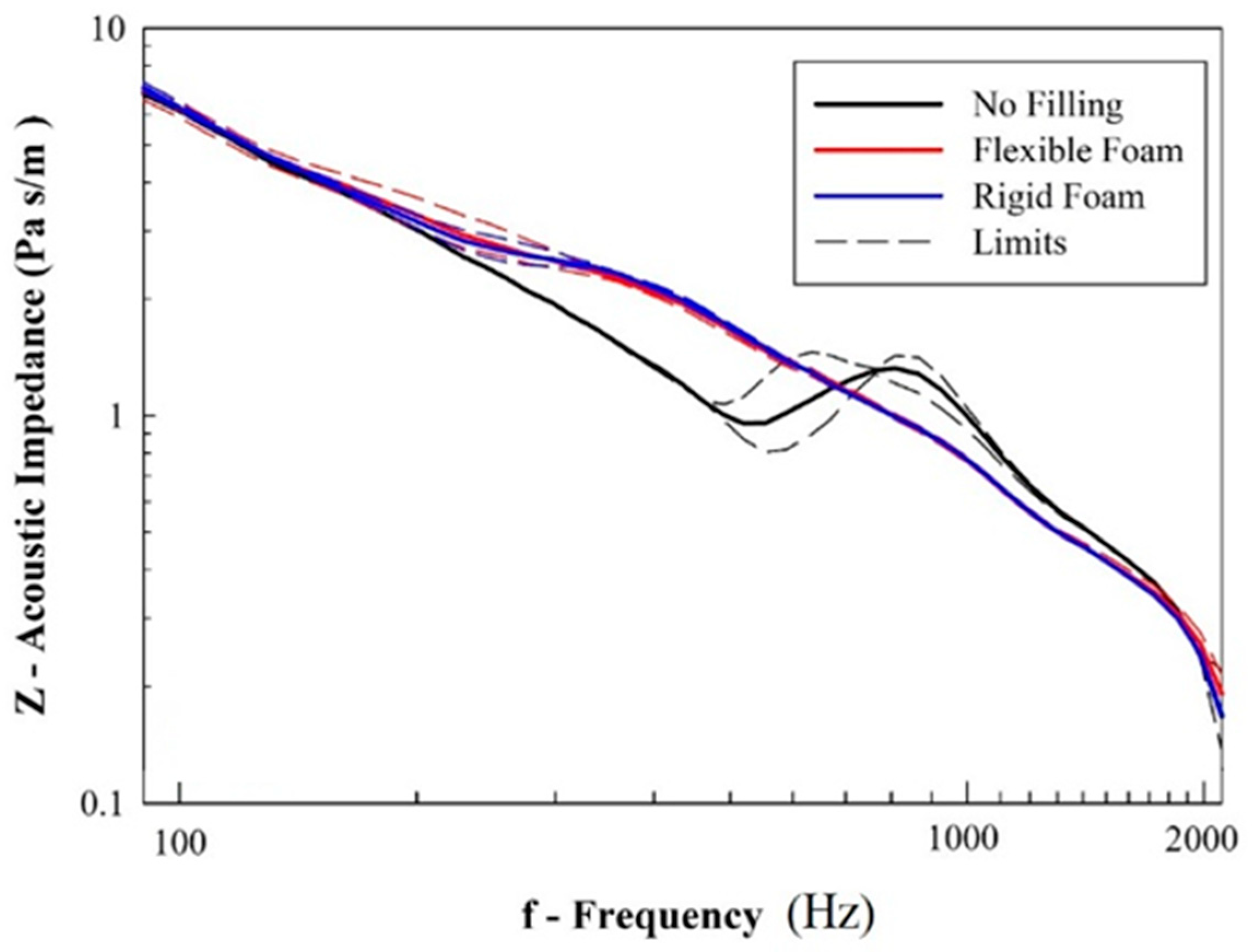
3. Results and Discussion
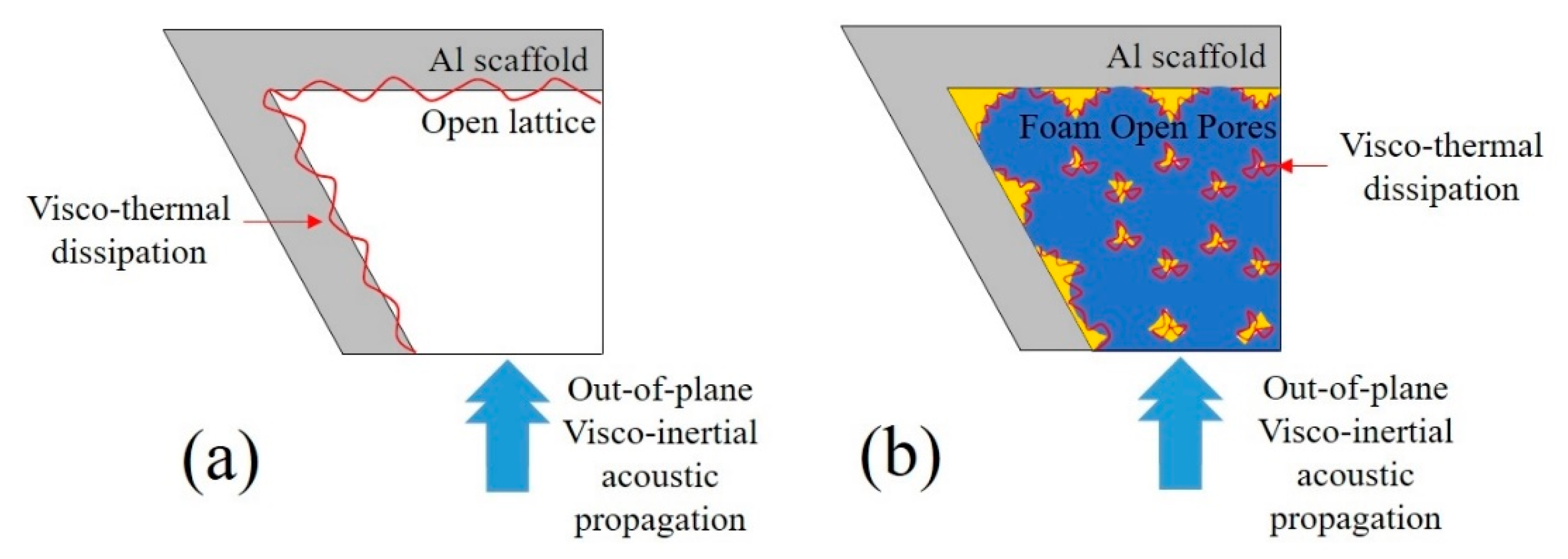
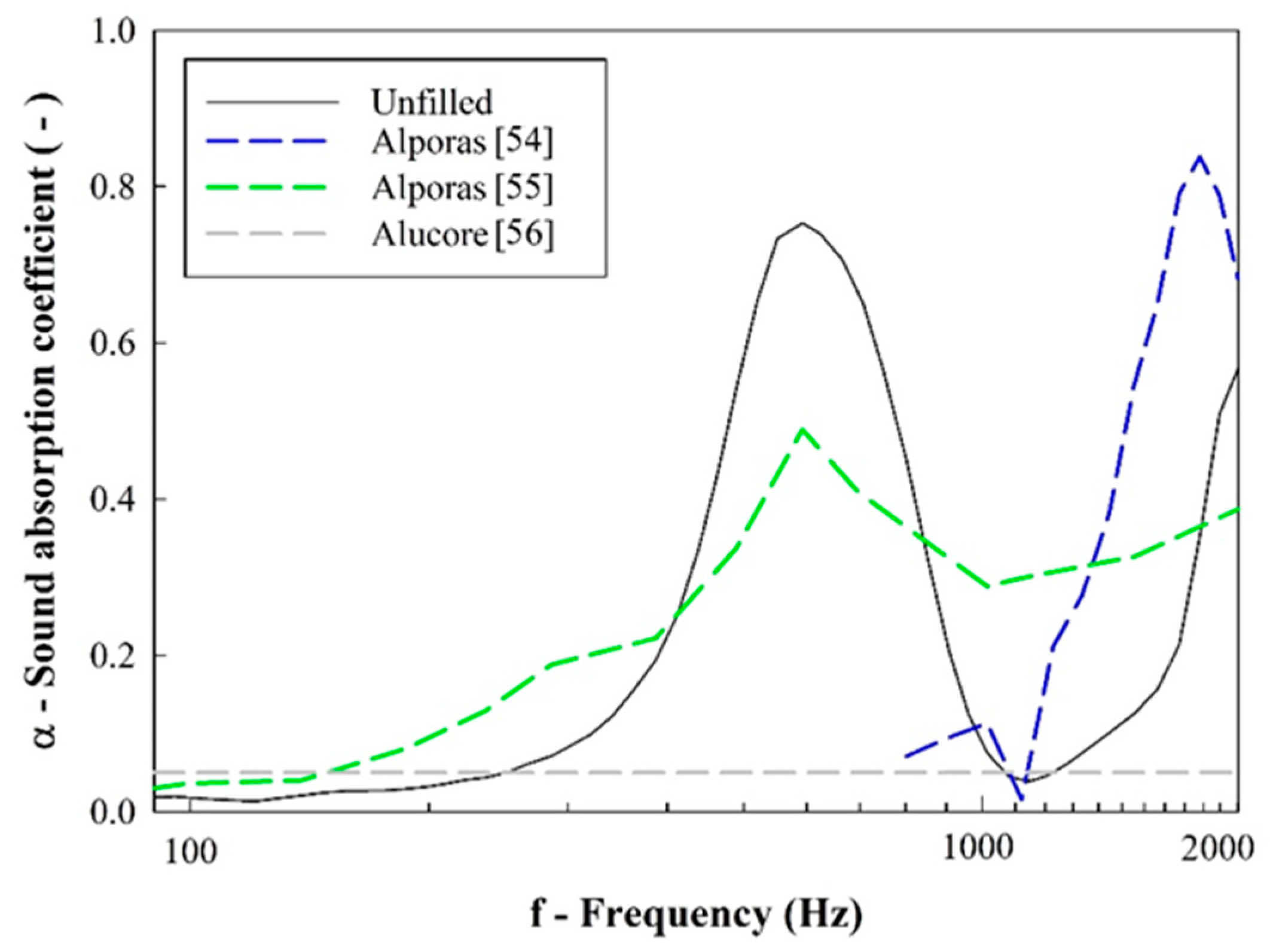
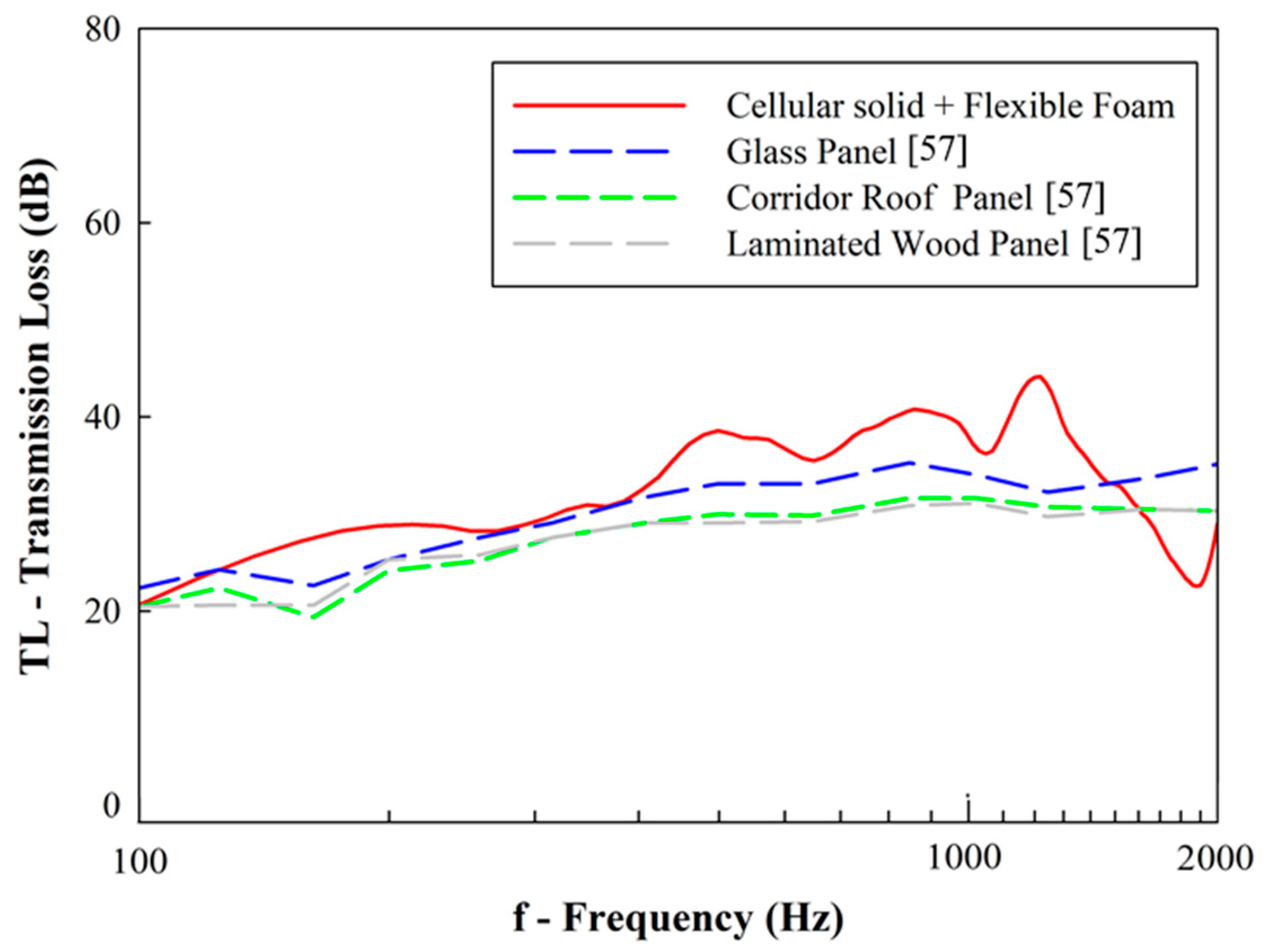
4. Comparison with Other Materials
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Variable | Description |
| A | Area (m2) |
| C | Speed of sound (m/s) |
| Cp | Heat capacity (J/K) |
| E | Young’s modulus (Pa) |
| G | Shear modulus (Pa) |
| K | Compressibility modulus (Pa) |
| Dynamic bulk modulus (Pa) | |
| k | Thermal conductivity (W/(m·K)) |
| k0 | Viscous static permeability (m2) |
| k′0 | Static thermal permeability (m2) |
| P | Pressure (Pa) |
| T | Temperature (°C) |
| Transmissibility (dB) | |
| TL | Transmission loss (dB) |
| u | Particle velocity (m/s) |
| V | Volume (m3) |
| v | Fluid velocity (m/s) |
| x | Measurement position (m) |
| Z | Acoustic impedance (Pa∙s/m) |
| c | Characteristic impedance (Pa∙s/m) |
| Zi | Incident acoustic impedance (Pa∙s/m) |
| Zt | Transmitted acoustic impedance (Pa∙s/m) |
| α | Sound absorption coefficient (—) |
| Dynamic tortuosity (—) | |
| High-frequency limit tortuosity (—) | |
| β | Dynamic compressibility (Pa−1) |
| γ | Specific heat (J/(kg·°C)) |
| ξ | Damping ratio (—) |
| η | Dynamic viscosity (Pa∙s) |
| Λ | Viscous characteristic length (m) |
| Λ′ | Thermal characteristic length (m) |
| μ | Fluid viscosity (N∙s/m2) |
| ρ | Air density (kg/m3) |
| Dynamic density (kg/m3) | |
| ρ* | Apparent density (kg/m3) |
| ρ0 | Bulk density (kg/m3) |
| ρf | Fluid density (kg/m3) |
| σ | Airflow resistivity (N∙s/m4) |
| τ | Temperature inside cellular solid (°C) |
| ν | Poisson’s ratio (—) |
| Φ | Porosity (—) |
| ω | Angular frequency (rad/s) |
References
- Vos, P. Railway Noise in Europe; International Union of Railways: Paris, France, 2016. [Google Scholar]
- European Comission Rail Freight Noise Reduction; European Commission: Brussels, Belgium, 2015.
- Gaulon, C.; Pierre, J.; Derec, C.; Jaouen, L.; Bécot, F.-X.; Chevillotte, F.; Elias, F.; Drenckhan, W.; Leroy, V. Acoustic Absorption of Solid Foams with Thin Membranes. Appl. Phys. Lett. 2018, 112, 261904. [Google Scholar] [CrossRef] [Green Version]
- Hilyard, N.; Cunningham, A. Low Density Cellular Plastics: Physical Basis of Behaviour; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 94-011-1256-8. [Google Scholar]
- Deshmukh, S.; Ronge, H.; Ramamoorthy, S. Design of Periodic Foam Structures for Acoustic Applications: Concept, Parametric Study and Experimental Validation. Mater. Des. 2019, 175, 107830. [Google Scholar] [CrossRef]
- Qiu, S.; Li, S.; Wang, X.; Mao, D. Enhanced Transmission Loss through Lattice-Supported Micro-Membranes. Appl. Acoust. 2019, 153, 127–131. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Puga, H.; Meireles, J. Positive, Zero and Negative Poisson’s Ratio Non-Stochastic Metallic Cellular Solids: Dependence between Static and Dynamic Mechanical Properties. Compos. Struct. 2019, 226, 111239. [Google Scholar] [CrossRef]
- Wang, R.; Shang, J.; Li, X.; Luo, Z.; Wu, W. Vibration and Damping Characteristics of 3D Printed Kagome Lattice with Viscoelastic Material Filling. Sci. Rep. 2018, 8, 9604. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Rayess, N.; Dukhan, N. Modeling of the Mechanical Properties of a Polymer-Metal Foam Hybrid. Proc. Mater. Sci. 2014, 4, 215–219. [Google Scholar] [CrossRef] [Green Version]
- Duarte, I.; Krstulović-Opara, L.; Dias-de-Oliveira, J.; Vesenjak, M. Axial Crush Performance of Polymer-Aluminium Alloy Hybrid Foam Filled Tubes. Thin-Walled Struct. 2019, 138, 124–136. [Google Scholar] [CrossRef]
- Duarte, I.; Vesenjak, M.; Krstulović-Opara, L.; Ren, Z. Crush Performance of Multifunctional Hybrid Foams Based on an Aluminium Alloy Open-Cell Foam Skeleton. Polym. Test. 2018, 67, 246–256. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Rawson, S.D.; Puga, H.; Meireles, J.; Withers, P.J. Additive Manufacturing Assisted Investment Casting: A Low-Cost Method to Fabricate Periodic Metallic Cellular Lattices. Addit. Manuf. 2020, 33, 101085. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Rawson, S.D.; Puga, H.; Withers, P.J. Macro-, Meso- and Microstructural Characterization of Metallic Lattice Structures Manufactured by Additive Manufacturing Assisted Investment Casting. Sci. Rep. 2021, 11, 4974. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Li, Y.; Zhang, A.; Bao, J. Epoxy Foams with Tunable Acoustic Absorption Behavior. Mater. Lett. 2017, 194, 234–237. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, Y.; Chen, J.; Wang, D. The Effects of Various Additive Components on the Sound Absorption Performances of Polyurethane Foams. Adv. Mater. Sci. Eng. 2015, 2015, 317561. [Google Scholar] [CrossRef] [Green Version]
- Verdejo, R.; Stämpfli, R.; Alvarez-Lainez, M.; Mourad, S.; Rodriguez-Perez, M.A.; Brühwiler, P.A.; Shaffer, M. Enhanced Acoustic Damping in Flexible Polyurethane Foams Filled with Carbon Nanotubes. Compos. Sci. Technol. 2009, 69, 1564–1569. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Lopes, D.; Puga, H.; Meireles, J. Numerical Inverse Engineering as a Route to Determine the Dynamic Mechanical Properties of Metallic Cellular Solids. Mater. Sci. Eng. A 2020, 800, 140428. [Google Scholar] [CrossRef]
- da Silva, C.C.B.; Terashima, F.J.H.; Barbieri, N.; de Lima, K.F. Sound Absorption Coefficient Assessment of Sisal, Coconut Husk and Sugar Cane Fibers for Low Frequencies Based on Three Different Methods. Appl. Acoust. 2019, 156, 92–100. [Google Scholar] [CrossRef]
- Eerden, F.J.M.; de Bree, H.-E.; Tijdeman, H. Experiments with a New Acoustic Particle Velocity Sensor in an Impedance Tube. Sens. Actuators A Phys. 1998, 69, 126–133. [Google Scholar] [CrossRef]
- Justus, C.G.; Woodrum, A. Atmospheric Pressure, Density, Temperature and Wind Variations between 50 and 200 Km; Nasa: Washington, DC, USA, 1972. [Google Scholar]
- Kuttruff, H. Acoustics: An Introduction; CRC Press: Boca Raton, FL, USA, 2007; ISBN 0-203-97089-6. [Google Scholar]
- Cats, P.; Tijs, E.; Comesana, D.F. Exploration of the Differences between a Pressure-Velocity Based in Situ Absorption Measurement Method and the Standardized Reverberant Room Method; ASA: Montereal, Canada, 2013; Volume 19, p. 15140. [Google Scholar]
- Rodriguez-Fernandez, C.; Fernandez-Comesana, D. In-Situ Estimation of Sound Transmission Loss Using a Scanning Sound Intensity Pu Probe. In Proceedings of the Simpósio Acústica Vibrações, Coimbra, Portugal, 3 February 2017. [Google Scholar]
- Buiat, M. Comparison Calibration of Low-Cost Prototypes of Acoustic Pressure-Velocity Probes and Some Applicatino Case-Studies. Ph.D. Thesis, Università degli Studi di Ferrara, Ferrara, Italy, 2015. [Google Scholar]
- Tijs, E. Study and Development of an in Situ Acoustic Absorption Measurement Method. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2013. [Google Scholar]
- Tiuc, A.E.; Nemeş, O.; Vermeşan, H.; Toma, A.C. New Sound Absorbent Composite Materials Based on Sawdust and Polyurethane Foam. Compos. Part B Eng. 2019, 165, 120–130. [Google Scholar] [CrossRef]
- Gwon, J.G.; Kim, S.K.; Kim, J.H. Sound Absorption Behavior of Flexible Polyurethane Foams with Distinct Cellular Structures. Mater. Des. 2016, 89, 448–454. [Google Scholar] [CrossRef]
- Allard, J.; Atalla, N. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials 2e; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 0-470-74734-X. [Google Scholar]
- Johnson, D.L.; Koplik, J.; Dashen, R. Theory of Dynamic Permeability and Tortuosity in Fluid-Saturated Porous Media. J. Fluid Mechan. 1987, 176, 379–402. [Google Scholar] [CrossRef]
- Lafarge, D.; Lemarinier, P.; Allard, J.F.; Tarnow, V. Dynamic Compressibility of Air in Porous Structures at Audible Frequencies. J. Acoust. Soc. Am. 1997, 102, 1995–2006. [Google Scholar] [CrossRef] [Green Version]
- Bruneau, M.; Potel, C. Materials and Acoustics Handbook; Wiley Online Library: Hoboken, NJ, USA, 2009; ISBN 1-84821-074-4. [Google Scholar]
- Chevillotte, F.; Perrot, C. Effect of the Three-Dimensional Microstructure on the Sound Absorption of Foams: A Parametric Study. J. Acoust. Soc. Am. 2017, 142, 1130–1140. [Google Scholar] [CrossRef]
- Trinh, V.H.; Perrot, C.; Langlois, V.; Pitois, O.; Khidas, Y. Achievement of Acoustical Properties of Foam Materials by Tuning Membrane Level: Elaborations, Models and Experiments. arXiv 2017, arXiv:1712.03849. [Google Scholar]
- Panneton, R.; Olny, X. Acoustical Determination of the Parameters Governing Viscous Dissipation in Porous Media. J. Acoust. Soc. Am. 2006, 119, 2027–2040. [Google Scholar] [CrossRef] [PubMed]
- Beranek, L.L. Acoustic Impedance of Porous Materials. J. Acoust. Soc. Am. 1942, 13, 248–260. [Google Scholar] [CrossRef]
- Wang, X.; Lu, T.J. Optimized Acoustic Properties of Cellular Solids. J. Acoust. Soc. Am. 1999, 106, 756–765. [Google Scholar] [CrossRef]
- Knapen, E.; Lanoye, R.; Vermeir, G.; Lauriks, W.; Van Gemert, D. Acoustic Properties of Sound Absorbing, Polymer-Modified Porous Cement Mortars. In Proceedings of the MSR VI, Karlsruhe, Germany, 15–18 September 2003; pp. 347–358. [Google Scholar]
- Cao, L.; Fu, Q.; Si, Y.; Ding, B.; Yu, J. Porous Materials for Sound Absorption. Compos. Commun. 2018, 10, 25–35. [Google Scholar] [CrossRef]
- Whitaker, S. Flow in Porous Media I: A Theoretical Derivation of Darcy’s Law. Transp. Porous Media 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Delany, M.; Bazley, E. Acoustical Properties of Fibrous Absorbent Materials. Appl. Acoust. 1970, 3, 105–116. [Google Scholar] [CrossRef]
- Pisani, L. Simple Expression for the Tortuosity of Porous Media. Transp. Porous Media 2011, 88, 193–203. [Google Scholar] [CrossRef]
- Liu, Z.; Fard, M.; Jazar, R. Development of an Acoustic Material Database for Vehicle Interior Trims; SAE Technical Paper; SAE: Warrendale, PA, USA, 2015. [Google Scholar]
- Hoang, M.T.; Bonnet, G.; Perrot, C. Multi-Scale Acoustics of Partially Open Cell Poroelastic Foams; ASA: Montereal, Canada, 2013; Volume 19, p. 65013. [Google Scholar]
- Leclaire, P.; Kelders, L.; Lauriks, W.; Melon, M.; Brown, N.; Castagnede, B. Determination of the Viscous and Thermal Characteristic Lengths of Plastic Foams by Ultrasonic Measurements in Helium and Air. J. Appl. Phys. 1996, 80, 2009–2012. [Google Scholar] [CrossRef] [Green Version]
- Olny, X.; Panneton, R. Acoustical Determination of the Parameters Governing Thermal Dissipation in Porous Media. J. Acoust. Soc. Am. 2008, 123, 814–824. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. II. Higher Frequency Range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Dib, L.; Bouhedja, S.; Amrani, H. Mechanical Parameters Effects on Acoustic Absorption at Polymer Foam. Adv. Mater. Sci. Eng. 2015, 2015, 896035. [Google Scholar] [CrossRef] [Green Version]
- Plona, T.J. Observation of a Second Bulk Compressional Wave in a Porous Medium at Ultrasonic Frequencies. Appl. Phys. Lett. 1980, 36, 259–261. [Google Scholar] [CrossRef] [Green Version]
- Bécot, F.-X.; Jaouen, L. An Alternative Biot’s Formulation for Dissipative Porous Media with Skeleton Deformation. J. Acoust. Soc. Am. 2013, 134, 4801–4807. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fung, Y. Foundations of Solid Mechanics; Prentice Hall: Englewood Cliffs, NJ, USA, 1965. [Google Scholar]
- Reyhanoglu, M. Computational and Experimental Studies of Acoustic Waves; BoD–Books on Demand: Zagreb, Croatia, 2018; ISBN 953-51-3715-8. [Google Scholar]
- Yahya, I. Analytical Expression for Sound Transmission Loss Calculation: An Improvement to the Existing Method after Singh and Katra. Adv. Acoust. Vib. 2010, 2009, 574604. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, T.; Fleck, N.A.; Hutchinson, J.; Wadley, H.; Gibson, L. Metal Foams: A Design Guide; Elsevier: New York, NY, USA, 2000; ISBN 0-08-051146-5. [Google Scholar]
- Miyoshi, T.; Itoh, M.; Akiyama, S.; Kitahara, A. Aluminum foam, “ALPORAS”: The Production Process, Properties and Applications. MRS Online Proc. Libr. Arch. 1998, 521, 133–138. [Google Scholar] [CrossRef]
- Lu, T.J.; Hess, A.; Ashby, M.F. Sound Absorption in Metallic Foams. J. Appl. Phys. 1999, 85, 7528–7539. [Google Scholar] [CrossRef]
- Dai, W.; Zheng, X.; Luo, L.; Hao, Z.; Qiu, Y. Prediction of High-Speed Train Full-Spectrum Interior Noise Using Statistical Vibration and Acoustic Energy Flow. Appl. Acoust. 2019, 145, 205–219. [Google Scholar] [CrossRef]
- Fan, R.; Meng, G.; Yang, J.; He, C. Experimental Study of the Effect of Viscoelastic Damping Materials on Noise and Vibration Reduction within Railway Vehicles. J. Sound Vibr. 2009, 319, 58–76. [Google Scholar] [CrossRef]




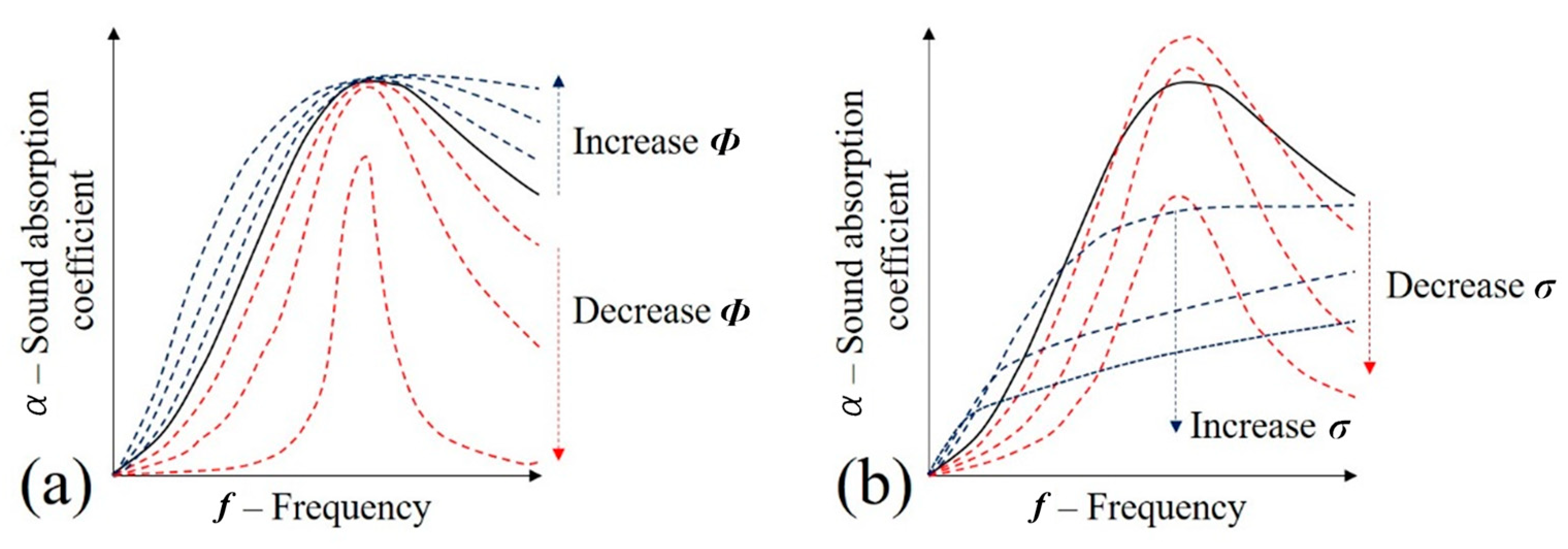

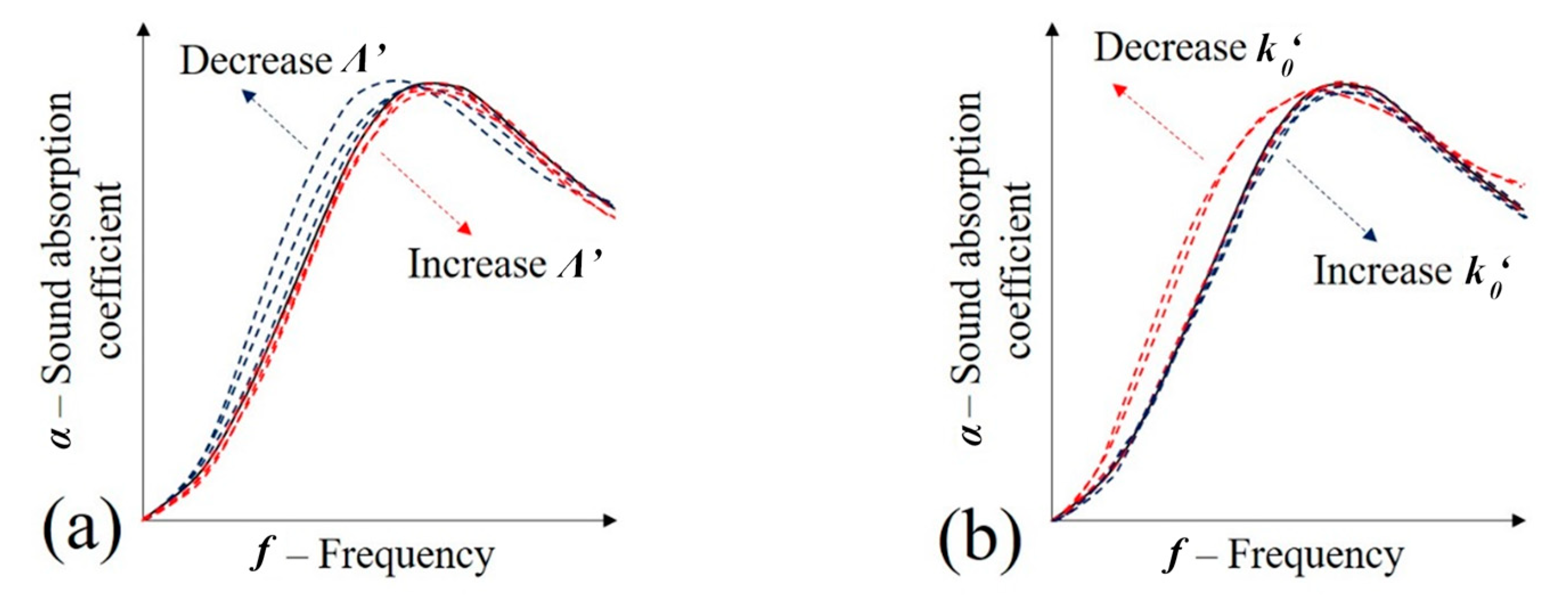

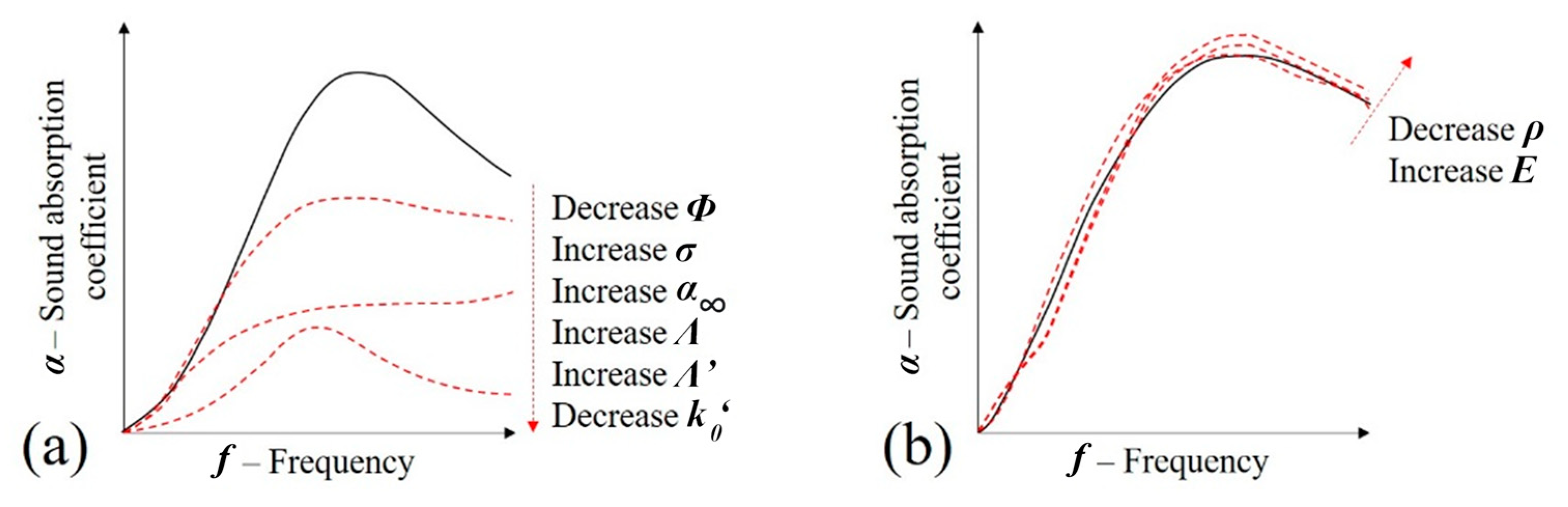
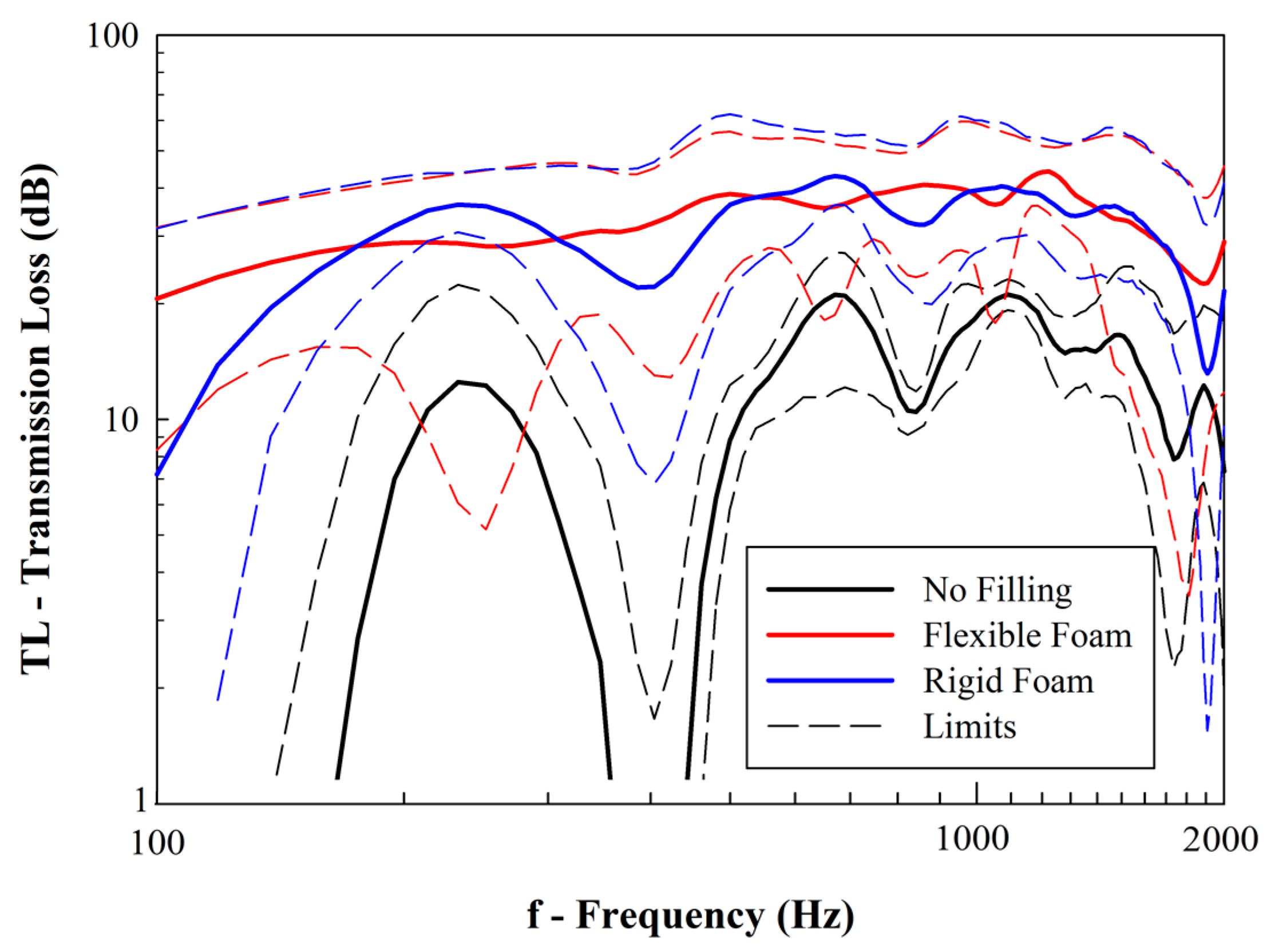

| Foam | Isocyanate/Polyol Ratio | Manufacturer |
|---|---|---|
| Rigid | 1:1 | Cronodur Foam 100 |
| Flexible | 1:2 | Cronodur Foam Flex |
| Foam | Flexible | Rigid |
|---|---|---|
| Optical microscopy (10×) |  |  |
| Apparent density (kg/m3) | 44.6 | 37.2 |
| Variable | Φ | ||||||
|---|---|---|---|---|---|---|---|
| Change |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carneiro, V.H.; Puga, H.; Meireles, J. Vibration Damping and Acoustic Behavior of PU-Filled Non-Stochastic Aluminum Cellular Solids. Metals 2021, 11, 725. https://doi.org/10.3390/met11050725
Carneiro VH, Puga H, Meireles J. Vibration Damping and Acoustic Behavior of PU-Filled Non-Stochastic Aluminum Cellular Solids. Metals. 2021; 11(5):725. https://doi.org/10.3390/met11050725
Chicago/Turabian StyleCarneiro, Vitor Hugo, Hélder Puga, and José Meireles. 2021. "Vibration Damping and Acoustic Behavior of PU-Filled Non-Stochastic Aluminum Cellular Solids" Metals 11, no. 5: 725. https://doi.org/10.3390/met11050725
APA StyleCarneiro, V. H., Puga, H., & Meireles, J. (2021). Vibration Damping and Acoustic Behavior of PU-Filled Non-Stochastic Aluminum Cellular Solids. Metals, 11(5), 725. https://doi.org/10.3390/met11050725








