Micro-Mechanisms and Modeling of Ductile Fracture Initiation in Structural Steel after Exposure to Elevated Temperatures
Abstract
:1. Introduction
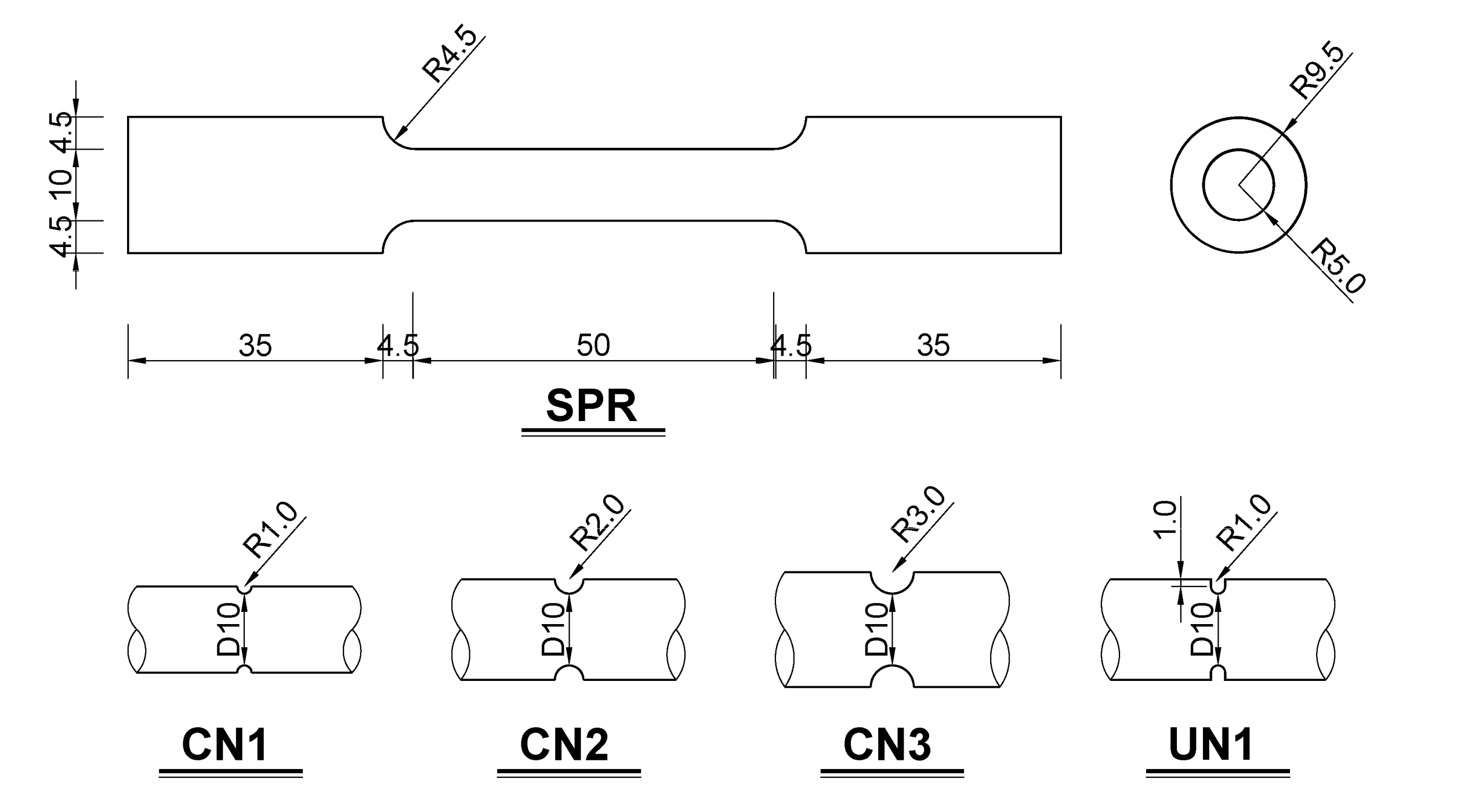
2. Review of Experimental Study
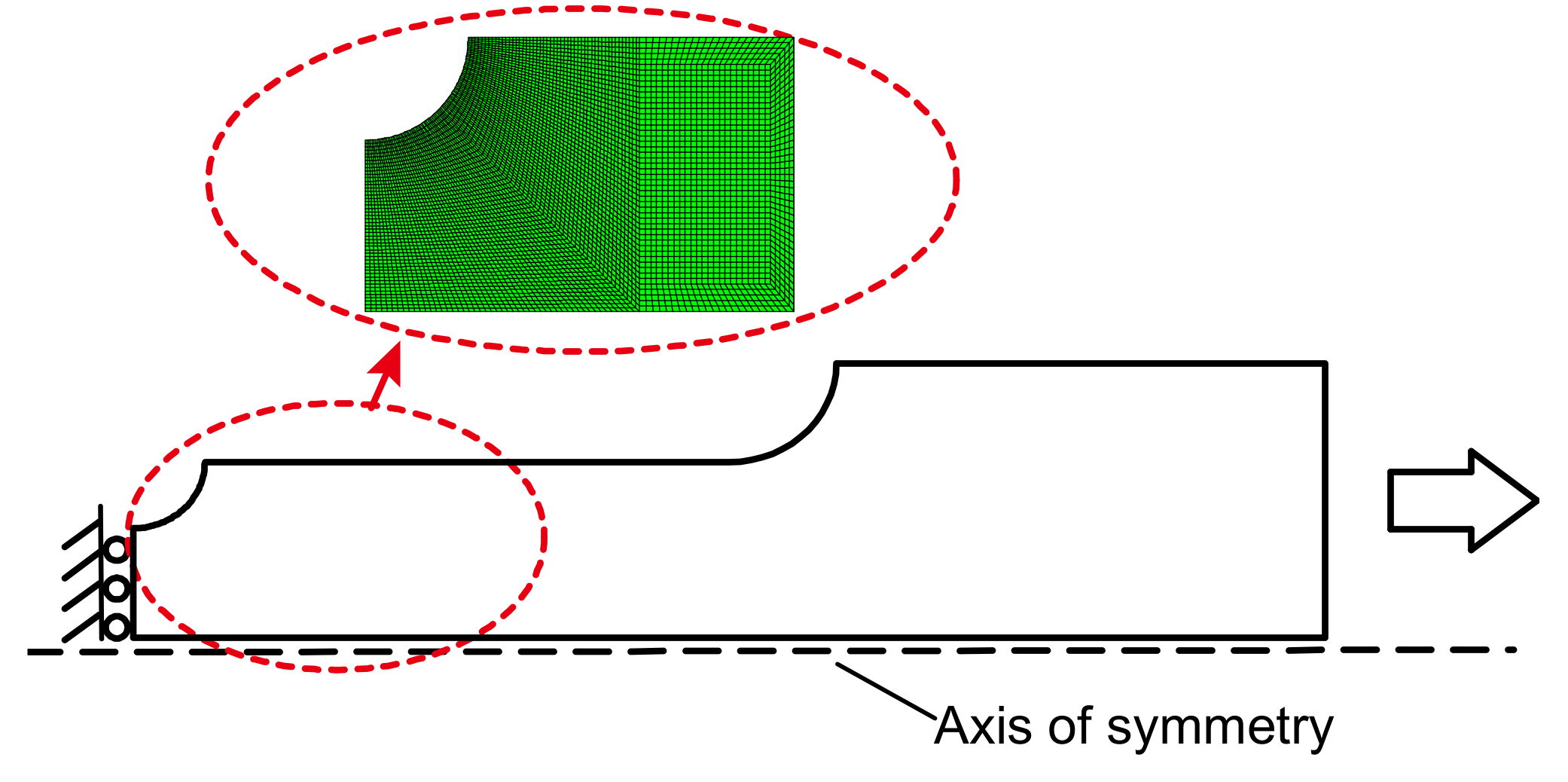
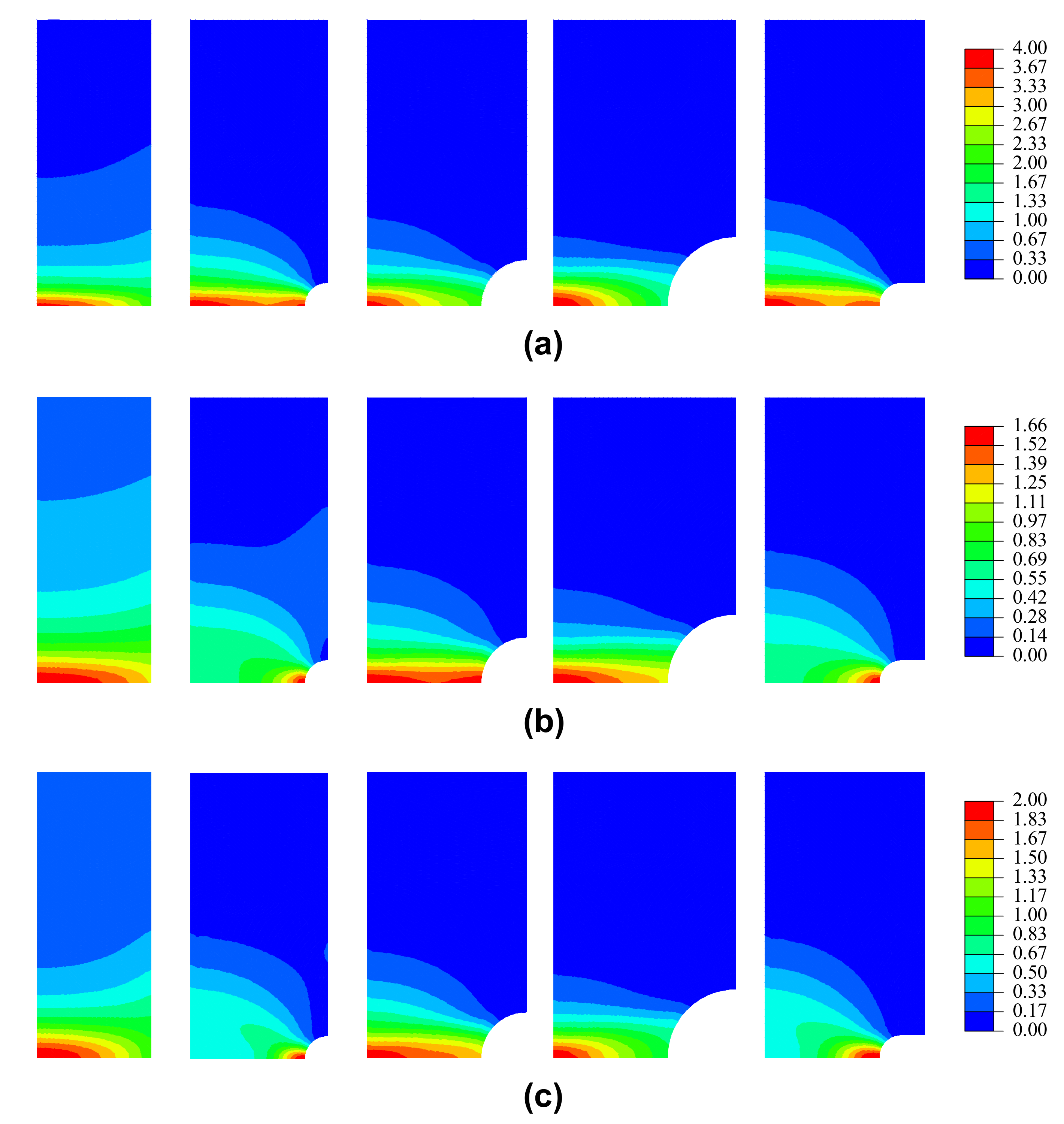
3. Finite Element Modeling
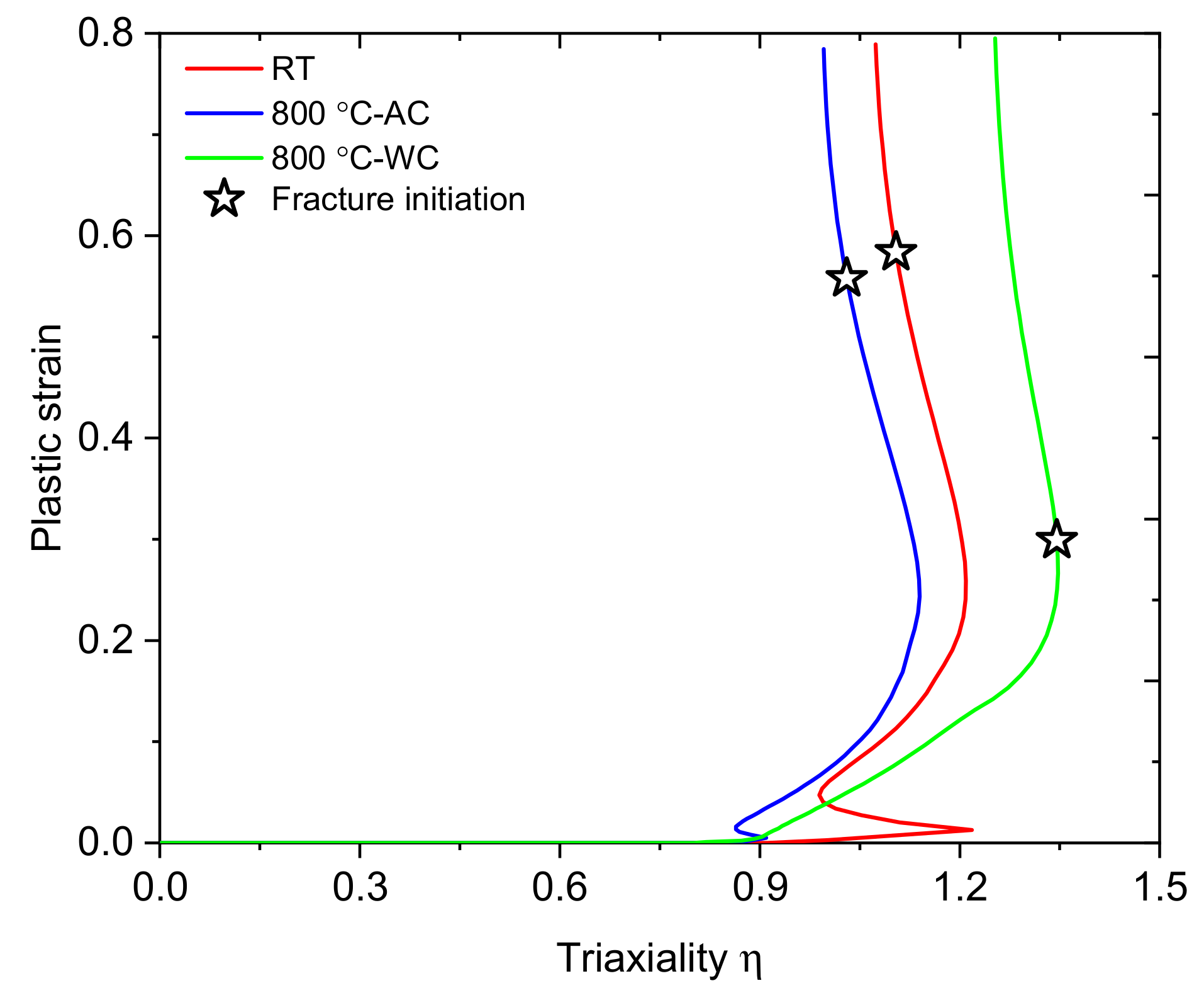
4. Micro-Mechanisms of Post-Fire Fracture in A572 Steels
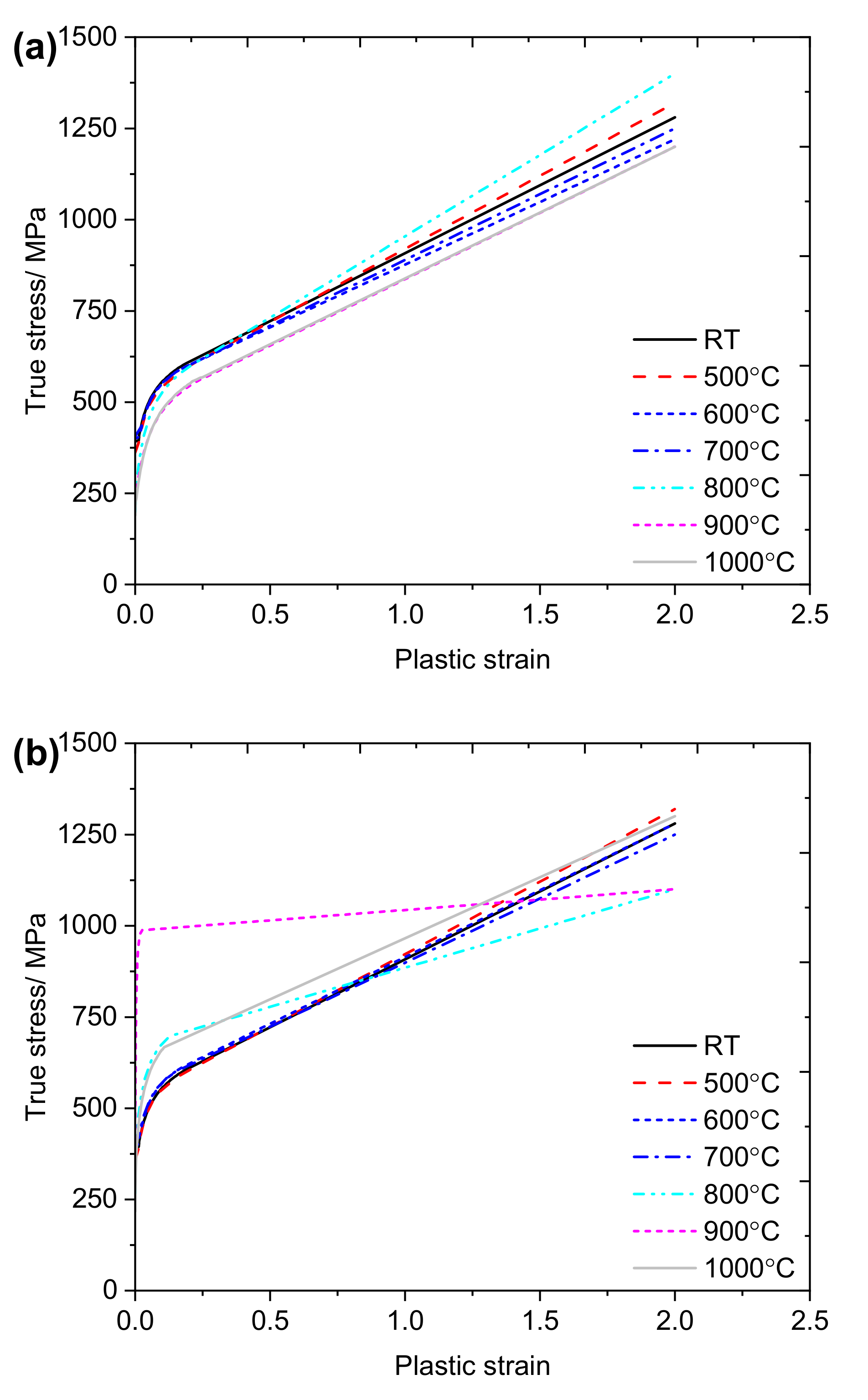
5. Micromechanics-Based Model for Post-Fire Ductile Fracture
5.1. Void Growth Model
5.2. Characteristic Length
5.3. Calibration of the Parameters β and VGIcr
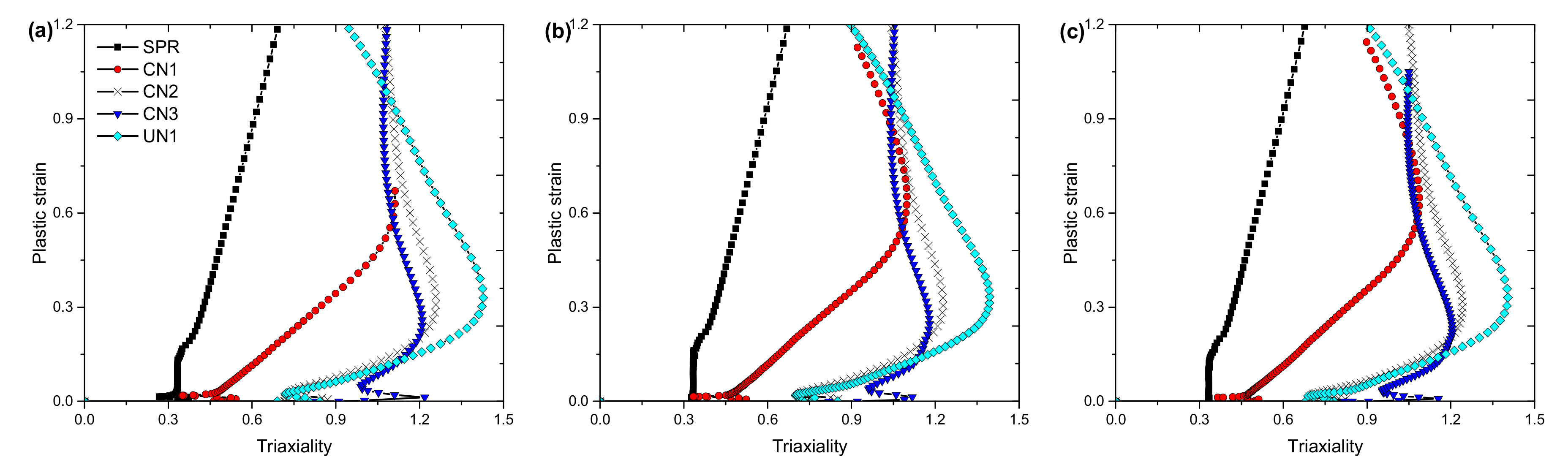
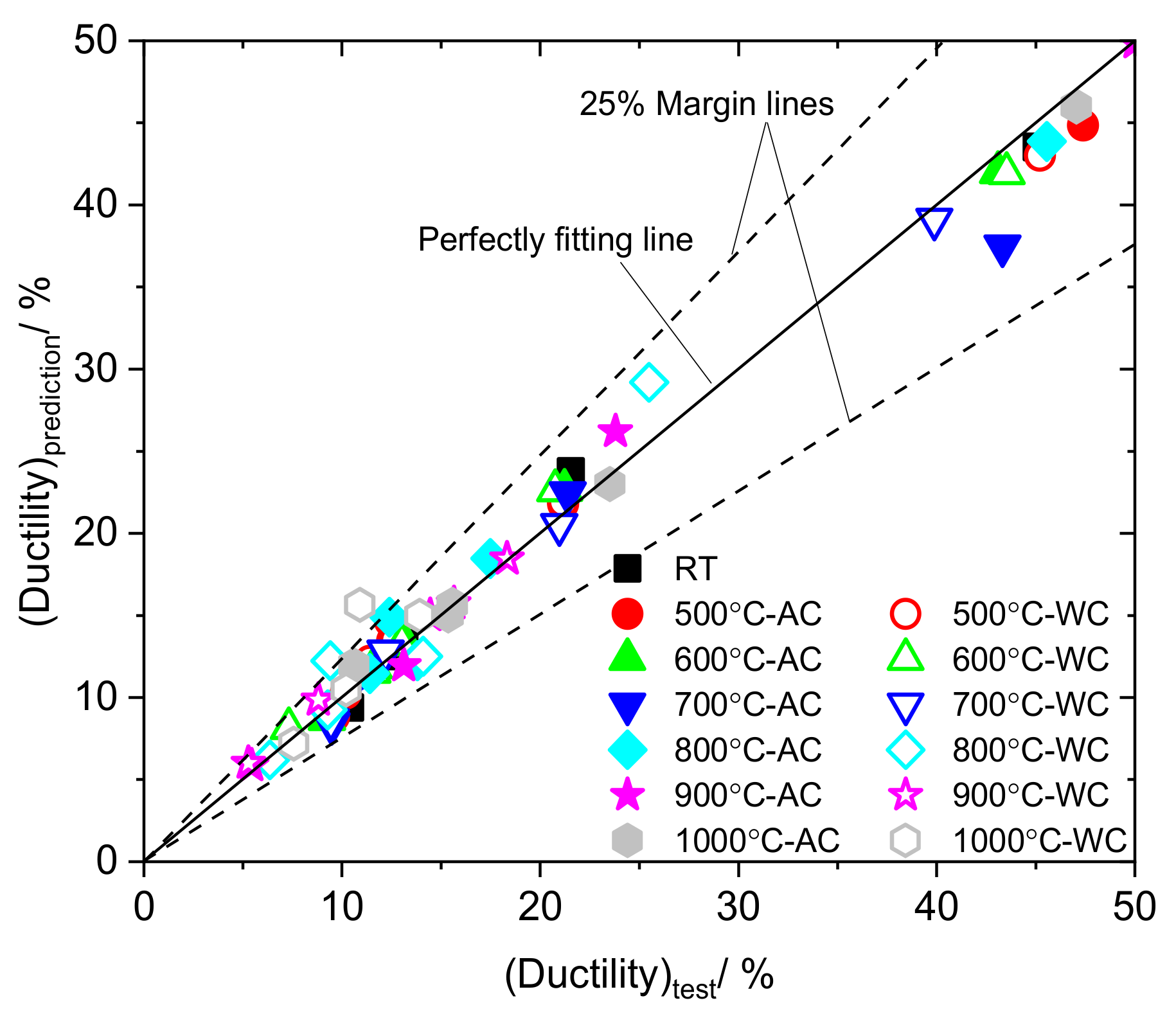
5.4. Simulation of Ductile Fracture Initiation Using VGM
6. Post-Fire VGM Model Incorporating Temperature and Cooling Method
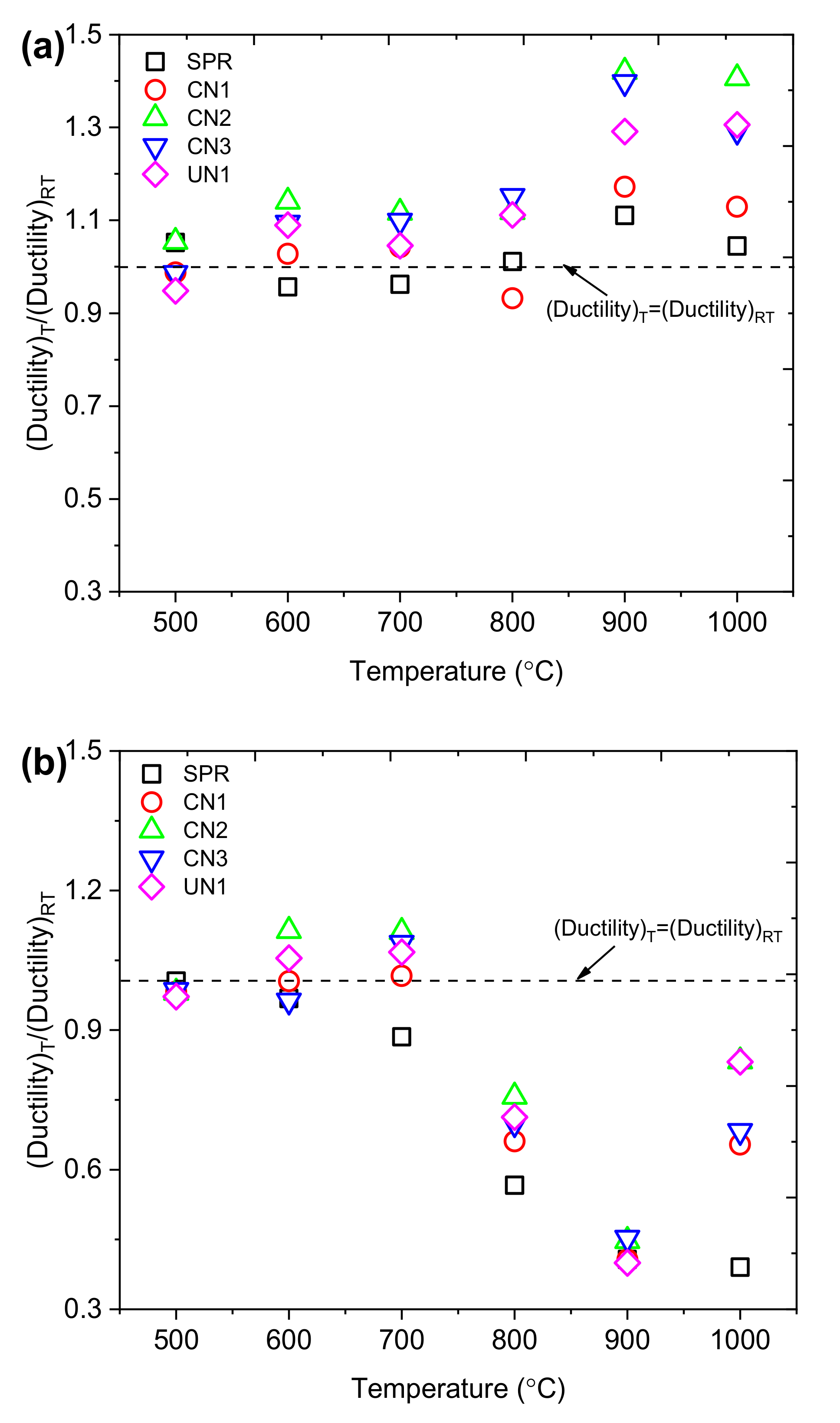
6.1. Effects of Temperature and Cooling Method on Fracture Initiation in A572 Steels
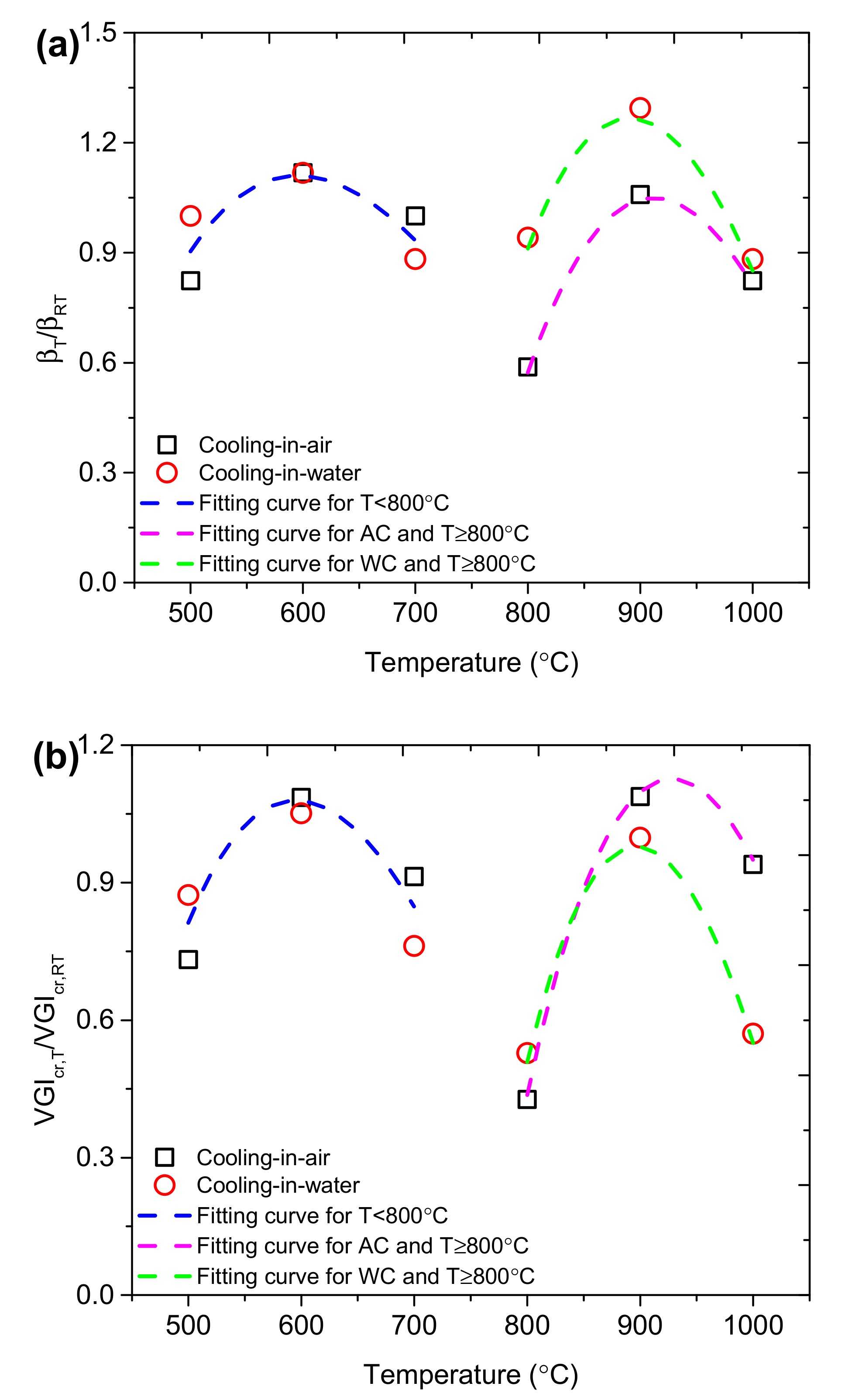
6.2. Dependence of Fracture Properties on Temperature and Cooling Method
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Sajid, H.U.; Kiran, R. Post-fire mechanical behavior of ASTM A572 steels subjected to high stress triaxialities. Eng. Struct. 2019, 191, 323–342. [Google Scholar] [CrossRef]
- Evarts, B. Fire Loss in the United States during 2017; National Fire Protection Association (NFPA): Quincy, MA, USA, 2018. [Google Scholar]
- American Society of Civil Engineers (ASCE). Structural Fire Protection; ASCE Committee on Fire Protection: Reston, VA, USA, 1992. [Google Scholar]
- American Institute of Steel Construction (AISC). AISC 360-16-Specification for Structural Steel Buildings; AISC: Chicago, IL, USA, 2016. [Google Scholar]
- Kodur, V.; Dwaikat, M.; Fike, R. High-Temperature Properties of Steel for Fire Resistance Modeling of Structures. J. Mater. Civ. Eng. 2010, 22, 423–434. [Google Scholar] [CrossRef]
- Garlock, M.; Paya-Zaforteza, I.; Kodur, V.; Gu, L. Fire hazard in bridges: Review, assessment and repair strategies. Eng. Struct. 2012, 35, 89–98. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, M.-C.; Kodur, V.; Li, G.-Q. Behavior of welded connections after exposure to elevated temperature. J. Constr. Steel Res. 2017, 130, 88–95. [Google Scholar] [CrossRef]
- Lou, G.-B.; Zhu, M.-C.; Li, M.; Zhang, C.; Li, G.-Q. Experimental research on slip-resistant bolted connections after fire. J. Constr. Steel Res. 2015, 104, 1–8. [Google Scholar] [CrossRef]
- Yu, L. Behavior of Bolted Connections during and after a Fire. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2006. [Google Scholar]
- Outinen, J.; Mäkeläinen, P. Mechanical properties of structural steel at elevated temperatures and after cooling down. Fire Mater. 2004, 28, 237–251. [Google Scholar] [CrossRef]
- Lu, J.; Liu, H.; Chen, Z.; Liao, X. Experimental investigation into the post-fire mechanical properties of hot-rolled and cold-formed steels. J. Constr. Steel Res. 2016, 121, 291–310. [Google Scholar] [CrossRef]
- Sajid, H.U.; Kiran, R. Influence of stress concentration and cooling methods on post-fire mechanical behavior of ASTM A36 steels. Constr. Build. Mater. 2018, 186, 920–945. [Google Scholar] [CrossRef]
- Yan, X.; Xia, Y.; Blum, H.B.; Gernay, T. Post-fire mechanical properties of advanced high-strength cold-formed steel alloys. Thin-Walled Struct. 2021, 159, 107293. [Google Scholar] [CrossRef]
- Zhang, C.; Jia, B.; Wang, J. Influence of artificial cooling methods on post-fire mechanical properties of Q355 structural steel. Constr. Build. Mater. 2020, 252, 119092. [Google Scholar] [CrossRef]
- Sajid, H.U.; Naik, D.L.; Kiran, R. Microstructure–Mechanical Property Relationships for Post-Fire Structural Steels. J. Mater. Civ. Eng. 2020, 32, 04020133. [Google Scholar] [CrossRef]
- Ding, F.; Zhang, C.; Yu, Y.; Lan, L.; Man, M. Hysteretic behavior of post fire structural steels under cyclic loading. J. Constr. Steel Res. 2019, 105847. [Google Scholar] [CrossRef]
- Wang, W.; Liu, T.; Liu, J. Experimental study on post-fire mechanical properties of high strength Q460 steel. J. Constr. Steel Res. 2015, 114, 100–109. [Google Scholar] [CrossRef]
- Li, G.-Q.; Lyu, H.; Zhang, C. Post-fire mechanical properties of high strength Q690 structural steel. J. Constr. Steel Res. 2017, 132, 108–116. [Google Scholar] [CrossRef]
- Qiang, X.; Bijlaard, F.S.; Kolstein, H. Post-fire mechanical properties of high strength structural steels S460 and S690. Eng. Struct. 2012, 35, 1–10. [Google Scholar] [CrossRef]
- Chiew, S.; Zhao, M.; Lee, C. Mechanical properties of heat-treated high strength steel under fire/post-fire conditions. J. Constr. Steel Res. 2014, 98, 12–19. [Google Scholar] [CrossRef]
- Lee, J.; Engelhardt, M.D.; Taleff, E.M. Mechanical Properties of ASTM A 992 Steel After Fire. Eng. J. 2012, 49, 33–44. [Google Scholar] [CrossRef] [Green Version]
- Aziz, E.M.; Kodur, V.K. Effect of temperature and cooling regime on mechanical properties of high-strength low-alloy steel. Fire Mater. 2016, 40, 926–939. [Google Scholar] [CrossRef]
- Cai, W.-Y.; Jiang, J.; Wang, Y.-B.; Li, G.-Q. Analysis of fracture behavior of high-strength steels in tension after fire exposure. Eng. Struct. 2021, 231, 111750. [Google Scholar] [CrossRef]
- Siwei, C.; Shaokun, J.; Houzuo, G.; Huixuan, C.; Yifeng, L.; Kang, L. Mechanical and ductile fracture performances of high strength structural steel Q690 after a fire: Experimental investigation. Procedia Eng. 2017, 210, 496–503. [Google Scholar] [CrossRef]
- Wang, F.; Lui, E.M. Experimental study of the post-fire mechanical properties of Q690 high strength steel. J. Constr. Steel Res. 2020, 167, 105966. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, R.; Song, G. Post-fire mechanical properties of Q460 and Q690 high strength steels after fire-fighting foam cooling. Thin-Walled Struct. 2020, 156, 106983. [Google Scholar] [CrossRef]
- Kang, L.; Suzuki, M.; Ge, H.; Wu, B. Experiment of ductile fracture performances of HSSS Q690 after a fire. J. Constr. Steel Res. 2018, 146, 109–121. [Google Scholar] [CrossRef]
- Azhari, F.; Heidarpour, A.; Zhao, X.-L.; Hutchinson, C.R. Mechanical properties of ultra-high strength (Grade 1200) steel tubes under cooling phase of a fire: An experimental investigation. Constr. Build. Mater. 2015, 93, 841–850. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, R.; Zhu, L. Mechanical properties of Q345 structural steel after artificial cooling from elevated temperatures. J. Constr. Steel Res. 2021, 176, 106432. [Google Scholar] [CrossRef]
- Lu, J.; Liu, H.; Chen, Z.; Bisby, L. Experimental investigation of the residual mechanical properties of cast steels after exposure to elevated temperature. Constr. Build. Mater. 2017, 143, 259–271. [Google Scholar] [CrossRef]
- Gunalan, S.; Mahendran, M. Experimental investigation of post-fire mechanical properties of cold-formed steels. Thin-Walled Struct. 2014, 84, 241–254. [Google Scholar] [CrossRef] [Green Version]
- Ren, C.; Dai, L.; Huang, Y.; He, W. Experimental investigation of post-fire mechanical properties of Q235 cold-formed steel. Thin-Walled Struct. 2020, 150, 106651. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, X.-Q.; Hassan, K.; Song, T.-Y.; Xie, L.-A. Behaviour of three types of stainless steel after exposure to elevated temperatures. J. Constr. Steel Res. 2018, 152, 296–311. [Google Scholar] [CrossRef]
- Ban, H.; Bai, R.; Chung, K.-F.; Bai, Y. Post-fire material properties of stainless-clad bimetallic steel. Fire Saf. J. 2020, 112, 102964. [Google Scholar] [CrossRef]
- Ha, N.S.; Le, V.T.; Goo, N.S.; Kim, J.Y. Thermal Strain Measurement of Austin Stainless Steel (SS304) during a Heating-cooling Process. Int. J. Aeronaut. Space Sci. 2017, 18, 206–214. [Google Scholar] [CrossRef]
- Le, V.T.; Ha, N.S.; Goo, N.S.; Kim, J.Y. Insulation System Using High-Temperature Fibrous Insulation Materials. Heat Transf. Eng. 2019, 40, 1523–1538. [Google Scholar] [CrossRef]
- Sajid, H.U.; Kiran, R. Influence of high stress triaxiality on mechanical strength of ASTM A36, ASTM A572 and ASTM A992 steels. Constr. Build. Mater. 2018, 176, 129–134. [Google Scholar] [CrossRef]
- Kanvinde, A.M.; Deierlein, G.G. The Void Growth Model and the Stress Modified Critical Strain Model to Predict Ductile Fracture in Structural Steels. J. Struct. Eng. 2006, 132, 1907–1918. [Google Scholar] [CrossRef]
- Jia, L.-J.; Kuwamura, H. Ductile Fracture Simulation of Structural Steels under Monotonic Tension. J. Struct. Eng. 2014, 140, 04013115. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. A comparative study of three groups of ductile fracture loci in the 3D space. Eng. Fract. Mech. 2015, 135, 147–167. [Google Scholar] [CrossRef]
- Wen, H.; Mahmoud, H. New Model for Ductile Fracture of Metal Alloys. I: Monotonic Loading. J. Eng. Mech. 2015, 142, 04015088. [Google Scholar] [CrossRef]
- Rice, J.; Tracey, D. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Kiran, R.; Xing, J.; Pan, Z.; Li, L. A modified micromechanics framework to predict shear involved ductile fracture in structural steels at intermediate and low-stress triaxialities. Eng. Fract. Mech. 2020, 225, 106860. [Google Scholar] [CrossRef]
- Dassault-Systèmes. ABAQUS/Standard Analysis User’s Manual; Dassault Systèmes Simulia: Providence, RI, USA, 2016. [Google Scholar]
- Kiran, R.; Khandelwal, K. Experimental Studies and Models for Ductile Fracture in ASTM A992 Steels at High Triaxiality. J. Struct. Eng. 2013, 140, 04013044. [Google Scholar] [CrossRef]
- Pineau, A.; Benzerga, A.; Pardoen, T. Failure of metals I: Brittle and ductile fracture. Acta Mater. 2016, 107, 424–483. [Google Scholar] [CrossRef] [Green Version]
- Bidulský, R.; Bidulská, J.; Gobber, F.S.; Kvačkaj, T.; Petroušek, P.; Actis-Grande, M.; Weiss, K.-P.; Manfredi, D. Case Study of the Tensile Fracture Investigation of Additive Manufactured Austenitic Stainless Steels Treated at Cryogenic Conditions. Materials 2020, 13, 3328. [Google Scholar] [CrossRef] [PubMed]
- McClintock, F. A Criterion for Ductile Fracture by the Growth of Holes. J. Appl. Mech. 1968, 35, 363–371. [Google Scholar] [CrossRef]
- Hancock, J.; Brown, D. On the role of strain and stress state in ductile failure. J. Mech. Phys. Solids 1983, 31, 1–24. [Google Scholar] [CrossRef]
- Zhu, Y.; Engelhardt, M.D.; Kiran, R. Combined effects of triaxiality, Lode parameter and shear stress on void growth and coalescence. Eng. Fract. Mech. 2018, 199, 410–437. [Google Scholar] [CrossRef]
- Liao, F.; Wang, M.; Tu, L.; Wang, J.; Lu, L. Micromechanical fracture model parameter influencing factor study of structural steels and welding materials. Constr. Build. Mater. 2019, 215, 898–917. [Google Scholar] [CrossRef]
- Myers, A.T.; Kanvinde, A.M.; Deierlein, G.G. Calibration of the SMCS Criterion for Ductile Fracture in Steels: Specimen Size Dependence and Parameter Assessment. J. Eng. Mech. 2010, 136, 1401–1410. [Google Scholar] [CrossRef]




| Temperature (°C) | Cooling Method | ASTM A36 | ASTM A572 Gr. 50 |
|---|---|---|---|
| RT | - | 40.31 | 45.06 |
| 500 | AC | 40.86 | 47.41 |
| WC | 40.17 | 45.29 | |
| 600 | AC | 44.13 | 43.10 |
| WC | 43.99 | 43.61 | |
| 700 | AC | 49.22 | 43.35 |
| WC | 34.06 | 39.90 | |
| 800 | AC | 38.77 | 45.57 |
| WC | 24.92 | 25.53 | |
| 900 | AC | 44.85 | 50.05 |
| WC | 15.73 | 18.33 | |
| 1000 | AC | 44.83 | 47.07 |
| WC | 12.60 | 14.17 |
| Temperature (°C) | Cooling Method | β | VGIcr | COV |
|---|---|---|---|---|
| RT | - | 1.7 | 3.84 | 0.118 |
| 500 | AC | 1.4 | 2.81 | 0.136 |
| WC | 1.7 | 3.35 | 0.147 | |
| 600 | AC | 1.9 | 4.17 | 0.095 |
| WC | 1.9 | 4.03 | 0.138 | |
| 700 | AC | 1.7 | 3.50 | 0.171 |
| WC | 1.5 | 2.92 | 0.126 | |
| 800 | AC | 1.0 | 1.64 | 0.151 |
| WC | 1.6 | 2.03 | 0.200 | |
| 900 | AC | 1.8 | 4.17 | 0.094 |
| WC | 2.2 | 3.83 | 0.127 | |
| 1000 | AC | 1.4 | 2.60 | 0.104 |
| WC | 1.5 | 2.19 | 0.126 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Huang, S.; Sajid, H.U. Micro-Mechanisms and Modeling of Ductile Fracture Initiation in Structural Steel after Exposure to Elevated Temperatures. Metals 2021, 11, 767. https://doi.org/10.3390/met11050767
Zhu Y, Huang S, Sajid HU. Micro-Mechanisms and Modeling of Ductile Fracture Initiation in Structural Steel after Exposure to Elevated Temperatures. Metals. 2021; 11(5):767. https://doi.org/10.3390/met11050767
Chicago/Turabian StyleZhu, Yazhi, Shiping Huang, and Hizb Ullah Sajid. 2021. "Micro-Mechanisms and Modeling of Ductile Fracture Initiation in Structural Steel after Exposure to Elevated Temperatures" Metals 11, no. 5: 767. https://doi.org/10.3390/met11050767






