Shape Memory Effect and Superelasticity of [001]-Oriented FeNiCoAlNb Single Crystals Aged under and without Stress
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Effect of Ageing under and without Stress on Temperatures of γ–α′ MT and the Precipitation of γ′- and β-Phase Particles
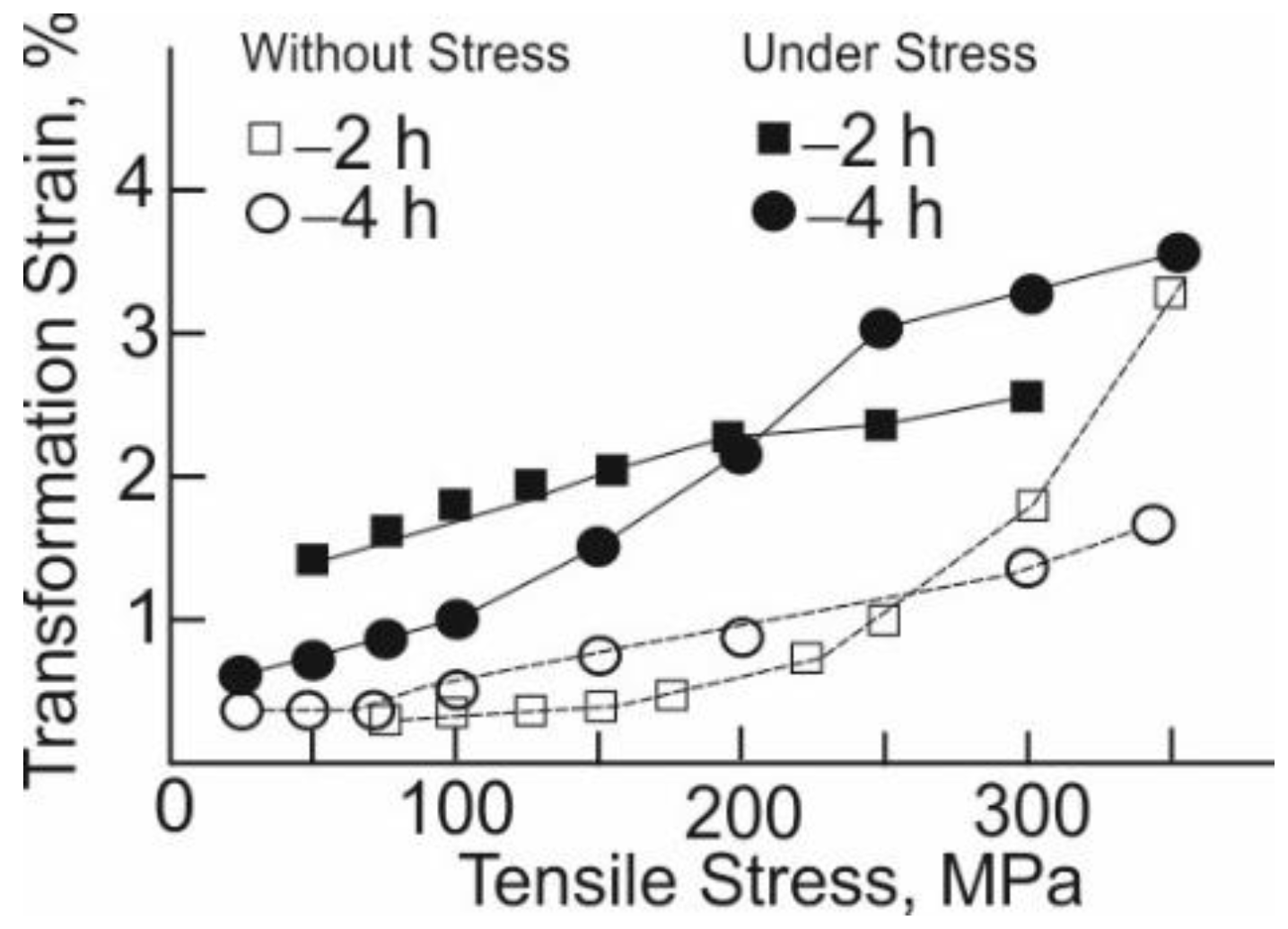
3.2. SE and SME in the [001]-Oriented FeNiCoAlNb Crystals Aged under and without Stress
4. Conclusions
- A new two-step ageing has been proposed for the FeNiCoAlNb single crystals, oriented along the [001]-direction for tensile strain, including ageing at the first step at 973 K for 5 h without stress and at the second step, at 873 K for 2 and 4 h without and under tensile stress at 120 MPa. At the first step of ageing at 973 K for 5 h, particles of the γ′-phase are precipitated, and at the second low-temperature step at 873 K for 2 and 4 h, a structure, consisting of particles of the γ′- and β-phases is formed.
- An increase in the ageing time at the second low-temperature step from 2 to 4 h leads to an increase in the Ms temperature, which is associated with a decrease in the nickel concentration in the matrix due to an increase in the volume fraction of the nickel-rich β-phase particles with the composition, (FeNiCo)(AlNb).
- Ageing under a tensile stress of 120 MPa at the second low-temperature step for 2 and 4 h leads to an increase in the Ms temperature, in comparison with ageing without stress by 11–15 K, which is associated with the generation of internal oriented tensile stresses during ageing under stress.
- In a structure containing particles of the γ′- and β-phases, conditions are created for observing SE within the temperature range from Ms to Af due to the formation of a high level of accumulated elastic energy, ΔGel, which significantly exceeds the value of the dissipated energy, ΔGdis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kokorin, V.V. Martensitic Transformations in Heterogeneous Solid Solutions. Naukova Dumka 1987, 1987, 165. (In Russian) [Google Scholar]
- Hornbogen, E. The effect of variables on martensitic transformation temperatures. Acta Met. 1985, 33, 595–601. [Google Scholar] [CrossRef]
- Hornbogen, E.; Jost, N. Alloys of iron and reversibility of martensitic transformations. J. Phys. Colloq. 1991, 1, C4-199–C4-210. [Google Scholar] [CrossRef]
- Maki, T. Ferrous shape memory alloys. In Book Shape Memory Material, 1st ed.; Otsuka, K., Wayman, C.M., Eds.; Cambridge University Press: Cambridge, UK, 1998; pp. 117–132. [Google Scholar]
- Tanaka, Y.; Himuro, Y.; Kainuma, R.; Sutou, Y.; Omori, T.; Ishida, K. Ferrous Polycrystalline Shape-Memory Alloy Showing Huge Superelasticity. Science 2010, 327, 1488–1490. [Google Scholar] [CrossRef]
- Choi, W.S.; Pang, E.L.; Choi, P.-P.; Schuh, C.A. FeNiCoAlTaB superelastic and shape-memory wires with oligocrystalline grain structure. Scr. Mater. 2020, 188, 1–5. [Google Scholar] [CrossRef]
- Cesari, E.; Chernenko, V.; Kokorin, V.; Pons, J.; Seguí, C. Physical properties of Fe-Co-Ni-Ti alloy in the vicinity of martensitic transformation. Scr. Mater. 1999, 40, 341–345. [Google Scholar] [CrossRef]
- Kokorin, V.V.; Kozlova, L.E.; Titenko, A.N.; Perekos, A.E.; Levchuk, Y.S. Charecteristic of thermoelastic martensitic trans-formation in ferromagnetic Fe-CoNi-Ti alloys alloyed with Cu. Phys. Metals Metallogr. 2008, 105, 564–567. [Google Scholar] [CrossRef]
- Gunko, L.P.; Takzei, G.A.; Titenko, A.N. Thermoplastic martensitic transformation in ferromagnetic materials and their superelastic properties. Funct. Mater. 2002, 9, 75–78. [Google Scholar]
- Geng, Y.; Lee, D.; Xu, X.; Nagasako, M.; Jin, M.; Jin, X.; Omori, T.; Kainuma, R. Coherency of ordered γ′ precipitates and thermoelastic martensitic transformation in FeNiCoAlTaB alloys. J. Alloy. Compd. 2015, 628, 287–292. [Google Scholar] [CrossRef]
- Chumlyakov, Y.I.; Kireeva, I.V.; Panchenko, E.; Kirillov, V.A.; Timofeeva, E.E.; Kretinina, I.V.; Danil’Son, Y.N.; Karaman, I.; Maier, H.J.; Cesari, E. Thermoelastic martensitic transformations in single crystals with disperse particles. Russ. Phys. J. 2011, 54, 937–950. [Google Scholar] [CrossRef]
- Ma, J.; Hornbuckle, B.; Karaman, I.; Thompson, G.; Luo, Z.; Chumlyakov, Y. The effect of nanoprecipitates on the superelastic properties of FeNiCoAlTa shape memory alloy single crystals. Acta Mater. 2013, 61, 3445–3455. [Google Scholar] [CrossRef]
- Czerny, M.; Maziarz, W.; Cios, G.; Wójcik, A.; Chumlyakov, Y.; Schell, N.; Fitta, M.; Chulist, R. The effect of heat treatment on the precipitation hardening in FeNiCoAlTa single crystals. Mater. Sci. Eng. A 2020, 784, 139327. [Google Scholar] [CrossRef]
- Jin, M.; Geng, Y.; Zuo, S.; Jin, X. Precipitation and its Effects on Martensitic Transformation in Fe-Ni-Co-Ti Alloys. Mater. Today Proc. 2015, 2, S837–S840. [Google Scholar] [CrossRef]
- Fu, H.; Li, W.; Song, S.; Jiang, Y.; Xie, J. Effects of grain orientation and precipitates on the superelasticity in directionally solidified FeNiCoAlTaB shape memory alloy. J. Alloy. Compd. 2016, 684, 556–563. [Google Scholar] [CrossRef]
- Fu, H.; Zhao, H.; Zhang, Y.; Xie, J. Enhancement of Superelasticity in Fe-Ni-Co-Based Shape Memory Alloys by Microstructure and Texture Control. Procedia Eng. 2017, 207, 1505–1510. [Google Scholar] [CrossRef]
- Krooß, P.; Holzweissig, M.J.; Niendorf, T.; Somsen, C.; Schaper, M.; Chumlyakov, Y.I.; Maier, H.J. Thermal cycling behavior of an aged FeNiCoAlTa single-crystal shape memory alloy. Scr. Mater. 2014, 81, 28–31. [Google Scholar] [CrossRef]
- Ma, J.; Kockar, B.; Evirgen, A.; Karaman, I.; Luo, Z.; Chumlyakov, Y. Shape memory behavior and tension–compression asymmetry of a FeNiCoAlTa single-crystalline shape memory alloy. Acta Mater. 2012, 60, 2186–2195. [Google Scholar] [CrossRef]
- Czerny, M.; Cios, G.; Maziarz, W.; Chumlyakov, Y.; Chulist, R. Studies on the Two-Step Aging Process of Fe-Based Shape Memory Single Crystals. Materials 2020, 13, 1724. [Google Scholar] [CrossRef] [PubMed]
- Krooß, P.; Niendorf, T.; Karaman, I.; Chumlyakov, Y.I.; Maier, H.J. Cyclic deformation behavior of aged FeNiCoAlTa single crystals. Funct. Mater. Lett. 2012, 5, 12500454. [Google Scholar] [CrossRef]
- Sehitoglu, H.; Karaman, I.; Zhang, X.; Chumlyakov, Y.; Maier, H.J. Deformation of FeNiCoTi shape memory single crystals. Scr. Mater. 2001, 44, 779–784. [Google Scholar] [CrossRef]
- Chumlakov, Y.I.; Kireeva, I.V.; Panchenko, E.Y.; Zakharova, E.G.; Kirillov, V.A.; Efimenko, S.P.; Sehitoglu, H. Shape memory effect in FeNiCoTi single crystals undergoing γ–α′ thermoelastic martensitic transformations. Doklady Phys. 2004, 49, 47–50. [Google Scholar] [CrossRef]
- Sehitoglu, H.; Efstathiou, C.; Maier, H.; Chumlyakov, Y. Hysteresis and deformation mechanisms of transforming FeNiCoTi. Mech. Mater. 2006, 38, 538–550. [Google Scholar] [CrossRef]
- Chumlyakov, Y.; Kireeva, I.; Kuksgauzen, I.; Poklonov, V.; Pobedennaya, Z.; Bessonova, I.; Kuksgauzen, D.; Kirillov, V.; Lauhoff, C.; Niendorf, T.; et al. Shape memory effect and superelasticity in high-strength FeNiCoAlTi single crystals hardened by nanoparticles. AIP Conf. Proc. 2019, 2167, 020064. [Google Scholar] [CrossRef]
- Chumlyakov, Y.I.; Kireeva, I.V.; Kuksgauzen, I.V.; Kuksgauzen, D.A.; Niendorf, T.; Krooß, P. Tension-compression asymmetry of the superelastic behavior of high-strength [001]-oriented FeNiCoAlNb crystals. Mater. Lett. 2021, 289, 129395. [Google Scholar] [CrossRef]
- Sehitoglu, H.; Zhang, X.Y.; Kotil, T.; Canadinc, D.; Chumlyakov, Y.; Maier, H.J. Shape memory behavior of FeNiCoTi single and polycrystals. Met. Mater. Trans. A 2002, 33, 3661–3672. [Google Scholar] [CrossRef]
- Chumlyakov, Y.; Kireeva, I.; Kutz, O.; Turabi, A.; Karaca, H.; Karaman, I. Unusual reversible twinning modes and giant superelastic strains in FeNiCoAlNb single crystals. Scr. Mater. 2016, 119, 43–46. [Google Scholar] [CrossRef]
- Dunne, D. Martens-ite. Metals 2018, 8, 395. [Google Scholar] [CrossRef]
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1998; p. 284. [Google Scholar]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti–Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, C.; Harrington, T.; Casalena, L.; Wang, H.; Shin, S.; Vecchio, K.S. Multifunctional Non-Equiatomic High Entropy Alloys with Superelastic, High Damping, and Excellent Cryogenic Properties. Adv. Eng. Mater. 2019, 21, 1800941. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, C.; Shin, S.; Casalena, L.; Vecchio, K. Grain boundary precipitation of tantalum and NiAl in superelastic FeNiCoAlTaB alloy. Mater. Sci. Eng. A 2019, 743, 372–381. [Google Scholar] [CrossRef]
- Chumlyakov, Y.; Kireeva, I.; Pobedennaya, Z.; Krooβ, P.; Niendorf, T. Rubber-like behaviour and superelasticity of [001]-oriented FeNiCoAlNb single crystals containing γ′- and β-phase particles. J. Alloy. Compd. 2021, 856, 158158. [Google Scholar] [CrossRef]
- Chumlyakov, Y.; Kireeva, I.; Kuksgauzen, I.; Poklonov, V.; Pobedennaya, Z.; Bessonova, I.; Kirillov, V.; Lauhoff, C.; Niendorf, T.; Krooβ, P. Effect of β- and γ’-phase particles on the shape memory effect and superelasticity in [001]-oriented FeNiCoAlTi single crystals. Mater. Lett. 2020, 260, 126932. [Google Scholar] [CrossRef]
- Li, D.; Chen, L. Selective variant growth of coherent Ti11Ni14 precipitate in a TiNi alloy under applied stresses. Acta Mater. 1997, 45, 471–479. [Google Scholar] [CrossRef]
- Li, D.; Chen, L. Morphological evolution of coherent multi-variant Ti11Ni14 precipitates in Ti-Ni alloys under an applied stress—A computer simulation study. Acta Mater. 1998, 46, 639–649. [Google Scholar] [CrossRef]
- Kireeva, I.; Picornell, C.; Pons, J.; Kretinina, I.; Chumlyakov, Y.; Cesari, E. Effect of oriented γ′ precipitates on shape memory effect and superelasticity in Co–Ni–Ga single crystals. Acta Mater. 2014, 68, 127–139. [Google Scholar] [CrossRef]
- Poster, D.A.; Easterling, K.E. Phase Transformation in Metals and Alloys; Chapman & Hall: London, UK, 1981; 165p. [Google Scholar]
- Khalil-Allafi, J.; Dlouhy, A.; Eggeler, G. Ni4Ti3-precipitation during aging of NiTi shape memory alloys and its influence on martensitic phase transformations. Acta Mater. 2002, 50, 4255–4274. [Google Scholar] [CrossRef]
- Li, J.-F.; Zheng, Z.-Q.; Li, X.-W.; Li, S.-C. Effect of compressive stress aging on transformation strain and microstructure of Ni-rich TiNi alloy. Mater. Sci. Eng. A 2009, 523, 207–213. [Google Scholar] [CrossRef]
- Tong, H.; Wayman, C. Characteristic temperatures and other properties of thermoelastic martensites. Acta Met. 1974, 22, 887–896. [Google Scholar] [CrossRef]
- Daróczi, L.; Palánki, Z.; Szabó, S.; Beke, D. Stress dependence of non-chemical free energy contributions in Cu–Al–Ni shape memory alloy. Mater. Sci. Eng. A 2004, 378, 274–277. [Google Scholar] [CrossRef]
- Palánki, Z.; Daróczi, L.; Beke, D.L. Method for the Determination of Non-Chemical Free Energy Contributions as a Function of the Transformed Fraction at Different Stress Levels in Shape Memory Alloys. Mater. Trans. 2005, 46, 978–982. [Google Scholar] [CrossRef]
- Beke, D.; Daróczi, L.; Samy, N.; Tóth, L.; Bolgár, M. On the thermodynamic analysis of martensite stabilization treatments. Acta Mater. 2020, 200, 490–501. [Google Scholar] [CrossRef]
- Wollants, P.; Roos, J.; Delaey, L. Thermally- and stress-induced thermoelastic martensitic transformations in the reference frame of equilibrium thermodynamics. Prog. Mater. Sci. 1993, 37, 227–288. [Google Scholar] [CrossRef]
- Vaidyanathan, R.; Bourke, M.; Dunand, D. Phase fraction, texture and strain evolution in superelastic NiTi and NiTi–TiC composites investigated by neutron diffraction. Acta Mater. 1999, 47, 3353–3366. [Google Scholar] [CrossRef]
- Dunand, D.C.; Mari, D.; Bourke, M.A.M.; Roberts, J.A. NiTi and NiTi-TiC composites: Part IV. Neutron diffraction study of twinning and shape-memory recovery. Met. Mater. Trans. A 1996, 27, 2820–2836. [Google Scholar] [CrossRef]
- Martin, J.W. Micromechanisms in Partical-Hardened Alloys; Cambridge Solid State Science Series; Cambridge University Press: Cambridge, UK, 1980; p. 197. [Google Scholar]
- Brown, L. Back-stresses, image stresses, and work-hardening. Acta Met. 1973, 21, 879–885. [Google Scholar] [CrossRef]
- Korotaev, A.D.; Chumlyakov, Y.I.; Esipenko, V.F.; Bushnev, L.S. Superelasticity effects in single crystals of Cu-15% Al-2% Co with non-coherent particles due to twinning. Phys. Status Solidi A 1984, 82, 405–412. [Google Scholar] [CrossRef]
- Chumlyakov, Y.; Kireeva, I.; Pobedennaya, Z.; Kuksgauzen, I.; Poklonov, V.; Krooß, P.; Niendorf, T.; Lauhoff, C.; Vollmer, M. Shape memory effect and superelasticity in high-strength FeNiCoAlTiNb single crystals. AIP Conf. Proc. 2020, 2310, 020065. [Google Scholar] [CrossRef]
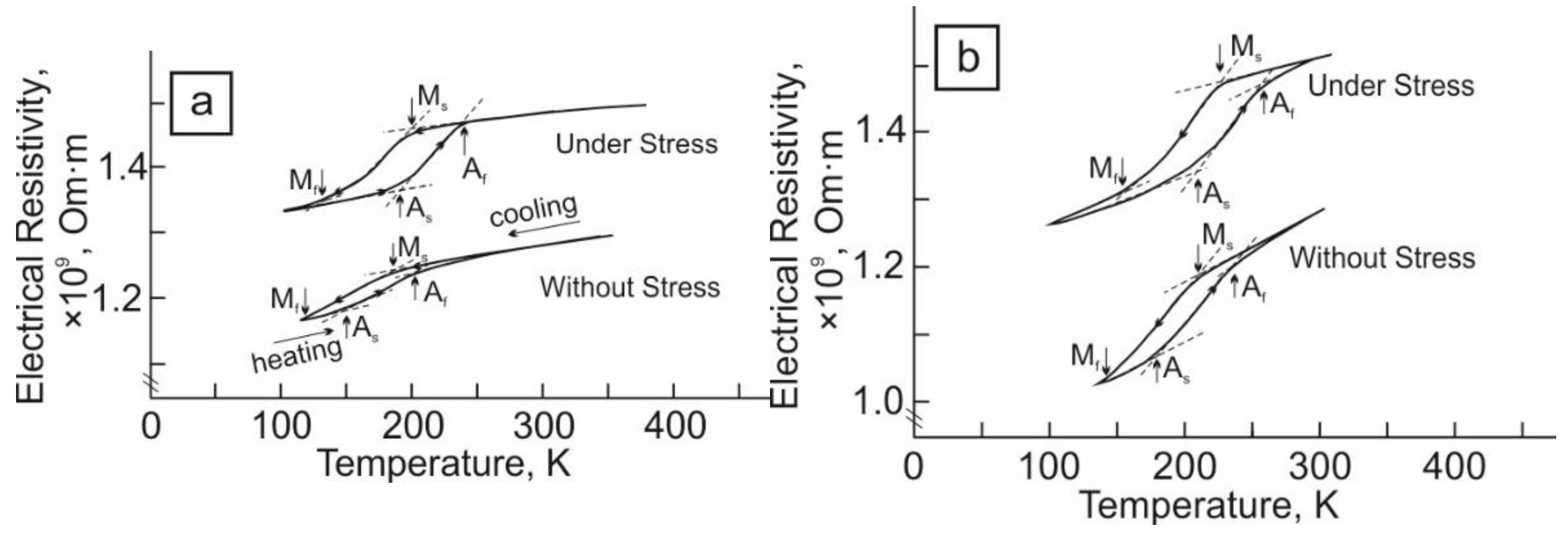



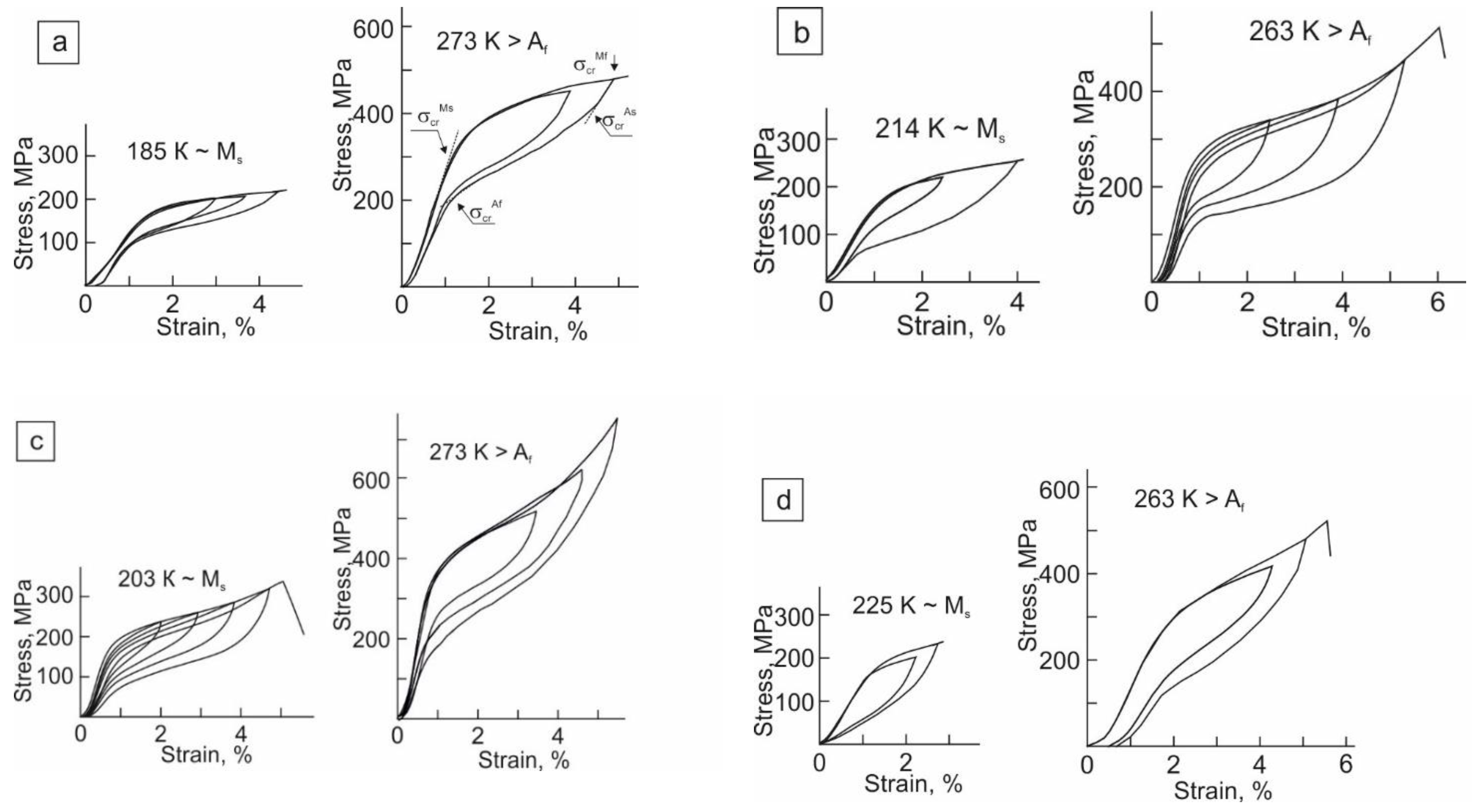


| Crystals | Ms, K | Mf, K | As, K | Af, K | ΔTh, K | ΔM, K | ΔA, K | ΔGel/ΔGdis |
|---|---|---|---|---|---|---|---|---|
| Crystal I | 185 | 120 | 150 | 203 | 18 | 65 | 53 | 6.6 |
| Crystal II | 200 | 130 | 190 | 240 | 40 | 70 | 50 | 3 |
| Crystal III | 214 | 140 | 180 | 235 | 21 | 74 | 55 | 6.5 |
| Crystal IV | 225 | 155 | 210 | 260 | 35 | 70 | 50 | 3.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chumlyakov, Y.I.; Kireeva, I.V.; Pobedennaya, Z.V.; Krooß, P.; Niendorf, T. Shape Memory Effect and Superelasticity of [001]-Oriented FeNiCoAlNb Single Crystals Aged under and without Stress. Metals 2021, 11, 943. https://doi.org/10.3390/met11060943
Chumlyakov YI, Kireeva IV, Pobedennaya ZV, Krooß P, Niendorf T. Shape Memory Effect and Superelasticity of [001]-Oriented FeNiCoAlNb Single Crystals Aged under and without Stress. Metals. 2021; 11(6):943. https://doi.org/10.3390/met11060943
Chicago/Turabian StyleChumlyakov, Yuriy I., Irina V. Kireeva, Zinaida V. Pobedennaya, Philipp Krooß, and Thomas Niendorf. 2021. "Shape Memory Effect and Superelasticity of [001]-Oriented FeNiCoAlNb Single Crystals Aged under and without Stress" Metals 11, no. 6: 943. https://doi.org/10.3390/met11060943
APA StyleChumlyakov, Y. I., Kireeva, I. V., Pobedennaya, Z. V., Krooß, P., & Niendorf, T. (2021). Shape Memory Effect and Superelasticity of [001]-Oriented FeNiCoAlNb Single Crystals Aged under and without Stress. Metals, 11(6), 943. https://doi.org/10.3390/met11060943








