Abstract
Electrical contacts involve complicated electrical, thermal, and mechanical phenomena. Fretting wear as a surface damage mechanism significantly weakens the performance of electrical contact components. In this study, a numerical approach is developed to investigate the electrical-thermal-mechanical-wear coupling behavior of electrical contacts. An electrical contact conductance law is used with the current conservation model to evaluate the electrical behavior. A transient heat transfer model, including the Joule heating behavior and a thermal contact conductance law, is employed to calculate the temperature field. Both contact conductance laws are related to the contact pressure distribution obtained by the contact stress analysis. Based on the predicted contact stress and relative slip on contact surfaces, the energy wear model is used to study the evolution of fretting wear depth and contact surface geometry. The material properties in these models are temperature-dependent. The proposed numerical approach is implemented in a finite element modeling of electrical contacts, which is validated by comparing the predicted and experimental results of the wear scar profile. The effects of the fretting wear on the electric potential, current density, contact resistance, temperature, and contact pressure are numerically studied.
1. Introduction
Electrical contacts are widely used to transmit electrical energy and signals in electrical and electronic devices. They involve several multi-physical phenomena including electrical, thermal, and mechanical aspects [1]. As current flows through two contacting components, materials in the contact zone are deformed under mechanical loads and also heated due to the Joule heating. The microhardness of the contacting metals is also affected by the applied electric potential [2,3]. Besides the current and the contact loads, electrical contacts are usually subjected to mechanical vibration which causes severe fretting wear damage to surface materials [4,5,6]. Several main wear mechanisms and damage types in electrical contacts have been identified and studied widely, as listed in Table 1. Fretting wear changes the contact surface geometry and contact pressure distribution, weakening the stability of electrical contacts. Moreover, it forms a debris layer with oxidation film, causing the increase of electrical contact resistance (ECR) and finally the failure of electrical contacts [7,8,9]. Therefore, fretting wear makes the coupling relationships among electrical, thermal, and mechanical behaviors more complicated.

Table 1.
Wear and damage mechanisms in electrical contacts.
Extensive experimental investigations focused on the fretting wear behavior of electrical contacts and its influence on ECR [10,11,12]. Based on common-used fretting testing equipment, the four-point method is widely used to measure the ECR of electrical contacts. Fouvry et al. [13] investigated the electrical contact failure of bronze alloy with three different coatings made of Sn, Ag, and Au. The coating materials and the applied slip amplitude affected the electrical contact endurance, i.e., the number of loading cycles to reach the threshold variation of ECR. Noh et al. [14] evaluated the effect of grain size on the fretting wear and ECR of copper. The medium grain size of around 60 μm had the shortest electrical contact endurance. Ren et al. [15] studied the effects of the current load on wear and fretting corrosion of gold-plated electrical contacts. He et al. [16] investigated the effects of oxidation layer and roughness on the fretting wear behavior of copper under electrical contacts. These experimental results revealed that the formation of the oxide debris layer during the fretting wear process resulted in a significant increase in the ECR. Generally, the experimental methods mainly focus on the evolution of ECR under different fretting wear conditions such as material type, contact force, slip amplitude, current value, surface features and so on. However, the coupling relationships among the electrical, thermal, and mechanical behaviors are not clearly described through experimental methods. Moreover, it is difficult to obtain the distributions and evolutions of internal variables including current density, electric potential, contact pressure, temperature and wear scar geometry by experimental methods.
Numerical methods have intrinsic advantages to reproduce electrical contact behavior and to study the effects of influencing factors. Weißenfels et al. [17] developed an electrical contact conductance model, in which surface asperities were considered as individual flux tubes with parallel connections. Ren et al. [18] conducted an electrical-thermal finite element analysis to evaluate the relationship between the voltage and temperature in spherical electrical contacts. The simulation results were used to make a correction of the classical Kohlrausch’s equation [1]. Terhorst et al. [19] developed an electro-thermo-mechanical contact model to calculate the current density and temperature in the bulk metal forming process. Jiang et al. [20] employed a frictional energy-based wear model to simulate the fretting wear profile of an electrical connector under the micro-slip loading condition. However, the electrical and thermal behaviors were ignored in the simulation. These numerical methods can provide reasonable predictions of electrical contact behavior under specific assumptions and simplifications. However, the effects of the fretting wear on the electrical, thermal and mechanical behavior are not considered.
Two types of wear models have been used to evaluate the effect of the wear on the mechanical behavior of contacting components. The Archard wear model [21] was firstly developed and used to investigate variations of wear volume and contact surface geometry. This model has been incorporated into the finite element method to evaluate wear-induced stress evolution and its effect on the fretting fatigue behavior of Ti-6Al-4V [22,23,24]. Fouvry et al. [25,26,27] conducted extensive fretting wear experiments and developed a new wear model relating the wear volume to the frictional dissipated energy in the contact zone. One wear coefficient could be used in the energy wear model to describe the fretting wear behavior under both partial slip and gross slip conditions, which is superior to the Archard wear model. Zhang et al. [28] incorporated the energy wear model in the finite element modeling to evaluate the influences of contact geometry on the fretting wear, fatigue, and cyclic plasticity behavior of Ti-6Al-4V. Shen et al. [29,30,31] combined the continuum damage mechanics-based method and this wear model to predict the evolutions of the fretting wear profile and fatigue damage. The obtained results of the fretting fatigue lifetimes agreed well with experimental results. In electrical contacts, fretting wear affects electrical, thermal, and mechanical behavior. Therefore, it should be included in the modeling of electrical contacts.
The motivation of the present study is that the published modeling work on electrical contacts mainly concerns the ECR and temperature while the fretting wear is not considered. Therefore, an electrical-thermal-mechanical-wear coupling model is proposed to evaluate electrical contact behavior. In the developed model, the current conservation model with an electrical contact conductance law is used to calculate the current density and electric potential distribution. A transient heat transfer model with a thermal contact conductance law is used to evaluate the temperature increase in the contact zone due to the Joule heating. An elastic material constitutive model with mechanical contact boundary conditions is used to evaluate the contact stress and subsurface stress. Based on the contact stress, the energy wear model is used to describe the wear profile evolution and contact geometry variation. The material properties in these models are temperature-dependent. All the models are incorporated in a finite element modeling of electrical contacts to evaluate the coupling relationship among electrical, thermal, mechanical, and wear behavior.
2. Electrical-Thermal-Mechanical-Wear Coupling Model
2.1. Current Conservation Model
Current flows through two contacting components. The current conservation model in bulk materials can be written as a group of equations [1]:
where is the current density, the electric field strength, the electric potential, and the temperature-dependent electrical conductivity. In the present study, the current-induced magnetic field is not considered. These three equations can be combined to form one equation as follows:
The current flows through contact surfaces resulting in constriction resistance. The actual contact surface has a certain roughness and oxidation area. Current can only flow through several small spots, i.e., a-spots. Moreover, the oxidation film also causes film contact resistance. Therefore, ECR consists of the constriction resistances from two components and the resistance from oxidation film on the contact surfaces. For a preliminary modeling study, the actual contact surface geometry with asperities and oxidation film is not considered. A Cooper–Mikic–Yovanovich (CMY) law [32] is used to model the electrical boundary conditions on both contact surfaces:
where is the normal direction of the contact surface. The subscripts ‘s’ and ‘m’ represent the slave surface and master surface, respectively. The contact in the modeling is usually implemented through the master-slave contact configuration. The contact surface on one body is selected as the master surface. The corresponding contact surface on the counterpart is treated as the slave surface. Some simple rules are used in the selection of the master and slave surfaces to achieve the best possible contact simulation: (a) the slave surface should be the more finely meshed surface, and (b) if the mesh densities are similar, the slave surface should be the surface with the softer underlying material. The contact electrical conductance is related to surface roughness features and contact pressure [32]:
where and characterize the average height and slope of surface asperities, respectively; is the contact pressure obtained from the contact stress calculation; is the micro-hardness of the softer material. The conductivity decreases with the increase of the average height of surface asperities. The applied current density or electric potential can be prescribed on non-contact surfaces.
where and are the prescribed current density and electric potential, respectively.
The current conservation model with the electrical contact boundary conditions is used to evaluate the distributions of current density , electric field strength , and electric potential . Therefore, ECR can be obtained by dividing the electric potential drop between two contact surfaces by the current value:
2.2. Transient Heat Transfer Model
Temperature increases obviously in contact zones of electrical contacts, which causes material softening and even melting. The main heat source is the Joule heating due to the current flowing through contact surfaces. The energy dissipation due to friction and plastic deformation of materials can also cause an increase in material temperature [33]. However, it is much smaller than the Joule heating energy in electrical contacts. Therefore, the transient heat transfer model only considers the Joule heating as follows
The joule heating energy density is calculated by the dot product of the current density and electric field strength. The temperature-dependent parameters , , and represent the density, specific heat capacity, and thermal conductivity, respectively.
Two types of thermal boundary conditions are applied on the surfaces of electrical contacts. On the contact surfaces, the thermal contact boundary conditions are expressed as:
The contact thermal conductance is a critical parameter for the evaluation of the temperature distribution. The CMY model is also used to describe the contact thermal conductance as follows:
On the non-contact surfaces, the natural convection boundary condition is applied as:
where is the natural convection coefficient and is the ambient temperature.
2.3. Material Constitutive Model
The material constitutive model considering elastic deformation and thermal expansion is used to evaluate the stress and strain distributions in electrical contacts. The total strain consists of elastic strain and thermal strain as follows:
The isotropic elastic model correlates the Cauchy stress tensor to the elastic strain tensor:
where is the temperature-dependent fourth-order elastic tensor which can be described by Young’s modulus and Poisson’s ratio for isotropic materials.
The thermal expansion is assumed to be isotropic, i.e., , is a second-order identity tensor. The thermal strain increment is determined by the temperature increase as follows
where is the temperature-dependent coefficient of thermal expansion (CTE) and is the temperature increment.
2.4. Frictional Energy-Based Wear Model
The frictional energy-based wear model developed by Fouvry et al. [26,34] relates the wear volume to the accumulated dissipated energy due to friction during the fretting wear process, i.e., where is the wear coefficient. The wear depth at each contact node can be expressed as:
where is the tangential frictional stress at position and time ; is the increment of the relative slip displacement. For a two-dimensional contact case, the wear depth is correspondingly written as:
In the simulation, the incremental form of the wear depth is commonly used in numerical implementation as follows:
where the subscript represents the ith time increment.
3. Computational Method
3.1. Fully Coupled Algorithm
The fully coupled relationships among the electrical, thermal, mechanical, and wear behavior of electrical contacts are considered in this study, as shown in Figure 1. The conventional electrical-thermal-mechanical coupling relationships are marked by solid black arrows. Electrical behavior affects the temperature field by providing the Joule heating energy as the main heat source. The change of temperature field leads to the variation of material electrical, thermal, and mechanical properties. The contact pressure distribution and the deformation affect the contact electrical and thermal conductance. Besides the conventional electrical-thermal-mechanical coupling behavior, the material wear behavior is also included in the modeling of electrical contacts. Its connections with the other three behaviors are marked by dot-line arrows in Figure 1. Wear behavior is related to mechanical behavior. Wear depth is determined by the frictional energy calculated by using the tangential frictional stress and relative slip displacement. The contact geometries of contact surfaces are then varied. The variation of contact geometries influences the other three behaviors.
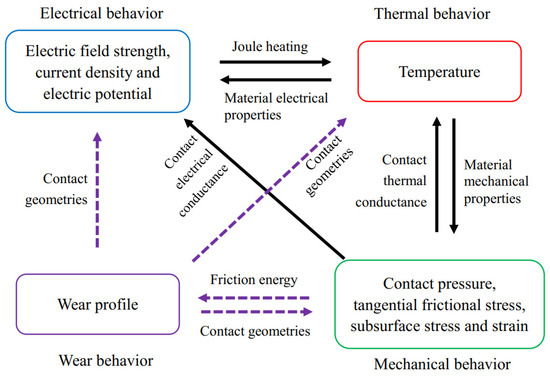
Figure 1.
Coupling relationships among electrical, thermal, mechanical, and wear behavior.
In the simulation, the electrical, thermal, and mechanical behaviors and their coupling relationships are calculated simultaneously at each time increment. Variables including the electric field strength, current density, electric potential, temperature, contact pressure, tangential frictional stress, subsurface stress, and strain are updated at the current time increment and then used as the initial conditions for the next time increment. However, the wear depth evaluation and contact geometry variation are conducted after the calculation of electrical, thermal, and mechanical variables. The wear depth increment of each node on the contact slave surface, , is calculated by using Equation (18). Then, the contact slave surface is moved a distance away from the corresponding contact master surface, as shown in Figure 2. Therefore, the contact geometry of the slave surface is changed at every time increment. The corresponding electrical, thermal, and mechanical variables are calculated again at the next time increment after the contact geometry variation [33,35].
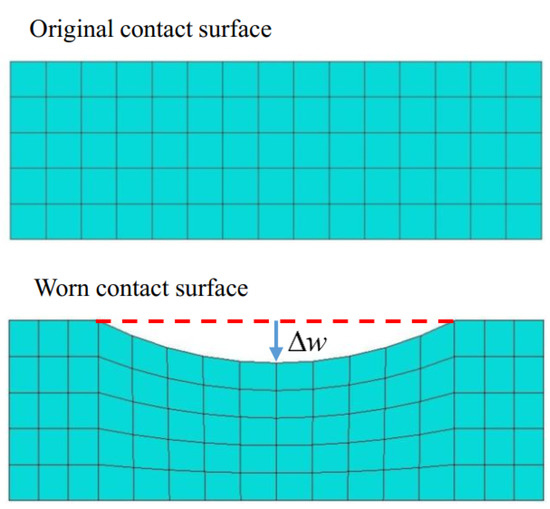
Figure 2.
Schematic of wear and contact geometry variation.
3.2. Finite Element Modeling of Electrical Contact
The electrical-thermal-mechanical-wear model is implemented in a finite element modeling of electrical contacts. A two-dimensional electrical contact model is established for simplicity. The specimen is made of copper without surface coating. The pad is made of 52,100 bearing steel. Normal force and cyclic horizontal displacement are applied on the top surface of the pad, as shown in Figure 3a. The bottom surface and two side surfaces of the specimen are fixed. Therefore, the pad can slide on the top surface of the specimen to reproduce the fretting wear process. On the top surface of the pad, a constant electric potential is prescribed. The corresponding ground is set on the bottom surface of the specimen. The total electric potential drop of the electrical contact remains unchanged, i.e., , in the simulation. The Joule heating behavior of the pad and specimen is considered. Figure 3b illustrates the histories of these three loads. Two steps are used to apply these loads. The normal force and the electric potential linearly increase to the prescribed values in the first step and then hold on in the second step. The reciprocating sliding displacement is applied in the second step. Figure 3c shows the finite element model of the electrical contact. In the modeling, the contact zone is finely meshed to obtain accurate predictions of the stress, strain, temperature, current density, and electric potential results. The other zones are coarsely meshed to save computational costs.
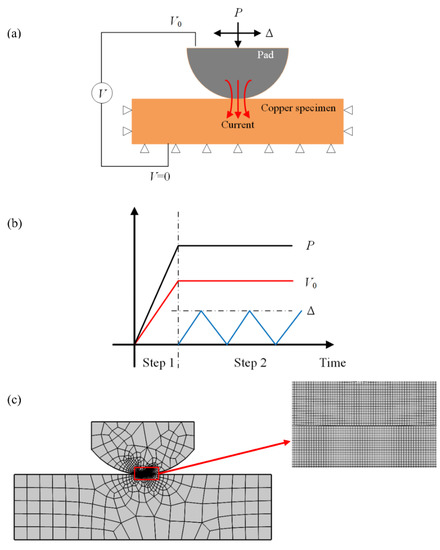
Figure 3.
(a) Schematic of electrical contact, (b) histories of applied loads, and (c) finite element mesh of electrical contact.
The contact behavior between the pad and specimen is defined in the modeling. As the study focuses on the wear behavior of the flat specimen, a partition of the top surface of the specimen is defined as the slave contact surface. A partition of the circular surface on the pad is defined as the master contact surface. In the study, the surface roughness is not considered by building contact surfaces based on the actual surface profiles. The ideal smooth surfaces of the specimen and the pad are used. The hard normal contact behavior is used so that there is no penetration between contacting components. The coefficient of friction (COF) between the contacting material is measured using a tribometer (Bruker, Billerica, MA, USA). Figure 4a shows the evolution of COF in the contact between the copper specimen and the steel ball. The stable COF value is used in the modeling. Figure 4b shows the surface morphology of a copper specimen measured using a 3D white-light interfering profilometer (ZYGO, Berwyn, PA, USA). The average height and slope of surface asperities in Equations (6) and (11) are determined by using the surface profile. It is noted that the surface morphology of the specimen is inevitably changed due to the contact and further material wear. The variation of the surface morphology will affect the contact electrical and thermal conductance. In this study, two constant values are used for simplicity.
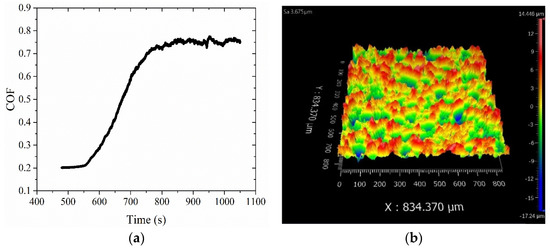
Figure 4.
(a) Evolution of COF between the copper specimen and the steel ball and (b) surface morphology of the copper specimen.
The parameters of the simulation cases are set as follows: the radius of the cylindrical pad 50.8 mm, the horizontal displacement range = 100 μm, the frequency of fretting loading 0.5 Hz, the normal force ranging from 30 to 90 N/mm, and the electric potential = 50 mV. The fretting sliding state between the pad and specimen is gross sliding, indicating no stick area occurs in the contact zone. The wear coefficient in Equation (18) is set as MPa−1 [36]. The ambient temperature is 293 K, and the free air convection coefficient of 10 W/(m2K) is used. It is noted that no actual experiments with the same loading conditions as the simulations are conducted. The simulation cases in Table 2 are chosen as examples to demonstrate the coupled electrical-thermal-mechanical-wear behavior in electrical contacts.

Table 2.
Parameters in the modeling of electrical contacts.
Figure 5 shows temperature-dependent material properties of copper used in the modeling, including Young’s modulus, yield stress, thermal conductivity, heat capacity, CTE, and electrical conductivity. Even though plastic deformation is not considered, the yield stress with the temperature dependence is also provided in the simulation. The influences of temperature on the Poisson’s ratio and density are insignificant, which is not considered in the modeling.
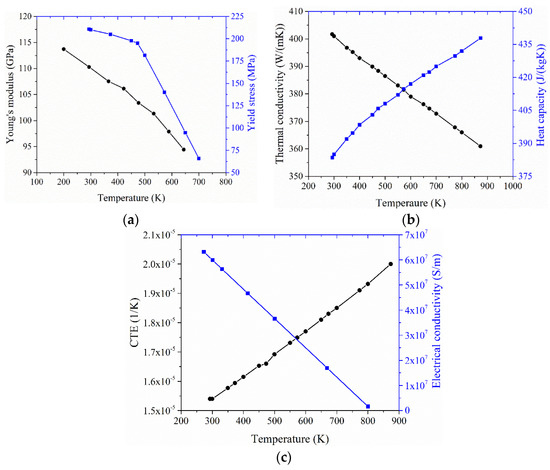
Figure 5.
Temperature-dependent properties of copper: (a) Young’s modulus and yield stress, (b) thermal conductivity and heat capacity, and (c) CTE and electrical conductivity [37].
4. Results and Discussion
4.1. Model Validation
4.1.1. Comparison with Theoretic Results of Contact Pressure and ECR
The comparison between the numerical and theoretic results is conducted through two steps. The Hertz contact model for the contact pressure and a theoretic model for the ECR are used. Both theoretic models are available without the presence of the fretting wear. Therefore, the corresponding numerical results without the fretting wear are used for the comparison.
The first step is to compare the predicted contact pressure distribution under the normal force with the classic Hertz contact solution. It is noted that electric potential and slip displacement are not applied in this validation step. Figure 6a illustrates the result comparison under a normal force of 90 N/mm. The predicted contact width is about 0.63 mm, close to the theoretic result (0.612 mm). The maximum contact pressure has a small deviation (less than 3%) from the Hertz solution. The main reason may be that the simulation domain is not an infinite half plane. It reveals that the simulation provides an accurate prediction of the contact pressure distribution.
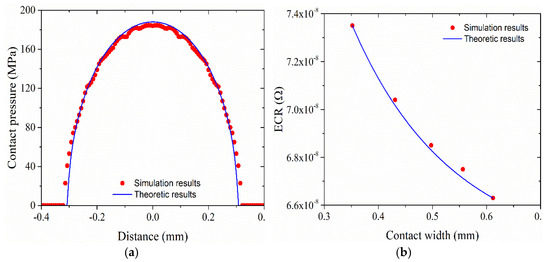
Figure 6.
Comparison between the simulation and theoretic results: (a) contact pressure distribution and (b) ECR. Both results are obtained without the consideration of fretting wear.
The second step is to compare the predicted the ECR with the theoretic solution developed by Aichi et al. [38]. The contact zone shape is a rectangle for the cylindrical pad and flat specimen. The relationship between the ECR and rectangle contact area was experimentally investigated and a simple equation between ECR and contact area was proposed as follows:
where is the equivalent electrical resistance of two components, is the contact area, and is a parameter defined as a linear function of the contact width. In the simulation, five normal forces ( = 30, 45, 60, 75, and 90 N/mm) are applied to obtain different contact widths. The potential is set as = 50 mV, and the slip displacement is not considered in this validation step. The simulation results including the contact width and ECR calculated by using Equation (8) are listed in Table 3. The results under two normal forces (30 and 90 N/mm) are used to determine the function as follows:
where is the contact width. Then the theoretic values of ECR can be obtained by using Equations (19) and (20). Figure 6b illustrates the comparison between the simulation and theoretic results of the ECR. The simulation results agree well with the theoretic results of ECR. It is noted that the validation does not include the effect of material wear.

Table 3.
Simulation results of contact width and ECR under different normal forces.
These ECR results are quite small compared with electrical contact experimental results [14,16,39,40,41]. In the electrical contact experiments of copper material, the ECR gradually increased to 0.1 Ω within 10,000 fretting cycles [14,16]. For some serve conditions, the number of fretting wear cycles to reach the ECR increase of 0.1 Ω was less than 2000 [14]. The deviation can attribute to two main reasons. The first one is that the surface roughness is not considered in the modeling. The actual conductive area on rough surfaces is much smaller than that under the smooth case in the simulation. Furthermore, the plastic deformation, crashing, and further compacting of materials on the asperities are also not modeled in the present study. The second one is that the surface oxidation and oxidation-induced non-conductive thin layer are ignored in the modeling. Further research will focus on these challenging issues.
4.1.2. Comparison with Experimental Fretting Wear Profile
Fretting wear experiments are conducted for model validation. The mechanical fretting wear is considered in the validation experiments. The electric potential cannot be applied in the experiments due to the limitation of the testing machine. The ball-on-disk contact configuration is used in the tribometer, as shown in Figure 7a. The normal force is set as 5 N and the amplitude of the reciprocating motion is 20 μm under a frequency of 10 Hz. Three specimens are used under the same condition and each test lasts for 1200 s. After the experiments, the three-dimensional profile and the wear depth of the fretting wear scar are measured using the white-light interfering profilometer, as shown in Figure 7b. The black arrow indicates the direction of the reciprocating motion. The maximum height of about 5.8 μm occurs around the wear scar due to the pile-up of the debris. The surface height along the A-B section is measured, as shown in Figure 7c. This section is parallel with the reciprocating motion direction. The maximum depth of the wear scar along the A-B section is about 1 μm. Based on the height information of the wear scar, the wear volume can be calculated. It is the volume of the wear scar with the height beneath the datum reference. The average wear volume of three specimens is about 11,502 μm3. Then the fretting wear experiments are simulated by using the developed numerical approach. The predicted wear profile is compared with the experimental results for the model validation, as shown in Figure 7d. The good agreement indicates the proposed model can provide an accurate prediction of the fretting wear scar.
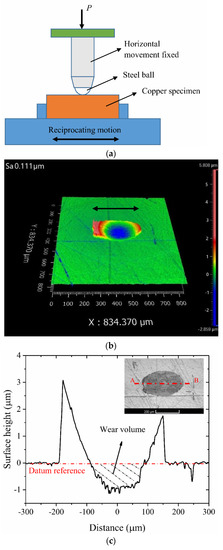
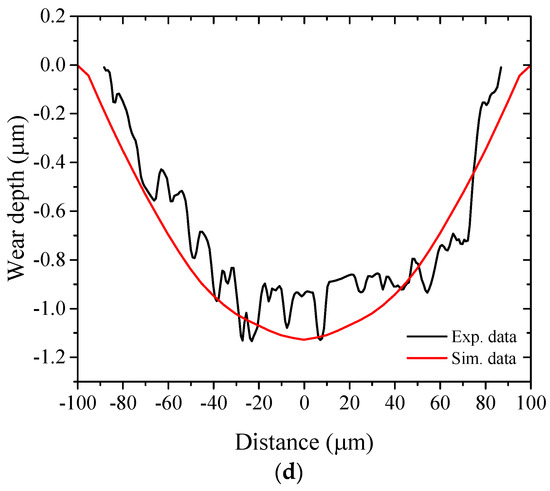
Figure 7.
(a) Schematic view of the fretting wear experiments, (b) surface morphology of the fretting wear scar, (c) surface height measured along the A-B section, and (d) comparison between the predicted and experimental wear scar profiles after 12,000 cycles.
4.2. Wear Profile, Contact Pressure, Temperature, and Electric Potential
The electrical, thermal, mechanical, and wear behavior of electrical contacts are investigated through the developed numerical approach. The simulation under Δ = 100 μm, P = 90 N/mm, and V0 = 50 mV is taken as an example to illustrate the evolutions of wear profile, electric potential, current density, temperature, and contact pressure as the number of the fretting cycles increases.
Figure 8a shows the evolution of the wear profile on the contact surface of the copper specimen. The wear width gradually increases from the initial 0.63 mm to nearly 2 mm after 50,000 cycles. Moreover, the wear depth grows from 0.66 to 7.61 μm as the number of fretting loading cycles increases from 2500 to 50,000 cycles. The maximum depth occurs at the middle of the contact zone. The increase of maximum wear depth is non-linear as shown in Figure 8b. The increase rate is higher at the beginning of the simulation. The main reason is that the tangential frictional stress reduces due to wear. The effect of the fretting wear on the contact pressure distribution will be discussed later.
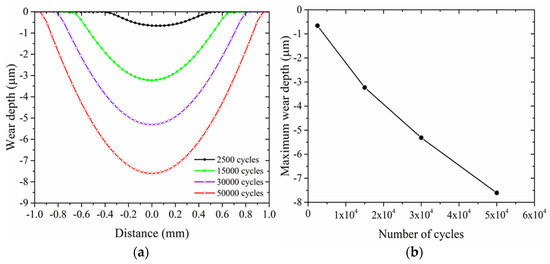
Figure 8.
(a) Evolution of fretting wear profile on the copper specimen and (b) evolution of the maximum fretting wear depth.
Figure 9a shows the evolution of electric potential distribution on the top surface of the copper specimen. The electric potential in the contact zone is stable and much higher than that in the non-contact zones. Since the contact width increases, the plateau on the distribution curve widens correspondingly. The maximum electric potential decreases from the initial 24.5 to 23.2 mV as the number increases to 50,000 cycles. Figure 9b shows the results without the consideration of the fretting wear. The contact width remains unchanged, but the maximum electric potential decreases with the increase of loading cycle number. It is attributed to the decrease in electrical conductivity due to the increase in temperature. Figure 9c illustrates the evolution of current density in the vertical direction on the contact surface. Two peaks of the current density occur at two contact edges, indicating the contraction of current lines. As the contact width increases, the current flows through the contact zone with a larger area. The evolution of the current density acts a similar behavior as the electric potential. The corresponding results without the consideration of wear are shown in Figure 9d. It is also similar to the evolution of electric potential in Figure 9b. The simulation without the consideration of wear only includes the Joule heating behavior. The Joule heating does not affect the contact width but the magnitude of the electric potential and current density. Fretting wear mainly changes the contact width and surface geometry. It works together with the Joule heating to cause significant variations of the electric potential and current density as shown in Figure 9a–c.
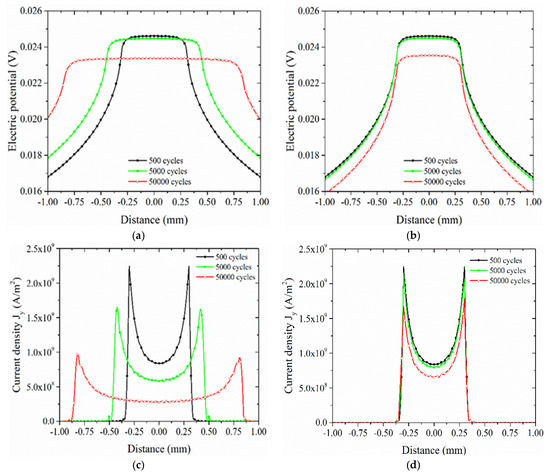
Figure 9.
Evolution of electric potential on the copper specimen with and without the consideration of fretting wear (a,b); evolution of current density with and without the consideration of fretting wear (c,d).
Figure 10 shows the evolution of ECR under the simulation cases with and without wear. If the fretting wear is not considered, the ECR increases rapidly in the first step and then grows smoothly in the subsequent loading cycles. It attributes to the temperature rise. However, the results with the consideration of the fretting wear have obvious fluctuations. The red dots indicate the maximum and minimum values in each loading block. As the pad is at the middle of the contact zone, i.e., , the contact width is about 1.5 mm which is largest than that at any other moment. Therefore, the ECR is minimum at this moment in one loading block. As the pad moves to two contact edges, the contact width reduces from 1.5 to about 1 mm, resulting in the maximum ECR at the contact edges. More importantly, the predicted ECR without the consideration of fretting wear is higher than that with fretting wear. It indicates that the effect of fretting wear on ECR is opposite to that of temperature rise. Fretting wear widens the contact zone, reducing the ECR. This result has been validated by electrical contact experiments [42]. In the simulation considering the fretting wear, there is a competition between the effects of the fretting wear and the temperature rise on ECR. The effect of the fretting wear is slightly dominant in the first 10,000 cycles so that ECR has a small reduction. In the subsequent cycles, the effect of temperature becomes to be dominant, causing the increase of ECR.
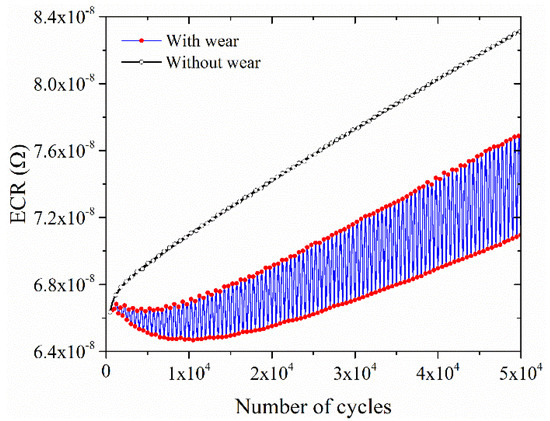
Figure 10.
Evolution of the ECR with and without the consideration of fretting wear.
Figure 11 shows the evolution of the temperature at the middle of the contact zone with the consideration of the fretting wear. It has a rapid temperature increase in the first step and then turns to a steady increase stage in the second step. The temperature increases from 293 to 425 K after 50,000 cycles. However, the temperature field is still not stable. The generated Joule heating energy is larger than the dissipated energy through the surface convection. The temperature evolution obtained under the condition without the consideration of wear is also shown in Figure 11. Two curves nearly coincide with each other at the first 20,000 cycles. The maximum difference is about 5 K at 50,000 cycles. It indicates that the material wear and the surface geometry variation have an insignificant effect on the temperature evolution.
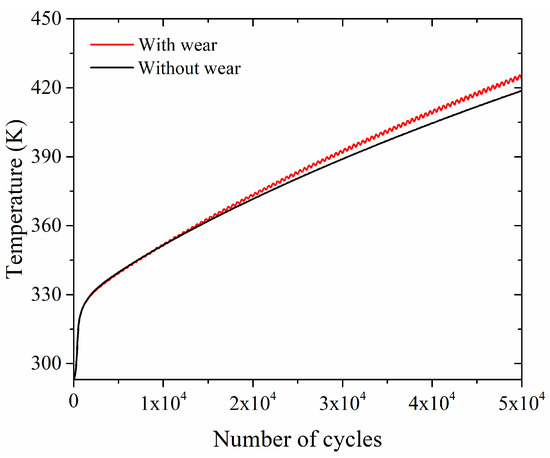
Figure 11.
Evolution of temperature on the copper specimen with and without the consideration of fretting wear.
Figure 12a illustrates the evolution of the contact pressure distribution on the contact surface. The contact pressure has an initial Hertz distribution. As the number of fretting cycles increases, contact width enlarges due to the material wear. A larger contact area is used to carry the applied normal force. Therefore, the maximum contact pressure reduces obviously from the initial 184 MPa to around 60 MPa at 50,000 cycles. Figure 12b shows the results without the consideration of wear. The distribution has a small variation during the simulation. In this case, the only influence factor is the temperature increase due to Joule heating. The material of both contacting components softens with the increase in temperature. However, Young’s modulus slightly decreases from 110 to about 106 GPa. Therefore, the maximum contact pressure has a small decrease under the condition of no fretting wear as the number increases to 50,000 cycles. The result comparison indicates that the fretting wear is the dominant influencing factor on the contact pressure distribution.
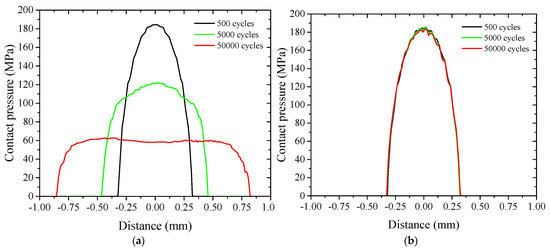
Figure 12.
Evolution of the contact pressure distribution on the copper specimen with the consideration of fretting wear (a) and without the consideration of fretting wear (b).
5. Conclusions
The electrical, thermal, mechanical, wear behavior and their interaction in electrical contacts are investigated through a numerical approach. An electrical-thermal-mechanical-wear coupling model is developed in this study. The frictional energy-based wear model is combined with the conventional electrical-thermal-mechanical coupling model to consider the effect of the fretting wear. This coupling model is implemented in the finite element modeling of electrical contacts under the fretting wear loading. The fretting wear experiments are conducted to validate the proposed numerical approach. After the model validation, the effects of the wear profile on the electric potential, current density, ECR, temperature, and contact pressure are studied.
Fretting wear width and depth both increase as the number of fretting wear cycles increases, resulting in the variation of the contact surface geometry. The electric potential and current density decrease due to the combined effects of the increase in the contact width and temperature. The numerical results reveal that the fretting wear plays a more important role than the temperature increase in changing the electric potential and current density distributions. The increase in the temperature causes the reduction of electrical conductivity, increasing the ECR. However, fretting wear increases the contact width, relieving the constriction of current lines and thus reducing the ECR. The effect of fretting wear competes with that of temperature increase. Both factors cause the ECR to decrease firstly and then gradually increase. The effect of the fretting wear on the temperature increase is insignificant. Its effect on the contact pressure is similar to that on the electric potential and current density.
Author Contributions
Conceptualization, F.S. and L.-L.K.; methodology, F.S. and L.-L.K.; software, F.S.; supervision, L.-L.K.; writing—original draft, F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Nos. 11725207, 12002234, and 12021002), the Research Start-up Foundation of Tianjin University, and the Open Fund Project of Tianjin Key Laboratory of Modern Engineering Mechanics.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Holm, R. Electric Contacts: Theory and Application; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Zuev, L.B.; Danilov, V.I.; Konovalov, S.V.; Filip’ev, R.A.; Gromov, V.E. Influence of contact potential difference and electric potential on the microhardness of metals. Phys. Solid State 2009, 51, 1137–1141. [Google Scholar] [CrossRef]
- Orlova, D.V.; Danilov, V.I.; Zuev, L.B.; Staskevich, O.S. Effect of low electrical potentials on the microhardness of metallic materials. Phys. Solid State 2016, 58, 9–11. [Google Scholar] [CrossRef]
- Slade, P.G. Electrical Contacts: Principles and Applications; CRC Press: London, UK, 2017. [Google Scholar]
- Hannel, S.; Fouvry, S.; Kapsa, P.; Vincent, L. The fretting sliding transition as a criterion for electrical contact performance. Wear 2001, 249, 761–770. [Google Scholar] [CrossRef]
- Maruschak, P.O.; Panin, S.V.; Zakiev, I.M.; Poltaranin, M.A.; Sotnikov, A.L. Scale levels of damage to the raceway of a spherical roller bearing. Eng. Fail. Anal. 2016, 59, 69–78. [Google Scholar] [CrossRef]
- Ito, T.; Sawada, S.; Hattori, Y.; Saitoh, Y.; Tamai, T.; Iida, K. Microscopy study of fretting corrosion caused by the tin plating thickness. In Proceedings of the 2008 54th IEEE Holm Conference on Electrical Contacts, Orlando, FL, USA, 27–29 October 2008; pp. 294–300. [Google Scholar]
- Gagnon, D.; Braunovic, M.; Masounave, J. Effect of fretting slip amplitude on the friction behaviour of electrical contact materials. In Proceedings of the Fifty-First IEEE Holm Conference on Electrical Contacts, Chicago, IL, USA, 26–28 September 2005; pp. 186–195. [Google Scholar]
- Heaton, C.E.; McCarthy, S.L. High cycle fretting corrosion studies on tin-coated contact materials. In Proceedings of the Forth-Seventh IEEE Holm Conference on Electrical Contacts (IEEE Cat. No. 01CH37192), Montreal, QC, Canada, 12 September 2001; pp. 209–214. [Google Scholar]
- Liu, X.-L.; Cai, Z.-B.; Cui, Y.; Liu, S.-B.; Xu, X.-J.; Zhu, M.-H. Effect of different atmospheres on the electrical contact performance of electronic components under fretting wear. J. Phys. D Appl. Phys. 2018, 51. [Google Scholar] [CrossRef]
- Liu, X.-L.; Cai, Z.-b.; He, J.-f.; Peng, J.-f.; Zhu, M.-h. Effect of elevated temperature on fretting wear under electric contact. Wear 2017, 376–377, 643–655. [Google Scholar] [CrossRef]
- Wang, P.; Yue, W.; Lu, Z.; Zhang, G.; Zhu, L. Friction and wear properties of MoS2-based coatings sliding against Cu and Al under electric current. Tribol. Int. 2018, 127, 379–388. [Google Scholar] [CrossRef]
- Fouvry, S.; Jedrzejczyk, P.; Chalandon, P. Introduction of an exponential formulation to quantify the electrical endurance of micro-contacts enduring fretting wear: Application to Sn, Ag and Au coatings. Wear 2011, 271, 1524–1534. [Google Scholar] [CrossRef]
- Noh, H.J.; Kim, J.W.; Lee, S.M.; Jang, H. Effect of grain size on the electrical failure of copper contacts in fretting motion. Tribol. Int. 2017, 111, 39–45. [Google Scholar] [CrossRef]
- Ren, W.; Wang, P.; Song, J.; Zhai, G. Effects of current load on wear and fretting corrosion of gold-plated electrical contacts. Tribol. Int. 2014, 70, 75–82. [Google Scholar] [CrossRef]
- He, L.-P.; Cai, Z.-B.; Peng, J.-F.; Deng, W.-L.; Li, Y.; Yang, L.-Y.; Zhu, M.-H. Effects of oxidation layer and roughness on the fretting wear behavior of copper under electrical contact. Mater. Res. Express 2020, 6. [Google Scholar] [CrossRef]
- Weißenfels, C.; Wriggers, P. Numerical modeling of electrical contacts. Comput. Mech. 2009, 46, 301–314. [Google Scholar] [CrossRef]
- Ren, W.; Wei, J.; Meng, X.; Zhi, H. Numerical Simulation of Temperature–Voltage Relation in Electrical Contacts and Correction of Classical Kohlrausch’s Equation. IEEE Trans. Electron Devices 2016, 63, 1217–1224. [Google Scholar] [CrossRef]
- Terhorst, M.; Ozhoga-Maslovskaja, O.; Trauth, D.; Shirobokov, A.; Mattfeld, P.; Solf, M.; Klocke, F. Electro-thermo-mechanical contact model for bulk metal forming under application of electrical resistance heating. Int. J. Adv. Manuf. Technol. 2016, 89, 3601–3618. [Google Scholar] [CrossRef]
- Jiang, X.; Pan, F.; Shao, G.; Huang, J.; Hong, J.; Zhou, A. Prediction of electrical contact endurance subject to micro-slip wear using friction energy dissipation approach. Friction 2018, 7, 537–550. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- McColl, I.R.; Ding, J.; Leen, S.B. Finite element simulation and experimental validation of fretting wear. Wear 2004, 256, 1114–1127. [Google Scholar] [CrossRef]
- Ding, J.; McColl, I.R.; Leen, S.B.; Shipway, P.H. A finite element based approach to simulating the effects of debris on fretting wear. Wear 2007, 263, 481–491. [Google Scholar] [CrossRef]
- Madge, J.J.; Leen, S.B.; Shipway, P.H. The critical role of fretting wear in the analysis of fretting fatigue. Wear 2007, 263, 542–551. [Google Scholar] [CrossRef]
- Paulin, C.; Fouvry, S.; Meunier, C. Finite element modelling of fretting wear surface evolution: Application to a Ti–6A1–4V contact. Wear 2008, 264, 26–36. [Google Scholar] [CrossRef]
- Fouvry, S.; Paulin, C.; Liskiewicz, T. Application of an energy wear approach to quantify fretting contact durability: Introduction of a wear energy capacity concept. Tribol. Int. 2007, 40, 1428–1440. [Google Scholar] [CrossRef]
- Arnaud, P.; Fouvry, S. A dynamical FEA fretting wear modeling taking into account the evolution of debris layer. Wear 2018, 412–413, 92–108. [Google Scholar] [CrossRef]
- Zhang, T.; McHugh, P.E.; Leen, S.B. Computational study on the effect of contact geometry on fretting behaviour. Wear 2011, 271, 1462–1480. [Google Scholar] [CrossRef]
- Shen, F.; Hu, W.; Meng, Q. A damage mechanics approach to fretting fatigue life prediction with consideration of elastic–plastic damage model and wear. Tribol. Int. 2015, 82, 176–190. [Google Scholar] [CrossRef]
- Shen, F.; Hu, W.; Voyiadjis, G.Z.; Meng, Q. Effects of fatigue damage and wear on fretting fatigue under partial slip condition. Wear 2015, 338–339, 394–405. [Google Scholar] [CrossRef]
- Shen, F.; Hu, W.; Meng, Q. A non-local approach based on the hypothesis of damage dissipation potential equivalence to the effect of stress gradient in fretting fatigue. Int. J. Fatigue 2016, 90, 125–138. [Google Scholar] [CrossRef]
- Cooper, M.G.; Mikic, B.B.; Yovanovich, M.M. Thermal contact conductance. Int. J. Heat Mass Transf. 1969, 12, 279–300. [Google Scholar] [CrossRef]
- Shen, F.; Zhou, K. Investigation on thermal response in fretting sliding with the consideration of plastic dissipation, surface roughness and wear. Int. J. Mech. Sci. 2018, 148, 94–102. [Google Scholar] [CrossRef]
- Paulin, C.; Fouvry, S.; Deyber, S. Wear kinetics of Ti–6Al–4V under constant and variable fretting sliding conditions. Wear 2005, 259, 292–299. [Google Scholar] [CrossRef]
- Fallahnezhad, K.; Oskouei, R.H.; Taylor, M. Development of a fretting corrosion model for metallic interfaces using adaptive finite element analysis. Finite Elem. Anal. Des. 2018, 148, 38–47. [Google Scholar] [CrossRef]
- El-Tayeb, N. The variation of hardness and wear coefficient in sliding wear of copper and aluminum alloys. Wear 1994, 174, 63–69. [Google Scholar] [CrossRef]
- Davis, J.R. Copper and Copper Alloys; ASM International: Novelty, OH, USA, 2001. [Google Scholar]
- Aichi, H. Analysis on the constriction resistance of the electric contact by the contact model using the electrolyte bath. In Proceedings of the 17th International Conference on Electrical Contacts, Nagoya, Japan, 4–9 July 1994; pp. 1–6. [Google Scholar]
- Liu, X.-L.; Cai, Z.-B.; Xiao, Q.; Shen, M.-X.; Yang, W.-B.; Chen, D.-Y. Fretting wear behavior of brass/copper-graphite composites as a contactor material under electrical contact. Int. J. Mech. Sci. 2020, 184. [Google Scholar] [CrossRef]
- Grandin, M.; Wiklund, U. Wear phenomena and tribofilm formation of copper/copper-graphite sliding electrical contact materials. Wear 2018, 398–399, 227–235. [Google Scholar] [CrossRef]
- Sung, I.H.; Kim, J.W.; Noh, H.J.; Jang, H. Effect of displacement and humidity on contact resistance of copper electrical contacts. Tribol. Int. 2016, 95, 256–261. [Google Scholar] [CrossRef]
- Zhao, H.; Feng, Y.; Zhou, Z.; Qian, G.; Zhang, J.; Huang, X.; Zhang, X. Effect of electrical current density, apparent contact pressure, and sliding velocity on the electrical sliding wear behavior of Cu–Ti3AlC2 composites. Wear 2020, 444–445. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).