Optimization of Activated Tungsten Inert Gas Welding Process Parameters Using Heat Transfer Search Algorithm: With Experimental Validation Using Case Studies
Abstract
1. Introduction
2. Materials and Methods
2.1. Selection of Process Parameter
2.2. Design Matrix as per the Response Surface Methodology
2.3. Experimentation as per Design Matrix
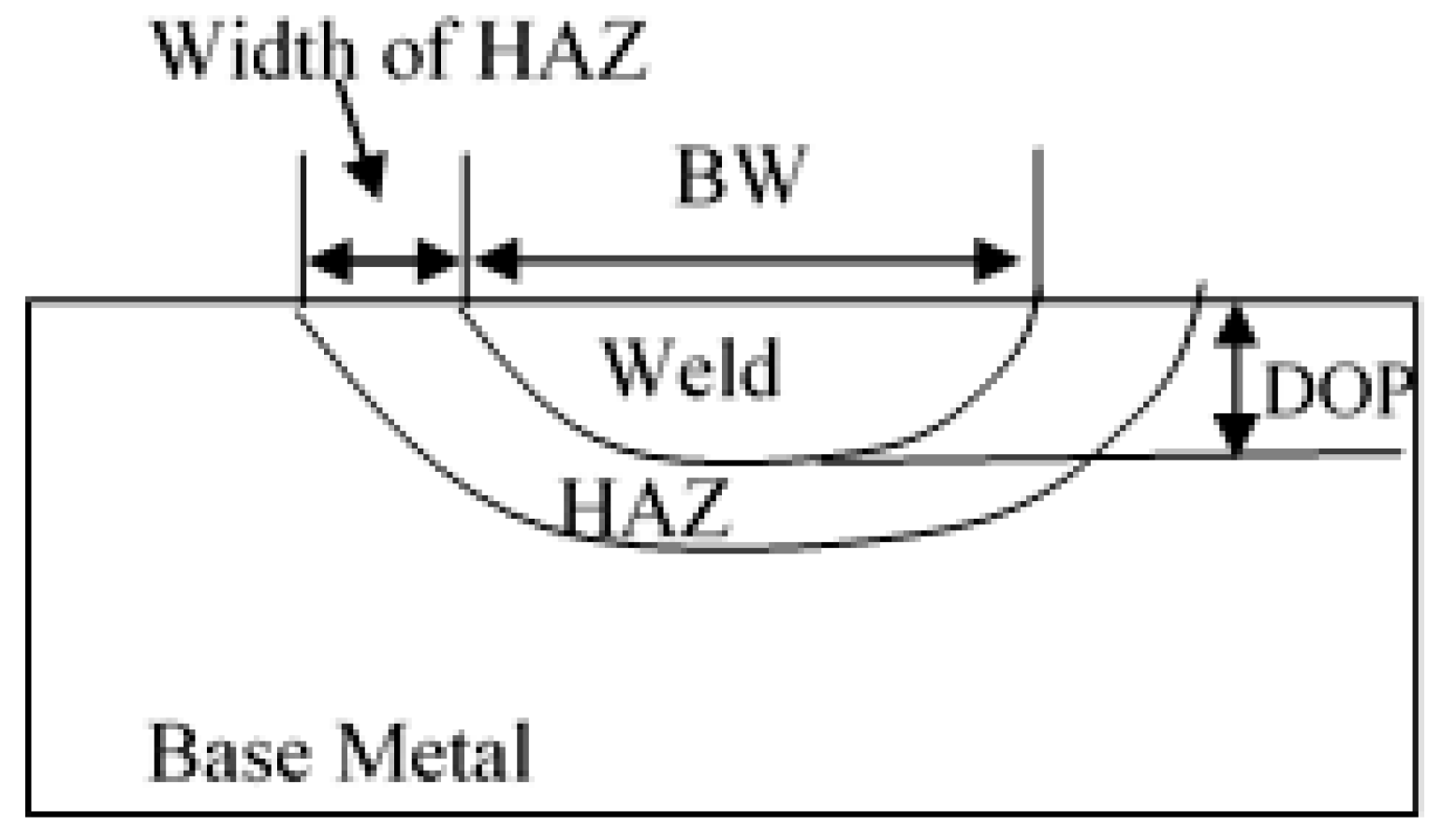
2.4. Evaluation of Bead-on-Plate Samples
2.5. Optimization Using HTS Algorithm
2.5.1. Conduction Phase
2.5.2. Convection Phase
2.5.3. Radiation Phase
2.6. Proposed Optimization Route
3. Results and Discussions
3.1. Analyzing Weld Bead Morphology
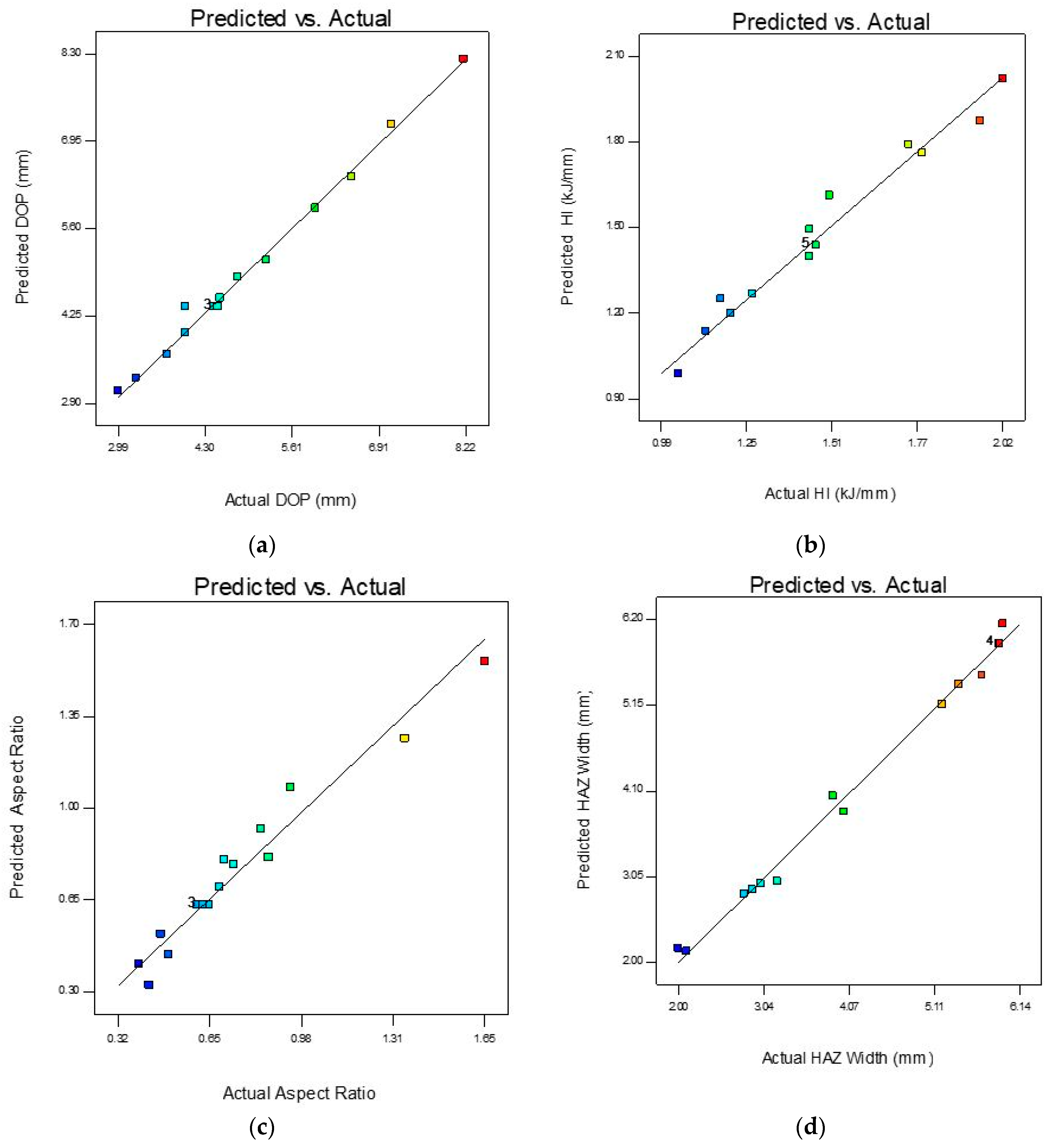
3.2. Mathematical Model Generation
3.3. Optimizing Efforts for Different Case Studies and Their Validation
3.3.1. Case I: Optimization of DOP
3.3.2. Case II: Optimization of HI (for DOP ≥ 6.2 mm)
3.3.3. Case III: Simultaneous optimization of D/w, HI, and HAZ width (for DOP ≥ 6.2 mm)
3.3.4. Case IV: Simultaneous optimization of DOP, D/w, HI and HAZ width
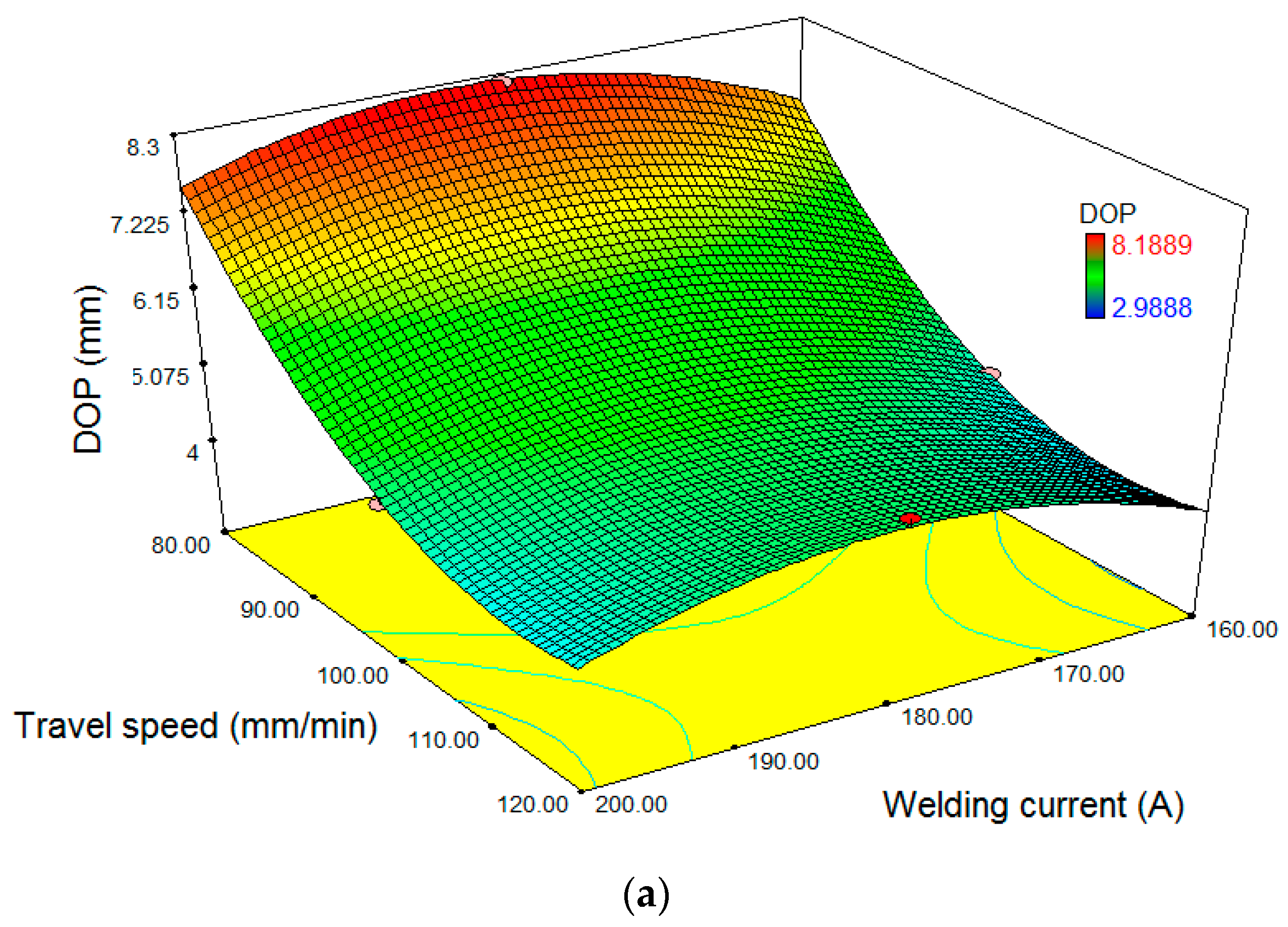
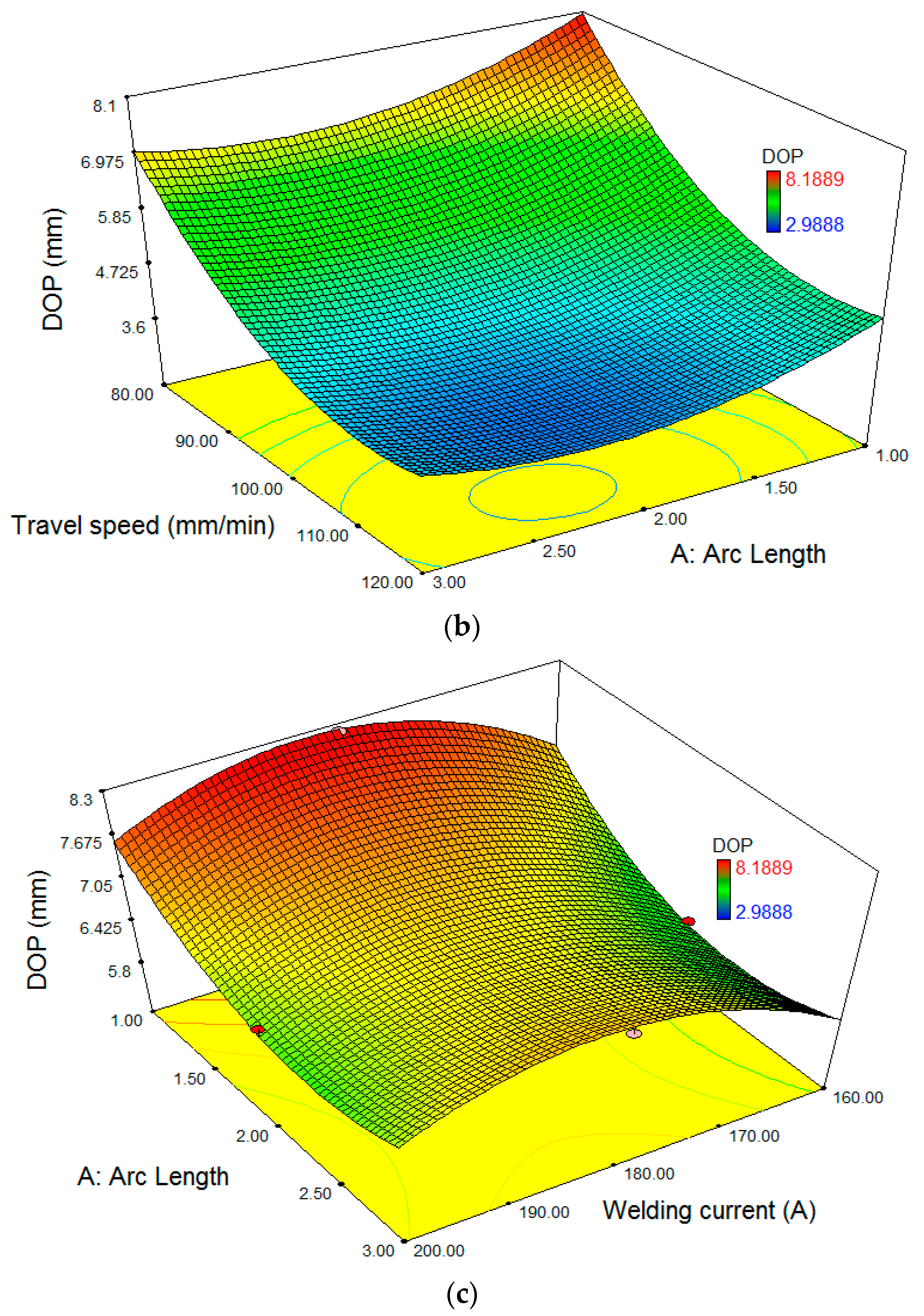
3.4. Validation of HTS Algorithm via 3D Surface Plots
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rezaei, A.; Ehsanifar, M.; Wood, D.A. Reducing welding repair requirements in refinery pressure vessel manufacturing: A case study applying six sigma principles. Int. J. Interact. Des. Manuf. 2019, 13, 1089–1102. [Google Scholar] [CrossRef]
- Rogalski, G.; Świerczyńska, A.; Landowski, M.; Fydrych, D. Mechanical and microstructural characterization of TIG welded dissimilar joints between 304L austenitic stainless steel and Incoloy 800HT nickel alloy. Metals 2020, 10, 559. [Google Scholar] [CrossRef]
- Jamrozik, W.; Górka, J.; Kik, T. Temperature-based prediction of joint hardness in TIG welding of inconel 600, 625 and 718 nickel superalloys. Materials 2021, 14, 442. [Google Scholar] [CrossRef] [PubMed]
- Arora, H.; Kumar, V.; Prakash, C.; Pimenov, D.; Singh, M.; Vasudev, H.; Singh, V. Analysis of sensitization in austenitic stainless steel-welded joint. In Advances in Metrology and Measurement of Engineering Surfaces; Springer: Singapore, 2021; pp. 13–23. [Google Scholar]
- Brykov, M.N.; Petryshynets, I.; Džupon, M.; Kalinin, Y.A.; Efremenko, V.G.; Makarenko, N.A.; Pimenov, D.Y.; Kováč, F. Microstructure and properties of heat affected zone in high-carbon steel after welding with fast cooling in water. Materials 2020, 13, 5059. [Google Scholar] [CrossRef]
- Stadler, M.; Freton, P.; Gonzalez, J.-J. Influence of welding parameters on the weld pool dimensions and shape in a TIG configuration. Appl. Sci. 2017, 7, 373. [Google Scholar] [CrossRef]
- Fujii, H.; Sato, T.; Lu, S.; Nogi, K. Development of an advanced A-TIG (AA-TIG) welding method by control of Marangoni convection. Mater. Sci. Eng. A 2008, 495, 296–303. [Google Scholar] [CrossRef]
- Tathgir, S.; Rathod, D.W.; Batish, A. Process enhancement using hydrogen-induced shielding: H2-induced A-TIG welding process. Mater. Manuf. Process. 2020, 35, 1084–1095. [Google Scholar] [CrossRef]
- Niagaj, J. Influence of Activated Fluxes on the Bead Shape of A-TIG Welds on Carbon and Low-Alloy Steels in Comparison with Stainless Steel AISI 304L. Metals 2021, 11, 530. [Google Scholar] [CrossRef]
- Balos, S.; Dramicanin, M.; Janjatovic, P.; Kulundzic, N.; Zabunov, I.; Pilic, B.; Klobčar, D. Influence of Metallic Oxide Nanoparticles on the Mechanical Properties of an A-TIG Welded 304L Austenitic Stainless Steel. Materials 2020, 13, 4513. [Google Scholar] [CrossRef] [PubMed]
- Balos, S.; Dramicanin, M.; Janjatovic, P.; Zabunov, I.; Klobcar, D.; Busic, M.; Grilli, M.L. Metal oxide nanoparticle-based coating as a catalyzer for A-TIG welding: Critical raw material perspective. Metals 2019, 9, 567. [Google Scholar] [CrossRef]
- Singh, A.K.; Kumar, M.; Dey, V.; Rai, R.N. A study to increase weld penetration in P91 steel during TIG welding by using activating fluxes. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Hyderabad, India, 3–4 July 2017; p. 012099. [Google Scholar]
- Vidyarthy, R.S.; Dwivedi, D.K. Microstructural and mechanical properties assessment of the P91 A-TIG weld joints. J. Manuf. Process. 2018, 31, 523–535. [Google Scholar] [CrossRef]
- Vora, J.J.; Badheka, V.J. Experimental investigation on mechanism and weld morphology of activated TIG welded bead-on-plate weldments of reduced activation ferritic/martensitic steel using oxide fluxes. J. Manuf. Process. 2015, 20, 224–233. [Google Scholar] [CrossRef]
- Nagaraju, S.; Vasantharaja, P.; Chandrasekhar, N.; Vasudevan, M.; Jayakumar, T. Optimization of welding process parameters for 9Cr-1Mo steel using RSM and GA. Mater. Manuf. Process. 2016, 31, 319–327. [Google Scholar] [CrossRef]
- Arivazhagan, B.; Vasudevan, M. Studies on A-TIG welding of 2.25 Cr-1Mo (P22) steel. J. Manuf. Process. 2015, 18, 55–59. [Google Scholar] [CrossRef]
- Kumar, S.A.; Sathiya, P. Experimental investigation of the A-TIG welding process of Incoloy 800H. Mater. Manuf. Process. 2015, 30, 1154–1159. [Google Scholar] [CrossRef]
- Tseng, K.-H.; Wang, N.-S. GTA welding assisted by mixed ionic compounds of stainless steel. Powder Technol. 2014, 251, 52–60. [Google Scholar] [CrossRef]
- Tseng, K.-H.; Hsu, C.-Y. Performance of activated TIG process in austenitic stainless steel welds. J. Mater. Process. Technol. 2011, 211, 503–512. [Google Scholar] [CrossRef]
- Tseng, K.-H. Development and application of oxide-based flux powder for tungsten inert gas welding of austenitic stainless steels. Powder Technol. 2013, 233, 72–79. [Google Scholar] [CrossRef]
- Vora, J.J.; Badheka, V.J. Improved penetration with the use of oxide fluxes in activated TIG welding of low activation ferritic/martensitic steel. Trans. Indian Inst. Met. 2016, 69, 1755–1764. [Google Scholar] [CrossRef]
- Vora, J.J.; Badheka, V.J. Experimental investigation on effects of carrier solvent and oxide fluxes in activated TIG welding of reduced activation ferritic/martensitic steel. Int. J. Adv. Mech. Automob. Eng. 2016, 3, 1–5. [Google Scholar]
- Vora, J.J.; Badheka, V.J. Experimental investigation on microstructure and mechanical properties of activated TIG welded reduced activation ferritic/martensitic steel joints. J. Manuf. Process. 2017, 25, 85–93. [Google Scholar] [CrossRef]
- Marya, M. Theoretical and experimental assessment of chloride effects in the A-TIG welding of magnesium. Weld. World 2002, 46, 7–21. [Google Scholar] [CrossRef]
- Tomków, J.; Sobota, K.; Krajewski, S. Series: Mechanical Engineering. Influence of tack welds distribution and welding sequence on the angular distortion of tig welded joint. Facta Univ. Ser. Mech. Eng. 2020, 3, 611–621. [Google Scholar]
- Zhao, D.; Wang, Y.; Sheng, S.; Lin, Z. Multi-objective optimal design of small scale resistance spot welding process with principal component analysis and response surface methodology. J. Intell. Manuf. 2014, 25, 1335–1348. [Google Scholar] [CrossRef]
- Muhammad, N.; Manurung, Y.H.; Jaafar, R.; Abas, S.K.; Tham, G.; Haruman, E. Model development for quality features of resistance spot welding using multi-objective Taguchi method and response surface methodology. J. Intell. Manuf. 2013, 24, 1175–1183. [Google Scholar] [CrossRef]
- do Valle Tomaz, I.; Colaço, F.H.G.; Sarfraz, S.; Pimenov, D.Y.; Gupta, M.K.; Pintaude, G. Investigations on quality characteristics in gas tungsten arc welding process using artificial neural network integrated with genetic algorithm. Int. J. Adv. Manuf. Technol. 2021, 113, 3569–3583. [Google Scholar] [CrossRef]
- Katherasan, D.; Elias, J.V.; Sathiya, P.; Haq, A.N. Simulation and parameter optimization of flux cored arc welding using artificial neural network and particle swarm optimization algorithm. J. Intell. Manuf. 2014, 25, 67–76. [Google Scholar] [CrossRef]
- Vasudevan, M.; Bhaduri, A.K.; Raj, B.; Rao, K.P. Genetic-algorithm-based computational models for optimizing the process parameters of A-TIG welding to achieve target bead geometry in type 304 L (N) and 316 L (N) stainless steels. Mater. Manuf. Process. 2007, 22, 641–649. [Google Scholar] [CrossRef]
- Vasudevan, M.; Arunkumar, V.; Chandrasekhar, N.; Maduraimuthu, V. Genetic algorithm for optimisation of A-TIG welding process for modified 9Cr–1Mo steel. Sci. Technol. Weld. Join. 2010, 15, 117–123. [Google Scholar] [CrossRef]
- Ansaripour, N.; Heidari, A.; Eftekhari, S.A. Multi-objective optimization of residual stresses and distortion in submerged arc welding process using Genetic Algorithm and Harmony Search. J. Mech. Eng. Sci. 2020, 234, 862–871. [Google Scholar] [CrossRef]
- Vora, J.J.; Abhishek, K.; Ramkumar, P.J. Different methodologies for the parametric optimization of welding processes. In Advances in Welding Technologies for Process Development; CRC Press: Boca Raton, FL, USA, 2019; Volume 55. [Google Scholar]
- Patel, V.K.; Savsani, V.J. Heat transfer search (HTS): A novel optimization algorithm. Inf. Sci. 2015, 324, 217–246. [Google Scholar] [CrossRef]
- Degertekin, S.; Lamberti, L.; Hayalioglu, M. Heat transfer search algorithm for sizing optimization of truss structures. Lat. Am. J. Solids Struct. 2017, 14, 373–397. [Google Scholar] [CrossRef]
- Raja, B.; Patel, V.; Jhala, R.L.; Progress, E. Thermal design and optimization of fin-and-tube heat exchanger using heat transfer search algorithm. Therm. Sci. Eng. Prog. 2017, 4, 45–57. [Google Scholar] [CrossRef]
- Tejani, G.G.; Savsani, V.J.; Patel, V.K.; Savsani, P.V.; Engineering. Size, shape, and topology optimization of planar and space trusses using mutation-based improved metaheuristics. J. Comput. Des. Eng. 2018, 5, 198–214. [Google Scholar] [CrossRef]
- Patel, V.; Savsani, V.; Mudgal, A. Efficiency, thrust, and fuel consumption optimization of a subsonic/sonic turbojet engine. Energy 2018, 144, 992–1002. [Google Scholar] [CrossRef]
- Vora, J.J.; Abhishek, K.; Srinivasan, S. Attaining optimized A-TIG welding parameters for carbon steels by advanced parameter-less optimization techniques: With experimental validation. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 261. [Google Scholar] [CrossRef]
- Lostado Lorza, R.; Escribano García, R.; Martínez Calvo, M.Á.; Múgica Vidal, R. Improvement in the design of welded joints of EN 235JR low carbon steel by multiple response surface methodology. Metals 2016, 6, 205. [Google Scholar] [CrossRef]
- Liao, B.; Shi, Y.; Cui, Y.; Cui, S.; Jiang, Z.; Yi, Y. Mathematical model for prediction and optimization of weld bead geometry in all-position automatic welding of pipes. Metals 2018, 8, 756. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, X.; Pan, K.; Wang, J. Multi-objective optimization of friction stir spot-welded parameters on aluminum alloy sheets based on automotive joint loads. Metals 2019, 9, 520. [Google Scholar] [CrossRef]
- Ibrahim, H.M.; Elkhidir, E.E. Response surface method as an efficient tool for medium optimisation. Trends Appl. Sci. Res. 2011, 6, 121–129. [Google Scholar] [CrossRef]
- Popović, O.; Prokić, R.; Burzić, M.; Milutinović, Z. The effect of heat input on the weld metal toughness of surface welded joint. In Proceedings of the 14th International Research/Expert Conference “Trends in the Development of Machinery and Associated Technology”, Mediterranean Cruise, Faculty of Mechanical Engineering, University of Belgrade, Belgrade, Serbia, 11–18 September 2010; pp. 11–18. [Google Scholar]


| C | S | P | Mn | Si | Al | Cu | Cr | Ni | Mo | V | Ti |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.01 | 0.013 | 1.1 | 0.21 | 0.023 | <0.02 | <0.015 | <0.015 | <0.015 | <0.01 | <0.005 |
| Crater current | 200 A |
| Electrode type | Tungsten (2% Thoriated) |
| Electrode diameter | 2.9 mm |
| Electrode angle | 18–20° (Blunt ground at the tip) |
| Shielding gas | Argon (99.999% purity) |
| Gas flow rate | 10–12 L/min |
| Welding position | 1G PA |
| Electrode extension | 5–6 mm |
| Nozzle diameter | 8 mm |
| Parameters | Units | Notations | Factor Levels | ||
|---|---|---|---|---|---|
| - | - | - | −1 | 0 | 1 |
| Arc length | mm | L | 1 | 2 | 3 |
| Welding current | A | I | 160 | 180 | 200 |
| Travel speed | mm/min | T | 80 | 100 | 120 |
| Exp. No. | Coded Values | Actual Values | ||||
|---|---|---|---|---|---|---|
| E (mm) | I (A) | TS (mm/min) | ||||
| 1 | 0 | 0 | 0 | 2 | 180 | 100 |
| 2 | −1 | −1 | 0 | 1 | 160 | 100 |
| 3 | −1 | 0 | 1 | 1 | 180 | 120 |
| 4 | −1 | 0 | −1 | 1 | 180 | 80 |
| 5 | 0 | 1 | −1 | 2 | 200 | 80 |
| 6 | 0 | −1 | −1 | 2 | 160 | 80 |
| 7 | −1 | 1 | 0 | 1 | 200 | 100 |
| 8 | 0 | 0 | 0 | 2 | 180 | 100 |
| 9 | 0 | 0 | 0 | 2 | 180 | 100 |
| 10 | 1 | 0 | −1 | 3 | 180 | 80 |
| 11 | 0 | 0 | 0 | 2 | 180 | 100 |
| 12 | 0 | 0 | 0 | 2 | 180 | 100 |
| 13 | 1 | −1 | 0 | 3 | 160 | 100 |
| 14 | 0 | 1 | 1 | 2 | 200 | 120 |
| 15 | 0 | −1 | 1 | 2 | 160 | 120 |
| 16 | 1 | 1 | 0 | 3 | 200 | 100 |
| 17 | 1 | 0 | 1 | 3 | 180 | 120 |
| Exp. No. | DOP (mm) | BW (mm) | Voltage | HI (kJ/mm) | D/w | HAZ (mm) |
|---|---|---|---|---|---|---|
| 1 | 4.49 | 7.15 | 13.50 | 1.46 | 0.63 | 5.90 |
| 2 | 4.52 | 6.41 | 13.20 | 1.27 | 0.71 | 4.01 |
| 3 | 5.22 | 3.85 | 12.50 | 1.13 | 1.36 | 2.00 |
| 4 | 8.19 | 4.98 | 13.20 | 1.78 | 1.65 | 5.20 |
| 5 | 6.50 | 7.50 | 13.50 | 2.03 | 0.87 | 5.40 |
| 6 | 5.96 | 8.64 | 12.50 | 1.50 | 0.69 | 5.96 |
| 7 | 4.79 | 5.71 | 12.00 | 1.44 | 0.84 | 2.10 |
| 8 | 4.49 | 7.15 | 13.50 | 1.46 | 0.63 | 5.90 |
| 9 | 4.48 | 7.14 | 13.50 | 1.46 | 0.63 | 5.94 |
| 10 | 7.10 | 7.51 | 14.50 | 1.96 | 0.95 | 5.68 |
| 11 | 4.50 | 6.92 | 13.50 | 1.46 | 0.65 | 5.89 |
| 12 | 4.00 | 6.56 | 13.50 | 1.46 | 0.61 | 5.90 |
| 13 | 3.72 | 8.56 | 12.50 | 1.20 | 0.44 | 3.00 |
| 14 | 3.26 | 6.80 | 14.40 | 1.44 | 0.48 | 3.20 |
| 15 | 2.99 | 7.53 | 13.00 | 1.04 | 0.40 | 2.90 |
| 16 | 4.00 | 7.91 | 14.50 | 1.74 | 0.51 | 3.88 |
| 17 | 4.42 | 5.98 | 13.00 | 1.17 | 0.74 | 2.80 |
| Response Feature | Model | R2 | Adj. R-Squared | Pred R-Squared | Adeq. Precision |
|---|---|---|---|---|---|
| DOP | Quadratic | 0.9915 | 0.9806 | 0.9575 | 35.153 |
| D/w | Forward regression | 0.9554 | 0.9286 | 0.8227 | 22.315 |
| HAZ | Quadratic | 0.9945 | 0.9873 | 0.9113 | 30.717 |
| HI | Back elimination regression | 0.9685 | 0.9542 | 0.9037 | 29.315 |
| Weld Bead Dimension Values | ||||||
|---|---|---|---|---|---|---|
| Condition | DOP (mm) | BW (mm) | Voltage (V) | HI (kJ/mm) | D/w | HAZ Width (mm) |
| Predicted by HTS Algorithm | 8.24 | 5.28 | 12.75 | 1.77 | 1.56 | 4.99 |
| Experimentally measured values | 8.1 | 5.33 | 12.54 | 1.74 | 1.52 | 5.14 |
| % ERROR | 1.72 | 0.94 | 1.67 | 1.72 | 2.63 | 2.91 |
 | ||||||
| Weld Bead Dimension Values | ||||||
|---|---|---|---|---|---|---|
| Condition | DOP (mm) | BW (mm) | Voltage (V) | HI (kJ/mm) | D/w | HAZ Width (mm) |
| Predicted by HTS Algorithm | 6.20 | 5.16 | 13.09 | 1.48 | 1.20 | 4.82 |
| Experimentally measured values | 6.32 | 5.01 | 12.54 | 1.46 | 1.15 | 4.40 |
| % ERROR | 1.89 | 2.99 | 4.38 | 1.36 | 4.34 | 9.5 |
 | ||||||
| Weld Bead Dimension Values | ||||||
|---|---|---|---|---|---|---|
| Condition | DOP (mm) | BW (mm) | Voltage (V) | HI (kJ/mm) | D/w | HAZ Width (mm) |
| Predicted by HTS Algorithm | 6.20 | 5.04 | 12.89 | 1.50 | 1.23 | 4.44 |
| Experimentally measured values | 6.41 | 6.05 | 14.25 | 1.62 | 1.06 | 4.32 |
| % ERROR | 3.27 | 16.7 | 9.5 | 7.4 | 16 | 2.7 |
 | ||||||
| Weld Bead Dimension Values | ||||||
|---|---|---|---|---|---|---|
| Condition | DOP (mm) | BW (mm) | Voltage (V) | HI (kJ/mm) | D/w | HAZ Width (mm) |
| Predicted by HTS Algorithm | 8.07 | 5.42 | 14.83 | 1.82 | 1.49 | 4.12 |
| Experimentally measured values | 8.15 | 6.03 | 13.33 | 1.90 | 1.35 | 4.32 |
| % ERROR | 0.98 | 10.1 | 11.2 | 4.2 | 10.4 | 4.6 |
 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vora, J.; Patel, V.K.; Srinivasan, S.; Chaudhari, R.; Pimenov, D.Y.; Giasin, K.; Sharma, S. Optimization of Activated Tungsten Inert Gas Welding Process Parameters Using Heat Transfer Search Algorithm: With Experimental Validation Using Case Studies. Metals 2021, 11, 981. https://doi.org/10.3390/met11060981
Vora J, Patel VK, Srinivasan S, Chaudhari R, Pimenov DY, Giasin K, Sharma S. Optimization of Activated Tungsten Inert Gas Welding Process Parameters Using Heat Transfer Search Algorithm: With Experimental Validation Using Case Studies. Metals. 2021; 11(6):981. https://doi.org/10.3390/met11060981
Chicago/Turabian StyleVora, Jay, Vivek K. Patel, Seshasai Srinivasan, Rakesh Chaudhari, Danil Yurievich Pimenov, Khaled Giasin, and Shubham Sharma. 2021. "Optimization of Activated Tungsten Inert Gas Welding Process Parameters Using Heat Transfer Search Algorithm: With Experimental Validation Using Case Studies" Metals 11, no. 6: 981. https://doi.org/10.3390/met11060981
APA StyleVora, J., Patel, V. K., Srinivasan, S., Chaudhari, R., Pimenov, D. Y., Giasin, K., & Sharma, S. (2021). Optimization of Activated Tungsten Inert Gas Welding Process Parameters Using Heat Transfer Search Algorithm: With Experimental Validation Using Case Studies. Metals, 11(6), 981. https://doi.org/10.3390/met11060981










