Atomic Simulations of U-Mo under Irradiation: A New Angular Dependent Potential
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Fitting Results
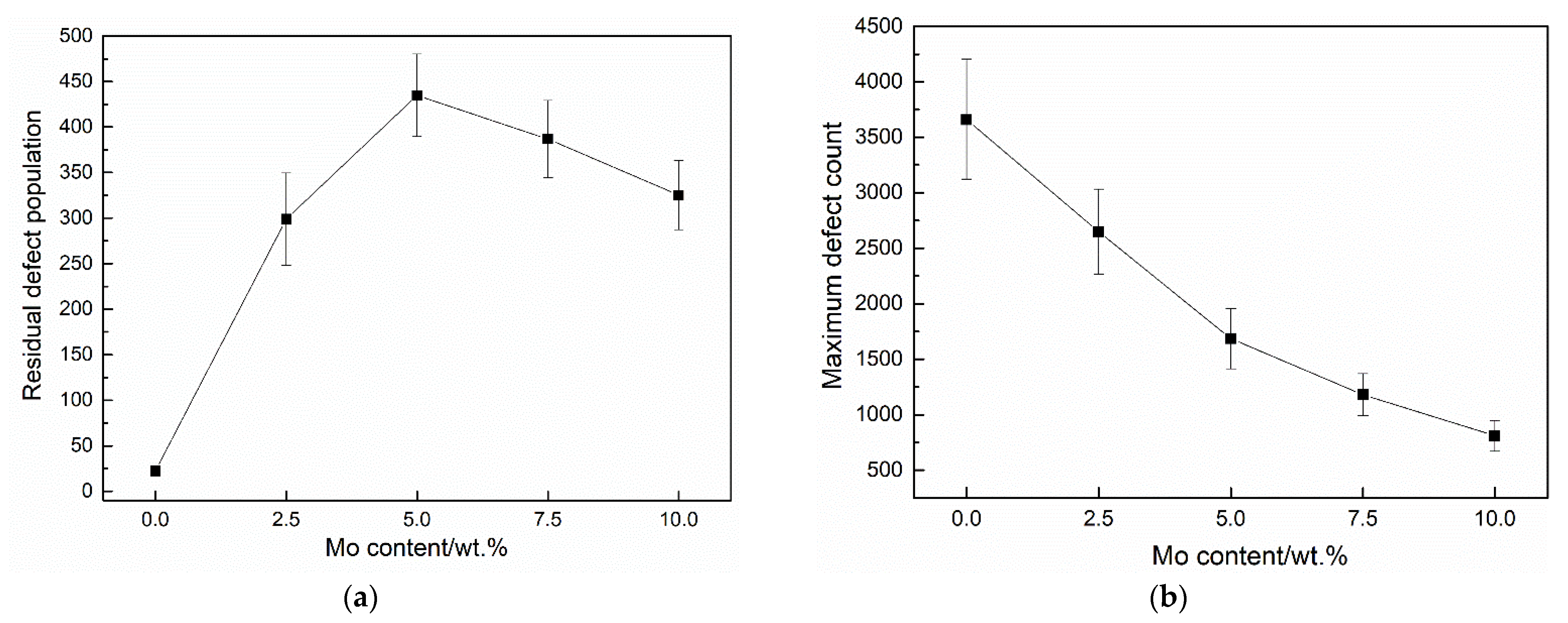
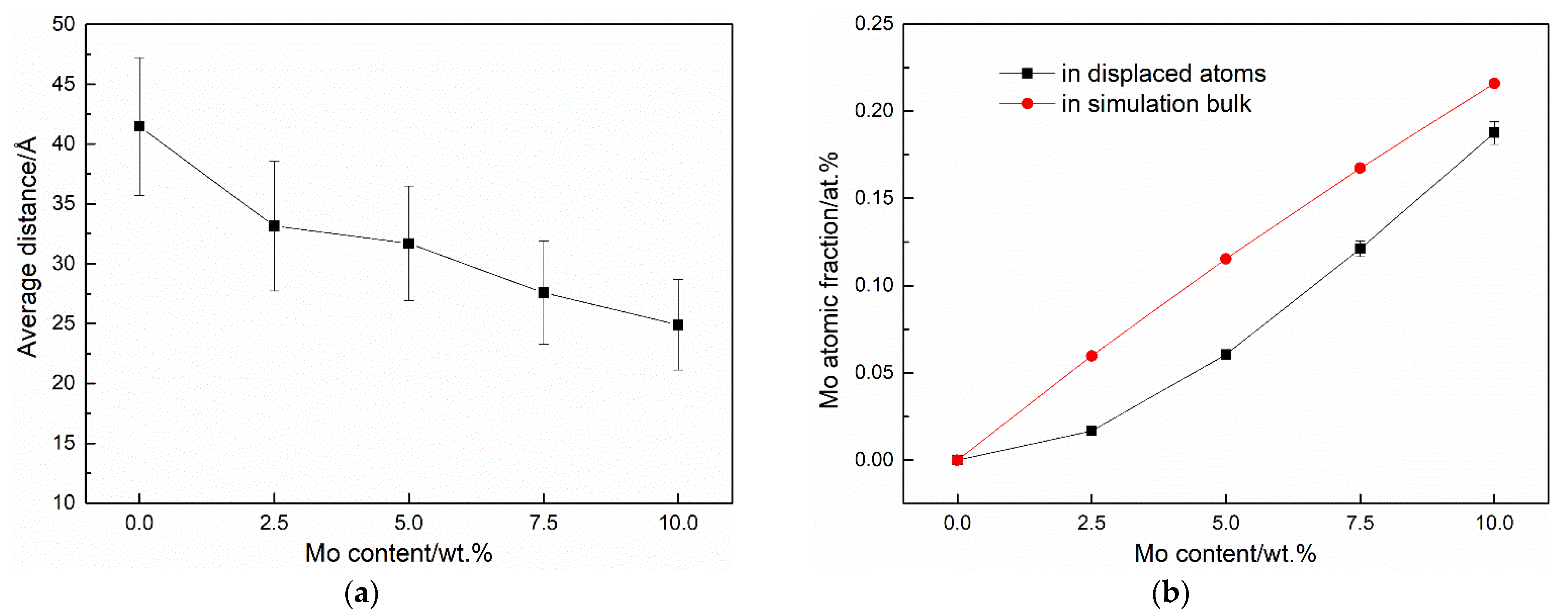
3.2. Cascade Simulations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kalashnikov, V.V.; Titova, V.V.; Sergeev, G.I.; Samoilov, A.G. Uranium-molybdenum alloys in reactor construction. Sov. J. At. Energy 1959, 5, 1315–1325. [Google Scholar] [CrossRef]
- Kulcinski, G.L.; Leggett, R.D.; Hann, C.R.; Mastel, B. Fission gas induced swelling in uranium at high temperatures and pressures. J. Nucl. Mater. 1969, 30, 303–313. [Google Scholar] [CrossRef]
- Landa, A.; Söderlind, P.; Turchi, P. Density-functional study of U–Mo and U–Zr alloys. J. Nucl. Mater. 2011, 414, 132–137. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.S.; Hofman, G.L. Fission product induced swelling of U–Mo alloy fuel. J. Nucl. Mater. 2011, 419, 291–301. [Google Scholar] [CrossRef]
- Tangri, K.; Williams, G.I. Metastable phases in the uranium molybdenum system and their origin. J. Nucl. Mater. 1961, 4, 226–233. [Google Scholar] [CrossRef]
- Yakel, H.L. Crystal structures of transition phases formed in U/16.60 at% Nb/5.64 at% Zr alloys. J. Nucl. Mater. 1969, 33, 286–295. [Google Scholar] [CrossRef]
- Williams, W.; Rice, F.; Robinson, A.; Meyer, M.; Rabin, B. Afip-6 mkii post-irradiation examination summary report. In Technical Report INL/LTD-15-34142; Idaho National Laboratory: Idaho Falls, ID, USA, 2015. [Google Scholar]
- Kim, Y.S.; Hofman, G.L.; Cheon, J.S. Recrystallization and fission-gas-bubble swelling of U–Mo fuel. J. Nucl. Mater. 2013, 436, 14–22. [Google Scholar] [CrossRef]
- Van den Berghe, S.; Van Renterghem, W.; Leenaers, A. Transmission electron microscopy investigation of irradiated U–7wt%Mo dispersion fuel. J. Nucl. Mater. 2008, 375, 340–346. [Google Scholar] [CrossRef]
- Smirnova, D.E.; Kuksin, A.Y.; Starikov, S.V.; Stegailov, V.V.; Insepov, Z.; Rest, J.; Yacout, A.M. A ternary EAM interatomic potential for U–Mo alloys with xenon. Model. Simul. Mater. Sci. Eng. 2013, 21, 035011. [Google Scholar] [CrossRef]
- Tian, X.; Xiao, H.; Tang, R.; Lu, C. Molecular dynamics simulation of displacement cascades in U–Mo alloys. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2014, 321, 24–29. [Google Scholar] [CrossRef]
- Hu, S.; Setyawan, W.; Joshi, V.V.; Lavender, C.A. Atomistic simulations of thermodynamic properties of Xe gas bubbles in U10Mo fuels. J. Nucl. Mater. 2017, 490, 49–58. [Google Scholar] [CrossRef] [Green Version]
- Smirnova, D.; Kuksin, A.Y.; Starikov, S. Investigation of point defects diffusion in bcc uranium and U–Mo alloys. J. Nucl. Mater. 2015, 458, 304–311. [Google Scholar] [CrossRef]
- Smirnova, D.E.; Kuksin, A.Y.; Starikov, S.V.; Stegailov, V.V. Atomistic modeling of the self-diffusion in γ-U and γ-U-Mo. Phys. Met. Metallogr. 2015, 116, 445–455. [Google Scholar] [CrossRef]
- Starikov, S.; Kolotova, L.; Kuksin, A.Y.; Smirnova, D.; Tseplyaev, V. Atomistic simulation of cubic and tetragonal phases of U-Mo alloy: Structure and thermodynamic properties. J. Nucl. Mater. 2018, 499, 451–463. [Google Scholar] [CrossRef]
- Chen, J.; Ouyang, W.; Lai, W.; Li, J.; Zhang, Z. A new type angular-dependent interatomic potential and its application to model displacement cascades in uranium. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2019, 451, 32–37. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Biersack, J.P. The Stopping and Range of Ions in Matter; Springer: Boston, MA, USA, 1985; pp. 93–129. [Google Scholar]
- Stoller, R.E.; Tamm, A.; Beland, L.K.; Samolyuk, G.D.; Stocks, G.M.; Caro, A.; Slipchenko, L.V.; Osetsky, Y.N.; Aabloo, A.; Klintenberg, M.; et al. Impact of Short-Range Forces on Defect Production from High-Energy Collisions. J. Chem. Theory Comput. 2016, 12, 2871–2879. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Fernández, J.R.; Pascuet, M.I. On the accurate description of uranium metallic phases: A MEAM interatomic potential approach. Model. Simul. Mater. Sci. Eng. 2014, 22, 055019. [Google Scholar] [CrossRef]
- Kittel, C.; McEuen, P.; McEuen, P. Introduction to Solid State Physics; Wiley: Hoboken, NJ, USA, 1996; Volume 8. [Google Scholar]
- Barrett, C.S.; Mueller, M.H.; Hitterman, R.L. Crystal Structure Variations in Alpha Uranium at Low Temperatures. Phys. Rev. 1963, 129, 625–629. [Google Scholar] [CrossRef]
- Yoo, C.-S.; Cynn, H.; Söderlind, P. Phase diagram of uranium at high pressures and temperatures. Phys. Rev. B 1998, 57, 10359–10362. [Google Scholar] [CrossRef]
- Taylor, C.D. Erratum: Evaluation of first-principles techniques for obtaining materials parameters of alpha-uranium and the (001) alpha-uranium surface. Phys. Rev. B 2009, 80, 149906. [Google Scholar] [CrossRef]
- Wilson, A.S.; Rundle, R.E. The structures of uranium metal. Acta Crystallogr. 1949, 2, 126–127. [Google Scholar] [CrossRef]
- Edwards, J.W.; Speiser, R.; Johnston, H.L. High Temperature Structure and Thermal Expansion of Some Metals as Determined by X-Ray Diffraction Data. I. Platinum, Tantalum, Niobium, and Molybdenum. J. Appl. Phys. 1951, 22, 424–428. [Google Scholar] [CrossRef]
- Errandonea, D.; Schwager, B.; Ditz, R.; Gessmann, C.; Boehler, R.; Ross, M. Systematics of transition-metal melting. Phys. Rev. B 2001, 63, 132104. [Google Scholar] [CrossRef]
- Stearns, M.B. Landolt-Bornstein: Numerical Data and Functional Relationships in Science and Technology, Group Ⅲ Condensed Matter. Atomic Defects Metals. 1991, 25. [Google Scholar] [CrossRef]
- Frazier, W.E.; Hu, S.; Burkes, D.E.; Beeler, B.W. A Monte Carlo model of irradiation-induced recrystallization in polycrystalline UMo fuels. J. Nucl. Mater. 2019, 524, 164–176. [Google Scholar] [CrossRef]
- Van Den Berghe, S.; Lemoine, P. Review of 15 years of high-density low-enriched umo dispersion fuel development for research reactors in europe. Nucl. Eng. Technol. 2014, 46, 125–146. [Google Scholar] [CrossRef] [Green Version]
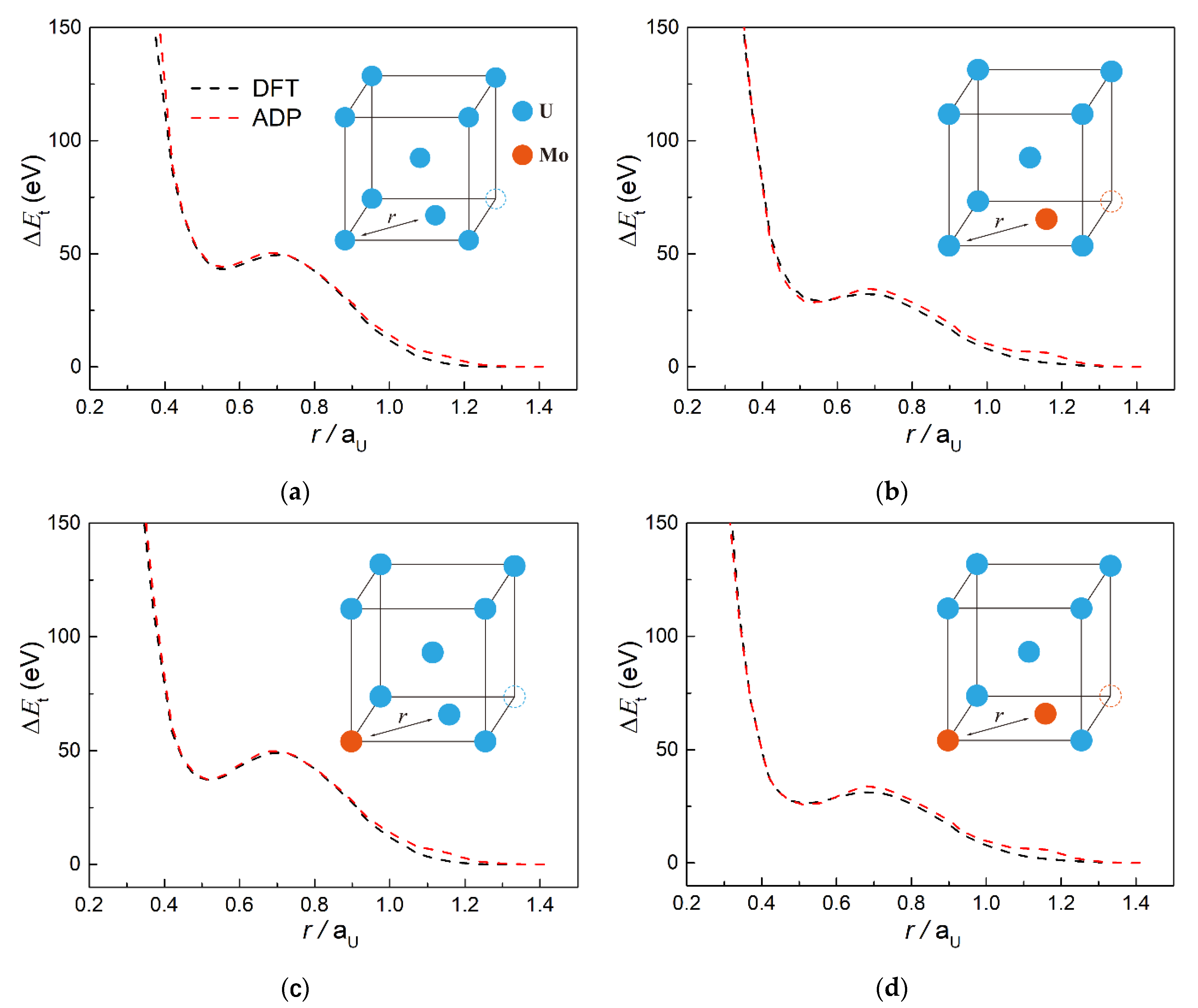

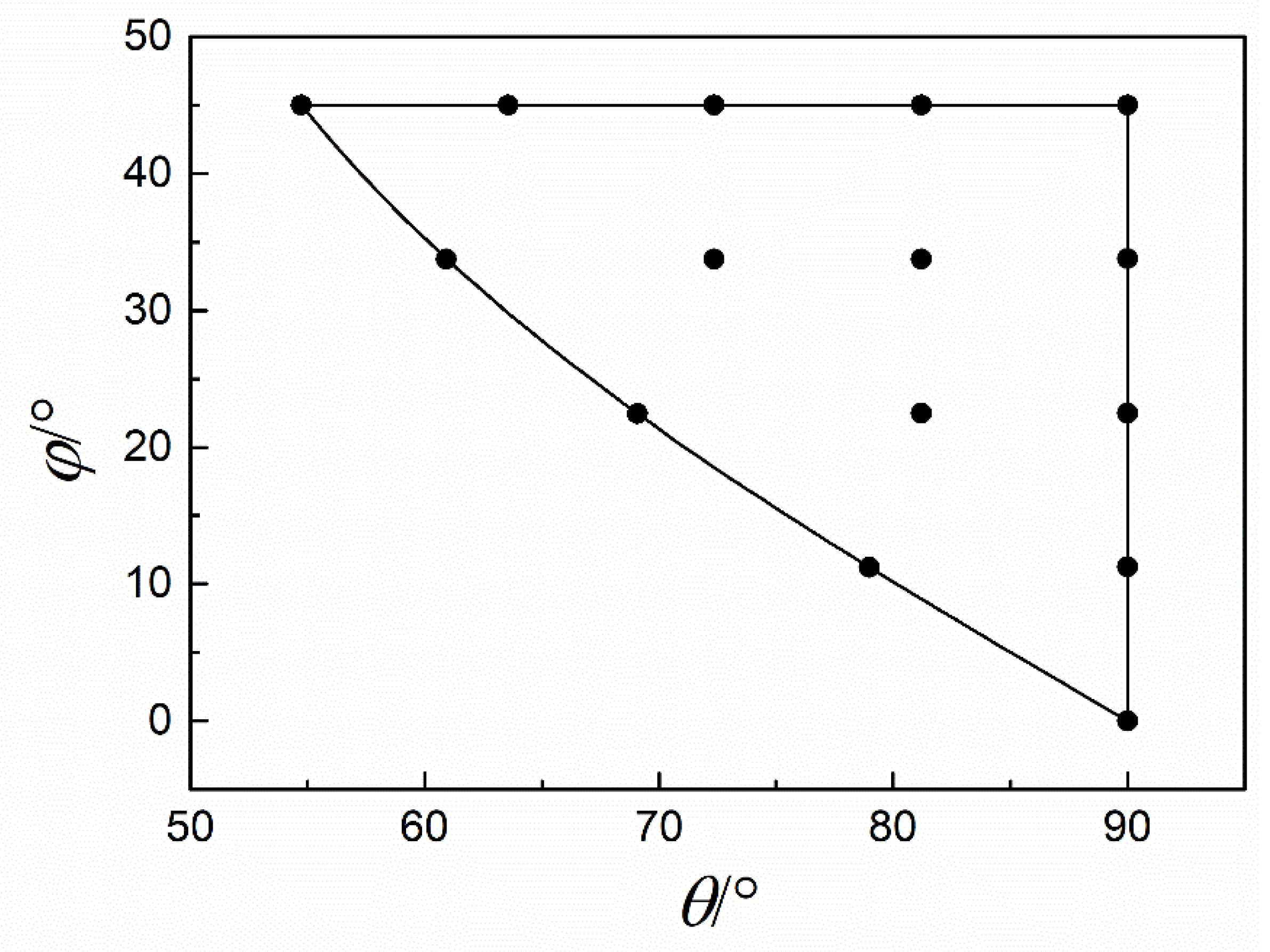

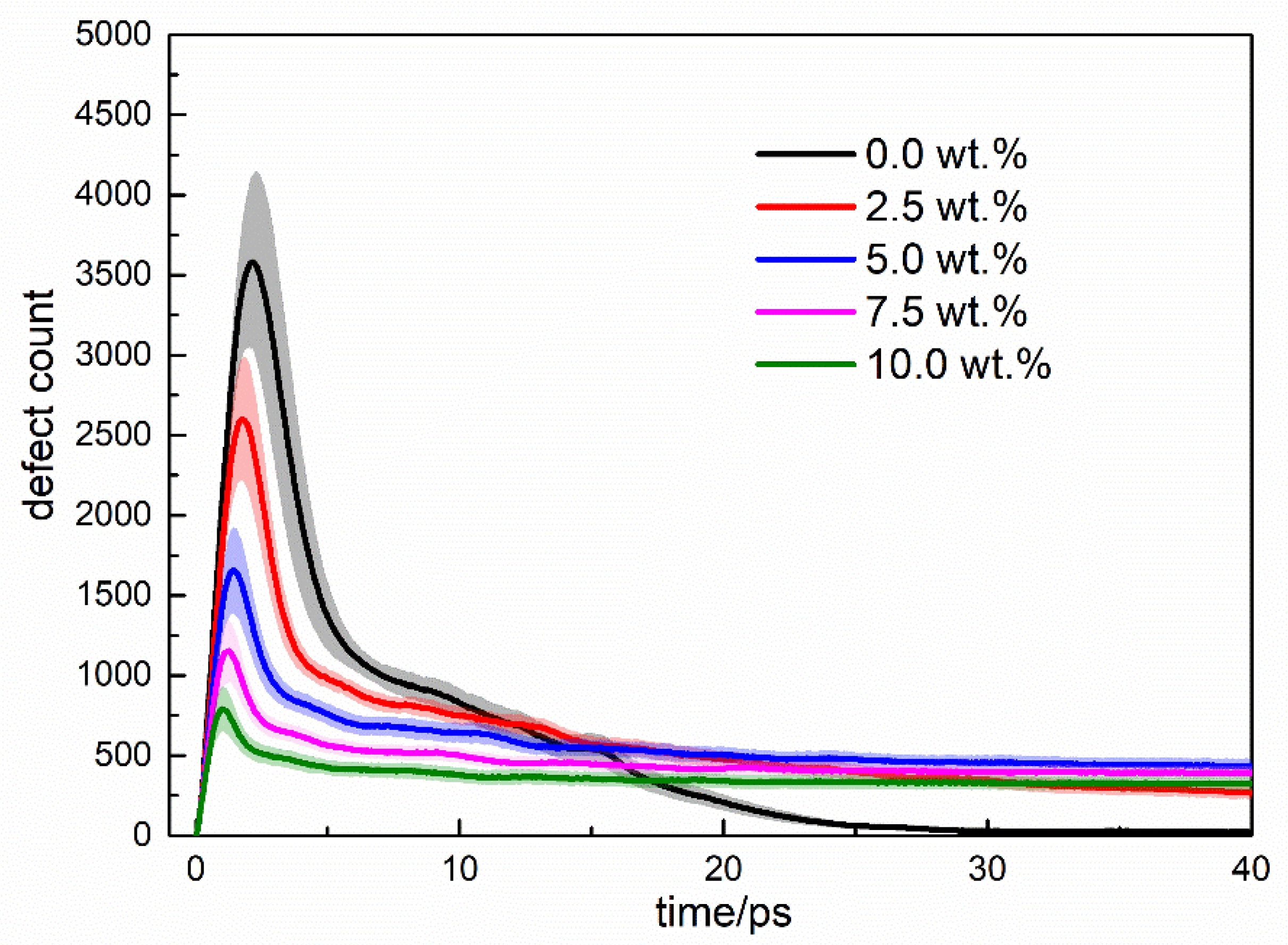
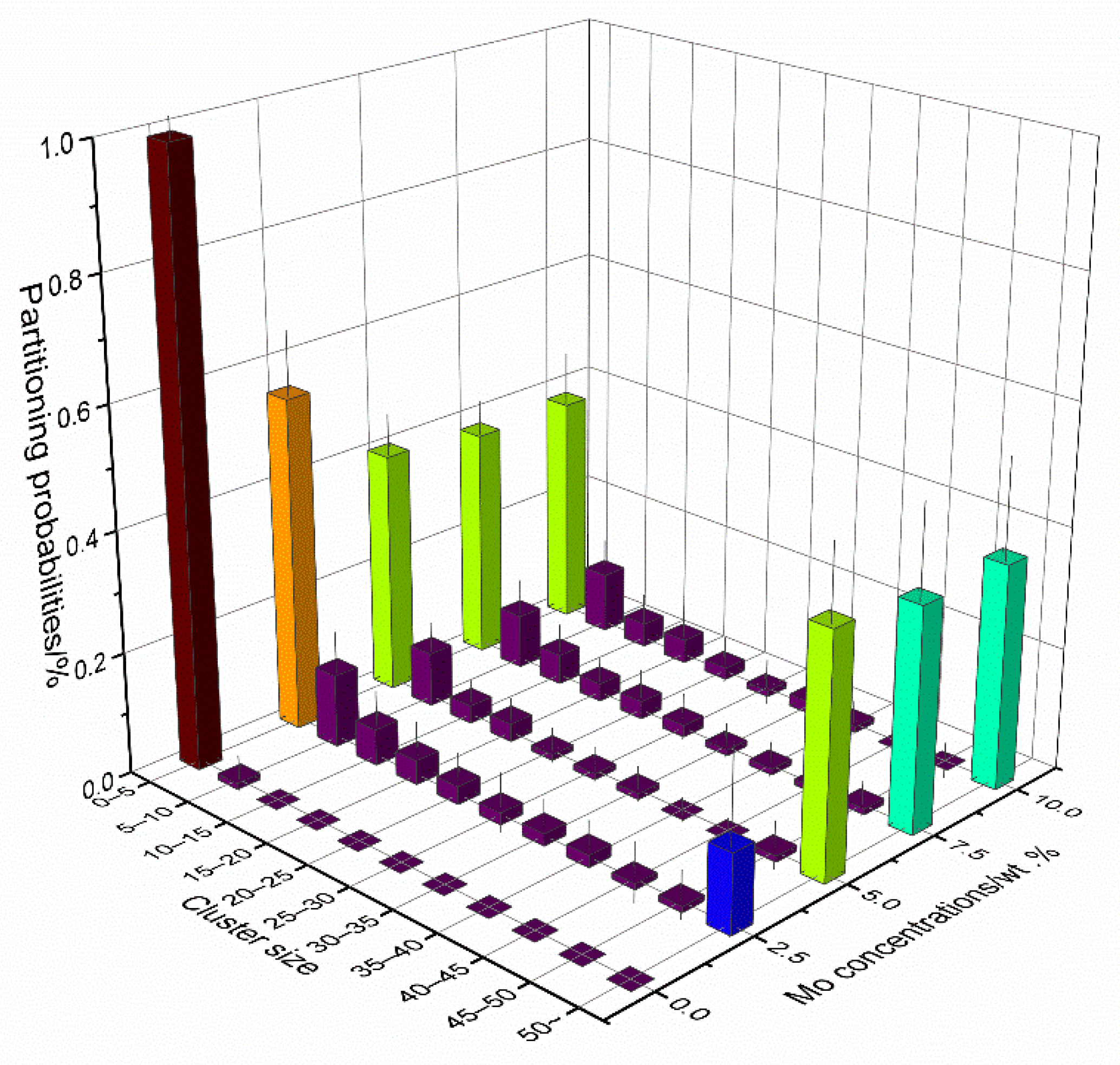
| Parameter | U–U | Mo–Mo | U–Mo |
|---|---|---|---|
| (eV∙Å−3) | −1.41881 | 1.75876 | 6.095612 |
| (eV∙Å−4) | 2.499597 | −3.74227 | −11.667 |
| (eV∙Å−5) | −1.40956 | 2.276131 | 7.291495 |
| (eV∙Å−6) | 0.279328 | −0.42748 | −1.48751 |
| α (eV∙Å−2) | 0.86737 | 0.255577 | - |
| β | −0.88394 | 2.017747 | - |
| (eV1/2) | 0.083778 | 0.369529 | −0.2 |
| (Å) | 2.825854 | 2.590854 | 3.173449 |
| (Å) | 0.151763 | 0.62249 | 0.312741 |
| (eV1/2) | 0.015177 | 0.225399 | 0.2 |
| (Å) | 3.153919 | 2.791784 | 3.208256 |
| (Å) | 0.149995 | 0.186653 | 0.409074 |
| (eV1/2) | 0.133803 | - | −0.2 |
| (Å) | 3.402176 | - | 2.952746 |
| (Å) | 0.359213 | - | 0.167571 |
| (Å) | 4.7 | 4.7 | 4.7 |
| (Å) | 2.7408 | 2.7387 | - |
| Structure | Properties | Present Work | MEAM [22] | ADP [15] | Experiment | FP |
|---|---|---|---|---|---|---|
| -U | (eV/at) | 5.46 | 5.547 | 4.23 | 5.550 [23] | - |
| a (Å) | 2.881 | 2.721 | 2.849 | 2.836 [24] | - | |
| b (Å) | 5.486 | 6.381 | 5.841 | 5.867 [24] | - | |
| c (Å) | 5.221 | 4.858 | 4.993 | 4.935 [24] | - | |
| y | 0.108 | 0.093 | 0.103 | 0.102 [24] | - | |
| B (GPa) | 153 | 143 | 147 | 136 [25] | - | |
| (eV) | 1.17 | 2.597 | - | - | 1.95 [26] | |
| -U | Δ (eV/at) | 0.01 | 0.15 | 0.09 | - | 0.278 |
| a (Å) | 3.479 | 3.463 | 3.52 | 3.47 [27] | 3.455 | |
| C11 (GPa) | 128.2 | 144.0 | 183.6 | - | 103.0 | |
| C12 (GPa) | 124.1 | 49.0 | 92.8 | - | 142.0 | |
| C44 (GPa) | 38.2 | −36.2 | 79.9 | - | 46.0 | |
| (eV) | 1.34 | - | - | - | 1.38 | |
| (eV) | 1.08 | - | - | - | 0.9 |
| Structure | Properties | Present Work | FP | Experiment [28,29,30] |
|---|---|---|---|---|
| bcc-Mo | (eV/atom) | 6.349 | 6.290 | - |
| (Å) | 3.171 | 3.162 | 3.147 | |
| C11 (GPa) | 473.9 | 488.8 | 465 | |
| C12 (GPa) | 143.3 | 146.6 | 176 | |
| C44 (GPa) | 67.0 | 108.3 | - | |
| 2.72 | 2.723 | 2.6–3.2 | ||
| fcc-Mo | Δ (eV/atom) | 0.439 | 0.327 | - |
| (Å) | 4.156 | 4.004 | - | |
| hcp-Mo | Δ (eV/atom) | 0.628 | 0.328 | - |
| (Å) | 2.842 | 2.948 | - | |
| (Å) | 4.212 | 4.263 | - |
| Structure | Properties | Present Work | FP |
|---|---|---|---|
| tetra-U2Mo | (eV/at) | 6.044 | 6.361 |
| (Å) | 3.304 | 3.427 | |
| (Å) | 9.921 | 9.833 | |
| y | 0.329 | 0.328 | |
| bcc-U15Mo | Δ (eV/at) | 0.391 | 0.116 |
| (Å) | 6.861 | 6.84 | |
| C11 (GPa) | 159.3 | 124.4 | |
| C12 (GPa) | 134.7 | 140.6 | |
| P6-U2Mo | Δ (eV/at) | 48.4 | 34.9 |
| (Å) | −0.119 | −0.035 | |
| (Å) | 4.823 | 4.818 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, W.; Lai, W.; Li, J.; Liu, J.; Liu, B. Atomic Simulations of U-Mo under Irradiation: A New Angular Dependent Potential. Metals 2021, 11, 1018. https://doi.org/10.3390/met11071018
Ouyang W, Lai W, Li J, Liu J, Liu B. Atomic Simulations of U-Mo under Irradiation: A New Angular Dependent Potential. Metals. 2021; 11(7):1018. https://doi.org/10.3390/met11071018
Chicago/Turabian StyleOuyang, Wenhong, Wensheng Lai, Jiahao Li, Jianbo Liu, and Baixin Liu. 2021. "Atomic Simulations of U-Mo under Irradiation: A New Angular Dependent Potential" Metals 11, no. 7: 1018. https://doi.org/10.3390/met11071018
APA StyleOuyang, W., Lai, W., Li, J., Liu, J., & Liu, B. (2021). Atomic Simulations of U-Mo under Irradiation: A New Angular Dependent Potential. Metals, 11(7), 1018. https://doi.org/10.3390/met11071018





