Effect of Load Combinations on Distortional Behaviors of Simple-Span Steel Box Girder Bridges

Abstract

When eccentric live loads are applied on the deck overhang of steel-box girder bridges, torsional moments, comprising pure torsional and distortional moments are generated on the box sections. The torsional moment on the bridge girders distorts the box girder cross-sections, inducing additional normal stress components and causing instability of the box girder sections in severe cases. Hence, it is essential to install intermediate diaphragms in the box sections to minimize distortional behaviors. Although the applied live loads are critical parameters that influence intermediate diaphragm spacings, the effects of live load combinations have rarely been addressed in the design of intermediate diaphragm spacings. Thus, load combinations should be evaluated to design the intermediate diaphragm spacing of the box girder bridges more thoroughly. In this study, the load combination effects on the distortional behavior and adequate intermediate diaphragm spacing were evaluated through a finite element analysis (FEA). Composite rectangular box girder bridges with different cross-sectional aspect ratios ($H/B$) and spans ($L$) were analyzed in the parametric study. It was found that the truck load, which represents the concentrated load, significantly influences the distortional warping normal stress, normal stress ratio, and intermediate diaphragm spacing. In addition, the FEA results showed that the controlling load combinations could be varied with the span.

1. Introduction

Steel-box girders exhibit higher torsional rigidity than plate-type girders and have been widely applied in bridge engineering, particularly in the interchanges of urban infrastructures. When eccentric live loads are applied to the deck overhang of a steel-box girder, they generate torsional moments, consisting of pure torsional and distortional moments, on the box sections (Figure 1). The distortional moment comprises distortional warping normal stress components (${\sigma }_{dw}$) and distortional deformation of the box section. Since the distortion may generate unstable cross-section states, resulting in the instability of the box girders, bridge design codes specify the installation of intermediate diaphragms to prevent distortion and excessive distortional stresses in the box section. Conventional provisions of the design code require installed intermediate diaphragms to control distortional stresses to values lower than 5% or 10% of the bending stress.

Since Dabrowski [1] theoretically analyzed the distortion behavior of a box girder, several researchers have contributed to distortional analysis and intermediate diaphragm design techniques to minimize the distortional behavior of box sections. Oleinik and Heins [2] derived differential equations for determining the cross-sectional deformation and conducted a parametric study on straight and curved girder composite bridges subjected to AASHTO truck (72k) loads and dead loads. Composite bridges of 50–150-ft spans were evaluated using a finite difference method. Based on their study, the design equations were included in the AASHTO design guidelines [3]. Sakai and Nagai [4] provided adequate intermediate diaphragm spacing for straight box girder bridges using the BEF (beam on an elastic foundation) analogy for cases where the distortional warping normal stress was limited to 5% of the bending normal stress. The design equations were later adopted in the Hanshin design guidelines [5]. Nakai and Yoo [6] derived design equations for determining the minimum intermediate diaphragm spacing in straight and curved girder bridges based on Nakai and Murayama [7], in which the design live loads specified in the Japan Specification for Highway Bridges [8] were used. Park et al. [9] investigated the adequate spacing of intermediate diaphragms with varying stress ratios for straight box girder bridges based on a beam element. Subsequently, Park et al. [10] presented a nine-degree curved-beam element based on Usami and Koh [11] and Kang and Yoo [12,13]. Based on the finite element analysis (FEA) of a curved beam element, a parametric study on straight and curved girder bridges of 30–100-m spans and 2–4-m widths was conducted for HS20-44 lane loading with a 33% live load impact, specified in an older version of AASHTO [3]. They extended their focus to distortion analyses of multicell box girders and the stiffness design of diaphragms [14,15,16]. Yoo et al. [17] established a procedure for calculating the distortional stresses of the curved tub-girder bridges by adopting an analogous theory of beams on elastic foundations. Lee et al. [18] conducted a parametric study on non-composite simple-span curved box girder bridges and presented simplified design charts. Later, Lee et al. [19] investigated the effects of the girder geometry of simple-span rectangular non-composite steel-box girder bridges. Zhang et al. [20] carried out a parametric study on non-composite girders to evaluate the torsional behavior of curved beams during construction. In their study, the simplified M/r and initial parameter methods were applied to determine the required diaphragm spacing. Ren et al. [21] performed a distortion analysis of cantilever box girders with intermediate diaphragms under concentrated loads using the initial parameter method. Li et al. [22] investigated the distortion behavior of a non-prismatic composite box girder with corrugated webs by solving the governing differential equation. Lee et al. [23] provided adequate intermediate diaphragm spacings for single-cell steel-box girder bridges, considering the cross-sectional aspect ratio; they also presented a simplified design equation based on the span and cross-sectional aspect ratio when the design live loads specified in AASHTO [24] were applied.

Despite the previous studies on intermediate diaphragm spacing, the equations proposed in the literature have not been extensively applied, because constant live loads of different magnitudes were used by different researchers. Although current design codes stipulate various live load combinations for the strength limit and service limit states, the load combinations for the distortional analysis were not defined clearly. Most of the applied load magnitudes and load combinations considered in previous studies were changed in the current design codes. Thus, load combinations should be evaluated in the current design codes to design the intermediate diaphragm spacing of box girder bridges. The aim of this study is to evaluate the distortional behavior and the required intermediate diaphragm spacing of steel-box girder bridges under different load combinations. In this parametric study, the load combinations provided in AASHTO [24] and the Koran Design Standard [25] were evaluated through FEA. Composite rectangular box girder bridges with different cross-sectional aspect ratios ($H/B$) and spans ($L$) were considered in a parametric study. Hence, the truck load, which represents a concentrated load, significantly influences the distortional warping normal stress, normal stress ratio, and intermediate diaphragm spacing. Additionally, the FEA results showed that the governing load combinations could be varied with the span.

2. Design Provisions for Box Girder Bridges

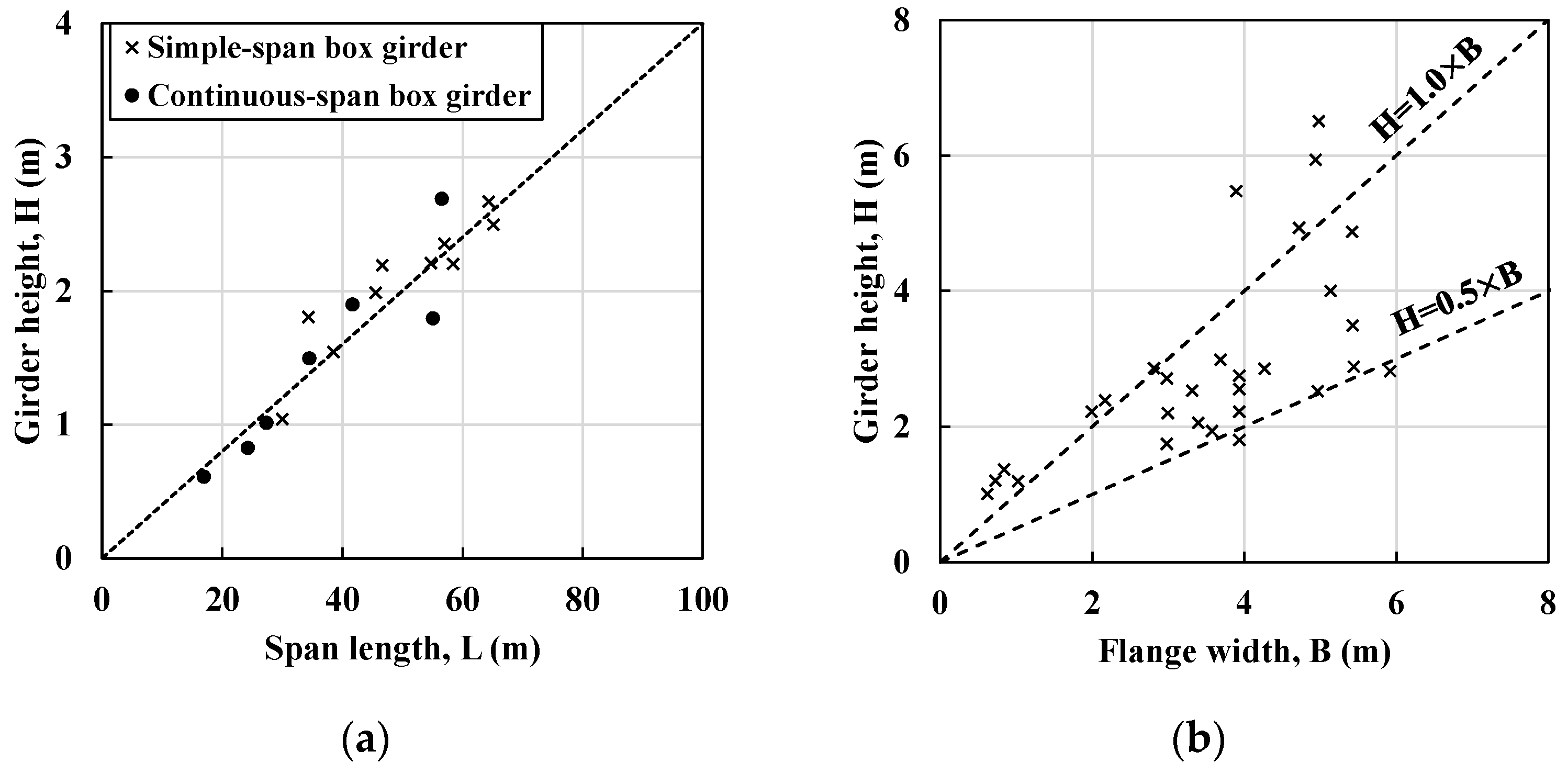
2.1. Design of Intermediate Diaphragm Spacing

The design provisions for intermediate diaphragm spacing ($L_d$) have been widely established in steel-box girder bridge design. According to article 6.7.4.3 of AASHTO [24], intermediate diaphragms must be installed to ensure that the distortional warping normal stress (${\sigma }_{dw}$) does not exceed 10 % of the bending normal stress (${\sigma }_b$). The maximum intermediate diaphragm spacing is also limited to 12 m (40 ft). In addition, the transverse bending normal stress (${\sigma }_t$) from the cross-section distortion for the strength limit state is limited to 138 MPa (20 ksi) in the C6.7.4.3 commentary. The design provisions of Article 6.7.4.3 of AASHTO [24] are summarized as expressed in Equation (1):

$$L_d\le 12 \mathrm{m} \left(\approx 40 ft\right), \frac{{\sigma }_{dw}}{{\sigma }_b}\le 0.1$$

(1)

where $L_d$ is the intermediate diaphragm spacing, ${\sigma }_{dw}$ is the distortional warping normal stress, ${\sigma }_b$ is the bending normal stress, and ${\sigma }_{dw}/{\sigma }_b$ is the normal stress ratio.

The Hanshin Guideline [5] stipulates design equations for calculating the adequate intermediate diaphragm spacing ($L_d$) of straight box girder bridges. In these design guidelines, the normal stress ratio (${\sigma }_{dw}/{\sigma }_b$) is limited to a maximum value of 5%. Moreover, the transverse bending stress (${\sigma }_{ts}$) from the cross-sectional distortion is limited to 4.9 MPa. The recommended minimum and maximum intermediate diaphragm spacings ($L_d$) are 6 and 20 m for spans shorter than 60 m and 160 m or longer, respectively. The design equations are expressed in Equation (2):

$$L_d=\{\begin{array}{ccc}6 \mathrm{m}& & for L<60 \mathrm{m}\\ \left(0.14L-2.4\right) \mathrm{m}& & for 60 \mathrm{m}\le L\le 160 \mathrm{m}\\ 20 \mathrm{m}& & for L>160 \mathrm{m}\end{array}$$

(2)

where $L_d$ is the intermediate diaphragm spacing of single-cell straight box girder bridges, and $L$ is the span.

The Korean Highway Bridge Design Code [26] presents a design equation similar to that of the Hanshin Guideline for designing intermediate diaphragm spacings. The design equations for the intermediate diaphragm spacing of the straight box bridges, according to Article 3.8.9.2, are expressed in Equation (3):

$$L_d=\{\begin{array}{ccc}6 \mathrm{m}& & L\le 50 \mathrm{m}\\ \left(0.14L-1.0\right) \mathrm{m}\le 20 \mathrm{m}& & L>50 \mathrm{m}\end{array}$$

(3)

Subsequently, the recent Korean Design Standard [25] stipulates in Article 4.11.3.5 that the box girder bridge must exhibit sufficient strength and rigidity to resist distortion, and an intermediate diaphragm with adequate spacing must be installed based on the structural analysis results.

2.2. Design Live Loads and Load Combinations

In previous studies on the adequate intermediate diaphragm spacing ($L_d$) of box girder bridges, design load combinations were practically applied by combining the concentrated and lane loads simultaneously. However, the current design codes worldwide recommend various load combinations with different live load magnitudes.

Table 1. Design live loads and load combinations specified in the design codes and applied load cases (LC) in this study.

Reference	Design Live Load	Load Combination (LC)	Applied Load Cases (LC) in This Study	Impact Coefficient
AASHTO (2020)	Design truck: 72 kips Design tandem: 50 kips Design lane: 0.64 k/ft	(1) Design truck with variable axle spacing + lane (2) Design tandem + lane	LC1: Design truck + lane load	0.33
AASHTO (1993)	Concentrated load: 18 kips Design lane: 0.64 k/ft	(1) Combined load (Concentrated + lane loads)	-	0.33
KDS (2016)	Design truck: 510 kN Design lane w = 12.7 kN/m for L ≤ 60 m w = 12.7(60/L)0.18 kN/m for L > 60 m	(1) 100% design truck (2) 75% design truck + lane load	LC2: 75% design truck + lane load LC3: 100% design truck	0.25
KMLIT (2010)	Design truck: 423 kN Design lane w = 12.7 kN/m Pm = 108 kN for moment Pm = 156 kN for shear	(1) Design truck (2) Design lane	-	15/(40 + L) ≤0.3

lists the design live loads and load combinations provided in different design codes. The older version of the AASHTO design code [3] stipulated the HS20-44 live load for bridge design, which comprises a concentrated live load of 18 kips and distributed live load of 0.64 k/ft. In the more recent AASHTO design standard [24], the design live loads comprise a design lane load of 0.64 k/ft with two different concentrated live loads of a 72-kip truck load and a 50-kip design tandem load. The live loads specified in the Korean Highway Bridge Design Code [26] recommends a 423-kN design truck load or 12.7-kN/m design lane load with concentrated loads (108 kN for the moment and 156 kN for the shear force), However, the current Korean Design Standard [25] specifies two different load combinations, consisting of a 100% design truck load (510 kN) and a 75% design truck load (382.5 kN) with a design lane load (12.7 kN/m). Since the effects of the current design load combinations have not been analyzed in detail, the effect of the live load magnitude and different load combinations should be evaluated to achieve an excellent preliminary design of intermediate diaphragms. Therefore, this study was focused on the parametric analysis of steel-box girder bridges under different live loads through three-dimensional (3D) FEA.

3. FEA

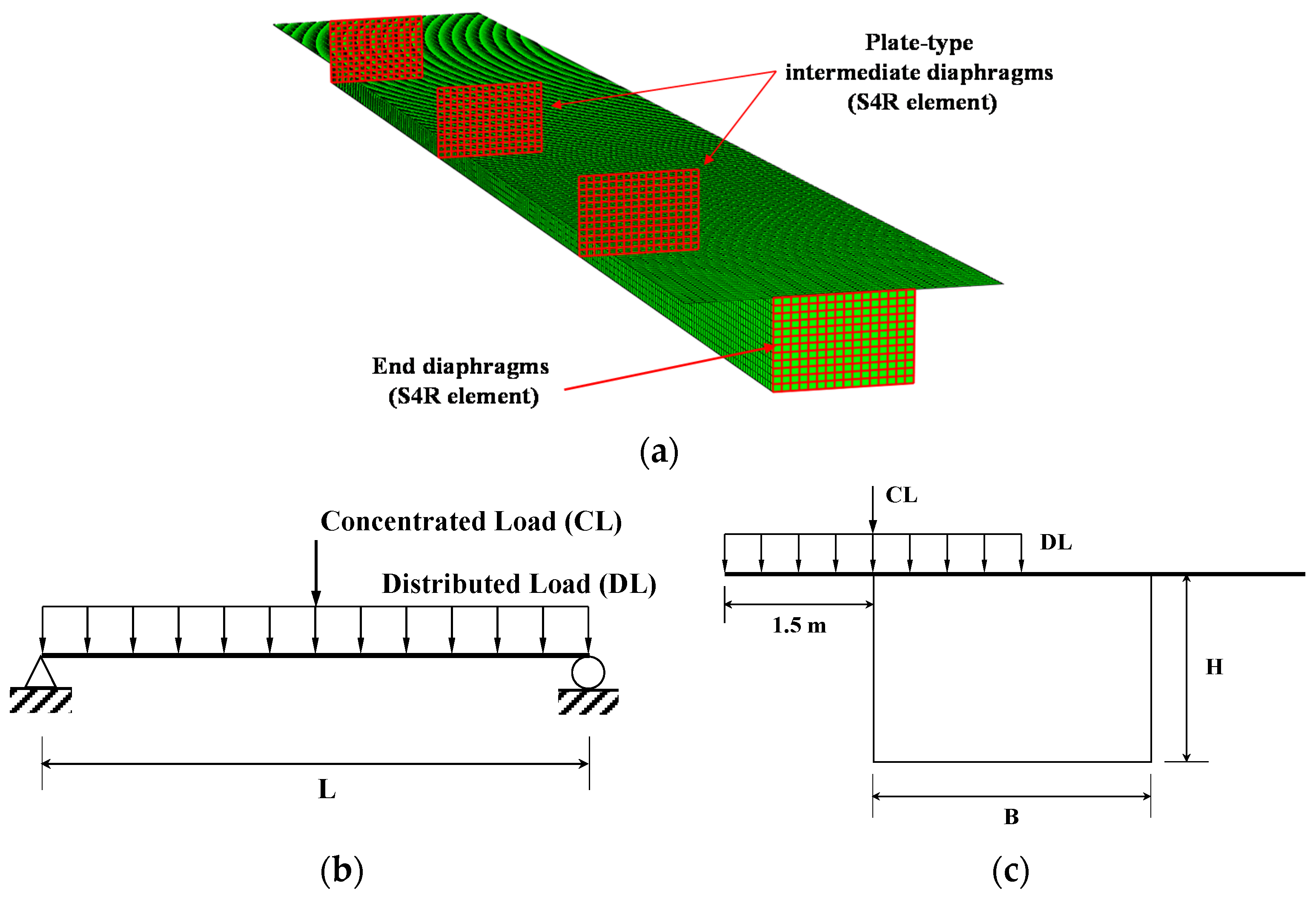
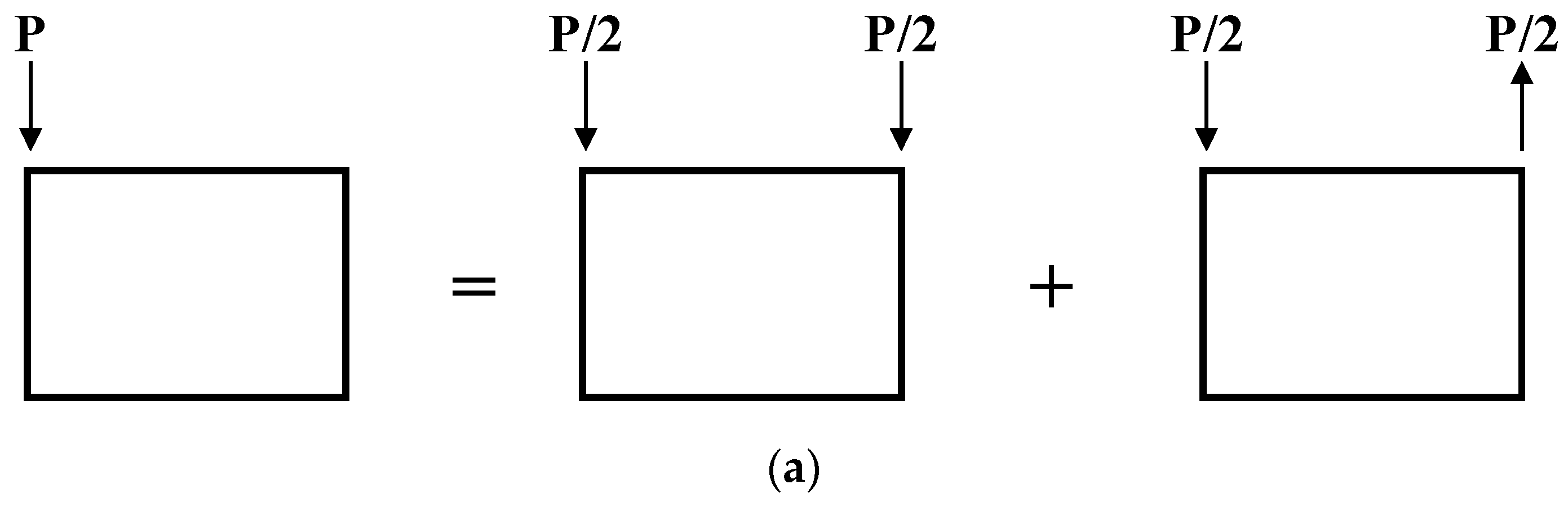
3.1. Overview of FEA

FEA was performed using ABAQUS [27] to evaluate the distortional warping normal stress and intermediate diaphragm spacing for different live loads. The composite box girder with plate-type intermediate diaphragms was modeled using a 3D shell element (S4R) (Figure 2). The box girders under simply supported the boundary conditions with torsional constraints to prevent overturning induced by the torsional moment at each end, which was free to undergo warping at each end. The applied live loads analyzed in this study consisted of load combinations of both trucks and lane loads (LC1 and LC2) and design truck load (LC3), as listed in Table 1. Load cases 1 and 2 (LC1 and LC2) represent the cases of the combined truck and lane loads specified in AASHTO [24] and the Korean Design Standard [25], respectively, whereas load case 3 (LC3) represents the case of the design truck load specified in the Korean Design Standard [25].

The concrete slab was assumed to have a 1.5-m overhang length with a 200-mm deck thickness ($t_c$). All live loads were applied along the span at the web locations. The effects of the dead load from the concrete deck were also included in the FEA results.

In this study, an elastic analysis for the bridge models was performed using Young’s modulus of 205,000 MPa for the steel-box girders and 25,000 MPa for the concrete deck. Poisson’s ratio of 0.3 for the steel and 0.16 for the concrete deck was used for the analysis. To simulate a fully composite action of the box girder bridges, all the structural components, such as the box girder and concrete decks, were merged so that no slip behavior between the concrete deck and box girder could occur.

3.2. Parameters for FEA Models

The box section dimensions and spans ($L$) were determined based on practical bridge data obtained from the Korean Design Manual [28] to establish the FEA models. Typically, the girder height ($H$) and span ($L$) are critical design parameters for designing the stiffness of the entire bridge system. An appropriate girder height ($H$) should be selected to prevent excessive girder deflections during construction, and it can be determined based on the span ($L$). In this study, the girder height ($H$) was assumed to be 1/25 times the span ($L$) to satisfy the provisions of AASHTO [24] and KDS [25] and to prevent excessive vertical deflection. Additionally, the span specified in the design codes [24,25] yielded more reasonable calculated values than the practical bridge data shown in Figure 3a.

Different design cases could be analyzed to determine the flange width of the box sections, depending on parameters, such as the total number of lanes, maximum deck width, and purpose of the bridges. In this study, the flange width was determined based on practical design cases for steel girder bridges presented in the Korea Bridge Design Manual [28]. Based on Figure 3b, a height-to-flange width ratio ($H/B$) of 0.5–1 was adopted for the parametric study.

Table 2. Dimensions of the box girder models for the FEA (unit: m).

L	H (=1/25L)	H/B	B	No. Diaphragms	tf	tw	tc
20	0.8	0.5	1.6	1 2 4 6 8 10	0.03	0.012	0.2
30	1.2		2.4
40	1.6		3.2
60	2.4		4.8
80	3.2		6.4
20	0.8	0.7	1.2
30	1.2		1.8
40	1.6		2.4
60	2.4		3.6
80	3.2		4.8
20	0.8	1.0	0.8
30	1.2		1.2
40	1.6		1.6
60	2.4		2.4
80	3.2		3.2

lists the dimensions of the box girder models used for the FEA. The thickness of the concrete ($t_c$), the thickness of the flange ($t_f$), and web ($t_w$) of the box girder were chosen as 200 mm, 30 mm, and 12 mm, respectively. Based on the literature [23], as the effects of the flange thickness on adequate intermediate diaphragm spacing were relatively marginal compared to the $H/B$ ratio, the effects of the flange thickness were not considered in this parametric study.

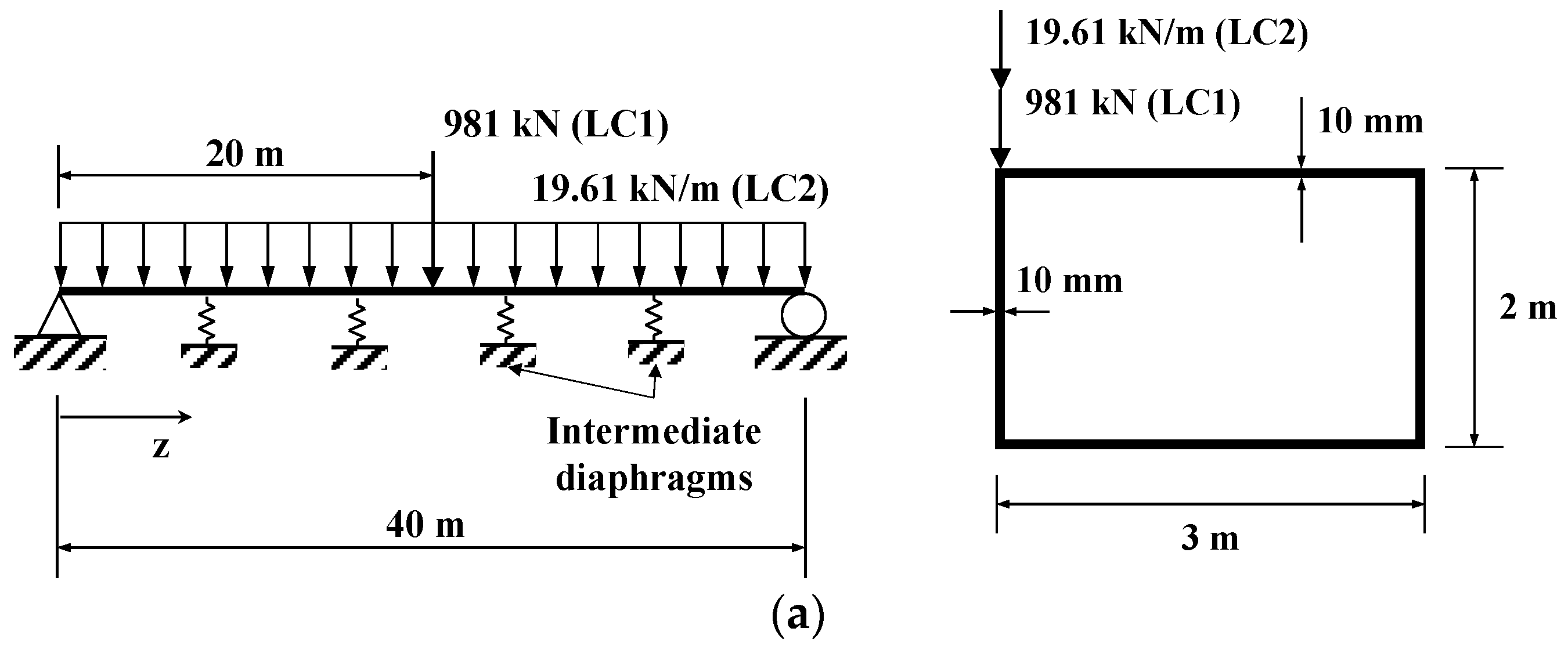
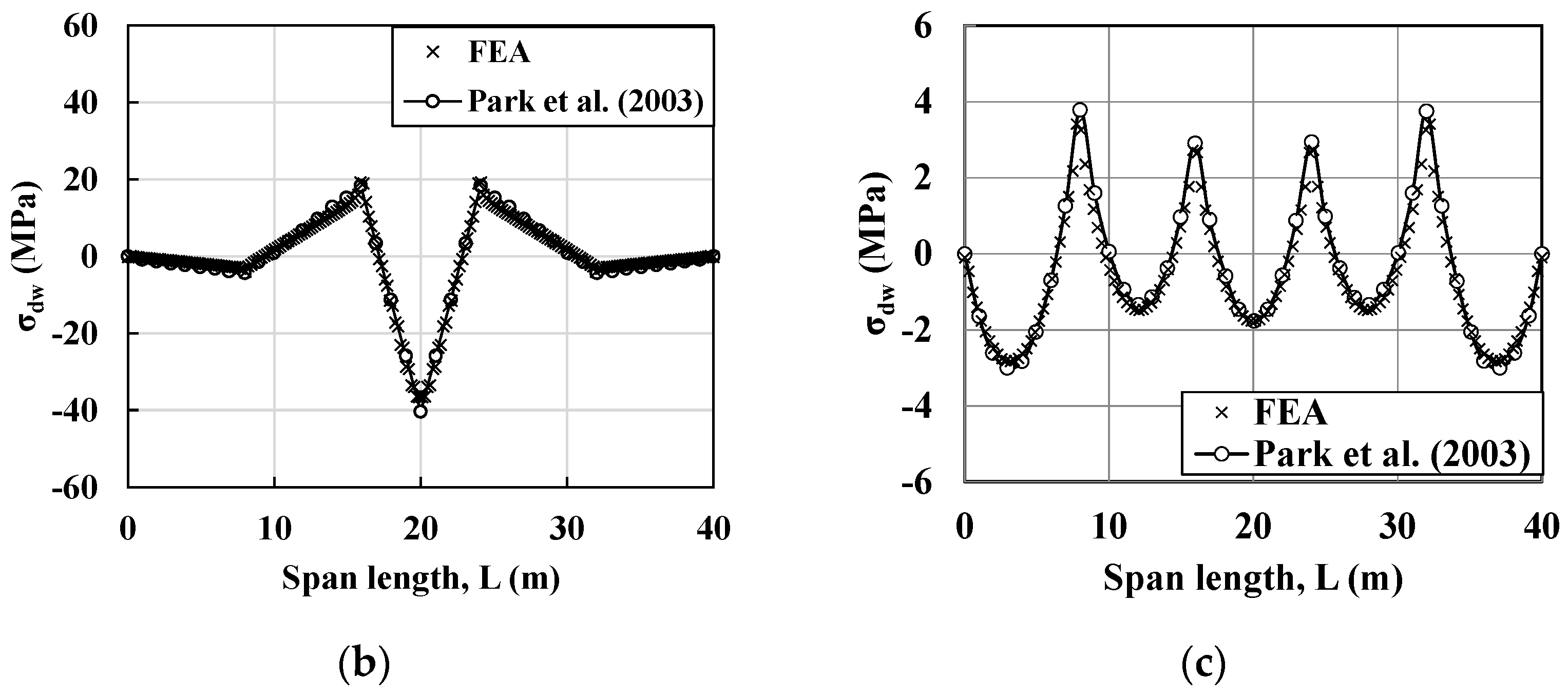
3.3. Verification of FEA

Before the load combination effects on the distortional behaviors of simple-span box girder bridges were evaluated, the FEA was verified using analytical data obtained from the literature. Park et al. [9] formulated nine degree-of-freedom beam elements to analyze the distortional behaviors of box girder bridges. An example of an FEA model of a box girder under eccentric loading is depicted in Figure 4. The model had a 40-m span with a 3-m flange width and 2-m girder height. The flange and web panels were 10 mm thick. A 981-kN concentrated load was applied at the box section edge in the middle of the span. This concentrated load had an eccentricity of 1.5 m from the centroid of the box section. Simply supported boundary conditions for flexure were adopted with torsional constraints at each end to prevent the overturning of the girder. A fine mesh with 16 elements along the flange width was used, and the same mesh size was adopted for the entire box girder modeling. The 3D FEA models established in this study showed good agreement with the analysis results reported in the literature (Figure 4b).

To achieve convergency of the FEA results, the fine mesh size, which is sixteen element numbers along the flange, was used based on the sensitivity analysis. The same mesh sizes along both longitudinal directions of the girders and vertical direction (web line) were used. The sensitivity analysis results are presented in Figure 5.

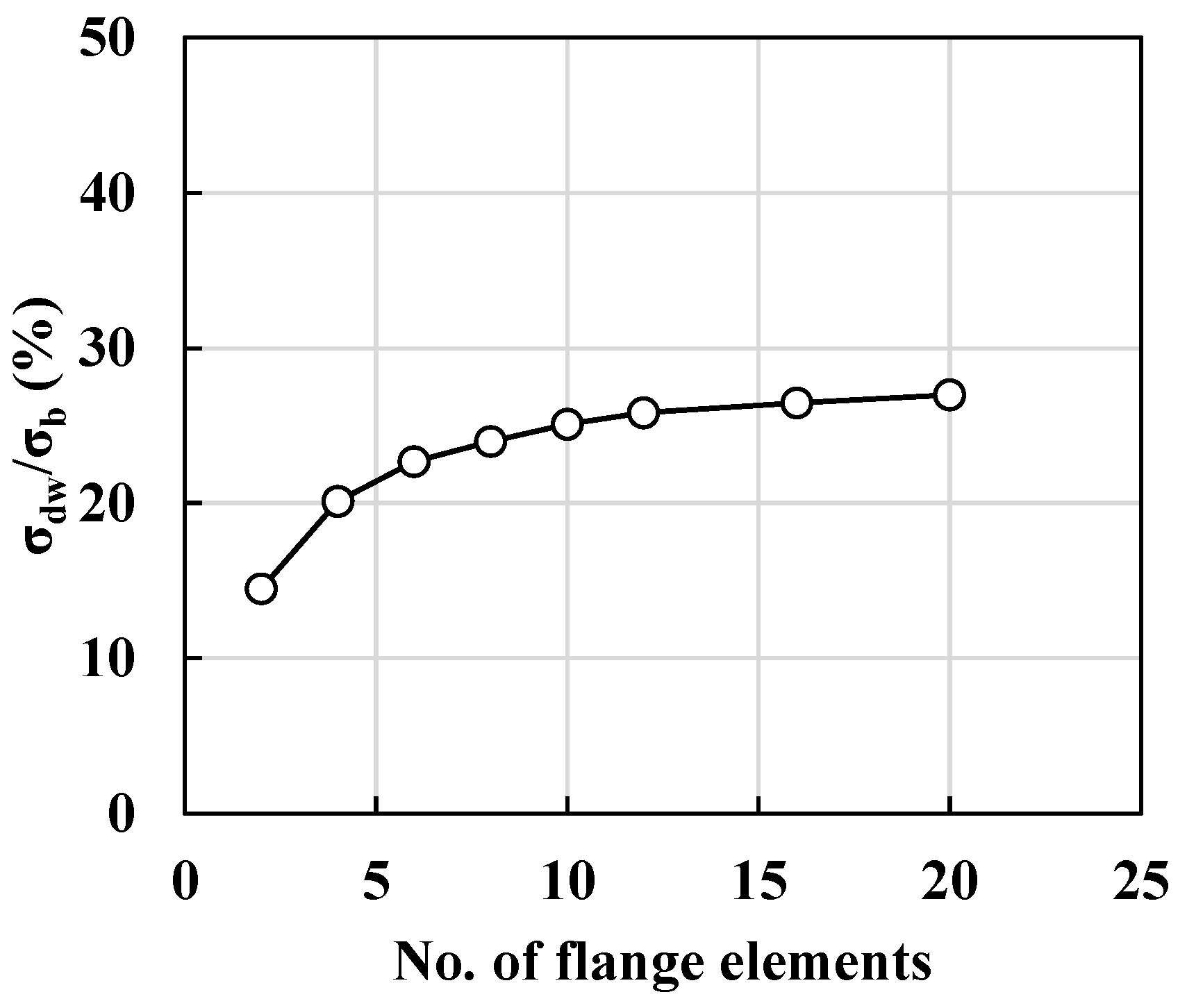
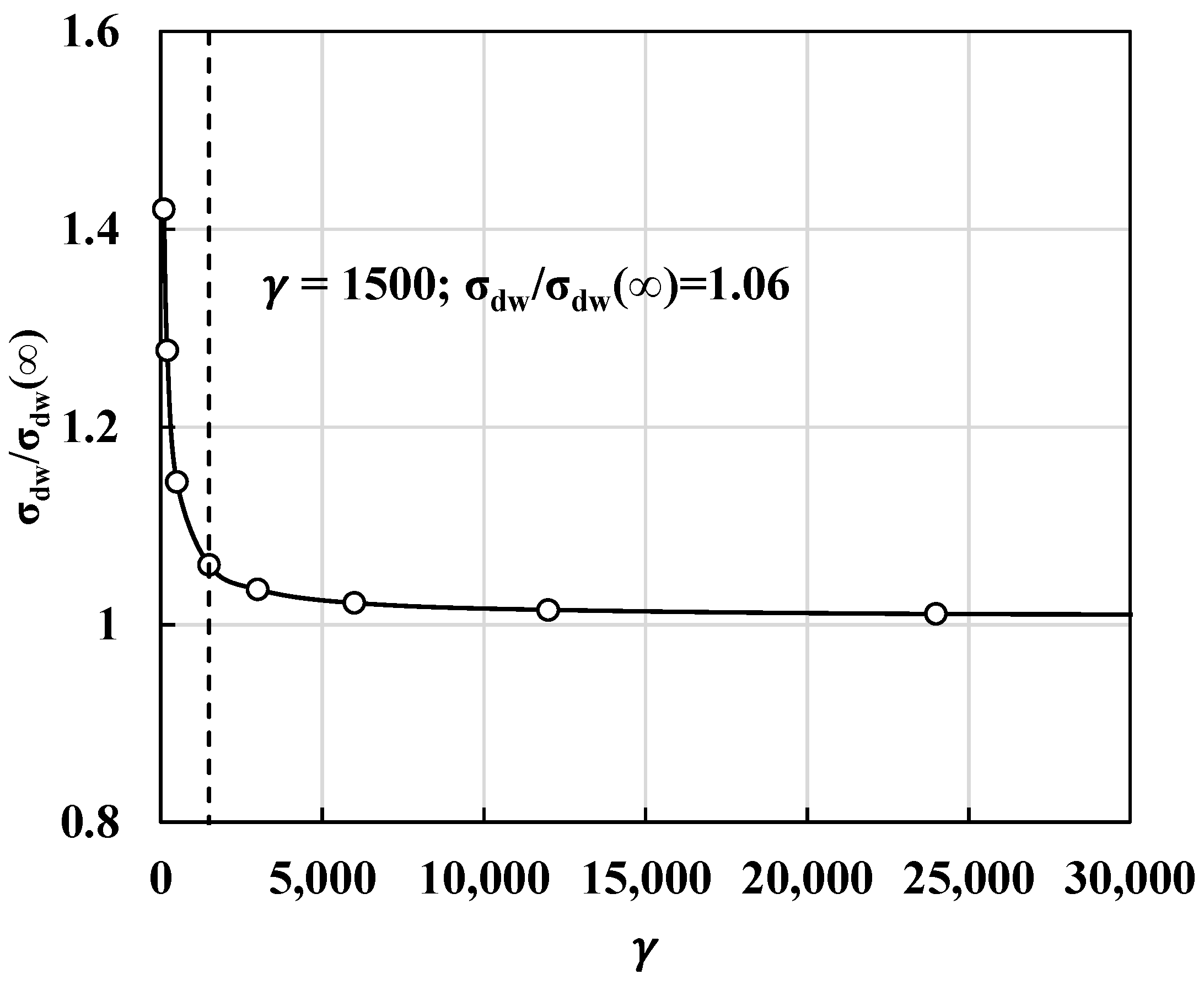
3.4. Stiffness of Intermediate Diaphragms Used for FEA Models

Intermediate diaphragms require sufficient rigidity to control distortional behavior. According to a previous study [6], the rigidity of intermediate diaphragms should be 1500 times higher than those of the box section between adjacent intermediate diaphragms, as expressed in Equation (4). Thus, the diaphragm thickness of each box girder model for the parametric study was determined using Equation (5). An example of the diaphragm stiffness results obtained through the FEA is shown in Figure 6.

$$\gamma =\frac{K_d}{K_{dw}{L}_d}\ge 1500$$

(4)

$$t_d=1500\frac{K_{dw}{L}_d}{GBH}$$

(5)

where

$$\begin{gathered} K_d=G{t}_{d}BH \\ {K}_{dw}=\frac{24E{I}_w}{{\alpha }_{0}H} \\ {\alpha }_0=1+\frac{\frac{2B}{H}+\frac{3\left(I_u+I_l\right)}{I_w}}{\frac{I_u+I_l}{I_w}+\left(\frac{6H}{B}\right)\left(\frac{I_u{I}_l}{I_w^2}\right)} \end{gathered}$$

In Equations (4) and (5), $K_{dw}$ is the distortional stiffness per unit length; $K_d$ is the distortional rigidity of the plate-type intermediate diaphragm; $E$ is the modulus of elasticity; $G$ is the shear modulus; $I_u$, $I_l$, and $I_w$ are the geometric moments of inertia of the upper flanges, lower flange, and web, respectively; $H$ is the web height; and $t_d$ is the intermediate diaphragm thickness.

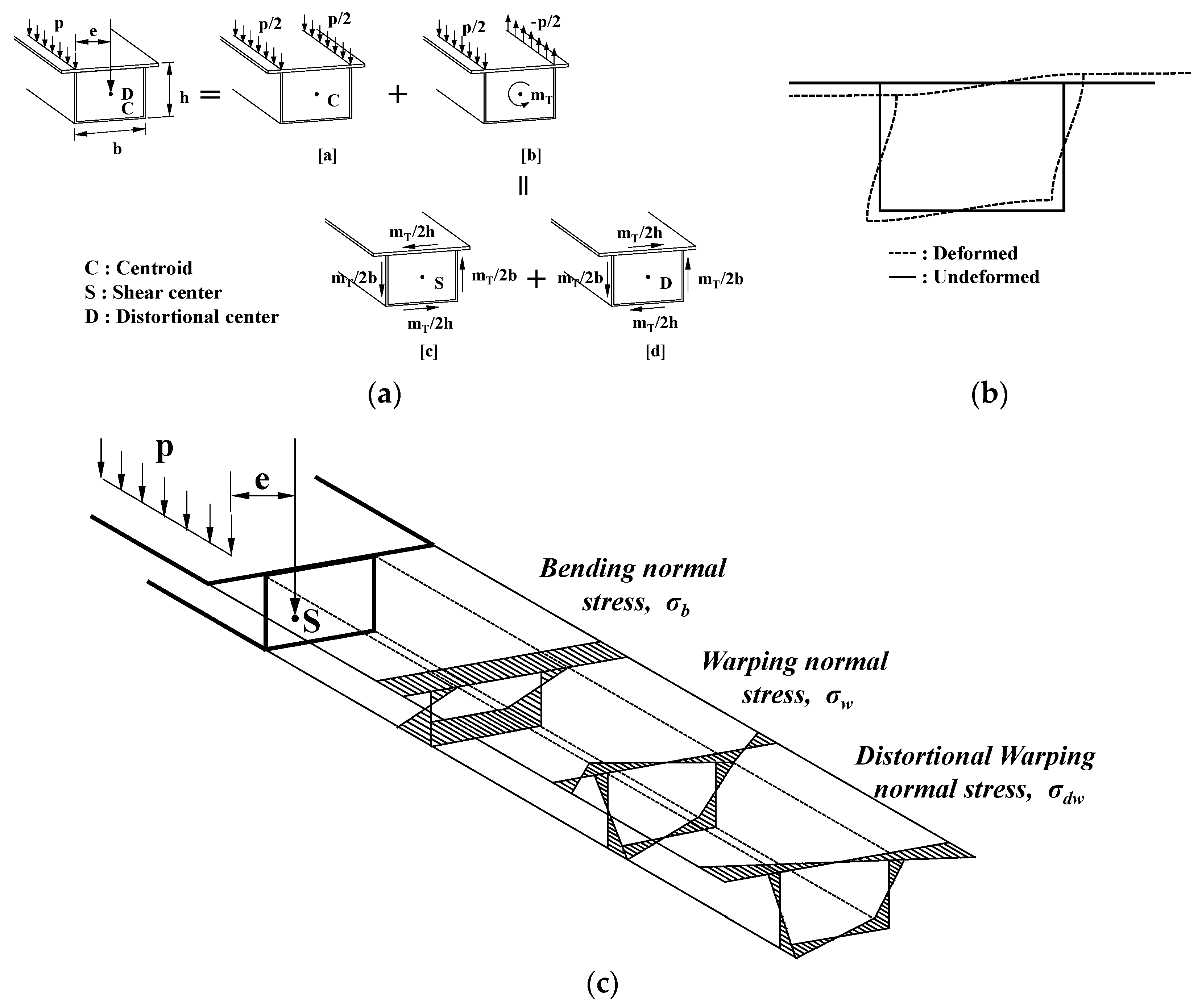
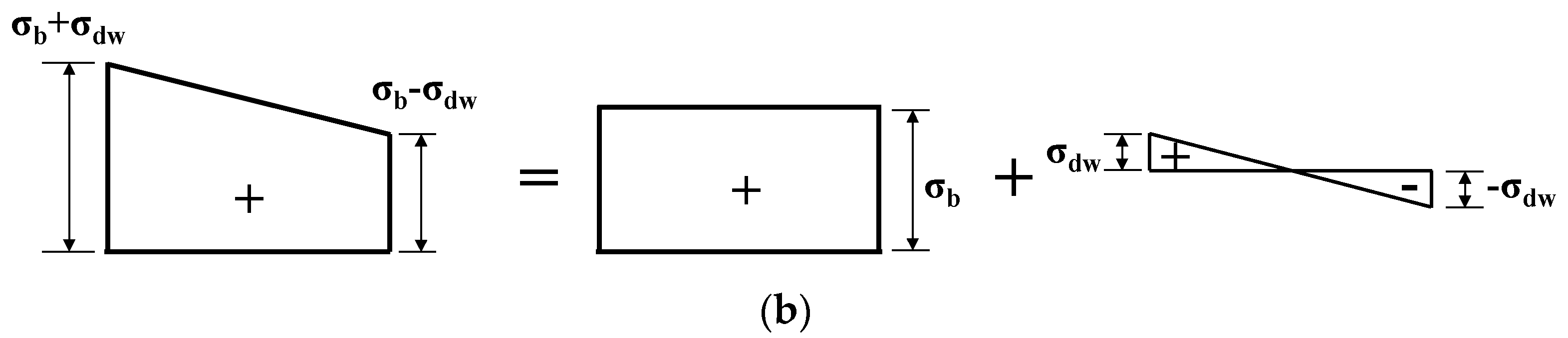
3.5. Estimated Distortional Warping Normal Stresses and Normal Stress Ratios

The distortional warping normal stress components developed at the bottom flanges were obtained from the FEA results. The components were determined by decomposing the normal stress resultants into the bending normal stress and distortional warping normal stress (Figure 7). The bending normal stress (${\sigma }_b$) could be obtained by calculating the average normal stress between each outer end of the bottom flanges, and the differences between the normal stress of each tip and the assumed bending normal stress were defined as the distortional warping normal stress (${\sigma }_{dw}$). Since the normal stress magnitude generated by pure torsion was negligible, the calculation process could yield reasonable distortional warping normal stress (${\sigma }_{dw}$) values.

The normal stress ratio ($R$) could be determined using the assumed distortional warping normal stress (${\sigma }_{dw}$). $R$ was obtained by calculating the sum of the distortional warping normal stresses divided by the sum of the bending normal stress from the self-weight and applied loads. The $R$-value should be less than 5% or 10%, depending on the design codes used, as expressed in Equation (6):

$$R=\frac{{\sigma }_{dw}}{{\sigma }_b}=\frac{{\sigma }_{dw,cl}+{\sigma }_{dw,dl}}{{\sigma }_{b,s}+{\sigma }_{b,cl}+{\sigma }_{b,dl}}\le 5\% \mathrm{or} 10\%$$

(6)

where ${\sigma }_{dw,cl}$ is the distortional warping normal stress generated by concentrated loads, ${\sigma }_{dw,dl}$ is the distortional warping normal stress induced by distributed loads, ${\sigma }_{b,sw}$ is the bending normal stress generated by the self-weight, ${\sigma }_{b,cl}$ is the bending normal stress produced by the concentrated load, and ${\sigma }_{b,dl}$ is the bending normal stress induced by the distributed load.

4. Evaluation of Analysis Results

4.1. Distortional Warping Normal Stress Based on FEA Results

Figure 8 shows the normal stress ratios (${\sigma }_{dw}/{\sigma }_b$) when different loads were combined, considering the intermediate diaphragm spacing ($L_d$), cross-sectional aspect ratio ($H/B$), and span ($L$). For the analysis, three load combinations, i.e., LC1, LC2, and LC3 listed in Table 1, were applied. All the FEA results in Figure 8 show similar trends of normal stress ratios according to the span length and the intermediate diaphragm spacing. The FEA results in Figure 8 were analyzed to provide more thorough analysis results considering the effects of the load combinations in the following sections. Figure 9 shows an example of distortional warping normal stress distributions along the span when LC1 is applied. In this example, bridges with a 40-m span and 0.7 $H/B$ with a varying number of diaphragms ($N$) were evaluated. The distortional warping normal stresses (${\sigma }_{dw}$) under each loading condition, comprising concentrated and distributed loads, were considered. The maximum distortional warping normal stresses under the design truck load were higher than those of the lane loads. Under concentrated loads, the maximum distortional warping normal stress (${\sigma }_{dw}$) existed at the midspan where the concentrated loads were applied, but the maximum stress under distributed loads existed near the diaphragm locations. A detailed analysis is presented in the following sections. As indicated in Figure 9, the maximum distortional stress values with respect to the different load types vary depending on the types of the design loads. Thus, the evaluation of the effects of the load combinations specified in the current design standards is necessary to provide a thorough analysis for the practical applications that were not mentioned in the literature.

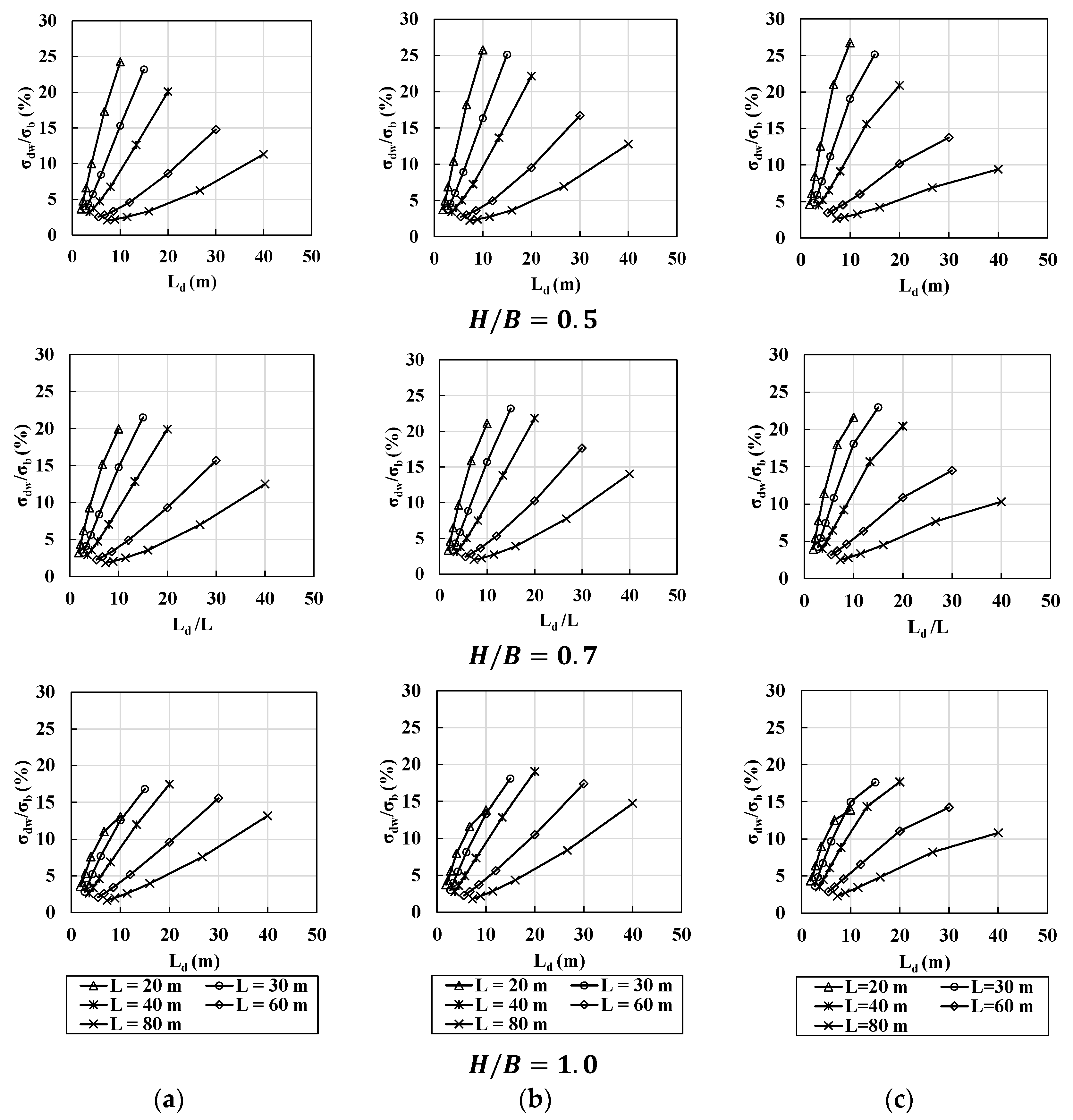
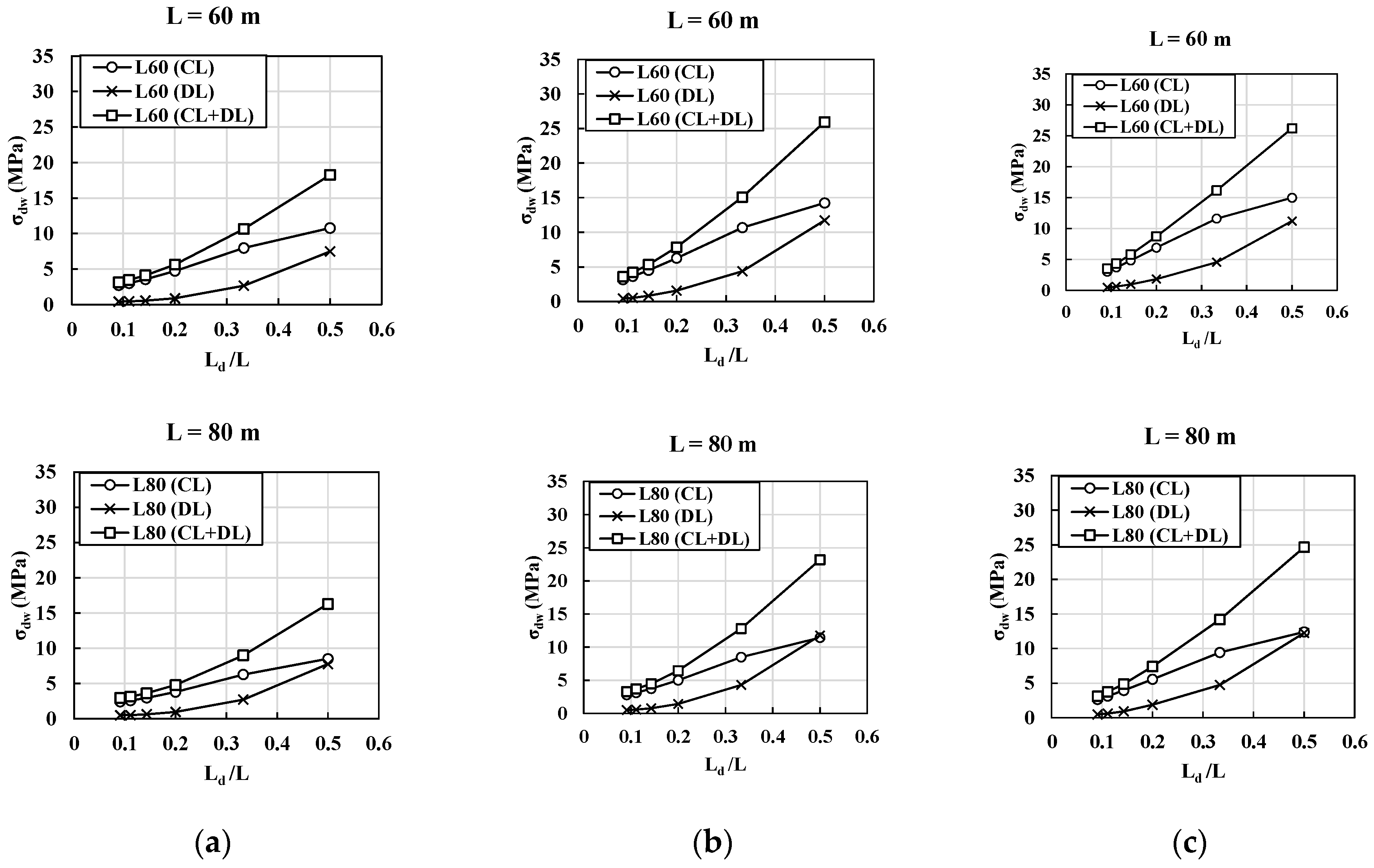
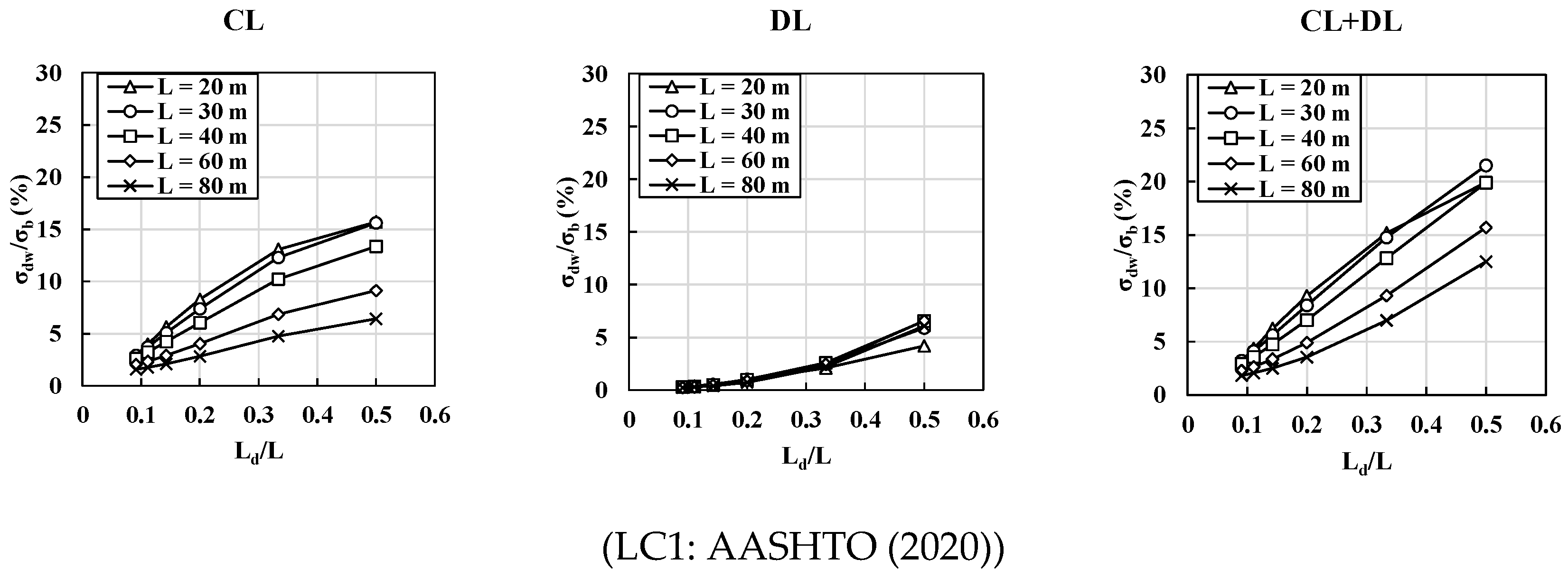
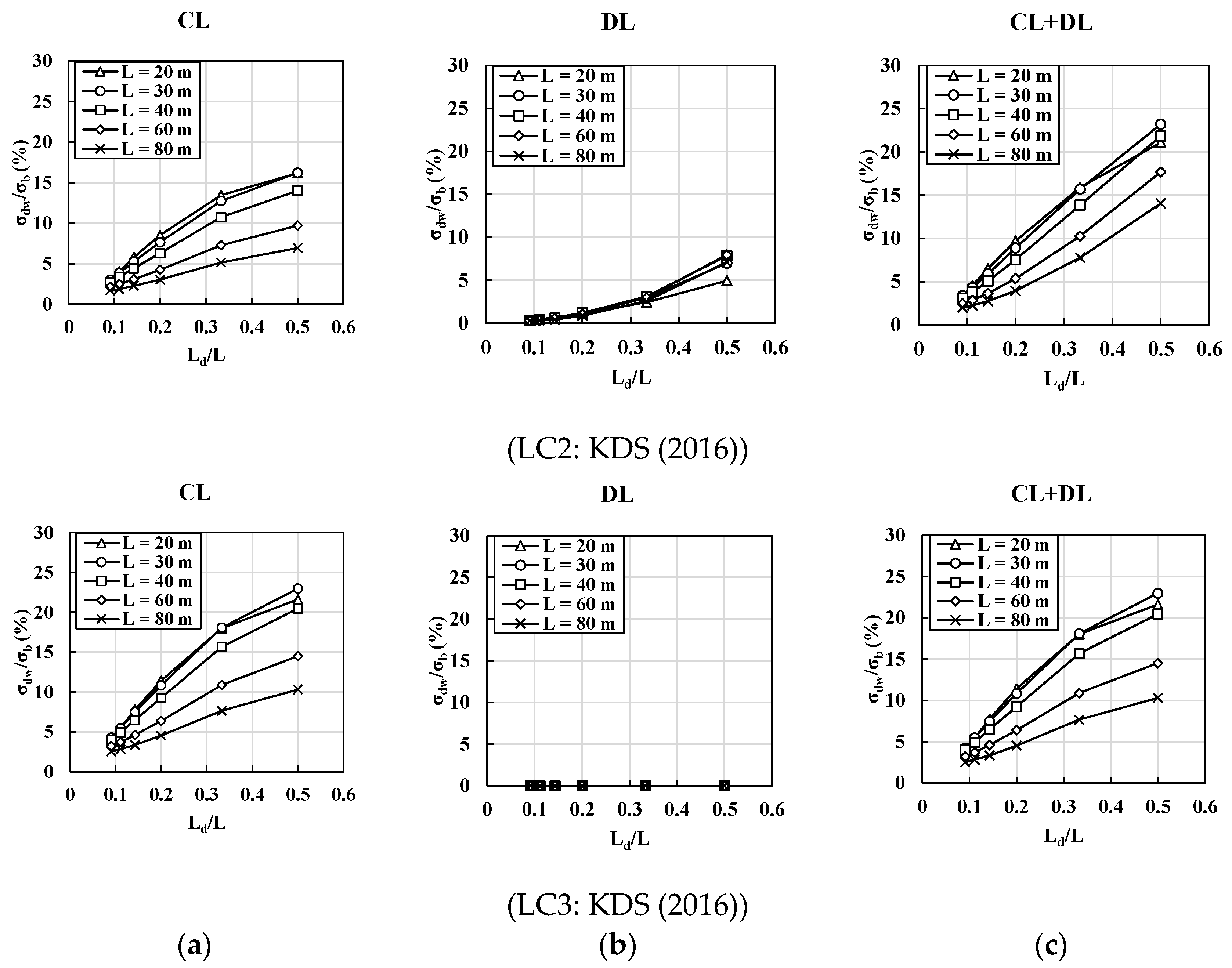
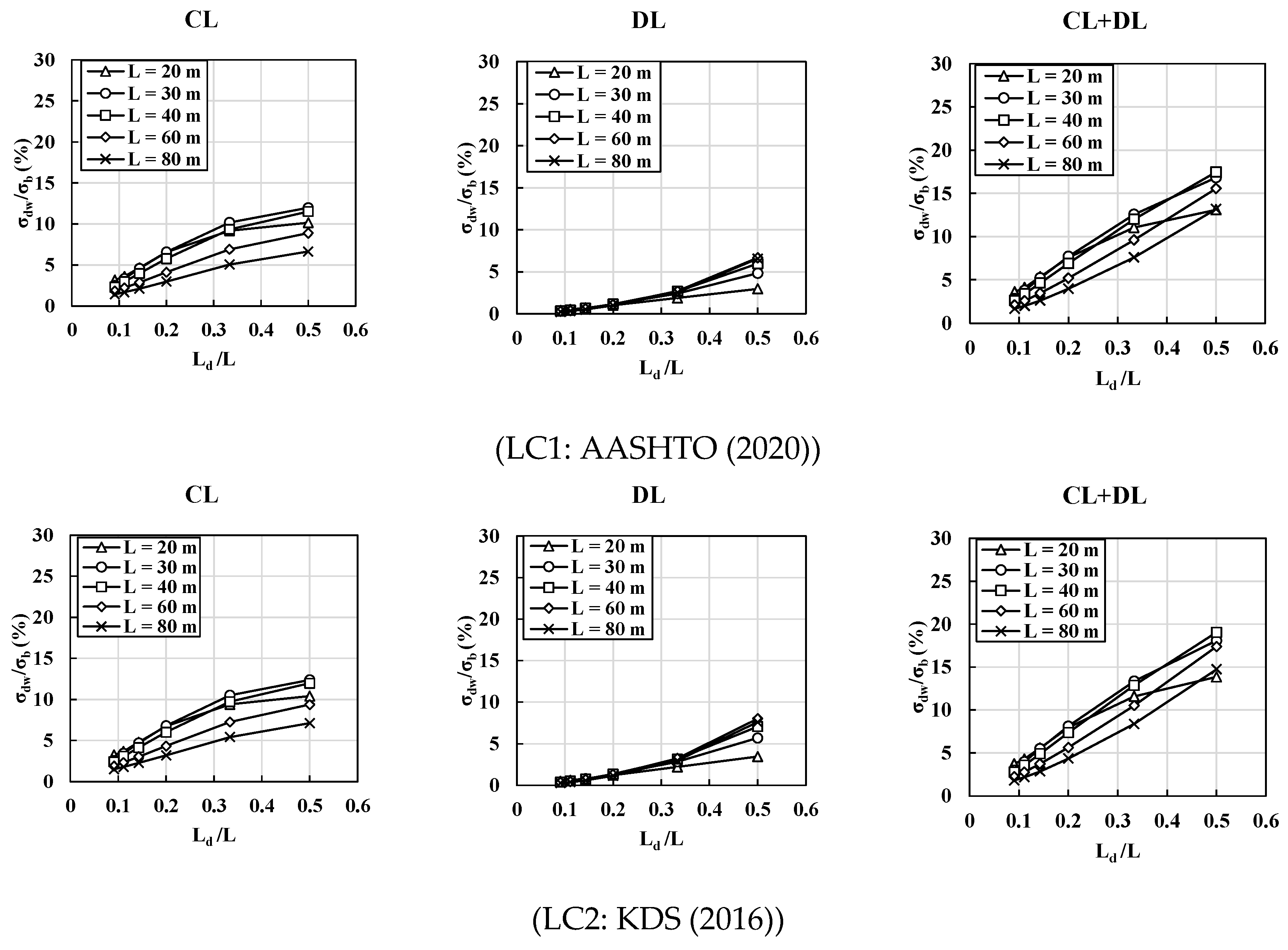
4.2. Effect of Load Combinations (LC) and Span Length (L)

Figure 10 shows the relationships between the maximum distortional warping normal stress (${\sigma }_{dw}$) and the normalized diaphragm spacing ($L_d/L$) for different loads and spans ($L$). In the analysis, LC1 comprising a load combination of a 425.6-kN design truck and 12.4-kN/m design lane load was applied, as stipulated in AASHTO [24]. The distortional warping normal stress values could be considered as the sum of the stresses induced by the concentrated and distributed loads. Thus, the FEA results were divided into two stress values for the concentrated load and distributed load, as shown in Figure 10. Several aspects of the distortional behavior were observed, considering the load type. All the distortional warping normal stresses under concentrated loads (CL in Figure 10) were significantly higher than those under distributed loads (DL in Figure 10), except for the case of the 80-m span. In contrast, the distortional stresses of the 80-m span cases under the distributed live loads had a close value with those under the concentrated loads. Hence, the effects of design lane loads were more significant when the span increased, whereas the concentrated load was more influential in smaller span bridge models.

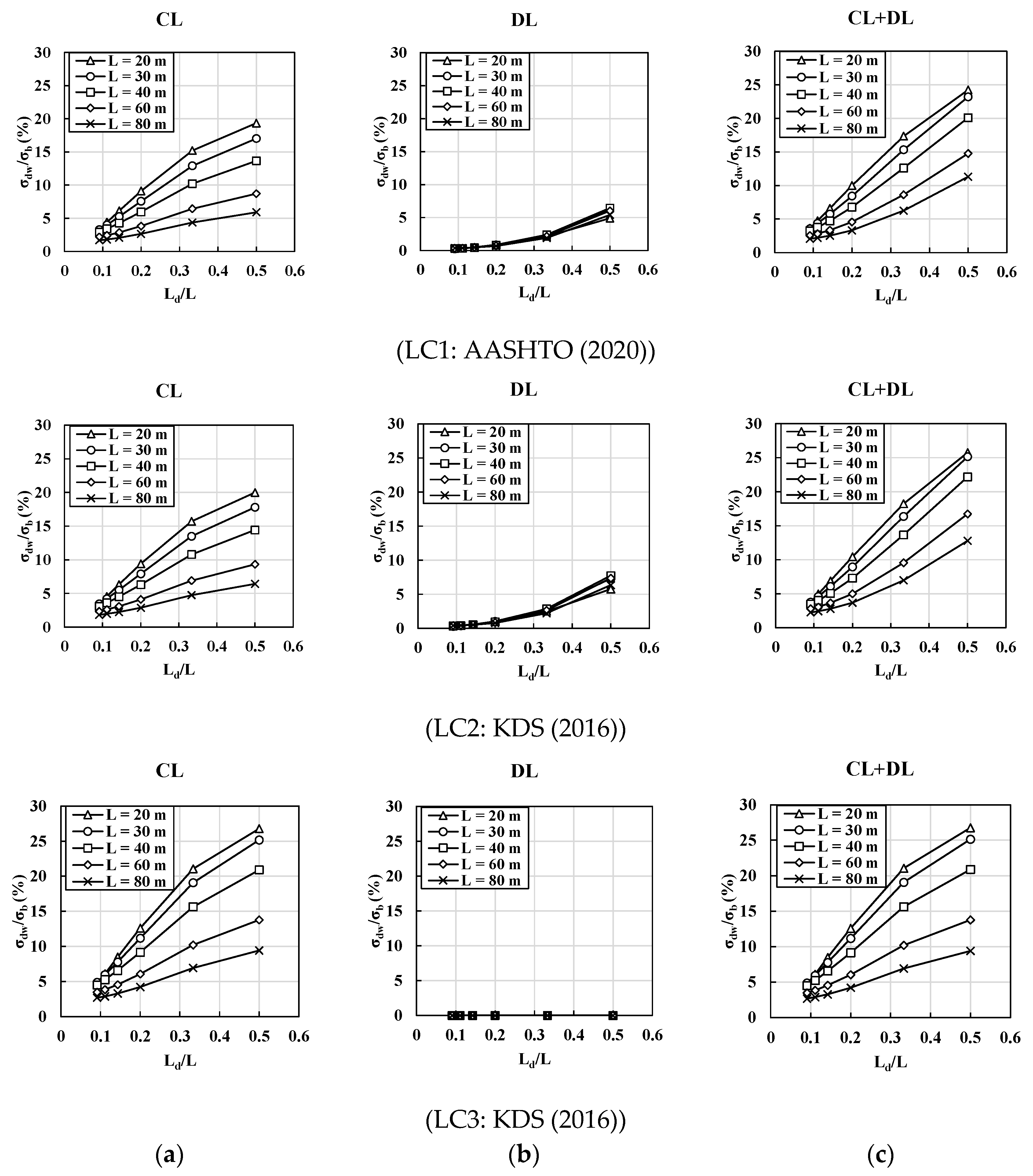
4.3. Comparisons of Normal Stress Ratios (${\mathsf{\sigma }}_{\mathrm{dw}}/{\mathsf{\sigma }}_{\mathrm{b}}$) for Different Design Loads

Figure 11, Figure 12 and Figure 13 show the relationships between the normal stress ratios (${\sigma }_{dw}/{\sigma }_b$) and normalized diaphragm spacing ($L_d/L$) for different design live load combinations and cross-sectional aspect ratios ($H/B$). All distortional and bending normal stresses were selected as the maximum stresses acting on the bottom flange sections, which were more critical in the strength limit state than on the concrete slabs. In Figure 11, Figure 12 and Figure 13, CL denotes concentrated load, DL denotes distributed load, and CL+DL denotes combined concentrated and distributed loads. The distortional warping normal stresses generated by the distributed loads had relatively less significant effects than the stresses induced by the concentrated loads. Under the concentrated loads, the normal stress ratio (${\sigma }_{dw}/{\sigma }_b$) was significantly influenced by the span ($L$). When the model bridge span was smaller, in which the smallest span was 20 m, the normal stress ratios become higher. However, in distributed loading cases, the span effects were marginal when the normalized diaphragm spacing ($L_d/L$) was smaller than 0.33 (when two intermediate diaphragms were installed). In this case, no significant change in the normal stress ratio was observed, because the amplitudes of the distortional warping normal stresses induced by the distributed loads were marginal, compared to the maximum bending normal stress.

Therefore, the concentrated load cases significantly influenced the normal stress ratio for different bridge spans, whereas the distributed load cases minimally influenced the span. In bridges with larger spans, the combined concentrated and distributed loads yielded higher normal stresses, whereas the concentrated loading influenced smaller span bridges.

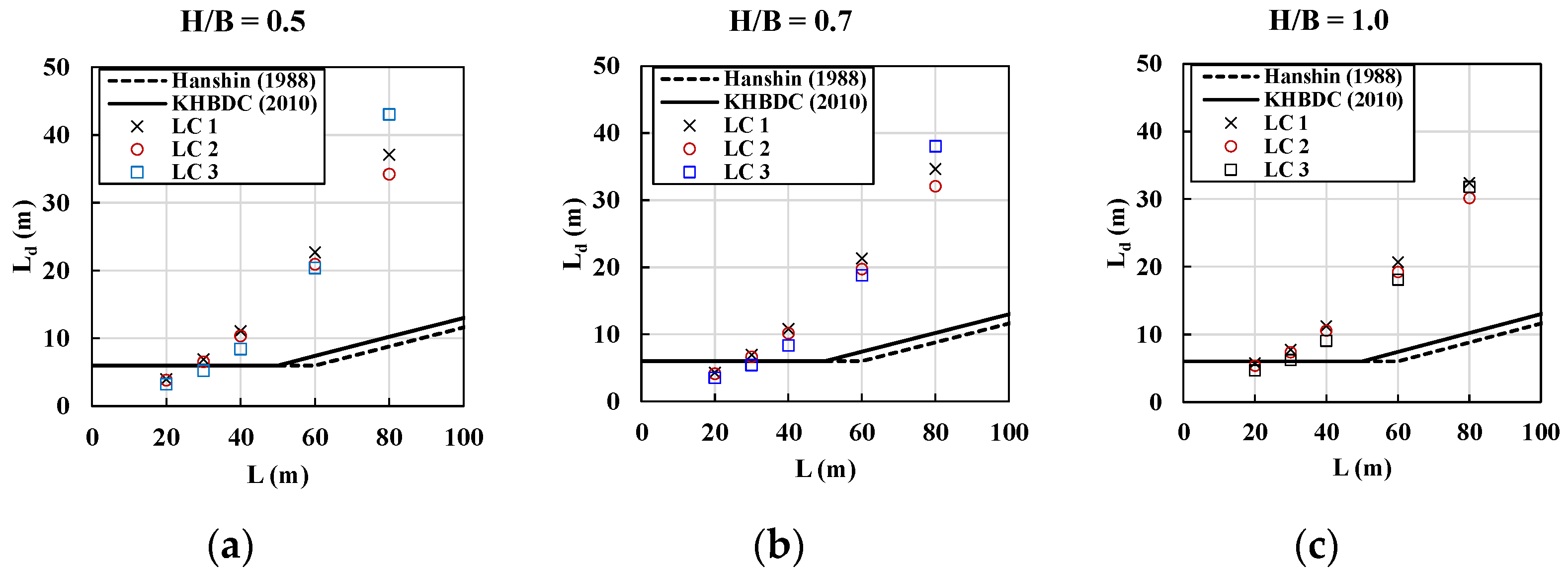
4.4. Comparisons of Minimum Requirements of Diaphragms between Different Live Loads

Based on the FEA results, the span ($L$), design live load combination, intermediate diaphragm spacing ($L_d$), cross-sectional aspect ratio ($H/B$), and minimum requirements of diaphragm spacing ($L_d$) were determined, as listed in

Table 3. Minimum requirements of the diaphragm spacing for different load combinations (unit: m).

σdw/σb	H/B	L	Ld, req
			LC1	LC2	LC3
5%	0.5	20	2.3	2.2	2.0
		30	3.7	3.6	2.9
		40	5.9	5.5	4.3
		60	12.7	11.7	9.1
		80	22.7	20.8	18.8
	0.7	20	2.2	2.2	1.9
		30	3.7	3.6	2.9
		40	6.0	5.8	4.2
		60	12.1	11.2	9.0
		80	21.0	19.4	17.0
	1.0	20	2.6	2.5	2.2
		30	4.1	4.0	3.4
		40	6.1	5.8	4.8
		60	11.7	10.9	9.2
10%	0.5	80	19.4	18.0	16.6
		20	4.0	3.8	3.2
		30	6.8	6.5	5.2
		40	11.1	10.4	8.4
		60	22.7	20.9	20.4
		80	37.1	34.2	43.0
	0.7	20	4.3	4.1	3.5
		30	7.0	6.6	5.4
		40	10.8	10.1	8.4
		60	21.3	19.7	18.8
		80	34.6	32.1	38.1
	1.0	20	5.7	5.4	4.7
		30	7.8	7.3	6.2
		40	11.2	10.6	9.0
		60	20.6	19.2	18.1
		80	32.4	30.2	31.8

Note: the bolded numbers in this table are minimum values.

. All the required diaphragm spacings ($L_d$) were determined through regression analysis using third-order polynomial equations based on the analysis results shown in Figure 11c, Figure 12c, and Figure 13c. The intermediate spacings with 5% and 10 % normal stress limits are listed in Table 3. Additionally, Figure 14 and Figure 15 show comparisons between the design intermediate diaphragm spacings from the Hanshin Guidelines [5] and the Korean Design Code [26] and the minimum required intermediate diaphragm spacings ($L_{d,req}$) for different spans ($L_d$) and load combinations based on the FEA.

Based on Figure 14 and Figure 15 and Table 3, it can be inferred that the different load combinations can significantly influence the required intermediate diaphragm spacing. For the 5% normal stress ratio, LC3 was the controlling load combination with 100% truck loading specified in the Korean Design Standards [25] for all the cross-sectional aspect ratios ($H/B$). The FEA with LC1 yielded the highest intermediate diaphragm spacing values. For the 10% normal stress ratio, LC3 was the controlling load combination, except for the case of an 80-m span. For the 80-m span case, LC2 yielded the second-highest concentrated load values with the maximum distributed load. Similar to the 5% normal stress ratio, LC1 resulted in the highest intermediate diaphragm spacing values.

Regarding the cross-sectional aspect ratios ($H/B$), higher $H/B$ values tended to require smaller minimum intermediate diaphragm spacings than those with smaller $H/B$ values, consistent with the results reported in the literature [23]. Additionally, when the spans were shorter than 40 and 30 m for the 5% and 10% stress ratios, respectively, the FEA results yielded lower values than the design intermediate diaphragm spacing values, which is 6 m in the Hanshin Guideline [5] and Korean Design Code [26]. Thus, it should be noted that spans shorter than 40 m for the 5% and 30 m for the 10% stress ratio limits should be thoroughly considered in the design phases. These aspects of the required intermediate diaphragm spacing ($L_d$) are only limited to the load combinations and applied load magnitudes listed in Table 1.

In the previous section, it was reported that the magnitude of the concentrated live load significantly influenced the normal stress ratios of box girder bridges, where higher concentrated live loads may result in higher normal stress ratios. LC3 had the highest concentrated live load of 100% [26] with a 637.5-kN truck load, which could be determined as 510 kN times (1 + 0.25). It tended to provide the minimum required intermediate diaphragm spacings, compared with the LC1 and LC2 cases. Moreover, the LC2 cases showed the minimum required intermediate diaphragm spacing when the span was 80 m, because the distributed loads exhibited a significant impact when the span increased. These aspects showed a similar tendency, regardless of the cross-sectional aspect ratio ($H/B$).

5. Conclusions

In this study, the effects of the design live-load combinations, cross-sectional aspect ratio ($H/B$), and span ($L$) on the required diaphragm spacings ($L_d$) were evaluated through 3D FEA. Based on the analysis results, several significant findings were obtained. The main conclusions of this study are summarized as follows.

• Based on literature reviews, it was revealed that the current bridge design codes stipulated various combinations of design live loads compared to the previous version of the bridge design codes. Therefore, this study conducted a series of parametric studies to evaluate the effects of the load combinations specified in the current bridge design codes on the distortional behaviors of box girder bridges.
• The distortional warping normal stress (${\sigma }_{dw}$) developed in box girder sections is more significantly influenced by concentrated live loads (representing truck loads in the current design codes) than distributed lane loads. In short-span bridges, the distortional warping normal stress generated by truck loads can be considered the governing load combination.
• For relatively long-span bridges, the distortional warping normal stress (${\sigma }_{dw}$) has similar values for both under the truck and the lane loads. The lane load effects are more significant in long-span bridges. Thus, the span ($L$) is a critical parameter for load combinations based on the FEA.
• In combined load cases, i.e., LC1 and LC2, the normal stress ratios (${\sigma }_{dw}/{\sigma }_b$) induced by the lane load have similar values, irrespective of the span, whereas those of the truck load are significantly influenced by the span. Hence, regarding the normal stress ratios, the truck loads are a controlling parameter with the $H/B$ and span for designing intermediate diaphragm spacings.
• Based on the analysis, the required intermediate diaphragm spacings specified in the Hanshin Guideline [5] and Korean Highway Bridge Design Code [26] can lead to a conservative design for determining the intermediate diaphragm spacing when the bridge span is longer than 30 or 40 m, depending on the normal stress ratio.
• The load combination effects can vary with the span, yielding sensitive design results in determining the intermediate diaphragm spacings. Therefore, various design live load combinations must be considered during the preliminary design phases to ensure the efficient design of intermediate diaphragms of the box girders.
• Although the load combinations specified in the current bridge design codes provided various combinations of design live loads, which influence the distortional behavior significantly, the importance of the live load combinations was not considered in the literature. Additionally, the distortional behavior of box girder bridges may be significantly influenced by the cross-sectional parameters. To consider the effects of load combinations and various design parameters, more efficient and accurate design methods should be provided in future works.