The Performance of 3D Printed Polymer Tools in Sheet Metal Forming

Abstract

Additively manufactured polymer tools are evaluated for use in metal forming as prototype tools and in the attempt to make sheet metal more attractive to small production volumes. Printing materials, strategies and accuracies are presented before the tools and tested in V-bending and groove pressing of 1 mm aluminum sheets. The V-bending shows that the tools change surface topography during forming until a steady state is reached at around five strokes. The geometrical accuracy obtained in V-bending is evaluated by the spring-back angle and the resulting bend radius, while bending to 90° with three different punch nose radii. The spring-back shows additional effects from the elastic deflection of the tools, and the influence from the punch nose radius is found to be influenced by the printing strategy due to the ratio between tool radius and the printed solid shell thickness enclosing the otherwise less dense bulk part of the tool. Groove pressing shows the combined effect of groove heights and angular changes due to spring-back. In all cases, the repeatability is discussed to show the potential of tool corrections for obtaining formed parts closer to nominal values.

1. Introduction

Sheet metal forming can be used to create a variety of complicated three-dimensional parts from flat sheet metal by, e.g., bending and deep drawing. Some of the advantages of sheet metal forming are the beneficial mechanical properties of the formed part, the minimal amount of scrap that is generated and the high production capacity that can be attained. The main disadvantage of the method is the cost and time necessary for setting up a new process line. To ensure economic production, sheet metal forming is therefore often limited to mass production [1].

One of the major costs related to sheet metal forming is the development and production of the forming tools. Conventionally, the tool is designed by a tool designer and machined out of metal, which can take a long time and be quite costly. During tool development, a tool may then go through one or more revisions before reaching its final form. Each revision would necessitate a new round of machining or other processing steps each time. This quickly adds up to massive costs, both money and time-wise.

Additive manufacturing has gained popularity as a method of rapid prototyping (RP) tool concepts. These prototypes can then serve as either a proof-of-concept or as tools for small series production [2]. Adopting this method reduces the time and money spent on the tool, and allows for increased flexibility in sheet metal forming [1]. Zaragosa et al. [3] found that implementing an RP solution is more expensive than fabricating a single metal tool due to the initial costs of purchasing equipment and configuring it. However, the cost of printing further tools becomes much smaller than the cost of machining metal tools. It is unlikely that a first tool design is perfect due to the increasing complexity of parts and new sheet materials, which, as noted by Durgun [4], makes the experience of conventional tool makers insufficient. Therefore, inevitable revisions and iterations on the tool design become cheaper with 3D printing of tools.

Various researchers have investigated the suitability of using 3D-printed tools for sheet forming. Zaragosa et al. [3] studied the use of 3D-printed tool inserts in a metal frame for use in V-bending and found the spring-back to be similar to using fully metal tools. Nakamura et al. [5] used fully plastic tools for V-bending and found that the accuracy of the final bend angle is reduced compared to metal tools due to the increased elastic deflection, nevertheless, the spring-back was repeatable for each material. They further noted that the spring-back remained mostly constant for the plastic tools over 100 bending operations. Nakamura et al. [5] also found, and Zaragosa et al. [3] later confirmed, that using plastic tools results in a better surface finish on the formed part compared to using metal tools. This is because the workpiece is unlikely to be scratched by the plastic tools. Klimyuk et al. [1] optimized their printing strategy and managed to deep draw a cup, noting that no wear was visible on the surface of the printed tools. Schuh et al. [6], on the other hand, after optimization of the printing strategy using a Design of Experiments approach, managed to deep draw a cup but noted that most of the wear occurs during the first operation. Aksenov and Kononov [7] fabricated heat exchanger plates using printed tools and noted that lubrication was not necessary, as the plastic had anti-friction properties. In all the above references, there is agreement that 3D printing of forming tools is suitable for rapid prototyping and small series production.

V-bending is one of the simplest sheet forming operations. It involves a V-shaped punch that presses a sheet into a die, forcing the sheet to bend to a predefined angle. The V-shape is typically designed to account for spring-back, and so that the radius of the corner of the bend is within the tolerance of part design. The ability to bend the sheet close to the nominal angle and dimension depends on the tool, meaning that the spring-back that occurs and the accuracy of the formed radius can be used as an indicator of tool performance [3].

In this work, the performance of 3D-printed tools is investigated under sheet metal forming conditions. After optimizing the printing strategy through V-bending tests and surface characterization, the optimized printing strategy is used to fabricate tools for a groove pressing process. This process is used to form a geometry that is more complex than the basic V-bending geometry to demonstrate the types of geometries that it is possible to form using polymer tools. Further, it serves as another way of evaluating the accuracy of formed parts when using polymer tools, bringing this method closer to an industrial application.

2. Materials and Methods

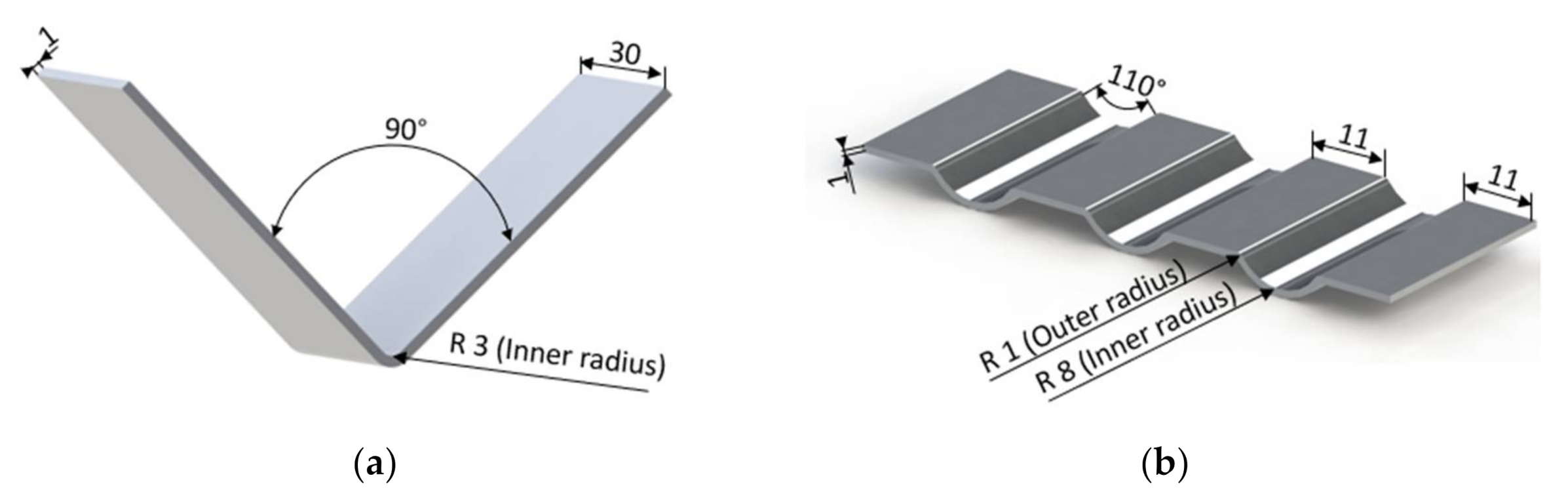
2.1. Equipment and Evaluation Geometries

The sheet material used in all parts of this study is commercially pure aluminum, EN AW-1050A H14, of 1.0 mm thickness (Sanistål, Aalborg, Denmark). Two forming processes are considered, V-bending and groove pressing. The initial blanks for each process have dimensions of 30 mm × 70 mm and 30 mm × 90 mm, respectively, with the target geometries of the processes shown in Figure 1.

Both forming processes were carried out in an electric press with a maximum capacity of 150 kN. A sub-press, designed for use with interchangeable tool inserts and is shown in Figure 2, is used to ensure proper guidance of the printed forming tools during forming. All experiments were conducted to fixed end positions with a vertical press speed of 3 mm/s.

All forming tools used in this study were printed using a Fused Filament Fabrication (FFF) printer of the Ultimaker 2+ type (Ultimaker, Utrecht, Netherlands). This printer extrudes a polylactic acid (PLA) filament of Ø2.85 mm through an Ø0.4 mm nozzle. From new, it has an XY-positioning (plane) accuracy of 12.5 μm and a Z-positioning (vertical) accuracy of 5 μm [8]. Using Vat Photopolymerization Additive Manufacturing (VPAM) as a method of producing tools was also investigated. The principle of the method is that liquid resin is selectively cured by a UV light in a layer-by-layer fashion. The printer used in this case was an Elegoo Mars 2 Pro, which has an XY-positioning (plane) accuracy of 50 µm, and an accuracy of 1 µm along the Z-axis (vertical).

2.2. Printing Material and Strategy

Among the different additive manufacturing processes, Fused Filament Fabrication (FFF) and Vat Photopolymerization (VPAM) are widely used in the field of rapid prototyping. In this work, both printing methods are investigated. FFF is an additive manufacturing process, where a molten polymer filament is extruded through a nozzle onto a build platform, layer by layer. In VPAM, a liquid resin is selectively cured through light activated polymerization by use of a UV light. Low costs and high manufacturing speeds are the core of rapid prototyping, so for the purpose of this study, the most commonly available materials were selected for both FFF and VPAM. PLA was used for the tools produced by FFF; this material is the most commonly used in FFF, it is biodegradable and produced from renewable resources such as corn starch and sugar cane. Furthermore, it is characterized by relatively low melting temperature and low shrinkage, reducing internal residual stresses [9]. The resin selected for VPAM is an acrylate-based photopolymer with phosphine oxide photo initiator. This photopolymer is affordable and is characterized by a great trade-off between market price and mechanical and printing properties. It was selected for its high hardness after curing compared to similar resins: 83 shore D hardness according to its datasheet. Some mechanical and physical properties of the materials that that are used in this work are shown in

Table 1. Typical mechanical and physical properties of materials that are used in this work.

Material	ρ (kg/m3)	E (GPa)	ν (-)
AL1050	2710	71	0.3
Polylactic acid (PLA)	1230	2	0.3
Photopolymer	1120	2.7	0.36

.

The final strength and quality of the 3D-printed tools are directly influenced by various printing parameters [1,10,11,12,13]. Klimyuk et al. [1] showed how layer thickness, wall thickness and infill density have a major impact on the final quality of the printed part. The authors of this work conducted an investigation on the influence of printing orientation, layer thickness, wall thickness and infill density in order to select the optimal parameters for printing the tools. In the case of VPAM, the effect of the exposure time was also studied. The selected printing parameters are shown in

Table 2. Printing process parameters for FFF and VPAM.

Printing Technology	Exposure Time	Orientation	Layer Thickness	Shell Thickness	Infill Density	Post Processing
FFF	-	Vertical	0.1 mm	2.10 mm	50%	-
VPAM	3.5 s	Vertical	0.1 mm	-	100%	UV curing at 45 °C for 30 min

.

The printing orientation is an important parameter due to the anisotropy of the properties of the printed part, which is generated by its layer structure [9]. The printing orientation was chosen to be in the out of plane direction in Figure 2, because parts printed in this direction withstand compressive forces during metal forming better by having the layers perpendicular to vertical forces. This minimizes the risk of delamination between layers.

The selected layer thickness is 0.1 mm. In FFF, thinner layers lead to improved adhesion of layers to one another and denser parts since the heat from the nozzle, being closer to the previous layer, helps the layers bond together. Kuznetsov et al. [9] showed that by decreasing the layer thickness, it is possible to decrease the generation of voids, which negatively affect layer adhesion and, therefore, tool strength. The layer thickness is also an important parameter for VPAM, where a smaller layer thickness ensures complete UV penetration through the layer and a higher degree of polymerization [11].

The shell thickness was fixed to 2.10 mm (double of the default wall thickness of 1.05 mm). Aslani et al. [12] investigated the influence of the shell thickness on the geometrical accuracy of the part showing higher accuracy when a double wall thickness was used.

The infill density is another important parameter. The higher the infill density, the larger the amount of material that the component is comprised of, and the greater the bonding areas between layers. The larger bonding area leads to an adhesion gain among the layers, reducing the likelihood of delamination and fracture and promoting the strength of the component. An infill density of 50% was selected for FFF as a balance between printing time/material volume and component strength. The infill density was set to 100% for the VPAM tools in order to ensure complete polymerization and to maximize the bonding between layers, reducing the risk of delamination.

The exposure time in VPAM directly affects the light penetration depth, which is the length by which the UV light is able to penetrate and cure the photopolymer. The light penetration depth needs to be equal to, or more than, the layer thickness in order to assure bonding between the layers. The optimal exposure time, for the specific resin used in this work, was found to be 30 s for the burn in layers and 3.5 s for the rest of the layers.

2.3. Precision, Accuracy and Surface Roughness of the Printed Parts

A study on the accuracy of the two printers was carried out after the printing parameters had been selected. The reference geometry in Figure 3 was printed five times with FFF and five times with VPAM and measured to evaluate accuracy and repeatability. Figure 4 shows the deviation in x, y and z directions from the nominal dimensions. The largest deviations can be detected in x and y directions on the parts printed with VPAM, showing how the photopolymer is more sensitive to shrinkage in comparison to PLA.

The standard deviation bars in Figure 4 depict the accuracy of the two printers relative to dimensions given in Figure 3. Overall, the VPAM printer showed better accuracies in comparison to FFF Accuracies of 0.03 mm and 0.02 mm were detected, respectively, for the x and y directions with the VPAM printer, while FFF showed accuracies of 0.02 mm in x and 0.06 mm in y. A particularly good accuracy was detected in the z direction for the VPAM with a value of 0.01 mm.

The surface roughness of the printed tools was investigated by using an Olympus LEXT confocal microscope. The linear mean height Ra of the tools was evaluated parallel and perpendicular to the printing direction. The Ra is comparable for both FFF and VPAM when looking at the surface parallel to the printing direction, with a value of 0.78 ± 0.45 µm and 0.81 ± 0.25 µm, respectively. The investigation of the roughness on the surface perpendicular to the printing direction showed instead higher Ra for FFF compared to VPAM, having Ra values of 2.96 ± 0.27 µm and 1.43 ± 0.21 µm, respectively. Even though VPAM was found to be more accurate than FFF, this additive manufacturing technology needs post-processing after the printing, increasing time and cost for the production of the tool. Therefore, FFF was selected as the preferred method of RP for further investigation.

2.4. Measurement Procedures and Strategy

The objective of this work is to study the geometrical accuracy of parts formed by RP polymer tools. The final shape of formed components and RP tools is compared to the nominal shape by use of a ZEISS DuraMax coordinate measuring machine. All measurements that are reported are averaged along the entire width of the respective component.

The nominal geometry of the component created by V-bending is shown in Figure 1a. The measurement strategy used to determine the geometrical accuracy of the formed component is outlined in Figure 5a. Five measurements of angles (M1–M5) are performed along the arms of the bent components at equal intervals of 6 mm. The radius (R) where the arms meet is also measured.

The geometrical accuracy of the part formed by groove pressing, shown in Figure 1b, is determined by the strategy outlined in Figure 5b. The angularity of the four flat parts (P1–P4) is measured with respect to the outer tangential plane touching the planes P2 and P3. The height of the three main grooves (H1, H2, H3) were measured with respect to the outer tangential plane touching the planes P1 and P2, P2 and P3, P3 and P4, respectively. The overall angularity of the workpiece is measured between P1 and P4.

For evaluating the geometrical accuracy of the printed punch, as shown in Figure 6, the strategy consists of five angle measurements (M1–M5) located at an equal distance from each other of 5 mm on the tilted surfaces and in five radius measurements (R1–R5) on the punch nose located at an equal distance of 8 mm from each other across the width.

3. Accuracy and Wear in V-Bending

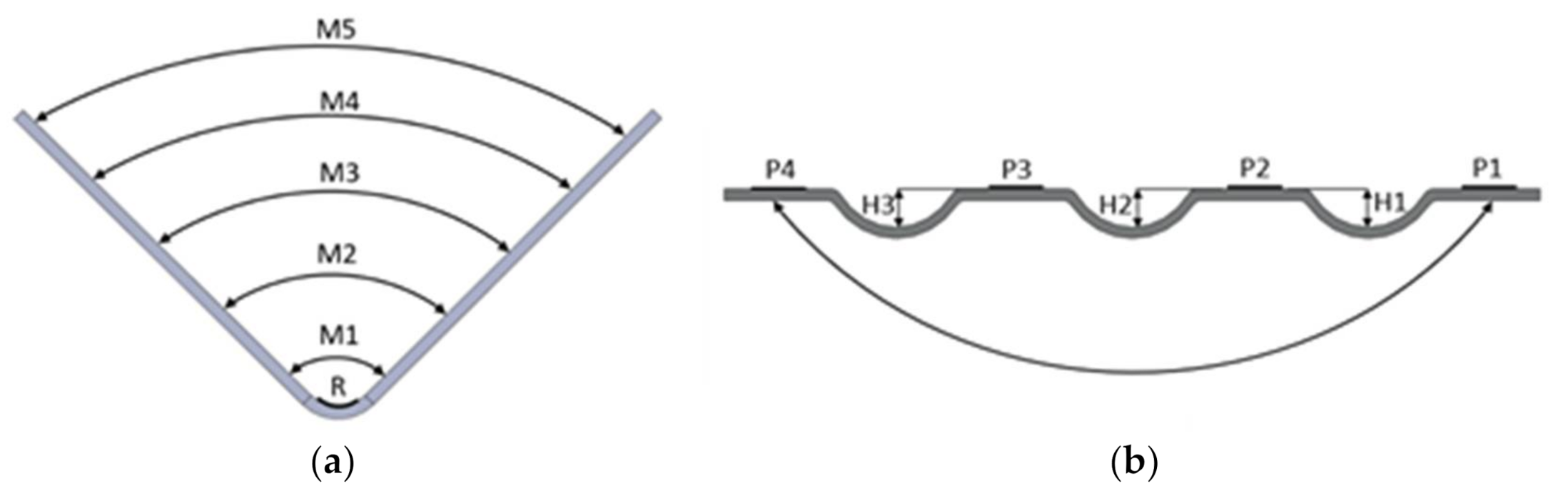
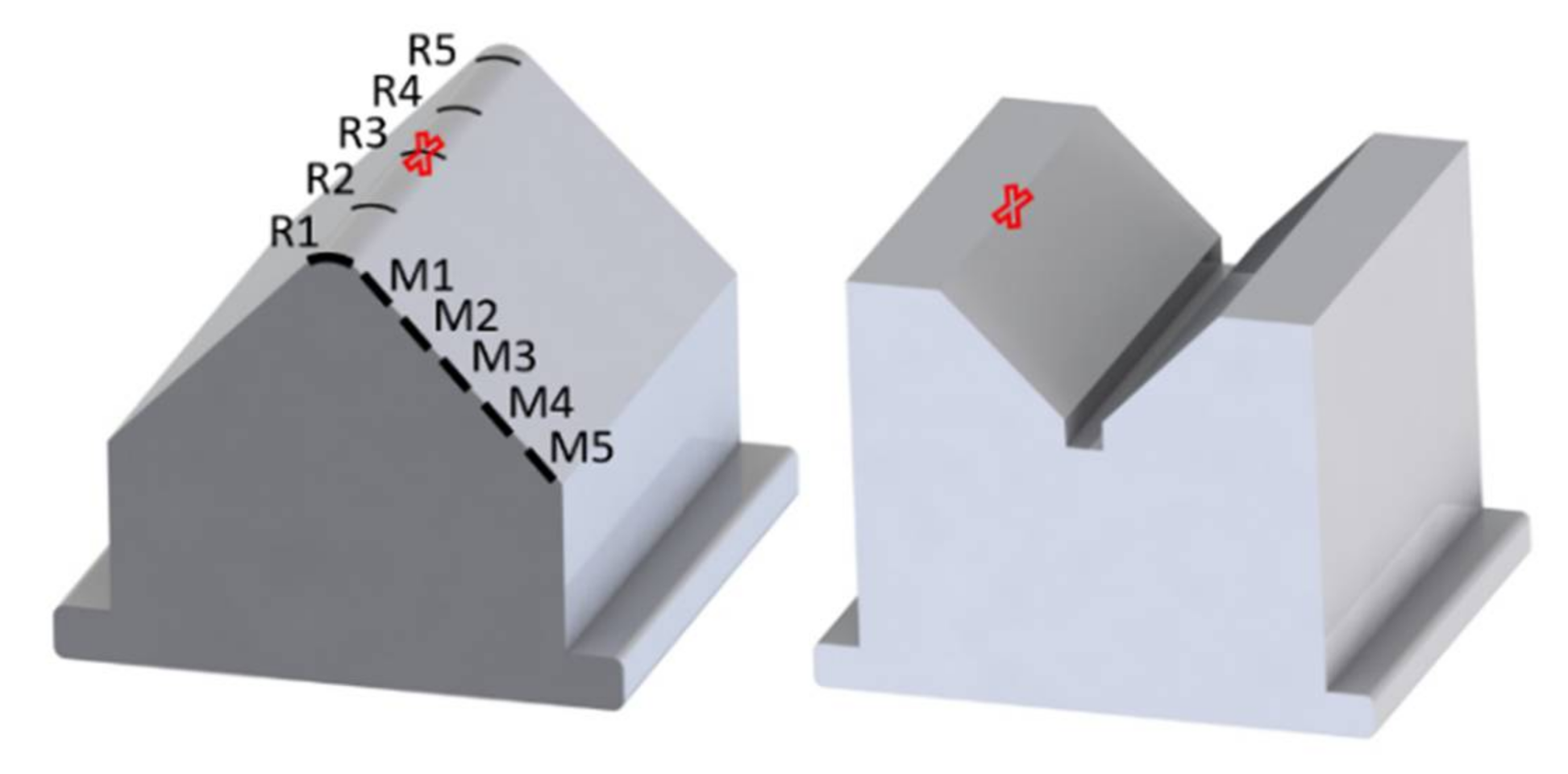
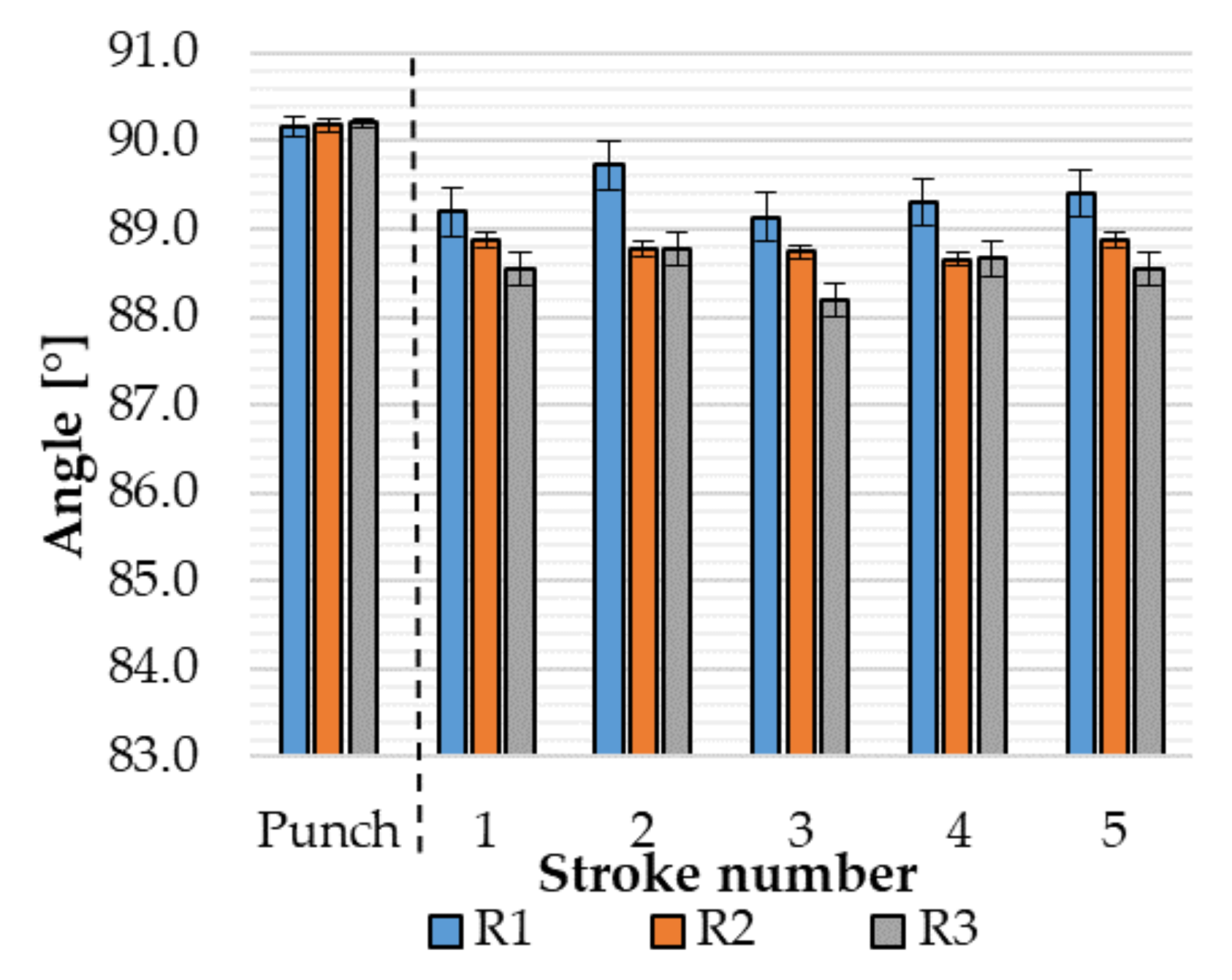
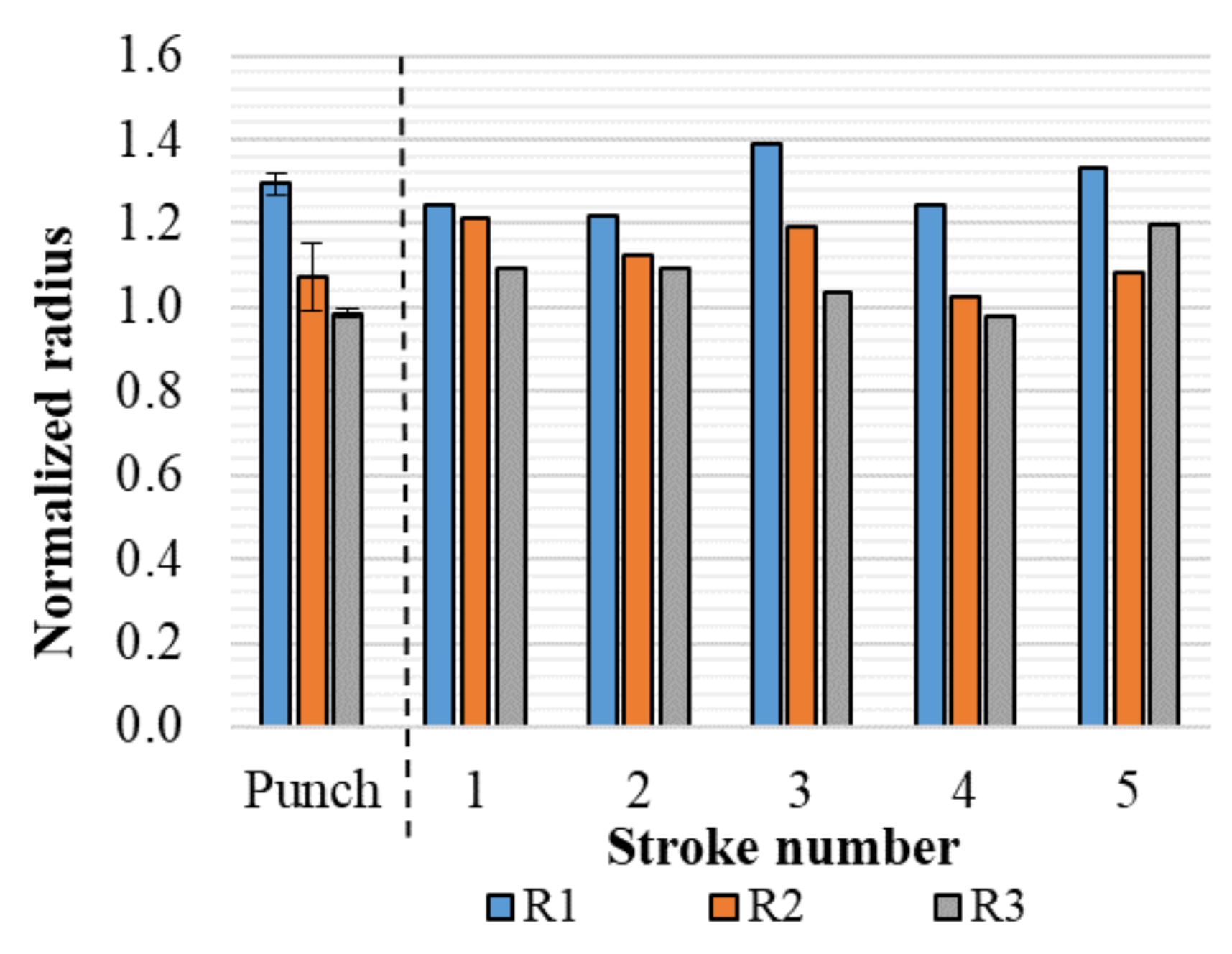
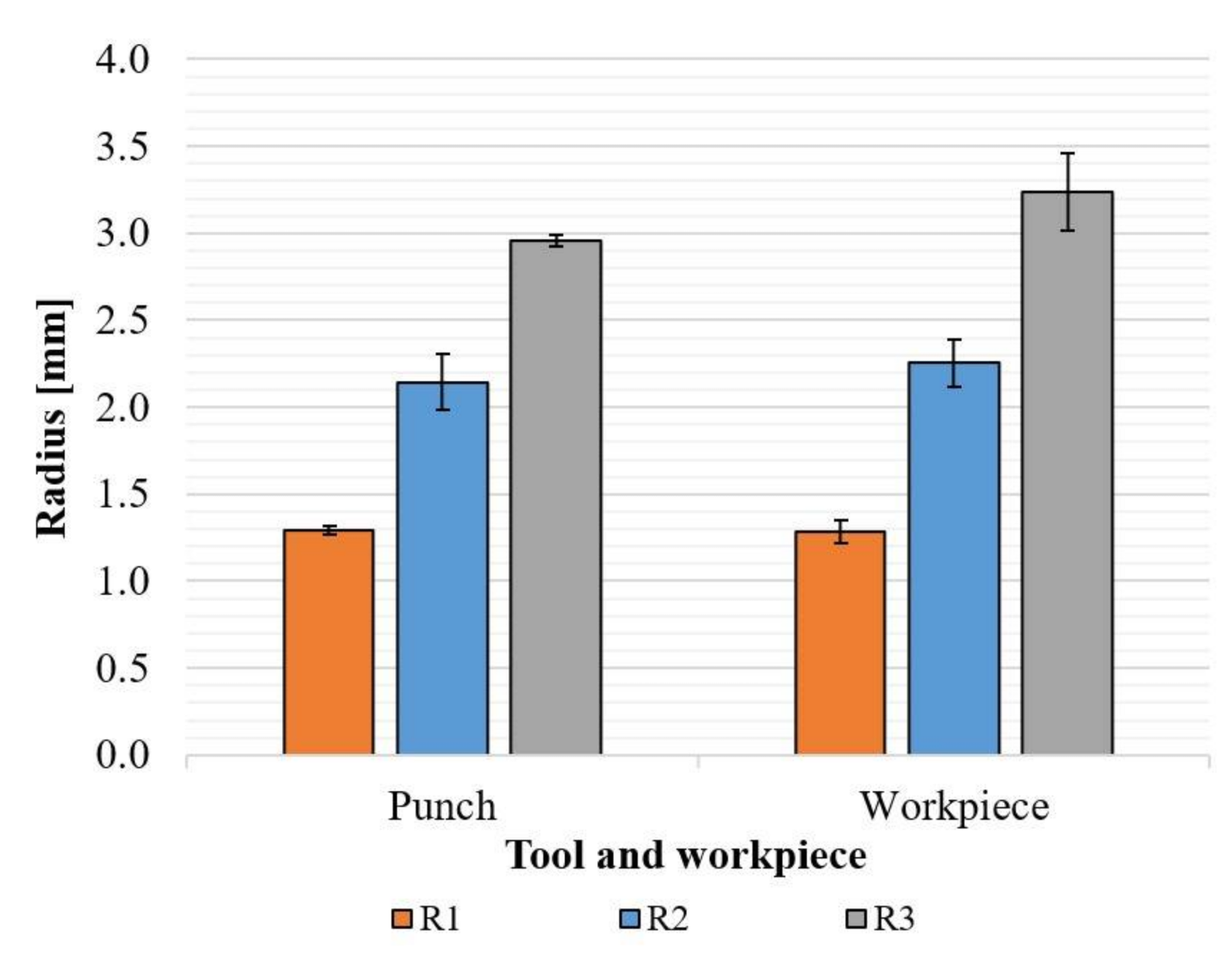
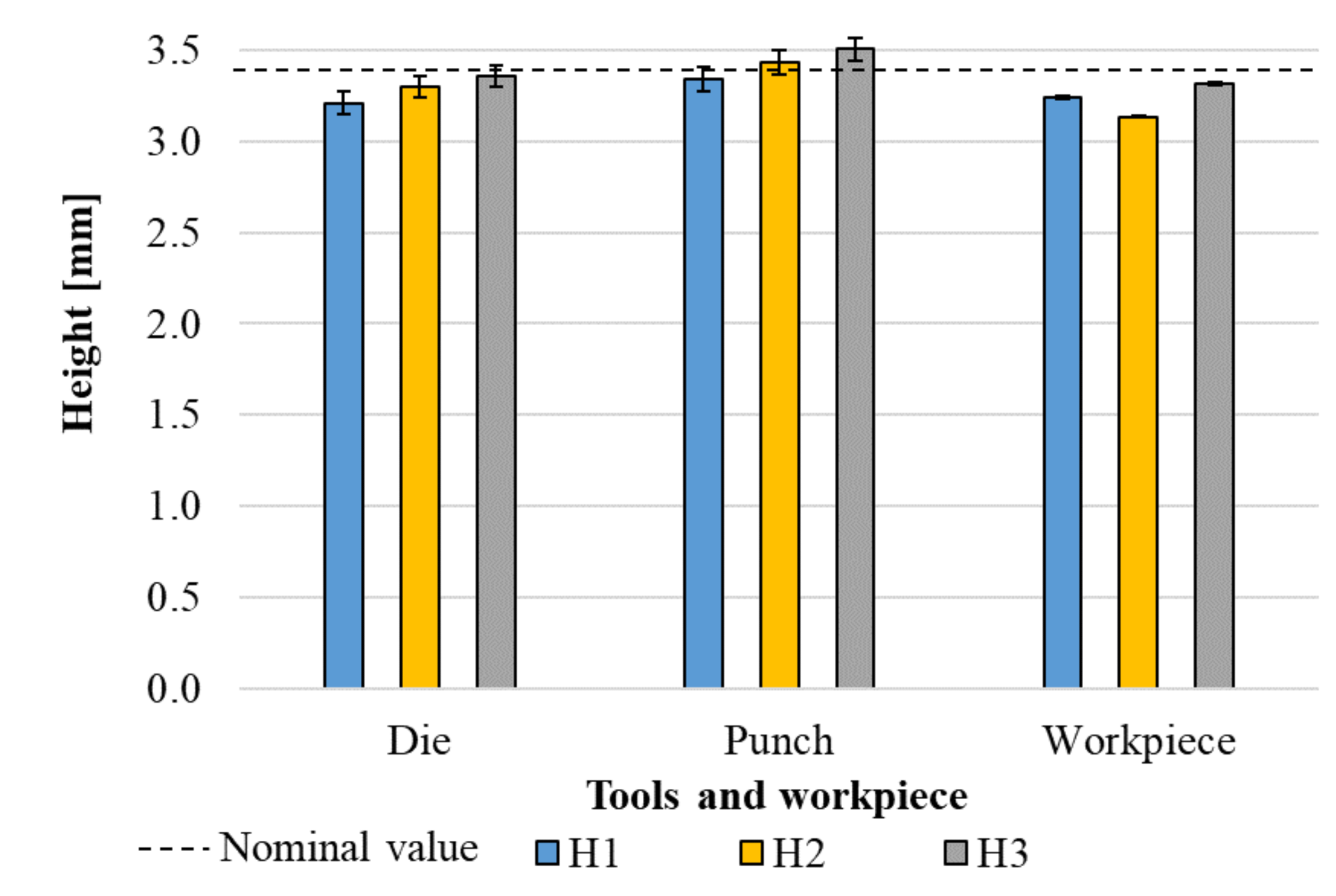
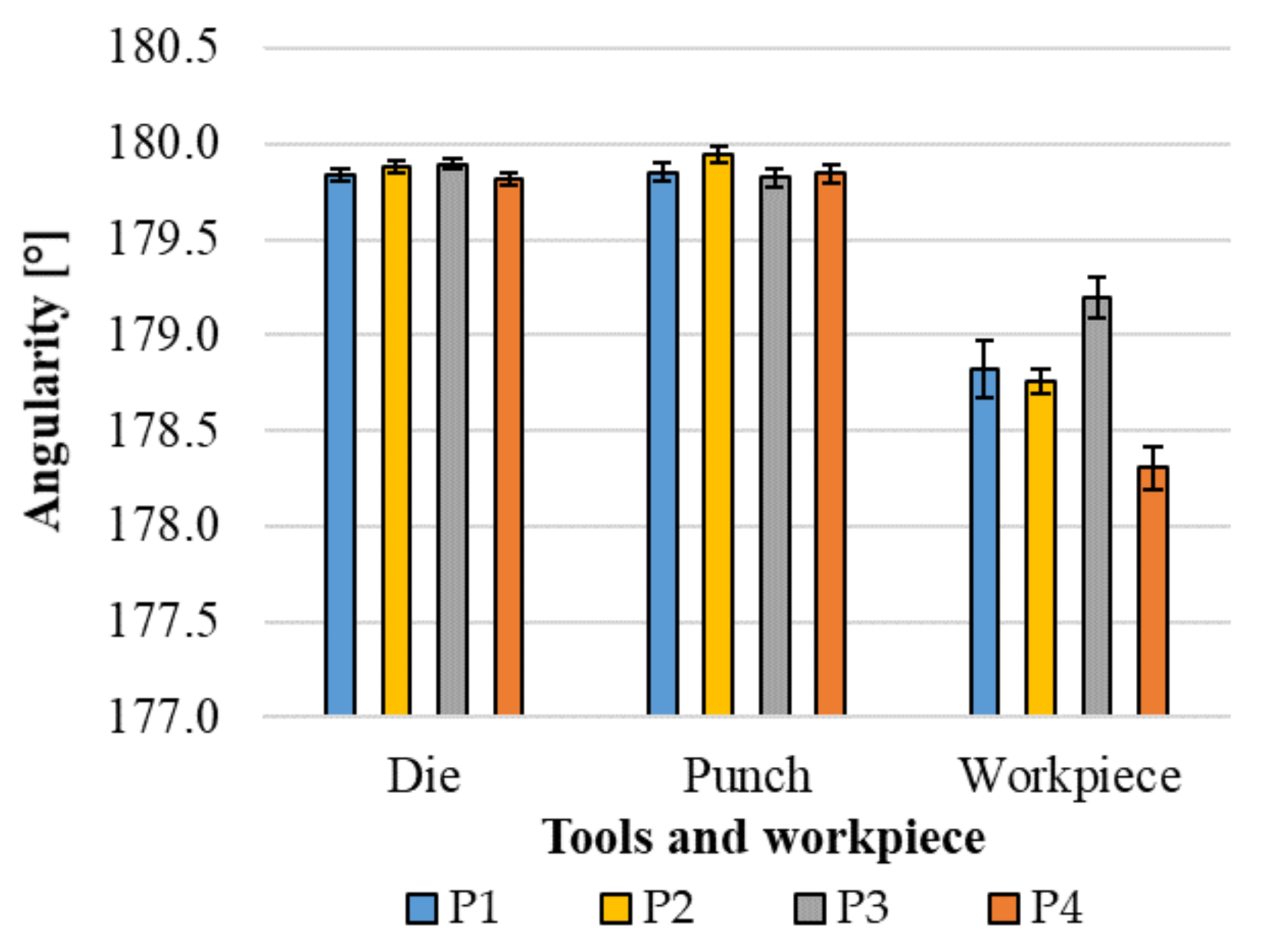
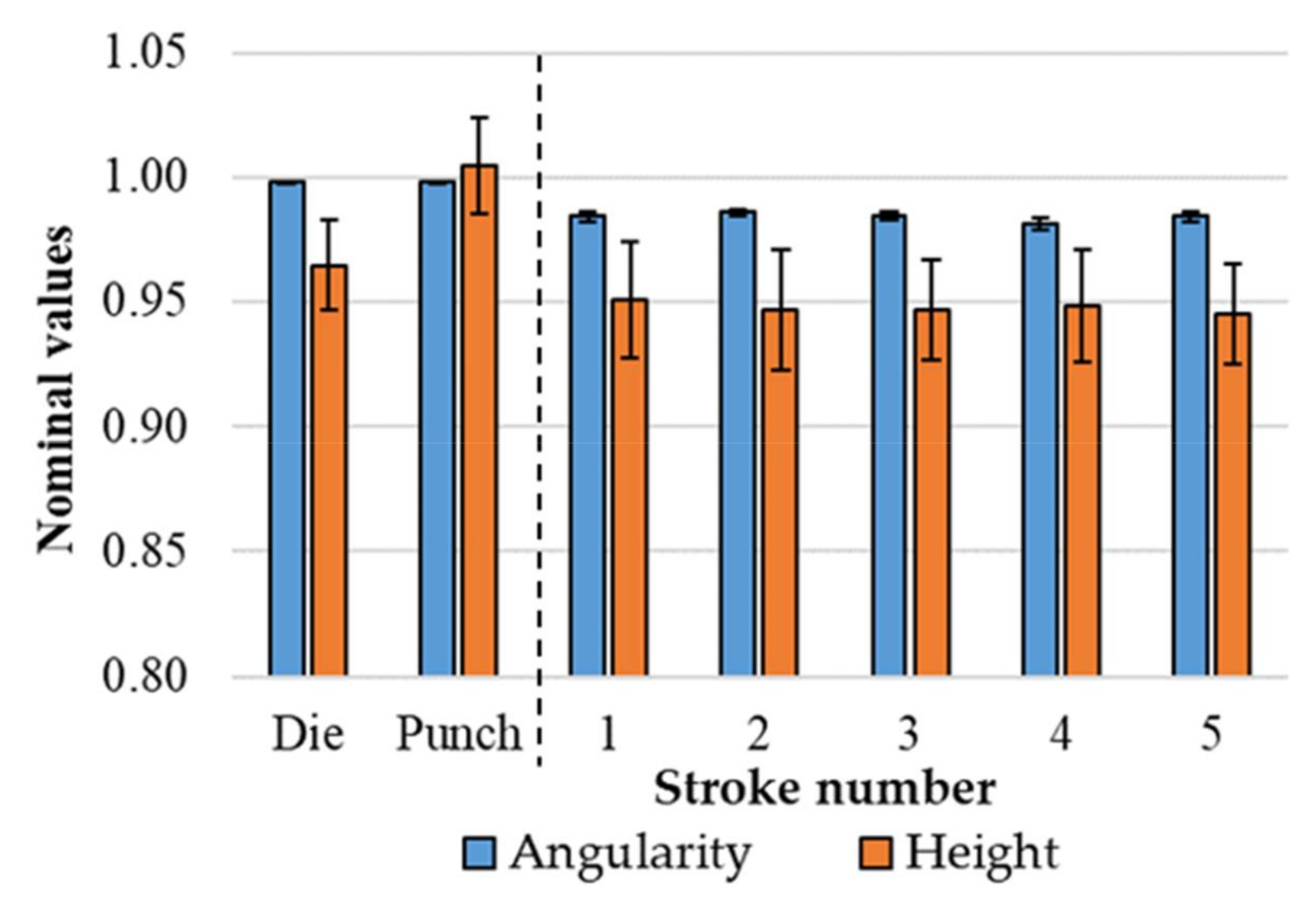
3.1. Change in Tool Geometry and Surface vs. Number of Strokes

A visual inspection at selected points of the tool surfaces was performed using a LEXT OLS4000 confocal microscope (Olympus, Tokyo, Japan). The locations, indicated by the red marks in Figure 6, were selected as the highest tribological load would be found there. The resulting pictures are shown in

Table 3. Images of tool surfaces for different numbers of strokes that have been performed. Each figure shows an area that is 600 µm by 600 µm.

Stroke (#)	0	3	5	10	30
Punch
Die

, as a function of the number of bending strokes. The picture taken for stroke #0 is not necessarily in the same location as others, as there were no existing marks which could be used as a reference point. It does, however, show that the surface is not perfect even before forming, with defects possibly having been caused by improper handling. Pictures taken for strokes #3–30 are taken in the same location to showcase how the wear progresses. The figures show that the punch does not experience significant changes to the surface, while the die does. The surface of the die changes more gradually after the fifth stroke, which may indicate some form of steady state. There is considerably less sliding occurring in the interface between the punch and the workpiece than in the interface between the die and the workpiece, which is likely the reason for the difference in wear between the two tools.

3.2. Springback, Geometrical Accuracy and Comparison to Tool Accuracy

The results of the geometrical accuracy study of the workpiece and punch, obtained by employing the measurement strategy described in Section 2.4, are shown in Figure 7 and Figure 8.

Figure 7 shows the geometrical accuracy of the 3D-printed punches after they have been used to form five parts. The mean angle that is measured is 90.2 ± 0.1°. The figure also shows the averaged angle over measurements of parts formed in five consecutive strokes. The angle is smaller than nominal and grows with distance from the punch nose. The deviation from nominal is largest at the punch nose. This behavior is most obvious for the tool with a 1 mm radius, where the mean angle grows from 86.1° to 89.8° as the measurements are taken further away from the punch nose.

Figure 8 shows the average angle measured in location M3 of the workpieces, over five strokes, for the three different punch nose radii. The largest difference from nominal is found when using the 3 mm radius tool after three strokes, where the measured value is 88.2 ± 0.8°. The smallest deviation from nominal is found when using the 1 mm radius tool at the second stroke, where the measured value is 88.7 ± 0.27°. The workpieces formed by the 2 mm radius tool have small deviations among them and a steady response over the five strokes, characterized by a standard deviation of 0.08°. This behavior is not observed for the workpieces formed by the 1 mm and 3 mm radii tools.

3.3. Bend Radius

Another aspect of the accuracy is the bend radius that is achievable by 3D-printed tools. Three different radii are tested in V-bending, with results shown in Figure 9 and Figure 10. The bend radii of the workpieces as function of the number of strokes in the same tool is shown in Figure 9. Figure 10 shows a comparison between the radius of the printed tools and the radius measured on the formed components. The nose radii of the R1 and R2 tools are not nominal, but the formed component adopts the measured nose radius closely. The scatter of measurements is also low, indicating that the repeatability is good. This implies that the deviation from nominal in the formed components is due to the accuracy of the printed tools, which could be compensated for. The R3 tool is different, in that the radius of the tool is close to nominal, but the radius of the formed component is not. The scatter in the measured radius is also larger than for components formed using the R1 and R2 tools. The shell thickness that is used when printing the tools is 2.1 mm for all punches regardless of the punch nose radius. As larger punch nose radius implies a larger contact area towards the workpiece, the constant shell thickness results in less stiff behavior from the punch nose when the radius is increased. The corresponding larger elastic deflection of the R3 tool would explain the increased radius and scatter measured on the bent workpieces.

4. Groove Pressing

The geometrical accuracy obtained by groove pressing (Figure 1b) is evaluated by the measurement strategy shown in Figure 5b. The geometrical accuracy of the tools, shown in Figure 2b, is also evaluated so that the analysis can be corrected for tool dimensions deviating from nominal. Two key features were selected for evaluating the workpiece accuracy: the angularity of the four flat parts and the height of the three grooves.

Figure 11 shows that the tools are printed with slight increasing height from H1 to H3. This is probably due to a slight tilting of the building plate during printing. The measured heights of the workpiece groove heights were relatively close to the heights imposed by the tools. The workpiece groove heights are very repeatable, with standard deviations between 0.6–1.1% across the three groves.

Figure 12 shows the angularity measured between the features that nominally sit on the same plane. The nominal angularity is therefore 180°. The figure shows that the tools are close to nominal. The average angularity measured on the workpiece is far from the nominal value of 180° due to spring-back and varies between the features. The largest deviation was observed on P4, which has an average value of 178.3 ± 0.12°. P3 has the closest value to nominal by 179.2 ± 0.11°. Spring-back after the nominally symmetric groove pressing is expected to increase angularity deviation from nominal with distance from the center. This explains why the deviation is larger in P4 than in P3. However, Figure 12 also shows that this cannot explain P1 and P2, because there is no symmetry in the resulting angularities. Since the tools are symmetrical in terms of angularity with respect to each other, the asymmetric angularity in the workpiece is due to the asymmetric groove heights in the tools, as shown in Figure 11.

The performance of the tools was also investigated over a small number of strokes. In this case, as mentioned in Section 2.4, the overall workpiece angularity is described by the angle between P1 and P4 and the reported height is an average value of H1, H2 and H3. Figure 13 shows the measured dimensions normalized with respect to the nominal values. The stability and repeatability of the measured values are good.

Regarding the height measurements, it is noticed that the standard deviations of both tools and workpieces are around 4%. The angularity is more stable and has standard deviations of 0.2%. The normalization shows that the angularity of the entire part is much closer to the nominal value than the height of the grooves. This is clearly linked to the deviation in the die, which could be compensated for. The angularity of the tools could also be altered by a small curvature to result in angularity of the workpieces after spring-back even closer to nominal.

5. Conclusions

This paper demonstrates the application of FFF to produce tools for sheet metal forming, exemplified by V-bending and grove pressing of aluminum sheets. The following conclusions can be drawn:

• Steady-state conditions were achieved in five strokes for the tool assembly with minimal wear detected in following strokes.
• The elastic deflection of the tools influence forming stroke and the final geometry after spring-back.
• The radius of the punch nose in V-bending should be considered relative to the shell-thickness used in printing the tools for optimal results.
• It is possible to form more complex shapes, which was here exemplified by groove pressing.
• Some compensation for spring-back will be possible due to low scatter in the final geometries.

The results of this work show the high potential of polymer tools in sheet metal forming for small series or prototyping, but also that there is room for improvement and further research in the field.