Prediction of Cracking Susceptibility of Commercial Aluminum Alloys during Solidification
Abstract
:1. Introduction
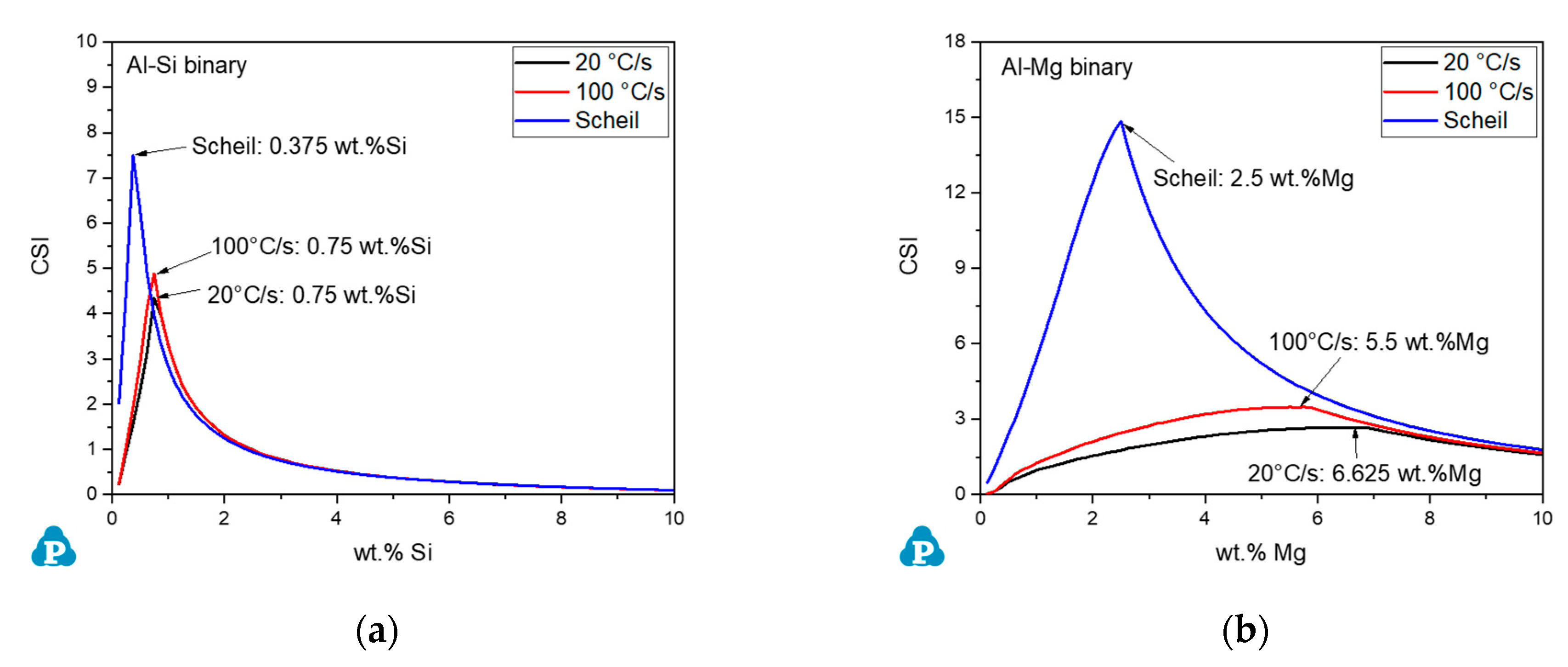
2. Solidification Simulation by the CALPHAD Method
3. Simulation of Hot Cracking Susceptibility of Commercial Aluminum Alloys
3.1. Hot Cracking Susceptibility of AA2xxx Series
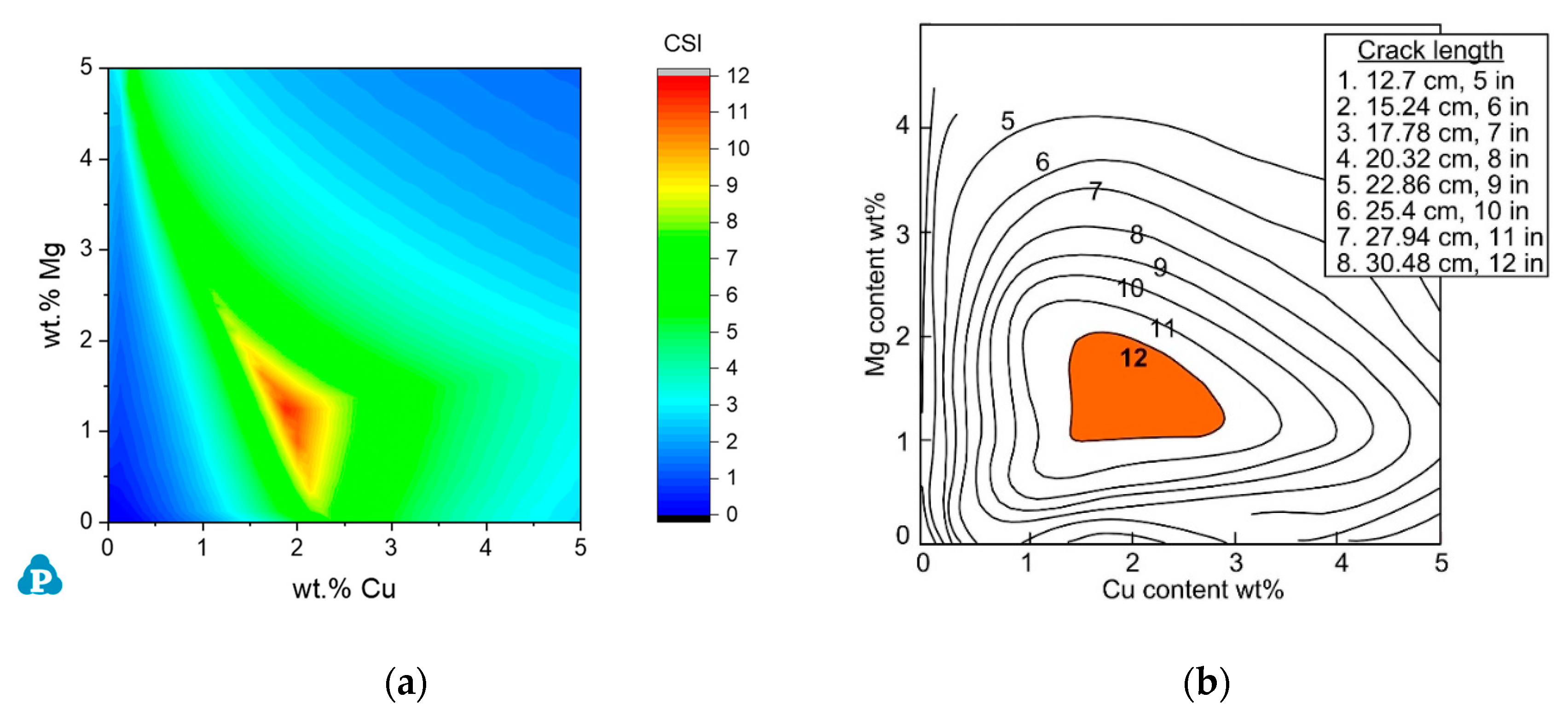
3.1.1. The Al-Cu-Mg Ternary System
3.1.2. Commercial AA2xxx Alloys
3.2. Hot Cracking Susceptibility of AA6xxx Series
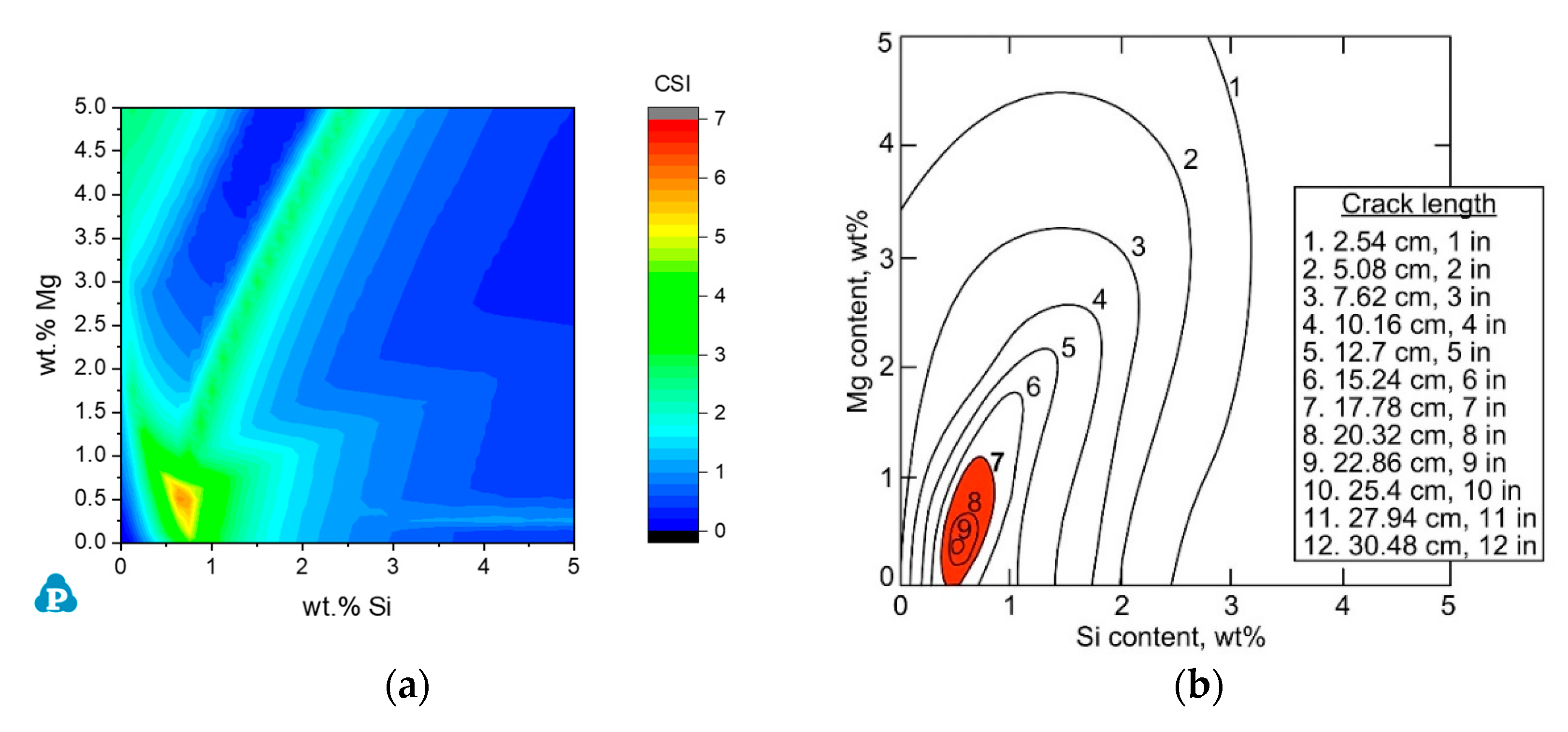
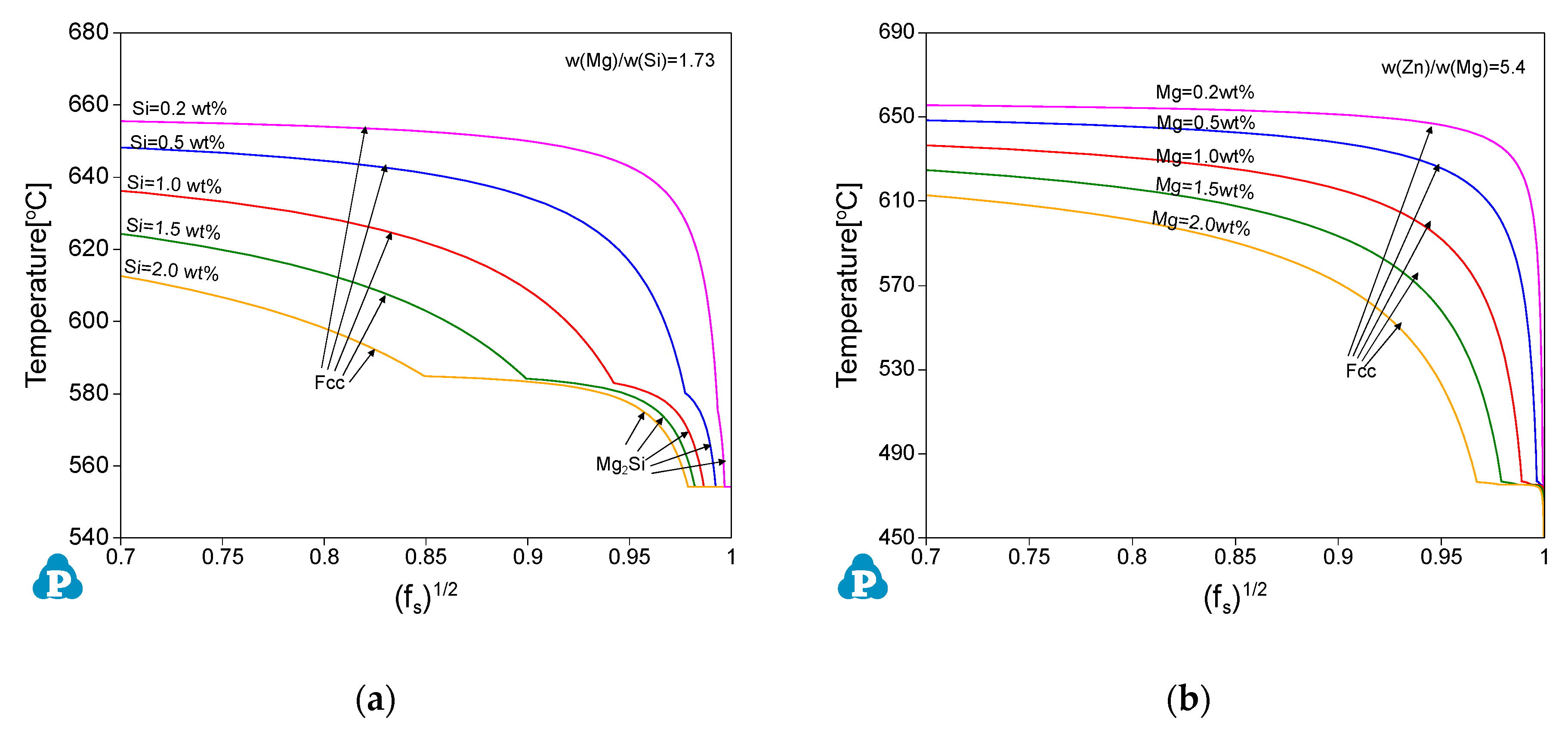
3.2.1. The Al-Mg-Si Ternary System
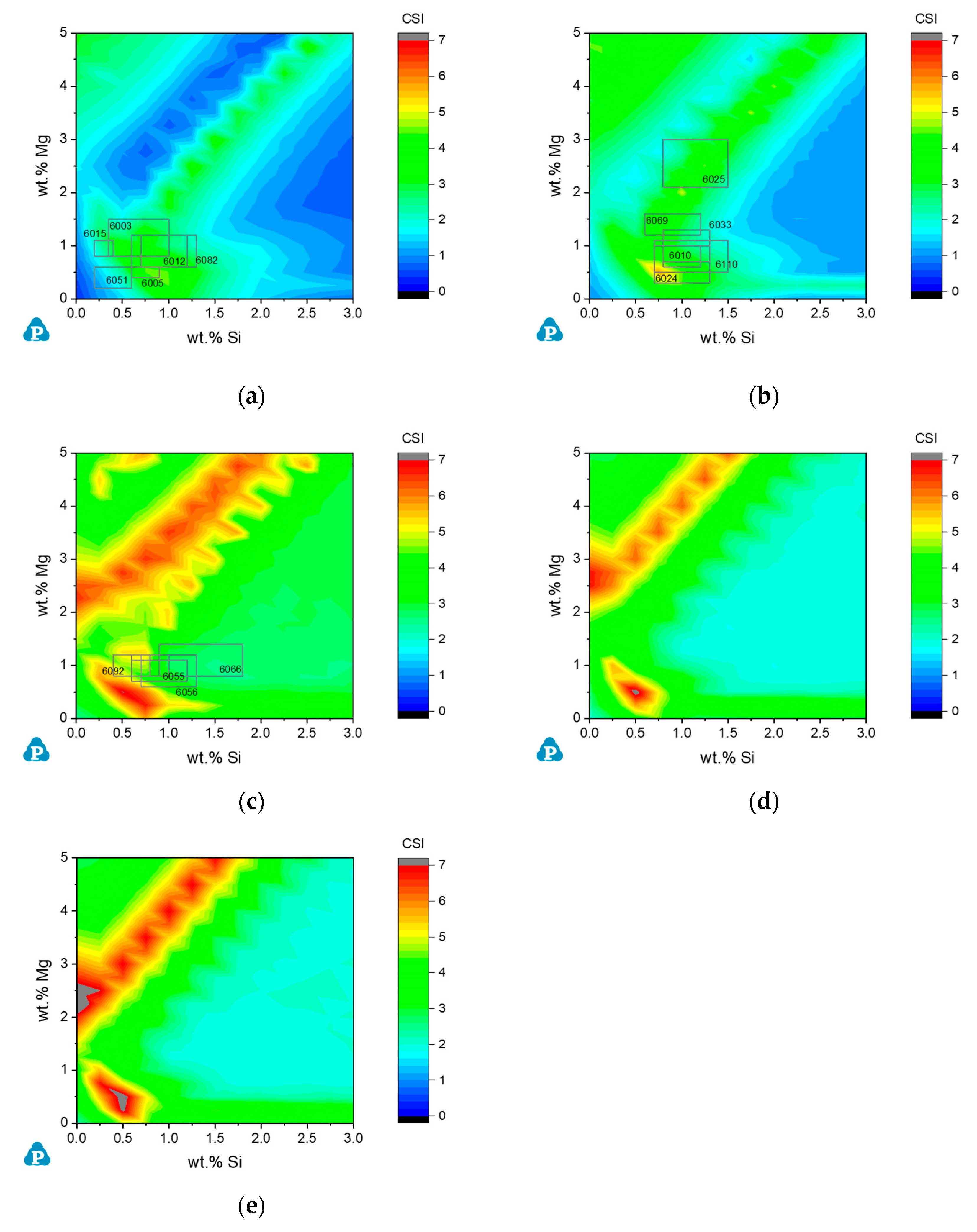
3.2.2. Commercial AA6xxx Alloys
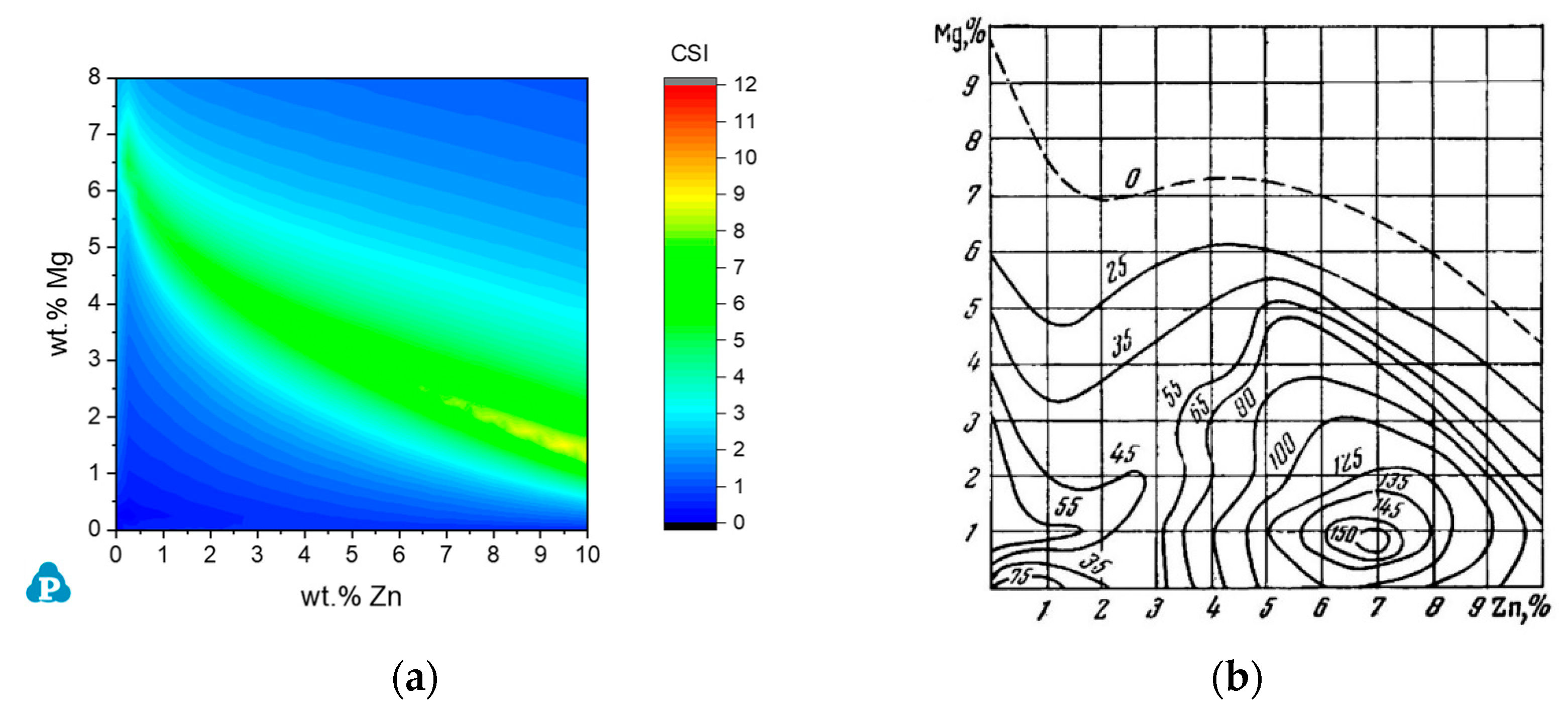
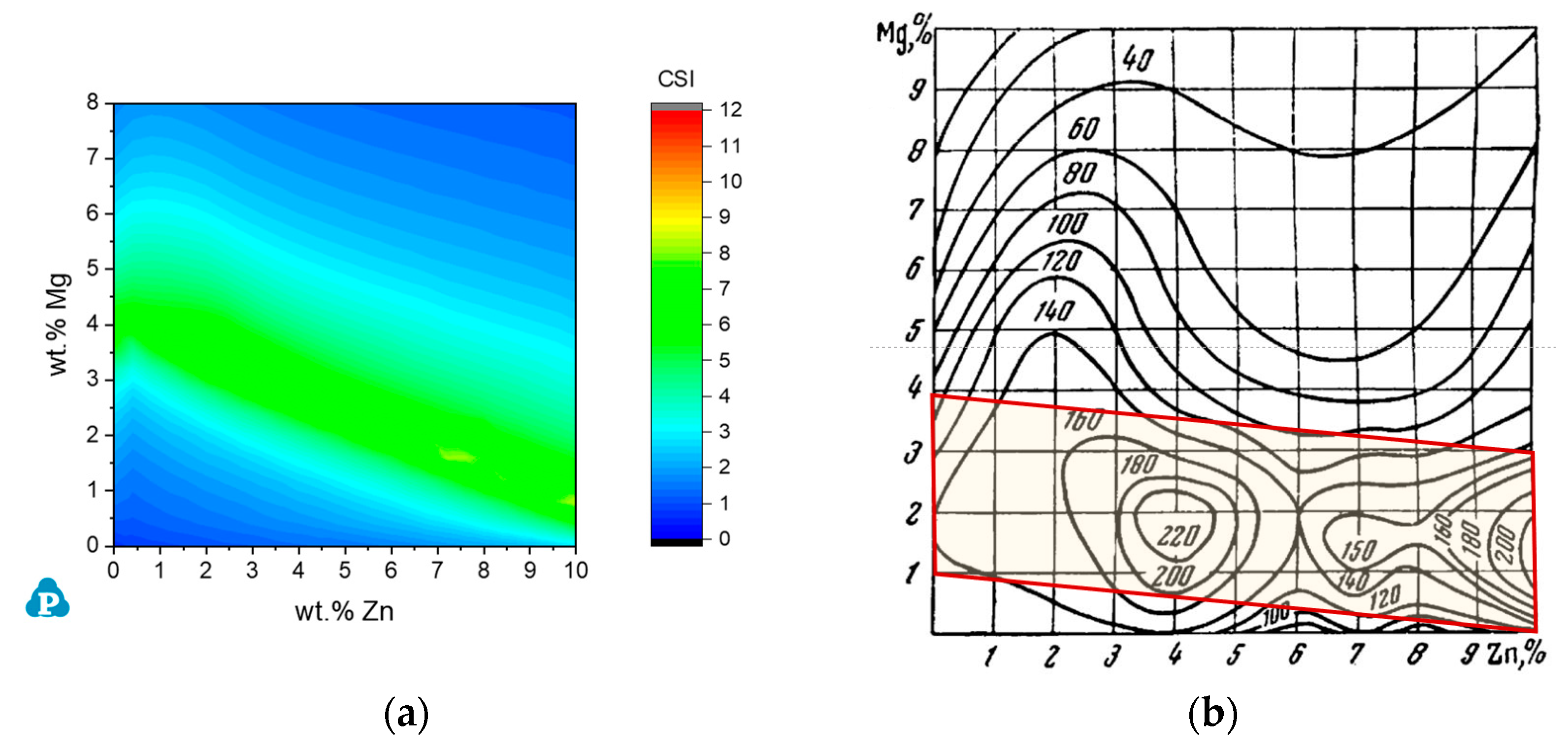
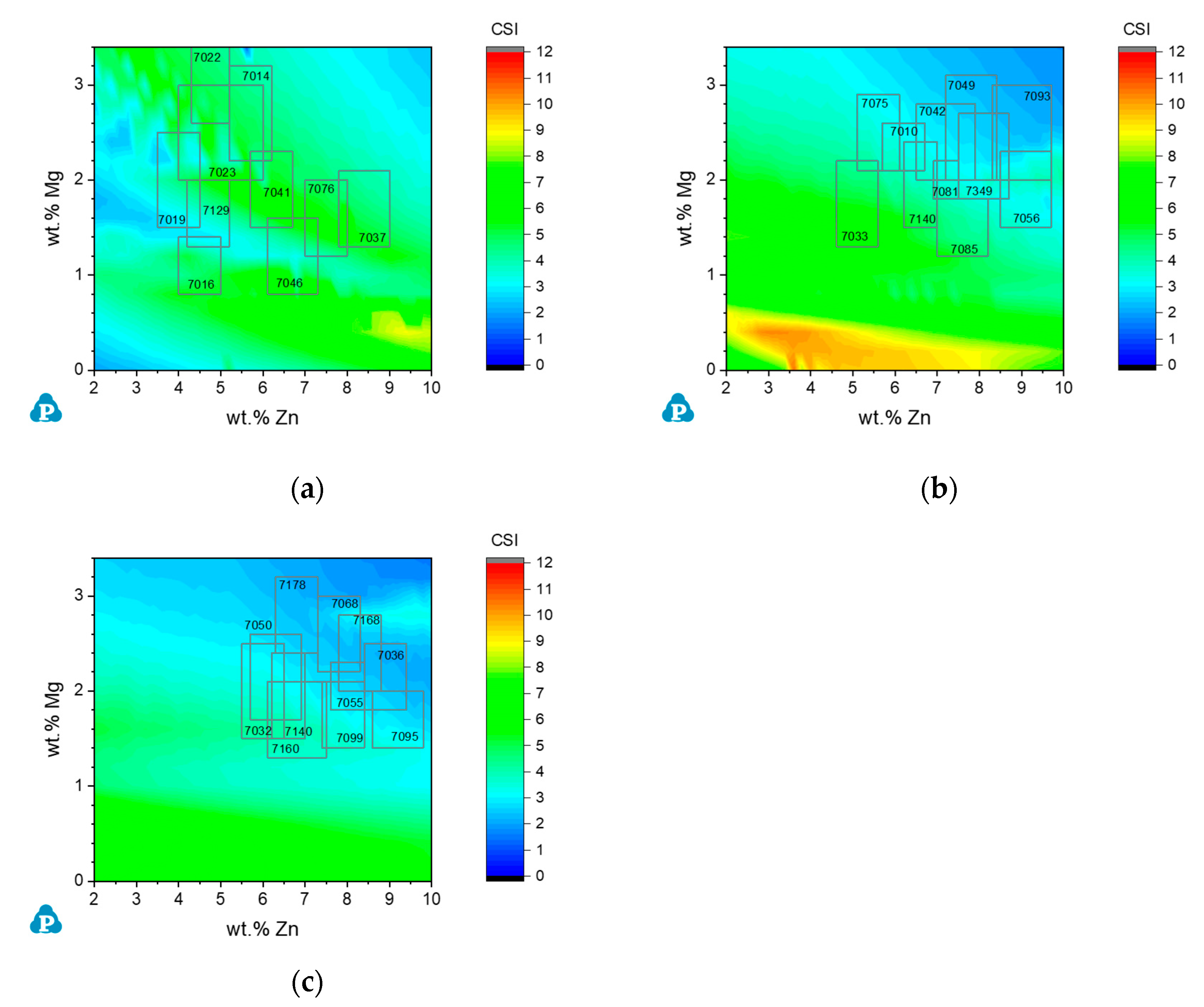
3.3. Hot Cracking Susceptibility of AA7xxx Series
3.3.1. The Al-Zn-Mg System
3.3.2. The Al-Mg-Zn-Cu System
3.3.3. Commercial AA7xxx Alloys
4. Discussion
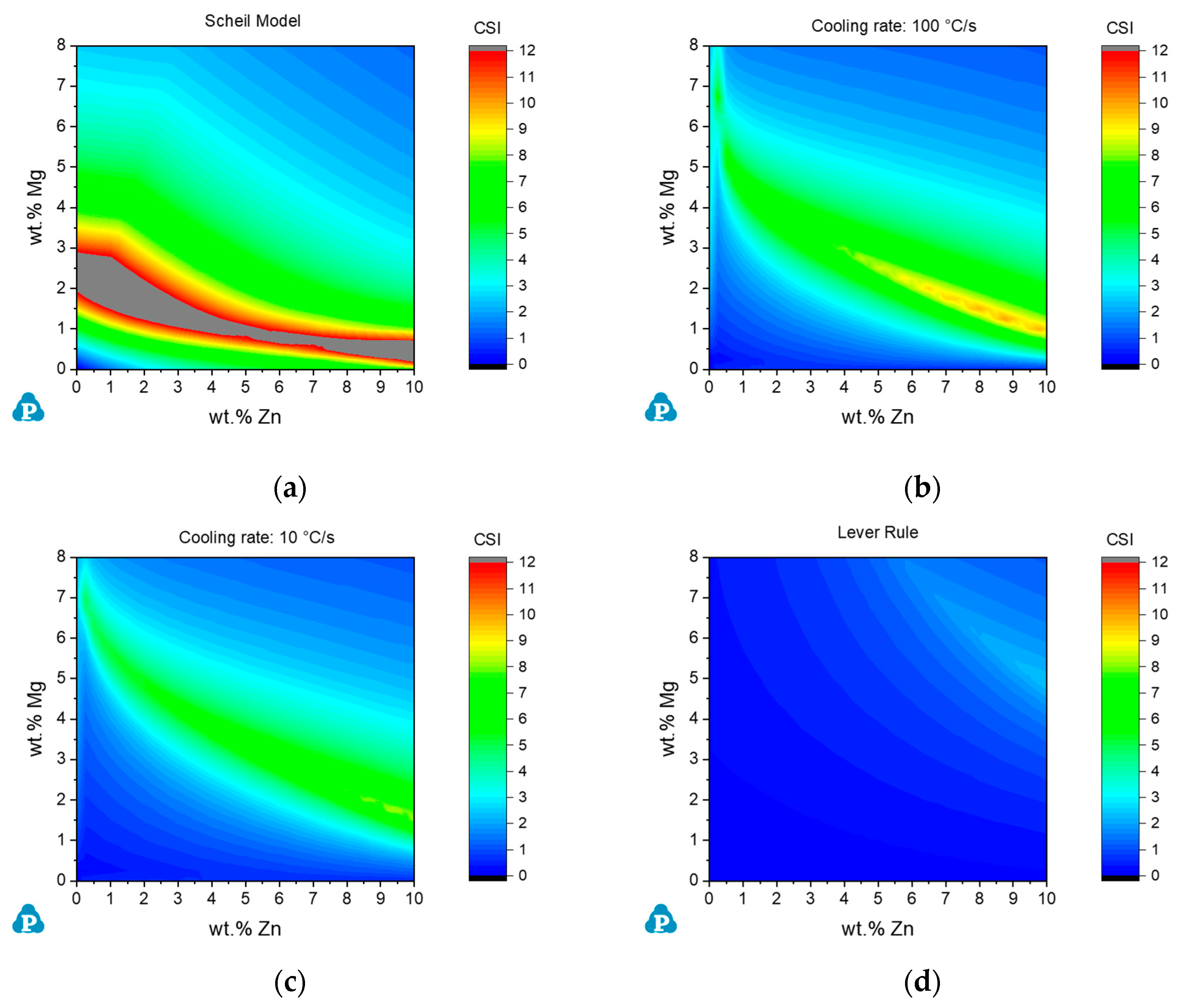
4.1. Effect of Cooling Rate
4.2. Comparison among AA2xxx, AA6xxx, and AA7xxx Alloys
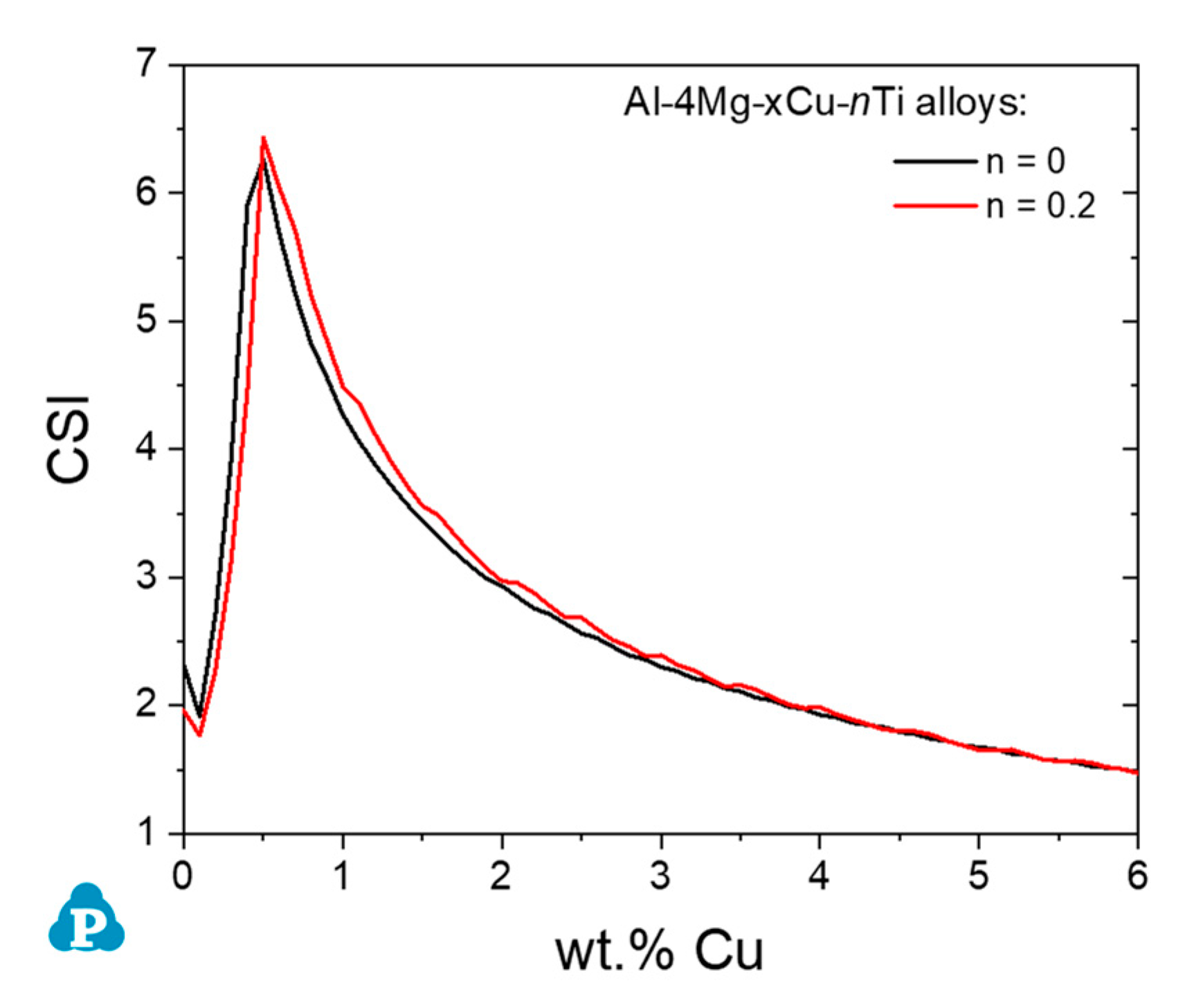
4.3. Effect of Minor Elements on Hot Cracking Behavior of Multi-Component Alloys
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Flemings, M.C. Solidification Processing; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Campbell, J. (Ed.) Castings, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2003. [Google Scholar]
- Kou, S. Welding Metallurgy, 3rd ed.; John Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Eskin, D.G.; Suyitno; Katgerman, L. Mechanical Properties in the Semi-Solid State and Hot Tearing of Aluminium Alloys. Prog. Mater. Sci. 2004, 49, 629–711. [Google Scholar] [CrossRef]
- Yan, X.; Lin, J.C. Prediction of Hot Tearing Tendency for Multicomponent Aluminum Alloys. Metall. Mater. Trans. B 2006, 37, 913–918. [Google Scholar] [CrossRef]
- Li, Y.; Li, H.; Katgerman, L.; Du, Q.; Zhang, J.; Zhuang, L. Recent Advances in Hot Tearing during Casting of Aluminium Alloys. Prog. Mater Sci. 2021, 117, 100741. [Google Scholar] [CrossRef]
- Prokhorov, N.N. Resistance to Hot Tearing of Cast Metals during Solidification. Russ. Cast. Prod. 1962, 2, 172–175. [Google Scholar]
- Feurer, U. Mathematisches Modell der Warmrissenigung von Binaeren Aluminiumlegierungen. Giesserei Forsch. 1976, 2, 75–80. [Google Scholar]
- Clyne, T.W.; Davies, G.J. The Influence of Composition on Solidification Cracking Susceptibility in Binary Alloy Systems. Br. Foundrym. 1981, 74, 65–73. [Google Scholar]
- Rappaz, M.; Drezet, J.M.; Gremaud, M. A New Hot-Tearing Criterion. Metall. Mater. Trans. A 1999, 30, 449–455. [Google Scholar] [CrossRef]
- Lees, D. The Hot Tearing Tendencies of Aluminium Casting Alloys. J. Inst. Met. 1946, 72, 343. [Google Scholar]
- Korolʹkov, A.M. Casting Properties of Metals and Alloys; Consultants Bureau: New York, NY, USA, 1963. [Google Scholar]
- Williams, J.; Singer, A. Deformation, Strength, and Fracture Above the Solidus Temperature. J. Inst. Met. 1968, 96, 5–12. [Google Scholar]
- Niyama, E. Japan-US Joint Seminar on Solidification of Metals and Alloys. Jpn. Soc. Promot. Sci. 1977, 271–282. [Google Scholar]
- Feurer, U. Quality Control of Engineering Alloys and the Role of Metals Science; Delft University of Technology: Delft, The Netherlands, 1977; pp. 131–145. [Google Scholar]
- Pellini, W.S. Strain Theory of Hot Tearing. Foundry 1952, 80, 124–133. [Google Scholar]
- Drezet, J.M.; Allehaux, D. Application of the Rappaz-Drezet-Gremaud Hot Tearing Criterion to Welding of Aluminium Alloys. In Hot Cracking Phenomena in Welds II; Böllinghaus, T., Herold, H., Cross, C.E., Lippold, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 27–45. [Google Scholar]
- Kou, S. A Criterion for Cracking during Solidification. Acta Mater. 2015, 88, 366–374. [Google Scholar] [CrossRef]
- Kou, S. A Simple Index for Predicting the Susceptibility to Solidification Cracking. Weld. J. 2015, 94, 374–388. [Google Scholar]
- Liu, J.; Kou, S. Effect of diffusion on susceptibility to cracking during solidification. Acta Mater. 2015, 100, 359–368. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Kou, S. Crack Susceptibility of Binary Aluminum Alloys during Solidification. Acta Mater. 2016, 110, 84–94. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Kou, S. Crack Susceptibility of Binary Aluminum Alloys: Analytical Equations. In Shape Casting: 6th International Symposium; Tiryakioǧlu, M., Jolly, M., Byczynski, G., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 11–18. [Google Scholar]
- Liu, J.; Duarte, H.P.; Kou, S. Evidence of Back Diffusion Reducing Cracking during Solidification. Acta Mater. 2017, 122, 47–59. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Kou, S. Susceptibility of Ternary Aluminum Alloys to Cracking during Solidification. Acta Mater. 2017, 125, 513–523. [Google Scholar] [CrossRef] [Green Version]
- Soysal, T.; Kou, S. A Simple Test for Assessing Solidification Cracking Susceptibility and Checking Validity of Susceptibility Prediction. Acta Mater. 2018, 143, 181–197. [Google Scholar] [CrossRef]
- Soysal, T.; Kou, S. Effect of Filler Metals on Solidification Cracking Susceptibility of Al Alloys 2024 and 6061. J. Mater. Process. Technol. 2019, 266, 421–428. [Google Scholar] [CrossRef]
- Stangeland, A.; Mo, A.; Nielsen, Ø.; M’Hamdi, M.; Eskin, D. Development of Thermal Strain in the Coherent Mushy Zone during Solidification of Aluminum Alloys. Metall. Mater. Trans. A 2004, 35, 2903–2915. [Google Scholar] [CrossRef]
- Spittle, J.A.; Brown, S.G.R. Numerical Modelling of Permeability Variation with Composition in Aluminium Alloy Systems and Its Relationship to Hot Tearing Susceptibility. Mater. Sci. Technol. 2005, 21, 1071–1077. [Google Scholar] [CrossRef]
- Kool, W.H.; Katgerman, L. Hot Tearing Criteria Evaluation for Direct-Chill Casting of an Al-4.5 Pct Cu Alloy. Metall. Mater. Trans. A 2005, 36, 1537–1546. [Google Scholar] [CrossRef]
- Savran, V.I.; Katgerman, L.; Eskin, D.G. Effects of Alloy Composition and Casting Speed on Structure Formation and Hot Tearing during Direct-Chill Casting of Al-Cu Alloys. Metall. Mater. Trans. A 2004, 35, 3551–3561. [Google Scholar] [CrossRef]
- Han, J.; Wang, J.; Zhang, M.; Niu, K. Susceptibility of Lithium Containing Aluminum Alloys to Cracking during Solidification. Materialia 2019, 5, 100203. [Google Scholar] [CrossRef]
- Liu, J.; Zeng, P.; Kou, S. Solidification Cracking Susceptibility of Quaternary Aluminium Alloys. Sci. Technol. Weld. Join. 2021, 26, 244–257. [Google Scholar] [CrossRef]
- Cao, W.; Chen, S.L.; Zhang, F.; Wu, K.; Yang, Y.; Chang, Y.A.; Schmid-Fetzer, R.; Oates, W.A. PANDAT Software with PanEngine, PanOptimizer and PanPrecipitation for Multi-Component Phase Diagram Calculation and Materials Property Simulation. Calphad 2009, 33, 328–342. [Google Scholar] [CrossRef]
- Pandat Software. Thermodynamic Calculations and Kinetic Simulations; CompuTherm LLC: Middleton, WI, USA, 2021. [Google Scholar]
- PanAluminum. Combined Thermodynamic and Mobility Database of Multicomponent Aluminum Alloys; PanAluminum: Middleton, WI, USA, 2021. [Google Scholar]
- Kaufman, L.; Bernstein, H. Computer Calculation of Phase Diagrams; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Saunders, N.; Miodownik, A.P. CALPHAD Calculation of Phase Diagrams: A Comprehensive Guide; Pergamon: New York, NY, USA, 1998. [Google Scholar]
- Chang, Y.A.; Chen, S.L.; Zhang, F.; Yan, X.Y.; Xie, F.Y.; Schmid-Fetzer, R.; Oates, W.A. Phase Diagram Calculation: Past, Present and Future. Prog. Mater. Sci. 2004, 49, 313–345. [Google Scholar] [CrossRef]
- Lukas, H.L.; Fries, S.G.; Sundman, B. Computational Thermodynamics: The CALPHAD Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Kattner, U.R. The CALPHAD Method and Its Role in Material and Process Development. Tecnol. Metal. Mater. Miner. 2016, 13, 3–15. [Google Scholar] [CrossRef]
- Andersson, J.O.; Agren, J. Models for Numerical Treatment of Multicomponent Diffusion in Simple Phases. J. Appl. Phys. 1992, 72, 1350–1355. [Google Scholar] [CrossRef]
- Campbell, C.E.; Boettinger, W.J.; Kattner, U.R. Development of a Diffusion Mobility Database for Ni-Base Superalloys. Acta Mater. 2002, 50, 775–792. [Google Scholar] [CrossRef]
- Campbell, C.E.; Kattner, U.R.; Liu, Z.-K. The Development of Phase-Based Property Data Using the CALPHAD Method and Infrastructure Needs. Integr. Mater. Manuf. Innov. 2014, 3, 12. [Google Scholar] [CrossRef] [Green Version]
- National Research Council. Integrated Computational Materials Engineering: A Transformational Discipline for Improved Competitiveness and National Security; The National Academies Press: Washington, DC, USA, 2008. [Google Scholar]
- Zhang, C.; Miao, J.; Chen, S.; Zhang, F.; Luo, A.A. CALPHAD-Based Modeling and Experimental Validation of Microstructural Evolution and Microsegregation in Magnesium Alloys During Solidification. J. Phase Equilib. Diffus. 2019, 40, 495–507. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, C.; Liang, S.M.; Lv, D.C.; Chen, S.L.; Cao, W.S. Simulation of the Composition and Cooling Rate Effects on the Solidification Path of Casting Aluminum Alloys. J. Phase Equilib. Diffus. 2020, 41, 793–803. [Google Scholar] [CrossRef]
- Gulliver, G.H. The Quantitative Effect of Rapid Cooling upon the Constitution of Binary Alloys. J. Inst. Met. 1913, 9, 120–157. [Google Scholar]
- Scheil, E. Remarks on the Crystal Layer Formation. Z. Metallkd. 1942, 34, 70–72. [Google Scholar]
- Pumphrey, W.I.; Lyons, J.V. Cracking during the Casting and Welding of the More Common Binary Aluminium Alloys. J. Inst. Met. 1948, 74, 439–455. [Google Scholar]
- Rosenberg, R.A.; Flemings, M.C.; Taylor, H.F. Nonferrous Binary Alloys Hot Tearing. AFS Trans. 1960, 69, 518–528. [Google Scholar]
- Novikov, I.I. Hot-Shortness of Nonferrous Metals and Alloys. Russ. Cast. Prod. 1962, 4, 167–172. [Google Scholar]
- Spittle, J.A.; Cushway, A.A. Influences of Superheat and Grain Structure on Hot-Tearing Susceptibilities of Al-Cu Alloy Castings. Met. Technol. 1983, 10, 6–13. [Google Scholar] [CrossRef]
- Cross, C.E.; Olson, D.L. Hot Tearing Model to Assess Aluminum Weldability. Alum. Alloy. Phys. Mech. Prop. 1986, 3, 1869–1875. [Google Scholar]
- Pumphrey, W.; Moore, D. Cracking during and After Solidification in Some Aluminium-Copper-Magnesium Alloys of High Purity. J. Inst. Met. 1948, 74, 425–438. [Google Scholar]
- Jennings, P.H.; Singer, A.R.E.; Pumphrey, W.I. Hot-Shortness of Some High-Purity Alloys in the Systems Aluminium-Copper-Silicon and Aluminium-Magnesium-Silicon. J. Inst. Met. 1948, 74, 227–248. [Google Scholar]
- Novikov, I.I. Hot-Shortness of Nonferrous Metals and Alloys; Defense Technical Information Center: Fort Belvoir, VA, USA, 1968. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Liang, S.; Zhang, C.; Chen, S.; Lv, D.; Cao, W.; Kou, S. Prediction of Cracking Susceptibility of Commercial Aluminum Alloys during Solidification. Metals 2021, 11, 1479. https://doi.org/10.3390/met11091479
Zhang F, Liang S, Zhang C, Chen S, Lv D, Cao W, Kou S. Prediction of Cracking Susceptibility of Commercial Aluminum Alloys during Solidification. Metals. 2021; 11(9):1479. https://doi.org/10.3390/met11091479
Chicago/Turabian StyleZhang, Fan, Songmao Liang, Chuan Zhang, Shuanglin Chen, Duchao Lv, Weisheng Cao, and Sindo Kou. 2021. "Prediction of Cracking Susceptibility of Commercial Aluminum Alloys during Solidification" Metals 11, no. 9: 1479. https://doi.org/10.3390/met11091479
APA StyleZhang, F., Liang, S., Zhang, C., Chen, S., Lv, D., Cao, W., & Kou, S. (2021). Prediction of Cracking Susceptibility of Commercial Aluminum Alloys during Solidification. Metals, 11(9), 1479. https://doi.org/10.3390/met11091479





