Damage-Based Assessment of the Fatigue Crack Initiation Site in High-Strength Steel Welded Joints Treated by HFMI
Abstract
:1. Introduction
2. Materials and Experimental Methods
2.1. Material Property and Specimen Detail
2.2. Residual Stress Measurement Methods
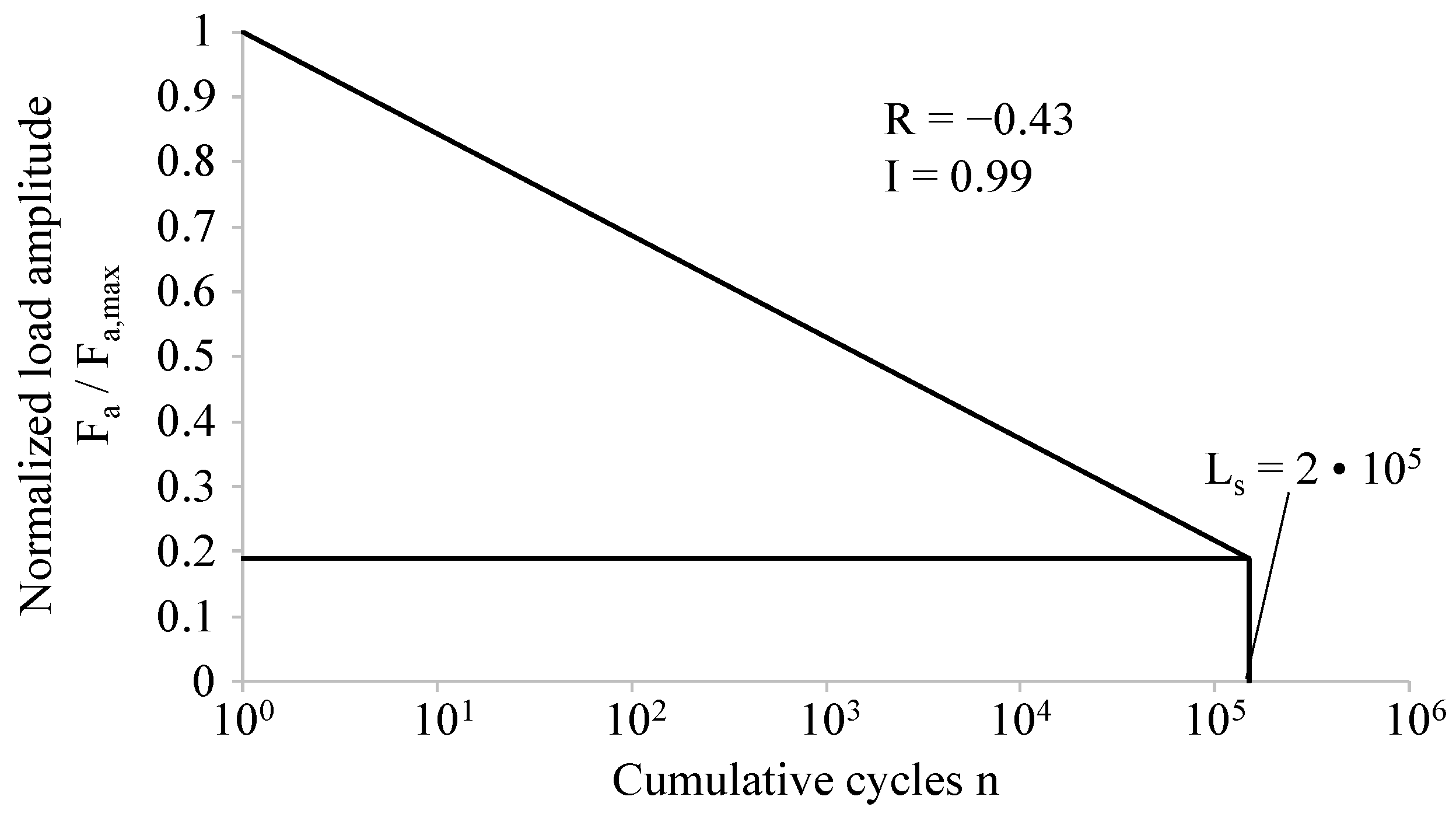
2.3. Fatigue Test Methods
3. Experimental Results
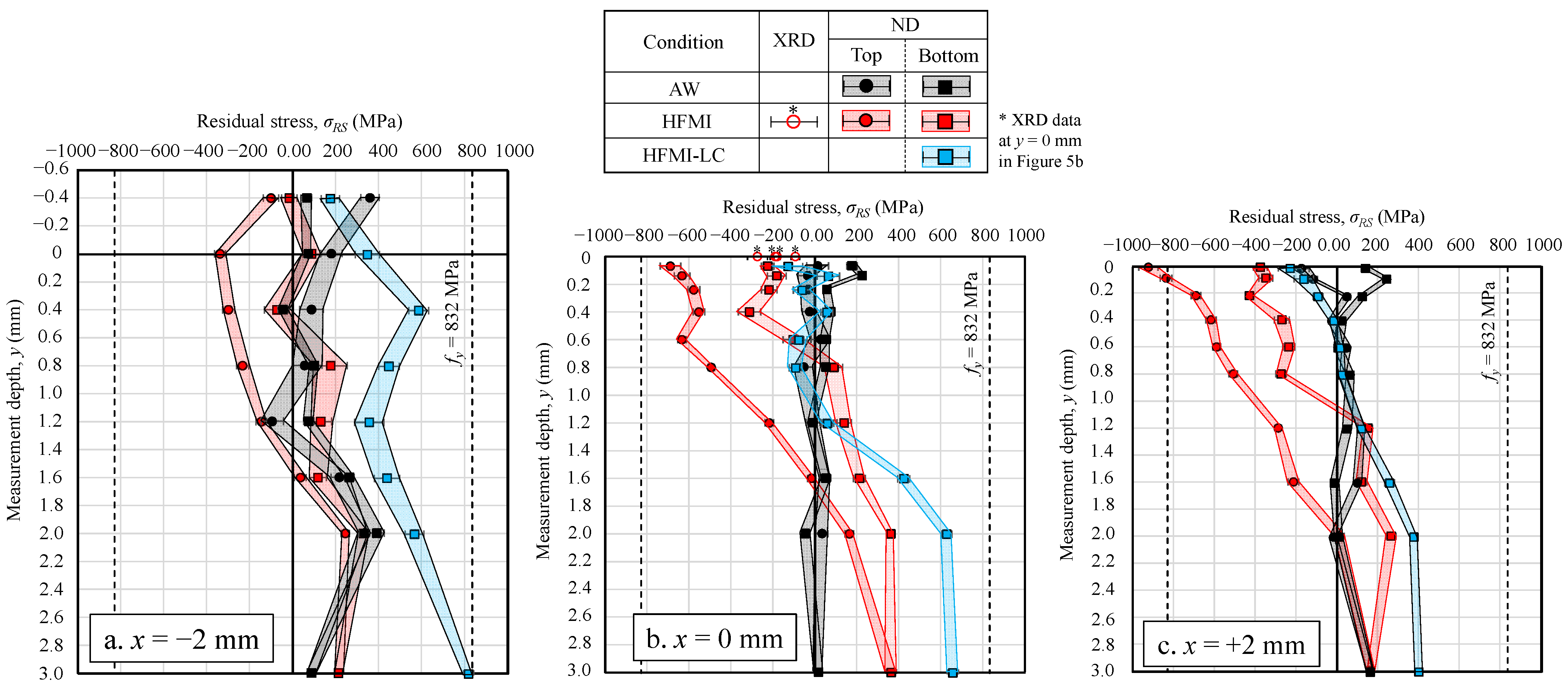
3.1. Results of the Residual Stress Measurement
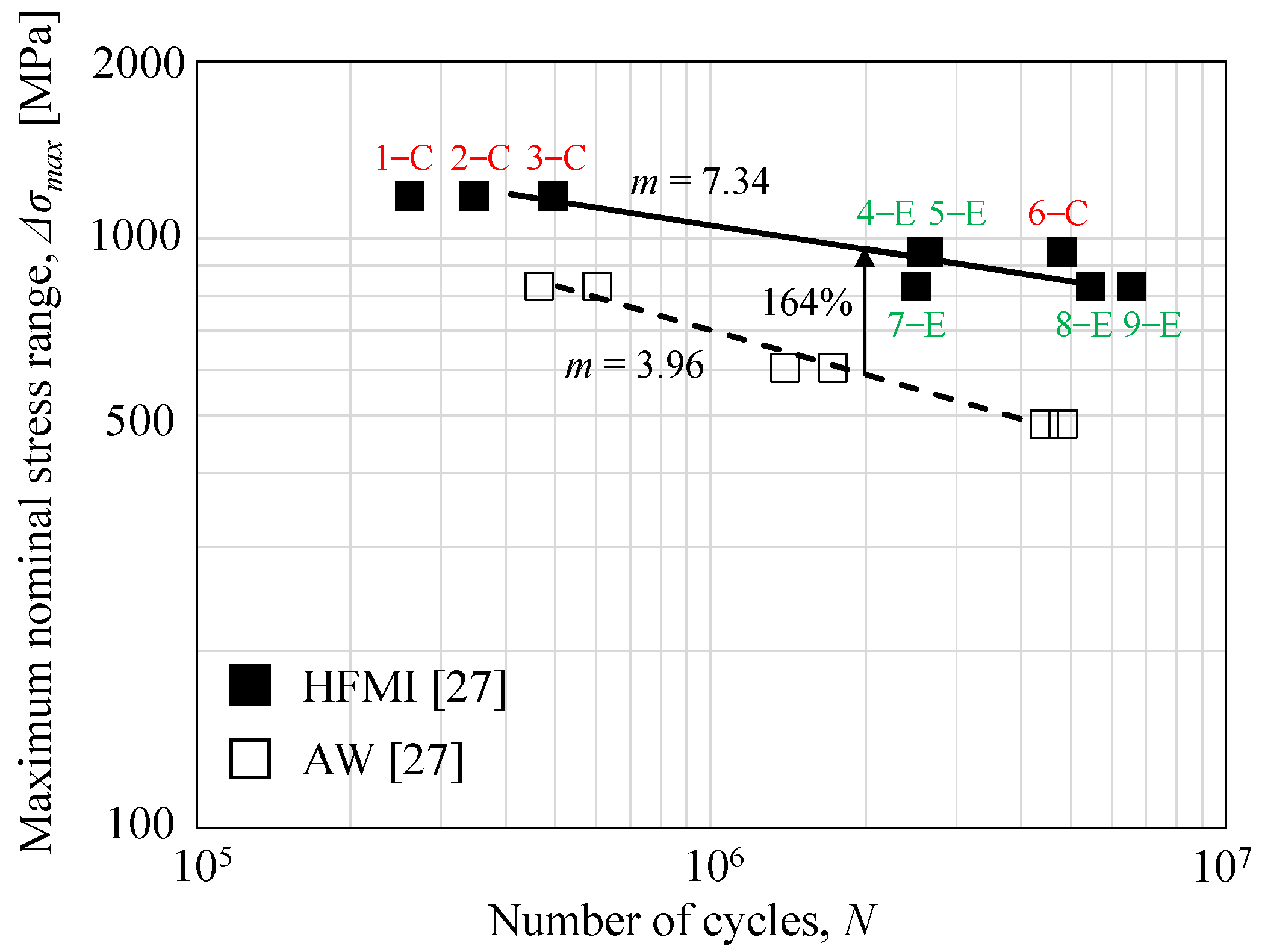
3.2. Results of the Fatigue Tests and Fracture Observations
4. Numerical Methods
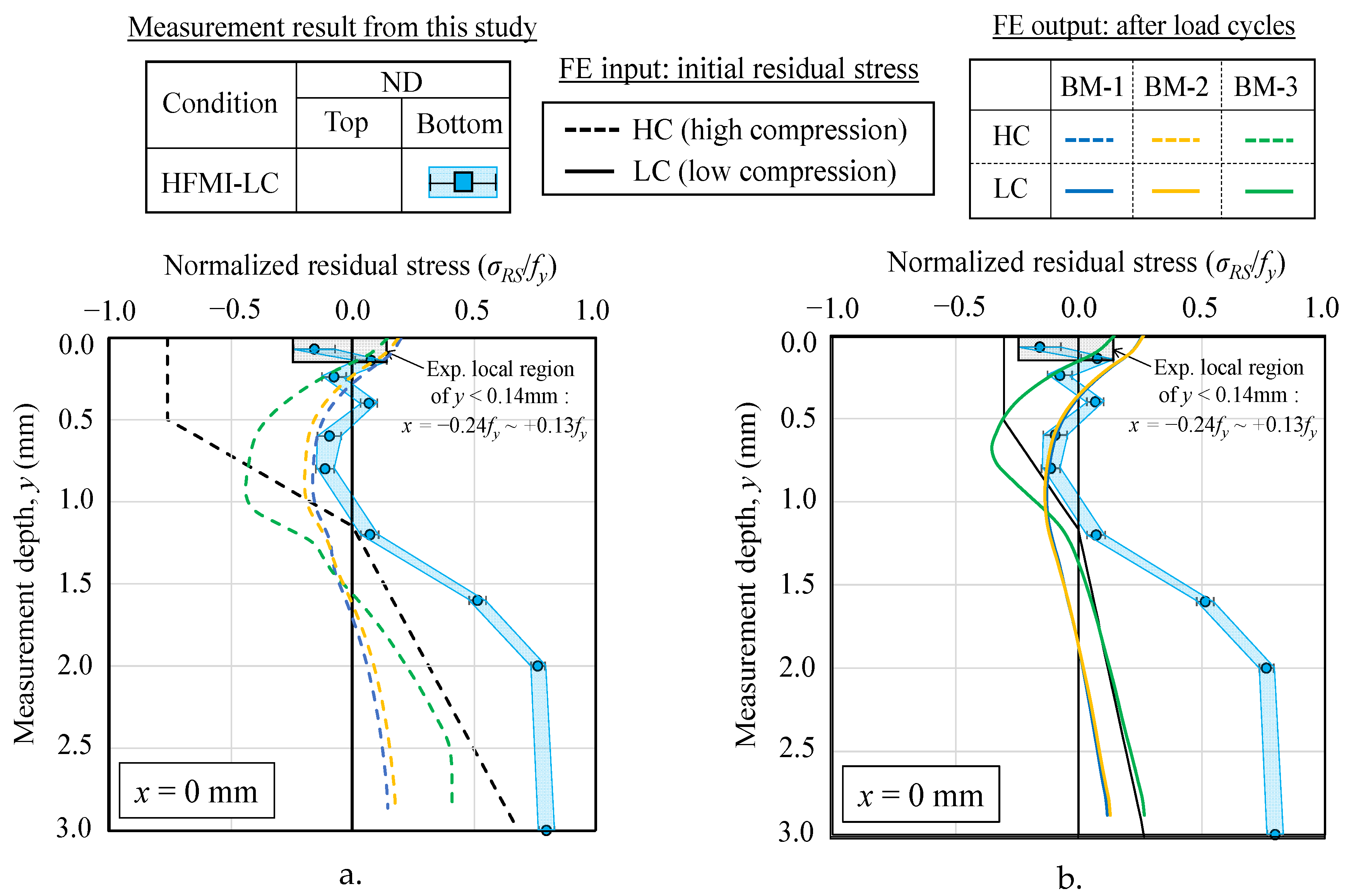
5. Numerical Results
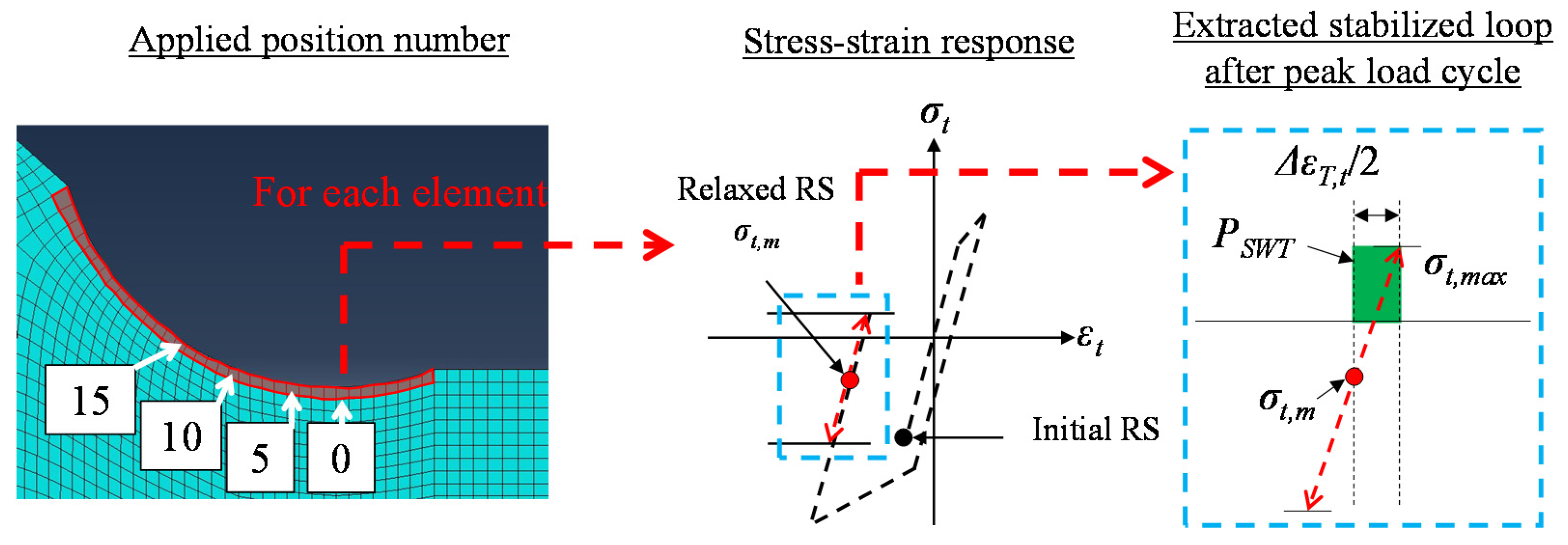
6. Fatigue Damage Assessment Considering Residual Stress Relaxation
7. Conclusions
- At the HFMI groove bottom, the in-depth profiles of residual stress showed the high compressive stress of about −0.30fy to −0.76fy within 0.5 mm of depth. The compressive stresses were maintained up to the depths in the range of 0.70 to 1.60 mm and were shifted to tensile stresses more deeply, which in-depth gradient was even steeper than that observed on available data of S355 steel grade. The high peak stress equal to 0.8fy led to a significant reduction of the beneficial compressive stresses, which, after relaxation, were close to zero near the surface and up to 1.2 mm, and remain tensile more deeply.
- Different features on fracture surface, crack pattern, crack initiation site, and crack initiation type were observed according to different applied high peak stresses. Particularly interesting, as the applied peak stress was lowered from 1.0fy to 0.7fy, the initiation site within the weld shifted from the HFMI groove to near the boundary between the HFMI-treated zone and the weld metal. In the latter case, the lap-type imperfections for the site near the boundary became the origin of crack initiation.
- The FE models developed, incorporating the measured in-depth residual stress profiles and applied load cycle with high peak load, was able to reproduce the residual stresses after relaxation; however, it was accurate only at the near surface with the HFMI treatment region.
- The simulation results with the FE models demonstrated that the significant reduction of compressive residual stress near the surface, observed in residual stress measurement, was mainly occurred by compressive peak stress, as it led to immediate local yielding on the compressive sides of the HFMI treatment region.
- The damage-based assessment considering the local mean stress after high peak stress equal to 1.0fy and 0.7fy confirmed a shift of the crack initiation most prone position along the surface of the HFMI groove, resulting from a combination of stress concentration and relaxation effect of residual stresses.
- When the peak stress was equal to 1.0fy, full relaxation of the compressive residual stress took place, such that cracks initiated from the HFMI groove where the stress concentration was dominant; less relaxation occurred under the peak stress equal to 0.7fy. Thus, in the latter case, the lap-type imperfections located near the boundary of the treatment became more critical for initiating the cracks even though the stress concentration was smaller than that of the HFMI groove. The above explains and confirms the experimental observations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Ref | Author | Steel Grade (fy) | Specimen Geometry | Method of Residual Stress Measurement | ||
|---|---|---|---|---|---|---|
| L × W × T | H × tg | h | ||||
| [31] | Kuhlman. 2006 | S690QL (813 MPa) | 23 × 160 × 12 | 18 × 12 | 5.7 | ·Hole drilling (1.80 mm hole): 1.5 mm away from weld toe |
| [32] | Kuhlman. 2009 | S690QL (830 MPa) | 26 × 80 × 12 | 40 × 12 | 7.1 | ·Hole drilling (1.77 mm hole): 1.0 mm away from weld toe |
| [35] | Ranjan. 2016 | A514 (793 MPa) | 19 × 30 × 9.5 | 25 × 6.4 | 6.4 | ·Laser X-ray diffaction (sin2ψ) & Layer removal by electronic poslihing |
| [27] | Yildirim. 2020 & This study | S690QL (832 MPa) | 14 × 40 × 6 | 40 × 6 | 4.2 | ·X-ray diffaction (sin2ψ, 1-mm collimator) ·Nutron diffraction at SALSA (0.6 × 2.0 × 0.6 mm3 or 2.0 × 2.0 × 2.0 mm3 collimator) |
| [33] | Tehrani Yekta. 2012 | 350W (396 MPa) | 19 × 30 × 9.5 | 25 × 6.4 | 6.4 | ·Laser X-ray diffaction (sin2ψ) & Layer removal by electronic poslihing |
| [14] | Quilliec. 2013 | S355K2 (490 MPa) | -×-×15 | -×15 | - | ·X-ray diffraction (2.5 × 1.0 × 0.006 mm3 collimator) |
| [34] | Suzuki. 2014 | SM490 (≥325 MPa) | -×100 × 16 | 50 × 16 | - | ·X-ray diffraction ·Neutron-diffraction (2.0 × 2.0 × 2.0 mm3 collimator) |
| [36] | Leitner. 2015 | S355 (≥350 MPa) | -×90 × 13 | 40 × 16 | - | ·X-ray diffaction (sin2ψ, 1-mm collimator) |
| [37] | Polezhayeva. 2015 | 080A15 (560 MPa) | 46 × 80 × 20 | 50 × 20 | 13 | ·Neutron-diffraction at UK’s ISIS neutron source (1-mm collimator ) |
| [22] | Schubnell. 2020 | S355J2 + N (420 MPa) | 21 × 50 × 10 | 50 × 10 | 5.7 | ·X-ray diffaction (2-mm collimator) ·Neutron diffraction (2.0 × 2.0 × 2.0 mm3 or 2.0 × 2.0 × 5.0 mm3 collimator) |
| Ref | Author | Method | Ultrasonic Frequency (kHz) | Ultrasonic Amplitude (μm) | Impact Frequency (Hz) | Indenter Diameter, D or Tip Radius, R (mm) | Travel Speed (m/mm) | Note |
|---|---|---|---|---|---|---|---|---|
| [31] | Kuhlman. 2006 | UIT | 27 | 3 (D) | Power consumption: 900 W | |||
| [32] | Kuhlman. 2009 | PIT | 90 | 2.0(R)8.0(D)/2.5(R)8.0(D) | 2–3 | Working pressure: 6 bars Angle for plate: 50–70 degree | ||
| [35] | Ranjan. 2016 | UIT | 20 | 50–60 | 220 | 3.0(R) | ||
| [27] | Yildirim. 2020 & This study | UNP | 20 | 30–60 | 100–400 | 1.5(R) | Angle for plate: 45 degree Angle for travel direction: 90 degree | |
| [33] | Tehrani Yekta. 2012 | UIT | 27–29 | 6.0 | Number of pass: 4 Angle for plate: 30–60 degree Groove radius: 1.69–2.37 Groove depth: 0.27–0.36 | |||
| [14] | Quilliec. 2013 | UIT | 27 | 3.0(D) | 4.0 | Power consumption: 1200 W Number of pass: 1 Indenter: 3 pins Angle for plate: 67 degree | ||
| [34] | Suzuki. 2014 | UIT | 27 | 30 | 3.0(R) | 6.0 | Power consumption: 1000 W | |
| [36] | Leitner. 2015 | PIT | 2.0(R) | 0.6–1.8 | Angle for plate: 30–60 degree Angle for travel direction: 90 degree | |||
| [37] | Polezhayeva. 2015 | UIT | ||||||
| [22] | Schubnell. 2020 | PIT | 90 | Working pressure: 6 bars |
References
- Statnikov, E.S. Application of Operational Ultrasonic Impact Treatment (UIT) Technologies in Production of Welded Joints; IIW Doc. XIII-1667-97; International Institute of Welding: Paris, France, 1997; Available online: http://www.appliedultrasonics.com/pdf/APPLICATIONS_OF_OPERATIONAL_ULTRASONIC_IMPACT_TREATMENT_(UIT)_TECHNOLOGIES_IN_PRODUCTION_OF_WELDED_JOINTS.html (accessed on 26 December 2021).
- Roy, S.; Fisher, J.W.; Yen, B.T. Fatigue resistance of welded details enhanced by ultrasonic impact treatment (UIT). Int. J. Fatigue 2003, 25, 1239–1247. [Google Scholar] [CrossRef]
- Huo, L.; Wang, D.; Zhang, Y. Investigation of the fatigue behaviour of the welded joints treated by TIG dressing and ultrasonic peening under variable-amplitude load. Int. J. Fatigue 2005, 27, 95–101. [Google Scholar] [CrossRef]
- Tominaga, T.; Matsuoka, K.; Sato, Y.; Suzuki, T. Fatigue improvement of weld repaired crane runway girder by ultrasonic impact treatment. Weld. World 2008, 52, 50–62. [Google Scholar] [CrossRef]
- Weich, I.; Ummenhofer, T.; Nitschke-Pagel, T.; Dilger, K.; Eslami, H. Fatigue behaviour of welded high-strength steels after high frequency mechanical post-weld treatments. Weld. World 2009, 53, 322–332. [Google Scholar] [CrossRef]
- Kudryavtsev, Y.; Kleiman, J. Increasing Fatigue Strength of Welded Joints by Ultrasonic Impact Treatment; IIW Document XIII- 2338-10; International Institute of Welding: Paris, France, 2010; Available online: http://sintes.ca/documents/IIWDocumentXIII-2338-10.2010UIT-UP.pdf (accessed on 26 December 2021).
- Maddox, S.J.; Dore, M.J.; Smith, S.D. A case study of the use of ultrasonic peening for upgrading a welded steel structure. Weld. World 2011, 55, 56–67. [Google Scholar] [CrossRef]
- Yıldırım, H.C.; Leitner, M.; Marquis, G.B.; Stoschka, M.; Barsoum, Z. Application studies for fatigue strength improvement of welded structures by high-frequency mechanical impact (HFMI) treatment. Eng. Struct. 2016, 106, 422–435. [Google Scholar] [CrossRef]
- Marquis, G.; Barsoum, Z. IIW Recommendation on High Frequency Mechanical Impact (HFMI) Treatment for Improving the Fatigue Strength of Welded Joints. In IIW Recommendations for the HFMI Treatment; Springer: Singapore, 2016; pp. 1–34. Available online: https://link.springer.com/chapter/10.1007/978-981-10-2504-4_1 (accessed on 26 December 2021).
- Yildirim, H.C. Recent results on fatigue strength improvement of high-strength steel welded joints. Int. J. Fatigue 2017, 101, 408–420. [Google Scholar] [CrossRef]
- Leitner, M.; Barsoum, Z. Effect of increased yield strength, R-ratio, and plate thickness on the fatigue resistance of high-frequency mechanical impact (HFMI)-treated steel joints. Weld. World 2020, 64, 1245–1259. [Google Scholar] [CrossRef]
- Mori, T.; Shimanuki, H.; Tanaka, M. Influence of steel static strength on fatigue strength of web-gusset welded joints with UIT. J. JSCE 2014, 70, 210–220. (In Japanese) [Google Scholar] [CrossRef]
- Lihavainen, V.M.; Marquis, G. Fatigue life estimation of ultrasonic impact treated welds using a local strain approach. Steel Res. Int. 2008, 77, 896–900. [Google Scholar] [CrossRef]
- Quilliec, L.G.; Lieurade, H.P.; Bousseau, M.; Drissi-Habti, M.; Inglebert, G.; Macquet, P.; Jubin, L. Mechanical and modelling of high-frequency mechanical impact and its effect on fatigue. Weld. World 2013, 57, 97–111. [Google Scholar] [CrossRef]
- Schubnell, J.; Hardenacke, V.; Farajian, M. Strain-based critical plane approach to predict the fatigue life of high frequency mechanical impact (HFMI)-treated welded joints depending on the material condition. Weld. World 2017, 61, 1199–1210. [Google Scholar] [CrossRef]
- Schubnell, J.; Pontner, P.; Wimpory, R.C.; Farajian, M.; Schulze, V. The influence of work hardening and residual stresses on the fatigue behavior of high frequency mechanical impact treated surface layers. Int. J. Fatigue 2020, 134, 105450. [Google Scholar] [CrossRef]
- Yıldırım, H.C.; Marquis, G.B. A round robin study of high frequency mechanical impact (HFMI)-treated welded joints subjected to variable amplitude loading. Weld. World 2013, 57, 437–447. [Google Scholar]
- Mikkola, E.; Doré, M.; Marquis, G.B.; Khurshid., M. Fatigue assessment of high-frequency mechanical impact (HFMI)-treated welded joints subjected to high mean stresses and spectrum loading. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 1167–1180. [Google Scholar] [CrossRef]
- Leitner, M.; Stoschka, M.; Ottersböck, M. Fatigue assessment of welded and high frequency mechanical impact (HFMI) treated joints by master notch stress approach. Int. J. Fatigue 2017, 101, 232–243. [Google Scholar] [CrossRef]
- Leitner, M.; Stoschka, M.; Barsoum, Z.; Farajian, M. Validation of the fatigue strength assessment of HFMI-treated steel joints under variable amplitude loading. Weld. World 2020, 64, 1681–1689. [Google Scholar] [CrossRef]
- Tai, M.; Miki, C. Improvement effects of fatigue strength by burr grinding and hammer peening under variable amplitude loading. Weld. World 2012, 56, 109–117. [Google Scholar] [CrossRef]
- Schubnell, J.; Carl, E.; Farajian, M.; Gkatzogianis, P.; Knodel, P.; Ummenhofer, T.; Wimpory, R.; Eslami, H. Residual stress relaxation in HFMI-treated fillet welds after single overload peaks. Weld. World 2020, 64, 1107–1117. [Google Scholar] [CrossRef]
- Yonezawa, T.; Shimanuki, H.; Mori, T. Influence of cyclic loading on the relaxation behaviour of compressive residual stress induced by UIT. Weld. World 2020, 64, 171–178. [Google Scholar] [CrossRef]
- Mikkola, E.; Remes, H.; Marquis, G. A finite element study on residual stress stability and fatigue damage in high-frequency mechanical impact (HFMI)-treated welded joint. Int. J. Fatigue 2017, 94, 16–29. [Google Scholar] [CrossRef] [Green Version]
- Nazzal, S.S.; Mikkola, E.; Yıldırım, H.C. Fatigue damage of welded high-strength steel details impoved by post-weld treatment subjected to critical cyclic loading conditions. Eng. Struct. 2021, 237, 111928. [Google Scholar] [CrossRef]
- Ruiz, H.; Osawa, N.; Rashed, S. Study on the stability of compressive residual stress induced by high-frequency mechanical impact under cyclic loadings with spike loads. Weld. World 2020, 64, 1855–1865. [Google Scholar] [CrossRef]
- Yıldırım, H.C.; Remes, H.; Nussbaumer, A. Fatigue properties of as-welded and post-weld-treated high-strength steel joints: The influence of constant and variable amplitude loads. Int. J. Fatigue 2020, 138, 105687. [Google Scholar] [CrossRef]
- Mikkola, E.; Marquis, G.; Lehto, P.; Remes, H.; Hänninen, H. Material characterization of high-frequency mechanical impact (HFMI)-treated high-strength steel. Mater. Des. 2016, 89, 205–214. [Google Scholar] [CrossRef]
- SONATS. Residual Stress Measurement by X-ray Diffraction. Available online: https://sonats-et.com/en/residual-stress/x-ray-diffraction-services/ (accessed on 26 September 2021).
- Pirlinga, T. Precise analysis of near surface neutron strain imaging measurements. Procedia Eng. 2011, 10, 2147–2152. [Google Scholar] [CrossRef] [Green Version]
- Kuhlmann, U.; Durr, A.; Bergmann, J.; Thumser, R. Fatigue Strength Improvement for Welded High Strength Steel Connections Due to the Application of Post-Weld Treatment Methods; FOSTA, Forschung fur die Praxis P 620: Dusseldorf, German, 2006. (In Germany) [Google Scholar]
- Kuhlmann, U.; Gunther, H. Experimentelle Untersuchungen zur Ermüdungssteigernden Wirkung des PIT-Verfahrens; Universität Stuttgart Institut für Konstruktion und Entwurf: Stuttgart, Germany, 2009. (In Germany) [Google Scholar]
- Tehrani Yekta, R. Acceptance Criteria for Ultrasonic Impact Treatment of Highway Steel Bridges. Ph.D. Thesis, University of Waterloo, Waterloo, AB, Canada, 2012. [Google Scholar]
- Suzuki, T.; Okawa, T.; Shimanuki, H.; Nose, T.; Suzuki, H.; Moriai, A. Effect of ultrasonic impact treatment (UIT) on fatigue strength of welded joints. Adv. Mat. Res. 2014, 996, 736–742. [Google Scholar] [CrossRef] [Green Version]
- Ranjan, R.; Ghahremani, K.; Walbridge, S.; Ince, A. Testing and fracture mechanic analysis of strength effects on the fatigue behaviour of HFMI-treated welds. Weld. World 2016, 60, 987–999. [Google Scholar] [CrossRef]
- Leitner, M.; Mossler, W.; Putz, W.; Stoschka, M. Effect of post-weld heat treatment on the fatigue strength of HFMI-treated mild steel joints. Weld. World 2015, 59, 861–873. [Google Scholar] [CrossRef]
- Polezhayeva, H.; Howarth, D.; Kumar, M.; Ahmad, B.; Fitzpatrick, M.E. The Effect of compressive fatigue loads on fatigue strength of non-load carrying specimens subjected to ultrasonic impact treatment. Weld. World 2015, 59, 713–721. [Google Scholar] [CrossRef]
- Anami, K.; Miki, C.; Tani, H.; Yamamoto, H. Improving fatigue strength of welded joints by hammer peening and Tig-dressing. J. JSCE 2000, 17, 67–78. [Google Scholar] [CrossRef] [Green Version]
- Fisher, W.J.; Sullivan, M.D.; Pense, W.A. Improving Fatigue Strength and Repairing Fatigue Damage; Fritz Laboratory Reports, Paper 2067; Lehigh University: Bethlehem, PA, USA, 1974. [Google Scholar]
- Voce, E. The relationship between stress and strain for homogeneous deformation. J. Met. 1948, 74, 537–562. [Google Scholar]
- Garcia, M. Multiaxial Fatigue Analysis of High-Strength Steel Welded Joints Using Generalized Local Approaches. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2020. [Google Scholar]
- Smith, M. Abaqus/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp.: Johnston, RI, USA, 2009. [Google Scholar]
- Smith., K.N.; Watson, P.; Topper, T.H. A stress-strain function for the fatigue of metals (stress-strain function for metal fatigue including mean stress effect). J. Mater. 1970, 5, 767–778. [Google Scholar]
- Kujawski, D. A deviation version of the SWT parameter. Int. J. Fatigue 2014, 67, 95–102. [Google Scholar] [CrossRef]











| Steel | Mechanical Properties | Chemical Composition | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yield Strength fy (N/mm2) | Tensile Strength fu (N/mm2) | Elongation (%), Minimum | C | Si | Mn | P | S | Al | Nb | V | Ti | Cu | Cr | Ni | Mo | Ca | N | EW | |
| S690QL | 832 | 856 | 0 | 0.14 | 0.29 | 1.21 | 0.011 | 0.001 | 0.047 | 0.021 | 0.028 | 0.10 | 0.010 | 0.28 | 0.05 | 0.150 | 0.0 | 0.002 | 0.43 |
| Condition Name | XRD | ND | Note | |||||
|---|---|---|---|---|---|---|---|---|
| Meas. Points 0 mm | Meas. Paths | Meas. Paths | Meas. Paths | |||||
| Top | Bottom | Top | Bottom | Top | Bottom | |||
| AW | - | 1 | 1 | 1 | 1 | 1 | 1 | Initial state |
| HFMI | 4 | 1 | 1 | 1 | 1 | 1 | 1 | Initial state |
| HFMI-LC | - | - | 1 | - | 1 | - | 1 | After load cycles in Figure 2 |
| Specimen Number | The Highest Peak Stress in a Part of Variable Amplitude Loading | The Number of Cycles to Complete Failure, N | Crack Location | ||
|---|---|---|---|---|---|
| Δσmax | σmax | σmin | |||
| 1−C | 1191 MPa | 1.00fy (833 MPa) | −0.43fy (358 MPa) | 258750 | Center |
| 2−C | 1191 MPa | 1.00fy (833 MPa) | −0.43fy (358 MPa) | 346500 | Center |
| 3−C | 1191 MPa | 1.00fy (833 MPa) | −0.43fy (358 MPa) | 492000 | Center |
| 4−E | 911 MPa | 0.80fy (665 MPa) | −0.37fy (246 MPa) | 2565750 | Edge |
| 5−E | 911 MPa | 0.80fy (665 MPa) | −0.37fy (246 MPa) | 2637000 | Edge |
| 6−C | 911 MPa | 0.80fy (665 MPa) | −0.37fy (246 MPa) | 4788750 | Center |
| 7−E | 780 MPa | 0.70fy (582 MPa) | −0.34fy (198 MPa) | 2499000 | Edge |
| 8−E | 780 MPa | 0.70fy (582 MPa) | −0.34fy (198 MPa) | 5466000 | Edge |
| 9−E | 780 MPa | 0.70fy (582 MPa) | −0.34fy (198 MPa) | 6579000 | Edge |
| Name | Author | Material | Linear-Elastic Behavior | Non-Linear Behavior | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Elastic Properties | Isotropic Properties | Kinematic Properties | |||||||||
| E [MPa] | ν | Q | q | σy [MPa] | C1 | γ1 | C2 | γ2 | |||
| BM-1 | Garcia | Base material | 210000 | 0.3 | 0 | 0 | 578 | 1832 | 8 | 17421 | 88 |
| BM-2 | Castro e Sousa | Base material | 206000 | 0.3 | 0 | 1 | 590 | 19018 | 83 | 771 | 5 |
| BM-3 | Mikkola | Base material | 200000 | 0.3 | 1 | 1 | 772 | 11478 | 395 | 11478 | 395 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ono, Y.; Yıldırım, H.C.; Kinoshita, K.; Nussbaumer, A. Damage-Based Assessment of the Fatigue Crack Initiation Site in High-Strength Steel Welded Joints Treated by HFMI. Metals 2022, 12, 145. https://doi.org/10.3390/met12010145
Ono Y, Yıldırım HC, Kinoshita K, Nussbaumer A. Damage-Based Assessment of the Fatigue Crack Initiation Site in High-Strength Steel Welded Joints Treated by HFMI. Metals. 2022; 12(1):145. https://doi.org/10.3390/met12010145
Chicago/Turabian StyleOno, Yuki, Halid Can Yıldırım, Koji Kinoshita, and Alain Nussbaumer. 2022. "Damage-Based Assessment of the Fatigue Crack Initiation Site in High-Strength Steel Welded Joints Treated by HFMI" Metals 12, no. 1: 145. https://doi.org/10.3390/met12010145
APA StyleOno, Y., Yıldırım, H. C., Kinoshita, K., & Nussbaumer, A. (2022). Damage-Based Assessment of the Fatigue Crack Initiation Site in High-Strength Steel Welded Joints Treated by HFMI. Metals, 12(1), 145. https://doi.org/10.3390/met12010145






