Hot Deformation Behavior of PM Ni with Harmonic Microstructure
Abstract
:1. Introduction
2. Materials and Methods
3. Results
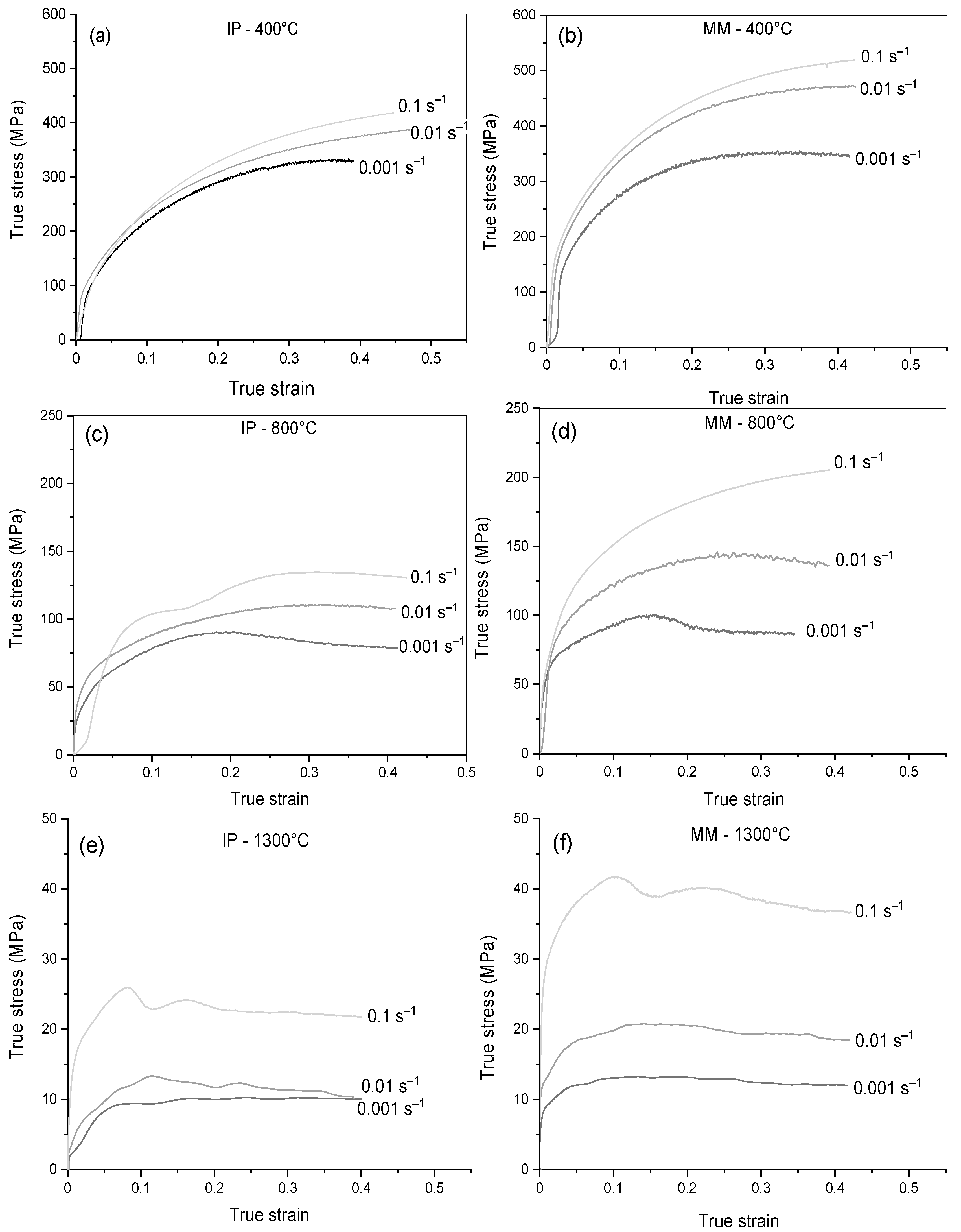
3.1. Hot Deformation Curves
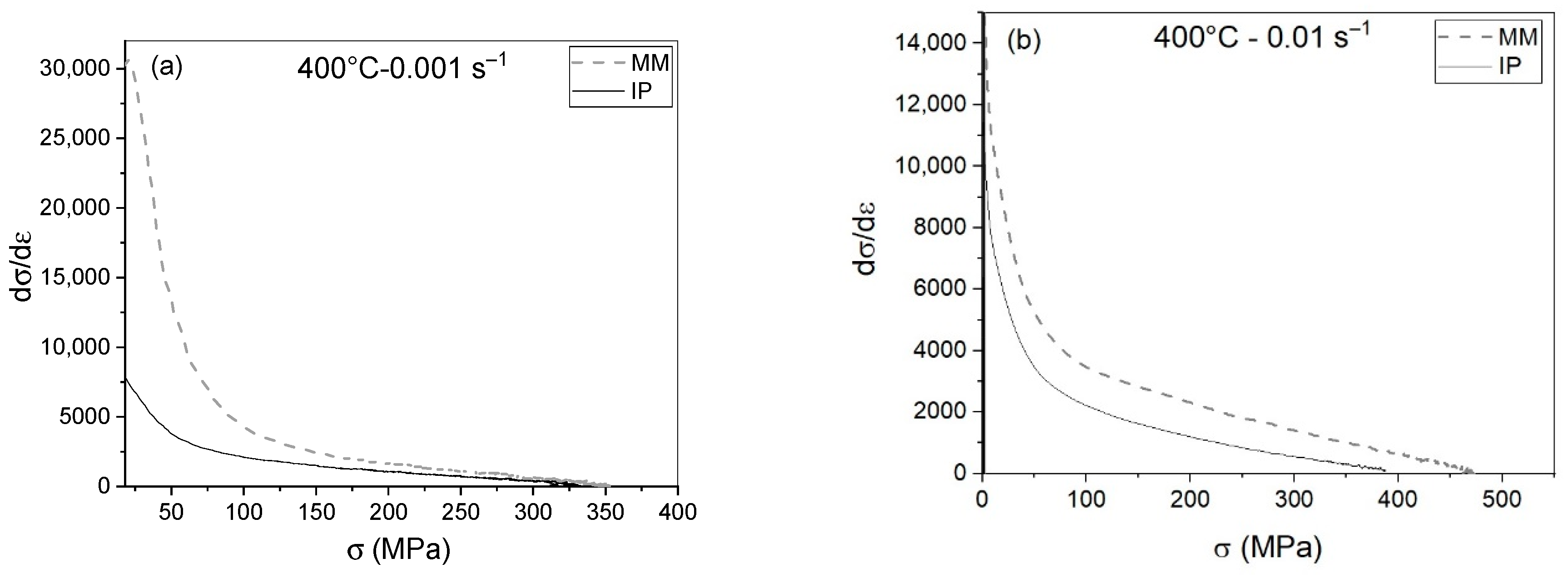
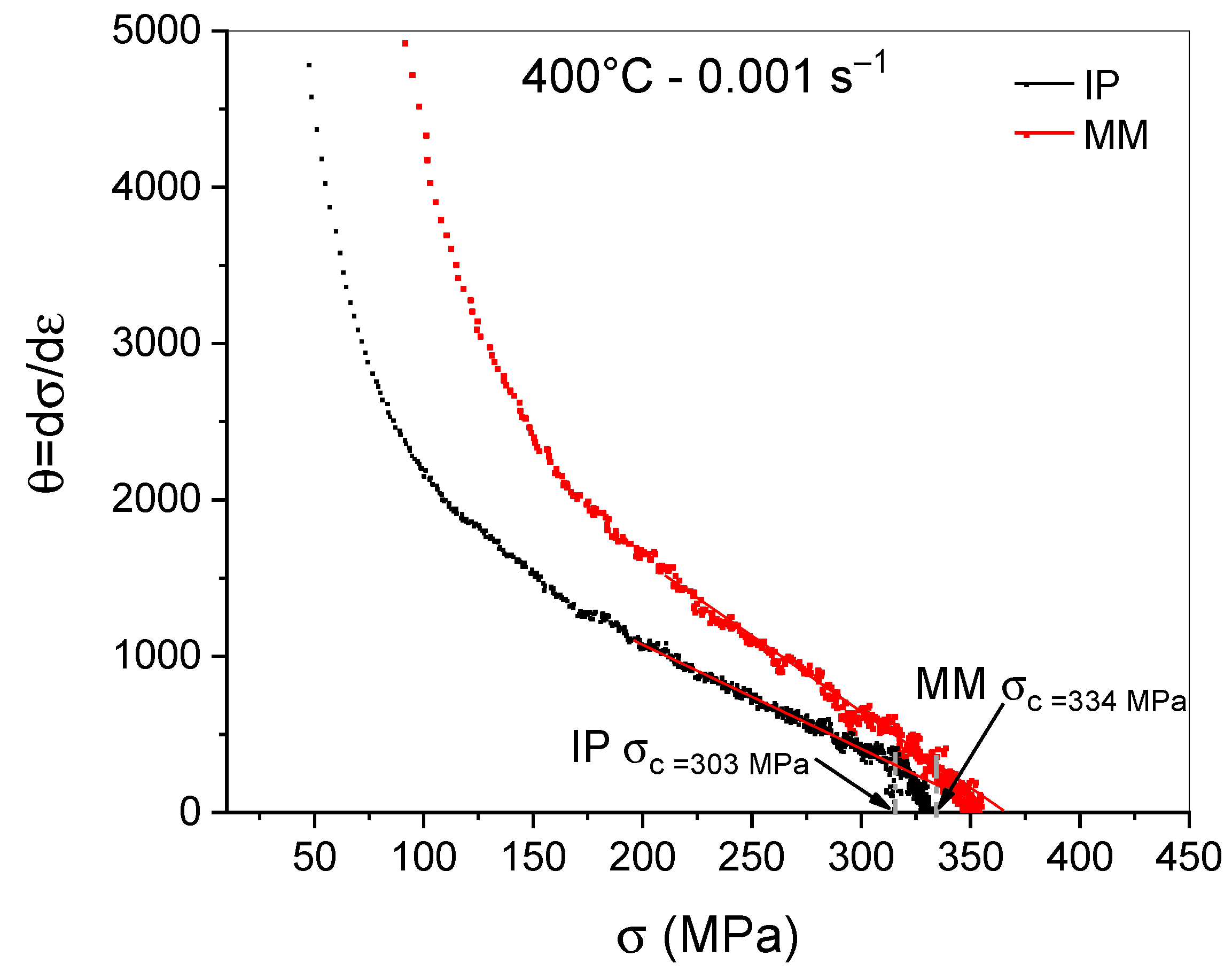
3.2. Initiation of Dynamic Recrystallization
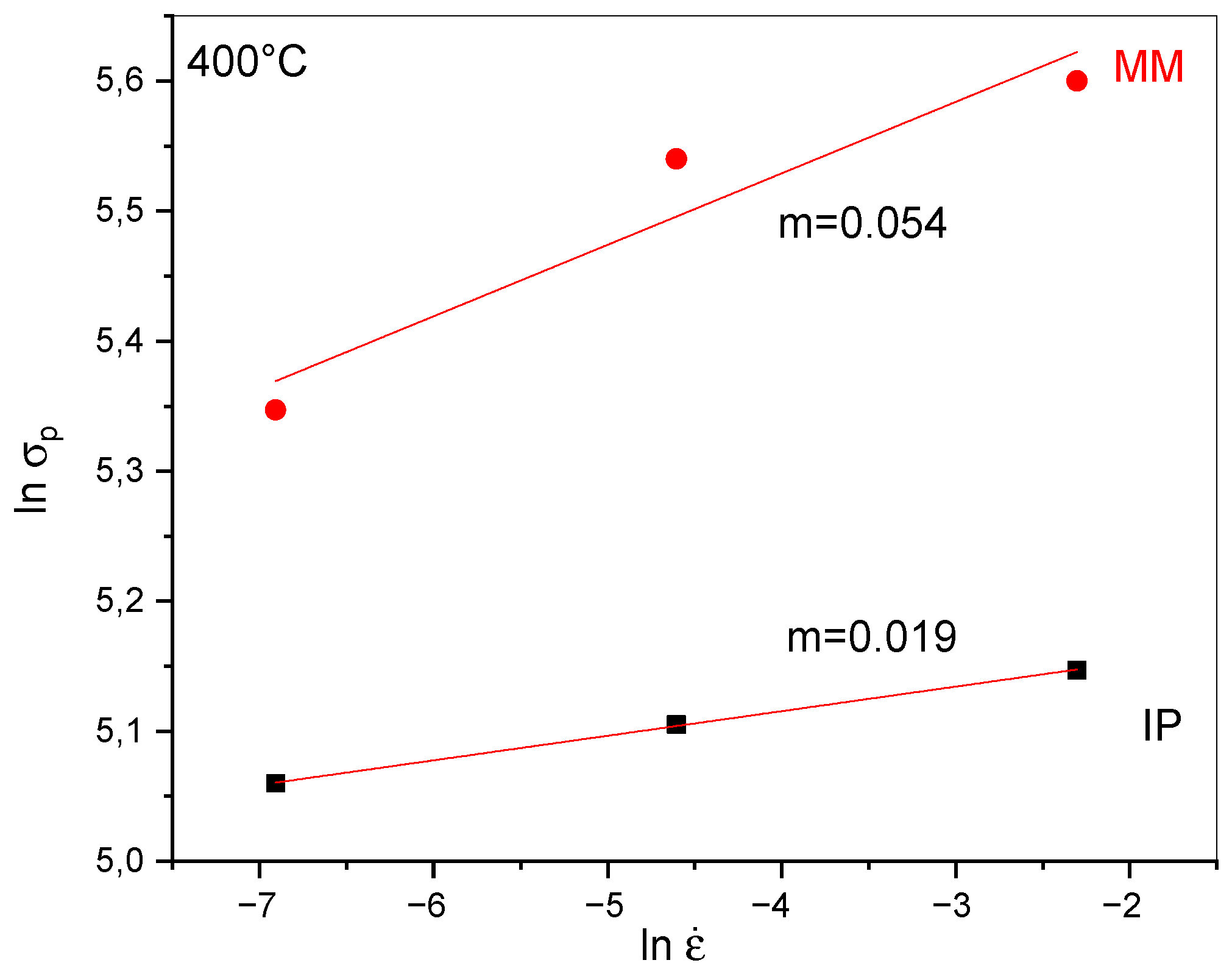
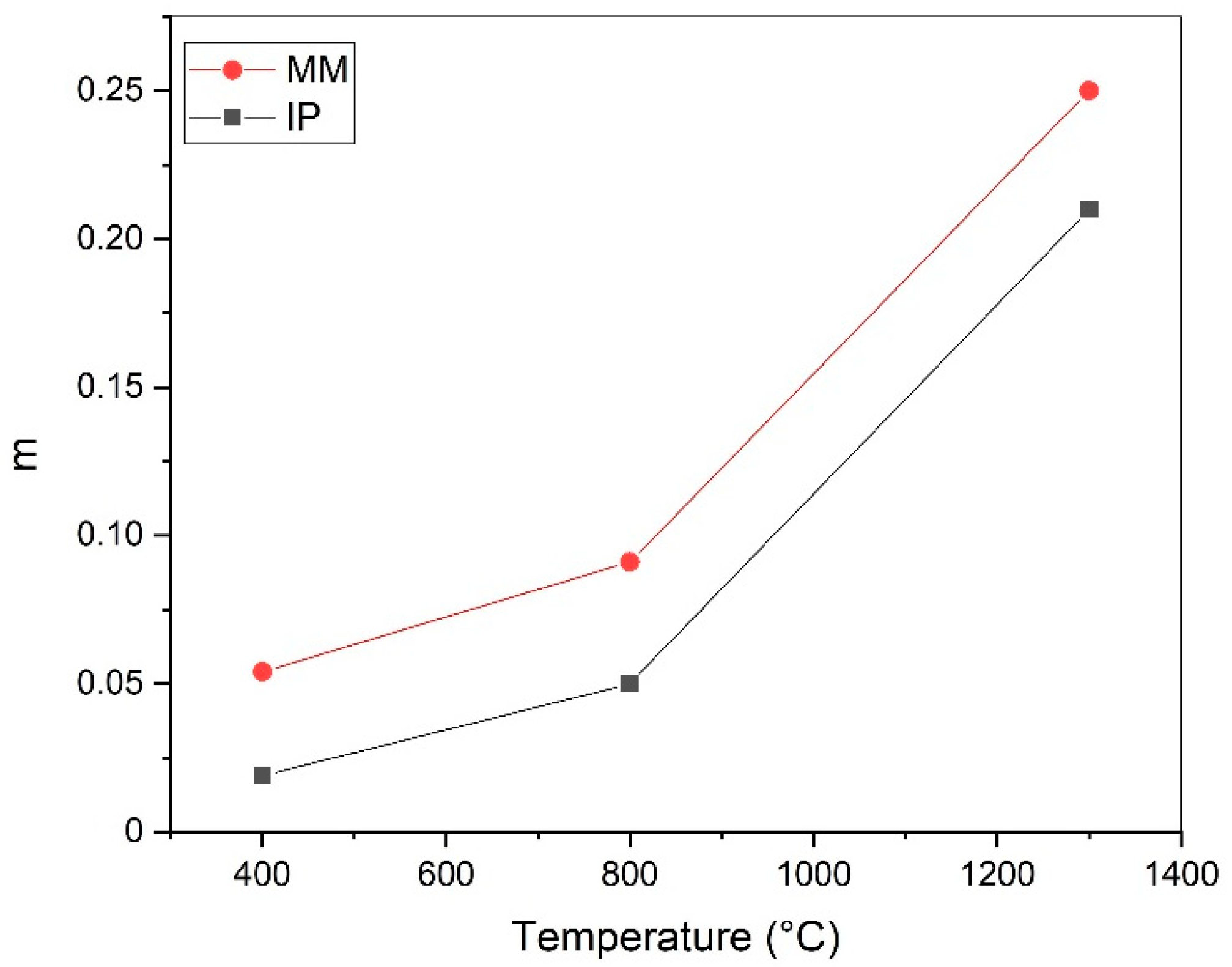
3.3. Strain Rate Sensitivity
3.4. Activation Volume
3.5. Microstructural Analysis
- At 400 °C, the IP samples show the original powder particles deformed perpendicularly to the compression direction (indicated with arrows in Figure 10a), together with a closure of the initial pores. No traces of recrystallized areas are visible at the lowest strain rate ( = 0.001 s−1) since DRX has just barely initiated at this temperature. In addition, in the MM samples, the grains (cores and shell) are elongated perpendicularly to the compression direction. Moreover, in this material, a consistent twinning phenomenon is observed. The nucleation of twins in high deformation energy areas such as grain boundaries, impurities, or dislocation pile-ups occurs in Ni, which has a low stacking fault energy, at this temperature. This phenomenon indicates that the MM samples have a greater deformation level than the IP samples, in which twinning was not detected. Twinning is shown in Figure 11, which reports sample MM deformed at 400 °C–0.1 s−1. In the MM sample deformed at the lowest strain rate, recrystallization starts to be evident, as shown in the SEM picture of Figure 12. The finer grain size in the cores and in the shell is indeed very clear. The recrystallization is induced by the higher deformation level of MM with respect to the corresponding IP sample and confirmed by the lower value of εc (Table 1).
- At 800 °C, both the IP and MM materials show a recrystallized microstructure (Figure 13a,b), even if the maximum peak stress is not observed on the compression curve of MM at the highest strain rate of 0.1 s−1, but the corresponding critical deformation value εc = 0.21 (Table 1) confirms the start of DRX. The grain size is higher in both materials at the lowest strain rate ( = 0.001 s−1) because a certain amount of grain growth occurs at this strain rate, which, on the contrary, has less time to occur when the test is carried out at = 0.01s−1 and = 0.1 s−1. Recrystallization is responsible for the flow softening observed in the stress–strain curves of both materials at the lowest strain rates, and for the consistent decrease in peak flow stress measured at this temperature. The sample MM, deformed at the lowest strain rate, shows, at this temperature, an increase in the grain size with respect to the same specimen deformed at 400 °C, which already exhibited a recrystallized microstructure. Comparing MM samples deformed at 800 °C and 400 °C at the same strain rate (Figure 13b vs. Figure 11), a smaller grain size is evident at 800 °C due to the recrystallization that occurred at this temperature.
- At 1300 °C, there is a significant grain growth in both IP and MM materials. In sample IP, deformed at the lowest strain rate, the formation of wedge-type pores was observed, because, at this temperature (homologous temperature TH = 0.91), diffusion creep mechanisms are active and induce grain boundary sliding and, therefore, the formation of wedge-type pores, occurring to accommodate space problems between simultaneously sliding grains, especially at the triple grain junctions. Flattened grains (grains with a preferred orientation) and the increase in grain size, which are clearly visible at this temperature, are other microstructural indications that the material was deformed by diffusion creep. In the MM specimens, the microstructure seems to also have harmonic features at this extremely high temperature, but the shell areas disappeared because of grain growth, leaving behind the traces of some oxides present on the grain boundaries of the shell zone, as shown in the SEM analysis of Figure 14. The EDXS analysis carried out on the area is shown in Figure 14b, which is rich in very small precipitates, and empty precipitate sites, from which they were probably removed during polishing, reveal the presence of oxygen. Ni oxides could have partially formed during the milling process and partially precipitated during the high-temperature tests [56].
4. Conclusions
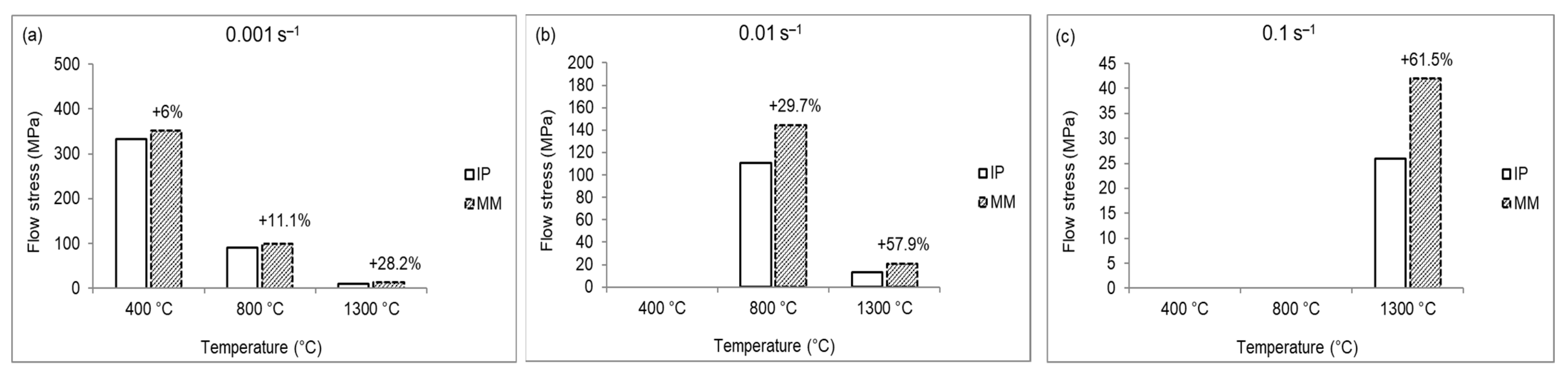
- The peak flow stress required for hot compression, strain hardening exponent n, and strain rate sensitivity m is higher for MM than in IP Ni;
- The occurrence of dynamic recrystallization is promoted by the peculiar bimodal microstructure of MM Ni, specifically by its heavily deformed shell having a finer grain size;
- The activation volumes of the MM Ni samples are lower than those of IP due to the lower grain size of this material and the consequent higher grain boundary surface, on which deformation mechanisms concentrate;
- Increasing the temperature, the difference in flow stress of MM and IP reduces, since both the materials undergo the same deformation mechanisms: DRX at 800 °C and creep at 1300 °C.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tsuji, N.; Okuno, S.; Koizumi, Y.; Minamino, Y. Toughness of ultrafine grained ferritic steels fabricated by ARB and annealing process. Mater. Trans. 2004, 45, 2272–2281. [Google Scholar] [CrossRef] [Green Version]
- Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Yang, M.; Yuan, F.; Wu, G.; Wei, Y.; Huang, X.; Zhu, Y. Heterogeneous lamella structure unites ultrafine-grain strength with coarse-grain ductility. Proc. Natl. Acad. Sci. USA 2015, 112, 14501–14505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Chen, M.; Zhou, F.; Ma, E. High tensile ductility in a nanostructured metal. Nature 2002, 419, 912–915. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Li, Y.; Zhu, L.; Liu, Y.; Lei, X.; Wang, G.; Wu, Y.; Mi, Z.; Liu, J.; Wang, H.; et al. Evading the strength-ductility trade-off dilemma in steel through gradient hierarchical nanotwins. Nat. Commun. 2014, 5, 3580. [Google Scholar] [CrossRef] [Green Version]
- Lu, K. Making strong nanomaterials ductile with gradients. Science 2014, 345, 1455–1456. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Jiang, P.; Chen, L.; Yuan, F.; Zhu, Y.T. Extraordinary strain hardening by gradient structure. Proc. Natl. Acad. Sci. USA 2014, 111, 7197–7201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Vajpai, S.K.; Orlov, D.; Ameyama, K. Improvement of mechanical properties in SUS304L steel through the control of bimodal microstructure characteristics. Mater. Sci. Eng. A 2014, 598, 106–113. [Google Scholar] [CrossRef] [Green Version]
- Vajpai, S.K.; Ota, M.; Watanabe, T.; Maeda, R.; Sekiguchi, T.; Kusaka, T.; Ameyama, K. The development of high performance Ti-6Al-4V alloy via a unique microstructural design with bimodal grain size distribution. Metall. Mater. Trans. A 2015, 46, 903–914. [Google Scholar] [CrossRef]
- Sharma, B.; Nagano, K.; Kawabata, M.; Ameyama, K. Microstructure and mechanical properties of hetero-designed Ti-25Nb-25Zr alloy fabricated by powder metallurgy route. Lett Mater. 2019, 9, 511–516. [Google Scholar] [CrossRef] [Green Version]
- Sekiguchi, T.; Ono, K.; Fujiwara, H.; Ameyama, K. New microstructure design for commercially pure titanium with outstanding mechanical properties by mechanical milling and hot roll sintering. Mater. Trans. 2010, 51, 39–45. [Google Scholar] [CrossRef] [Green Version]
- Ameyama, K.; Horikawa, N.; Kawabata, M. Unique mechanical properties of harmonic structure designed materials. Tetsu ToHagane J. Iron Steel Inst. Jpn. 2019, 105, 124–126. [Google Scholar] [CrossRef] [Green Version]
- Orlov, D.; Ameyama, K. Critical Assesment 37: Harmonic-structure materials—Idea, status and perspectives. Mater. Sci. Technol. 2020, 36, 517–526. [Google Scholar] [CrossRef] [Green Version]
- Mirzadeh, H.; Parsa, M.H.; Ohadi, D. Hot deformation behavior of austenitic stainless steel for a wide range of initial grain size. Mater. Sci. Eng. A 2013, 569, 54–60. [Google Scholar] [CrossRef]
- Nagata, M.; Horikawa, N.; Kawabata, M.; Ameyama, K. Effects of microstructure on mechanical properties of harmonic structure designed pure Ni. Mater. Trans. 2019, 60, 1914–1920. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhen, L.; Shao, W.Z.; Yang, L.; Zhang, X.M. Hot working characteristics and dynamic recrystallization of delta-processed superalloy 718. J. Alloys Compd. 2009, 474, 341–346. [Google Scholar] [CrossRef]
- Chen, X.M.; Lin, Y.C.; Wen, D.X.; Zhang, J.L.; He, M. Dynamic recrystallization behavior of a typical nickel-based superalloy during hot deformation. Mater. Des. 2014, 57, 568–577. [Google Scholar] [CrossRef]
- Menapace, C.; Sartori, N.; Pellizzari, M.; Straffelini, G. Hot deformation behavior of four steels: A comparative study. J. Eng. Mater. Technol. Trans. ASME 2018, 140, 021006. [Google Scholar] [CrossRef]
- Yagi, K.; Sharma, B.; Kawabata, M.; Ameyama, K. Fabrication of SUS316L harmonic structure compacts by bi-modal milling process. J. Jpn. Soc. Powder Powder Metall. 2020, 67, 239–244. [Google Scholar] [CrossRef]
- Molinari, A.; Bisoffi, E.; Menapace, C.; Torralba, J. Shrinkage kinetics during early stage sintering of cold isostatically compacted iron powder. Powd Met. 2014, 57, 61–69. [Google Scholar] [CrossRef]
- Gandhi, C. On fracture initiation mechanisms and dynamic recrystallization during hot deformation of pure nickel. Metall Trans. A Phys. Metall. Mater. Sci. 1982, 13, 1233–1238. [Google Scholar] [CrossRef]
- Srinivasan, N.; Prasad, Y.V.R.K. Characterisation of dynamic recrystallisation in nickel using processing map for hot deformation. Mater. Sci. Technol. 1992, 8, 206–212. [Google Scholar] [CrossRef]
- Gao, W.L.; Lai, S.Z.; Teng, J.; Du, Z.T.; Liu, X.S.; Chang, Y.W. Flow behavior and microstructural evolution in nickel during hot deformation. Rare Met. 2019, 38, 675–682. [Google Scholar] [CrossRef]
- Matougui, N.; Piot, D.; Fares, M.L.; Montheillet, F.; Semiatin, S.L. Influence of niobium solutes on the mechanical behavior of nickel during hot working. Mater. Sci. Eng. A 2013, 586, 350–357. [Google Scholar] [CrossRef]
- Luton, M.J.; Sellars, C.M. Dynamic recrystallization in nickel and nickel-iron alloys during high temperature deformation. Acta Metall. 1969, 17, 1033–1043. [Google Scholar] [CrossRef]
- Sakai, T.; Jonas, J.J. Overview no. 35 dynamic recrystallization: Mechanical and microstructural considerations. Acta Metall. 1984, 32, 189–209. [Google Scholar] [CrossRef]
- Meagher, S.; Borch, R.S.; Groza, J.; Mukherjee, A.K.; Green, H.W. Activation parameters of high-temperature creep in polycrystalline nickel at ambient and high pressures. Acta Met. Mater. 1992, 40, 159–166. [Google Scholar] [CrossRef]
- Rice, J. The localization of plastic deformation. In Proceedings of the 14th International Congress on Theoretical and Applied Mechanichs, Delft, The Netherlands, 30 August–4 September 1976; Volume 1, pp. 207–220. [Google Scholar]
- Narayana Murty, S.V.S.; Nageswara Rao, B.; Kashyap, B.P. Instability criteria for hot deformation of materials. Int. Mater. Rev. 2000, 45, 15–26. [Google Scholar] [CrossRef]
- Staker, M.R.; Stayer, M.R. The relation between adiabatic shear instability strain and material properties. Acta Met. 1981, 29, 683–689. [Google Scholar] [CrossRef]
- Sellars, C.M. Recrystallization of metals during hot deformation. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1978, 288, 147–158. [Google Scholar] [CrossRef]
- Ota, M.; Shimojo, K.; Okada, S.; Vajpai, S.K.; Ameyama, K. Harmonic structure design and mechanical properties of pure ni compact. J. Powder Metall. Min. 2014, 3, 122. [Google Scholar] [CrossRef]
- Garcia de la Cruz, L.; Martinez Celis, M.; Keller, C.; Hug, E. Exploring the strain hardening mechanisms of ultrafine grained nickel processed by spark plasma sintering. Metals 2021, 11, 65. [Google Scholar] [CrossRef]
- Khodabakhshi, F.; Haghshenas, M.; Eskandari, H.; Koohbor, B. Hardness-strength relationships in fine and ultra-fine grained metals processed through constrained groove pressing. Mater. Sci. Eng. A 2015, 636, 331–339. [Google Scholar] [CrossRef]
- Bowen, A.W.; Partridge, P.G. Limitations of the Hollomon strain-hardening equation. J. Phys. D Appl. Phys. 1974, 7, 969–978. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization. Acta Mater. 1996, 44, 127–136. [Google Scholar] [CrossRef]
- Altan, T.; Boulger, F.W. Flow stress of metals and its application in metal forming analyses. ASME Pap. 1973, 95, 1009–1019. [Google Scholar] [CrossRef]
- Tjong, S.C.M.Y. Fundamental theories and mechanisms of failure. In Comprehensive Structural Integrity; Elsevier Science, Ltd.: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Maryuama, K. Fundamental Aspects of Creep Deformation and Deformation Mechanism Map; Abe, F., Kern, T.-U., Viswanathan, R., Eds.; Creep-Resistant Steels—A Volume in Woodhead Publishing Series in Metals and Surface Engineering; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Jenkins, W.D.; Digges, T.G.; Johnson, C.R. Creep of high-purity nickel. J. Res. Natl. Bur. Stand. 1954, 53, 329. [Google Scholar] [CrossRef]
- Movchan, B.A.; Dabizha, E.V. A phenomenological model for high-temperature creep in pure nickel. Strength Mater. 1975, 7, 278–283. [Google Scholar] [CrossRef]
- Dalla Torre, F.; Spätig, P.; Schäublin, R.; Victoria, M. Deformation behaviour and microstructure of nanocrystalline electrodeposited and high pressure torsioned nickel. Acta Mater. 2005, 53, 2337–2349. [Google Scholar] [CrossRef]
- Bui, Q.H.; Dirras, G.; Ramtani, S.; Gubicza, J. On the strengthening behavior of ultrafine-grained nickel processed from nanopowders. Mater Sci. Eng. A 2010, 527, 3227–3235. [Google Scholar] [CrossRef]
- Wang, Y.M.; Hamza, A.V.; Ma, E. Temperature-dependent strain rate sensitivity and activation volume of nanocrystalline Ni. Acta Mater. 2006, 54, 2715–2726. [Google Scholar] [CrossRef]
- Gray, G.T.; Lowe, T.C.; Cady, C.M.; Valiev, R.Z.; Aleksandrov, I.V. Influence of strain rate & temperature on the mechanical response of ultrafine-grained Cu, Ni, and Al-4Cu-0.5Zr. Nanostruct. Mater. 1997, 9, 477–480. [Google Scholar] [CrossRef]
- Schwaiger, R.; Moser, B.; Dao, M.; Chollacoop, N.; Suresh, S. Some critical experiments on the strain-rate sensitivity of nanocrystalline nickel. Acta Mater. 2003, 51, 5159–5172. [Google Scholar] [CrossRef]
- Li, Y.J.; Mueller, J.; Höppel, H.W.; Göken, M.; Blum, W. Deformation kinetics of nanocrystalline nickel. Acta Mater. 2007, 55, 5708–5717. [Google Scholar] [CrossRef]
- Dalla Torre, F.; Van Swygenhoven, H.; Victoria, M. Nanocrystalline electrodeposited Ni: Microstructure and tensile properties. Acta Mater. 2002, 50, 3957–3970. [Google Scholar] [CrossRef]
- Wei, Q.; Jia, D.; Ramesh, K.T.; Ma, E. Evolution and microstructure of shear bands in nanostructured Fe. Appl. Phys. Lett. 2002, 81, 1240–1242. [Google Scholar] [CrossRef]
- Sharma, G.; Chatterjee, A.; Paul, B.; Varshney, J.; Chakravartty, J.K. High temperature mechanical behavior of nanocrystalline Ni. Mater. Sci. Eng. A 2013, 576, 69–73. [Google Scholar] [CrossRef]
- Maier, V.; Durst, K.; Mueller, J.; Backes, B.; Höppel, H.W.; Göken, M. Nanoindentation strain-rate jump tests for determining the local strain-rate sensitivity in nanocrystalline Ni and ultrafine-grained Al. J. Mater. Res. 2011, 26, 1421–1430. [Google Scholar] [CrossRef] [Green Version]
- Wei, Q.; Cheng, S.; Ramesh, K.T.; Ma, E. Effect of nanocrystalline and ultrafine grain sizes on the strain rate sensitivity and activation volume: Fcc versus bcc metals. Mater. Sci. Eng. A 2004, 381, 71–79. [Google Scholar] [CrossRef]
- Morris, D. Strengthening mechanisms in nanocrystalline metals. In Nanostructured Metals and Alloys; Series in Metals and Surface Engineering; Woodhead Publishing: Sawston, UK, 2011. [Google Scholar]
- Höppel, H.W.; May, J.; Eisenlohr, P.; Göken, M. Strain rate sensitivity of ultrafine grained materials. Z. Met. 2005, 96, 566–571. [Google Scholar] [CrossRef]
- Caillard, D.; Martin, J.L. Thermally Activated Mechanisms in Crystal Plasticity; Pergamon Materials Series; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Haugsrud, R. On the high-temperature oxidation of nickel. Corros. Sci. 2003, 45, 211–235. [Google Scholar] [CrossRef]









| Strain Rate s−1 | 400 °C | 800 °C | 1300 °C | |||
|---|---|---|---|---|---|---|
| IP | MM | IP | MM | IP | MM | |
| 0.001 | 0.230 | 0.193 | 0.133 | 0.099 | 0.049 | 0.016 |
| 0.01 | - | - | 0.216 | 0.196 | 0.051 | 0.040 |
| 0.1 | - | - | 0.222 | 0.210 | 0.066 | 0.058 |
| Temperature | IP | MM |
|---|---|---|
| 400 °C | 0.019 | 0.054 |
| 800 °C | 0.050 | 0.091 |
| 1300 °C | 0.21 | 0.25 |
| Hot Compression Parameters | IP | MM |
|---|---|---|
| 400 °C–0.001 s−1 | 22 | 6 |
| 400 °C–0.01 s−1 | 21 | 5 |
| 400 °C–0.1 s−1 | 20 | 4 |
| 800 °C–0.001 s−1 | 33 | 14 |
| 800 °C–0.01 s−1 | 28 | 11 |
| 800 °C–0.1 s−1 | 26 | 9 |
| 1300 °C–0.001 s−1 | 84 | 34 |
| 1300 °C–0.01 s−1 | 74 | 23 |
| 1300 °C–0.1 s−1 | 31 | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menapace, C.; Sharma, B.; Ameyama, K. Hot Deformation Behavior of PM Ni with Harmonic Microstructure. Metals 2022, 12, 90. https://doi.org/10.3390/met12010090
Menapace C, Sharma B, Ameyama K. Hot Deformation Behavior of PM Ni with Harmonic Microstructure. Metals. 2022; 12(1):90. https://doi.org/10.3390/met12010090
Chicago/Turabian StyleMenapace, Cinzia, Bhupendra Sharma, and Kei Ameyama. 2022. "Hot Deformation Behavior of PM Ni with Harmonic Microstructure" Metals 12, no. 1: 90. https://doi.org/10.3390/met12010090
APA StyleMenapace, C., Sharma, B., & Ameyama, K. (2022). Hot Deformation Behavior of PM Ni with Harmonic Microstructure. Metals, 12(1), 90. https://doi.org/10.3390/met12010090








