Identification of Active Slip Mode and Calculation of Schmid Factors in Magnesium Alloy
Abstract
:1. Introduction
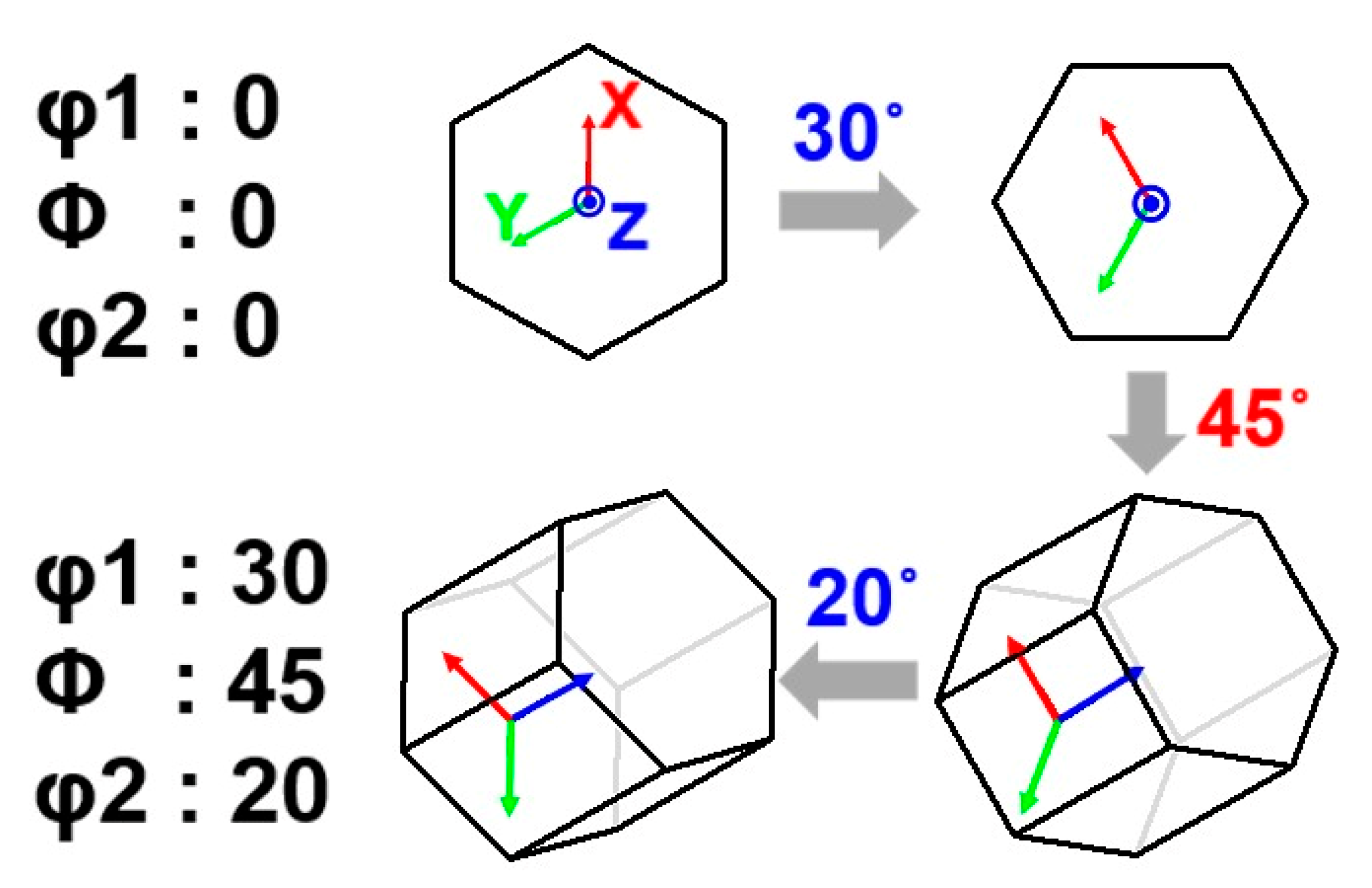
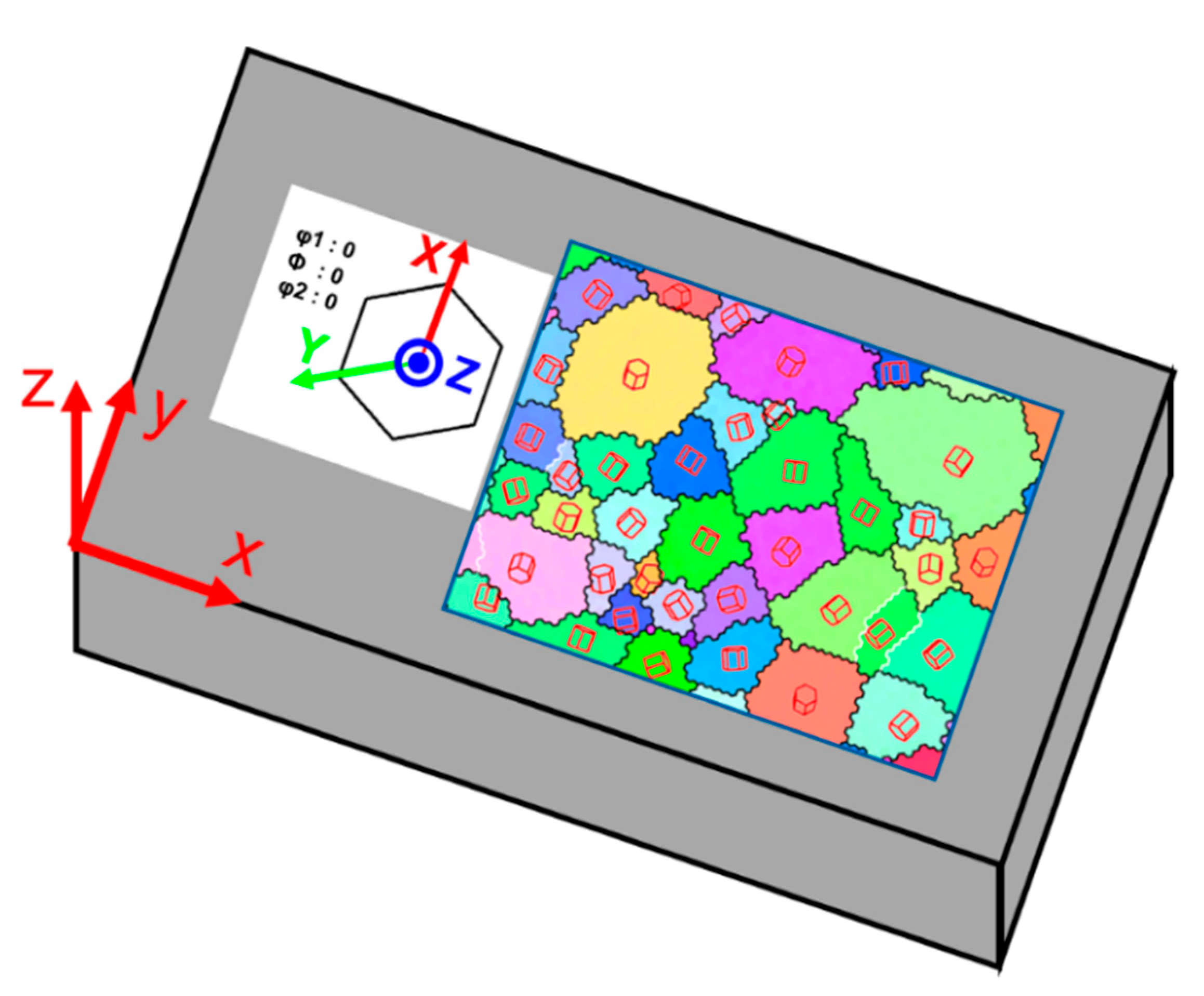
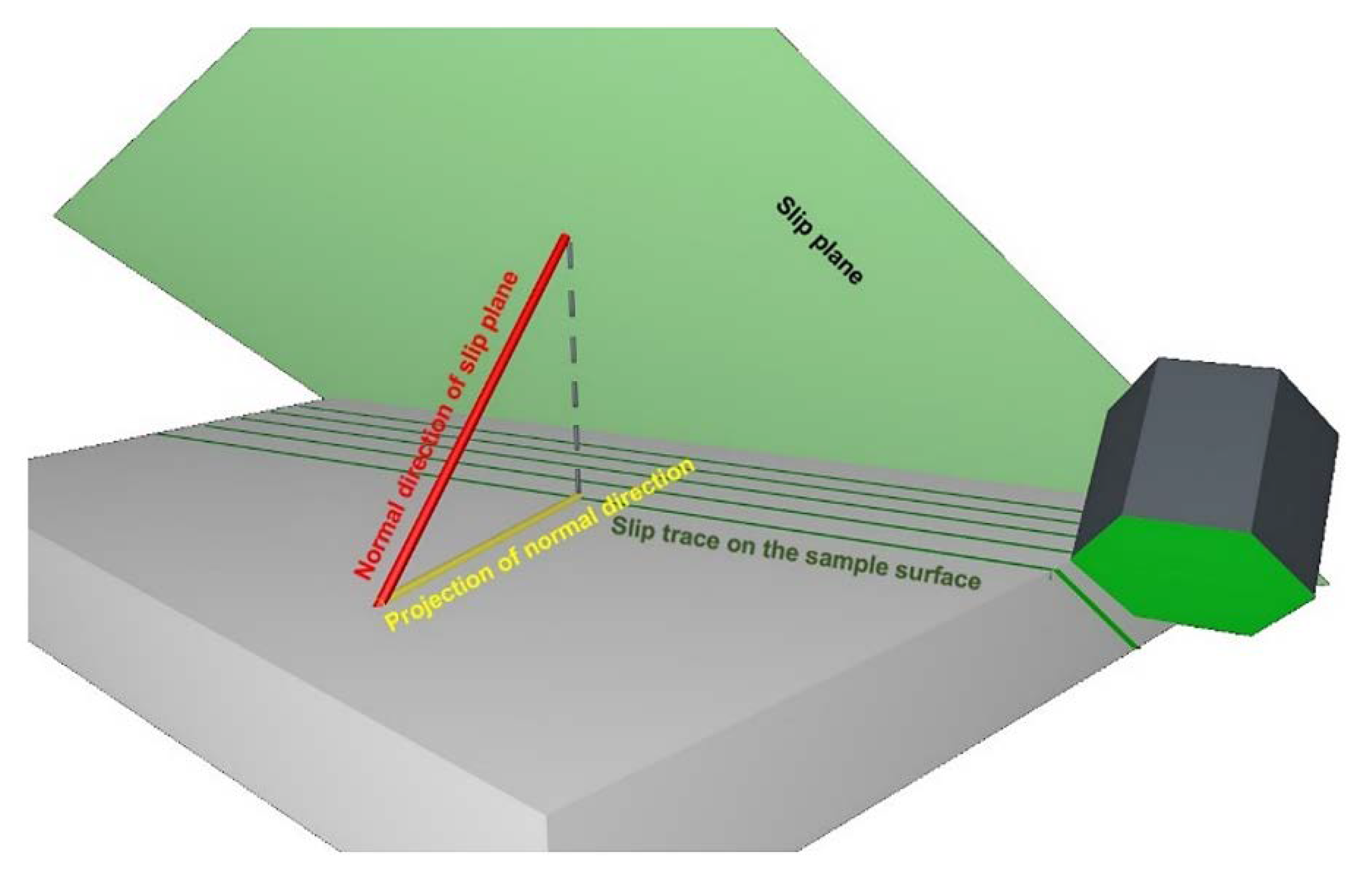
2. Methodology
3. Calculation of Possible Slip Systems and Schmid Factor
3.1. Calculation of Possible Slip Systems
3.2. Calculation of Schmid Factor
4. Case Analysis
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Takagi, K.; Yamasaki, M.; Mine, Y.; Takashima, K. Temperature Dependence of Prismatic Slip in a Single-Crystalline Long-Period Stacking Ordered Mg–Zn–Y Alloy. Scr. Mater. 2020, 178, 498–502. [Google Scholar] [CrossRef]
- Razavi, S.M.; Foley, D.C.; Karaman, I.; Hartwig, K.T.; Duygulu, O.; Kecskes, L.J.; Mathaudhu, S.N.; Hammond, V.H. Effect of Grain Size on Prismatic Slip in Mg–3Al–1Zn Alloy. Scr. Mater. 2012, 67, 439–442. [Google Scholar] [CrossRef]
- Victoria-Hernández, J.; Yi, S.; Letzig, D. Role of Non-Basal Slip Systems on the Microstructure and Texture Development of ZXK-Mg Alloy Deformed in Plane Strain Compression at Elevated Temperature. Scr. Mater. 2022, 208, 114322. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Li, Z. Dynamic Tension Deformation of Rare-Earth Containing Mg-1.9Mn-0.3Ce Alloy Sheet along the Rolling Direction at Various Temperatures. Metals 2020, 10, 1473. [Google Scholar] [CrossRef]
- Agnew, S.R. 2—Deformation Mechanisms of Magnesium Alloys. In Advances in Wrought Magnesium Alloys; Bettles, C., Barnett, M., Eds.; Woodhead Publishing: Sawston, UK, 2012; pp. 63–104. [Google Scholar]
- Xu, J.; Guan, B.; Xin, Y.; Huang, G.; Wu, P.; Liu, Q. Revealing the Role of Pyramidal Slip in the High Ductility of Mg-Li Alloy. J. Magnes. Alloys, 2021; in press. [Google Scholar] [CrossRef]
- Ullmann, M.; Kittner, K.; Prahl, U. Hot Rolling of the Twin-Roll Cast and Homogenized Mg-6.8Y-2.5Zn (WZ73) Magnesium Alloy Containing LPSO Structures. Metals 2021, 11, 1771. [Google Scholar] [CrossRef]
- Barnett, M.R. Twinning and the Ductility of Magnesium Alloys. Mater. Sci. Eng. A 2007, 464, 1–7. [Google Scholar] [CrossRef]
- Koike, J.; Ohyama, R. Geometrical Criterion for the Activation of Prismatic Slip in AZ61 Mg Alloy Sheets Deformed at Room Temperature. Acta Mater. 2005, 53, 1963–1972. [Google Scholar] [CrossRef]
- Kim, Y.M.; Mendis, C.; Sasaki, T.; Letzig, D.; Pyczak, F.; Hono, K.; Yi, S. Static Recrystallization Behaviour of Cold Rolled Mg-Zn-Y Alloy and Role of Solute Segregation in Microstructure Evolution. Scr. Mater. 2017, 136, 41–45. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, B.; Tang, A.; Fu, J.; Jiang, Z.; Sheng, H.; Zhang, D.; Huang, G.; Pan, F. Unveiling Annealing Texture Formation and Static Recrystallization Kinetics of Hot-Rolled Mg-Al-Zn-Mn-ca Alloy. J. Mater. Sci. Technol. 2020, 43, 104–118. [Google Scholar] [CrossRef]
- Xu, X.; Lunt, D.; Thomas, R.; Babu, R.P.; Harte, A.; Atkinson, M.; da Fonseca, J.Q.; Preuss, M. Identification of Active Slip Mode in a Hexagonal Material by Correlative Scanning Electron Microscopy. Acta Mater. 2019, 175, 376–393. [Google Scholar] [CrossRef]
- Wang, S.; Schuman, C.; Bao, L.; Lecomte, J.S.; Zhang, Y.; Raulot, J.M.; Philippe, M.J.; Zhao, X.; Esling, C. Variant Selection Criterion for Twin Variants in Titanium Alloys Deformed by Rolling. Acta Mater. 2012, 60, 3912–3919. [Google Scholar] [CrossRef]
- Guan, D.; Wynne, B.; Gao, J.; Huang, Y.; Rainforth, W.M. Basal Slip Mediated Tension Twin Variant Selection in Magnesium WE43 Alloy. Acta Mater. 2019, 170, 1–14. [Google Scholar] [CrossRef]
- Bian, M.; Huang, X.; Chino, Y. Substantial Improvement in Cold Formability of Concentrated Mg–Al–Zn–ca Alloy Sheets by High Temperature Final Rolling. Acta Mater. 2021, 220, 117328. [Google Scholar] [CrossRef]
- Shou, H.; Zheng, J.; Zhang, Y.; Long, D.; Rao, J.; Liu, Q. Quasi-In-Situ Analysis of Dependency of Deformation Mechanism and Work-Hardening Behavior on Texture in Mg-2Zn-0.1Ca Alloy. J. Alloys Compd. 2019, 784, 1187–1197. [Google Scholar] [CrossRef]
- Wang, H.; Boehlert, C.J.; Wang, Q.D.; Yin, D.D.; Ding, W.J. In-Situ Analysis of the Tensile Deformation Modes and Anisotropy of Extruded Mg-10Gd-3Y-0.5Zr (Wt.%) at Elevated Temperatures. Int. J. Plast. 2016, 84, 255–276. [Google Scholar] [CrossRef]
- Boehlert, C.J.; Chen, Z.; Gutiérrez-Urrutia, I.; Llorca, J.; Pérez-Prado, M.T. In Situ Analysis of the Tensile and Tensile-Creep Deformation Mechanisms in Rolled AZ31. Acta Mater. 2012, 60, 1889–1904. [Google Scholar] [CrossRef]
- Jang, H.-S.; Lee, J.-K.; Tapia, A.J.S.F.; Kim, N.J.; Lee, B.-J. Activation of non-basal <c + a> slip in multicomponent Mg alloys. J. Magnes. Alloys 2022, 10, 585–597. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, W.; Sung, H.; Li, S.; Zhang, D.; Zhao, Y.; Lavernia, E.J.; Zhu, Y. Origins and dissociation of pyramidal <c + a> dislocations in magnesium and its alloys. Acta Mater. 2018, 146, 265–272. [Google Scholar] [CrossRef]
- Ganeshan, S.; Shang, S.L.; Wang, Y.; Liu, Z.-K. Effect of Alloying Elements on the Elastic Properties of Mg from First-Principles Calculations. Acta Mater. 2009, 57, 3876–3884. [Google Scholar] [CrossRef]
- Wu, L.; Agnew, S.R.; Brown, D.W.; Stoica, G.M.; Clausen, B.; Jain, A.; Fielden, D.E.; Liaw, P.K. Internal Stress Relaxation and Load Redistribution during the Twinning–Detwinning-Dominated Cyclic Deformation of a Wrought Magnesium Alloy, ZK60A. Acta Mater. 2008, 56, 3699–3707. [Google Scholar] [CrossRef]
- Agnew, S.R.; Duygulu, Ö. Plastic Anisotropy and the Role of Non-Basal Slip in Magnesium Alloy AZ31B. Int. J. Plast. 2005, 21, 1161–1193. [Google Scholar] [CrossRef]
- Nan, X.-L.; Wang, H.-Y.; Zhang, L.; Li, J.-B.; Jiang, Q.-C. Calculation of Schmid Factors in Magnesium: Analysis of Deformation Behaviors. Scr. Mater. 2012, 67, 443–446. [Google Scholar] [CrossRef]
- Christian, J.W.; Mahajan, S. Deformation Twinning. Prog. Mater. Sci. 1995, 39, 1–157. [Google Scholar] [CrossRef]


| Type | Basal <a> | Prismatic <a> | ||||||
|---|---|---|---|---|---|---|---|---|
| Slip plane | Plane normal in cartesian coordinate system <x, y, z> | SF (m) | Slop (k) | Slip plane | Plane normal in cartesian coordinate system <x, y, z> | SF (m) | Slop (k) | |
| <001> | 0.48 | 17.88 | <, 1, 0> | 0.13 | 3.1 | |||
| 0] | <001> | 0.13 | 17.88 | 20] | , 1, 0> | 0.25 | −0.69 | |
| 20] | <001> | 0.35 | 17.88 | 0] | <−1, 0, 0> | 0.13 | 0.19 | |
| Type | Pyramidal <a> | Pyramidal <a + c> | ||||||
| Slip plane | Plane normal in cartesian coordinate system <x, y, z> | SF (m) | Slop (k) | Slip plane | Plane normal in cartesian coordinate system <x, y, z> | SF (m) | Slop (k) | |
| 0] | , 1, a/c> | 0.05 | 1.56 | 23] | , 1, 2a/c> | 0.05 | 0.11 | |
| 0] | ,1, a/c> | 0.06 | −0.17 | 3] | , 1, 2a/c> | 0.15 | 0.25 | |
| 110] | , 0, a/c> | 0.11 | −0.20 | 13] | , −1, 2a/c> | 0.31 | −0.65 | |
| 20] | , −1, a/c> | 0.39 | −1.23 | 113] | <0, 2, 2a/c> | 0.20 | −0.79 | |
| 10] | , −1, a/c> | 0.17 | 4.39 | 3] | <0, −2, 2a/c> | 0.37 | −4.12 | |
| 0] | , 0, a/c> | 0.34 | 0.57 | 3] | , −1, 2a/c> | 0.37 | 1.33 | |
| Type | Extension twinning {102} | Contraction twinning {101} | ||||||
| Slip plane | Plane normal in cartesian coordinate system <x, y, z> | SF (m) | Slop (k) | Slip plane | Plane normal in cartesian coordinate system <x, y, z> | SF (m) | Slop (k) | |
| 011] | , 1, 2a/c> | 0.04 | −0.36 | 2] | , 1, a/c> | 0.25 | 1.56 | |
| 101] | ,1, 2a/c> | 0.15 | 0.32 | 02] | ,1, a/c> | 0.09 | −0.17 | |
| 11] | , 0, 2a/c> | 0.26 | −0.62 | ] | , 0, a/c> | −0.12 | −0.20 | |
| 01] | , −1, 2a/c> | 0.24 | −1.81 | 102] | , −1, a/c> | −0.38 | −1.23 | |
| 1] | , −1, 2a/c> | 0.17 | 5.47 | 012] | , −1, a/c> | −0.41 | 4.39 | |
| 1] | , 0, 2a/c> | 0.30 | 0.94 | 12] | , 0, a/c> | −0.30 | 0.57 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Kim, C.; Kim, Y.-M. Identification of Active Slip Mode and Calculation of Schmid Factors in Magnesium Alloy. Metals 2022, 12, 1604. https://doi.org/10.3390/met12101604
Li L, Kim C, Kim Y-M. Identification of Active Slip Mode and Calculation of Schmid Factors in Magnesium Alloy. Metals. 2022; 12(10):1604. https://doi.org/10.3390/met12101604
Chicago/Turabian StyleLi, Lichao, Chunjoong Kim, and Young-Min Kim. 2022. "Identification of Active Slip Mode and Calculation of Schmid Factors in Magnesium Alloy" Metals 12, no. 10: 1604. https://doi.org/10.3390/met12101604
APA StyleLi, L., Kim, C., & Kim, Y.-M. (2022). Identification of Active Slip Mode and Calculation of Schmid Factors in Magnesium Alloy. Metals, 12(10), 1604. https://doi.org/10.3390/met12101604





